Resumo
The main subject of this article is to show the parallelism betwen the Ellingham and Van't Hoff diagrams. The first one is a graphic representation of the changes in the standard Gibbs free energy (deltarGtheta) as a function of T and was introduced by Ellingham in 1944, in order to study metallurgic processes involving oxides and sulphides. On the other hand, the Van't Hoff diagram is a representation of the function ln K versus (1/T). The equivalence between both diagrams is easily demonstrated, making simple mathematical manipulations. In order to show the parallelism between both diagrams, they are presented briefly and two examples are discussed. The comparison of the both diagrams surely will be helpful to students and teachers in their learning and teaching activities, and will certainly enrich important aspects of chemical thermodynamics.
Ellingham diagram; Van't Hoff diagram; chemical thermodynamics
Ellingham diagram; Van't Hoff diagram; chemical thermodynamics
EDUCAÇÃO
Diagramas de Ellingham e de Van't Hoff: algumas considerações
Ellingham and Van't Hoff diagrams: some considerations
José de Alencar Simoni; Aécio Pereira Chagas* * e-mail: aecio@iqm.unicamp.br
Instituto de Química, Universidade Estadual de Campinas, CP 6154, 13084-971 Campinas - SP, Brasil
ABSTRACT
The main subject of this article is to show the parallelism betwen the Ellingham and Van't Hoff diagrams. The first one is a graphic representation of the changes in the standard Gibbs free energy (DrGq) as a function of T and was introduced by Ellingham in 1944, in order to study metallurgic processes involving oxides and sulphides. On the other hand, the Van't Hoff diagram is a representation of the function ln K versus (1/T). The equivalence between both diagrams is easily demonstrated, making simple mathematical manipulations. In order to show the parallelism between both diagrams, they are presented briefly and two examples are discussed. The comparison of the both diagrams surely will be helpful to students and teachers in their learning and teaching activities, and will certainly enrich important aspects of chemical thermodynamics.
Keywords: Ellingham diagram; Van't Hoff diagram; chemical thermodynamics.
Os diagramas de Ellingham, ou seja, representações gráficas das funções DrG (T), foram introduzidos por H. J. T. Ellingham, em 1944, para estudo de processos metalúrgicos envolvendo óxidos e sulfetos1. Foram, posteriormente, difundidos por Richardson, porém seu uso ficou restrito à área metalúrgica2.
Recentemente, livros mais gerais3-5 têm apresentados estes diagramas, inclusive para nitretos6 e haletos metálicos7. Usos não metalúrgicos são mais raros, porém, recentemente Maia e Osório8 relataram uma aplicação. A Figura 1 traz um diagrama de Ellingham para óxidos5.
As funções DrG (T) são praticamente lineares em relação à T, ou melhor, quando representadas graficamente em um diagrama de coordenadas DrG em função de T, são retas quebradas em que as inflexões, muitas vezes pouco acentuadas, são devidas às mudanças de fases (fusão, vaporização etc.) de um dos componentes. A função DrG (T) tem a forma de uma das equações fundamentais da Termodinâmica Química:
sendo DrH (T) o coeficiente linear e DrS (T) o coeficiente angular (o significado dos símbolos encontra-se no final do artigo). A rigor, as grandezas H e S são também funções de T, conforme indicado, porém elas são praticamente constantes com a mesma, fazendo com que DrG (T) se torne, portanto, praticamente linear. Esta independência de H e S em relação a T é devida ao fato de DrCp (T) ser pequeno. Explicitando melhor, os valores de H e S a uma dada temperatura T são dados, respectivamente, pelas equações:
em que Tr é a temperatura de referência, usualmente 298,15 K, e a notação das integrais foi simplificada5,9.
Como os valores das integrais acima são pequenos em relação aos outros dois respectivos termos do segundo membro, DrH (Tr) e DrS (Tr), praticamente DrH (T) e DrS (T) não variam. Como exemplo, tem-se o sistema representado pela equação química:
Será considerada a faixa de 298 a 1100 K, larga o suficiente para se verificar as variações de cada termo e sem nenhuma mudança de fase dos componentes. A Tabela 1 apresenta os valores dos termos das Equações 2 e 3 em algumas temperaturas. Na Figura 2 tem-se um gráfico mostrando a variação da Int S(T) (Equação 3) e de DrS (T) com a T. Observar que DrS (T) é dezenas de vezes maior (em valor absoluto) que a respectiva integral. Na Figura 3 tem-se a variação de Int H(T) (Equação 2), DrH (T), DrG (T) e DrS (T)T com a T. Observar que DrH (T) é centenas de vezes maior (em valor absoluto) que Int H(T), além da linearidade dos outros termos. Nestes cálculos utilizaram-se as tabelas JANAF10.
Da literatura, de modo geral, capta-se a impressão de que os diagramas de Ellingham só funcionam para substâncias que interessam à metalurgia (óxidos, sulfetos etc.), mas, como será mostrado a seguir, estes diagramas são de uso geral, como os de Van't Hoff, que são equivalentes.
Os diagramas de Van't Hoff são representações da função lnK (1/T), obtidas da integração da conhecida equação do mesmo nome5,9,11:
que integrada resulta em:
sendo C uma constante de integração. Note que essa equação tem a forma y = ax + b (x = 1/T), ou seja, a equação de uma reta. O gráfico, como o da Figura 4, correspondente ao sistema12
em que Kq = p(CO2, g) / pq, representa a variação linear de ln Kq com o inverso da temperatura (1/T), sendo possível calcular DrH (T) e DrS (T) da respectiva reação.
A equivalência de ambos os diagramas pode ser facilmente demonstrada. Os diagramas de Ellingham baseiam-se na Equação 1. Dividindo-a por 1/RT (obviamente T > 0, pela 2ª Lei da Termodinâmica5,13) tem-se:
O primeiro membro dessa equação é igual a ln K, é a relação conhecida por "lei do equilíbrio químico" ou "isóbara de Van't Hoff"5,9,11:
O primeiro termo do segundo membro da Equação 8 é igual ao termo correspondente da Equação 6 e o segundo termo é a respectiva constante de integração. Os dois diagramas permitem, utilizando-se dados experimentais de DrG (T) ou de ln K, a diversas temperaturas, obter DrH (T) e DrS (T). DrG (T) pode ser obtido de medidas de força eletromotriz de células galvânicas (pilhas eletroquímicas), E, através da conhecida equação fundamental da Eletroquímica5,9,11:
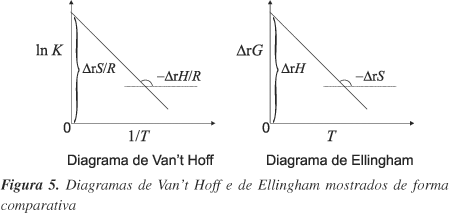
sendo n(e) o coeficiente estequiométrico dos elétrons nas equações químicas balanceadas dos dois lados da célula. A constante de equilíbrio termodinâmica K pode ser obtida também de experimentos onde se pode medir concentrações (e daí as atividades) ou pressões parciais (e daí as fugacidades) do sistema em equilíbrio. O uso do diagrama de Ellingham ou de Van't Hoff passa a ser decorrente dos dados experimentais obtidos. A Figura 5 apresenta, de forma comparativa, os dois diagramas.
Apesar da equivalência de ambos, nem sempre se obtêm os mesmos resultados, devido à precisão dos dados experimentais e aos valores numéricos que serão ajustados à equação da reta. Este ajuste pode ser feito utilizando-se planílhas eletrônicas (Origin, Sigmaplot etc.), através do método dos mínimos quadrados (correlação linear).
Vamos ver dois exemplos, utilizando-se dados da literatura bem distantes entre si, para mostrar o paralelismo de ambos os diagramas. O primeiro deles refere-se à dissociação do iodo em fase gasosa:
estudada por Starck e Bodenstein14, em 1910, medindo-se a pressão do sistema a diversas temperaturas e depois calculando-se K. Utilizamos a faixa de 1073 a 1473 K (5 pontos). Os correspondentes diagramas de Van't Hoff e Ellingham estão nas Figuras 6 e 7 e na Tabela 2 estão os valores encontrados. DrG foi calculado pela Equação 9. Note que os valores de DrH (T) e DrS (T) são concordantes dentro dos desvios estimados. A pequena diferença entre os valores dos desvios é devido ao ajuste.
O segundo exemplo é a formação do óxido de rutênio:
estudada por Cordfunke e Konings15, em 1988, que construíram uma célula galvânica baseada nesta reação e mediram a força eletromotriz da mesma, juntamente com a pressão de oxigênio, a diversas temperaturas. Utilizamos a faixa de 961,8 a 1056,7 K (5 pontos). Os correspondentes diagramas de Van't Hoff e Ellingham estão nas figuras 8 e 9 e os valores encontrados, na Tabela 2. Pela Equação 10 calculou-se DrG e pela Equação 9, ln K. Note que os valores de DrH (T) e DrS (T) são também concordantes.
CONCLUSÃO
Apesar de conhecidos há muito tempo, os diagramas de Van't Hoff e de Ellingham são equivalentes e complementares. Na literatura científica e técnica tradicionalmente utiliza-se um ou outro e o uso de ambos pode ser desnecessário na maior parte das vezes. Entretanto, a comparação dos dois diagramas certamente ajudará aos professores e estudantes, em suas atividades de ensino e aprendizagem, a compreenderem melhor certos aspectos da Termodinâmica Química.
SÍMBOLOS UTILIZADOS
 sendo nB o coeficiente estequiométrico da espécie B, associado à equação química genérica
sendo nB o coeficiente estequiométrico da espécie B, associado à equação química genérica  .
.
X = funções termodinâmicas de estado: G, H, S, ST, Cp.
G = função de Gibbs ou energia livre de Gibbs.
H = entalpia.
S = entropia.
Cp = capacidade calorífica molar à pressão constante.
T = temperatura termodinâmica.
p = pressão.
pq = pressão padrão = 0,1 MPa.
K = constante de equilíbrio termodinâmica.
E = força eletromotriz de uma célula galvânica.
F = constante de Faraday = 96485 C/mol.
REFERÊNCIAS
1. Ellingham, H. J. T.; J. Soc. Chem. Ind. (London) 1944, 63, 125.
2. DeHof, R. T.; Thermodynamics in Materials Science, McGraw-Hill: New York, 1993.
3. Lupis, C. H. P.; Chemical Thermodynamics of Materials, North-Holland and Elsevier: New York, 1983.
4. Atkins, P. W.; Physical Chemistry, 6th ed., Oxford: Oxford, 1998; Shriver, D. F.; Atkins, P. W.; Inorganic Chemistry, 3rd ed., Oxford University Press: Oxford, 1999; Shriver, D. F.; Atkins, P. W.; Química Inorgânica, 3rd ed., Bookman: Porto Alegre, 2006.
5. Chagas, A. P.; Termodinâmica Química, Ed. Unicamp: Campinas, 1999.
6. Put, P. J. van der; Inorganic Chemistry of Materials, Plenum Press: New York, 1998.
7. Swaddle, T. W.; Inorganic Chemistry, Academic Press: San Diego (CA), 1997.
8. Maia, A. de S.; Osorio, V. K. L.; Quim. Nova 2003, 26, 595.
9. McGlashan, M. L.; Chemical Thermodynamics, Academic Press: London, 1979.
10. Chase Jr., M. W.; Davies, C. A.; Downey Jr., J. R.; Frurip, D. J.; McDonald, R. A.; Syverud, A. N.; JANAF Thermochemical Tables, 3rd ed., J. Phys. Chem. Ref. Data 1985, 14, suppl. 1.
11. DeVoe, H.; Thermodynamics and Chemistry, Prentice Hall: Upper Saddle River (NJ), 2001.
12. Smyth, F. H.; Adams, L. H.; J. Am. Chem. Soc. 1923, 45, 1167.
13. Denbigh, K.; The Principles of Chemical Equilibrium, 4th ed., Cambridge University Press: Cambridge, 1981.
14. Stark, G.; Bodenstein, M.; Z. Elektroch. 1910, 16, 961.
15. Cordfunke, E. H. P.; Konings, R. J. M.; Thermochim. Acta 1988, 129, 63.
Recebido em 14/3/06; aceito em 14/6/06; publicado na web em 19/1/07
- 1. Ellingham, H. J. T.; J. Soc. Chem. Ind. (London) 1944, 63, 125.
- 2. DeHof, R. T.; Thermodynamics in Materials Science, McGraw-Hill: New York, 1993.
- 3. Lupis, C. H. P.; Chemical Thermodynamics of Materials, North-Holland and Elsevier: New York, 1983.
- 4. Atkins, P. W.; Physical Chemistry, 6th ed., Oxford: Oxford, 1998;
- Shriver, D. F.; Atkins, P. W.; Inorganic Chemistry, 3rd ed., Oxford University Press: Oxford, 1999;
- Shriver, D. F.; Atkins, P. W.; Química Inorgânica, 3rd ed., Bookman: Porto Alegre, 2006.
- 5. Chagas, A. P.; Termodinâmica Química, Ed. Unicamp: Campinas, 1999.
- 6. Put, P. J. van der; Inorganic Chemistry of Materials, Plenum Press: New York, 1998.
- 7. Swaddle, T. W.; Inorganic Chemistry, Academic Press: San Diego (CA), 1997.
- 8. Maia, A. de S.; Osorio, V. K. L.; Quim. Nova 2003, 26, 595.
- 9. McGlashan, M. L.; Chemical Thermodynamics, Academic Press: London, 1979.
- 10. Chase Jr., M. W.; Davies, C. A.; Downey Jr., J. R.; Frurip, D. J.; McDonald, R. A.; Syverud, A. N.; JANAF Thermochemical Tables, 3rd ed.,
- J. Phys. Chem. Ref. Data 1985, 14, suppl. 1.
- 11. DeVoe, H.; Thermodynamics and Chemistry, Prentice Hall: Upper Saddle River (NJ), 2001.
- 12. Smyth, F. H.; Adams, L. H.; J. Am. Chem. Soc. 1923, 45, 1167.
- 13. Denbigh, K.; The Principles of Chemical Equilibrium, 4th ed., Cambridge University Press: Cambridge, 1981.
- 14. Stark, G.; Bodenstein, M.; Z. Elektroch. 1910, 16, 961.
- 15. Cordfunke, E. H. P.; Konings, R. J. M.; Thermochim. Acta 1988, 129, 63.
Datas de Publicação
-
Publicação nesta coleção
13 Mar 2007 -
Data do Fascículo
Abr 2007
Histórico
-
Recebido
14 Mar 2006 -
Aceito
14 Jun 2006