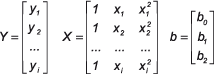Validação da metodologia da avaliação de incerteza em curvas de calibração melhor ajustadas por polinômios de segundo grau

Methodology validation for evaluation of the uncertainty in the calibration curves better adjusted for second-degree polynomials

second order calibration uncertainty; Monte Carlo Simulation; GUM Supplement

ARTIGO

Validação da metodologia da avaliação de incerteza em curvas de calibração melhor ajustadas por polinômios de segundo grau

Methodology validation for evaluation of the uncertainty in the calibration curves better adjusted for second-degree polynomials

Elcio Cruz de Oliveira^I,*; Paula Fernandes de Aguiar^II

^IPETROBRAS TRANSPORTE S.A. - Gerência Geral de Engenharia, Av. Pres. Vargas, 328, 20091-060 Rio de Janeiro - RJ, Brasil

^IIDepartamento de Química Analítica, Instituto de Química, Universidade Federal do Rio de Janeiro, Cidade Universitária - Ilha do Fundão, CT, Bl. A, 21949-900 - Rio de Janeiro - RJ, Brasil

ABSTRACT

The most widespread literature for the evaluation of uncertainty - GUM and Eurachem - does not describe explicitly how to deal with uncertainty of the concentration coming from non-linear calibration curves. This work had the objective of describing and validating a methodology, as recommended by the recent GUM Supplement approach, to evaluate the uncertainty through polynomial models of the second order. In the uncertainty determination of the concentration of benzatone (C) by chromatography, it is observed that the uncertainty of measurement between the methodology proposed and Monte Carlo Simulation, does not diverge by more than 0.0005 unit, thus validating the model proposed for one significant digit.

Keywords: second order calibration uncertainty; Monte Carlo Simulation; GUM Supplement.

INTRODUÇÃO

Na calibração univariada clássica, n pontos de calibração y definem a curva de calibração (y = f (x)), e a quantidade desconhecida (x₀) é determinada pela solução da equação (y₀ = f (x₀)), onde y₀ é a resposta para uma concentração desconhecida. O caso mais simples e mais largamente utilizado é o seguinte modelo linear: (y = b₀ + b₁x), onde os valores da variável independente x e incerteza dos padrões utilizados na construção da curva de calibração são considerados com incerteza desprezível, além da variável de resposta y assumir ter erros aleatoriamente distribuídos de desvio padrão constante - homocedástica.¹ A regressão linear não ponderada é usada para obter estimativas dos parâmetros de calibração b₀ e b₁, a partir de x₀ = (y₀ - b₁)/b₀.

Se os valores de b₀ e b₁, suas variâncias var b₀, var b₁e sua covariância, cov(b_o,b₁), são determinadas pelo método dos mínimos quadrados; a variância em x, var(x_o), obtida usando a expansão da série de Taylor e desprezando os termos de ordem superior, é dada pela Equação 1:²

onde a incerteza correspondente u(x_o, y_o) é .

Em uma regressão não ponderada, a partir de n pontos de dados da curva de calibração e para p números de medições para determinar y₀, a incerteza padrão em x₀ é geralmente calculada a partir da Equação 2:^3,4

onde, S é o desvio padrão residual do ajuste linear.

Entretanto, em algumas situações, o melhor ajuste pode não ser o linear. O objetivo deste trabalho é descrever uma metodologia e sua validação para avaliação de incerteza, onde o ajuste mais adequado é o quadrático.

FUNDAMENTOS TEÓRICOS

Análise de regressão

É a maneira tradicional de se construir a melhor curva, de tal maneira que a soma dos quadrados dos resíduos seja mínima, razão pela qual este método é chamado de ajuste por mínimos quadrados.

Podem-se calcular os valores dos coeficientes b_i, resolvendo uma única equação matricial: b = (X^t X)^-1 X^t Y, desde que a matriz (X^t X) não seja singular. Para um modelo de segunda ordem, y_i = b₀ + b₁x_i + b₂x²_i, onde x_i representa a variável independente no i-ésimo nível, o sistema matricial é representado por:⁵

Variância e covariância

Neste trabalho, matrizes são utilizadas para expressar o cálculo das incertezas nas estimativas dos parâmetros. Para isto, foi definida a matriz de covariância de e b₀, b₁ e Equação 3:

onde:⁶

que, para o modelo quadrático, assume a seguinte forma:

Através da raiz quadrada dos elementos da diagonal principal, é possível se chegar às incertezas padrão de b₀, b₁ e b₂.

Incerteza do modelo quadrático

A incerteza padrão combinada é calculada a partir da expansão da série de Taylor (LPU). Supondo que uma grandeza de saída = f (b₁, b₂, ..., b_n) dependa de n grandezas de entradas b₁, b₂, ..., b_n, onde cada b_i seja descrito por uma distribuição de probabilidade apropriada, a incerteza padrão combinada assume a forma da Equação 5, ao se levar em consideração que as grandezas são correlacionadas entre si:⁷

Para o seguinte modelo de segunda ordem: = b₀ + b₁x + b₂x², os x valores de são explicitados nas Equações 6 e 7:

Aplicando, então, a Equação 5 na Equação 6, desprezando os termos de ordem superior e a correlação entre e os coeficientes estimados, se obtém a Equação 8:

Considerando cov(x,y) = r(x.y)u_xu_y e substituindo as derivadas parciais, se chega à Equação 13, que calcula a incerteza padrão combinada de x em uma curva de calibração com ajuste quadrático:

onde, ; para n números de medições para determinar y₀.

Simulação de Monte Carlo (SMC)

A simulação de Monte Carlo tem este nome devido à famosa roleta de Monte Carlo, no Principado de Mônaco. Seu nome, bem como o desenvolvimento sistemático do método, data de 1944, durante a Segunda Guerra Mundial, utilizada como ferramenta de pesquisa para o desenvolvimento da bomba atômica.

A simulação de Monte Carlo gera, aleatoriamente, inúmeros dados para variáveis consideradas incertas, simulando assim, baseado nas suas distribuições de probabilidade, combinações de valores dessas variáveis que levam a resultados que são o foco da análise.

Este método consiste na substituição do estudo de um processo físico ou matemático por um modelo probabilístico que possa tratar problemas determinísticos por meio de amostras aleatórias ou por meio de números pseudo-aleatórios gerados por um computador.

Uma importante utilidade da simulação de Monte Carlo^8,9 consiste na possibilidade de validação dos cálculos executados pela abordagem do ISO GUM.⁷ Contudo, é complexo quantificar os efeitos das aproximações envolvidas, tais como não linearização do modelo matemático, inaplicabilidade da fórmula de Welch-Satterthwaite e a distribuição não normal da grandeza de saída. Neste sentido, sempre quando houver dúvidas com relação à adequação do método do ISO GUM, os cálculos devem ser validados de alguma forma. A simulação de Monte Carlo, associada à utilização de softwares computacionais, pode ser uma alternativa para validar tais cálculos, já que a propagação de distribuições é uma generalização da lei de propagação de incertezas (LPU).⁹

De acordo com Cox e Harris,¹⁰ o método de Monte Carlo, diferentemente do ISO GUM, utiliza o conceito de propagação das distribuições de probabilidade das grandezas de entrada e não somente a propagação das incertezas das grandezas de entrada, como preconiza o outro método. Ou seja, toda a distribuição de probabilidade de cada fonte de incerteza é propagada através da equação da medição.

De acordo com o BIPM,⁹ com o método de Monte Carlo, as funções densidade de probabilidade das grandezas de entrada são propagadas pelo modelo matemático da medição para obter uma função densidade de probabilidade (PDF) para a grandeza de saída, o mensurando. Desta forma, a distribuição da grandeza de saída não é assumida a priori, como acontece no método do ISO GUM, mas calculada a partir das distribuições de probabilidade das grandezas de entrada.¹¹

As bases para a aplicação da simulação de Monte Carlo no cálculo da incerteza consistem em selecionar aleatoriamente um número de uma distribuição de possíveis valores para uma grandeza de entrada e repetir o procedimento para as outras grandezas de entrada.

Cada valor obtido aleatoriamente é considerado no modelo matemático da medição e um resultado é, então, obtido para a grandeza de saída. Este passo é repetido n vezes, de forma independente, a fim de avaliar a função densidade de probabilidade do mensurando.

Para a estimativa x de um valor da grandeza multivariada X e matriz de incerteza correspondente (matriz de covariância) V, a PDF Gaussiana multivariada N(x, V) é a apropriada para o valor de X.⁹

Validação do modelo

Para a comparação de resultados de incerteza calculados pelos métodos do ISO GUM e de Monte Carlo, BIPM recomenda um procedimento baseado no número de algarismos significativos expressos nos cálculos.⁹

O procedimento de comparação é baseado na seguinte premissa: determinar se os intervalos de abrangência obtidos pela lei de propagação de incerteza e SMC concordam com o grau estipulado de aproximação. Este grau de aproximação é determinado em termos dos limites dos intervalos de abrangência e corresponde àquele dado pela expressão da incerteza padrão, que é observada em termos de algarismos significativos.

A seguir, são apresentados os passos recomendados para esta comparação, segundo BIPM:⁹ calcular a incerteza expandida de acordo com a metodologia do ISO GUM; aplicar os procedimentos de cálculo de incerteza segundo o método de Monte Carlo; determinar o número de algarismos significativos n que se deseja ter na incerteza padrão combinada, geralmente n = 1 ou n = 2; expressar o valor da incerteza padrão combinada pelo método do ISO GUM como a x 10^r-, onde a é um número com n algarismos inteiros e r- um número inteiro; calcular a Equação 14 para determinar um valor crítico de diferenças entre as incertezas:

comparar as incertezas de acordo com a Equação 15:

onde: x é a estimativa da média pelo método de Monte Carlo; U é a incerteza expandida pelo método do ISO GUM, para um determinado nível de confiança; x_abaixo e x_acima são os valores obtidos pelo método de Monte Carlo nos correspondentes percentis, tendo em vista o nível da confiança estipulado no cálculo pelo método do ISO GUM.

Se a Equação 15 gerar números menores que o valor crítico calculado pela Equação 14, os resultados das incertezas são compatíveis para aquele dado número de algarismos significativos e para aquele nível da confiança. Caso contrário, os resultados não são compatíveis no dado número de algarismos significativos e nível de confiança.

RESULTADOS E DISCUSSÃO

O modelo proposto foi aplicado à avaliação de incerteza na determinação cromatográfica de benzatona (C) a partir da construção de curva de calibração para seis diferentes concentrações. Estes dados foram adaptados da ref. 5. Foram feitos dois ajustes de curvas de calibração pelo método de mínimos quadrados: linear e quadrático. A variância homocedástica é considerada e se assume que as incertezas dos valores da abscissa são desprezíveis em relação às incertezas dos valores da ordenada. Por esta razão, os procedimentos usuais de cálculo da incerteza para a concentração da benzatona (C) somente refletem a incerteza na altura do pico e não na incerteza dos padrões de calibração, nem nas inevitáveis correlações induzidas pela sucessiva correlação da solução estoque.

O desvio padrão e a covariância foram calculados pelo software Matlab, a partir da Equação 3.

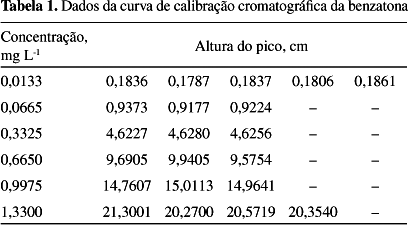
Seis padrões de calibração foram utilizados, fornecendo os valores apresentados na Tabela 1.

Curva de calibração linear: = b₀ + b₁x

Os resultados do ajuste linear são dados na Tabela 2, com um coeficiente de correlação r de 0,9992. O desvio padrão residual S é 0,2296 e a covariância entre b₀ e b₁ é -0,0054.

Analisando somente o coeficiente de correlação que está muito próximo à unidade, sugere que o ajuste da equação está excelente, mas na verdade apresenta falta de ajuste. Quando se calcula a relação entre a média quadrática da falta de ajuste e a média quadrática do erro puro, MQ_faj/ MQ_ep, se encontra um valor de 19,56, que é maior que F_4,15 = 3,06 (95% de confiança). Tal afirmativa é ratificada pelo gráfico de resíduos da regressão, que não está distribuído aleatoriamente em torno do zero, apresentando um padrão que se assemelha a uma parábola (Figura 1).

É possível se observar pela Figura 1, que representa a análise de resíduos deste ajuste, que este modelo não é adequado.

Curva de calibração não-linear: = b₀ + b₁x + b₂x²

Para tentar eliminar a falta de ajuste, foi acrescentado um termo quadrático, e se chega a um modelo com três parâmetros. Os resultados encontram-se na Tabela 3, com um coeficiente de correlação r de 0,9998. O desvio padrão residual S é 0,1034.

O aumento do valor de coeficiente de correlação não aparenta ser significativo, mas examinando o gráfico de resíduos - distribuição aleatória em torno do zero (Figura 2) é possível se constatar que o modelo quadrático é superior, e já não apresenta falta de ajuste. Para ele, aliás, MQ_faj/ MQ_ep = 0,142, valor que, por ser inferior a um, nos dispensa de fazer o teste F.

Validação da metodologia

Os valores obtidos, para os modelos linear e quadrático, respectivamente, são utilizados nas Equações 2 e 13, para o cálculo da incerteza da concentração.

Em seguida, a fim de validar o modelo quadrático desenvolvido na Equação 13, por simulação de Monte Carlo, conforme recomendação do Suplemento 1 do GUM, 30.000 dados aleatórios para os coeficientes b₀, b₁ e b₂ foram gerados, utilizando a distribuição Gaussiana multivariada, pela função RMVNORM, no software R versão 2.4.0 (2006) e para a grandeza utilizando a distribuição retangular pelo Excel.

Neste trabalho, a incerteza expandida a um nível de confiança de 95,45% foi considerada, baseada no fator de abrangência de 2, como recomendado na literatura em Química Analítica.²

Para resultados de incerteza padrão em torno de 0,007 mg L^-1, usando a regressão quadrática por SMC, estes podem ser expressos como 7 × 10^-3 mg L^-1, e assim a = 7 e r- = -3. Logo .

As colunas U(x)_linear e U(x)_quadrático apresentam a incerteza expandida pela LPU, para regressões linear e quadrática, respectivamente. As colunas SMC e d_abaixo; d_acima foram calculadas para os percentis 2,275 e 97,725% e V define se os resultados foram validados para um algarismo significativo, porque o valor crítico é 0,0005.

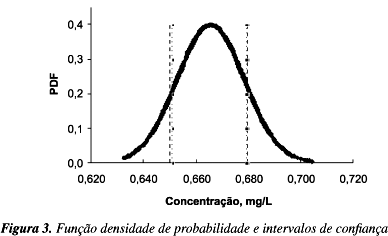
Na Figura 3, observa-se a curva da função densidade de probabilidade Gaussiana, a partir da lei de propagação de incerteza para o ponto em negrito da Tabela 4. O par interno de linhas verticais define um intervalo de confiança de 95,45% para a concentração proveniente da LPU baseada na PDF. O par externo de linhas verticais define um intervalo de confiança de 95,45% para a concentração proveniente do histograma a partir da SMC baseada na PDF. Como a faixa de incerteza pela LPU está contida no intervalo dado pela SMC, confirma-se a validação do modelo proposto.

CONCLUSÕES

O presente trabalho descreve uma metodologia para avaliação de incerteza, baseada na LPU, em curvas onde o melhor ajuste é o de ordem dois e a valida para um algarismo significativo, contra o SMC.

Ao se comparar valores de incerteza determinados caso a distribuição tivesse sido ajustada através de um polinômio de primeiro grau, observou-se que a incerteza de medição chega a ser superestimada em mais de 100%, em relação ao ajuste quadrático.

Em um ajuste não-linear, deve-se avaliar o efeito da covariância/correlação entre as grandezas de saída, que normalmente é desprezado em Química Analítica.

Um elevado coeficiente de correlação ( >0,999) não determina por si só o melhor ajuste de uma curva; deve-se sempre realizar uma análise de resíduos e o teste F.

Este estudo é específico para comportamento de dados homocedásticos e considera desprezível a incerteza dos padrões de calibração, eixo x. Estes casos serão assuntos de próximos trabalhos.

Recebido em 14/10/08; aceito em 5/2/09; publicado na web em 3/7/09

• 1. Tellinghuisen, J.; Analyst 2005,130, 370.
• ²
  EURACHEM; Quantifying uncertainty in analytical measurement, 2^nd ed., Eurachem/CITAC Working Group: Helsinki, 2000.
• 3. Miller, J. N.; Analyst 1991, 116, 3.
• ⁴
  Massart, D. L.; Handbook of Chemometrics and Qualimetrics, Part A, Elsevier: Amsterdam, 1997.
• ⁵
  Barros Neto, B.; Scarminio, I. S.; Bruns, R. E.; Como Fazer Experimentos - Pesquisa e Desenvolvimento na Ciência e na Indústria, Ed. da Unicamp: Campinas, 2001.
• 6. Meinrath, G.; Chemo. Intel. Lab. Systems 2000, 51, 175.
• 7. International Standard Organization; Guide to the Expression of Uncertainty in Measurement, 1^st ed., International Organization for Standardization: Geneva, 1993.
• 8. Satterthwaite, F. E.; Psychometrika 1941, 6, 309.
• ⁹
  Joint Committee for Guides in Metrology; Evaluation of measurement data - Supplement 1 to the "Guide to the expression of uncertainty in measurement" - Propagation of distributions using a Monte Carlo method, Final draft, BIPM: Sèvres, 2006.
• 10. Cox, M. G.; Harris, P. M.; GUM Supplements. CIE Expert Symposium on Uncertainty Evaluation, Method for Analysis of Uncertainties in Optical Radiation Measurement, Proceedings of the CIE expert simposium: Vienna, 2001.
• 11. Meyer, V. R.; J. Chromatogr., A 2007, 1158, 15.

Datas de Publicação

• Publicação nesta coleção
  22 Set 2009
• Data do Fascículo
  2009

Histórico

• Aceito
  05 Fev 2009
• Recebido
  14 Out 2008