Bound state solutions of schrödinger equation for a more general exponential screened coulomb potential via Nikiforov-Uvarov method

ARTICLE

Bound state solutions of schrödinger equation for a more general exponential screened coulomb potential via Nikiforov-Uvarov method

Benedict I. Ita^I; P. Ekuri^I; Idongesit O. Isaac^II; Abosede O. James^III

^IQuantum Chemistry Group, Department of Pure and Applied Chemistry, University of Calabar, P. O. Box 3700, Calabar, CRS, Nigeria

^IIDepartment of Mathematics/Statistics and Computer Science, University of Calabar, Calabar, Cross River State, Nigeria

^IIIDepartment of Pure and Industrial Chemistry, University of Port Harcourt, Nigeria

ABSTRACT

The arbitrary angular momentum solutions of the Schrödinger equation for a diatomic molecule with the general exponential screened coulomb potential of the form V(r) = (- a / r){1+ (1+ b )e-2^b } has been presented. The energy eigenvalues and the corresponding eigenfunctions are calculated analytically by the use of Nikiforov-Uvarov (NU) method which is related to the solutions in terms of Jacobi polynomials. The bounded state eigenvalues are calculated numerically for the 1s state of N₂ CO and NO

Keywords: Nikiforov-Uvarov method, Eigenvalues, Eigenfunctions, General Exponential Screened Coulomb Potential.

Introduction

The exact analytic solutions of the wave equations (non-relativistic and relativistic) are only possible for certain potentials of physical interest under consideration since they contain all the necessary information on the quantum system [1]. It is known that for certain potentials, the Schrödinger equation can be solved for the angular momentum quantum numbers =0 [2]. However, in some cases, like for the ≠ 0 states, some approximations are often used to obtain analytic solutions of the Schrödinger equation [3 - 5].

A more general exponential screened coulomb (MGESC) potential used in this paper is of the form [6]:

where a is the strength coupling constant and b is the screened parameter. The potential in equation (1) is known to describe adequately the effective interaction in many-body environments of a variety of fields [6]. In this paper, we have decided to explore the possibility of also using it in obtaining bound state solutions of the Schrödinger equation for diatomics using Nikiforov-Uvarov (NU) method.

Overview of Nikiforov-Uvarov (NU) Method

The NU method is based on the solutions of general second order linear differential equations with some orthogonal functions [7]. For the given potential, the Schrödinger equation in the spherical coordinates is reduced to a generalized equation of hypergeometric type with an appropriate s =s(r) coordinate transformation. Thus, it has the form [8]:

where σ(s) and (s) are polynomials, at most , second-degree, and (s) is a first-degree polynomial. To find a particular solution of equation (2), we use the following transformation [9]:

This reduces Schrödinger equation (2) to an equation of hyper-geometric type:

where Φ(s) satisfies

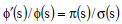y(s) is the hyper-geometric type function whose polynomial solutions are given by the Rodrigues relation:

where B_n is a normalization constant and the weight function ^ρ must satisfy the condition [9]:

The function ^π and the parameter λ required for this method are defined as:

and

Here, ^π(s) is a polynomial with the parameter s and the determination of k is necessary for ^π(s) to be obtained. To find k, the expression under the square root must be square of a polynomial. A new eigenvalue equation for the Schrödinger equation thus becomes:

where

and ^τ'(s) must be negative.

Bound State Solutions via Nikiforov-Uvarov (NU) Method

The potential in equation (1) is substituted into the radial Schrödinger equation given as:

where n denotes the radial quantum number which together with are both named as the vibration-rotation quantum numbers in molecular chemistry, r is the internuclear separation, ^En is the exact bound state energy eigenvalues and V(r) is the internuclear potential energy function and we obtain:

Equation (12) can be rearranged to give:

Introducing the following dimensional parameters:

equation (13) is written as:

A comparison of equations (2) and (17) reveals the following polynomials:

Substituting these polynomials into equation (7), we get ^π(r) as:

and ^σ'(r) is taken equal to 1. The discriminant of the expression under the square root in equation (19) has to be zero for it to have equal roots. Therefore, we get:

On solving equation (20) for k we get:

where

and

Substituting ^k± into equation (19), gives the following four possible solutions obtained for ^π(r) as:

From the four possible forms of ^π(r) in equation (24), we select the one for which the function ^τ(s) in equation (10) has a negative derivative. ^τ(s) satisfies these requirements with:

and

From equation (8), we obtain:

and also

We then obtain the parameters ε² as:

Substituting the values of ε² , ^β and ^γ from equations (14) - (16) into equation (29), yields:

To find y(r), we first obtain ^ρ(r) from equation (6) as:

Substituting this into the Rodrigues relation given in equation (5), we get:

B_n is the normalization constant. The polynomial solutions of y_n(r) in equation (32) are expressed in terms of the associated Laguerre polynomials, which is one of the orthogonal polynomials. We write:

where ^{v= 2iεr,} therefore,

By substituting ^π(r) and ^σ(r) into the expression and solving the resulting differential equation, the other part of the wave function in equation (3) is obtained as:

or in terms of v,

Combining the Laguerre polynomials and φ(v) in equation (3), enables the radial wave function to be constructed as:

If we introduce the variable

equation (38) becomes:

To find A_n , a new normalization constant, we write:

Therefore,

The above integral can be evaluated by using the recursion relation for Laguerre polynomials and A_n is found to be:

Therefore, R_n (r) becomes:

Conclusion

The analytical solutions of the Schrödinger equation for the general exponential screened coulomb potential has been presented. The Nikiforov-Uvarov method employed in the solutions enables us to explore an effective way of obtaining the eigenvalues and corresponding eigenfunctions of the Schrödinger equation for any - state.

Finally, we calculate the energies of the exponential screened coulomb potential for diatomic molecules by means of equation (30) for the - state. The explicit values of the energy at different values of the screened parameter are shown in Table 1.

Corresponding author: e-mail: iserom [e-mail]

• [1] S. M. Ikhdair and R. Sever (2008). Improved analytical approximation to arbitrary - state solutions of the Schrödinger equation for the hyperbolical potentials. Personal Communication.
• [2] C. Berkdemir and J. Han (2005). Chem. Phys. Lett. 409, 203 - 207.
• [3] E. Aydmer and C. Orta (2008). Quantum information entropies of the eigenstates of the eigenvalues of the Morse potential. Personal Communication.
• [4] H. Taseli (1997). Int. J. Quantum Chemistry, 63(5), 949 - 959.
• [5] M. W. Kermode, M. L. J. Allen, J. P. McTavish and A. Kervell (1984). J. Phys. G: Nucl. Phys. 773 - 783.
• [6] S. M. Ikhdair and R. Sever (2008). Bound states of a more general exponential screened coulomb potential. Personal Communication.
• [7] A. F. Nikiforov and U. B. Uvarov (1988). Special Functions of Mathematical Physics, Birkhauser: Basel.
• [8] C. Tezcan and R. Sever (2008). Quantum Physics. 15, 1 - 20.
• [9] S. Ikhdair and R. Sever (2008). Cent. Eur. J. Physics. 6, 141 - 152.

Publication Dates

• Publication in this collection
  09 Dec 2010
• Date of issue
  Sept 2010