Abstract
In the paper Busaniche and Cignoli (2009) we presented a quasivariety of commutative residuated lattices, called NPc-lattices, that serves as an algebraic semantics for paraconsistent Nelson's logic. In the present paper we show that NPc-lattices form a subvariety of the variety of commutative residuated lattices, we study congruences of NPc-lattices and some subvarieties of NPc-lattices.
Nelson logic; Paraconsistency; Residuated Lattices; Substructural Logic; Twist Structures
Remarks on an algebraic semantics for paraconsistent Nelson's logic1 1 Dedicated to Newton A. C. Da Costa on his 80th birthday.
Manuela BusanicheI; Roberto CignoliII
IInstituto de Matemática Aplicada del Litoral, CONICET - UNL, Guemes 3450, S3000gln-Santa Fe, ARGENTINA, manuelabusaniche@yahoo.com.ar
IIDepartamento de Matemática, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires, Ciudad Universitaria 1428 Buenos Aires, ARGENTINA, cignoli@dm.uba.ar
ABSTRACT
In the paper Busaniche and Cignoli (2009) we presented a quasivariety of commutative residuated lattices, called NPc-lattices, that serves as an algebraic semantics for paraconsistent Nelson's logic. In the present paper we show that NPc-lattices form a subvariety of the variety of commutative residuated lattices, we study congruences of NPc-lattices and some subvarieties of NPc-lattices.
Keywords: Nelson logic. Paraconsistency. Residuated Lattices. Substructural Logic. Twist Structures.
INTRODUCTION
The well known disjunction property of intuitionistic propositional calculus asserts that a disjunction α ∨ β is provable if and only if α is provable or β is provable. The constructive character of disjunction is not shared by negation: ¬(α ∧ β) in general does not imply ¬ α or ¬ β. This motivated D. Nelson (1949) to introduce constructive logic with strong negation (CLN) as an expansion of intuitionistic logic by a new negation symbol ~. The propositional fragment of CLN can be axiomatized by adding to axioms of propositional positive intuitionistic logic the axioms:
N1 ~ ~ α  α,
α,
N2 ~ (α ∨ β)  (~ α ∧ ~ β),
(~ α ∧ ~ β),
N3 ~(α ∧ β)  (~ α ∨ ~ β),
(~ α ∨ ~ β),
N4 ~(α → β)  (α ∧ ~ β),
(α ∧ ~ β),
N5 ~ α → (α → β).
The deduction rules are modus ponens and substitution.
In the short paper Almukdad and Nelson (1984) it is observed that by deleting N5 one obtains "a constructive logic which may be applied to inconsistent subject matter without necessarily generating a trivial theory." The system obtained by deleting N5 is known as paraconsistent Nelson's logic.
Both, CLN and paraconsistent Nelson's logic are algebraizable. The corresponding algebraic structures are Nelson algebras and N4-lattices, respectively. Nelson algebras and N4-lattices can be represented as twist-structures of Heyting algebras and generalized Heyting algebras (also known as implicative lattices) respectively. This representation, due to Sendlewski (1990) for Nelson algebras and to Odinstov (2004) for N4-lattices, has been the main tool to study the algebraic semantics of CLN and its paraconsistent version. For details see the monograph Odintsov (2008).
Many important logics are particular cases of substructural logics (Galatos, Jipsen, Kowalski and Ono (2007)), i.e., logics that lack some of the three structural rules of contraction, weakening and exchange. Due to this fact, in the recent years the study of substructural logics have been greatly developed to provide a common framework to treat and compare these different logics. Residuated lattices are the algebraic counterpart of substructural logics. With the aim of situating Nelson's logic within this framework, M. Spinks and R. Veroff (2008a, 2008b) showed that Nelson algebras are term equivalent to a class of residuated lattices. This class of residuated lattices is a variety, the variety of Nelson residuated lattices (see also Busaniche and Cignoli, 2010). Spinks and Veroff's result allows us to use the well-developed theory of residuated lattices to investigate the algebraic semantics of CLN. More important, it shows that CNL can be considered as an axiomatic extension of FLew, the Full Lambek Calculus with Exchange and Weakening (see Galatos, Jipsen, Kowalski and Ono (2007)).
Following these ideas, in Busaniche and Cignoli (2009) we presented a quasivariety of commutative residuated lattices that serves as an algebraic semantics for paraconsistent Nelson's logic. The elements of this quasivariety are called NPc-lattices. As a matter of fact NPc-lattices form the algebraic semantics of a conservative expansion of paraconsistent Nelson's logic by a constant e that correspond to the unit of the underlying monoids of the residuated lattices.
In this note we improve the results of Busaniche and Cignoli (2009) by showing that NPc-lattices form a subvariety of the variety of commutative residuated lattices. This means that the mentioned expansion of paraconsistent Nelson's logic by the constant e is an axiomatic extension of FLe, the full Lambek calculus with exchange (Galatos, Jipsen, Kowalski and Ono (2007)). We show that the negative cone of an NPc-lattice is a generalized Heyting algebra, and that the congruence lattice of an NPc-lattice is isomorphic to the congruence lattice of its negative cone. This provides an interesting tool to investigate subvarieties of NPc-lattices. We prove that semisimple NPc-lattices form a subvariety of the variety of NPc-lattices, and that the representable NPc-lattices form a proper subvariety of the variety of semisimple NPc-lattices. Therefore semisimple NPc-lattices and representable NPc-lattices form the algebraic semantics of axiomatic extensions of FLe. It is worthwhile to notice that these algebraic results were obtained for the more general variety of Pc-lattices (see Definition 2.1), and hence do not depend on the representation as twist-structures of generalized Heyting algebras, in contrast with the results of Busaniche and Cignoli (2009).
All the notions from universal algebra used in this paper can be found in the book Burris and Sankappanavar (1981).
1. PREMILINARIES
By a commutative residuated lattice we mean an algebra A = (A, ∨, ∧, *, ⇒, e) of type (2,2,2,2,0) such that (A, ∨, ∧) is a lattice, (A, *, e) is a commutative monoid and the following residuation condition is satisfied:
where x, y, z denote arbitrary elements of A and < is the order given by the lattice structure.
The residuated condition (1) can be replaced by the following set of equations (see Hart, Rafter and Tsinakis (2002)):
R1x * (y ∨ z) = (x * y) ∨ (x * z),
R2x ⇒ (y ∧ z) = (x ⇒ y) ∧ (x ⇒ z),
R3 (x * (x ⇒ y)) ∨ y = y,
R4 (x ⇒ (x * y)) ∧ y = y.
Therefore commutative residuated lattices form a variety, that we shall denote by
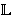 .
.
If the underlying lattice of A ∈ 
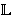 is distributive, we say that A is a commutative distributive residuated lattice.
is distributive, we say that A is a commutative distributive residuated lattice.
It follows from R1 that * is monotonic:
A residuated lattice A is called integral provided x < e for all x ∈ A.
The negative cone of A ∈ 
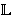 is the set A− = {x ∈ A : x < e}. It follows from (2) that A− is closed under the operations ∨,∧, *, and if the binary operation ⇒e is defined as
is the set A− = {x ∈ A : x < e}. It follows from (2) that A− is closed under the operations ∨,∧, *, and if the binary operation ⇒e is defined as
x ⇒e y = (x ⇒ y) ∧ e,
then it is easy to check that A− = (A−,∨,∧,*,⇒e, e) is an integral commutative residuated lattice.
A residuated lattice with involution was defined in Busaniche and Cignoli (2009) as a commutative residuated lattice which satisfies the equation:
and it was shown that if we define on a residuated lattice with involution A the unary operation ~ by the prescription ~x = x ⇒ e for all x ∈ A, then the following properties are satisfied:
M1 ~~x = x,
M2 ~(x ∨ y) = ~x ∧ ~y,
M3 ~(x ∧ y) = ~x ∨ ~y,
M4 ~(x * y) = x ⇒ ~y.
Moreover, we have that ~e = e. Then the system A = (A,∨,∧, *, ⇒, e) is an involutive residuated lattice in the sense of Galatos and Raftery (2004) and Tsinakis and Wille (2006).
2. NPc-LATTICES
Definition 2.1. A Paraconsistent residuated lattice (Pc-lattice for short), is a commutative distributive residuated lattice with involution A = (A,∧,∨, *,⇒, e) satisfying the following equations, where ~x = x ⇒ e and x2 = x * x:
A Nelson Pc-lattice (NPc-lattice) is a Pc-lattice that satisfies the equation:
We denote
c and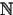 c the varieties of Pc-lattices and NPc-lattices, respectively.
c the varieties of Pc-lattices and NPc-lattices, respectively.
In Definition 4.1 of Busaniche and Cignoli (2009) NPc-lattices were defined as commutative residuted lattices with involution satisfying, besides equations (4), (5) and (6), the equation
and the quasiequation
Since ~e = e, by M1 and M3, (8) is equivalent to:
It was observed in Remark 4.9 in Busaniche and Cignoli (2009) that the lattice reduct of each NPc-lattice A is distributive. On the other hand it is well known, and easy to check, that for elements x, y, z of a distributive lattice, x ∨ y = x ∨ z and x ∧ y = x ∧ z imply y = z. Hence the requirement that the lattice be distributive turns the quasiequation (8) and the equation (7) redundant. Consequently the characterization of NPc-residuated lattices as a variety given here is equivalent to the definition of NPc-lattices given in Definition 4.1 in Busaniche and Cignoli (2009).
Given a Pc-lattice A, its positive cone given by
A+ = {x ∈ A : x > e}
satisfies that A+ = {x ∈ A : ~x ∈ A−}, because of M2 and M3. Because of M1, the set A = A− ∪ A+ is symmetric with respect to e.
A generalized Heyting algebra (called implicative lattice by Odintsov (2003, 2004)) is an integral residuated lattice
H = (H,∨,∧,*,⇒, e)
that satisfies the equation:
Notice that e is definable by x ⇒ x for any x ∈ H. For simplicity, when we refer to a generalized Heyting algebra we omit the operation * and we write simply H = (H,∨,∧,⇒, e). Generalized Heyting algebras can be thought of as bottom-free reducts of Heyting algebras.
Since (5) implies that (10) holds in the negative cone of each Pc-lattice, we have:
Theorem 2.2. IfA = (A,∨,∧,*,⇒, e) ∈  c, then A− = (A−,∨,∧, ⇒e, e) is a generalized Heyting algebra.
c, then A− = (A−,∨,∧, ⇒e, e) is a generalized Heyting algebra.
The next theorem, whose proof follows from straightforward computations (cf. Corollary 3.4 in Tsinakis and Wille (2006)), besides providing examples of NPc-lattices shows that every generalized Heyting algebra is (isomorphic to) the negative cone of a Pc-lattice.
Theorem 2.3.LetH = (H,∨,∧,⇒, e) be a generalized Heyting algebra. Then
I(H) = (H × H,∨,∧,*,⇒, (e, e))
with the operations ∨,∧,*,⇒ given by
is a NPc-lattice. Moreover, the correspondence
a (a, e)
(a, e)
defines an isomorphism fromHontoI(H)−.
With the notation of the previous theorem, for every element (a, b) ∈ H × H we have
The reader can verify that the following equation
holds in every A ∈  c (a proof is given in Lemma 4.2 of Busaniche and Cignoli (2009)).
c (a proof is given in Lemma 4.2 of Busaniche and Cignoli (2009)).
3. CONGRUENCES OF Pc-LATTICES
A convex subalgebra of A ∈ 
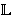 is a subalgebra S of A such that if x, y ∈ S, then the whole segment [x, y] = {z ∈ A : x < z < y} is in S. Given a congruence θ of A, Sθ = {x ∈ A : (x, e) ∈ θ} is a convex subalgebra of A. The following result is proved in §2 of Hart, Rafter and Tsinakis (2002):
is a subalgebra S of A such that if x, y ∈ S, then the whole segment [x, y] = {z ∈ A : x < z < y} is in S. Given a congruence θ of A, Sθ = {x ∈ A : (x, e) ∈ θ} is a convex subalgebra of A. The following result is proved in §2 of Hart, Rafter and Tsinakis (2002):
Theorem 3.1.The correspondence θ  Sθestablishes an order isomorphism from the set Subc(A) of convex subalgebras of A onto the set Cong(A) of congruences of A, when both sets are ordered by inclusion.
Sθestablishes an order isomorphism from the set Subc(A) of convex subalgebras of A onto the set Cong(A) of congruences of A, when both sets are ordered by inclusion.
An implicative filter (i-filter for short) of an integral commutative residuated lattice A is a subset F ⊆ A such that e ∈ F and it is closed under modus ponens: x ∈ F and x ⇒ y ∈ F imply y ∈ F. Implicative filters can also be characterized as subsets of A that are nonempty, upwards closed and closed by *. It follows easily that implicative filters are precisely the convex subalgebras of integral commutative residuated lattices. Hence by Theorem 3.1, there is an order isomorphism from Cong(A) onto the set Filt(A) of i-filters of A, ordered by inclusion.
Let A ∈ 
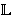 and let F ∈ Filt(A−). It follows from Lemma 2.7 in Hart, Rafter and Tsinakis (2002) that
and let F ∈ Filt(A−). It follows from Lemma 2.7 in Hart, Rafter and Tsinakis (2002) that
C(F) = {x ∈ A : z < x < z ⇒ e for some z ∈F}
is the universe of a convex subalgebra of A. Moreover, from the results of Hart, Rafter and Tsinakis (2002) the following theorem can be deduced.
Theorem 3.2.LetA be a Pc-lattice. The correspondence Φ Filt(A−) → Subc(A) given by
F C(F)
C(F)
is an order isomorphism.2 2 The result of this Theorem can be generalized to commutative residuated lattices and their negative cones.
Proof. Let F be an i-filter of the integral residuated lattice A−. First observe that F = C(F) ∩ A−. Indeed, if z ∈ F, then z ∈ A− and z < z < z ⇒ e, thus F ⊆ C(F) ∩ A−. For the opposite inclusion, take x ∈ C(F) ∩ A−. By definition there is z ∈ F such that z < x < z ⇒ e. Since F is upwards closed we get x ∈ F. We can conclude that Φ is injective.
To check surjectivity, let S ∈ Subc(A). First we see that F = S∩A− is an implicative filter of the negative cone of A. Clearly e ∈ S ∩ A− and if x, y ∈ S∩A−, then x*y ∈ S∩A−. To see that S∩A− is upwards closed, let x ∈ S ∩ A− and x < y < e. Then x * y < e * e = e, and y < x ⇒ e. Hence we have x < y < x ⇒ e and since S is convex we get y ∈ S ∩ A−.
Now we prove that S = C(F). The inclusion C(F) ⊆ S follows immediately from the convexity of S. For the opposite inclusion, take s ∈ S. Since S is a subalgebra of A, the element h = s ∧ e ∧ (s ⇒ e) belongs to S ∩ A−. We have
s * h = s * (s ∧ e ∧ (s ⇒ e)) < s * (s ⇒ e) < e.
Then h < s < h ⇒ e and S ⊆ C(F).
It is left as an easy exercise to corroborate that Φ is order preserving.
Notice that the inverse of the isomorphism Φ in the above theorem is the correspondence S  S ∩ A−. As an immediate corollary we get:
S ∩ A−. As an immediate corollary we get:
Corollary 3.3. The lattices Cong(A) and Cong(A−) are isomorphic.
Theorem 3.2 provides a useful tool to analize some classes and subvarieties of
c and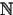 c. Two of its most important consequences are summarized in the next lemma.
c. Two of its most important consequences are summarized in the next lemma.
Lemma 3.4. Let A be a Pc-lattice. Then:
1. A is simple if and only if A−is the two-element Boolean algebra.
2. A is subdirectly irreducible if and only if A−has a coatom.
4. SEMISIMPLE AND REPRESENTABLE Pc-LATTICES
We first prove a result that will help us deal with semisimplicity.
Lemma 4.1.LetA ∈  c. Then A−is the bottom-free reduct of a boolean algebra if and only if A satisfies the equation
c. Then A−is the bottom-free reduct of a boolean algebra if and only if A satisfies the equation
Proof. It is well known that the generalized Heyting algebra A− is the bottom-free reduct of a boolean algebra if and only if it satisfies the Peirce equation
Observe that for every pair of elements a, b ∈ A−, since equation (16) holds in A we get that
(a ⇒e b) ⇒e a = ((a ∧ e) ⇒e (b ∧ e)) ⇒e (a ∧ e) =
(((a ∧ e ⇒ b ∧ e) ∧ e) ⇒ a ∧ e) ∧ e =
(((a ∧ e ⇒ b) ∧ e) ⇒ a ∧ e) ∧ e =
(((a ∧ e ⇒ b) ∧ e) ⇒ a) ∧ e.
With this information, the reader can easily check that equation (17) holds in A if and only if equation (18) holds in A−.
Let B be the two-element boolean algebra with universe {0, 1}. Then I(B) is an NPc-lattice with universe {(0, 1), (1, 1), (1, 0), (0, 0)}, where e = (1, 1). We define P3, as the unique nontrivial proper subalgebra of I(B), i.e., the subalgebra with universe P3 = {(0, 1), (1, 1), (1, 0)}.
In Figure 1 one can see the lattice reducts of the algebras I(B) and P3.
The proof of the following lemma is left as an easy exercise.
Lemma 4.2. Each of the lattices of Figure 1 admits a unique (up to isomorphism) structure of a Pc-lattice (an NPc-lattice), given by I(B) and P3respectively.
We will see that these are the only nontrivial simple Pc-lattices.
Lemma 4.3. Let C ∈  c be a simple algebra. Then C is a subalgebra of I(B).
c be a simple algebra. Then C is a subalgebra of I(B).
Proof. Assume that C is a nontrivial simple algebra in  c. From Lemma 3.4 we know that C− is the two-element boolean algebra B. We will prove that C is a subalgebra of I(B). Since e is the greatest element in C−, without danger of confusion we can denote by ┴ the other element in C−, thus C− = {┴ < e}.
c. From Lemma 3.4 we know that C− is the two-element boolean algebra B. We will prove that C is a subalgebra of I(B). Since e is the greatest element in C−, without danger of confusion we can denote by ┴ the other element in C−, thus C− = {┴ < e}.
After defining ~┴ = ┬, we have that C− ∪ C+ is the set
{┴ < e < ┬}.
Observe that this totally ordered set is order isomorphic to the lattice reduct of the algebra P3. Let c ∈C be such that c ∉ C− ∪ C+. Since c ∧ e is an element in C− less than e we must have c ∧ e = ┴. Similarly c ∨ e = ┬. If there were c, d ∉ C− ∪C+, then c ∧ e = d ∧ e and c ∨ e = d ∨ e. As previously mentioned, the distributivity of C implies the quasiequation (9), thus c = d. From the result of Lemma 4.2 we can conclude that either C ≅ P3 or C ≅ I(B).
Theorem 4.4.The class of semisimple Pc-lattices is the subvariety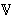 of
of cgenerated byI(B), and it is characterized by equation (17). Moreover, the class of semisimple Pc-lattices coincides with the class of semisimple NPc-lattices.
cgenerated byI(B), and it is characterized by equation (17). Moreover, the class of semisimple Pc-lattices coincides with the class of semisimple NPc-lattices.
Proof. As an immediate consequence of Lemma 4.3, any semisimple algebra in  c must be in
c must be in 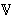 .
.
The algebra I(B) satisfies equation (17), because I(B)− is the reduct of a boolean algebra. Since this algebra generates 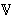 , every algebra in
, every algebra in 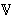 satisfies equation (17). Due to Lemma 4.1, we can assert that the negative cone of every algebra in
satisfies equation (17). Due to Lemma 4.1, we can assert that the negative cone of every algebra in 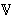 is a boolean algebra. In particular, if C is a subdirectly irreducible algebra in
is a boolean algebra. In particular, if C is a subdirectly irreducible algebra in 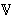 , then C− is a subdirectly irreducible boolean algebra. This means that C− is the two element boolean algebra. Thus C is a simple Pc-lattice. We can conclude that subdirectly irreducible algebras in
, then C− is a subdirectly irreducible boolean algebra. This means that C− is the two element boolean algebra. Thus C is a simple Pc-lattice. We can conclude that subdirectly irreducible algebras in 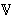 are simple. Hence all the elements of
are simple. Hence all the elements of 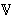 are semisimple Pc-lattices.
are semisimple Pc-lattices.
The last statement of the theorem follows from the fact that I(B) is an NPc-lattice.
It is easy to see that P3 generates a proper subvariety of the variety of semisimple Pc-lattices, characterized by (17) and the following Kleene equation:
We are going to show that this variety coincides with the variety of representable Pc-lattices.
A residuated lattice is representable if it is a subdirect product of linearly ordered residuated lattices. Given a subvariety 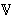 ⊆
⊆ 
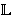 , it is shown in §3 in Tsinakis and Wille (2006) that the representable residuated lattices in
, it is shown in §3 in Tsinakis and Wille (2006) that the representable residuated lattices in 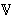 form a subvariety of
form a subvariety of 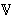 characterized by equation (7) and the equation
characterized by equation (7) and the equation
We have already observed that (7) holds in any Pc-lattice. Therefore we will search for subvarieties of
c that satisfy (20).To achieve such an aim, we will investigate the possible structure of totally ordered Pc-lattices. Obviously the trivial Pc-lattice whose only element is e is totally ordered.
Theorem 4.5. The Pc-lattice P 3 is the only nontrivial totally ordered Pc-lattice.
Proof. Let L be a nontrivial totally ordered Pc-lattice. Obviously L = L− ∪ L+, thus the chain L must be symmetric with respect to e.
Then it can not be the case that L has only two elements. If L has three elements, the result of Lemma 4.2 yields that L ≅ P3.
Assume that L has more than three elements. By symmetry with respect to e, L has at least five elements b < a < e < ~a < ~b.
Observe that ~b * a > e. Indeed, if ~b * a < e then the residuation law (1) yields
~b < a ⇒ e = ~a
which is a contradiction. Then (~b * a) ∧ e = e. On the other hand, from equation (4) we have
(~b * a) ∧ e = (~b ∧ e) * (a ∧ e) = e * a = a < e.
The contradiction arises from the hypothesis that L has more than three elements.
Corollary 4.6. The subvariety of representable Pc-lattices is generated by P 3 and it is characterized by (20). Moreover, it coincides with the subvariety of representable NPc-lattices.
Clearly, the variety of representable Pc-lattices is the only nontrivial proper subvariety of the variety of semisimple Pc-lattices.
REFERENCES
ALMUKDAD, A. and NELSON, D. "Constructible falsity and inexact predicates", J. Symb. Logic 49, p. 231–233, 1984.
BURRIS, S. And SANKAPPANAVAR, H. P. A Course in Universal Algebra Graduate Texts in Mathematics, Vol. 78. Springer-Verlag, New York - Heidelberg - Berlin, 1981.
BUSANICHE, M. and CIGNOLI, R. "Constructive logic with strong negation as a substructural logic", J. Log. Comput., 20, p. 761–793, 2010.
______. "Residuated lattices as an algebraic semantics for paraconsistent Nelson logic", J. Log. Comput., 19, p. 1019–1029, 2009.
GALATOS, N. and RAFTERY, J. G. "Adding involution to residuated structures", Stud. Log., 77, p. 181-207, 2004.
GALATOS, N., JIPSEN, P., KOWALSKI, T. and ONO, H. Residuated Lattices: An Algebraic Glimpse at Substructural Logics, Studies in Logics and the Foundations of Mathematics, Volume 151, Elsevier, New York, 2007.
HART, J.B., RAFTER, L. and TSINAKIS, C. "The structure of commutative residuated lattices", Int. J. Algebra Comput. 12, p. 509–524, 2002.
NELSON, D. "Constructible falsity", J. Symb. Logic. 14, p.16–26, 1949.
ODINTSOV, S.P. "Algebraic semantics for paraconsistent Nelson's logic", J. Log. Comput. 13, p. 453–468, 2003.
______. "On the representation of N4-lattices", Stud. Log. 76, p. 385–405, 2004.
______. Negations and Paraconsistency, Trends in Logic–Studia Logica Library 26. Springer. Dordrecht, 2008.
SENDLEWSKI, A. "Nelson algebras through Heyting ones. I", Stud. Log. 49, p. 105–126, 1990.
SPINKS, M. and VEROFF, R. "Constructive logic with strong negation is a substructural logic. I", Stud. Log., 88, p. 325–348, 2008.
______. "Constructive logic with strong negation is a substructural logic. II", Stud. Log., 89, p. 401– 425, 2008.
TSINAKIS, C. and WILLE, A.M. "Minimal Varieties of Involutive Residuated Lattices", Stud. Log., 83, p. 407– 423, 2006.
- BURRIS, S. And SANKAPPANAVAR, H. P. A Course in Universal Algebra Graduate Texts in Mathematics, Vol. 78. Springer-Verlag, New York - Heidelberg - Berlin, 1981.
- GALATOS, N. and RAFTERY, J. G. "Adding involution to residuated structures", Stud. Log., 77, p. 181-207, 2004.
- GALATOS, N., JIPSEN, P., KOWALSKI, T. and ONO, H. Residuated Lattices: An Algebraic Glimpse at Substructural Logics, Studies in Logics and the Foundations of Mathematics, Volume 151, Elsevier, New York, 2007.
Publication Dates
-
Publication in this collection
31 July 2012 -
Date of issue
June 2011



















