Resumos
Este trabalho teve como objetivo desenvolver um modelo de programação dinâmica, para determinar o momento ótimo de substituição de equipamentos, incorporando-se as receitas geradas pelo uso e descarte da máquina. Tal modelo deverá procurar maximizar os lucros através de uma relação de recorrência referente às receitas e aos custos ao longo dos anos. Desse modo, comparou-se o modelo proposto com um tradicional de substituição, que inclui apenas custos, utilizado por Filgueiras (1997). O modelo proposto foi satisfatório, de acordo com o objetivo do trabalho, pois com o seu desenvolvimento foi possível oferecer decisões ótimas de substituir ou reter o equipamento. Tal modelo se apresentou mais flexível, podendo ser utilizado em situações em que o equipamento gera receitas diretas (como no caso de aluguel ou receitas de fretes) ou não. Quando não se utilizam receitas, os resultados são idênticos aos do modelo tradicional. Constatou-se, também, que o modelo proposto é mais suscetível a aumentos no valor de aquisição do equipamento, enquanto o modelo sem receita é mais sensível a variações na taxa de juros. Observou-se que a aplicação da Programação Dinâmica oferece ao planejador uma gama de alternativas bem maior para auxiliar a tomada de decisão.
Programação dinâmica; substituição de equipamento; receita e custos
The objective of this work was to develop a dynamic programming model to determine the optimal time to replace equipment, including the incomes generated by the use and removal of the machine, aiming at the maximization of profits through a recurrence relation related to the incomes and costs along the years. Thus, the proposed model was compared to the traditional replacement model using the dynamic programming that does not include the income generated by the equipment, used by Filgueiras (1997). The model proposed was satisfactory according to the objective of the work, as its development made it possible to offer optimal decisions to replace or maintain the equipment. The model that includes only the costs showed to be best recommended in situations where the equipment is used without concern of generating annual incomes. On the other hand, the model developed can be used in situations where the equipment generates direct incomes or not. The model developed with the income showed to be efficient, and a greater susceptibility to a raise in the purchase value of the equipment was observed, whereas the model without concern to income is more susceptible to variations of interest rates. The advantage in using the dynamic programming (PD) in this case is that this tool offers a much greater range of alternatives at the moment of the decision making.
Dynamic programming; equipment replacement; income and, costs
Aplicação da programação dinâmica na substituição de equipamentos
Application of dynamic programming in equipment substitution
Gláucio Marcelino MarquesI; Márcio Lopes da SilvaII; Hélio Garcia LeiteII; Alessandro Albino FontesIII
IMestre em Ciência Florestal pelo DEF/UFV
IIDepartamento de Engenharia Florestal da Universidade Federal de Viçosa
IIIDoutorando em Ciência Florestal pelo DEF/UFV
RESUMO
Este trabalho teve como objetivo desenvolver um modelo de programação dinâmica, para determinar o momento ótimo de substituição de equipamentos, incorporando-se as receitas geradas pelo uso e descarte da máquina. Tal modelo deverá procurar maximizar os lucros através de uma relação de recorrência referente às receitas e aos custos ao longo dos anos. Desse modo, comparou-se o modelo proposto com um tradicional de substituição, que inclui apenas custos, utilizado por Filgueiras (1997). O modelo proposto foi satisfatório, de acordo com o objetivo do trabalho, pois com o seu desenvolvimento foi possível oferecer decisões ótimas de substituir ou reter o equipamento. Tal modelo se apresentou mais flexível, podendo ser utilizado em situações em que o equipamento gera receitas diretas (como no caso de aluguel ou receitas de fretes) ou não. Quando não se utilizam receitas, os resultados são idênticos aos do modelo tradicional. Constatou-se, também, que o modelo proposto é mais suscetível a aumentos no valor de aquisição do equipamento, enquanto o modelo sem receita é mais sensível a variações na taxa de juros. Observou-se que a aplicação da Programação Dinâmica oferece ao planejador uma gama de alternativas bem maior para auxiliar a tomada de decisão.
Palavras-chave: Programação dinâmica, substituição de equipamento, receita e custos.
ABSTRACT
The objective of this work was to develop a dynamic programming model to determine the optimal time to replace equipment, including the incomes generated by the use and removal of the machine, aiming at the maximization of profits through a recurrence relation related to the incomes and costs along the years. Thus, the proposed model was compared to the traditional replacement model using the dynamic programming that does not include the income generated by the equipment, used by Filgueiras (1997). The model proposed was satisfactory according to the objective of the work, as its development made it possible to offer optimal decisions to replace or maintain the equipment. The model that includes only the costs showed to be best recommended in situations where the equipment is used without concern of generating annual incomes. On the other hand, the model developed can be used in situations where the equipment generates direct incomes or not. The model developed with the income showed to be efficient, and a greater susceptibility to a raise in the purchase value of the equipment was observed, whereas the model without concern to income is more susceptible to variations of interest rates. The advantage in using the dynamic programming (PD) in this case is that this tool offers a much greater range of alternatives at the moment of the decision making.
Key words: Dynamic programming, equipment replacement, income and, costs.
1. INTRODUÇÃO
Parte significativa dos ativos das empresas florestais refere-se a máquinas e equipamentos, que apresentam custos de aquisição e operacionais elevados, exigindo das empresas cuidados com a sua utilização e com a determinação da sua vida útil.
A substituição, seja tardia, seja prematura, de máquinas e equipamentos leva a organização a incorrer em perdas financeiras, respectivamente, na recuperação de capital ou nos elevados custos operacionais do bem (VALVERDE e REZENDE, 1997). Ao otimizar a troca de equipamentos, pressupõe-se a definição e prévia análise do horizonte de planejamento, do futuro do investimento, dos custos operacionais, da depreciação, da taxa de juros, da utilização correta do ativo, dos programas de manutenção e reparos e dos critérios econômicos a serem considerados (VALVERDE e REZENDE, 1997). A substituição de equipamentos mostra-se, dessa forma, uma atividade complexa, que resultará em importante tomada de decisão. Além disso, outras possibilidades devem ser consideradas pelas empresas, como: adiar o investimento, reformar o equipamento velho, alugar o equipamento, "leasing", terceirizar a operação, dentre outras opções (MOTTA e CALÔBA, 2002; SAMANEZ, 2002).
Segundo Gupta e Cozzolino (1974), a estrutura mais simples de substituição de um equipamento é caracterizada quando o processo de depreciação é conhecido e representado por um aumento de custo operacional e uma diminuição do valor de revenda e da sua capacidade de trabalho constante ou decrescente com o tempo.
Apresentam-se como motivadores da substituição de equipamentos: melhores tecnologias, mudanças nos requerimentos dos serviços e nos próprios equipamentos, mudança na legislação tributária e casualidades (GRANT, 1960). A substituição é efetuada quando o equipamento inicia um processo de incapacidade de realização de suas funções, podendo, entretanto, ser substituído por outro mais funcional, que resulte em redução de custos operacionais e aumento de eficiência (MASSÉ, 1962). Nota-se que aspectos como a vida útil do equipamento e o seu valor residual são freqüentemente considerados na determinação do tempo ótimo de troca de máquinas e equipamentos. Dentre os métodos utilizados para determinação da substituição ótima de equipamentos, destacam-se o do custo médio total, o do custo anual equivalente e o de equações diferenciais (ciclo terminal, substituição parcial ou retirada e cadeia de substituição) e o uso da programação dinâmica (PD), como ferramentas para definir a substituição.
A PD pode ser determinística ou estocástica. A primeira considera todas as variáveis conhecidas ou predefinidas e foi o foco deste estudo. Já a PD estocástica, tal como o método da Opção Real, assume que o comportamento das variáveis está associado a dada probabilidade de ocorrência. Esses métodos são muito úteis e aplicados em análises de investimentos (DRAYFUS, 1977; MOTTA e CALÔBA, 2002; MONTEIRO, 2003).
Apesar de cada método apresentar suas características próprias, a programação dinâmica é um instrumental útil, pois, além de flexível, permite gerar soluções de forma rápida e otimizada dentro de um leque maior de opções. É um método de decomposição que se baseia no princípio da otimalidade de Bellman, aplicável em situações em que diversas decisões são requeridas na determinação da solução ótima de um sistema composto de distintos estágios, no qual as decisões em estágios subseqüentes não afetam os resultados de estágios anteriores (NENHAUSER, 1966; BEVERIDGE e SCHECHTER, 1970; DREYFUS e LAW, 1977).
Os modelos de PD determinística aplicados na substituição de equipamentos objetivaram minimizar custos, sem considerar as receitas geradas conforme o modelo utilizado por Filgueiras (1997). Contudo, sabe-se que as máquinas e os equipamentos podem gerar receitas (aluguéis e fretes). O fato de incluir a receita do equipamento como variável de decisão pode alterar o resultado da análise.
Na área florestal é grande o investimento em máquinas e equipamentos que, em sua maioria, apresentam custos elevados, daí a necessidade de eles operarem em jornadas extensas de uso intensivo, para redução de custos fixos. As máquinas são submetidas a condições de trabalho adversas, gerando elevados custos de reparos, manutenção e consertos. Nas últimas décadas, observou-se a introdução de modernas técnicas de mecanização, principalmente no que diz respeito à colheita florestal. Grandes organizações utilizam equipamentos de forma experimental, buscando mais produtividade nos serviços florestais. Nota-se, dessa forma, que várias empresas do segmento florestal estão intensificando seu investimento em maquinário. Assim, estudos sobre substituição de máquinas e equipamentos são fundamentais na tomada de decisão.
O objetivo geral deste estudo foi desenvolver um modelo com o uso de programação dinâmica, incorporando a receita do equipamento, a fim de proporcionar ao planejador florestal subsídios relativos à inversão de capital em novos equipamentos ao longo do horizonte de planejamento.
2. MATERIAL E MÉTODOS
2.1. Modelo de Programação Dinâmica para Substituição de Equipamentos Minimizando Custos
Um dos modelos empregados neste trabalho como ferramenta para definir o momento ideal para a substituição de equipamento foi o mesmo utilizado por Filgueiras (1997) e também por Gupta e Cozzolino (1974), com o objetivo de minimizar os custos operacionais. Foram adotados algumas notações e termos básicos para a formulação do problema e o desenvolvimento do modelo, conforme mostrado a seguir:
Horizonte de planejamento: conjunto de períodos sucessivos no decorrer do qual há interesse em se otimizar determinada variável ou função; corresponde ao número de estágios.
Estágios: são os períodos anuais, em que as ações de substituição são conduzidas. O número que identifica o estágio corresponde ao número de anos futuros em que a capacidade do equipamento é necessária; coincide com o horizonte de planejamento.
Estado: situação do sistema em determinado estágio, caracterizada por uma ou mais variáveis quantitativas ou qualitativas.
Transição: passagem do sistema do estado em que se encontra em determinado estágio para um estado associado ao estágio seguinte; a transição de estados é caracterizada pela mudança dos valores especificativos das variáveis de um estado para outro.
Decisão: a decisão no início de cada estágio consiste em reter o equipamento em uso por mais um ano ou substituí-lo e começar o ano seguinte com o equipamento novo.
Política: conjunto de decisões sucessivas ao longo do horizonte de planejamento.
N = número total de estágios ou tamanho do horizonte de planejamento.
n = idade do equipamento com a qual o processo é iniciado, em anos, n = 1, 2, ..., N.
Po = valor de aquisição de um equipamento novo, em US$.
Cn = custo operacional anual de um equipamento no início do ano n, n = 1, 2, ..., N, em US$; Cn é determinado pelo produto do custo/hora e pelo número de horas em operação no ano n.
Rn = valor de revenda de um equipamento, no final do ano n, n = 1, 2, ...N, em US$.
pn = fator de custos anuais não-controláveis de um tipo ou classe de equipamento, expresso em termos porcentuais em relação a Cn, que varia em função da idade do equipamento.
i = taxa de desconto anual.
Com base nas variáveis anteriormente definidas, formulou-se, então, a seguinte relação de recorrência:
em que fN(n) = custo total atualizado dos N estágios futuros, tendo o equipamento em consideração n anos de uso no início do processo e sendo tomadas decisões ótimas em todos os futuros estágios.
Observa-se que no final do processo (fo(n)) ocorre a venda do equipamento ou sucata, por isso fo(n) = -Rn * (1+i) -n.
A decisão econômica ótima é tomada comparando-se os valores da relação de recorrência referentes a manter ou substituir o equipamento para o ano seguinte do processo, isto é, ele é mantido quando o custo de retenção é menor que o custo de substituição; caso contrário, o equipamento deve ser substituído.
2.2. Modelo com Programação Dinâmica Incluindo Receita do Equipamento
Para se incluir a receita, apesar de a dinâmica ser a mesma, neste novo modelo se procuram maximizar os lucros, enquanto no anterior, minimizar os custos. Nesse caso, será introduzida a receita (anual) gerada pelo equipamento, seja pelo aluguel da máquina, seja pela sua utilização no processo produtivo, ou a receita do frete, no caso de veículos.
A definição das variáveis do modelo desenvolvido para este trabalho, associada ao objetivo de maximização dos lucros anuais do equipamento, proporcionou a formulação da seguinte relação de recorrência:
em que Rfné a receita gerada pelo equipamento no ano n; as demais variáveis foram definidas conforme anteriormente.
2.3. Estudo de Caso
A utilização dos modelos propostos se deu através de dados atualizados, que representam a rotina de atividades do setor florestal. Dessa forma, foi elaborado um estudo de caso de um trator de porte médio, com informações que podem ser observadas no Quadro 1. Todo o modelo foi desenvolvido em planilha do Excell.
2.4. Pós-otimização
A pós-otimização foi realizada efetuando-se alterações nas variáveis valor de aquisição de um equipamento novo, taxa de juros, receita e custo operacional, da seguinte forma. Essas alterações foram aplicadas nos dois modelos, a fim de verificar o efeito que a mudança em cada variável causaria sobre a decisão final.
3. RESULTADOS E DISCUSSÃO
3.1. Aplicação dos Modelos
Para testar a aplicabilidade dos modelos e compará-los, considerou-se um trator de porte médio com valor de aquisição de US$60.000,00, sendo os demais dados conforme apresentado nos Quadros 1 e 2.
Nota-se, na Figura 1, um rápido decréscimo do valor de revenda do equipamento, principalmente nos primeiros anos.
O custo operacional, por sua vez, demonstra um crescimento aproximadamente linear; em contrapartida, pode-se observar a tendência descendente da linha da receita anual que é superada pelo custo a partir do décimo ano de vida útil do equipamento. Nesse momento, o valor de revenda deste se mostra muito baixo, devido à depreciação sofrida pelo equipamento no decorrer do processo.
O fator de custo (pn) considerado também é crescente, componente esse que faz que o custo sofra aumento maior com o tempo.
Esses dados, embora aproximados, seguem uma tendência esperada para essas variáveis ao longo da vida útil do equipamento.
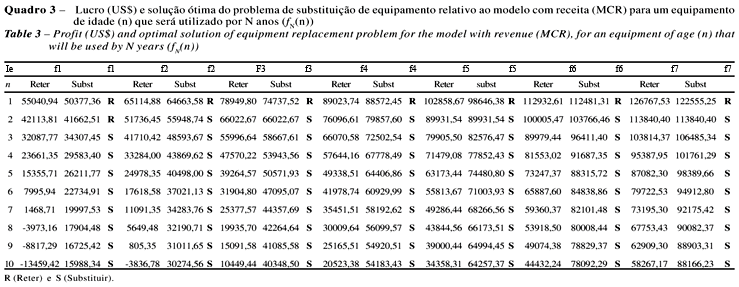
A partir dos dados do Quadro 2 e da taxa de juros de 6% a.a., obtiveram-se os resultados para o modelo com receita (MCR), que são apresentados no Quadro 3 e para o modelo sem receita (MSR), no Quadro 4. Os Quadros 3 e 4 são tabelas de dupla entrada que permitem analisar uma série de situações possíveis, dependendo da idade atual da máquina (n) e do horizonte de planejamento (N).
No Quadro 3 são ilustrados os resultados obtidos com a utilização do modelo com receita gerada por um equipamento com valor de aquisição de US$60.000,00, trabalhando 2.000 horas por ano e com taxa de juros de 6% ao ano. O Quadro 3 representa uma tabela de dupla entrada, em que a primeira coluna representa a idade atual do equipamento (n) que está variando de 1 a 10 anos, e na horizontal tem-se o tempo que se pretende operar com a máquina (N). Desse modo, obtém-se o valor do lucro, caso a máquina seja retida (R) ou substituída (S), sendo a melhor opção apontada pela letra correspondente.
Observa-se que o equipamento com 1 ano de uso (n=1) seria retido em todos os estágios (de f1 a f7). Já o equipamento com 2 anos de uso (n=2), utilizado por mais 1 ano (f1), seria retido, porém, se esse equipamento fosse utilizado por 2 anos ou mais (f2, f3, fn), deveria ser substituído. O modelo indica que, para as demais situações, o equipamento seria substituído. Isso se deve ao fato de que, apesar do elevado custo de aquisição e da influência das demais variáveis envolvidas, os equipamentos novos proporcionaram maiores lucros.
No Quadro 4, encontram-se os resultados obtidos com a utilização do modelo sem receita. Nesse caso, para a maioria das situações a melhor opção, ou seja, a que minimiza os custos, seria reter o equipamento por mais tempo; em poucos casos ocorre a substituição. Para interpretação do modelo, um equipamento que fosse utilizado por mais 1 ano (f1) seria retido, seja qual for a sua idade. Já no (f2), ou seja, caso o equipamento fosse utilizado por 2 anos e tivesse até 7 anos de uso, ele seria retido. Entretanto, um equipamento com 8 anos seria substituído.
Comparando o MCR e o MSR, observa-se que foram apresentados resultados diferentes em virtude da inclusão da receita do equipamento.
Para facilitar a interpretação, a partir do Quadro 3 (MCR) confeccionou-se um diagrama ou "árvore de decisão" (Figura 2), que ilustra a melhor alternativa ou o caminho que proporciona maior lucro nos três últimos anos do processo ou tempo em que o equipamento é necessário. Nesse caso, um trator com 4 anos de uso seria substituído por um equipamento novo (pois este proporcionaria um lucro maior de US$53.943,00); no estágio seguinte teria uma máquina com 1 ano de idade, que seria retida (pois este proporcionaria um lucro maior de US$65.114,00) e, no último estágio, essa máquina estaria com 2 anos e também seria retida até o final do processo. Desse modo, o Quadro 3 permite identificar o caminho ótimo para qualquer situação ou idade da máquina.
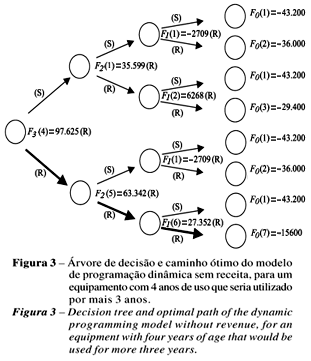
A Figura 3 foi gerada a partir do Quadro 4 (MSR) e ilustra a melhor alternativa ou o caminho que proporciona menor custo, nos três anos finais do processo. Nesse caso, um equipamento com 4 anos seria retido até o final do processo.
3.2. Pós-otimização
Para comparar a "performance" e a aplicação dos modelos, desenvolveu-se uma planilha, onde foi possível variar o valor de aquisição, a taxa de juros, o total de horas trabalhadas no ano, o custo/hora da máquina e a receita/hora desta.
Ao alterar essas variáveis, observou-se o seguinte: quando não se considerou a receita do equipamento, os dois modelos se igualaram e apresentaram a mesma solução, indicando que ambos estão corretos.
Pequenas alterações nas variáveis, embora possam alterar um pouco o lucro no MCR e o custo no MSR, não apresentaram mudanças significativas nos resultados, ou seja, na decisão de reter ou substituir a máquina. Porém, ao se aumentar o valor de aquisição de US$60.000,00 para US$150.000,00, por exemplo, notou-se que tanto o MCR quanto o MSR resultaram na retenção do equipamento por mais tempo, significando que, em função do maior valor do bem, seria necessário maior prazo para o retorno do capital investido.
Elevando-se a taxa de juros de 6 para 18%, ambos os modelos resultaram em soluções que recomendaram a retenção do equipamento por mais tempo.
O aumento de receita teve efeito inverso, possibilitando retorno mais rápido do capital. Assim, ao aumentar o valor da receita de US$30,00 para US$50,00, obtiveram-se soluções que recomendaram a retenção do equipamento por menos tempo.
Ao considerar custos operacionais mais elevados, é recomendado que o equipamento seja substituído mais cedo por um novo. Assim, ao elevar os custos operacionais de US$14,00 para US$25,00, tanto no modelo MCR quanto no MSR, isso resultou em menor tempo de retenção do equipamento.
Observou-se que o modelo com receita (MCR) é mais afetado pelo valor de aquisição, ou seja, quanto mais se eleva o valor de aquisição, mantendo as demais variáveis constantes, o modelo com receita resulta em retenções do equipamento por mais tempo.
O modelo sem receita (MSR) foi mais sensível a variações na taxa de juros. Assim, quanto mais elevada essa taxa, mais se recomenda reter o equipamento; taxas acima de 8% resultaram em soluções recomendando a retenção do equipamento para todas as situações.
Além das variáveis citadas, a solução ótima pode ser afetada pelas formas das curvas: de custo operacional, de valor de revenda e de receita da máquina, enfim, depende do tipo ou modelo do equipamento.
O resumo da análise de sensibilidade é apresentado no Quadro 4.
4. CONCLUSÕES
O desenvolvimento do referido modelo e a análise dos respectivos resultados permitiram chegar às seguintes conclusões:
A vantagem de se usar a PD, neste caso, é que esta ferramenta oferece ao planejador uma gama de alternativas bem maior na hora da tomada de decisão.
O modelo proposto foi satisfatório de acordo com o objetivo do trabalho, pois com o seu desenvolvimento foi possível oferecer decisões ótimas de substituir ou reter o equipamento.
Um aumento no valor de aquisição do equipamento pode acarretar o adiamento na substituição ótima da capacidade de serviço do equipamento em análise.
O modelo que inclui apenas custos é mais indicado para situações em que o equipamento utilizado não gera receita direta; neste caso, o que mais afetou a decisão foi a taxa de juros utilizada.
O modelo com receita é mais flexível, podendo ser utilizado em situações que o equipamento gera receitas diretas (como no caso de aluguel ou frete do equipamento) ou não.
A escolha da taxa de juros deve ser criteriosa, pois afeta a rentabilidade do investimento e também para que o processo de substituição apresente coerência com a realidade do problema.
5. REFERÊNCIAS BIBLIOGRÁFICAS
Recebido em 15.09.2003 e aceito para publicação em 10.08.2005.
- BEVERIDGE, G. S. D.; SCHECHTER, R .S. Optimization: theory and practice. Tókio: McGraw-Hill Kogakusha, 1970. 773 p.
- DREYFUS, S. E.; LAW, A. M. The art and theory of dynamic programming San Diego: 1977. 284 p.
- FILGUEIRAS, J. F. Um modelo de substituição de equipamentos para minimizar custos operacionais em uma empresa florestal 1997. 54 f. Dissertação (Mestrado em Ciência Florestal) - Universidade Federal de Viçosa, Viçosa, 1997.
- GUPTA, S. K.; COZZOLINO, J. M. Fundamentals of operations research for management: an introduction to quantitative methods. San Francisco: Holden Day, 1974. 405 p.
- GRANT, E. L. Principles of engineering economy New York: Ronald Press, 1960. 623 p.
- KAUFMANN, A.; CRUON, R. La programation dynamique México, D.C.: Continental, 1967. 308 p.
- MASSÉ, P. Optimal investment decisions: rules for action and criteria for choice. New Jersey: Prentice-Hall, 1962. 500 p.
- MONTEIRO, R.C. Contribuições da abordagem de avaliação de opções reais em ambientes econômicos de grande volatilidade - uma ênfase no cenário latino-americano 2003. 200f. Dissertação (Mestrado em Controladoria e Contabilidade) - Universidade de São Paulo, São Paulo, 2003.
- MOTTA, R. R; CALÔBA, G.M. Análise de investimentos São Paulo: Atlas, 2002. 392p.
- NENHAUSER, G. L. Introduction to dynamique programming New York: John Wiley and Sons, 1966. 256 p.
- SAMANEZ, C.P. Matemática financeira: aplicações à análise de investimentos. 3. ed. São Paulo: Makron Books, 2002. 340p.
- VALVERDE, S. R.; REZENDE, J. L. P. Princípio de substituição de máquinas e equipamentos. Revista Árvore, v. 21, n. 3, p. 353-364, 1997.
Datas de Publicação
-
Publicação nesta coleção
30 Nov 2005 -
Data do Fascículo
Out 2005
Histórico
-
Aceito
10 Ago 2005 -
Recebido
15 Set 2003