Resumos
Este estudo examinou a integração espacial via preços entre quatro mercados regionais de carvão vegetal em Minas Gerais. Após a realização do Teste de Raiz Unitária e do Teste de Causalidade de Granger e estimação de um modelo VAR, concluiu-se que os mercados são integrados espacialmente, ou seja, um choque de oferta ou demanda em um desses mercados afeta os preços do carvão vegetal nos demais mercados. Embora se tenha analisado o preço do carvão vegetal em apenas quatro regiões do Estado, os resultados deste estudo apontaram que o mercado mineiro de carvão vegetal vem funcionando eficientemente.
Integração de mercado; comercialização; preços; carvão vegetal
This study examined the spatial price integration among four regional markets of wood charcoal in Minas Gerais, Brasil. After performing Unit Root Tests, Granger Causality Tests and estimating a VAR, it was concluded that the markets are integrated, in other words, a supply or a demand shock in one of those markets affects the prices of the wood charcoal in other markets. Although the price of the wood charcoal has been analyzed in only four areas of the state, this study suggests that the wood charcoal market in Minas Gerais is working efficiently.
Market integration; commercialization; prices; wood charcoal
Integração espacial no mercado mineiro de carvão vegetal
Spatial price integration the market of wood charcoal in Minas Gerais, Brasil
Alessandro Albino FontesI; Márcio Lopes da SilvaII; João Eustáquio de LimaIII
IPrograma de Pós-Graduação em Ciência Florestal do DEF/UFV. E-mail: <aafontes@alunos.ufv.br>
IIDepartamento de Engenharia Florestal da Universidade Federal de Viçosa. E-mail: <marlosil@ufv.br>
IIIDepartamento de Economia Rural da Universidade Federal de Viçosa. E-mail: <jelima@ufv.br>
RESUMO
Este estudo examinou a integração espacial via preços entre quatro mercados regionais de carvão vegetal em Minas Gerais. Após a realização do Teste de Raiz Unitária e do Teste de Causalidade de Granger e estimação de um modelo VAR, concluiu-se que os mercados são integrados espacialmente, ou seja, um choque de oferta ou demanda em um desses mercados afeta os preços do carvão vegetal nos demais mercados. Embora se tenha analisado o preço do carvão vegetal em apenas quatro regiões do Estado, os resultados deste estudo apontaram que o mercado mineiro de carvão vegetal vem funcionando eficientemente.
Palavras-chave: Integração de mercado, comercialização, preços e carvão vegetal.
ABSTRACT
This study examined the spatial price integration among four regional markets of wood charcoal in Minas Gerais, Brasil. After performing Unit Root Tests, Granger Causality Tests and estimating a VAR, it was concluded that the markets are integrated, in other words, a supply or a demand shock in one of those markets affects the prices of the wood charcoal in other markets. Although the price of the wood charcoal has been analyzed in only four areas of the state, this study suggests that the wood charcoal market in Minas Gerais is working efficiently.
Keywords: Market integration, commercialization, prices and wood charcoal.
1. INTRODUÇÃO
O carvão vegetal é um subproduto florestal resultante da pirólise da madeira, também conhecida como carbonização ou destilação seca da madeira; um método destrutivo. No processo de carbonização, a madeira é aquecida em ambiente fechado, na ausência ou presença de quantidades controladas de oxigênio, a temperaturas acima de 300 ºC, desprendendo vapor d'água, líquidos orgânicos e gases não condensáveis, ficando como resíduo o carvão.
A produção nacional de carvão vegetal, considerando-se a variação de estoques, perdas e ajustes, é aproximadamente equivalente ao consumo, haja vista que as exportações e as importações são praticamente inexpressivas e quase se equivalem. A maior parcela de carvão vegetal produzida e consumida no país provém de florestas plantadas (74%) contra 26% de florestas nativas (AMS, 2004).
O Estado de Minas Gerais destaca-se, no cenário nacional, como o maior produtor e consumidor de carvão vegetal, em razão de seu parque siderúrgico, tendo consumido, em 2003, cerca de 67% da demanda nacional (29,2 milhões de metros de carvão) (AMS, 2004).
Os principais mercados consumidores de carvão vegetal no Estado de Minas localizam-se nas regiões de Sete Lagoas, Belo Horizonte, Divinópolis, Vertentes, João Monlevade, Rio Piracicaba, Rio Doce, Santos Dumont, Pirapora, Montes Claros e Ouro Preto. Entretanto, ao longo das duas últimas décadas algumas dessas regiões deixaram de ser importantes para a composição do preço do carvão vegetal no Estado, enquanto, ao mesmo tempo, outras regiões adquiriram destaque. Nesse aspecto, é de suma importância um estudo atualizado para saber se os mercados regionais são integrados, quais mercados possuem maior destaque e quais mercados influenciam os preços nos demais ou qual o sentido de transmissão de preços.
O acompanhamento dos preços praticados na compra do carvão vegetal deixou de ser realizado, por uma série de razões, em algumas das regiões anteriormente mencionadas, fazendo que várias dessas séries de preços ficassem interrompidas ou não tivessem continuidade. No entanto, durante esse período de tempo, quatro séries de preços de carvão vegetal se mantiveram: as de Sete Lagoas, Belo Horizonte, Divinópolis e Vertentes.
Segundo Faminon e Benson (1990), citados por Costa e Ferreira Filho (2000), um sistema de mercado é integrado quando os preços são determinados de maneira interdependente. Alterações de preços em um mercado são transmitidas aos preços de outros mercados (COSTA e FERREIRA FILHO, 2000). Um sistema de mercado é espacialmente integrado quando os preços praticados em cada um deles respondem não apenas às ofertas e demandas locais, mas às ofertas e demandas de todos eles (SANTANA, 1998). Mais precisamente, a integração espacial de mercados refere-se à medição do grau de co-movimentação dos preços em diferentes locais, por meio da correlação entre os preços (FACKLER e GOODWIN, 2000).
De acordo com Goodwin e Schroeder (1991), mercados que não são integrados podem carregar informações imprecisas de preços que podem distorcer as decisões de comercialização dos produtores e contribuir para a movimentação ineficiente de produtos. Assim, medir a integração espacial (co-movimentação de preços em diferentes locais, medida pela correlação entre os preços) de um mercado pode ser visto como um dado básico para o entendimento de como esse mercado funciona e, segundo Nogueira (2001), é de suma importância para a formulação de políticas governamentais para o setor visando tornar o mercado mais eficiente, bem como para os agentes da cadeia produtiva, pois choques de preços em uma região podem ser transmitidos a outras, levando a incertezas a respeito dos preços e renda.
Nesse contexto, o presente estudo tem como objetivo analisar a integração do mercado de carvão vegetal no Estado de Minas Gerais, principal produtor e consumidor desse energético no país. Especificamente, pretendeu-se identificar o comportamento dos preços no mercado físico das principais regiões consumidoras de carvão vegetal no Estado de Minas Gerais e testar a existência de relação de longo prazo entre os preços.
2. METODOLOGIA
2.1. Referencial Teórico
O conceito de mercados integrados deriva da proposição da "Lei do Preço Único" (LPU) que postula que bens idênticos obedecem à regra de perfeita arbitragem, ou seja, esses bens idênticos são vendidos a um preço equivalente nos diferentes mercados, independentemente da moeda nas quais são fixados (no caso de mercado internacional), após descontar os custos de transferência (custo de transferir o produto entre regiões). O que garante a verificação da LPU é o mecanismo de arbitragem. Por isso, a LPU é uma relação que se cumpre no longo prazo, sem excluir a possibilidade de desajustes de preços no curto prazo (COSTA e FERREIRA FILHO, 2000).
A base da análise da integração dos mercados encontra-se na LPU, garantida pela arbitragem dos mercadores. Na arbitragem espacial, os arbitradores são agentes que asseguram que os preços de bens homogêneos de quaisquer duas localidades diferem, no máximo, pelo custo de transferência do bem da região de menor preço para a região de maior preço (FACKLER e GOODWIN, 2000), ou seja:
em que pi representa o preço do bem na região "i"; pj, o preço do bem na região "j"; e rij, o custo de movimentação do bem da região "i" para a região "j".
Entende-se custo de transferência (custo de transação) o custo relevante de transações entre locais espacialmente separados (NOGUEIRA, 2001).
A condição (1) se manterá com regularidade se houver comércio direto entre as regiões "i" e "j". Essa condição é denominada condição de arbitragem espacial e constitui um conceito de equilíbrio (FACKLER e GOODWIN, 2000).
A LPU é freqüentemente testada, com a ressalva de que tais testes devem ser interpretados não somente como testes de condições de equilíbrio, mas como testes que são condicionados a hipóteses, considerando-se ligações de comércio. Violações da LPU podem indicar uma falta de relações de negócios estáveis ou uma situação de desequilíbrio, ou ambas (FACKLER e GOODWIN, 2000).
Arbitragem espacial, "Lei do Preço Único" e integração espacial de mercados são termos que se confundem e se inter-relacionam. No entanto, o que diferencia integração espacial de mercados dos demais termos é que este se refere à medida do grau de integração de mercados, ou seja, por um lado, existem mercados completamente isolados e, por outro, aqueles perfeitamente integrados (em que a LPU é observada). Integração espacial de mercado diz respeito ao grau de co-movimentação dos preços em diferentes locais, sendo medido pela correlação entre os preços (FACKLER e GOODWIN, 2000).
A integração espacial de mercados é importante à medida que pode ocorrer transmissão de preços indiretamente. Não é necessário que duas regiões sejam parceiras diretas de comércio para existir alto grau de integração entre elas. Suponha a existência de duas localidades "A" e "B", ambas fornecedoras de determinado bem para uma localidade "C". As localidades "A" e "B" podem estar fortemente integradas, apesar de não comerciarem diretamente. É justamente a ligação comercial com "C" que pode fazer que "A" e "B" estejam integradas. Assim, choques de preços podem ser transmitidos, indiretamente, por meio da rede de comércio via ligações de comércio entre regiões a ela conectadas (FACKLER e GOODWIN, 2000).
2.2. Modelo Analítico
Uma das formas de se avaliar a integração espacial de mercados via preços é utilizando a teoria da co-integração, empregada para avaliar relações lineares entre séries de preços de vários mercados, a serem estabelecidas no longo prazo. A ocorrência de tais relações, de forma estável, faz que as séries de preços sejam co-integradas, havendo, portanto, um indicativo de que os mercados também sejam co-integrados (SANTANA, 1998).
Para testar a co-integração das regiões consumidoras de carvão vegetal no Estado de Minas Gerais, inicialmente testou-se a estacionariedade das séries, pois a co-integração requer que todas as variáveis do modelo sejam integradas de mesma ordem. Isso pode ser feito pelo Teste da Raiz Unitária, introduzido por DICKEY e FULLER (1979). Os modelos que podem ser considerados são:
Subtraindo yt-1 de ambos os lados das equações (2) a (4), estas podem ser reescritas como:
em que Dyt = yt - yt-1; e d = r - 1; sendo t a variável tempo ou tendência.
Considera-se a hipótese nula H0: d = 0 (r = 1) contra a hipótese alternativa Ha: d < 0 (r < 1). Caso a hipótese nula não seja rejeitada, haverá raiz unitária no modelo, e a série será não-estacionária; caso contrário, a série será estacionária. Nesse teste, utiliza-se a estatística t (semelhante à estatística t), cujos valores foram tabulados por Dickey e Fuller, com base em simulações de Monte Carlo (DICKEY e FULLER, 1979). Na literatura, o teste t é conhecido como Teste de Dickey-Fuller (DF).
Caso o termo de erro do modelo seja autocorrelacionado, incluem-se no modelo os termos diferenciados defasados. O número de termos diferenciados defasados a serem incluídos no modelo é determinado, de forma que o termo de erro seja serialmente independente. O Teste de Dickey-Fuller, aplicado aos modelos (5), (6) e (7), acrescido dos termos diferenciados e defasados, é conhecido como Teste de Dickey-Fuller Aumentado (ADF), para o qual se utilizam os valores tabulados por Mackinnon (VACONCELOS e ALVES, 2000; EVIEWS, 1997).
Definida a estacionariedade das séries e se estas são co-integradas, e caso sejam, aplica-se o Teste de Causalidade de Granger (GRANGER, 1969). Esse teste possibilita aferir o sentido de causalidade entre os preços, no estudo da integração espacial.
A abordagem de Granger (1969), para a questão se "X" causa "Y", consiste em verificar quanto do "Y" corrente pode ser explicado por valores passados de "Y" e, então, se a adição de valores passados de "X" pode melhorar a explicação de "Y". "Y" será Granger causado por "X" se "X" ajudar na predição de "Y" ou, equivalentemente, se os coeficientes defasados de "X" forem estatisticamente significativos.
A afirmativa "X" Granger causa "Y" não implica "Y" seja efeito ou resultado de "X". A causalidade de Granger mede a procedência e o volume da informação, mas não indica a causalidade no uso mais comum do termo (GRANGER, 1969).
Seja a equação:
em que Yt-j são valores defasados da variável Yt; Xt-j, valores defasados da variável Xt; gj e qj, parâmetros; e et, erro aleatório.
Considerando a equação (8), o teste para verificar se "Y" é causado por "X" consiste em testar se os coeficientes de "X" são nulos, ou melhor, se q1= q2= ... = qp = 0, que é a hipótese nula. Tal verificação pode ser feita pelo teste "F". Caso a hipótese nula seja rejeitada, diz-se que "X" Granger causa "Y".
Para testar se "X" é causado por "Y", estima-se uma equação de "X" em razão de valores de "Y" e de "X" defasados (semelhante à equação (8)), e procede-se da mesma forma com relação ao tese "F", para verificar se g1 = g2 = ... = gp = 0, que é a hipótese nula. Caso essa hipótese seja rejeitada, diz-se que "Y" Granger causa "X".
Os resultados possíveis do Teste de Causalidade de Granger são os seguintes (considerando-se que também é realizado um teste de causalidade de Y em X, de maneira análoga):
a) Causalidade unidirecional de X para Y (X®Y): ocorre quando se rejeita H0 para X®Y e não se rejeita H0 para Y®X.
b) Causalidade unidirecional de Y para X (Y®X) ocorre quando se rejeita H0 para Y®X e não se rejeita H0 para X®Y.
c) Causalidade bidirecional (X«Y): ocorre quando as duas hipóteses nulas são rejeitadas.
d) Ausência de causalidade (independência): ocorre quando as duas hipóteses nulas não são rejeitadas.
O Teste de Causalidade de Granger será realizado nas variáveis em nível, atentando-se para seus pressupostos básicos de que as variáveis testadas são estocásticas; as séries estudadas são estacionárias, ou seja, suas propriedades estocásticas não variam ao longo do tempo, e o futuro não causa o presente e o passado, tendo-se em vista que o número de defasagens escolhidas pode influenciar a direção da causalidade (GUJARATI, 2000).
Definido o sentido de causalidade entre os preços, passa-se à estimação de um modelo Vetor de Auto-Regressão (VAR) para verificar o efeito de uma variação de preços ocorrido em determinado mercado sobre os demais.
O uso da metodologia de Auto-Regressão Vetorial (VAR) permite a obtenção de elasticidades de impulso para k períodos à frente. Essas elasticidades de impulso possibilitam avaliar o comportamento das variáveis em resposta a choques (inovações) individuais em qualquer dos componentes do sistema, podendo-se, assim, analisar, através de simulação, efeitos de eventos que tenham alguma probabilidade de ocorrer. A metodologia VAR possibilita, também, a decomposição histórica da variância dos erros de previsão, k períodos à frente, em porcentagens, a serem atribuídas a cada variável componente do sistema ou, de outra forma, trata-se da análise da importância de cada choque (em cada variável do modelo) ocorrido no passado por explicação dos desvios dos valores observados nas variáveis em relação à sua previsão realizada no início do período considerado.
A metodologia VAR tem como limitação o fato de possuir estrutura recursiva para as relações contemporâneas entre as variáveis. Bernanke (1986) desenvolveu o modelo conhecido como VAR estrutural, que supera tal restrição e permite estabelecer relações contemporâneas, tomando a teoria econômica como referência.
Um modelo VAR estrutural pode ser representado por:
em que yt é um vetor com variáveis de interesse; Bj são matrizes (n x n) para qualquer j, com B0 sendo a matriz de relações contemporâneas e et um vetor n x 1 de choques ortogonais. Além de considerar que os componentes de et são não correlacionados serialmente, adota-se a suposição de que eles não têm causa comum, tratando-os como mutualmente não-correlacionados, de tal forma que E(et et') = D.
O modelo, conforme descrito, requer o uso de séries estacionárias ou séries que se tornam estacionárias após a diferenciação.
2.3. Dados e Procedimentos
As séries utilizadas neste estudo referem-se aos preços médios mensais praticados na compra de carvão vegetal nas regiões de Sete Lagoas, Belo Horizonte, Divinópolis e Vertentes, no período de janeiro de 1981 a dezembro de 2003 (Consumer Price Index (CPI) Base 1982/84 = 100), elaboradas pela Associação Brasileira de Florestas Renováveis (ABRACAVE), obtidas em Coelho Junior (2004), compreendendo-se o total de 276 ocorrências em cada uma das séries de preço.
Os dados utilizados foram transformados em logaritmos e processados por meio do uso do software Eviews, versão 3.0, da QMS.
3. RESULTADOS E DISCUSSÃO
A variabilidade de preços no mercado de carvão vegetal se deve, em parte, ao grande número de produtores e fornecedores (GUIMARÃES e JARDIM, 1982), a exemplo do produtor profissional, do fazendeiro, do intermediário, das reflorestadoras e do produtor eventual, e à oferta de que, dadas as condições edafoclimáticas, está sujeita às flutuações estacionais e aleatórias (SILVA e SILVA, 1996), visto que a demanda desse produto é estável. Além disso, o carvão vegetal é um energético consumido nas diversas regiões do Brasil, com destaque para o Estado de Minas Gerais (maior consumidor devido ao parque siderúrgico) e para a região siderúrgica de Carajás, nos Estados do Maranhão e Pará. Tais fatos, aliados às condições climáticas, pressões ecológicas por parte da sociedade civil organizada, legislação (os grandes consumidores ficam obrigados a se auto-abastecerem), conjunturas interna e externa e concorrência do carvão mineral importado, entre outros, favorecem um ambiente de elevada incerteza para os agentes dessa cadeia agroindustrial.
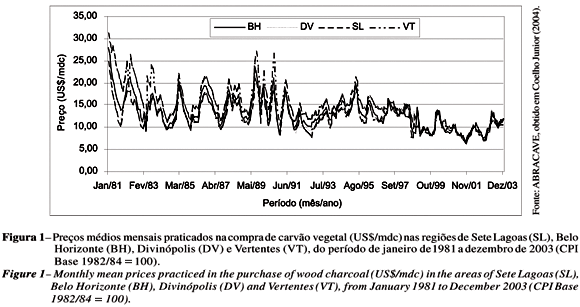
Para se ter uma idéia da integração espacial entre as regiões consumidoras de carvão vegetal deste estudo, é interessante verificar o esboço do gráfico com as quatro séries mensais de preço: Sete Lagoas, Belo Horizonte, Divinópolis e Vertentes (Figura 1).
Pode-se verificar, na Figura 1, que essas séries obedecem a uma mesma formação, dando a entender que se movimentam juntas ao longo do tempo, principalmente na década de 1990 e início da década de 2000. Assim, aparentemente, tais séries seriam integradas, ou seja, haveria integração espacial entre os mercados representados na referida figura.
Tal afirmação, no entanto, deve ser examinada criteriosamente. Dessa forma, procedeu-se à verificação econométrica da integração espacial dos mercados de carvão vegetal no Estado de Minas Gerais.
3.1. Análise de Estacionariedade dos Preços de Carvão
O Teste de Raiz Unitária tem por objetivo verificar se as séries em estudo são estacionárias. Gujarati (2000) mencionou que uma série é fracamente estacionária se suas médias e variâncias forem constantes ao longo do tempo e o valor da co-variância entre dois períodos de tempo depender apenas da distância ou defasagem entre os dois períodos e não do período de tempo efetivo em que a co-variância é calculada.
Utilizou-se o Teste de Dickey-Fuller Aumentado (ADF), que foi estimado para os casos da série com intercepto, com intercepto e com tendência e sem intercepto e sem tendência, utilizando-se a defasagem ("lags") de zero a 5. Tais estimativas foram feitas das séries mensais de preço do carvão, em nível. Utilizou-se, então, o menor valor do Critério de Akaike para selecionar a melhor opção (EVIEWS, 1997).
No Quadro 1, mostra-se que a hipótese nula de que a série tem uma raiz unitária foi rejeitada nas séries de preços de carvão vegetal de Sete Lagoas, Belo Horizonte, Divinópolis e Vertentes.
Pelos resultados apresentados no Quadro 1, verificou-se que as séries de preços de carvão vegetal de Sete Lagoas, Belo Horizonte, Divinópolis e Vertentes são estacionárias em nível, ou seja, são integradas de ordem zero, I (0).
Concluindo que as séries de preços de carvão vegetal são estacionárias, pode-se afirmar que os mercados considerados são espacialmente integrados, uma vez que séries estacionárias são co-integradas (ENDERS, 1995). Isso significa que choques de oferta, devido a condições climáticas, por exemplo, que afetam os preços em Sete Lagoas, irão refletir em variações de preços nos outros mercados.
3.2. Relações de Causalidade entre os Preços de Carvão
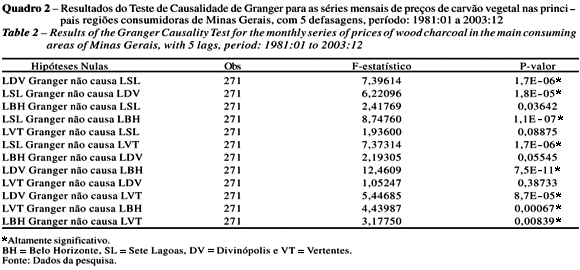
Após concluir que os mercados são integrados, passou-se ao teste para verificar como ocorre a transmissão das variações de preços entre os mercados e qual mercado lidera essas variações. Aplicou-se o Teste de Causalidade de Granger, que foi executado com até sete defasagens. Analisaram-se todos os resultados, sendo interessante reportar o resultado com cinco defasagens, por ser esse o caso mais provável e adequado para representar as relações de preços nesses mercados (Quadro 2). Os resultados com uma, duas, três e cinco defasagens diferiram entre si, sendo os resultados com três e quatro defasagens semelhantes entre si, e os resultados com cinco, seis e sete defasagens também foram semelhantes si.
Ao analisarem os resultados do Quadro 2, obtiveram-se as seguintes relações de casualidade de Granger (a 1% de significância): a) Sete Lagoas Granger causa Belo Horizonte; b) Sete Lagoas Granger causa Vertentes; c) Sete Lagoas Granger causa Divinópolis; d) Divinópolis Granger causa Sete Lagoas; e) Divinópolis Granger causa Belo Horizonte; f) Divinópolis Granger causa Vertentes; g) Belo Horizonte Granger causa Vertentes; e h) Vertentes Granger causa Belo Horizonte.
É interessante observar, nos resultados do Quadro 2 (com cinco defasagens), que existem relações de causalidade de Granger bidirecional entre as regiões de Sete Lagoas e Divinópolis e entre as regiões de Belo Horizonte e Vertentes e relações de causalidade de Granger unidirecional de Sete Lagoas para Belo Horizonte, Sete Lagoas para Vertentes, Divinópolis para Belo Horizonte e Divinópolis para Vertentes (Figura 2). Outro fato a notar é que os preços das regiões de Belo Horizonte e Vertentes são conseqüências dos demais mercados, no sentido Granger, enquanto os preços das regiões de Sete Lagoas e Divinópolis são causa dos demais mercados. Pode-se sugerir que as regiões de Sete Lagoas e Divinópolis são pólos que transmitem os choques (alterações) de preços aos demais mercados. Aparentemente, essas relações têm sentido econômico, pois se esperava que a região Sete Lagoas, maior consumidora de carvão vegetal em Minas Gerais, fosse Granger causa dos demais mercados, ou seja, a expectativa era de que a região de Sete lagoas se antecipasse nas variações de preços em relação aos demais mercados.
Cabe ressaltar que a Causalidade de Granger mede a precedência e o volume de informação, mas não indica, por si só, causalidade no uso mais comum do termo (GRANGER, 1969). Assim, o fato de Sete Lagoas e Divinópolis serem Granger causa dos demais mercados não significa que os choques (alterações) de preços dos demais mercados sejam o efeito ou o resultado dos choques (alterações) de preços ocorridos em Sete Lagoas e Divinópolis.
3.3. Vetor de Auto-Regressão
Após verificada a direção de transmissão dos preços de carvão nas regiões consumidoras de Minas Gerais, passou-se à estimação do modelo VAR para verificar o efeito de uma variação de preços ocorrido em determinado mercado sobre os demais. O Vetor de Auto-Regressão foi especificado na forma irrestrita, com duas defasagens, nas séries LSL, LDV, LBH e LVT, incluindo intercepto. O impulso de resposta nas variáveis foi definido para 12 períodos, adotando-se o método analítico (assintótico) para as respostas aos erros-padrão, com 100 repetições.
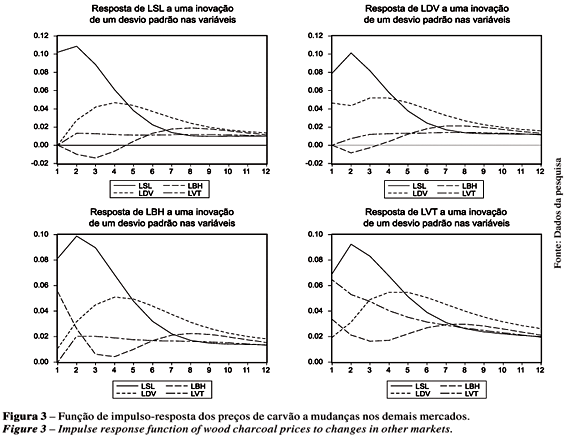
Na Figura 3, mostram-se os efeitos de choques nas variáveis consideradas (preço de carvão) nos primeiros 12 períodos (meses) seguintes ao instante do choque inicial.
Os resultados indicam que uma variação do preço de carvão vegetal na região de Sete Lagoas não tem efeito, no primeiro momento, em nenhum dos demais mercados, passando a ser expressivo, no segundo mês após o choque, no preço de carvão da região de Vertentes, no terceiro mês no preço de carvão da região de Belo Horizonte, e no quarto mês no preço de carvão da região de Divinópolis. Ou seja, uma variação de 1% no preço de carvão de Sete Lagoas provoca, após dois meses, uma variação de aproximadamente 0,01% no preço de Vertentes; de -0,01% no preço de Belo Horizonte (após três meses) e de 0,04% no preço de Divinópolis (após quatro meses). Observou-se que uma variação do preço de carvão em Sete Lagoas reflete positivamente nos preços de Vertentes e Divinópolis e negativamente no preço de Belo Horizonte.
O efeito de uma variação do preço de carvão vegetal na região de Divinópolis não reflete, no primeiro momento, nos mercados de carvão de Vertentes e de Belo Horizonte. Esse efeito passa a ser expressivo, no segundo mês após o choque, no preço de carvão da região de Belo Horizonte e, no terceiro mês após, no preço de carvão da região de Vertentes. Assim, uma variação de 1% no preço de carvão de Divinópolis provoca, após dois meses, uma variação de aproximadamente 0,10% no preço de Sete Lagoas e de -0,01% no preço de Belo Horizonte; e, após três meses, de 0,01% no preço de Vertentes. Observou-se que uma variação no preço de carvão em Divinópolis reflete positivamente nos preços de Vertentes e Sete Lagoas e negativamente nos preços de Belo Horizonte.
O efeito de uma variação do preço de carvão vegetal na região de Belo Horizonte reflete, no primeiro momento, nos demais mercados de carvão vegetal, à exceção de Vertentes. Esse efeito atinge valores máximos, no segundo mês após o choque, nos preços de carvão da região de Vertentes e Sete Lagoas; e, no quarto mês após, no preço de carvão da região de Divinópolis. Ou seja, uma variação de 1% no preço do carvão de Belo Horizonte provoca, após dois meses, variação de aproximadamente 0,02% no preço de Vertentes e de 0,10% no preço de Sete Lagoas; e, após quatro meses, de 0,055% no preço de Divinópolis. Verificou-se que variação no preço de carvão em Belo Horizonte reflete positivamente nos preços nos demais mercados de carvão vegetal.
Por último, o efeito de uma variação do preço de carvão vegetal na região de Vertentes reflete positivamente, no primeiro momento, nos demais mercados de carvão vegetal. Esse efeito atinge valores máximos, no segundo mês após o choque, no preço de carvão da região de Sete Lagoas; no terceiro mês após, no preço de carvão da região de Belo Horizonte; e, no quinto mês após, no preço de carvão da região de Divinópolis. Assim, uma variação de 1% no preço de carvão de Vertentes provoca, após dois meses, uma variação de aproximadamente 0,09% no preço de Sete Lagoas; de 0,017% no preço de Belo Horizonte (após três meses); e de 0,055% no preço de Divinópolis (após cinco meses). Observou-se que uma variação do preço de carvão em Vertentes reflete positivamente nos preços nos demais mercados de carvão vegetal.
4. CONCLUSÃO
As informações obtidas neste trabalho permitiram a conclusão de que:
- As séries de preços de carvão vegetal de Sete Lagoas, Belo Horizonte, Divinópolis e Vertentes são estacionárias em nível, ou seja, são integradas de ordem zero, I (0).
- Os mercados de carvão vegetal das regiões de Sete Lagoas, Belo Horizonte, Divinópolis e Vertentes são integrados espacialmente via preços, ou seja, existem relações estáveis de longo prazo entre eles ou, em outras palavras, um choque de oferta ou demanda em um desses mercados afeta os preços de carvão vegetal nos demais mercados.
- Os mercados de carvão vegetal das regiões de Sete Lagoas e Divinópolis são Granger causa dos demais mercados, o que leva a inferir que as regiões de Sete Lagoas e Divinópolis são pólos que transmitem os choques de preços (alterações) aos demais mercados.
5. REFERÊNCIAS BIBLIOGRÁFICAS
Recebido em 06.10.2004 e aceito para publicação em 10.08.2005.
- ASSOCIAÇÃO MINEIRA DE SILVICULTURA-AMS. Anuário. [08.09.2004]. (http://www.silviminas.com.br/anuario.htm).
- BERNANKE, B.S. Alternative explanations of the money-income correlation. Carnegie-Rochester Conference Series on Public Policy, v.25, p.49-100, 1986.
- COELHO JUNIOR, L.M. Análise temporal dos preços do carvão vegetal, no estado de Minas Gerais. 2004. 160f. Dissertação (Mestrado em Engenharia Florestal) - Universidade Federal de Lavras, Lavras, 2004.
- COSTA, S.M.A.L.; FERREIRA FILHO, J.B.S. Liberação comercial no Brasil e integração nos mercados de commodities agrícolas: os mercados do algodão, milho e arroz. Revista de Economia e Sociologia Rural, v.38, n.2, p.41-70, 2000.
- DICKEY, D.A.; FULLER, W.A. Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association, v.74, n.366, p.427-431, 1979.
- ENDERS, W. Applied econometric time series. New York: John Wiley & Sons, 1995. 433p.
- EVIEWS User's Guide. Irvine: QMS, 1997. 656p. (Versão 3.0).
- FACKLER, P.L.; GOODWIN, B.K. Spatial price analysis. forthcoming, Handbook of Agricultural Economics. North-Holland: 2000. p.1-59.
- GOODWIN, B.K.; SCHROEDER, T.C. Cointegration tests and spatial price linkages in regional cattle markets. American Journal of Agricultural Economics, v.73, p.452-464, 1991.
- GRANGER, C.W.J. Investigating causal relations by econometric models and cross spectral methods. Econometrica, v.37, n.3, p.424-438, 1969.
- GUIMARÃES, S.T.A.; JARDIM, L.S.B. Aspectos econômicos da produção de carvão vegetal. Transporte, manuseio, estocagem. In: FUNDAÇÃO CENTRO TECNOLÓGICO DE MINAS GERAIS-CETEC. Produção e utilização de carvão vegetal. Belo Horizonte: 1982. p.125-140.
- GUJARATI, D.N. Econometria básica. 3. ed. São Paulo: Makron Books, 2000. 846p.
- NOGUEIRA, F.T.P. Integração espacial e efetividade do "Hedge" no mercado brasileiro de café arábica. 2001. 147f. Dissertação (Mestrado em Economia Rural) - Universidade Federal de Viçosa, Viçosa, 2001.
- SANTANA, A.C. Comercialização e integração de mercado na pecuária de corte do estado do Pará. In: AGRUIAR, D.R.D.; PINHO, J.B. (Org.). O agronegócio brasileiro: desafios e perspectivas. Brasília: 1998. p.653-668..
- SILVA, M.L.; SILVA, J.M.A. Análise do comportamento temporal dos preços do carvão vegetal: aplicação e avaliação da metodologia "Box and Jenkins". Revista Árvore, v.20, n.1, p.57-67, 1996.
- VASCONCELOS, M.A.S.; ALVES, D. Manual de econometria. São Paulo: Atlas, 2000. 308p.
Datas de Publicação
-
Publicação nesta coleção
15 Maio 2006 -
Data do Fascículo
Dez 2005
Histórico
-
Aceito
10 Ago 2005 -
Recebido
06 Out 2004