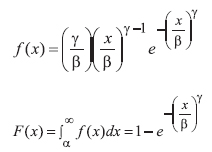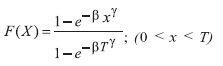Resumos
A projeção da distribuição diamétrica e produção é de grande importância para o planejamento e tomada de decisão sobre manejo de povoamentos florestais. Este estudo objetivou a aplicação de um modelo de distribuição diamétrica na projeção de distribuição e produção de um povoamento de eucalipto, por meio do ajuste e aplicação da função Weibull de duas variáveis e truncada. Verificou-se que a utilização da Weibull truncada proporcionou estimativas ligeiramente superiores à Weibull com duas variáveis.
Crescimento; Função densidade probabilidade; Função Weibull
The projection of the diametrical distribution and production is of great importance for the planning and decision taking in the management of forest stands. The objective of this work was to apply a diametric distribution model in the prediction of distribution and yield of a eucalyptus stand by adjusting and application of the Weibull function with two fitting parameters and truncated. The use of the truncated Weibull estimates provided slightly superior estimates than the Weibull function with two fitting parameters.
Growth; Probability density function; Weibull function
Projeção da distribuição diamétrica e produção de povoamentos de eucalipto empregando diferentes formas da função weibull
Projection of yield and distribution diametrical of eucalyptus stands with different forms of weibull function
Thelma Shirlen SoaresI; Helio Garcia LeiteII; Carlos Pedro Boechat SoaresII; Antonio Bartolomeu do ValeII
IUniversidade Federal de Goiás, Campus Jataí, UFG, Brasil, E-mail: thelmasoares@terra.com.br
IIDepartamento de Engenharia Florestal, Universidade Federal de Viçosa, UFV, MG, Brasil, E-mail: hgleite@gmail.com, csoares@ufv.br; abvale@superig.com.br
RESUMO
A projeção da distribuição diamétrica e produção é de grande importância para o planejamento e tomada de decisão sobre manejo de povoamentos florestais. Este estudo objetivou a aplicação de um modelo de distribuição diamétrica na projeção de distribuição e produção de um povoamento de eucalipto, por meio do ajuste e aplicação da função Weibull de duas variáveis e truncada. Verificou-se que a utilização da Weibull truncada proporcionou estimativas ligeiramente superiores à Weibull com duas variáveis.
Palavras chave: Crescimento, Função densidade probabilidade e Função Weibull.
ABSTRACT
The projection of the diametrical distribution and production is of great importance for the planning and decision taking in the management of forest stands. The objective of this work was to apply a diametric distribution model in the prediction of distribution and yield of a eucalyptus stand by adjusting and application of the Weibull function with two fitting parameters and truncated. The use of the truncated Weibull estimates provided slightly superior estimates than the Weibull function with two fitting parameters.
Keywords: Growth, Probability density function and Weibull function.
1. INTRODUÇÃO
Estudos referentes à distribuição dos diâmetros de povoamentos florestais datam de 1898 quando De Liocourt propôs um modelo simples baseado na progressão geométrica dos diâmetros. A distribuição diamétrica, de acordo com Soares et al. (2007), tem sido a mais simples e eficiente maneira de descrever as propriedades de um povoamento.
Neste contexto, o ajuste de distribuições de probabilidades às estruturas diamétricas se tornou uma ferramenta clássica no manejo florestal de povoamentos florestais equiâneos (NÁVAR-CHÁIDEZ; CONTRERAS-AVINÃ, 2000). Entre as diversas funções de densidade de probabilidade (f d p), a função Weibull tem sido a mais utilizada na modelagem de povoamentos florestais.
Segundo Campos e Turnbull (1981), a função Weibull apresenta superioridade em relação às demais para os propósitos florestais devido a sua flexibilidade e à facilidade de relacionar, de forma significativa, suas variáveis com características importantes do povoamento.
Usualmente, a função Weibull é empregada com três variáveis (responsáveis pela escala, forma e locação da distribuição) ou duas variáveis (parâmetros de escala e forma). Um quarto parâmetro, definido como um ponto de truncamento sendo o limite superior da maior classe diamétrica tem sido utilizado para aprimorar as estimativas das distribuições diamétricas. A função Weibull truncada à direita é utilizada quando se deseja considerar que a distribuição estimada deve estar dentro de um intervalo determinado pelos diâmetros mínimo e máximo, corrigindo o inconveniente de se estimar um número de árvores para classes não observadas nas medições das parcelas em campo.
Este estudo foi realizado com o objetivo de avaliar um sistema de predição presente e futura da produção por classe diamétrica, empregando a distribuição Weibull sob duas formas: com duas variáveis e truncada à direita.
2. MATERIAL E MÉTODOS
Foram utilizados dados de povoamentos do híbrido Eucalyptus grandis W. Hill ex Maiden x Eucalyptus urophylla S. T. Blake, em espaçamento 3 x 2 m, localizados na região nordeste do Estado da Bahia, de 64 parcelas de área de 471 m2, cujas medições foram realizadas aos 38, 50, 62, 74 e 86 meses.
Os dados são de parcelas permanentes circulares com raio de 12,25 m. Em cada parcela, foram medidos os diâmetros a 1,3 m de altura do solo (dap) de todas as árvores e a altura total (Ht) de 20 árvores por parcela, aos 38, 50, 62, 74 e 86 meses.
Foram testadas duas variações da função Weibull: função Weibull de duas variáveis e função Weibull truncada à direita.
A função Weibull com duas variáveis é da forma (BAILEY; DELL, 1973):
em que: β = variável de escala;
γ = variável de forma;
x = variável aleatória, no caso centro de classe de dap, sendo x > 0, b > 0, γ > 0.
A função Weibull truncada à direita é da forma (WINGO, 1988):
em que: β, < γ e x = definidos anteriormente;
T = ponto de truncamento (diâmetro máximo). O valor de T foi considerado o maior diâmetro observado para cada parcela, e o limite inferior da distribuição calculada foi o mínimo.
Os dados foram agrupados em classes com intervalos regulares de 2 cm de amplitude. O número de classes por parcela variou em função da quantidade de árvores e da diferença entre os diâmetros mínimo e máximo observados em cada unidade amostral. As funções foram ajustadas aos dados de distribuição diamétrica observada de cada parcela em todas as medições. A estimação dos parâmetros da função densidade de probabilidade (f d p), para ambas as funções, foi realizada empregando o método da máxima verossimilhança, conforme Gove e Fairweather (1989).
O modelo de distribuição diamétrica empregado para a recuperação das variáveis das f d p em uma idade futura é composto pelo seguinte sistema de equações obtido de Soares et al. (2010):
= 6,620468 0,052552 N + 0,406683 Hd
R2aj = 0,86 ∴ Syx% = ± 3,96%
γ = 1,810831 - 0,016685 I +0,296597  - 0,085201Hd
- 0,085201Hd
R2aj = 0,42 ∴ Syx% = ± 2,20%
β = -2,11962 + 0,004404 I +0,46773
R2aj = 0,88 ∴ Syx% = ± 7,92%
N2 = N1 e-93,72493(I20,004192 - I10,004282)
R2aj = 0,92 ∴ Syx% = ± 6,27%
em que: I = idade (meses);
 = diâmetro médio na idade atual (cm);
= diâmetro médio na idade atual (cm);
N = número de árvores;
Hd = altura dominante (m);
γ = parâmetro de forma da função Weibull;
β = parâmetro de escala da função Weibull;
I1 = idade atual (meses);
I2 = idade futura (meses);
N1 = número de árvores por hectare, na idade atual I1;
N2 = número de árvores por hectare, na idade futura I2;
ln = logaritmo neperiano.
Com os dados dos parâmetros estimados para cada uma das equações do modelo de distribuição diamétrica, os parâmetros de forma e escala das funções densidade de probabilidade foram recuperados.
A projeção da distribuição diamétrica foi realizada a partir de uma distribuição em uma idade atual (I1) para uma idade futura (I2), partindo-se de uma distribuição inicial observada.
De acordo com a metodologia descrita por Soares et al. (2007), aplicou-se um teste de compatibilidade, que consistiu em analisar se a distribuição diamétrica projetada do início para o final de um período é compatível com a distribuição diamétrica projetada ano a ano. Para isso, empregou-se o teste de aderência de Kolmogorov-Smirnov a 5%.
A partir das distribuições teóricas simuladas, foram obtidas estimavas da produção em volume total e por classe de diâmetro em diferentes idades. A estimação foi realizada para todas as parcelas e em todas as medições. A altura total e os volumes foram obtidos por meio das seguintes equações obtidas de Soares et al. (2007):
In Ht = 0,81574 + 0,48837dap-1 - 2,53925 In(Hd)
R2aj = 0,89 ∴ Syx% = ± 9,10%
V = 0,00008dap1,53553.Ht1,44819 .[e-2,25669(Tx/dap)].[1-(d.dap -1)1-0,00077.d]
R2aj = 0,95 ∴ Syx% = ± 5,23%
em que: Ht = altura total (m);
dap = diâmetro medido a 1,3 m de altura do solo (cm);
d = diâmetro comercial (cm);
V = volume (m3);
e = base dos logaritmos neperianos;
Tx = variável binária (0 para volume ou diâmetro d com casca e 1 para volume ou diâmetro d sem casca);
Hd, ln = conforme definido anteriormente.
O modelo volumétrico foi empregado para a obtenção do volume total, do volume comercial (neste caso considerado até o diâmetro aproveitável de 6 cm) e para energia com casca. As estimativas volumétricas foram comparadas por meio da aplicação do teste L&O (LEITE; OLIVEIRA, 2002), utilizado para comparar os volumes observados com os volumes estimados.
3. RESULTADOS
3.1 Simulação das distribuições diamétricas
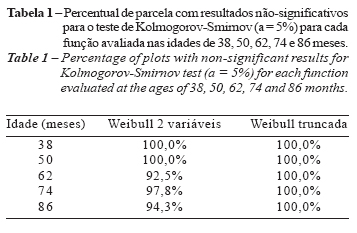
O teste Kolmogorov-Smirnov apresentou resultados não significativos para todas parcelas em todas as idades para a avaliação dos ajustes realizados, com a função Weibull truncada. Já quando foi aplicada a Weibull com duas variáveis, ocorreu diferença significativa nas idades de 62, 74 e 86 meses (Tabela 1).
Na Figura 1 são apresentados exemplos das distribuições observadas e recuperadas para cada uma das formas da função Weibull, empregando o modelo de distribuição diamétrica.
Com o teste de Kolmogorov-Smirnov foram avaliadas as distribuições observadas e recuperadas. O teste foi não significativo para 93,8% e 98,4% das parcelas, respectivamente, para a recuperação empregando a Weibull de duas variáveis e a Weibull truncada.
3.2 Avaliação da projeção da produção volumétrica
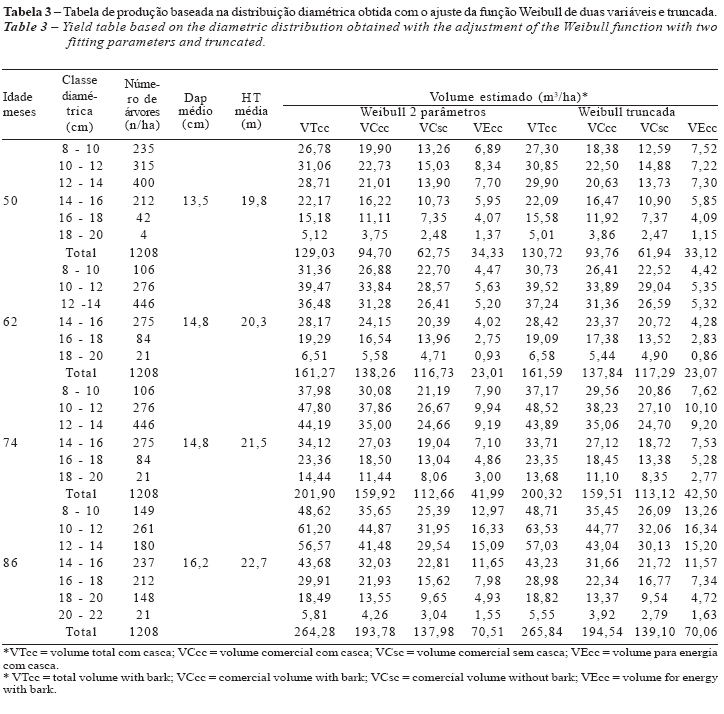
A fim de averiguar a similaridade entre as projeções volumétricas obtidas pelo emprego da distribuição Weibull não truncada e truncada, utilizou-se o teste de L&O cujo resultado indicou não haver diferenças significativas (p > 0,05) entre os valores observados e ajustados em ambos os casos (Tabela 2). As projeções efetuadas são apresentadas na Tabela 3.
4. DISCUSSÃO
Os resultados do teste Kolmogorov-Smirnov demonstraram, para a maioria dos casos, a inexistência de diferenças significativas entre as projeções observadas e estimadas tanto pelo emprego da distribuição Weibull de duas variáveis quanto pela Weibull truncada. Entretanto, observa-se maior proporção de redistribuições não significativas, ou seja, valores estimados iguais aos observados para as projeções realizadas com a f d p truncada quando a mesma é comparada com a f d p Weibull sem o truncamento.
Verifica-se, então, que o truncamento da função Weibull aumenta a eficiência do modelo, uma vez que corrige as probabilidades totais cujo valor é menor que 1. O truncamento da função fez com que as estimativas do número de árvores permanecessem dentro do intervalo dapmínino < dap < dapmáximo observado.
Comparando os resultados obtidos da aplicação da função Weibull completa e truncada, observou-se que a diferença entre os resultados é indiferente, e o truncamento da função propicia maior porcentagem de estimativas estatísticamente iguais aos valores observados. Tais resultados corroboram o uso do truncamento na função, principalmente em situações em que se faz necessário considerar limites superior, inferior ou bilateral nas distribuições a serem estimadas.
Apesar de apresentar resultados estatísticos similares em termos de aceitação do ajuste realizado, as funções analisadas diferem-se no que se refere à exata distribuição das árvores em classes de diâmetro, sendo a função Weibull truncada à direita a que melhor se comporta. Sendo assim, infere-se que qualquer um dos métodos pode ser empregado para a modelagem da distribuição diamétrica e projeção da produção volumétrica de povoamentos florestais, sendo a escolha uma opção particular do usuário.
5. CONCLUSÕES
A f d p Weibull de duas variáveis e truncada propiciam estimativas precisas das variáveis avaliadas.
O truncamento da f d p Weibull contribuiu para eliminar as estimativas de probabilidades cujos números de árvores por classe diamétrica eram menor que 1, sem superestimar ou subestimar o número de árvores nas maiores classes.
6. REFERÊNCIAS
Recebido em 26.09.2009 e aceito para publicação em 02.05.2011.
- BAILEY, R. L.; DELL, J. R. Quantifying diameter distributions with the Weibull function. Forest Science, v.19, n.2, p.97-104, 1973.
- CAMPOS, J. C. C.; TURNBULL, K. J. Um sistema para estimar produção por classe de diâmetro e sua aplicação na interpretação de efeitos de desbaste. Árvore, v.5, n.1, p.1-16, 1981.
- GOVE, J. H.; FAIRWEATHER, S. E. Maximum-likelihood estimation of Weibull function parameters using a general interactive optimizer and grouped data. Forest Ecology and Management, v.28, n.1, p.61-69, 1989.
- LEITE, H. G.; OLIVEIRA, F. H. T. Statistical procedure to test the identity of analytical methods. Communications in Soil Science Plant Analysis, v.33, n.7/8, p.1105-1118, 2002.
- NÁVAR-CHÁIDEZ, J. J.; CONTRERAS-AVIÑA, J. Ajuste de la distribución Weibull a las estructuras diamétricas de rodales irregulares de pino en Durango, México. Agrociencia, v.34, n.3, p.353-361, 2000.
- SOARES, T. S. et al. Avaliação de um modelo de passo invariante na predição da estrutura de um povoamento de Eucalyptus sp. Revista Árvore, v.31, n.2, p.275-283, 2007.
- SOARES, T. S. et al. Procedures for theoretical redistribution of diameters in eucalyptus stands. Cerne, v.16, n.1, p.68-76, 2010.
- WINGO, D. R. Methods for fitting the right-truncated weibull distribution to life-test and survival data. Biometrical Journal, v.30, n.5, p.545-551, 1988.
Datas de Publicação
-
Publicação nesta coleção
10 Out 2011 -
Data do Fascículo
Out 2011
Histórico
-
Recebido
26 Set 2009 -
Aceito
02 Maio 2011