Abstracts
In the last two centuries, papers have been published including measurements of the germination process. High diversity of mathematical expressions has made comparisons between papers and some times the interpretation of results difficult. Thus, in this paper is included a review about measurements of the germination process, with an analysis of the several mathematical expressions included in the specific literature, recovering the history, sense, and limitations of some germination measurements. Among the measurements included in this paper are the germinability, germination time, coefficient of uniformity of germination (CUG), coefficient of variation of the germination time (CVt), germination rate (mean rate, weighted mean rate, coefficient of velocity, germination rate of George, Timson’s index, GV or Czabator’s index; Throneberry and Smith’s method and its adaptations, including Maguire’s rate; ERI or emergence rate index, germination index, and its modifications), uncertainty associated to the distribution of the relative frequency of germination (U), and synchronization index (Z). The limits of the germination measurements were included to make the interpretation and decisions during comparisons easier. Time, rate, homogeneity, and synchrony are aspects that can be measured, informing the dynamics of the germination process. These characteristics are important not only for physiologists and seed technologists, but also for ecologists because it is possible to predict the degree of successful of a species based on the capacity of their harvest seed to spread the germination through time, permitting the recruitment in the environment of some part of the seedlings formed.
germinability; germination rate; germination synchrony; germination time; germination uniformity
Nos dois últimos séculos, trabalhos têm sido publicados incluindo medidas do processo de germinação. A diversidade das expressões matemáticas existente na literatura tem tornado difícil comparações entre os trabalhos e, algumas vezes, a interpretação dos resultados. Assim, este trabalho apresenta uma revisão sobre medidas de germinação, incluindo a análise de várias expressões matemáticas contidas na literatura específica. Entre as medidas analisadas estão a germinabilidade, tempo de germinação, coeficiente de uniformidade de germinação (CUG), coeficiente de variação do tempo de germinação (CVt), velocidade de germinação (velocidade média, velocidade média ponderada, coeficiente de velocidade, velocidade de germinação de George, índice de Timson, GV ou índice de Czabator; método de Throneberry e Smith e suas adaptações, incluindo a velocidade de Maguire; ERI ou índice de velocidade de emergência, índice de germinação e suas modificações), incerteza associada à distribuição das freqüências relativas de germinação (U) e índice de sincronia (Z). Os limites dessas medidas foram incluídos para facilitar a interpretação e a tomada de decisões durante as comparações. Tempo, velocidade, homogeneidade e sincronia são aspectos que podem ser medidos, e que informam a dinâmica do processo de germinação. Essas características são interessantes não somente para fisiólogos e tecnologistas de sementes, mas também para ecólogos, uma vez que é possível predizer o grau de sucesso das espécies, com base na capacidade da safra de sementes em distribuir a germinação através do tempo, permitindo o recrutamento no ambiente de parte das plântulas formadas.
germinabilidade; sincronia de germinação; tempo de germinação; uniformidade de germinação; velocidade de germinação
REVIEW PAPER ARTIGO DE REVISÃO
How and why to measure the germination process?
Como e por que medir o processo de germinação?
Marli A. RanalI,1 1 Corresponding author: ranal@ufu.br ; Denise Garcia de SantanaII
IUniversidade Federal de Uberlândia, Instituto de Biologia, Caixa Postal 593, 38400-902 Uberlândia, MG, Brasil
IIUniversidade Federal de Uberlândia, Instituto de Ciências Agrárias, Caixa Postal 593, 38400-902 Uberlândia, MG, Brasil
ABSTRACT
In the last two centuries, papers have been published including measurements of the germination process. High diversity of mathematical expressions has made comparisons between papers and some times the interpretation of results difficult. Thus, in this paper is included a review about measurements of the germination process, with an analysis of the several mathematical expressions included in the specific literature, recovering the history, sense, and limitations of some germination measurements. Among the measurements included in this paper are the germinability, germination time, coefficient of uniformity of germination (CUG), coefficient of variation of the germination time (CVt), germination rate (mean rate, weighted mean rate, coefficient of velocity, germination rate of George, Timsons index, GV or Czabators index; Throneberry and Smiths method and its adaptations, including Maguires rate; ERI or emergence rate index, germination index, and its modifications), uncertainty associated to the distribution of the relative frequency of germination (U), and synchronization index (Z). The limits of the germination measurements were included to make the interpretation and decisions during comparisons easier. Time, rate, homogeneity, and synchrony are aspects that can be measured, informing the dynamics of the germination process. These characteristics are important not only for physiologists and seed technologists, but also for ecologists because it is possible to predict the degree of successful of a species based on the capacity of their harvest seed to spread the germination through time, permitting the recruitment in the environment of some part of the seedlings formed.
Key words: germinability, germination rate, germination synchrony, germination time, germination uniformity
RESUMO
Nos dois últimos séculos, trabalhos têm sido publicados incluindo medidas do processo de germinação. A diversidade das expressões matemáticas existente na literatura tem tornado difícil comparações entre os trabalhos e, algumas vezes, a interpretação dos resultados. Assim, este trabalho apresenta uma revisão sobre medidas de germinação, incluindo a análise de várias expressões matemáticas contidas na literatura específica. Entre as medidas analisadas estão a germinabilidade, tempo de germinação, coeficiente de uniformidade de germinação (CUG), coeficiente de variação do tempo de germinação (CVt), velocidade de germinação (velocidade média, velocidade média ponderada, coeficiente de velocidade, velocidade de germinação de George, índice de Timson, GV ou índice de Czabator; método de Throneberry e Smith e suas adaptações, incluindo a velocidade de Maguire; ERI ou índice de velocidade de emergência, índice de germinação e suas modificações), incerteza associada à distribuição das freqüências relativas de germinação (U) e índice de sincronia (Z). Os limites dessas medidas foram incluídos para facilitar a interpretação e a tomada de decisões durante as comparações. Tempo, velocidade, homogeneidade e sincronia são aspectos que podem ser medidos, e que informam a dinâmica do processo de germinação. Essas características são interessantes não somente para fisiólogos e tecnologistas de sementes, mas também para ecólogos, uma vez que é possível predizer o grau de sucesso das espécies, com base na capacidade da safra de sementes em distribuir a germinação através do tempo, permitindo o recrutamento no ambiente de parte das plântulas formadas.
Palavras-chave: germinabilidade, sincronia de germinação, tempo de germinação, uniformidade de germinação, velocidade de germinação
Introduction
During the last two centuries, several methods and mathematical expressions to measure the germination process have been proposed or discussed (Czabator 1962, Nichols & Heydecker 1968, Goodchild & Walker 1971, Heydecker 1973, Labouriau 1983a, Scott et al. 1984, Brown & Mayer 1988, Hilhorst & Karssen 1988, Carneiro et al. 1993, Bewley & Black 1994, Santana & Ranal 2004). It is wholesome and welcome, but the diversity of expressions has made comparisons difficult. Several of these expressions have the same name, measuring different characteristics of the germination process, some of them have the same meaning, although expressed using different symbols, while different mathematical expressions are used to measure the same characteristic. Besides, some practical attempts were also proposed to analyse the germination process, associating rate and capacity in generic expressions. As pointed out by Bewley & Black (1994), the attempts to incorporate two distinct characteristics of the germination process in the same mathematical expression are not entirely satisfactory.
Despite this diversity, several papers have discussed results based only on germinability and the behaviour of seeds during the germination process has several quantitative aspects that must be considered (Labouriau 1983a, Brown & Mayer 1988, Bewley & Black 1994). Time, rate, homogeneity, and synchrony are important aspects that can be measured, informing the dynamics of this process. These characteristics are important not only for physiologists and seed technologists, but also for ecologists because it is possible to predict the degree of success of a species based on the capacity of their harvest seed to spread the germination through time, permitting the recruitment in the environment of some part of the seedlings formed.
Thus, in this review the history, the sense, and limitations of some germination measurements were recovered and discussed. Mathematical expressions were adequate to the actual notation.
Measurement of germination capacity
As pointed out by Bewley & Black (1994), the term germination is often used loosely and sometimes incorrectly, being confounded with seedling growth, which begins when germination finishes. The global germination process is constituted by three partial processes, including the imbibition, the activation process, and intra-seminal growth that is completed with embryo protrusion (Labouriau 1983a). In the practical sense, it is difficult to establish the beginning and the end of each partial process because molecular and cellular events are involved in a multicellular and complex tissue and the reactivation of the process is gradual. Thus, the precision in determining the exact moment of the beginning of the germination process by means of some molecular or cellular criterion is substituted by macroscopic criteria, such as embryo protrusion, that confers some rigor because the same reference point can be used by several people. As was appropriately written by Bewley & Black (1994), the only stage of germination that can time fairly precisely is its termination. In this manner, the establishment of an easy and common criterion was important because in the absence of this common point, the germination capacity could be under or overestimated, decreasing the chance of comparing results among laboratories and increasing contradictory information about the species.
The germination capacity of one seed, based on a binary answer (germinated/non germinated), is one qualitative attribute of the germination process, generally converted in a quantitative attribute, commonly percentage. According to Labouriau (1983a), germinability of one seed sample is the percentage of seeds in which the germination process reaches the end, in the experimental conditions, by means of the intra-seminal growth that results in the protrusion (or emergence) of one live embryo. In general, it is presented as percentage, accompanied by some dispersion measurement, but it is possible to use proportion rather than percentage, and the proportion values for one or several samples can be submitted to statistical tests (Carvalho et al. 2005). As the majority of papers include the germinability through time or at the end of the observations, it should be clear that its importance, meaning, and method of calculation are a consensus among researchers.
Measurements of germination time
The time for the first germination (to) that expresses the time of germination of the faster seeds has been used by some authors since 1865 (Edwards 1932, Czabator 1962, Goloff & Bazzaz 1975, Labouriau 1983a, Ranal 1999, Quintanilla et al. 2000). According to Labouriau (1983a), when used alone, it is an excessive simplification, since this method disregards the behaviour of the majority of seeds of one sample. The use of the two extreme times, time for the first germination (to) and time for the last germination (tg) was proposed in 1878 (Edwards 1932), perhaps to correct the partiality expressed when only to is used, although this method is also limited, concentrating its attention only on the slower and faster seeds (Labouriau 1983a).
A more efficient method to solve this inconvenience is to use measurements of central tendency. Among them is the median, used in the context of germination since 1913 (Czabator 1962, Thompson 1970, Simon et al. 1976, Scott et al. 1984, Drake 1993, Ranal 1999) to study the time for 50% of germination (t1/2). If the frequency distribution of germination is symmetric, the mean time and the median time can be used to express central tendency of the data. On the other hand, if distribution is asymmetric, mean and median are distant, with the mean located in the tails of distribution where there are smaller frequencies and, in this case, the median is more representative then the mean, as discussed by Costa Neto (1977). The modal time is the point of the distribution in which the highest frequency of germinated seeds is observed. It represents the peak of germination, although sometimes it is not unique. There are seed samples whose distributions present two or more peaks of germination (germination with polymodal time) and, in this case, this measurement is inadequate to synthetize the information.
Labouriau and collaborators used in their papers the mean germination time ( ), proposed by Haberlandt in 1875 (Labouriau 1983a). It is calculated as the weighted mean of the germination time. The number of seeds germinated in the intervals of time established for data collection is used as weight. In this case, the use of the weighted mean is indispensable, since it considers that a different number of seeds germinate each time. In this manner,
), proposed by Haberlandt in 1875 (Labouriau 1983a). It is calculated as the weighted mean of the germination time. The number of seeds germinated in the intervals of time established for data collection is used as weight. In this case, the use of the weighted mean is indispensable, since it considers that a different number of seeds germinate each time. In this manner,  , where ti: time from the start of the experiment to the ith observation (day or hour); ni: number of seeds germinated in the time i (not the accumulated number, but the number correspondent to the ith observation), and k: last time of germination. This measurement was mentioned by Czabator (1962) as mean length of incubation time. According to the author, it is a measurement of the average length of time required for maximum germination of a seed lot, and is expressed in terms of the same units of time used in making germination counts (hours or days). It was denoted as MLIT= (G1T1 + G2T2 +...+ GnTn) / (G1 + G2 +...+ Gn), where G: germination count on any counting period; T: time. For Czabator (1962), the expression of MLIT apparently has been used since 1875. Probably it was used by Haberlandt since this year as the mean germination time mentioned by Labouriau (1983a). The variance of germination time is given by
, where ti: time from the start of the experiment to the ith observation (day or hour); ni: number of seeds germinated in the time i (not the accumulated number, but the number correspondent to the ith observation), and k: last time of germination. This measurement was mentioned by Czabator (1962) as mean length of incubation time. According to the author, it is a measurement of the average length of time required for maximum germination of a seed lot, and is expressed in terms of the same units of time used in making germination counts (hours or days). It was denoted as MLIT= (G1T1 + G2T2 +...+ GnTn) / (G1 + G2 +...+ Gn), where G: germination count on any counting period; T: time. For Czabator (1962), the expression of MLIT apparently has been used since 1875. Probably it was used by Haberlandt since this year as the mean germination time mentioned by Labouriau (1983a). The variance of germination time is given by  , where
, where  : mean germination time; ti: time between the start of the experiment and the ith observation (day or hour); ni: number of seeds germinated in the time i, and k: last time of germination. The standard deviation is calculated by st =
: mean germination time; ti: time between the start of the experiment and the ith observation (day or hour); ni: number of seeds germinated in the time i, and k: last time of germination. The standard deviation is calculated by st =  . The standard error of the mean germination time is another important measurement of variability and is adequate to measure the accuracy of the calculation of the mean germination time. Thus,
. The standard error of the mean germination time is another important measurement of variability and is adequate to measure the accuracy of the calculation of the mean germination time. Thus,  , where st: standard deviation of the germination time; ni: number of seeds germinated in the time i, and k: last time of germination. Labouriau and collaborators used the values of the confidence intervals to measure the dispersion of mean germination time and to visualize statistical differences between samples or treatments. For the confidence interval the expression is
, where st: standard deviation of the germination time; ni: number of seeds germinated in the time i, and k: last time of germination. Labouriau and collaborators used the values of the confidence intervals to measure the dispersion of mean germination time and to visualize statistical differences between samples or treatments. For the confidence interval the expression is  ± e, being e = ta/2;v
± e, being e = ta/2;v  , were
, were  : mean germination time; t: critical value of the "Student" distribution for the significance a/2 and v =
: mean germination time; t: critical value of the "Student" distribution for the significance a/2 and v =  -1 = degrees of freedom, and
-1 = degrees of freedom, and  : standard error of the mean germination time.
: standard error of the mean germination time.
Edmond & Drapala (1958) used an expression denoted by them as mean days for emergence and expressed by Mdays = (N1G1 + N2G2 +...+ NnGn)/(G1 + G2 +...+ Gn), where G1, G2,..., Gn: number of seedlings emerged on the day of observation and N1, N2,..., Nn: number of days counted since the day of sowing until the day of observation. This expression is the mean germination time with different notation. If this expression were to be written in summation, it would be given by Mdays =  , that is the mean germination time, used to evaluate seedling emergence.
, that is the mean germination time, used to evaluate seedling emergence.
Measurements of germination rate
Among the germination measurements, rate has received especial attention of the researchers. According to Labouriau (1983a), the first idea of germination rate was expressed by Kotowski (1926). The author presented the coefficient of velocity for 17 cultivated species, using the expression as coefficient of velocity = 100 (A1 + A2 +...+ Ax)/(A1T1 + A2T2 +...+ AxTx), where A1, A2,..., Ax: number of seedlings counted on the first day, second day, and so on until the last day (c), and T1, T2,..., Tx: number of days between sowing and the first collection, between the sowing and the second collection, and so on until the last collection (c).
Czabator (1962) mentioned that this coefficient of velocity is the reciprocal of the mean length of incubation time (MLIT), whose quotient is multiplied by 100. As Kotowski (1926) wrote that the value of the coefficient of velocity increases when the number of seedlings increases, this information brought several authors to consider this characteristic as a negative point for this coefficient, limiting its use. However, the number of seeds germinated (or seedlings emerged) is only a weight of this measurement. Thus, the coefficient of velocity is free from the influence of the number of seeds germinated (or seedlings emerged) in the samples or treatments. This mistake was noted by Brown & Mayer (1988) when they analyzed the Kotowskis coefficient of velocity and related methods. According to them, CV is really only the reciprocal of the average germination time, and so is independent of the extent of germination. These authors considered that the usefulness of CV is further limited by its failure to provide any information on the spread of germination.
Later, Nichols & Heydecker (1968) presented the coefficient of velocity of Kotowski as coefficient of velocity of germination, denoting it as CVG =  , where fi: number of seeds newly germinating on day i; ci: number of days from sowing, and k: last day of germination. Nichols & Heydecker (1968) also observed that the CVG is a reciprocal of the mean germination time. Then, Labouriau (1970) demonstrated that the coefficient of velocity of Kotowski (1926) could be used to calculate the mean germination rate as
, where fi: number of seeds newly germinating on day i; ci: number of days from sowing, and k: last day of germination. Nichols & Heydecker (1968) also observed that the CVG is a reciprocal of the mean germination time. Then, Labouriau (1970) demonstrated that the coefficient of velocity of Kotowski (1926) could be used to calculate the mean germination rate as  = CV/100 = 1/
= CV/100 = 1/ , where
, where  : mean germination time, and CV: coefficient of velocity. In this manner, the mean germination rate (
: mean germination time, and CV: coefficient of velocity. In this manner, the mean germination rate ( ) is defined as reciprocal of the mean germination time, since the mean rate increases and decreases with 1/
) is defined as reciprocal of the mean germination time, since the mean rate increases and decreases with 1/ , not with
, not with  (Labouriau 1983b). As the distribution of the reciprocal of time is unknown, the variance of the rate is approximated. Labouriau (1983b) presented in detail the development of the function j (t) = 1/t, according to the expansion in Taylor series, suggesting a correction to the expression of the variance of the germination rate given by Heydecker (1973). Thus, the variance proposed for rate is
(Labouriau 1983b). As the distribution of the reciprocal of time is unknown, the variance of the rate is approximated. Labouriau (1983b) presented in detail the development of the function j (t) = 1/t, according to the expansion in Taylor series, suggesting a correction to the expression of the variance of the germination rate given by Heydecker (1973). Thus, the variance proposed for rate is  , where
, where  : variance of germination time and
: variance of germination time and  : mean germination rate (Labouriau 1983b).
: mean germination rate (Labouriau 1983b).
Sometimes the sense of  , a pure rate measurement without the interference of the germinability, is difficult to understand because it is a non-linear measurement of rate. It is similar to that used to measure velocity of chemical reactions (molecules per time unity). It seems compatible with germination process which is a result of a series of chemical reactions inside metabolic complex routes. In physics, frequency is the reciprocal of period. As period is the interval of time to complete one cycle, frequency is the reciprocal of time (f = 1/T, where T: period). It is the well known concept of hertz (1/s = Hz, where s: second) that means cycle per second or the reciprocal of second (s-1). In this sense,
, a pure rate measurement without the interference of the germinability, is difficult to understand because it is a non-linear measurement of rate. It is similar to that used to measure velocity of chemical reactions (molecules per time unity). It seems compatible with germination process which is a result of a series of chemical reactions inside metabolic complex routes. In physics, frequency is the reciprocal of period. As period is the interval of time to complete one cycle, frequency is the reciprocal of time (f = 1/T, where T: period). It is the well known concept of hertz (1/s = Hz, where s: second) that means cycle per second or the reciprocal of second (s-1). In this sense,  is a frequency, since it is the reciprocal of the mean germination time, being expressed in hour-1 or day-1.
is a frequency, since it is the reciprocal of the mean germination time, being expressed in hour-1 or day-1.
In the same way, it is possible to calculate the germination rate as the reciprocal of the median time (Went 1957, apud Labouriau 1983a). Thus, v1/2 = 1/t1/2, where t1/2: time for 50% of germination. The use of this expression is not common because its interpretation is more difficult than the mean. Moreover, the variance and the standard deviation calculated in relation to the median present higher values than when they are calculated in relation to the mean. According to Labouriau (1983a), this inconvenience for the use of median was pointed out by Dixon & Massey (1969).
Another alternative to measure the germination rate is to calculate the weighted mean germination rate, using the mean germination rate of each replication of one treatment (or sample) and its variance (Labouriau, 1983c). It can be denoted as  , for wj = nj /
, for wj = nj / , where wj : weight of the jth replication;
, where wj : weight of the jth replication;  : mean germination rate of the jth replication; nj: number of seeds germinated in the jth replication;
: mean germination rate of the jth replication; nj: number of seeds germinated in the jth replication;  : variance of the germination rate of the jth replication, and r: number of replications or sample size (n). This weighted mean germination rate is more representative than the unweighted rate (
: variance of the germination rate of the jth replication, and r: number of replications or sample size (n). This weighted mean germination rate is more representative than the unweighted rate ( or
or  ), since it considers and detaches differences between equal mean rate that present different variances (Labouriau & Osborn 1984). Although
), since it considers and detaches differences between equal mean rate that present different variances (Labouriau & Osborn 1984). Although  is a single mean, unaccompanied by dispersion values, it can be used for comparisons because its mathematical expression includes the variances of the samples or replications involved in its calculation. Thus, its use in the last decades is justifiable, once the statistics programs for computers were scarce. As presently data are more easily processed, the values of
is a single mean, unaccompanied by dispersion values, it can be used for comparisons because its mathematical expression includes the variances of the samples or replications involved in its calculation. Thus, its use in the last decades is justifiable, once the statistics programs for computers were scarce. As presently data are more easily processed, the values of  for the replications of each treatment can be submitted to the conventional multisample and pairwise comparisons.
for the replications of each treatment can be submitted to the conventional multisample and pairwise comparisons.
Mixed measurements of germination rate
Timson (1965) suggested a measurement named by him as "ten summation" (S 10). According to the author, this measurement was defined based on the number of days required for seeds of weed species to complete the germination process. In his proposal Timson (1965) presented only a theoretical explanation without any mathematical expression. According to Nichols & Heydecker (1968), this index was originally proposed by George in 1961 as "germination rate". Goodchild & Walker (1971) denoted this index as  , where gi: germination in time interval i (i varying from 1 to t); t: total number of time intervals, being j = i 1. Goodchild & Walker (1971) emphasized that T cannot be of universal application. As it combines germination rate with the final germination percentage, it is useful for comparisons only when samples have equal germinabilities. Brown & Mayer (1988) wrote clearly that Timson (1965) proposed an index of germination based on the progressive total of daily cumulative germination over 10 days, with supplementary totals over other periods being quoted as S 5 for five days, S 20 for 20 days, and so on. The same understanding was given by Baskin & Baskin (1998) who expressed this index as S n = S gi(t - j), where n is the cumulative daily germination percentage for each day of the study. It means that , i. e., in the first term of this equality the germinability (n) is cumulative as written by Baskin & Baskin (1998) and in the second term the germinability is partial (gi) as written by Goodchild & Walker (1971). These two expressions, producing the same value, can carry doubts in relation to the use of partial or cumulative germinabilities. According to Tucker & Wright (1965), George proposed a method which involves the sum of the products between the number of seeds germinated and days remaining until completion of the germination test. This method produces a number ranging from NK down to N, where N is the number of seeds included in the test, and K the number of days until the end of the test. Timson (1965) changed the number of seeds germinated proposed by George per percentage of germination. Certainly, the use of percentage of germination is better than number of seeds germinated because the transformation to percentage cancels the effect of the sample size. Allan et al. (1962) described a measurement, denoted by them as ERI, that is exactly the description of the George method. Labouriau (personal communication) proposed to divide both members of the expression denoted by Goodchild & Walker (1971) as Timson index, by the sum of partial germinabilities (gi); thus,Tmod = T /
, where gi: germination in time interval i (i varying from 1 to t); t: total number of time intervals, being j = i 1. Goodchild & Walker (1971) emphasized that T cannot be of universal application. As it combines germination rate with the final germination percentage, it is useful for comparisons only when samples have equal germinabilities. Brown & Mayer (1988) wrote clearly that Timson (1965) proposed an index of germination based on the progressive total of daily cumulative germination over 10 days, with supplementary totals over other periods being quoted as S 5 for five days, S 20 for 20 days, and so on. The same understanding was given by Baskin & Baskin (1998) who expressed this index as S n = S gi(t - j), where n is the cumulative daily germination percentage for each day of the study. It means that , i. e., in the first term of this equality the germinability (n) is cumulative as written by Baskin & Baskin (1998) and in the second term the germinability is partial (gi) as written by Goodchild & Walker (1971). These two expressions, producing the same value, can carry doubts in relation to the use of partial or cumulative germinabilities. According to Tucker & Wright (1965), George proposed a method which involves the sum of the products between the number of seeds germinated and days remaining until completion of the germination test. This method produces a number ranging from NK down to N, where N is the number of seeds included in the test, and K the number of days until the end of the test. Timson (1965) changed the number of seeds germinated proposed by George per percentage of germination. Certainly, the use of percentage of germination is better than number of seeds germinated because the transformation to percentage cancels the effect of the sample size. Allan et al. (1962) described a measurement, denoted by them as ERI, that is exactly the description of the George method. Labouriau (personal communication) proposed to divide both members of the expression denoted by Goodchild & Walker (1971) as Timson index, by the sum of partial germinabilities (gi); thus,Tmod = T /  . This proposition minimizes the effect of the final germination percentage and then the Timson index can measure the germination rate with some precision.
. This proposition minimizes the effect of the final germination percentage and then the Timson index can measure the germination rate with some precision.
Czabator (1962) proposed other index named by him as "germination value" and expressed as GV = PV MDG, where PV: peak value of germination, and MDG: mean daily germination, which is the mean number of seeds germinating per day. The value of PV represents the maximum cumulative germination percentage divided by the number of days to reach this percentage. In the interpretation of Brown & Mayer (1988), this index is an expression of speed and totality of germination, and their interaction. According to these authors, the values of PV and MDG can be counterbalanced, resulting in equal values for GV for samples or treatments with different behaviour in relation to germination process.
Maguire (1962) presented the germination rate for field or laboratory conditions to evaluate the seedlings vigour. According to the author, the method is an adaptation of the daily counting method used by some researchers, like Throneberry & Smith (1955), for determination of the seedlings vigour. In fact, Maguire (1962) gave a generic mathematical expression for the method presented by Throneberry & Smith (1955) that permits one to obtain the measurement for any intervals of time. The mathematical expression is given by  .
.
High values obtained using this expression mean higher seedling vigour of one sample in relation to another. In seed technology this value, named index of velocity of germination or emergence, is used to predict the relative vigour of samples, especially for cultivated species, since samples with the same quantity of seeds germinated can present different values for this index. Although Maguire (1962) had not presented the unit of this measurement, the value calculated using the expression proposed denotes a number of normal seedlings per day.
According to Brown & Mayer (1988), the Maguires index is a time-weighted cumulative germination that measures the speed of germination and quantifies the seedling vigour, being expressed as Tmod = T /  , where Gi: percentage of seedlings that germinated during the time interval tiand n: last day of germination. In their comments, the authors inform that there is confusion about what this expression measures, since the expression is not arithmetically equivalent to any accepted measurement of germination rate. The use of percentage of seedlings proposed by Bouton and collaborators in 1976, as commented by Brown & Mayer (1988), is important because it cancels the effect of the sample size. In spite of this modification, the value obtained using this expression is influenced by the total number of seeds that germinated in the experimental conditions. Thus, it is useful for comparisons only when samples or treatments present the same germinabilities.
, where Gi: percentage of seedlings that germinated during the time interval tiand n: last day of germination. In their comments, the authors inform that there is confusion about what this expression measures, since the expression is not arithmetically equivalent to any accepted measurement of germination rate. The use of percentage of seedlings proposed by Bouton and collaborators in 1976, as commented by Brown & Mayer (1988), is important because it cancels the effect of the sample size. In spite of this modification, the value obtained using this expression is influenced by the total number of seeds that germinated in the experimental conditions. Thus, it is useful for comparisons only when samples or treatments present the same germinabilities.
Another modification of the method presented by Throneberry & Smith (1955) was presented by Kendrick & Frankland (1969) that proposed a germination index  for comparisons of germination times, expressed as
for comparisons of germination times, expressed as  = S(1/t) where t: time for each seed to germinate. Apparently this expression does not have any relation to the method presented by Throneberry & Smith (1955) and Maguire (1962). Nevertheless, when n1, n2, n3, ..., nk seeds germinated on the first day, second, third, and kth days, the expression could be written as
= S(1/t) where t: time for each seed to germinate. Apparently this expression does not have any relation to the method presented by Throneberry & Smith (1955) and Maguire (1962). Nevertheless, when n1, n2, n3, ..., nk seeds germinated on the first day, second, third, and kth days, the expression could be written as  that is in itself the Throneberry and Smiths method, adopted by Maguire (1962).
that is in itself the Throneberry and Smiths method, adopted by Maguire (1962).
The emergence rate index proposed by Shmueli & Goldberg (1971) is given by  , where Xn: number of emerged seedlings per linear meter, counted on the day n; c: number of days counted from sowing until the end of the emergence; n: day of the counting, expressed as number of days after sowing, and no: day when the emergence started, expressed as number of days after sowing. Allan et al. (1962) used this name and abbreviation to nominate another mathematical expression, as was commented previously. The value of ERI can be divided by total number of emerged seedlings (or germinated seeds), to minimize the effect of germinability (Santana & Ranal 2004). Then, the new expression is
, where Xn: number of emerged seedlings per linear meter, counted on the day n; c: number of days counted from sowing until the end of the emergence; n: day of the counting, expressed as number of days after sowing, and no: day when the emergence started, expressed as number of days after sowing. Allan et al. (1962) used this name and abbreviation to nominate another mathematical expression, as was commented previously. The value of ERI can be divided by total number of emerged seedlings (or germinated seeds), to minimize the effect of germinability (Santana & Ranal 2004). Then, the new expression is  .
.
The germination index proposed by Melville et al. (1980) was expressed by  , where n: number of germination counting (days, hours or other type of time unit); : total number of days spent in the germination test plus 1; Di: number of days until the ith reading; Gi: number of normal seeds germinated in the ith day, and S: total number of seeds used in the test. It means that non germinated seeds are included in the calculus. The S value of the GI expression, index proposed by Melville et al. (1980), can be replaced by the number of seeds germinated at the end of the experiment to cancel the effect of the seed sample size (Santana & Ranal 2004).
, where n: number of germination counting (days, hours or other type of time unit); : total number of days spent in the germination test plus 1; Di: number of days until the ith reading; Gi: number of normal seeds germinated in the ith day, and S: total number of seeds used in the test. It means that non germinated seeds are included in the calculus. The S value of the GI expression, index proposed by Melville et al. (1980), can be replaced by the number of seeds germinated at the end of the experiment to cancel the effect of the seed sample size (Santana & Ranal 2004).
General considerations about rate germination measurements
One important aspect in relation to these rate measurements is that when the quantity of seeds that completed the germination process is similar among treatments, all rate measurements have similar accuracy. On the contrary, when germinabilities are different among treatments, high values of G increase values of all mixed rate measurements because they include germination capacity and rate in the same mathematical expression. Negligible to low correlation (sensu Davis 1971) between  and germinability, obtained by simulations on a set data show that the first is not influenced by the second. Very high correlation sensu Davis (1971) between germinability and each one of the mixed rate measurements obtained for the same set data show the influence of the germinability on these measurements. It means that germinability and germination rate are counterbalanced in these indices. These associations were demonstrated for the first time for Myracrodruon urundeuva Allemão diaspores (Dorneles et al. 2005). As pointed out by Goodchild & Walker (1971) and Brown & Mayer (1988), this inherent ambiguity is the greatest weakness in Timsons method. As the idea of these measurements is the same, this observation is valid for all mixed measurements.
and germinability, obtained by simulations on a set data show that the first is not influenced by the second. Very high correlation sensu Davis (1971) between germinability and each one of the mixed rate measurements obtained for the same set data show the influence of the germinability on these measurements. It means that germinability and germination rate are counterbalanced in these indices. These associations were demonstrated for the first time for Myracrodruon urundeuva Allemão diaspores (Dorneles et al. 2005). As pointed out by Goodchild & Walker (1971) and Brown & Mayer (1988), this inherent ambiguity is the greatest weakness in Timsons method. As the idea of these measurements is the same, this observation is valid for all mixed measurements.
Among the rate measurements here discussed, CV, CVG, v1/2,  ,
,  , GV, Rate, GR, and
, GV, Rate, GR, and  measure the germination frequency. Timsons index, Tmod, ERI, ERImod, GI, and GImod do not have this characteristic and the germination frequency is substituted by the time in decreasing order. Thus, to the faster seeds a weight corresponding to the greater time is attributed.
measure the germination frequency. Timsons index, Tmod, ERI, ERImod, GI, and GImod do not have this characteristic and the germination frequency is substituted by the time in decreasing order. Thus, to the faster seeds a weight corresponding to the greater time is attributed.
Measurements of uniformity of germination
The coefficient of uniformity of germination measures the variability among seeds in relation to the mean germination time of the sample (Heydecker 1973, Bewley & Black 1994) and is expressed by
where ni : number of seeds germinated on the ith day and Di : number of days counted from the day of sowing to the collection of the datum (i). It is important to note that CRG is the Kotowskis coefficient of velocity with a different mathematical notation, and  the mean germination time. This mathematical expression is the reciprocal of the variance of the germination time, exc ept the "-1" that appears in the expression of variance as the degrees of freedom of the measurement. If CUG was expressed as variance, high values would indicate germination spread over time. Certainly the author had the intention that this expression would have a direct interpretation on the sense that high values would be associated with concentrated germination in time. Thus, it is important that it be expressed as a reciprocal measurement of variance, given information about the uniformity of seeds in relation to the germination process. This coefficient can be applied only if the germination frequencies have normal distribution (Heydecker 1973, Bewley & Black 1994). This is a limitation because, in general, seeds in germination process show some deviation from normality in their behaviour in relation to time. Another limitation for the use of this measurement is that the mean germination time of samples or treatments must be the same for comparisons. This is the same limitation associated with variances and standard deviations because the variability measured by them depends on the magnitude of the mean.
the mean germination time. This mathematical expression is the reciprocal of the variance of the germination time, exc ept the "-1" that appears in the expression of variance as the degrees of freedom of the measurement. If CUG was expressed as variance, high values would indicate germination spread over time. Certainly the author had the intention that this expression would have a direct interpretation on the sense that high values would be associated with concentrated germination in time. Thus, it is important that it be expressed as a reciprocal measurement of variance, given information about the uniformity of seeds in relation to the germination process. This coefficient can be applied only if the germination frequencies have normal distribution (Heydecker 1973, Bewley & Black 1994). This is a limitation because, in general, seeds in germination process show some deviation from normality in their behaviour in relation to time. Another limitation for the use of this measurement is that the mean germination time of samples or treatments must be the same for comparisons. This is the same limitation associated with variances and standard deviations because the variability measured by them depends on the magnitude of the mean.
To solve this inconveniency, the coefficient of variation of the germination time was proposed to evaluate the germination uniformity or variability in relation to the mean germination time and was applied to seeds of Myracrodruon urundeuva Allemão (Dorneles et al. 2005) and Anacardium humile A. St.-Hil. (Carvalho et al. 2005). It is calculated as  , where st: standard deviation of the germination time and
, where st: standard deviation of the germination time and  : mean germination time. The unit of CVt (%) is easier to interpret than the unit of the coefficient of uniformity of germination (day-2). This inconvenience of the CUG unit is the same related to variances, as commented above. Another important point is that the CVt is a relative dispersion measurement that permits comparisons, independently of the magnitude of the mean germination time.
: mean germination time. The unit of CVt (%) is easier to interpret than the unit of the coefficient of uniformity of germination (day-2). This inconvenience of the CUG unit is the same related to variances, as commented above. Another important point is that the CVt is a relative dispersion measurement that permits comparisons, independently of the magnitude of the mean germination time.
Measurements of germination synchrony
As seed germination, in general, is assynchronized, it is possible to quantify this characteristic by means of a measurement named synchronization index ( ), uncertainty associated to the distribution of the relative frequency of germination (U), or informational entropy (H), expressed by Labouriau & Valadares (1976) as
), uncertainty associated to the distribution of the relative frequency of germination (U), or informational entropy (H), expressed by Labouriau & Valadares (1976) as  , being
, being  , where fi: relative frequency of germination; ni: number of seeds germinated on the day i, and k: last day of observation. This expression was proposed by Shannon in 1948 to measure the informational entropy or uncertainty associated to the frequency distribution fi = j (t) (Labouriau 1983a). This expression is used by ecologists to measure the diversity of one environment (Magurran 1988). Thus, high values for this index indicate high diversity and numbers in direction of zero indicate low diversity. When applied to seed germination, the conventional interpretation is in the opposite direction, that is, low values indicate more synchronized germination. The use and sense of this measurement for seed germination were clearly demonstrated by Labouriau & Pacheco (1978) for seeds of Dolichos biflorus L., using several frequency polygons with relative frequencies of germination as functions of the time of isothermal incubation of the seeds. The unit of this index is bit, since log2 is used (Labouriau & Valadares 1976, Labouriau 1983a, Magurran 1988). Each bit is a binary measurement that counts, in this case, germinated/non germinated. Thus, the transformation of the germination frequencies (fi) for each time of observation (ti) in the logaritm of the frequency in base 2 (log2fi) transform a binary measurement (bit) in a weigh. In this manner, log2fi is the weigh of each frequency registered, being expressed as fi log2fi. The maximum limit of the Shannon index is the log of the total number of species established in a given area (Hutcheson 1970). For seeds, this limit is thelog2 of S ni, that is, the log2 of the total number of seeds germinated in a given condition.
, where fi: relative frequency of germination; ni: number of seeds germinated on the day i, and k: last day of observation. This expression was proposed by Shannon in 1948 to measure the informational entropy or uncertainty associated to the frequency distribution fi = j (t) (Labouriau 1983a). This expression is used by ecologists to measure the diversity of one environment (Magurran 1988). Thus, high values for this index indicate high diversity and numbers in direction of zero indicate low diversity. When applied to seed germination, the conventional interpretation is in the opposite direction, that is, low values indicate more synchronized germination. The use and sense of this measurement for seed germination were clearly demonstrated by Labouriau & Pacheco (1978) for seeds of Dolichos biflorus L., using several frequency polygons with relative frequencies of germination as functions of the time of isothermal incubation of the seeds. The unit of this index is bit, since log2 is used (Labouriau & Valadares 1976, Labouriau 1983a, Magurran 1988). Each bit is a binary measurement that counts, in this case, germinated/non germinated. Thus, the transformation of the germination frequencies (fi) for each time of observation (ti) in the logaritm of the frequency in base 2 (log2fi) transform a binary measurement (bit) in a weigh. In this manner, log2fi is the weigh of each frequency registered, being expressed as fi log2fi. The maximum limit of the Shannon index is the log of the total number of species established in a given area (Hutcheson 1970). For seeds, this limit is thelog2 of S ni, that is, the log2 of the total number of seeds germinated in a given condition.
Z index was proposed to evaluate the degree of overlapping in flowering among individuals of one population. Adopting the idea expressed by Primack (1980), the synchrony of one seed with another included in the same replication of one treatment is defined as  , being
, being  and N = Sni (Sni - 1) / 2, where
and N = Sni (Sni - 1) / 2, where  : combination of the seeds germinated in the time i, two together, and ni: number of seeds germinated in the time i. Then, Z = 1 when the germination of all seeds occur at the same time and Z = 0 when at least two seeds could germinate, one at each time.
: combination of the seeds germinated in the time i, two together, and ni: number of seeds germinated in the time i. Then, Z = 1 when the germination of all seeds occur at the same time and Z = 0 when at least two seeds could germinate, one at each time.
U is an adaptation of the Shannon index that measures the degree of uncertainty in predicting the informational entropy or the uncertainty associated with the distribution of the relative frequency of germination (Labouriau & Valadares 1976, Labouriau 1983a). In function of this, uncertainty index appears to be better for denomination of this index, as used by Labouriau in his papers published before 1983, than synchronization index. Low values of U indicate frequencies with few peaks, that is, germination more concentrated in time. Only one seed germinating changes the value of U. It means that U measures the degree of spreading of germination through time and can be used, by inference, to measure the synchrony of germination. On the contrary, Z produces a number if and only if there are two seeds finishing the germination process at the same time. Thus, the value of Z measures, in fact, the synchrony of germination, that is, the degree of germination overlapping.
The mathematical limits of each expression here presented represent an important contribution and a good point of reference that make it easier to distinguish between good and bad treatments (table 1).
When zero exists for the germination measurements
Zero and null values are surrounded by doubts that make the statistical analysis difficult. Zero for germinability exists when none seed is able to complete the germination process in a given condition (table 1). The same is valid for Timsons index, GV, Rate, ERI, GR, and  . Zero for
. Zero for  , CVt, CUG, CVG,
, CVt, CUG, CVG,  ,
,  , Tmod, ERImod, GI, GImod, U, and Z do not exist, that is, the values are nulls when germination does not occur. Mathematically all fractional measurements must have as divisor a number different from zero. Thus, when germinability is zero,
, Tmod, ERImod, GI, GImod, U, and Z do not exist, that is, the values are nulls when germination does not occur. Mathematically all fractional measurements must have as divisor a number different from zero. Thus, when germinability is zero,  and
and  must not be calculated. In addition, CVt and CUG measure variability. It means that both of them exist only when at least two seeds were able to complete the germination process in the experimental condition, at different times. U is zero when one seed was able to complete the germination process. Z is zero when no overlapping will be observed for n germinated seeds and will be null when no seed could complete the germination process.
must not be calculated. In addition, CVt and CUG measure variability. It means that both of them exist only when at least two seeds were able to complete the germination process in the experimental condition, at different times. U is zero when one seed was able to complete the germination process. Z is zero when no overlapping will be observed for n germinated seeds and will be null when no seed could complete the germination process.
How to work statistically with germination measurements using samples
When few seeds are produced by one species, the conventional experimental designs are limited. According to the seed analysis rules (ISTA 1985, Brasil 1992), four hundred seeds per treatment are necessary to give representativity for the results. As this number is very high for several native species, Brazilian researchers are preparing specific rules for forest species based on two hundred seeds as a reliable sample, although not always this minimum could be collected. In this case, all germination measurements with variability associated to them can be calculated because t Student test can be used to compare samples if they have normal distribution. This technique was applied to evaluate the emergence of Anacardium humile seedlings (Carvalho et al. 2005).
The proportion of seeds germinated (or seedlings emerged) is a discrete variable, with binomial distribution and the method of the approximation of the binomial by normal distribution can be used, since n1
1 > 5, n11 > 5, n22> 5, and n22 > 5, for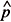 1 = X1/ n1;
1 = X1/ n1; 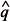 1 = 1
1 = 1 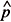 1;
1; 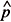 2 = X2/n2, and
2 = X2/n2, and 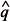 2 = 1
2 = 1 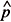 2 , where
2 , where 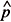 1 and
1 and 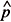 2 are the estimation of the proportion of seeds germinated in the first and second samples; X1 and X2 are the number of seeds germinated in the first and second samples; n1 and n2 are the initial number of seeds included in the first and in the second samples, respectively. If these conditions are met, comparisons between samples can be processed using the expression of the t Student test for variances heterogeneous to compare proportions,
2 are the estimation of the proportion of seeds germinated in the first and second samples; X1 and X2 are the number of seeds germinated in the first and second samples; n1 and n2 are the initial number of seeds included in the first and in the second samples, respectively. If these conditions are met, comparisons between samples can be processed using the expression of the t Student test for variances heterogeneous to compare proportions, 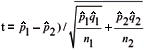 .
.
For  , t Student test can be processed by the expression
, t Student test can be processed by the expression  , where
, where  1 and
1 and  2 are the mean germination time of the first and second samples;
2 are the mean germination time of the first and second samples;  and
and  the variances of the first and second samples; and and the number of seeds germinated in the first and in the second samples, respectively. The same is valid for the mean germination rate (
the variances of the first and second samples; and and the number of seeds germinated in the first and in the second samples, respectively. The same is valid for the mean germination rate ( ), using the expression of variance proposed by Labouriau (1983b), in the expression
), using the expression of variance proposed by Labouriau (1983b), in the expression  , where
, where  1 and
1 and  2 are the mean germination rate of the first and second samples;
2 are the mean germination rate of the first and second samples;  and
and  the variances of the first and second samples; and n1 and n2 the number of seeds germinated in the first and in the second samples, respectively.
the variances of the first and second samples; and n1 and n2 the number of seeds germinated in the first and in the second samples, respectively.
Comparisons between samples for the uncertainty of the seed germination (U) can be made using the method proposed by Hutcheson (1970) and described by Zar (1999).
For the other germination measurements here presented, variability is unknown and its approximation was not proposed by the authors. Then, no statistical test for comparisons can be processed, using samples without replications.
How to work statistically with germination measurements within experimental designs
Within the conventional experimental designs, all germination measurements here discussed can be analysed. In a treatment with five replications, five values of each measurement can be used to calculate the mean and to process the multisample comparisons. In this case, the variability inherent in the germinability, mean germination time and rate, and uncertainty is not considered because only the variability of the experiment can be measured.
Relationships among germination measurements
When statistical analysis are processed, the results are not always the same for  and
and  in relation to normality, homogeneity, in the magnitude of the variances, and in relation to the number of categories formed after pairwise comparisons in one experiment. It means that both of them are non linearly associated. Mathematically
in relation to normality, homogeneity, in the magnitude of the variances, and in relation to the number of categories formed after pairwise comparisons in one experiment. It means that both of them are non linearly associated. Mathematically  and
and  are proportionally inverse. Thus, when the first increases, the second obligatorily decreases, but non linearly. These relationships are also valid when the rate of the germination process is measured using mathematical expressions free of the action of the number of seeds germinated as Tmod, ERImod, and GImod. For mixed rate measurements, increases or decreases as a consequence of the balance between germinability and rate germination can give rise to associations without the same tendency observed for
are proportionally inverse. Thus, when the first increases, the second obligatorily decreases, but non linearly. These relationships are also valid when the rate of the germination process is measured using mathematical expressions free of the action of the number of seeds germinated as Tmod, ERImod, and GImod. For mixed rate measurements, increases or decreases as a consequence of the balance between germinability and rate germination can give rise to associations without the same tendency observed for  and
and  .
.
High or low values of  are not associated with high or low values of CVt or CUG, neither with high or low values of U or Z, because seeds could germinate spending a little time (low
are not associated with high or low values of CVt or CUG, neither with high or low values of U or Z, because seeds could germinate spending a little time (low  value) and the germination process could be spread through time or could germinate spending more time (high
value) and the germination process could be spread through time or could germinate spending more time (high  value), concentrating the process after the first germination.
value), concentrating the process after the first germination.
Another important point is related to the interval between two consecutive evaluations. Depending on this interval, seeds could be considered synchronized and homogeneous or unsynchronized and heterogeneous. Short intervals between two consecutive evaluations makes the determination of  more accurate because the history of each seed is registered. On the other hand, short intervals between two consecutive evaluations, show low synchrony, because few seeds are counted at the same evaluation. It means that the mean germination time and synchrony are overestimated using high intervals between observations. On the contrary, if short intervals are used to count germination, all seeds appear to be without synchrony because it is possible to detect the end of germination (embryo protrusion) for each seed individually. The germination process of Gossypium hirsutum L. cv. DeltaOPAL seeds were evaluated in different intervals (Cunha 2002) and confirmed the influence of the interval size on the accuracy of these measurements.
more accurate because the history of each seed is registered. On the other hand, short intervals between two consecutive evaluations, show low synchrony, because few seeds are counted at the same evaluation. It means that the mean germination time and synchrony are overestimated using high intervals between observations. On the contrary, if short intervals are used to count germination, all seeds appear to be without synchrony because it is possible to detect the end of germination (embryo protrusion) for each seed individually. The germination process of Gossypium hirsutum L. cv. DeltaOPAL seeds were evaluated in different intervals (Cunha 2002) and confirmed the influence of the interval size on the accuracy of these measurements.
After these considerations, it is clear that the researcher must choose the measurements and the interval of evaluations, according to their objectives. Besides, correlations among the germination measurements prove the nature of each measurement and can help the researchers in their options. It is important to take into account that correlations between variables in completely randomized design models must to be done after the standardization of the effect of treatment (Santana & Ranal 2006). When correlations are applied to the residuals and to the original data, this makes it possible to identify if the association between variables (in this case, germination measurements) is algebraic, physiological, or due to the effect of treatment included in the model. The analysis of the germination can be enriched if in addition to the germinability,  and/or
and/or  , CVt, Z and/or U values were communicated, because they measure different aspects of the germination process. Finally, all germination measurements could be applied to evaluate seed germination and seedling emergence. Details and intermediate tables to calculate all of them were presented by Santana & Ranal (2004) and the practical and biological sense by Dorneles et al. (2005).
, CVt, Z and/or U values were communicated, because they measure different aspects of the germination process. Finally, all germination measurements could be applied to evaluate seed germination and seedling emergence. Details and intermediate tables to calculate all of them were presented by Santana & Ranal (2004) and the practical and biological sense by Dorneles et al. (2005).
Acknowledgments Important assistance for the understanding and calculus of the Z index was given by Dr. Richard B. Primack and Dr. Fernando Pedroni. Useful discussions about  as a frequency were established with Dr. Roberto Hiroki Miwa (Physicist) and Cláudio Franco Muniz (Master Degree Student). The English revision was done by Mr. John David Bagnall. The authors register their sincere thanks, adding a special word of thanks to the Editorial Board of the Revista Brasileira de Botânica for the invitation and opportunity to present and publish this review.
as a frequency were established with Dr. Roberto Hiroki Miwa (Physicist) and Cláudio Franco Muniz (Master Degree Student). The English revision was done by Mr. John David Bagnall. The authors register their sincere thanks, adding a special word of thanks to the Editorial Board of the Revista Brasileira de Botânica for the invitation and opportunity to present and publish this review.
(received: August 18, 2005; accepted: January 26, 2006)
- ALLAN, R.E., VOGEL, A.O. & PETERSON, C.J. 1962. Seedling emergence rate of fall-sown wheat and its association with plant height and coleoptile length. Agronomy Journal 54:347-350.
- BASKIN, C.C. & BASKIN, J.M. 1998. Seeds: ecology, biogeography, and evolution of dormancy and germination. Academic Press, San Diego.
- BEWLEY, J.D. & BLACK, M. 1994. Seeds: physiology of development and germination. 2nd ed. Plenum Press, New York.
- BRASIL. 1992. Ministério da Agricultura e Reforma Agrária. Regras para análise de sementes. SNDA/DNDV/CLAV, Brasília.
- BROWN, R.F. & MAYER, D.G. 1988. Representing cumulative germination. 1. A critical analysis of single-value germination indices. Annals of Botany 61:117-125.
- CARNEIRO, J.W.P., DOLIS, M., SHIMONISHI, M.L.S. & TOLEDO, E.A. 1993. Avaliação do desempenho germinativo de sementes de stevia (Stevia rebaudiana (Bert.) Bertoni) utilizando parâmetros da função de distribuição Weibull. Anais. Informativo Abrates 3:81.
- CARVALHO, M.P., SANTANA, D.G. & RANAL, M.A. 2005. Emergência de plântulas de Anacardium humile A. St.-Hil. (Anacardiaceae) avaliada por meio de amostras pequenas. Revista Brasileira de Botânica 28:627-633.
- COSTA NETO, P.L.O. 1977. Estatística. Edgard Blücher, São Paulo.
- CUNHA, C.M.G. 2002. Avaliação da qualidade fisiológica de sementes de algodoeiro (Gossipium hirsutum L. cv. DeltaOPAL) em função de tamanho e local de produção. Dissertação de mestrado, Universidade Federal de Uberlândia, Uberlândia.
- CZABATOR, F.J. 1962. Germination value: an index combining speed and completeness of pine seed germination. Forest Science 8:386-396.
- DAVIS, J.A. 1971. Elementary survey analysis. Prentice-Hall, Englewood.
- DIXON, W.J. & MASSEY JR., F.J. 1969. Introduction to statistical analysis. 3rd ed. McGraw-Hill Book Company, New York.
- DORNELES, M.C., RANAL, M.A. & SANTANA, D.G. 2005. Germinação de diásporos de Myracrodruon urundeuva Allemão (Anacardiaceae) ocorrente no cerrado do Brasil Central. Revista Brasileira de Botânica 28:399-408.
- DRAKE, D.R. 1993. Germination requirements of Metrosideros polymorpha, the dominant tree of hawaiian lava flows and rain forests. Biotropica 25:461-467.
- EDMOND, J.B. & DRAPALA, W.J. 1958. The effects of temperature, sand and soil, and acetone on germination of okra seed. Proceedings of the American Society for Horticultural Science 71:428-434.
- EDWARDS, T.I. 1932. Temperature relations of seed germination. Quarterly Review of Biology 7:428-443.
- GOLOFF JR., A.A. & BAZZAZ, F.A. 1975. A germination model for natural seed populations. Journal of Theoretical Biology 52:259-283.
- GOODCHILD, N.A. & WALKER, M.G. 1971. A method of measuring seed germination in physiological studies. Annals of Botany 35:615-621.
- HEYDECKER, W. 1973. Glossary of terms. In Seed ecology (W. Heydecker, ed.). Butterworths, London, p.553-557.
- HILHORST, H.W.M. & KARSSEN, C.M. 1988. Dual effect of light on the gibberellin- and nitrate- stimulated seed germination of Sisymbrium officinale and Arabidopsis thaliana. Plant Physiology 86:591-597.
- HUTCHESON, K. 1970. A test for comparing diversities based on the Shannon formula. Journal of Theoretical Biology 29:151-154.
- ISTA. International Seed Testing Association. 1985. International rules for seed testing. Seed Science and Technology 13:307-513.
- KENDRICK, R.E. & FRANKLAND, B. 1969. Photocontrol of germination in Amaranthus caudatus Planta 85:326-339.
- KOTOWSKI, F. 1926. Temperature relations to germination of vegetable seed. Proceedings of the American Society for Horticultural Science 23:176-184.
- LABOURIAU, L.G. 1970. On the physiology of seed germination in Vicia graminea Sm. I. Anais da Academia Brasileira de Ciências 42:235-262.
- LABOURIAU, L.G. 1983a. A germinação das sementes. Organização dos Estados Americanos. Programa Regional de Desenvolvimento Científico e Tecnológico. Série de Biologia. Monografia 24.
- LABOURIAU, L.G. 1983b. Uma nova linha de pesquisa na fisiologia da germinação das sementes. In Anais do XXXIV Congresso Nacional de Botânica. SBB, Porto Alegre, p.11-50.
- LABOURIAU, L.G. 1983c. Some effects of deuterium oxide on the isothermal germination of tomato seeds. Boletin de la Sociedad Venezolana de Ciencies Naturales 38:153-166.
- LABOURIAU, L.G. & OSBORN, J.H. 1984. Temperature dependence of the germination of tomato seeds. Journal of Thermal Biology 9:285-294.
- LABOURIAU, L.G. & PACHECO A.A. 1978. On the frequency of isothermal germination in seeds of Dolichos biflorus L. Plant & Cell Physiology 19:507-512.
- LABOURIAU, L.G. & VALADARES, M.E.B. 1976. On the germination of seeds of Calotropis procera (Ait.) Ait. f. Anais da Academia Brasileira de Ciências 48:263-284.
- MAGUIRE, J.D. 1962. Speed of germination - aid in selection and evaluation for seedling emergence and vigor. Crop Science 2:176-177.
- MAGURRAN, A.E. 1988. Ecological diversity and its measurement. 1. Ecological communities. Diversity. Mathematical models. Croom Helm Limited, London.
- MELVILLE, A.H., GALLETTA, G.J., DRAPER, A.D. & NG, T.J. 1980. Seed germination and early seedling vigour in progenies of inbred strawberry selections. HortScience 15:749-750.
- NICHOLS, M.A. & HEYDECKER, W. 1968. Two approaches to the study of germination data. Proceedings of the International Seed Testing Association 33:531-540.
- PRIMACK, R.B. 1980. Variation in the phenology of natural populations of montane shrubs in New Zealand. Journal of Ecology 68:849-862.
- QUINTANILLA, L.G., PAJARÓN, S., PANGUA, E. & AMIGO, J. 2000. Effect of temperature on germination in northernmost populations of Culcita macrocarpa and Woodwardia radicans Plant Biology 2:612-617.
- RANAL, M.A. 1999. Effects of temperature on spore germination in some fern species from semideciduous mesophytic forest. American Fern Journal 89:149-158.
- SANTANA, D.G. & RANAL, M.A. 2004. Análise da germinação: um enfoque estatístico. Editora UnB, Brasília.
- SANTANA, D.G. & RANAL, M.A. 2006. Linear correlation in experimental design models applied to seed germination. Seed Science and Technology 34:241-247.
- SCOTT, S.J., JONES, R.A. & WILLIANS, W.A. 1984. Review of data analysis for seed germination. Crop Science 24:1192-1199.
- SHMUELI, M. & GOLDBERG, D. 1971. Emergence, early growth, and salinity of five vegetable crops germinated by sprinkle and trickle irrigation in an arid zone. HortScience 6:563-565.
- SIMON, E., MINCHIM, A., MCMENAMIN, M.M. & SMITH, J.M. 1976. The low temperature limit for seed germination. New Phytology 77:301-311.
- THOMPSON, P.A. 1970. Characterization of the germination response to temperature of species and ecotypes. Nature 225:827-831.
- THRONEBERRY, G.O. & SMITH, F.G. 1955. Relation of respiratory and enzymatic activity to corn seed viability. Plant Physiology 30:337-343.
- TIMSON, J. 1965. New method of recording germination data. Nature 207:216-217.
- TUCKER, H. & WRIGHT, L.N. 1965. Estimating rapidity of germination. Crop Science 5:398-399.
- ZAR, J.H. 1999. Biostatistical analysis. 4th ed. Prentice Hall, New York.
Publication Dates
-
Publication in this collection
14 Aug 2006 -
Date of issue
Mar 2006
History
-
Received
18 Aug 2005 -
Accepted
26 Jan 2006



