Abstract
The use of limiting dilution assay (LDA) for assessing the frequency of responders in a cell population is a method extensively used by immunologists. A series of studies addressing the statistical method of choice in an LDA have been published. However, none of these studies has addressed the point of how many wells should be employed in a given assay. The objective of this study was to demonstrate how a researcher can predict the number of wells that should be employed in order to obtain results with a given accuracy, and, therefore, to help in choosing a better experimental design to fulfill one's expectations. We present the rationale underlying the expected relative error computation based on simple binomial distributions. A series of simulated in machina experiments were performed to test the validity of the a priori computation of expected errors, thus confirming the predictions. The step-by-step procedure of the relative error estimation is given. We also discuss the constraints under which an LDA must be performed.
limiting dilution assay: accuracy; wells; number of; relative error
Braz J Med Biol Res, August 2000, Volume 33(8) 937-947
A priori estimation of accuracy and of the number of wells to be employed in limiting dilution assays
J.G. Chaui-Berlinck1 and J.A.M. Barbuto2
Departamentos de 1Fisiologia, Instituto de Biociências, and 2Imunologia, Instituto de Ciências Biomédicas, Universidade de São Paulo, São Paulo, SP, Brasil
Conclusion
References
Correspondence Correspondence Correspondence
Abstract
The use of limiting dilution assay (LDA) for assessing the frequency of responders in a cell population is a method extensively used by immunologists. A series of studies addressing the statistical method of choice in an LDA have been published. However, none of these studies has addressed the point of how many wells should be employed in a given assay. The objective of this study was to demonstrate how a researcher can predict the number of wells that should be employed in order to obtain results with a given accuracy, and, therefore, to help in choosing a better experimental design to fulfill one's expectations. We present the rationale underlying the expected relative error computation based on simple binomial distributions. A series of simulated in machina experiments were performed to test the validity of the a priori computation of expected errors, thus confirming the predictions. The step-by-step procedure of the relative error estimation is given. We also discuss the constraints under which an LDA must be performed.
Key words: limiting dilution assay: accuracy, wells, number of, relative error
Introduction
The use of limiting dilution assay (LDA) for assessing the frequency of responders in a cell population is a method extensively used by immunologists. A series of studies addressing the adequate estimator (the statistical method of choice) in an LDA have been published (1-6). Interestingly, however, none of these studies has clearly addressed the point of how many wells should be employed in a given assay. Many qualitative propositions are available, mainly of heuristic value instead of a quantitative one. For example: "Numbers of replicates ... 180 per dilution and not less than 60 ..." (Lefkovits and Waldmann, quoted in 2); "... reliable estimates with replicates of the order of 20." (2); "Our experiments indicate that values between 24 and 72 are efficient ..." (3); "In our laboratory we use 12 dilution steps with 8 wells per dilution ..." (4).
The objective of the present study was to demonstrate how a researcher, when setting up a limiting dilution assay, can predict how many wells should be employed in order to obtain results with a given accuracy, and, therefore, to help choose a better experimental design to fulfill one's expectations.
Rationale
The observation of clusters in place of discrete events. Consider a finite population of cells, some of which are responders to a given stimulus while the others are non-responders. This defines a relative frequency of responders in such a population as the number of responders divided by the total number of cells. This has the same general form of the frequentist definition of probability (Footnote 1), and thus the probability p of finding a responder among cells of that population is equal to the relative frequency f:
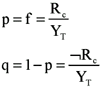
(Equation 1)
where YT stands for the sum of the cells of the population, Rc for the sum of the responder cells, and ØRc for the sum of the non-responder cells. Obviously, p and q end up by defining a binomial distribution. If a certain number of cells (events) are observed, say n, there shall be an expected p.n number of positive events (i.e., responding cells) among n. This was defined at the level of the discrete individual event, i.e., each cell in the population.
Consider that instead of observing n individual events one observes clusters of events, and classifies a cluster as positive if there is at least one positive discrete event within it (but how many of these discrete positive events are present in a positive cluster is unknown) and as negative otherwise. The question is how can we infer p (or q) by observing these clusters instead of the particular events themselves. As stated by Strijbosch et al. (3), it is easy to demonstrate how one is truly observing what is going on in the realm of the discrete events by observing the realm of clusters of those events.
Consider a cluster, Ck, composed of discrete yk events (cells). The probability of a cluster of this size being negative is the probability that all yk events within it are negative:
where Cki = - is "the cluster i is negative". Take N of these clusters. What is the probability of zero positive events, at the cluster level, in N clusters?
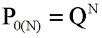
(Equation 3)
However, the number of discrete events composing these N clusters (of the same size) is N.yk and the probability of zero positive events at the individual level will be:
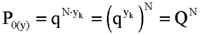
(Equation 4)
and, therefore, the probability of zero positive events at the cluster level is equal to the probability of zero positive events at the individual level, as it was expected to be demonstrated. We will use, without further considerations, the result in which, for small p (i.e., f) and big sample sizes, the Poisson distribution fits well the underlying binomial one (i.e., Stirling's approximation; 7,8):
In an LDA, yk is the number of cells per well in a given dilution (e is the natural logarithm base). The parameter p is interchangeable with f, the relative frequency of responders (see above).
The map from P0(C) = Q to f: features of a binomial distribution. An interesting result emerges from equation 2. If a set of N clusters (of the same size at this point) is observed, the binomial distribution observed is defined by Prob(Cki = -) = Q and Prob(Cki = +) = P = 1 - Q, therefore, (P + Q)N = 1. The final objective of an LDA is to estimate p (or f, equation 5) from the observed Qob. The best estimate one can make of p by observing these N clusters is mapped to the best estimate one can make of Q from Qob.
Given the binomial distribution resulting from (P + Q)N = 1, let us consider a coin that has a probability Q of tail-up in a flip (and 1 - Q of head-up). A clear quantitative question is how many outcomes do we need to observe in order to believe that the Qob estimator we have (Qob, in this example, is the tail outcome/N outcome ratio) is equal to the true Q? Obviously, stated as this, the question has two possible and useless answers: if Q is determined in a finite population of events then Qob = Q only if the entire population has been sampled; if Q is determined in an infinite population of events then Qob = Q only when we observe infinite outcomes. However, the question allows a change from its inclusive form to the exclusive one that maintains the essential quantitative feature: how many events should we observe in order to be sure, at a given precision level, that the true Q is a value neither lower than a given Qlow nor higher than another given Qhigh? Because each of these probabilities, Qlow and Qhigh, defines a binomial distribution in a sample of size N, we can define beforehand the limiting cases:

(Equation 6b)
where t is a tabulated value from the Student distribution with N degrees of freedom at the desired confidence level (for example, t = 1.96 for a 95% confidence interval with degrees of freedom tending to infinite). Therefore, the best map one can track down from the observed Qob in N clusters to p (or f) is the range from Qlow to Qhigh. Two features of equations 6a and b are: 1) the limits Qlow and Qhigh are asymmetrical in relation to Qob (unless Qob = 0.5) and 2) the limits have to be found iteratively. Because equations 6a and b are the best that can be done, any estimator of p should not result in a range greater than Qlow to Qhigh in order to obtain the best accuracy allowed by the observed Qob in N clusters. At the same time, no estimator can result in a range smaller than those limits, in order to be fair.
A note on estimators of LDA. The solution of equations 6a and b results in limits that are asymmetrical to the observed fraction of negative wells (Qob). The estimators given as adequate (maximum likelihood and its jackknife version; 3) or inadequate (e.g., linear regression) result in symmetrical limits (confidence interval). Therefore, one can predict some level of bias to be present in these estimators. However, the large number of wells observed (i.e., N) tends to result in more symmetrical limits in relation to Qob (see below). It is not the aim of this study to address the adequacy of estimators, but it is worth calling attention to this point.
Taking the ratio between the difference Qhigh - Qlow and Qob one obtains the relative error of the estimated Q. In its logarithmic transformed version, ln(Qhigh/Qlow)/ - ln(Qob), one obtains the relative error of the estimated p (or of the estimated frequency f). Figure 1 shows this relative error of f in relation to values of Qob for a given N. Notice that the logarithmic transformed version of the relative error has a nadir around Qob = 0.21. The relative error is the quantitative version of the heuristic "most informative range" found in studies concerning the estimators of LDA (2,3).
Let us define trivial cases such as those outcomes that generate only one limit by equations 6a and b. There are two possible trivial outcomes: zero positive events (Qob = 1) and all positive events (Qob= 0) (Footnote 2). Due to the indetermination of the trivial outcomes they should be disregarded as valuable in the estimation of f (and they regularly are, implicitly or explicitly). So, when one observes N events, the non-trivial outcomes go from 1/N to (N - 1)/N. This limits, on an a priori basis, the range of possible Q (or f) to be estimated by a given N. At the same time, the more distant Qob falls from 0.21 as the relative error increases (Figure 1).
From a single dilution assay to a limiting dilution one. Up to now we were considering N events observed under the same Q (i.e., the same f.yk product). Basically, what limits the estimation of f in a single dilution assay is the increase of the relative error and the possibility of trivial outcomes. Dividing N observable events with the same Q into d subsets of h observable events of different values of Q expands the estimation range of f. This occurs when one can be sure that at least some of the subsets will have non-trivial outcomes. For the sake of simplicity, let us consider that each subset di comprises the same number of observable events as the other subsets (i.e., there is the same number of wells, h, at each dilution i, in a total of d dilutions), and, therefore, d.h = N. Each dilution di has a range of non-trivial results and every Qobi coming from each di has a relative error much greater than a putative error that would be obtained by observing a single Qob in N events. As stated before, an estimator of f should not result in a range greater than Qlow to Qhigh in order to have the best accuracy allowed by N observations and no estimator can result in a range smaller than those limits, in order to be fair. Therefore, a map from the Qobi outcomes (subset level) is to be tracked down to a single putative Qpu at the N level by an adequate estimator in order to reduce uncertainty to the minimum allowed by the number of events observed (remember that N is the total number of wells employed). This is illustrated in Figure 2. Therefore, the problem that now remains is to evaluate the possibility of knowing, on an a priori basis, the value of Qpu that would be obtained from the set of Qobi. In Appendix A Appendix A we show that the value of Qpu at N is the conjunction of the independent values of Qobi. Such a conjunction of independent events results in:
Suppose h (e.g., 100) events were observed and the resulting probability of positive events (i.e., positive outcomes/h) among these events is p1 (e.g., p1 = 0.1). Suppose another set of h events resulted in another p2 (e.g., p2 = 0.4). What one should expected if, instead of observing two separate sets of h events, one had observed one set of 2.h events? These being independent events, the conjunction of p1 and p2 is the unbiased expectation one should have to obtain at the 2.h level. This means:
In the numerical example above, the expected number of positive events is 200.(0.04 + 0.03 + 0.18) = 50. Obviously, this ends up as the mean between p1 and p2, (p1 + p2)/2. The extension to any number X of subsets of hi events is straightforward: Prob(X.h) = mean(Prob(hi)).
Qpu = mean (Qobi)
(Equation 7)
in a straightforward computation (see Appendix A Appendix A ). An adequate estimator should yield, for a set of d different (and non-trivial) Qobi, a relative error related to a putative Qpu = mean(Qobi) that would be obtained if the experimental setup consisted of a single dilution assay with N observable events. This is what happens, as shown in the present study.
Equations 6a and b are the best estimates of the possible values of a true Q resulting in an observed Qob in N events at a given confidence level. As stated before, the solution is an iterative numerical procedure. However, as N increases, the approximate estimation would become close to the best one. Therefore, equations 6a and b could be approximated by equation 8 for a large N:
where the limits Qlow and Qhigh are taken as the subtractive and the additive operations, respectively (t has the same meaning as in equations 6a and b). Notice that the limits are now (wrongly) symmetrical. Also, equation 8 allows a direct a priori computation of the expected limits for a Q to be observed. Thus, equations 8 and 7 can be used to estimate, on an a priori basis, the accuracy expected to be obtained by a given LDA experimental setup.
Methods
In machina experiments were performed with a PC with a Pentium® processor using the MatLab 4.2b software (The MathWorks Inc., Natick, MA, USA). Data were obtained using a built-in function of random uniformly distributed variables generating a binomial distribution with a desired probability Q related to f (equation 5). A maximum likelihood estimator (fML) was employed to estimate f in the in machina experiments (numerical procedure given in Ref. 1). The relative error of a particular result k is 2.SE(k)/fML(k), where SE stands for the standard error given by the maximum likelihood procedure. The ("real") relative error for a given f within a given experimental setup was taken as the mean of the relative errors obtained.
The estimated relative error for a given f within a given experimental setup is obtained as follows: 1) the exact expected value of Qobi for each dilution di is computed; 2) all expected trivial results (steps in which Qobi<1/h or Qobi>(h - 1)/h) are discarded; 3) the mean value of the remaining non-trivial expected Qobi is computed (equation 7), and this is the putative Qpu; 4) Nnt as the sum of h in the non-trivial steps is computed; 5a) the exact limits Qlow and Qhigh are numerically computed (equations 6a and b with N = Nnt and Qob = Qpu) or 5b) the approximate limits Qlow and Qhigh are directly computed (equation 8 with N = Nnt and Qob = Qpu); 6) the expected relative error of f in the given experimental setup is then:
Example 1 in the Discussion gives the complete, step-by-step, procedure described above to compute the expected relative error. From now on, e.r.e. stands for expected relative error, the relative error computed by the best or by the approximate procedure.

Several different experimental setups were simulated and the estimation of the relative error evaluated. The Strijbosch et al. (3) procedure for experimental designs was employed (see Appendix B Appendix B ). In this procedure, the number of cells per dilution is computed by means of an algorithm concerned with the range of possible frequencies to be covered, a high (P2) and a low (P1) value of P0(C), and the number d' of dilutions falling between P1 and P2.
The first step in the Strijbosch et al. (3) procedure is to determine the frequency range to be evaluated, f1 (the lower boundary) and f2 (the upper boundary, 0<f1£f2<1). Then, the two boundaries (P1 and P2) in the fraction of negative wells (i.e., 0<P1<P2<1) and the number of dilutions d' to be found between P1 and P2 are set. The computation below (taken from Ref. 3) shows how many dilutions and what number of cells per dilution are to be employed to satisfy the conditions established a priori:
The best estimation of the relative error. Using the procedure of equations 6a and b one can numerically construct exclusion tables for different values of N and obtain the relative error of each non-trivial observable Q (equation 9), as Figure 1 graphically shows. Table 1 shows the e.r.e. obtained by this procedure for some experimental setups and the "real" mean relative error coming from the maximum likelihood estimator of data generated under these different settings. The agreement between the two errors (estimated and obtained) is as exact as can be expected for numerical processes. Obviously, such an agreement is independent of Nnt, as also expected.
Table 1 - Comparison between the relative error obtained and those predicted both by the best procedure (equations 6a and b) and by the approximate procedure (equation 8) for a series of different experimental designs.
The experimental designs were generated by the Strijbosch procedure (Ref. 3; Appendix B). The number of wells per dilution, h, varied within each experimental setup. Each sub-table also presents the expected number of non-trivial results for each value of h within the experimental setup under analysis. The experimental designs analyzed were:
C1 = [3, 0.15, 0.65, (1:300 to 1:4000)]
C2 = [4, 0.10, 0.30, (1:500 to 1:1000)]
C3 = [3, 0.70, 0.90, (1:400 to 1:40000)]
C4 = [2, 0.10, 0.90, (1:600 to 1:120000)]
C5 = [5, 0.35, 0.85, (1:300 to 1:4000)]
C6 = [5, 0.15, 0.65, (1:300 to 1:4000)]
where 1) d', the number of dilutions between P1 and P2; 2) P1; 3) P2, and 4) the upper and the lower boundaries of a frequency range are given within brackets. Thus, [d', P1, P2, (f2 to f1)]. The letters U and L after an experimental setup stand for the results obtained at the upper and at the lower boundaries of the frequency range, respectively. Notice the fine agreement between the obtained relative error and the predicted ones. On the one hand, such an agreement is independent of the experimental design and the frequency range. On the other hand, such an agreement is jeopardized when the expected non-trivial dilutions comprise a low number of events to be observed. The cases of non-agreement between the predicted and the obtained errors are given in bold (on the "predicted best" lines). This non-agreement is explained by spurious experimental designs resulting in extreme low numbers of non-trivial dilutions associated with high numbers of expected trivial steps. Such a conjunction leads to the emergence of unexpected non-trivial results in putative trivial steps. As an example, consider the experimental setup C3L. The obtained error was 1.529 (italics underlined). This setup comprises 14 dilutions with a putative fraction of negative wells at the lower boundary of the frequency range of Qob(%) = [99.9 99.8 99.7 99.5 99.3 99 98.4 97.7 96.5 94.8 92.3 88.6 83.4 76.2]. Such a Qob leads to only 3 dilutions (underlined) with non-trivial results when h = 10 wells per dilution (therefore, Nnt = 30). However, there are 110 wells comprising fractions above 90%, and thus non-trivial results are now expected to emerge within this set of wells (and this is what occurs). When the results are reevaluated after eliminating those 11 trivial steps, the error obtained goes to 1.903, which is now within 5% of the predicted ones. Another problem that emerges at those extremely low numbers of wells comprising the results of an LDA is related to the loss of the nominal confidence interval of the estimator (Chaui-Berlinck JG, unpublished results). However, this is not the subject of this study.
Continued on the next page
Next, we will focus on the approximate direct estimation procedure (step 5b, equation 8). This is because a) we are mainly concerned with an a priori estimation of the approximate accuracy a given experimental setup is expected to yield, b) most of the time N is large (N>100) in an LDA, and c) directly solving equation 8 is easier than numerically solving equations 6a and b.
The approximate estimation of the relative error. Table 1 presents relative errors estimated by the approximate procedure (equation 8) for different experimental setups, as well as the mean relative errors coming from the maximum likelihood estimator of data generated under these different settings. Notice that the agreement between the two errors is warranted only when the total non-trivial dilution, Nnt, is greater than 100. Otherwise, the e.r.e. by the approximate procedure shall overestimate such a parameter.
Results

Despite the intense use of LDA by immunologists in general, its proper employment seems to escape most of them. Two striking problems are the absence of references to how an experimental design is set up (i.e., the range of frequencies that the given setup is prepared to adequately cover) and the use of linear regression by least squares (Footnote 3) as the estimator of the frequency (in circa 40 to 50% of published studies, our personal observation). Thus, see below five basic statements about constraints of the estimation of frequencies in an LDA: 1) in an LDA there is a fixed range of frequencies that can be estimated in a given experimental setup; 2) prior knowledge about a putative range of frequencies to be estimated is a sine qua non condition in an LDA with the aim of truly determining a certain frequency; 3) such a range should be determined previously, when setting up the experimental design; 4) when the outcome of an experiment falls outside the prior expected range, loss of confidence and power of the estimate occurs, and 5) analysis of the outcome of a particular experiment requires programming because there is no good direct analytical LDA estimator (e.g., linear regression) and the adequate ones are not found in common commercial packages.
Discussion
These features can be found in published papers about the subject (e.g., 2-4). The empiricist must be aware of these constraints when planning an LDA. Closely related to these problems is the absence of knowledge of what should be expected from a given experimental setup in terms of accuracy. No quantitative prescriptions about the number of wells per dilution (i.e., the number of events to be observed) are found among these constraints (see Introduction). The present study provides such a quantitative prescription, which is based on the relative error of a measure and is thus related to the desired accuracy of such measure. The prescription can be presented as follows: 6) the number of wells in non-trivial steps must be set to match the desired level of accuracy determined a priori.
This putative sixth constraint can be read in either direction, that is, the necessity of increasing the number of wells in a given experiment or the possibility of decreasing such a number in another setting. Let us illustrate these points by means of some "real" problems to be solved. Basically, accuracy is expected to be equal to or greater than a given value (thus the relative error is expected to be less than a given value), the number of wells is limited to some maximum N, and the true frequency lies within some range. To these indisputable limits we will add one more: the lower the number of different dilutions to be prepared the less time and energy consuming the experiment will be.
Example 1. The unknown frequency lies in a 20-fold range, d' = 4, P1 = 0.1, P2 = 0.8 (see Methods). What is the error expected in an experimental setup employing 25 wells per dilution (i.e., h = 25)? What is the gain if h = 40 instead of 25? The experimental setup will comprise 9 dilutions (d = 9) by the Strijbosch et al. (3) procedure (see Appendix B Appendix B , for computation). For the upper limit in the frequency range, the expected Qob (expected P0(C)) in each dilution (di) is, respectively, Qob expected (in %) = [73.3 57.3 36.9 16.7 4.1 0.3 0 0 0]. For the lower limit in the frequency range, the expected Qob for each di is, respectively, Qob expected (in %) = [98.5 97.3 95.1 91.5 85.2 75 59.8 39.7 19.1]. At the upper limit, the number of non-trivial steps expected (for h = 25 wells) comprises dilutions 1 to 5. At the lower limit, the number of non-trivial steps expected comprises dilutions 3 to 9. These numbers of non-trivial expected dilutions are the result of 1/h being equal to 4%, thus excluding dilutions below 4% and above 96% as possible non-trivial dilutions. Therefore, for both extremities in the frequency range, the number of non-trivial dilutions expected, with h = 25, results in Nnt>100 (125 for the upper limit and 175 for the lower one). On this basis, the direct approximate procedure will be employed (equation 8, step 5b). The e.r.e. at the extremities is 0.470 and 0.517, respectively. This represents, roughly speaking, 25% plus and 25% minus around the estimated frequency in a real experiment (e.g., f = fML ± 0.25.fML). When h is increased to 40 wells, the e.r.e. decreases to 0.369 and 0.405 at the extremities. One should expect to obtain (approximately) 20% plus and minus around the estimated frequency, representing a 20% increase in accuracy from the h = 25 design. This increase is obtained by a 60% increase (15/25) in the number of wells.
Example 2. The relative error is expected to be less than 0.45, N is limited to 300 wells, the expected frequency lies in a 10-fold range. What is best: to set the experiment as A: (d' = 2, P1 = 0.15, P2 = 0.30, h = 25) or B: (d' = 4, P1 = 0.10, P2 = 0.60, h = 30)? Notice that setup A concentrates results around the nadir of the relative error curve (see Figure 1), the so-called "most informative range". Setup A comprises 12 dilutions (d = 12) and setup B comprises d = 10. As in the above example, the expected Q at the upper and at the lower extremities of the frequency range is computed. Then, by computing the expected relative error at the extremities of the frequency range in each experimental setup one finds e.r.e. = [0.537 0.355] for A and e.r.e. = [0.412 0.379] for B. Therefore, experimental design B is more consistent with the maximum relative error desired in the entire range of the expected frequencies to be estimated. Coincidentally, it is also the less expensive in terms of dilutions to be prepared. All these relevant parameters could be determined beforehand.
Example 3. The relative error is expected to be £0.50, the unknown frequency is within a 15-fold range, N is limited to 240 wells. Does a general setting with d' = 3, P1 = 0.10, P2 = 0.70 and h adjusted as h = integer(N/d) fit the expectations? When the number of cells per dilution is computed under the Strijbosch et al. (3) procedure, one finds that d = 7 and, therefore, h = 34. The expected relative errors for the extremities of the frequency range are 0.434 and 0.466. Therefore, such a general setting fits well the expectations of relative errors of less than 0.50 for a 15-fold range of the unknown frequency.
Example 4. Consider a problem similar to the above example, but with the unknown frequency restricted to a 5-fold range. The experimental setup is now reduced to 5 dilutions, and thus h = 48. Accuracy increases, as indicated by the e.r.e. of 0.361 and 0.413 at the extremities.
Example 5. Employing the general setup used in example 3, one needs the relative error to be less than 0.2, in a 100-fold range of the unknown frequency. How many wells per dilution are needed to fulfill the expectations? The number of dilutions to cover such a frequency range (in this setting) is d = 10. Then, at the frequency extremities, e.r.e. = [0.183 0.199] when h = 183 (and, therefore, N = 1830 wells). In view of these figures, one would ask whether the experiment is feasible or not (either in terms of how many of these determinations are to be made or in terms of relaxing the relative error expected).
The use of dilutions related to each other by a power rule (e.g., y(n) = Z(n-1) ·y(1)) is given as an inadequate experimental setup procedure by Fazekas de St. Groth (2). When one computes the relationship between the number of cells in each dilution of the experimental setup given in example 5 each step is found to contain approximately 1.862 times the number of cells of the preceding one (i.e., the power scaling factor Z = 1.862). In fact, a given composition of d', P1 and P2 under the Strijbosch et al. (3) procedure generates a power scaling factor (notice that the frequency range does not matter for such an underlying rule). In example 1, the power scaling factor is 1.792. In example 2, the power scaling factor is 1.255 for setup A and 1.457 for setup B. Despite an underlying power scaling factor, it is possible to attain relative errors at a desired level, contradicting Fazekas de St. Groth's statement about the power rule. What this investigator means must be read as "one should not employ a fixed power scaling factor for every frequency determination". Strijbosch et al. (3) provide an easy way to find the adequate power scaling factor. This study provides an easy way to evaluate the accuracy such a scaling factor shall yield under empirical conditions.
Conclusion 
This study provides an easy way to estimate beforehand the relative error (i.e., the accuracy) of an LDA experimental setup. This can be done following steps 1, 2, 3, 4, 5b and 6 in Methods and in equations 7, 8 and 9, when the expected number of non-trivial dilutions(Footnote 4) is large (i.e., non-trivial dilutions comprise, overall, more than 100 wells). When such an expected number is less than 100, care must be taken because both the relative error and the nominal confidence level of the estimator can be wrongly estimated.
Footnotes
Footnote 1) It is not our concern to consider the arguments about the various definitions of probability.
Footnote 2). Notice that if Qob = 0, the best one can do is to state "f³z", thereby defining just one boundary. This implies the need to observe the whole population in order to accept the limit included by such an outcome. Mutatis mutandis, the same applies to Qob = 1.
Footnote 3) A method repeatedly shown to be inadequate for the purpose of frequency estimation in LDA in the last 20 years.
Footnote 4) Non-trivial dilutions are those in which the expected number of positive wells in the dilution is different from 100% and from 0%.
Address for correspondence: J.G. Chaui-Berlinck, Departamento de Fisiologia, Instituto de Biociências, USP, 05508-900 São Paulo, SP, Brasil. Fax: +55-11-818-7422, E-mail: jgcb@usp.br
J.G. Chaui-Berlinck was the recipient of a FAPESP post-doctoral fellowship (No. 97/10492-3). Received June 23, 1999. Accepted March 10, 2000.
- 1. Taswell C (1981). Limiting dilution assays for the determination of immunocompetent cell frequencies. I. Data analysis. Journal of Immunology, 126: 1614-1619.
- 2. Fazekas de St. Groth S (1982). The evaluation of limiting dilution assays. Journal of Immunological Methods, 49: R11-R23.
- 3. Strijbosch LWG, Buurman WA, Does RJMM, Zinken PH & Groenewegen G (1987). Limiting dilution assays: experimental design and statistical analysis. Journal of Immunological Methods, 97: 133-140.
- 4. Cobb L, Cyr L, Schmehl MK & Bank HL (1989). Comparison of statistical methods for the analysis of limiting dilution assays. In Vitro Cellular and Developmental Biology, 25: 76-81.
- 5. Schmehl MK, Cobb L & Bank HL (1989). Power analysis of statistical methods for comparing treatment differences from limiting dilution assays. In Vitro Cellular and Developmental Biology, 25: 69-75.
- 6. Burleson JÁ, Binder TA & Goldschneider I (1993). Use of logistic regression in comparing multiple limiting dilution analyses of antigen-reactive T cells. Journal of Immunological Methods, 159: 47-52.
- 7. Vuolo JH (1996). Fundamentos da Teoria dos Erros 2nd edn. Editora Edgard Blücher Ltda., Săo Paulo.
- 8. Sokal RR & Rohlf FJ (1995). Biometry: the Principles and Practice of Statistics in Biological Research 3rd edn. W.H. Freeman and Company, New York.
Appendix A
Appendix B
Correspondence
Publication Dates
-
Publication in this collection
31 July 2000 -
Date of issue
Aug 2000
History
-
Accepted
10 Mar 2000 -
Received
23 June 1999








