Abstract
Synthetic dyes bind to proteins causing selective coprecipitation of the complexes in acid aqueous solution by a process of reversible denaturation that can be used as an alternative method for protein fractionation. The events that occur before precipitation were investigated by equilibrium dialysis using bovine trypsin and flavianic acid as a model able to cause coprecipitation. A two-step mode of interaction was found to be dependent on the incubation periods allowed for binding, with pronounced binding occurring after 42 h of incubation. The first step seems to involve hydration effects and conformational changes induced by binding of the first dye molecule, following rapid denaturation due to the binding of six additional flavianate anions to the macromolecule.
dye binding; binding isotherm; coprecipitation
Braz J Med Biol Res, August 2001, Volume 34(8) 1047-1054
A time-dependent, two-step binding mode of the nitro dye flavianic acid to trypsin in acid media
J.M. Schneedorf1, M.M. Santoro2, R.E. Lovrien3 and M. Mares-Guia2
1Laboratório de Fitofármacos, Faculdade de Medicina, Universidade de Alfenas, Alfenas, MG, Brasil
2Departamento de Bioquímica e Imunologia, Instituto de Ciências Biológicas, Universidade Federal de Minas Gerais, Belo Horizonte, MG, Brasil
3Departmentof Biochemistry, University of Minnesota, St. Paul, MN, USA
References
Correspondence and Footnotes Correspondence and Footnotes Correspondence and Footnotes
Abstract
Synthetic dyes bind to proteins causing selective coprecipitation of the complexes in acid aqueous solution by a process of reversible denaturation that can be used as an alternative method for protein fractionation. The events that occur before precipitation were investigated by equilibrium dialysis using bovine trypsin and flavianic acid as a model able to cause coprecipitation. A two-step mode of interaction was found to be dependent on the incubation periods allowed for binding, with pronounced binding occurring after 42 h of incubation. The first step seems to involve hydration effects and conformational changes induced by binding of the first dye molecule, following rapid denaturation due to the binding of six additional flavianate anions to the macromolecule.
Key words: dye binding, binding isotherm, coprecipitation
Introduction
The earliest evidence for the interaction of dyes with proteins dates from 1909 when Sørenson observed indicator errors in pH determinations of protein solutions (1). A few years later, Chapman et al. (2) observed the correspondence between the amount of dye bound and the number of proton-binding groups in the protein. With the application of the mass action law to multiple equilibria, a theoretical basis became available for the thermodynamic treatment of dye-protein complexes (3). The ability of ionic dyes to precipitate proteins has long since been used in studying protein behavior upon unfolding, protection against denaturants, preservation of macromolecule conformation during stress, and bioseparation (4). The methodology for bioseparation of proteins using synthetic dyes includes affinity chromatography, aqueous two-phase partitioning and selective precipitation (5). The last method, initially suggested by Bertrand et al.(6), has the advantage that both enrichment and concentration are accomplished in a single step. Furthermore, there is less experimental variation as found in chromatographic procedures, and the possibility of working with large volumes of crude extract (7). Selective coprecipitation surveys were renewed during the last decade aiming at understanding crystallization and bioseparation processes, due to their simple execution and the low cost of the chemicals involved (4,8). Since Bertrand and co-workers (6) suggested protein precipitation induced by dyes as a useful complementary method for protein purification, much effort has been devoted to protein isolation by matrix ligand coprecipitation (4,6), including two US application patents (9,10). Recently, Wu and co-workers (11) were able to isolate lectins in a single-step procedure from crude extract using Little Rock Orange ligand, recovering the total specificity of the lectin similar to that of the product sold by Sigma Chemical Co. (St. Louis, MO, USA).
In the present study we investigated a generic dye-protein coprecipitating model, the binding of the organic sulfonated nitro dye flavianic acid to bovine trypsin, as a part of a program for screening potential dyes for protein isolation by matrix coprecipitation. Flavianic acid, 2,4-dinitro-1-naphthol-7-sulfonic acid, is a yellow textile dye first used in the thirties to fractionate basic amino acids from crude protein extracts, aiming at sample purification and the development of lysine- and histidine-free diets (12). Lately it has been used for histonase detection (13) and total protein determination (14). We were able to disclose a time-dependent feature occurring before the aggregation and precipitation phenomena that may be relevant to fractionation procedures through selective coprecipitation.
Material and Methods
General
Bovine trypsin was purchased from Sigma. The concentration of enzyme active centers was determined with p-nitrophenyl-p'-guanidinobenzoate according to Chase and Shaw (15). Enzyme samples were prepared daily, centrifuged in a Sorvall instrument at 45,000 g (SS-34 rotor) for 45 min to remove a small insoluble residue, and filtered through a nitrocellulose membrane. The concentration of purified flavianic acid as a twice-crystallized monosodium salt was determined spectrophotometrically using extinction coefficients calculated for the solvent equilibrium system. Other chemicals used were of analytical grade.
Dialysis equilibrium
The experiments were carried out in acrylic cells assembled according to the specifications of Teraoka and Nierhaus (16). Membranes of 5000 MW cut-off were used to separate the chamber half-cells. Concentrations of flavianic acid up to 4 mM in 1.1 ml of 50 mM sodium citrate buffer, pH 3.0, were used. Dye was applied in buffer at 4oC to one half-cell; the other half-cell contained an identical volume with 0.5 mg of trypsin in the buffer. Data were collected by withdrawing 20 µl of dye solution from the free ligand half-cell at fixed time intervals. The activity coefficients of the free ligand were assumed to be equal at the end of the experiment as relatively high concentrations of protein and salts were used in the cells, thus limiting Donnan effects (17). The binding rate was determined spectrophotometrically according to the following equation:
where n = binding ratio of the interaction (moles of bound dye per mole of enzyme), PLi = number of moles of the bound ligand (complex), Pt = total number of moles of protein added, Lt = total number of moles of ligand added, Lm = number of moles of adsorbed ligand on the membrane, and L = number of moles of free ligand per half-cell.
Results and Discussion
Equilibrium assays
The data obtained from dialysis experiments were of satisfactory quality, with an information content for each isotherm ranging from 4.4 to 6.0 bits, which represents 65-84% of maximum information available for the different incubation periods assayed (18). The thermodynamic value for n, the maximum binding ratio of interaction, was found to be related to the time period allowed for the chemical species to interact (upper panel of Figure 1). The binding mode of the interaction also seemed to change depending on the incubation period used: equilibrium dialysis conducted from 18 to 139 h of incubation periods showed a sharp change in Scatchard profiles (19) as can be seen in the lower panel of Figure 1. The deviations from a straight line in Scatchard plots may be attributed to several effects including interactions due to cooperativity between neighboring binding sites, heterogeneity of population of sites and/or creation of new binding sites. Assuming no statistical effects (19), heterogeneity can be distinguished from cooperativity by structural differences at the binding sites, which are present from the start for the former, and generated in the course of the reaction for the latter. Ligand isomerization (20) seems also to occur, since the maximum molar ratio found at 139 h of incubation indicates a number of bound ligands that is twice larger than the 23 positive groups available on trypsin at pH 3.0 (21). Furthermore, the trend shown in the upper panel of Figure 1 indicates a non-asymptotic character of n values with increasing periods of incubation after 42 h. These observations suggest a two-step binding mode for the flavianate-trypsin system.
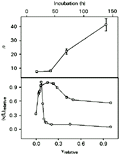 Upper panel: n, maximum molar ratio of binding with increasing incubation times of 18, 42, 70 and 139 h. Solutions of trypsin and flavianate were 21 µM and 0.8 mM, respectively. Lower panel: Scatchard plots of the interaction at incubation times of 18 (circles) and 139 h (squares); the values are relative to the maximal ones. Dye concentration range was 1 µM to 0.8 mM with trypsin at 21 µM.
Upper panel: n, maximum molar ratio of binding with increasing incubation times of 18, 42, 70 and 139 h. Solutions of trypsin and flavianate were 21 µM and 0.8 mM, respectively. Lower panel: Scatchard plots of the interaction at incubation times of 18 (circles) and 139 h (squares); the values are relative to the maximal ones. Dye concentration range was 1 µM to 0.8 mM with trypsin at 21 µM.
Figure 1. Binding of flavianate to trypsin at different incubation periods. Upper panel: n, maximum molar ratio of binding with increasing incubation times of 18, 42, 70 and 139 h. Solutions of trypsin and flavianate were 21 µM and 0.8 mM, respectively. Lower panel: Scatchard plots of the interaction at incubation times of 18 (circles) and 139 h (squares); the values are relative to the maximal ones. Dye concentration range was 1 µM to 0.8 mM with trypsin at 21 µM.
[View larger version of this image (7 K GIF file)]
As binding models are poorly resolved in graphic representations (22), nonlinear regression based on the Marquadt algorithm was applied to discriminate between rival models for cooperativity, site heterogeneity and one-site creator models of binding data at 18 and 139 h. The binding equations are provided by Dahlquist (19), Olsen et al. (23) and Parsons and Vallner (24), and can be viewed in Figure 2. All adjustments were convergent, with tolerance satisfied and no ill-matrix conditions. The chi-square values obtained from the fitting are summarized in Table 1. The data point to a statistical superiority of the one-site creator model against cooperativity and heterogeneity models (25). Since a two-step model for the binding of flavianate to trypsin seems to be seen only after 42 h of incubation and with a possible non-asymptotic trend (upper panel of Figure 1 and Figure 3), we investigated the apparently more stable binding at 18 h of incubation, which precedes the second step of massive binding of flavianate. The maximum number of sites filled by the dye on the trypsin surface at 18 h of incubation was estimated to be close to seven under the experimental conditions (Figure 1). This value was close to the five flavianate molecules found upon binding to serum albumin at pH 5.0 (26) and also to lysozyme at pH 5.5 (27). It also shows the role of basic groups on trypsin in the adsorption process, as the increase of binding ratio was attained by lowering the pH value. The maximum molar ratio found was obtained from nonlinear estimation fitting (Sigma Plot 2.0, Jandel Scientific, Chicago, IL, USA) of the overall values of free ligand concentration, L, and binding ratios, v, applied to a single hyperbola derived from the Adair relation (18).
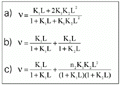 i is the binding constant for the interaction, L is the free ligand concentration, and ni is the i site population for the interaction.
i is the binding constant for the interaction, L is the free ligand concentration, and ni is the i site population for the interaction.
Figure 2. Equations provided for nonlinear adjustments of cooperativity (a; 23), heterogeneity (b; 19), and one-site creator (c; 24). Models were applied to the equilibrium data at 18 and 139 h. Ki is the binding constant for the interaction, L is the free ligand concentration, and ni is the i site population for the interaction.
[View larger version of this image (6 K GIF file)]
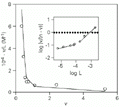 Inset: Hill plot of the data. The lines represent values calculated by linear regressions applied to the two population sites filled by flavianate (see text).
Inset: Hill plot of the data. The lines represent values calculated by linear regressions applied to the two population sites filled by flavianate (see text).
Figure 3. Scatchard representation of the binding of flavianic acid to trypsin at 18 h of incubation. The line was fitted to the heterogeneity model with binding constants calculated according to the deconvolution method of Schreier and Schimmel (31). Inset: Hill plot of the data. The lines represent values calculated by linear regressions applied to the two population sites filled by flavianate (see text).
[View larger version of this image (5 K GIF file)]
The nonlinearity of the Scatchard plot (Figure 3) suggests a dependence of microscopic binding constants during enzyme saturation (19). This relationship is also reinforced by the outline found in the Hill plot shown in the inset of Figure 3, although the plot seems to be linear up to 0.1 mM of free dye concentration (28). Scatchard representation was chosen for this analysis due to its better sensitivity for detection of complex systems such as site heterogeneity than Hill plots or Langmuir-like isotherms (22). Although inspection of binding curves was used in the past to distinguish between cooperativity and heterogeneity models, they are only discriminated definitely with the aid of direct measurements such as optical rotation or X-ray diffraction (19,27). These two models cannot be distinguished graphically, since they predict identical profiles despite their distinct equations (22). Furthermore, curvature in a Scatchard-type plot does not necessarily indicate different orders of cooperativity or interference effects (29). The subtractive method of equilibrium dialysis is able to offer only indirect measurements and indications about conformational properties of macromolecules (27). However, the straightforward analysis of binding data for detecting cooperativity phenomena is mainly done by estimating the Hill coefficient, nH (30). This parameter indicates changes in the chemical potential of bound and free sites as a function of the chemical potential of the free ligand.
The Hill plot shown in the inset of Figure 3 seems to present a curvilinear trend with a free ligand concentration above 0.1 mM, which results in distinct apparent nH values at different free dye concentration ranges. This result suggested an apparent cooperativity between sites on trypsin arising from the first site filled on the enzyme. Up to 0.1 mM of dye, however, the data fit reasonably well to the unitary Hill value. This observation suggested an interaction of flavianate with trypsin with two different populations of binding sites. A deconvolution method of successive approximations was applied to the biphasic Scatchard plot to determine the binding constants for two populations of sites (31). The method was chosen due to its independence of the mechanistic model involved. The dissociation constant for the interaction of trypsin with flavianic acid obtained by this approach is shown in Table 2, together with some values referring to other dye-protein interactions for comparison (see Refs. 7,32,33). With two classes of binding sites for flavianate on trypsin found at 18 h of incubation, the ordinate values in the Hill plot should better fall into two straight lines rather than a curvilinear one (inset of Figure 3). In this way, the first site classes gave an nH value of 0.28 (R = 0.978) and the stronger site population an nH value of 1.09 (R = 0.995) as calculated by linear regression applied to the data, suggesting an apparent negative cooperativity taking place during the filling of the first site class.
Cooperative effects in the binding of ligands to proteins can be positive or negative and involve the occupation of two or more binding sites (24). Positively cooperative effects may be accompanied by conformational adaptations in the protein structure to attain the most favorable energetics for ligand binding. Negative cooperativity, however, is generally viewed as the difficulty of a ligand to cross over the energy barrier implied in a previous binding. In this sense, a pure cooperativity obligatorily involves two or more binding events, because it has a conceptual need of two or more binding sites. Therefore, the outline of the first binding of a flavianate molecule to trypsin rules out any pure cooperative effect, and suggests that an apparent negative cooperativity takes place in the system.
This apparent negative cooperativity could then be explained by a difficulty to cross the energy barrier for initial dye binding rather than being pure cooperativity. Apparent cooperativity was also found in other dye-protein systems, being related to protein self-associations (34) and to hydration effects on the protein surface due to water displacement (35). The occurrence of two classes of binding sites on trypsin could also arise from changes in the shape of the protein as a consequence of a progressive rearrangement of the residues following an entropic disturbance introduced by the dye. The small nH value found up to 0.1 mM of free ligand concentration (Figure 3) could also be due to the energetic imbalance resulting from the binding of the first flavianate molecule, against the positive free energy generated from a strong conformational change on trypsin. Scatchard analysis alone is insufficient to establish conformational changes in proteins. This occurs because a linearity deviation from a Scatchard profile can also arise from ligand self-association (20), heterogeneity of binding sites (22), cooperativity (24), site creation (19), and protein denaturation (35), among others (29). In order to evaluate the hypothesis of flavianate-induced trypsin transconformation, another approach using the same experimental data was employed.
We adopted a procedure suggested by Tandford (36) and based on the treatment of electrostatic approximation of Debye and Hueckel to rigid and impenetrable ellipsoid models of proteins, as the flavianate ion has two negative charges at pH 3.0 (37). This approach relates the electrostatic work required to bring a charged molecule from infinite to the macromolecule surface as follows (36):
Eq. 2where a = fraction of bound sites n/n, pL = -log L, Kint = intrinsic constant of the association, w = electrostatic factor of Debye and Hueckel, zi = charge of the ion under the conditions assayed, and Z = net charge of the ligand-protein complex under the conditions assayed.
Figure 4 shows a continuous decrease of the plot slopes up to the filling of the first site on the trypsin molecule, suggesting that the saturation process could occur as a denaturation mechanism of a biphasic character, since decreasing values for the slopes point to asymmetry and penetrability, leading to a protein configuration spatially more disordered (35). The decrease in these values may also suggest electrostatic repulsion and hydrogen bond disruption (27). In this case, the initial saturation of the protein could be facilitated by a swelling of trypsin, supplying intermolecular space and enhancing the transconformation mediated by the dye. Dye-induced conformational changes were also found in the interaction of auramine O with alcohol dehydrogenase (38).
After formation of the trypsin-flavianate complex with a 1:1 stoichiometry (Figure 4), additional flavianate molecules will lead to aggregation reactions and transconformation in trypsin, resulting in the coprecipitation phenomena observed at high ligand concentrations. The initial coprecipitation would be enhanced by dye bridges produced from large aromatic areas offered by the naphthalene ring of flavianate, both adsorbed on trypsin or in solution. The latter could also be produced from isomerization of dye molecules since self-interactions are common in organic dye binding, contributing to the concavity found in the Scatchard plot (Figure 3 and Ref. 20).
Figure 4. Dependence of the saturation of binding sites on trypsin by flavianate after 18-h incubation upon the net charge on the enzyme (Equation 2). The dotted lines represent linear adjustments applied to each data set. The a parameter represents the fraction of bound sites n/n in trypsin.
[View larger version of this image (14 K GIF file)]
Nature of the binding
When a protein adsorbs ions in aqueous solution, the resulting Langmuir-like isotherm may be interpreted by assuming coulombic attraction between independent charged centers on the polymer and the anion (35). The strength of this interaction could be due mainly to the aromatic surface area of the ligand (8). Increasing ion size seems to lead to stronger binding, as nonpolar interactions are viewed as a second requirement of organic ligands upon binding to proteins. The average contribution of free binding energy of seven flavianate anions to trypsin is of the order of -0.9 kJ/mol. This is within the -1.7 kJ/mol range suggested by Rosemberg (17) as typical entropy-driven force of weak interactions due to water displacement from the hydration shell of the protein surface. At the molecular level, a higher affinity for some larger anions may be due to a greater degree of dehydration of the complex rather than to increased van der Walls interactions (39). In this way, anions of the size of flavianate, methyl orange, Biebrich scarlet and Congo red should have aromatic surface areas directly related to their values of free binding energy (Table 2). The entropy-driven character of flavianate binding to trypsin was not tested at different temperatures since a negligible or neutral thermal effect was found in the past on isotherms of organic dyes with proteins (39). Meanwhile, preliminary calorimetric assays performed by us showed a positive enthalpy value of the same order of magnitude as the free energy of binding, with an entropy change DS of +26.3 entropy units. This value is in agreement with those found for binding of alkyl sulfates to serum albumin and for polymerizing reactions of antigen-antibody systems of bovine serum albumin and ovalbumin (35). It also applies to entropy-driven interactions in hydrophobic and electrostatic binding, the latter accomplished by water release from the protein surface (35). Similar results were obtained on displacement of five water molecules from the avidin surface by 2-(4'-hydroxyazobenzene) benzoic acid (40). Furthermore, calculations of binding surface area carried out with the Insight II Builder (release 2.2.0, Biosym, San Diego, CA, USA) resulted in a maximum area occupied by seven flavianate molecules equal to 10% of the trypsin surface area, pointing to the dependence on the electrostatic effects of the groups on the protein, assuming that positively charged groups on trypsin are not restricted to 10% of the surface (18). This picture is consistent with the hypothesis of interacting hydration effects in trypsin (33). The trypsin molecule has 900 water molecules accessible in its first hydration shell inside the crystal, with displacement of one water molecule on the binding of a sulfonic group, leading to five hydrogen bonds between the latter and five external water molecules (21).
The overall treatment of Scatchard, Hill and Tandford analyses showed the binding of flavianate to trypsin to be a ligand-induced protein transconformation process. After the first dye molecule is bound to trypsin, new binding sites are created on the enzyme, proportional to the time of the interaction, together with ligand isomerization at high dye concentrations. The kinetic dependence of the binding also indicated the maintenance of the first step mode of binding for a relatively long period of time (42 h, upper panel in Figure 1). The other interplaying hypotheses discussed earlier, such as ligand isomerization and protein transconformation, should be considered to explain the Scatchard deviation from a straight line shown in Figure 3. For the whole binding process, this is reflected on the difficulty of placing all variables considered in a two-dimensional plot (28). Furthermore, the incubation periods should be taken into account for improvement of protein fractionation through selective coprecipitation with dyes. In our case, a massive coprecipitation of the flavianate-trypsin system was observed with time-dependent binding steps.
Acknowledgments
We thank Mr. Carlos Henrique Silveira for his help with the surface area calculations.
Address for correspondence: J.M. Schneedorf, Laboratório de Fitofármacos, Faculdade de Medicina, Universidade de Alfenas, Rodovia MG 179, km 0, 37130-000 Alfenas, MG, Brasil. Fax: +55-35-299-3239. E-mail: jose.silva@unifenas.br
Research supported by CNPq, FAPEMIG and BioBRAS S.A. Received October 18, 2000. Accepted May 2, 2001.
- 1. Klotz IM & Walker FM (1947). Spectral changes in some dye ions and their relation to the protein error in indicators. Journal of Physical and Colloidal Chemistry, 51: 666-680.
- 2. Chapman L, Greenberg DM & Schmidt CLA (1927). Studies on the nature of the combination between certain acid dyes and proteins. Journal of Biological Chemistry, 72: 707-729.
- 3. Klotz IM, Walker FM & Pivan RB (1946). The binding of organic ions by proteins. Journal of the American Chemical Society, 68: 1486-1490.
- 4. Conroy MJ & Lovrien RE (1992). Matrix coprecipitating and cocrystallizing ligands (MCC ligands) for bioseparations. Journal of Crystal Growth, 122: 213-222.
- 5. Garg N, Galaev IYU & Mattiasson B (1996). Dye-affinity techniques for bioprocessing: recent developments. Journal of Molecular Recognition, 9: 259-274.
- 6. Bertrand D, Cochet S & Kroviarski Y (1985). Protein precipitation induced by a textile dye. Precipitation of human plasminogen in the presence of procion red HE3B. Journal of Chromatography, 346: 111-114.
- 7. Neiderauer MQ & Glatz CE (1992). Selective precipitation. In: Niederauer MQ (Editor), Advances in Biochemical Engineering/Biotechnology Springer-Verlag, Berlin, 159-188.
- 8. Gupta MN, Kaul R, Guoqiang D, Dissing U & Mattiasson B (1996). Affinity precipitation of proteins. Journal of Molecular Recognition, 9: 356-359.
- 9. Mattiasson BG & Galaev IY (1993). Affinity purification of a target substance by the use of an immobilized ligand complexed with a second target substance. PCT International Application WO 94 15, 951 (Cl. C07K3/20).
- 10. Nuijens JH & Van Corven EJ (1994). Separation of human serum albumin. PCT International Application WO 96 02, 573 (Cl. C07K14/765).
- 11. Wu CW, Lovrien R & Matutis D (1998). Lectin coprecipitative isolation from crudes by Little Rock Orange ligand. Analytical Biochemistry, 257: 33-39.
- 12. Bunney HE & Rose WC (1928). Growth upon diets practically devoid of arginine, with some observations upon the relation of glutamic and aspartic acid to nutrition. Journal of Biological Chemistry, 76: 521-534.
- 13. Kass L (1974). Demonstration of histonase with flavianic acid. Journal of Histochemistry and Cytochemistry, 22: 1159-1162.
- 14. Noel-Courtney B (1975). Effects of colchicine on the content of ribonucleic acids and total proteins of culture nerve cells. Preliminary study. Bulletin de l'Association des Anatomistes, 59: 235-240.
- 15. Chase T & Shaw E (1967). p-Nitrophenyl-p'-guanidinobenzoate-HCl: A new active site titrant for trypsin. Biochemical and Biophysical Research Communications, 29: 508-514.
- 16. Teraoka H & Nierhaus KH (1979). Measurement of the binding of antibiotics to ribosomal particles by means of equilibrium dialysis. Methods in Enzymology, 59: 862-866.
- 17. Rosemberg RM (1960). Dye binding methods. In: Alexander R & Block RT (Editors), Analytical Methods of Protein Chemistry Pergamon Press, London.
- 18. Weber G & Anderson SR (1965). Multiplicity of binding range of validity and practical test of Adair's equation. Biochemistry, 4: 1942-1947.
- 19. Dahlquist FW (1978). The meaning of Scatchard and Hill plots. Methods in Enzymology, 48: 270-298.
- 20. Ishida T, Horiike K, Tojo H & Nozaki M (1988). Interaction of protein with a self-associating ligand. Deviation from a hyperbolic binding curve and the apparent cooperativity in the Scatchard plot. Journal of Theoretical Biology, 130: 49-66.
- 21. Bartunik HD, Summers LJ & Bartsch HH (1989). Crystal structure of bovine ß-trypsin at 1.5 Å resolution in a crystal form with low molecular packing density. Active site geometry, ion pairs and solvent structure. Journal of Molecular Biology, 210: 813-828.
- 22. José MV & Larralde C (1982). Alternative interpretation of unusual Scatchard plots: contribution of interactions and heterogeneity. Mathematical Biosciences, 58: 159-170.
- 23. Olsen RW, Bergman MO, Van Ness PC, Lummis SC, Watkins AE, Napias C & Greenlee DV (1981). g-Aminobutyric acid receptor binding in mammalian brain. Heterogeneity of binding sites. Molecular Pharmacology, 19: 217-227.
- 24. Parsons DL & Vallner JJ (1978). Theoretical models for cooperative binding. Mathematical Biosciences, 41: 189-240.
- 25. Bevington PR (1969). Data Reduction and Error Analysis for the Physical Sciences McGraw-Hill, New York.
- 26. Lewin J (1951). Preparation and properties of serum and plasma proteins XXX. Crystaline derivatives of human serum albumin and of certain other proteins. Journal of the American Chemical Society, 73: 3906-3911.
- 27. Steinhardt J & Reynolds JÁ (1969). Multiple Equilibria in Proteins Academic Press, New York.
- 28. Cornish-Bowden A & Koshland DE (1975). Diagnostic uses of the Hill (Logit and Nernst) plots. Journal of Molecular Biology, 95: 201-212.
- 29. Shimitz KS (1977). Inapplicability of "Scatchard-type" analysis to highly cooperative binding systems. Biopolymers, 16: 143-155.
- 30. Neet EK (1980). Cooperativity in enzyme function: equilibrium and kinetic aspects. Methods in Enzymology, 64: 139-192.
- 31. Schreier AA & Schimmel PR (1974). Interaction of manganese with fragments, complementary fragment recombinations, and whole molecules of yeast phenylalanine specific transfer RNA. Journal of Molecular Biology, 86: 601-620.
- 32. Glazer NA (1967). The specific binding of Biebrich scarlet to the active site of a-chymotrypsin. Journal of Biological Chemistry, 242: 4528-4533.
- 33. Klunk WE, Pettegrew JW & Abraham DJ (1989). Two simple methods for quantifying low-affinity dye-substrate binding. Journal of Histochemistry and Cytochemistry, 37: 1293-1297.
- 34. Johnson ML, Formisano S & Edelhoch H (1978). Self-association of glucagon as measured by the optical properties of rhodamine 8G. Journal of Biological Chemistry, 253: 1353-1356.
- 35. Kauzmann W (1959). Some factors in the interpretation of protein denaturation. Advances in Protein Chemistry, 14: 1-63.
- 36. Tandford C (1961). Electrostatics. In: Tandford C (Editor), Physical Chemistry of Macromolecules John Wiley & Sons, New York, 526-586.
- 37. Schneedorf JM, Santoro MM & Mares-Guia M (1998). Flavianate, an amino acid precipitant, is a competitive inhibitor of trypsin at pH 3.0. Brazilian Journal of Medical and Biological Research, 31: 1105-1111.
- 38. Weers JG & Maki AH (1986). Triplet-singlet energy transfer in the complex of auramine O with horse liver alcohol dehydrogenase. Biochemistry, 25: 2897-2904.
- 39. Klotz IM & Urquhart H (1949). The binding of organic ions by proteins. Effect of temperature. Journal of the American Chemical Society, 71: 847-851.
- 40. Livnah O, Bayer EA, Wilchek M & Sussman JL (1993). The structure of the complex between avidin and the dye, 2-(4'-hydroxyazobenzene) benzoic acid (HABA). FEBS Letters, 328: 165-168.
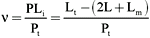
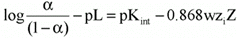
Correspondence and Footnotes
Publication Dates
-
Publication in this collection
20 July 2001 -
Date of issue
Aug 2001
History
-
Accepted
02 May 2001 -
Received
18 Oct 2000



