Abstract
We measured human frequency response functions for seven angular frequency filters whose test frequencies were centered at 1, 2, 3, 4, 8, 16 or 24 cycles/360º using a supra-threshold summation method. The seven functions of 17 experimental conditions each were measured nine times for five observers. For the arbitrarily selected filter phases, the maximum summation effect occurred at test frequency for filters at 1, 2, 3, 4 and 8 cycles/360º. For both 16 and 24 cycles/360º test frequencies, maximum summation occurred at the lower harmonics. These results allow us to conclude that there are narrow-band angular frequency filters operating somehow in the human visual system either through summation or inhibition of specific frequency ranges. Furthermore, as a general result, it appears that addition of higher angular frequencies to lower ones disturbs low angular frequency perception (i.e., 1, 2, 3 and 4 cycles/360º), whereas addition of lower harmonics to higher ones seems to improve detection of high angular frequency harmonics (i.e., 8, 16 and 24 cycles/360º). Finally, we discuss the possible involvement of coupled radial and angular frequency filters in face perception using an example where narrow-band low angular frequency filters could have a major role.
Spatial frequency; Angular frequency; Narrow-band frequency filters; Polar gratings; Radial frequency
Braz J Med Biol Res, February 2002, Volume 35(2) 243-253
Narrow-band 1, 2, 3, 4, 8, 16 and 24 cycles/360 o angular frequency filters
M.L.B. Simas1 and N.A. Santos2
1LabVis, Departamento de Psicologia, Universidade Federal de Pernambuco, Recife, PE, Brasil
2Programa de Neurociências e Comportamento, Departamento de Psicologia, Universidade de São Paulo, São Paulo, SP, Brasil
References
Correspondence and Footnotes Correspondence and Footnotes Correspondence and Footnotes
Abstract
We measured human frequency response functions for seven angular frequency filters whose test frequencies were centered at 1, 2, 3, 4, 8, 16 or 24 cycles/360º using a supra-threshold summation method. The seven functions of 17 experimental conditions each were measured nine times for five observers. For the arbitrarily selected filter phases, the maximum summation effect occurred at test frequency for filters at 1, 2, 3, 4 and 8 cycles/360º. For both 16 and 24 cycles/360º test frequencies, maximum summation occurred at the lower harmonics. These results allow us to conclude that there are narrow-band angular frequency filters operating somehow in the human visual system either through summation or inhibition of specific frequency ranges. Furthermore, as a general result, it appears that addition of higher angular frequencies to lower ones disturbs low angular frequency perception (i.e., 1, 2, 3 and 4 cycles/360º), whereas addition of lower harmonics to higher ones seems to improve detection of high angular frequency harmonics (i.e., 8, 16 and 24 cycles/360º). Finally, we discuss the possible involvement of coupled radial and angular frequency filters in face perception using an example where narrow-band low angular frequency filters could have a major role.
Key words: Spatial frequency, Angular frequency, Narrow-band frequency filters, Polar gratings, Radial frequency
Introduction
The existence of narrow-band spatial frequency filters first demonstrated by psychophysical work (1,2) is now well established. This information integration seems to occur mainly in the striate and extrastriate cortex. Integration at higher levels in the visual system has been extensively investigated in many psychophysical and physiological studies. However, literature involving angular frequency stimuli is scattered and somewhat scarce. One of the main streams has been based on the proposition by Dodwell (3) derived from the work of Hoffman (4) who introduced the application of Lie Transformation Groups Algebra to visual processes. For these authors, spatial filtering in polar coordinates is a by-product of the Lie Transformation Group for Neuropsychology (LTG-NP) model. A variety of psychophysical (5,6) and physiological studies (7,8) have been obtaining evidence in favor of the LTG-NP model. Other physiological studies by the group of Tanaka (9,10) dealing with motion vectors having polar organizations also have shown the existence of cells that could conform to this model. However, these investigators do not address this specific theory. Other physiological studies have used traditional sine wave gratings, checkerboard-like stimuli or complex form stimuli (11-13) as well as faces and hands (14) to investigate cell responses from striate cortex to higher visual areas (15,16). Pasupathy and Connor (15) measured cell responses to angles and found "strong bias towards" responses to convex angles. Such a finding is in agreement with our psychophysical findings for angular frequency stimuli. The study of Hedge and Van Essen (16) also measured responses of cells to angles and polar gratings in V2. Furthermore, at least another study used functional magnetic resonance imaging (MRI) in humans together with stimuli defined in polar coordinates to evaluate responses of V1 and neighboring retinotopic areas (17).
Our work since 1985 (18,19) has focused mainly on characterizing the human visual system through its psychophysical responses to contrast of spatial frequency targets defined in polar coordinates and, since 1995, is trying to relate this processing to face perception (Simas MLB and Santos NA, unpublished data).
Angular frequency stimuli
Angular frequency stimuli have appeared in the literature under a variety of names. Some studies have used terms like radial targets, radial gratings, polar gratings, windmill stimuli, star-like, among others (e.g., 7,8,10,17). For the sake of consistency we have kept our original nomenclature since it was adopted in 1985 (18). Thus, we define angular frequency as a spatial frequency varying sinusoidally (or cosinusoidally, depending on how phase is considered) with angle within a circle being an adimensional integer stimulus whose frequency is independent of the distance of the observer.
This stimulus was conceived as the orthogonal component based on equation 4 of reference 19 derived from Sneddon (20). Such equation coupling radial and angular components is:
Radial frequency stimuli
We call radial frequency the spatial frequency varying along the radius of a circle. Amidor (21) and Wilkinson and colleagues (22) recently used this same terminology (but not the same modulation profile, i.e., Bessel functions). This is the orthogonal component of angular frequency stimuli in Equation 1.
More recent research concerning radial frequency has been directed mainly towards local filtering of spatial characteristics employing Gabor's or DOG functions as elementary stimuli to probe local processing (e.g., 23,24).
We have been using Bessel functions as suggested by Kelly (25) as well as by Sneddon's (20) equation, but we will show our results with radial frequencies elsewhere. Some of our results are presented in a previous paper (26).
Other theoretical perspectives using polar coordinates
Other approaches involving or discussing models of visual processing related to polar stimuli are those used by Koenderink and van Doorn (27) and by the group of Wilson (e.g. 28-30). While Koenderink argues for a wavelet, a Cartesian and a polar representation of the receptive fields of the cell, Wilson argues for nonlinear interactions (28) and uses random dot "Glass patterns" (29).
Narrow-band angular frequency filters
We first tried to demonstrate the existence of many narrow-band angular frequency filters in 1992 (31). We used the arbitrary trigonometric definition of phase for background frequencies of 1, 2, 3, 4, 6, 9, 13, 16, 24, 32, 47, 64 and 96. We measured seven filters at test angular frequencies of 2, 4, 9, 13, 16, 24 and 47 cycles/360º using the same supra-threshold method of the present study, which is based on that of sub-threshold summation (32). Instead of using sub-threshold levels of contrast to measure the peak of the function, we used supra-threshold summation whereby the test frequency is summed to a background frequency of higher contrast (i.e., 42%). While contrast of the test frequency is varied according to observer sensitivity, contrast of the background frequency is fixed above threshold (i.e., supra-threshold). In this manner, if a stimulus containing only the background frequency is compared to a stimulus in which the background frequency is summed to the test frequency the only way of differentiating between the pair will be to detect the presence of the test frequency in one of them. Our results showed absolute or relative summation effects at the test frequencies used surrounded by strong inhibition. We concluded for the existence of some selectivity for specific ranges of angular frequencies.
Phase selection
Our earlier studies involving angular frequency (18,19,31,33) used arbitrary phases based on the origin of the trigonometric circle, i.e., maximum luminance set to the right. All stimuli generated had the same origin in common.
The present study uses differently selected phases based on some known psychological phenomenon. For instance, when we observe a circle with shadows such that the lighter part is placed at the top and the darker at the bottom we perceive the stimulus as protruding from the plane while inversion produces a converse effect. Other orientations were selected on the assumption that angular frequency might be involved in face processing and other related perceptual phenomena.
Thus, we have selected phases based on symmetries of hemispheres and quadrants. Our axis choice was vertical versus horizontal. So, under these conditions, n-even angular frequencies present symmetric quadrants while n-odd ones present symmetric vertical hemispheres. We arbitrarily set minimum luminance for all n-even and n-odd (except for one cycle as well as for multiples of odd numbers) at position north (i.e., traditionally 90º). These exceptions for one cycle and for multiples of odd numbers will be discussed elsewhere. They are based on a configuration after-effect phenomenon we found which will be presented elsewhere. Figure 1 shows the phases used for six of the seven test angular frequencies in the experiment reported here. All additions were made in phase.

Phases used for six (1, 2, 3, 4, 8, and 16 cycles/360º) of the seven test angular frequencies in the experiment here reported.
[View larger version of this image (40 K JPG file)]
Contrast sensitivity to angular frequencies
Why work with angular frequencies when evidence from cells in the striate cortex points to orientation selectivity? Figure 2 shows contrast thresholds for angular frequencies (new phase definition) as compared to sine wave gratings. This result is a replicate of that reported in 1997 (33). We found that the visual system is at least two-fold more sensitive to angular frequencies than to sine wave gratings in the respective maximum sensitivity ranges. This would not necessarily be expected because some studies have shown inhibition among sine wave gratings at orthogonal or other orientations (e.g., 34).
Working with angular frequencies and psychophysical methods since 1985 based only on the Equation 1 derived from Sneddon (20) was not in tune with many physiological data. At that time evidence from the work of Hubel and Wiesel (35) did not lead in this direction. Only recently did physiological evidence favoring this type of stimulus configuration become available (7,8). Additional evidence comes from studies of cells sensitive to expansion/contraction and rotation (9,10) and involves movement.
Indeed, if angular frequency is being used by any visual system it requires integration over wide areas assembling information across hemispheres and quadrants. This implies integration across higher areas of the visual system. Furthermore, in our view, the processing of angular frequencies is coupled to that of radial frequencies except for n = 0 (refer to Equation 1). In this case, we would be looking at global aspects of spatial processing.

Contrast thresholds for angular frequencies (new phase definition) as compared to sine wave gratings. This result is a replicate of that reported in 1997 (33).
[View larger version of this image (8 K GIF file)]
The present study
In the experiments reported here we assume that higher areas of the visual system (e.g., V4 and IT) might be processing information in terms of coupled radial and angular frequencies.
Gallant and colleagues (7,8) showed the existence of groups of cells for detecting angular frequency in V4. We take this to be strong encouragement to follow the theoretical line underlying the present psychophysical work.
In the present study we set out to measure angular frequency filters centered at 1, 2, 3, 4, 8, 16 and 24 cycles/360º using the different phases as stated in the Phase selection section. We used the same supra-threshold method and increased the sample to 17 background angular frequencies. We also used a monitor with higher contrast resolution.
The main objectives were to establish the existence of narrow-band angular frequency filters using the new phase selection and observe how integration may be made as we shift from lower fundamental angular frequencies (e.g., 1 through 4 cycles/360º) to higher harmonics.
We must keep in mind that as angular frequency is increased to 24 cycles/360º, sensitivity increases and information becomes more redundant (presenting symmetric quadrants). So, it is important to establish how higher angular frequencies are related to lower ones (that require more integration).
Material and Methods
Subjects
Five 19-30-year-old naive subjects with normal or corrected vision participated in the measurements.
Equipment and stimulus material
All images were displayed on a 20-inch Sony BVM-1910 monitor (30 Hz, interlaced RGBsync, resolution: 900 lines) controlled by a 386-IBM compatible microcomputer through a DT-2853 frame grabber. Experiments were run on-line. Measurements were made using pairs of stimuli composed of a single-background angular frequency or of the sum of a background angular frequency-plus-test frequency. Background angular frequencies were 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 16, 24, 32, 48, 64 or 96 cycles/360º. The test angular frequencies were 1, 2, 3, 4, 8, 16 or 24 cycles/360º. Figure 1 shows six of the seven test frequencies used at their arbitrarily selected phases: at top left, 1 cycle, top right, 2 cycles/360º, center left, 3 cycles/360º, center right, 4 cycles/360º, bottom left, 8 cycles/360º, and bottom right, 16 cycles/360º. Please observe the selected phases.
Procedure
The supra-threshold summation procedure for an experimental condition consisted of having the observer select which of the components of a stimulus pair contained the sum background-plus-test frequency. Only contrast of the test frequency was increased or decreased according to a forced-choice method (36). Contrast of the background in both images of a stimulus pair was constant at 42%. The criterion for varying contrast of the test frequency was that of three correct choices to decrease contrast of a unit, and one incorrect choice to increase it by the same amount. All measurements were made binocularly at a distance of 150 cm, and the mean luminance was 2.0 fL. Maximum and minimum luminance was 2.2 and 1.8 fL, respectively.
The temporal sequence was initiated by a warning signal immediately followed by a 2-s presentation of the first stimulus followed by a 1-s interstimulus interval, followed in turn by a 2-s presentation of the second stimulus and the answer of the observer. The 2-s presentation was selected because we want to eliminate accommodation effects and assure enough time for steady fixation. We had already observed that deliberate fixation at the borders increased thresholds (15). The order of the stimulus pair was randomly selected. If the response was a correct one, it was followed by a beep and a 3-s intertrial interval would start. The whole experimental session would vary in length depending on the errors and correct choices made by the observer since a total of 10 pairs of peaks and valleys (i.e., 20 threshold estimates per experimental session) were necessary to end the session. Generally, a session lasted about 15-25 min.
Each of the 17 experimental conditions required to measure each of the seven filters was run at least three times on different days by at least three different observers. Thus, a total of nine functions were measured for each filter yielding a sample of 180 values to be averaged across observers for each of the 17 points. The distribution of the five subjects among the filter measurements was as follows: for F1(q), i.e., 1 cycle/360º filter (NAS:3, MMM:3, MC:3); for F2(q), i.e., 2 cycles/360º (NAS:3, ERB:3, TPL:3); for F3(q), i.e., 3 cycles/360º (NAS:3, MC:3, MMM:3); for F4(q), i.e., 4 cycles/360º (NAS:3, TPL:3, ERB:3); for F8(q), i.e., 8 cycles/360º (NAS:3, MMM:3, ERB:3); for F16(q), i.e., 16 cycles/360º (NAS:3, MC:3, ERB:3), and for F24(q), i.e., 24 cycles/360º (NAS:3, MMM:3, MC:3).
Figure 3 illustrates pairs of stimuli for filters at test angular frequencies of 1, 2, 3, 4, 8, 16 and 24 cycles/360º. Figure 3A shows pairs 1 and 1 + 1 cycles/360º (top), 3 and 3 + 1 cycles/360º (center), and 10 and 10 + 1 cycles/360º (bottom) for filter F1(q) centered at 1 cycle. Figure 3B shows pairs 1 and 1 + 2 cycles/360º (top), 2 and 2 + 2 cycles/360º (center), and 3 and 3 + 2 cycles/360º (bottom) for filter F2(q) centered at 2 cycles/360º. Figure 3C shows pairs 2 and 2 + 3 cycles/360º (top), 3 and 3 + 3 cycles/360º (center), and 4 and 4 + 3 cycles/360º (bottom) for filter F3(q) centered at 3 cycles/360º. Figure 3D shows pairs 3 and 3 + 4 cycles/360º (top), 4 and 4 + 4 cycles/360º (center), and 5 and 5 + 4 cycles/360º (bottom) for F4(q) centered at 4 cycles/360º. Figure 3E shows pairs 4 and 4 + 8 cycles/360º (top), 8 and 8 + 8 cycles/360º (center), and 10 and 10 + 8 cycles/360º (bottom) for F8(q) centered at 8 cycles/360º. Figure 3F shows pairs 4 and 4 + 16 cycles/360º (top), 8 and 8 + 16 cycles/360º (center), and 16 and 16 + 16 cycles/360º (bottom) for F16(q) centered at 16 cycles/360º, and Figure 3G shows pairs 12 and 12 + 24 cycles/360º (top), 24 and 24 + 24 cycles/360º (center), and 48 and 48 + 24 cycles/360º (bottom) for filter F24(q) centered at 24 cycles/360º.
 A shows pairs 1 and 1 + 1 cycles/360º (top), 3 and 3 + 1 cycles/360º (center), and 10 and 10 + 1 cycles/360º (bottom) for filter F1(q) centered at 1 cycle. B shows pairs 1 and 1 + 2 cycles/360º (top), 2 and 2 + 2 cycles/360º (center), and 3 and 3 + 2 cycles/360º (bottom) for filter F2(q) centered at 2 cycles/360º. C shows pairs 2 and 2 + 3 cycles/360º (top), 3 and 3 + 3 cycles/360º (center), and 4 and 4 + 3 cycles/360º (bottom) for filter F3(q) centered at 3 cycles/360º. D shows pairs 3 and 3 + 4 cycles/360º (top), 4 and 4 + 4 cycles/360º (center), and 5 and 5 + 4 cycles/360º (bottom) for F4(q) centered at 4 cycles/360º. E shows pairs 4 and 4 + 8 cycles/360º (top), 8 and 8 + 8 cycles/360º (center), and 10 and 10 + 8 cycles/360º (bottom) for F8(q) centered at 8 cycles/360º. F shows pairs 4 and 4 + 16 cycles/360º (top), 8 and 8 + 16 cycles/360º (center), and 16 and 16 + 16 cycles/360º (bottom) for F16(q) centered at 16 cycles/360º. G shows pairs 12 and 12 + 24 cycles/360º (top), 24 and 24 + 24 cycles/360º (center), and 48 and 48 + 24 cycles/360º (bottom) for filter F24(q) centered at 24 cycles/360º.
A shows pairs 1 and 1 + 1 cycles/360º (top), 3 and 3 + 1 cycles/360º (center), and 10 and 10 + 1 cycles/360º (bottom) for filter F1(q) centered at 1 cycle. B shows pairs 1 and 1 + 2 cycles/360º (top), 2 and 2 + 2 cycles/360º (center), and 3 and 3 + 2 cycles/360º (bottom) for filter F2(q) centered at 2 cycles/360º. C shows pairs 2 and 2 + 3 cycles/360º (top), 3 and 3 + 3 cycles/360º (center), and 4 and 4 + 3 cycles/360º (bottom) for filter F3(q) centered at 3 cycles/360º. D shows pairs 3 and 3 + 4 cycles/360º (top), 4 and 4 + 4 cycles/360º (center), and 5 and 5 + 4 cycles/360º (bottom) for F4(q) centered at 4 cycles/360º. E shows pairs 4 and 4 + 8 cycles/360º (top), 8 and 8 + 8 cycles/360º (center), and 10 and 10 + 8 cycles/360º (bottom) for F8(q) centered at 8 cycles/360º. F shows pairs 4 and 4 + 16 cycles/360º (top), 8 and 8 + 16 cycles/360º (center), and 16 and 16 + 16 cycles/360º (bottom) for F16(q) centered at 16 cycles/360º. G shows pairs 12 and 12 + 24 cycles/360º (top), 24 and 24 + 24 cycles/360º (center), and 48 and 48 + 24 cycles/360º (bottom) for filter F24(q) centered at 24 cycles/360º.
[View larger version of this image (95 K JPG file)]
Results
Figure 4 shows the frequency response functions for the seven filters F1(q), F2(q), F3(q), F4(q), F8(q), F16(q) and F24(q). Angular frequency of the background stimulus is plotted as a function of the amount of contrast necessary to identify the presence of the test angular frequency in the summated pair. We are calling this threshold for the test angular frequency summated to each background frequency contrast threshold of test in sum. Legends at top right indicate the test frequency.
Our statistical treatment was to estimate the standard error of the mean for each distribution of 180 values measured per point and to correct for sample size using the Student t-test to obtain the 99% confidence level.
In previous studies we established that this estimate is more rigorous than testing means either by comparison of two correlated samples or by ANOVA statistical treatment. In the statistical treatment using the confidence level, when two error bars show a 50% overlap, the t-statistics obtained for testing the difference between means for correlated samples has been found to be significant at least at the P<0.05 level and sometimes at a lower level. Most of the error bars that do not overlap show significance at the P<0.000 level, as shown by the SPSS-PC program. The use of ANOVA tends to show significant effects in all factors and interactions and does not add much information.
We can classify the resulting measured functions into two types of characteristic responses. For filters F1(q), F2(q), F3(q) and F4(q), the maximum summation effect surrounded by somewhat strong inhibition occurred at test frequencies with a secondary maximum at their neighboring higher and lower harmonics, respectively.
For filter F8(q) this tendency started to change. At F8(q) a relative maximum summation effect occurred at the test frequency but an absolute maximum summation effect occurred at 2 cycles/360º (lower harmonic) followed by another effect at 64 cycles/360º. For F16(q), the tendency was definitely changed. Maximum summation occurred at 8 cycles/360º (neighbor lower harmonic) as well as at 1 cycle and 96 cycles/360º. At the test frequency of 16 cycles/360º, summation was minimum or, in other words, inhibition was almost maximum. The same tendency occurred for F24(q). A maximum summation effect occurred at 12 cycles/360º (neighbor lower harmonic) followed by another effect at 8 cycles/360º. Maximum inhibition occurred at 32 cycles/360º.
We should note, however, that background frequency contrast was set at 42% for all filters regardless of the absolute threshold for each test angular frequency. As we can observe from Figure 2, contrast thresholds for 8, 16 and 24 cycles/360º were considerably lower than those for 1, 2, 3 and 4 cycles/360º.
Nevertheless, the ratio between maximum summation and maximum inhibition for all filters ranged from 2.19 to 2.47, indicating clear filtering effects. F1(q) showed a band pass at 1 cycle, F2(q) showed a band pass at 2 and 24-64 cycles/360º, F3(q) showed a band pass at 3 cycles/360º and a weaker one at 32-64 cycles/360º, and F4(q) showed a band pass at 4, 2 and 48 cycles/360º. These results were less clear for test frequencies at 8, 16 and 24 cycles/360º. F8(q) showed a band pass at 2 cycles/360º, 8 cycles/360º and 48-64 cycles/360º, while F16(q) showed a band pass at 8 cycles/360º, 1-5 cycles/360º and 96 cycles/360º. Furthermore, F16(q) showed a significant increase in sensitivity at its higher harmonic, 32 cycles/360º, and strongly inhibited passage at 9-24 cycles/360º. For F24(q), maximum summation surrounded by significant inhibition occurred at 12 and 8 cycles/360º. Another minor band pass occurred at 48 and 96 cycles/360º. For all results, a main observation was that generally the frequency of passage was surrounded on both sides by stronger inhibition.
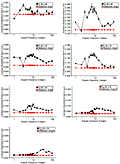 1(q), F2(q), F3(q), F4(q), F8(q), F16(q) and F24(q). Angular frequency of the background stimulus is plotted as a function of the amount of contrast necessary to identify the presence of the test angular frequency in the summated pair. We are calling this threshold for the test angular frequency summated to each background frequency contrast threshold of test in sum. Legends at top right indicate the test frequency.
1(q), F2(q), F3(q), F4(q), F8(q), F16(q) and F24(q). Angular frequency of the background stimulus is plotted as a function of the amount of contrast necessary to identify the presence of the test angular frequency in the summated pair. We are calling this threshold for the test angular frequency summated to each background frequency contrast threshold of test in sum. Legends at top right indicate the test frequency.
[View larger version of this image (109 K GIF file)]
Discussion
The results clearly show filter selectivity for the test frequencies used. This was not true for F16(q) and F24(q). All filters again showed a main result observed in our work of 1992 (31), that is, the test frequencies showed summation surrounded on both sides by strong inhibition. We see a trend for filters F1(q), F2(q), F3(q) and F4(q) which differs from F8(q), F16(q) and F24(q). In the former, summation was very sharp and inhibition at higher frequencies (e.g., 5-12 cycles/360º for F2(q) and F4(q)) was present. Inhibition at 1 and 3 cycles/360º was also clear. As for F8(q), although summation was sharp at 8 cycles/360º, we observed that adding frequencies in the ranges of 1-4 cycles/360º and 32-96 cycles/360º also increased sensitivity to the test frequency, i.e., 8 cycles/360º. The cases of F16(q) and F24(q) were quite different, i.e., adding frequencies in the range of 1-5 or 6 cycles/360º as well as its lower harmonic, 8 or 12 cycles/360º, increased sensitivity to 16 or 24 cycles/360º. On the other hand, frequencies at 9-24 strongly inhibited detection of 16 cycles/360º, while those at 24-32 strongly inhibited 24 cycles/360º perception. We should remember at this point that additions were made in phase within the vertical/horizontal axis.
While results for test frequencies at 1, 2, 3, 4 and 8 cycles/360º conform to our expectations, the characteristic responses for F16(q) and for F24(q) are not so easy to interpret. One possibility is that the visual system is integrating primarily in a lower range of angular frequencies (i.e., 1-8 cycles/360º) and interpolates higher frequencies. Another possibility is the fact that we used 42% contrast for all the background frequencies, an amount of contrast corresponding to 2.5, 3.5, 4.6, 5.9, 11, 15 and 20 times the absolute threshold for 1, 2, 3, 4, 8, 16 and 24 cycles/360º, respectively. So, we could replicate the experiment for 8, 16 and 24 cycles/360º using background frequency contrasts adjusted to be no higher than five times their respective absolute thresholds. Indeed, we are currently running experiments for 1, 2, 3, 4, 8, 16, 24, 32, 48, 64 and 96 cycles/360º angular frequency filters in the latter condition, i.e., background contrast equals five times thresholds for respective test frequencies. Our preliminary results confirm our hypothesis since we are finding summation at the test frequency for all filters already measured, including those for the high angular frequencies.
In addition, we would like to emphasize our interest in evaluating a main involvement of lower angular frequencies in face processing as explained in some detail by Simas and Santos (26) and by Simas MLB and Santos NA (unpublished data). We find, for instance, that the coupling of low radial frequencies to 2, 3 and 4 cycles/360º angular frequencies, as shown in Figure 5, bears some relationship to the white/black areas of the night monkey1 1 The night monkeys face was found at the site http://primates.com/monkeys/nightmonk.htm aotus, even more particularly under scotopic conditions. While the angular frequency content of the face seems to be enhanced, the radial content is also present as shown by the black contour. The exact radial frequency to be coupled to the angular part would have to be estimated on the basis of the monkey's face size and the more frequent distances of observation. The fact that we found narrow-band angular frequency filters centered at 1, 2, 3 and 4 cycles/360º would reinforce this view.
We believe that at least some of the cells found to be selective for faces in primates (37) may be responding to coupled and uncoupled angular/radial frequencies as in Equation 1. The fact that Gallant and colleagues (7,8) found cells responding selectively to angular as well as radial frequencies may indicate that this hypothesis is not too speculative.
We should point out that there are no psychophysical or physiological studies in the literature attempting to model face perception in terms of neural processing through narrow-band coupled/uncoupled angular and/or radial frequency filters working simultaneously or not. We do believe that narrow-band low angular/radial frequency filters operate best under scotopic conditions and as a viable example of this fact we are presenting the aotus face to illustrate an organism which possibly involves a very short set of such filters (Figure 5). The processing of human faces requires a much greater number of narrow-band filters operating at higher luminance levels (for identification and full recognition) and most likely involves higher narrow-band angular/radial frequency filters as well as pure narrow-band radial frequency filters. We present no human examples because we do not have programs for computer simulations of angular frequency filtering effects of such faces. We hope to be able to do that soon. Two recent reports would be in agreement with our statements in pointing out the similarity of human/primate face/form processing (38) and showing that higher radial frequencies are more involved in human face perception (39).
Another issue to be raised is the role of phase in angular frequency filtering. The work of Wilson and colleagues (40) addresses the problem of head rotation frontal-face/profile. In our view, theoretically, frontal rotation should be invariant. But if "pre-wiring" is assumed for determined phases as we do in the Phase selection section this would not be necessarily true. Upright and upside down would not be the same, particularly due to odd frequencies. On the other hand, the type of rotation studied by Wilson et al. (40) with a high frequency band pass would be viewed differently from our standpoint. We are emphasizing the role of low angular frequency filters. From this perspective, frontal views would indeed be somewhat different as we approach a profile view. Complexity would be dependent on the number of filters simultaneously considered. We have done a very rough simulation for the aotus (considering only filters 2, 3 and 4) and found very different luminance distributions. This will be presented elsewhere.
Finally, at this point it is not entirely clear to us how information from V1 contributes to the sensitivity to polar elementary stimuli. As we think about it, more and more we find ourselves believing we are investigating a more global processing mechanism involving higher visual areas that might work better at medium and low levels of illumination and may involve large portions of peripheral form processing. Furthermore, we do not believe that all input for this type of discrimination passes through V1. We believe in parallel input to other areas. This is not to say that foveal input may not be involved, but it is interesting to observe that one of our best examples like the aotus (whose faces seem to involve low angular and radial frequencies) is a night monkey.
In sum, we think that angular frequencies could involve more peripheral processing (i.e., near maximum rod population) and prove to be very relevant in the study of face perception of various species, including humans.

The coupling of low radial frequencies to 2, 3 and 4 cycles/360º angular frequencies, as shown at top right, bottom left and bottom right, respectively, bear some relationship to the white/black areas of the night monkey aotus (top left), even more particularly under scotopic conditions.
[View larger version of this image (54 K JPG file)]
Address for correspondence: M.L.B. Simas, LabVis, Departamento de Psicologia, Universidade Federal de Pernambuco, Rua Acadêmico Hélio Ramos, s/n, 9º andar, 50670-901 Recife, PE, Brasil. E-mail: mlbslabv@elogica.com.br and mlbs@npd.ufpe.br
Research supported by CNPq (No. 52.3791/95-0), FINEP and FACEPE (No. APQ-0606-7.07/97). Publication supported by FAPESP. Part of this work was presented at the XI International Symposium on Computer Graphics, Image Processing and Vision, Rio de Janeiro, RJ, Brazil, 1998. Received April 11, 2001. Accepted October 24, 2001.
- 1. Blakemore C & Campbell FW (1969). On the existence of neurones in the human visual system selectively sensitive to the orientation and size of retinal images. Journal of Physiology, 203: 237-260.
- 2. Graham N (1972). Spatial frequency channels in the human visual system: effects of luminance and pattern drift rate. Vision Research, 12: 53-68.
- 3. Dodwell PC (1983). The Lie group transformation model of visual perception. Perception and Psychophysics, 34: 1-16.
- 4. Hoffman WC (1966). The Lie algebra of visual perception. Journal of Mathematical Psychology, 3: 65-98. Errata, ibid., 4 (1967), 348-440.
- 5. Flanagan P & Dodwell PC (1991). Pattern-specific contrast threshold elevation. Spatial Vision, 5: 159-187.
- 6. Von Grünau M, Kwas M & Dube S (1994). The interaction of depth parameters in motion integration with polar plaids. Spatial Vision, 8: 119-140.
- 7. Gallant JL, Braun J & Van Essen DC (1993). Selectivity for polar, hyperbolic, and Cartesian gratings in macaque visual cortex. Science, 259: 100-103.
- 8. Gallant JL, Connor CE, Rakshit S, Lewis JW & Van Essen DC (1996). Neural responses to polar, hyperbolic, and Cartesian gratings in area V4 of the macaque monkey. Journal of Neurophysiology, 76: 2718-2739.
- 9. Tanaka K & Saito H-A (1989). Analysis of motion of the visual field by direction, expansion/contraction, and rotation cells clustered in the dorsal part of the medial superior temporal area of the macaque monkey. Journal of Neurophysiology, 62: 626-641.
- 10. Tanaka K, Fukada Y & Saito H-A (1989). Underlying mechanisms of the response specificity of expansion/contraction and rotation cells in the dorsal part of the medial superior temporal area of the macaque monkey. Journal of Neurophysiology, 62: 642-656.
- 11. Gershon ED, Wiener MC, Latham PE & Richmond BJ (1998). Coding strategies in monkey V1 and inferior temporal cortices. Journal of Neurophysiology, 79: 1135-1144.
- 12. Morley JW & Vickery RM (1997). Spatial and temporal frequency selectivity of cells in area 21a of the cat. Journal of Physiology, 501: 405-413.
- 13. Kobatake E & Tanaka K (1994). Neuronal selectivities to complex object features in the ventral visual pathway of macaque cerebral cortex. Journal of Neurophysiology, 71: 856-867.
- 14. Desimone R (1991). Face-selective cells in the temporal cortex of monkeys. Journal of Cognitive Neuroscience, 3: 1-8.
- 15. Pasupathy A & Connor CE (1999). Responses to contour features in macaque area V4. Journal of Neurophysiology, 82: 2490-2502.
- 16. Hedge J & Van Essen DC (2000). Selectivity for complex shapes in primate visual area V2. Journal of Neuroscience, 20: RC61.
- 17. Tootell RB, Hadjikhani NK, Vanduffel W, Liu AK, Mendola JD, Sereno MI & Dale AM (1998). Functional analysis of primary visual cortex (V1) in humans. Proceedings of the National Academy of Sciences, USA, 95: 811-817.
- 18. Simas ML de B (1985). Linearity and domain invariance in the visual system. Doctoral thesis, Queen's University at Kingston, Ontario, Canada. University Microfilms International, Ann Arbor, MI, 1985. "Publication No. 86-17940".
- 19. Simas ML de B & Dodwell PC (1990). Angular frequency filtering: a basis for pattern decomposition. Spatial Vision, 5: 59-74.
- 20. Sneddon IN (1961). Special Functions of Mathematical Physics and Chemistry Interscience Publishers, New York, NY, USA, 105.
- 21. Amidor I (1997). Fourier spectrum of radially periodic images. Journal of the Optical Society of America. A, Optics, Image Science, and Vision, 14: 816-826.
- 22. Wilkinson F, Wilson HR & Habak C (1998). Detection and recognition of radial frequency patterns. Vision Research, 38: 3555-3568.
- 23. Westheimer G (1998). Lines and Gabor functions compared as spatial visual stimuli. Vision Research, 38: 487-491.
- 24. Graham N, Sutter A & Venkatesan C (1993). Spatial-frequency- and orientation-selectivity of simple and complex channels in region segregation. Vision Research, 33: 1893-1911.
- 25. Kelly DH (1960). Stimulus pattern for visual research. Journal of the Optical Society of America, 50: 1115-1116.
- 26. Simas ML de B & Santos NA (1997). Human visual contrast detection of radial frequency stimuli defined by Bessel profiles j0, j1, j2, j4, j8 and j16 and its relation to angular frequency. Proceedings of the II Workshop on Cybernetic Vision, IEEE Computer Science, December 9-11, 1996, São Carlos, SP, Brazil, 219-224.
- 27. Koenderink JJ & van Doorn AJ (1990). Receptive field families. Biological Cybernetics, 63: 291-297.
- 28. Wilson HR & Wilkinson F (1997). Evolving concepts of spatial channels in vision: from independence to nonlinear interactions. Perception, 26: 939-960.
- 29. Wilson HR & Wilkinson F (1998). Detection of global structure in Glass patterns: implication for form vision. Vision Research, 38: 2933-2947.
- 30. Wilson HR, Wilkinson F & Asaad W (1997). Concentric orientation summation in human form vision. Vision Research, 37: 2325-2330.
- 31. Simas ML de B, Frutuoso JT & Vieira FM (1992). Inhibitory side bands in multiple angular frequency filters in the human visual system. Brazilian Journal of Medical and Biological Research, 25: 919-923.
- 32. Kulikowski JJ & King-Smith PE (1973). Spatial arrangement of line, edge and grating detectors revealed by sub-threshold summation. Vision Research, 13: 1455-1478.
- 33. Simas ML de B, Santos NA dos & Thiers FA (1997). Contrast sensitivity to angular frequency stimuli is higher than that for sinewave gratings in respective middle range. Brazilian Journal of Medical and Biological Research, 30: 633-636.
- 34. Tyler CW (1975). Spatial frequency filters in cat visual cortex? Vision Research, 15: 303-304.
- 35. Hubel DH & Wiesel TN (1968). Receptive fields and functional architecture of monkey striate cortex. Journal of Physiology, 195: 215-243.
- 36. Wetherill GB & Levitt H (1965). Sequential estimation of points on a psychometric function. British Journal of Mathematical and Statistical Psychology, 18: 1-10.
- 37. Bruce CJ, Desimone R & Gross CG (1981). Visual properties of neurons in a polysensory area in superior temporal sulcus of the macaque. Journal of Neurophysiology, 46: 369-384.
- 38. Connor CE (2000). Monkeys see thinks our way. Current Biology, 10: R836-R838.
- 39. Wilkinson F, James TW, Wilson HR, Gati JS, Menon RS & Goodale MA (2000). An fMRI study of the selective activation of human extrastriate form vision areas by radial and concentric gratings. Current Biology, 10: 1455-1458.
- 40. Wilson HR, Wilkinson F, Lin L & Castillo M (2000). Perception of head orientation. Vision Research, 40: 459-472.
Correspondence and Footnotes
Publication Dates
-
Publication in this collection
08 Feb 2002 -
Date of issue
Feb 2002
History
-
Accepted
24 Oct 2001 -
Received
11 Apr 2001



