Abstract
The present study compares the performance of stochastic and fuzzy models for the analysis of the relationship between clinical signs and diagnosis. Data obtained for 153 children concerning diagnosis (pneumonia, other non-pneumonia diseases, absence of disease) and seven clinical signs were divided into two samples, one for analysis and other for validation. The former was used to derive relations by multi-discriminant analysis (MDA) and by fuzzy max-min compositions (fuzzy), and the latter was used to assess the predictions drawn from each type of relation. MDA and fuzzy were closely similar in terms of prediction, with correct allocation of 75.7 to 78.3% of patients in the validation sample, and displaying only a single instance of disagreement: a patient with low level of toxemia was mistaken as not diseased by MDA and correctly taken as somehow ill by fuzzy. Concerning relations, each method provided different information, each revealing different aspects of the relations between clinical signs and diagnoses. Both methods agreed on pointing X-ray, dyspnea, and auscultation as better related with pneumonia, but only fuzzy was able to detect relations of heart rate, body temperature, toxemia and respiratory rate with pneumonia. Moreover, only fuzzy was able to detect a relationship between heart rate and absence of disease, which allowed the detection of six malnourished children whose diagnoses as healthy are, indeed, disputable. The conclusion is that even though fuzzy sets theory might not improve prediction, it certainly does enhance clinical knowledge since it detects relationships not visible to stochastic models.
Epidemiologic methods; Stochastic models; Fuzzy models; Clinical signs; Diagnosis; Data analysis
Braz J Med Biol Res, May 2004, Volume 37(5) 701-709
Clinical signs of pneumonia in children: association with and prediction of diagnosis by fuzzy sets theory
J.C.R. Pereira1, P.A. Tonelli3, L.C. Barros4 and N.R.S. Ortega2
1Departamento de Epidemiologia, 2Laboratório de Investigação Médica, Hospital das Clínicas, Faculdade de Saúde Pública, and 3Instituto de Matemática e Estatística, Universidade de São Paulo, São Paulo, SP, Brasil
4Instituto de Matemática, Estatística e Computação Científica, Universidade Estadual de Campinas, Campinas, SP, Brasil
 References
References
 Correspondence and Footnotes
Correspondence and Footnotes
Correspondence and Footnotes
Correspondence and Footnotes
Correspondence and Footnotes
Correspondence and Footnotes
Abstract
The present study compares the performance of stochastic and fuzzy models for the analysis of the relationship between clinical signs and diagnosis. Data obtained for 153 children concerning diagnosis (pneumonia, other non-pneumonia diseases, absence of disease) and seven clinical signs were divided into two samples, one for analysis and other for validation. The former was used to derive relations by multi-discriminant analysis (MDA) and by fuzzy max-min compositions (fuzzy), and the latter was used to assess the predictions drawn from each type of relation. MDA and fuzzy were closely similar in terms of prediction, with correct allocation of 75.7 to 78.3% of patients in the validation sample, and displaying only a single instance of disagreement: a patient with low level of toxemia was mistaken as not diseased by MDA and correctly taken as somehow ill by fuzzy. Concerning relations, each method provided different information, each revealing different aspects of the relations between clinical signs and diagnoses. Both methods agreed on pointing X-ray, dyspnea, and auscultation as better related with pneumonia, but only fuzzy was able to detect relations of heart rate, body temperature, toxemia and respiratory rate with pneumonia. Moreover, only fuzzy was able to detect a relationship between heart rate and absence of disease, which allowed the detection of six malnourished children whose diagnoses as healthy are, indeed, disputable. The conclusion is that even though fuzzy sets theory might not improve prediction, it certainly does enhance clinical knowledge since it detects relationships not visible to stochastic models.
Key words: Epidemiologic methods, Stochastic models, Fuzzy models, Clinical signs, Diagnosis, Data analysis
Introduction
Poincaré, in the preface to his XIX century "Science and Hypothesis", remarked that "the aim of science is not things themselves, as the dogmatists in their simplicity imagine, but the relations between things; outside those relations there is no reality knowable" (1). In the medical sciences, relations among phenomena are mainly studied as associations assessed by a stochastic or deterministic paradigm in order to provide cause and effect relationships. On the basis of Hume's principle of uniformity of nature ("like objects placed in like circumstances will always produce like effects") (2), predictions are made for future situations on the basis of relations drawn from past experience.
Much knowledge has undoubtedly been obtained in the medical sciences using these frames of reference. Nonetheless, it may be proposed that inspecting any given phenomenon from different standpoints should afford additional information and eventually more complete and accurate knowledge. Conversely, restricting choice to specific frames of reference should lead to restrictions in mapping relationships and, thus, ultimately, to restrictions in knowledge. In this respect, Susser (3), when discussing causality, stated that "to choose a frame of reference is to choose a limited set of causal relationships within an ecological system".
The theory of fuzzy sets was introduced by Lotfi A. Zadeh in the 1960's as a means to model the uncertainty that is present in natural language, e.g., expressions like big, small, strong, weak, etc. This was a turning point in what Klir and Yuan (4) called a grand paradigm shift, remarking that "Among the various paradigmatic changes in science and mathematics in this century, one such change concerns the concept of uncertainty. &ldots; According to the traditional view, science should strive for certainty in all its manifestations (precision, specificity, sharpness, consistency, etc.); hence, uncertainty (imprecision, non-specificity, vagueness, inconsistency, etc.) is regarded as unscientific. According to the alternative (or modern) view, uncertainty is considered essential to science."
According to Rouvray (5), the problem of vagueness and rigidity of the fundamental axioms in Aristotelian logic reasoning was probably first discussed by the logician George Boole in 1854. At the beginning of the XX century, Peirce acknowledged that "All that exists is continuous and such continuum governs knowledge" and some years later, in 1923, Russell stated that "both vagueness and precision are features of language, not reality. Vagueness clearly is a matter of degree" (6). But, again according to Rouvray (5), it was Lukasiewicz who, in 1930, took the first step towards a formal model of vagueness, an early logic based on more values than true and false, and was later followed by Black, in 1937, who outlined his proto-fuzzy logic with the "suggestion that degrees of vagueness could be measured by a consistency function". Eventually, it was Zadeh (7) who, in 1965, settled the matter of vagueness setting forth the mechanics of fuzzy set theory. Zadeh's key concept is graded membership, according to which a set can have members that partly belong to it. So, if one assumes that X is a set serving as the universe of discourse, a fuzzy subset A of X is associated with a function: µA: X ® [0,1] which is generally called membership function. The idea is that for each x, µA(x) indicates the extent to which x is a member of the fuzzy set A. This membership degree indicates the degree of compatibility of the assertion "x is A".
Ever since Zadeh outlined the first principles of fuzzy sets theory, both its contents and applications have experienced an extraordinary development. From then to June 2003, when these annotations were made, the databases of scientific literature of the Institute for Scientific Information (Science Citation Expanded®, Social Sciences Citation Index®, and Arts and Humanities Citation Index) record that 21,187 articles containing the term "fuzzy" were published. Concerning the medical sciences, Medline® recorded 1,777 such articles, beginning with just one in 1971 and increasing exponentially to 181 in 2002 (a mean yearly increment rate of 15%).
The present study was conceived as a proposal to determine whether fuzzy relations could add information to that provided by customary stochastic relations about the association and prediction of events of medical interest.
Material and Methods
Data were taken from a study about the relationship between clinical signs and diagnosis (8). The study comprised 153 children who were randomly divided into an analysis sample (115 cases) and a validation sample (38 cases). No criteria other than random allocation separated these two samples, the former being meant to draw relationships and the latter conceived as a trial sample to test the value of such relationships in terms of prediction. Since testing predicted values yielded by any function against the same real values used to derive such a function is not more than assessing residuals and goodness-of-fit, a validation sample is required to properly assess prediction, so that data processed to give prediction have nothing to do with the way they are processed.
Diagnoses (pneumonia, non-pneumonia diseases, healthy) were originally ascertained as either present (1) or absent (0), and were mutually exclusive. Two pediatricians, on grounds of identical clinical investigations, independently made the diagnoses, and an X-ray was required for the diagnosis of pneumonia. Entry condition, apart from ethical issues, was agreement between the two specialists.
The following clinical signs were considered for analysis: dyspnea, measured on a scale from absent (0) to severe (4) taking into account the following signs: mild discomfort, lower rib in-drawing with tachypnea, intercostal in-drawing with severe tachypnea and/or presence of nasal flaring, full retraction of ribs plus cyanosis and/or poor peripheral blood perfusion; toxemia, measured as a scale from absent (0) to severe (4), according to the presence of pallor, pallor and listlessness, irritability, drowsiness; radiological signs, measured as a counting scale for the presence of signs from absent (0) up to seven: alveolar and interstitial infiltrates, atelectasis, pleural effusion, pneumatoceles, airtrapping, pneumothorax; auscultation signs, measured on a counting scale for the presence of signs from absent (0) up to three: rales, crackles, bronchial breathing; temperature, measured on a scale from normal (0) to severe fever (3): normal (£37ºC), mild fever (>37ºC and <38.5ºC), fever (³38.5ºC and <40ºC), severe fever (³40ºC); heart rate, according to age group, measured on an ordinal scale from normal (0) to highly tachycardic (4); respiratory rate, according to age group, measured on an ordinal scale from normal (0) to highly tachypneic (4).
All of these measurements were made using a scale in order to have a single definition of a fuzzy membership function to map original values into grades of membership: scales were all normalized to the unit so that full membership would mean a clinical sign present at its most severe expression. This license was allowed by taking into account that the focus of the study was neither the diagnosis nor the signs, but, as indicated above, the comparison of two different methodological approaches, namely stochastic and fuzzy. Indeed, for such a goal any other sort of measurement should equally do, which would not be true if knowledge about the subject was being sought. Under these circumstances, one would better consider signs as linguistic variables and endeavor to develop a specific fuzzy membership function for each variable according to its symbolic and semantic characteristics (9). Thus, the fact that measurement precision is excused, should not jeopardize the clinical appreciation of the argument concerning an alternative reasoning for decision about the diagnosis of children's pneumonia, or any other sort of diagnosis.
To obtain relationships between clinical signs and diagnoses under a stochastic model, multi-discriminant analysis (10) was conducted, following the pattern of the original study from which the data were taken. Mahalanobis distances were used, and functions best discriminating diagnoses were derived by stepwise selection of variables. Relationships between multi-discriminant functions and clinical signs were examined in the rotated structure matrix. These functions were used to predict the diagnoses of patients in the validation sample and overall agreement was calculated.
To run a similar analysis under fuzzy theory, a max-min composition (11) was used to combine information from two fuzzy binary relations organized as membership matrices: one concerning the relationships between clinical signs (x) and patients (y) and the other concerning the relationships between patients (y) and diagnoses (z). This yielded a matrix of relationships between clinical signs (x) and diagnoses (z) [R(x,z)]. This max-min composition may be described as follows: given S and T, two binary relations of U x V and V x W (e.g., signs x patients and patients x diagnosis), the max-min composition S*T of U x W (e.g., signs x diagnoses) is a fuzzy binary relationship with membership function given by
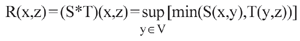
(Eq. 1)
To predict the diagnoses (D) of patients from the validation sample the following function was used: for each patient (Pn), his/her relationship with each diagnosis (dm) was drawn from the composition of his/her vector of clinical signs (si) with the composite relationship previously identified (R(x,z), relationships between signs and diagnoses), as follows:
The D(Pn)(dm) value can be seen as the possibility of diagnosis dm for patient Pn, from his signs si, 1 £ i £ 7, since seven signs were considered. Hence, D(Pn) stands for the membership function of patient Pn in the universe of diagnoses.
To finalize the allocation of a patient to a single diagnosis, a defuzzification rule is needed to make a choice from the relationships he shows with each diagnosis category. This rule was defined as the highest value of the resulting membership functions. In other words, one patient should be allocated to the diagnosis for which he had highest membership. Since for allocation of a patient to the healthy category he/she should have no relation with any clinical sign, healthy patients were defined as those whose membership for pneumonia or other disease was null. In the case of ties, a complementary analysis treating diagnosis as a multi-response variable should be considered.
Results
Multi-discriminant analysis identified two functions that together could represent 100% of total variance (function 1 = 98.4%, function 2 = 1.6%). As shown in Figure 1, function 1 separates pneumonia cases from other cases, and function 2 separates healthy cases from others, with increasing values towards patients with any type of disease (Figure 1).
The rotated structure matrix provided information about the relationships between clinical signs and diagnoses as shown in Table 1.
Clinical signs of pneumonia in children: association with and prediction of diagnosis by fuzzy sets theory. J.C.R. Pereira, P.A. Tonelli, L.C. Barros and N.R.S. Ortega. Brazilian Journal of Medical and Biological Research, 37 (5): 701, 2004.
Using function coefficients, patients from the validation sample were classified regarding diagnosis, with 75.7% being correctly classified, as shown in Table 2. The classification of one patient could not be predicted because of missing data concerning body temperature.
Clinical signs of pneumonia in children: association with and prediction of diagnosis by fuzzy sets theory. J.C.R. Pereira, P.A. Tonelli, L.C. Barros and N.R.S. Ortega. Brazilian Journal of Medical and Biological Research, 37 (5): 701, 2004.
By applying relation (1) to the analysis sample data, the matrix of relations presented in Table 3 was obtained: surprisingly, heart rate was found to have some relationship with the healthy condition, and analysis of the patients' records showed that, actually, six children in this group had mild tachycardia [three at a level of 0.25 (+) and three at a level of 0.50 (++)], with the weight of four of them being below the 25th percentile. Thus, these children probably were not perfectly healthy but were malnourished and perhaps had the not rarely accompanying condition of anemia, which could account for the tachycardia.
Clinical signs of pneumonia in children: association with and prediction of diagnosis by fuzzy sets theory. J.C.R. Pereira, P.A. Tonelli, L.C. Barros and N.R.S. Ortega. Brazilian Journal of Medical and Biological Research, 37 (5): 701, 2004.
By applying Equation 2, a vector of values representing membership of each patient in the diagnoses was obtained. An example of such vector is (5, 0.75, 0.5, 0.5), meaning that patient No. 5 had a 0.75 membership grade for pneumonia, a 0.5 membership grade for other diseases, and 0.5 membership grade for the healthy condition.
By applying the pre-defined defuzzification rule, the classification of 20 of the 38 patients (52.6%) remained indeterminate
due to ties. Agreement between the original and predicted classification is presented in Table 4.
Clinical signs of pneumonia in children: association with and prediction of diagnosis by fuzzy sets theory. J.C.R. Pereira, P.A. Tonelli, L.C. Barros and N.R.S. Ortega. Brazilian Journal of Medical and Biological Research, 37 (5): 701, 2004.
The 18 cases that could be classified by the pre-defined classification rule showed perfect agreement with the classification due to multi-discriminant functions: the same 3 were classified as pneumonia and the same 15 were classified as healthy by both methods.
In cases of ties concerning patients equally belonging to both the `pneumonia' and `non-pneumonia disease' categories, agreement between the original and predicted classification was as presented in Table 5. In this table one should appreciate the difference between cases (patients seen) and records (diagnoses made) that follows the transformation of diagnosis from a categorical variable with mutually exclusive categories to a multi-response variable which allows more than one diagnosis per patient. Thus, counts in each cell do not add up to marginal frequency (total number of patients with a given real status) which, nevertheless, is kept as the denominator for relative frequencies so that one can determine the proportion of agreement for each diagnosis separately (diagonal line in boldface).
Clinical signs of pneumonia in children: association with and prediction of diagnosis by fuzzy sets theory. J.C.R. Pereira, P.A. Tonelli, L.C. Barros and N.R.S. Ortega. Brazilian Journal of Medical and Biological Research, 37 (5): 701, 2004.
Thus, treating diagnosis as a multi-response variable allowed ties to be dealt with and the 38 cases of the validation sample could be analyzed. Thirty-seven of these cases were available for comparison against the results of multi-discriminant classification since one case had been missed in this analysis. Among these 37 patients, only one had a conflicting allocation: a patient classified as healthy in multi-discriminant analysis was classified as both pneumonia (membership grade = 0.25) and non-pneumonia disease (membership grade = 0.25) in fuzzy classification, which was due to his having toxemia at a level of 0.25 (linguist equivalent = pallor). This patient's real status was non-pneumonia disease.
Territorial map for diagnoses according to multi-discriminant analysis. Each circle stands for a case and each spike (short bars) represents additional cases overlying the first case.
Discussion
Evaluation of methodological strategies should be a major concern to any scientific investigator. Under the influence of Claude Bernard (12), medical sciences used to fight against statistical methods in favor of deterministic approaches, which were then paradigms of scientific knowledge. Nevertheless, statistics and probability theories overcame prejudices and became a major tool for medical research, significantly contributing to the progress of knowledge. If a lesson is to be drawn from the history of the medical sciences, it is that doubts about established methodologies are an unequivocal driving force for the advancement of science.
In the present study, we cast doubts over the ability of stochastic methods to comprehensively contribute to medical diagnosis, arguing that some information might be missed by using their strategies for data processing. An alternative approach drawn from fuzzy sets theory is used to provide evidence in support of this thesis. Thus, multi-discriminant analysis was compared with max-min composition, and their performances concerning predictions and description of relationships between clinical signs and diagnoses were examined. Both techniques yield a relation matrix from which predictions can be drawn. In multi-discriminant analysis this is a correlation matrix (as shown in Table 1) and prediction is made through regression, while in fuzzy logic this is a membership grade matrix (as in Table 3) and prediction is made by logical compositions (as in Equation 2) and defuzzification rules.
In correlation, relationships are described as covariance, how variations of one thing are accompanied by variations of other things, the correlation coefficient being just a standardized measurement of covariance. Fuzzy relations examine interspersing, how things are intertwined together, and express this as grades of membership. Regression draws predictions from line fitting and thus odd extreme data points contribute less than central values. Fuzzy predictions are drawn from the composition of Cartesian products of sets, in the present case a max-min composition that could tentatively be translated as "if at least, then up to", and thus odd extreme data points are taken into account.
Concerning prediction, the comparison of the two methods studied here easily leads to the conclusion that they are almost identical. Indeed, they only disagreed in the single instance of one patient who, having presented some degree of toxemia, was classified as healthy by multi-discriminant analysis and as somehow ill by fuzzy relations. Moreover, the performances of the two methods in allocating patients to diagnosis groups when compared to the real status of patients were very close, scoring within the interval of 75.7% in multi-discriminant classification (Table 2) and 78.3% in fuzzy classification with diagnosis as a multi-response variable (Table 5). Perhaps some advantage for the fuzzy classification could be acknowledged since it achieved slightly higher figures and, in addition, it did more properly classify the `non-pneumonia disease' patient who was missed as such by multi-discriminant classification.
One could argue that fuzzy models might not work well when mutually exclusive allocation is sought, since due to ties 52.6% of the cases could not conform to a defuzzification rule for patient allocation to a single diagnosis category. On the other hand, it should be emphasized that restrictions of use are present in any method. Actually, multi-discriminant analysis did also hint its limitations when it could not deal with one case with missing information for just one variable, while fuzzy relations were robust enough to circumvent this problem. The same way as it is not in the nature of multi-discriminant analysis to deal with missing data, it is not in the nature of fuzzy relations to deal with exclusive membership in one set.
Since both methods were almost equivalent in terms of prediction, we may ask whether it would be worth going through all the trouble of mastering up fuzzy sets theory to eventually end up with the same conclusions. In this respect, first of all, one should not be surprised by the fact that looking at a phenomenon from different standpoints, the views one arrives at are congruent: all in all, it is always the same phenomenon and remarkable it would be if, instead, something completely different could emerge. As Einstein put it when lecturing at Princeton, 1921, "Raffiniert ist der Herrgott, aber boshaft ist er nicht", or in his own humorous translation "God is slick, but He ain't mean" (13). Secondly, one should revisit Poincaré's remarks cited in the opening of this paper and consider that knowledge lies in relations, not in predictions, which are just a corollary of relations.
Now, turning our attention to relations themselves, we can better appreciate how fuzzy sets theory can contribute to medical knowledge. Indeed, comparing the two relations presented in Tables 1 and 3, one realizes that, in contrast with what happens with their derived predictions, they are not equivalent but complementary. While in multi-discriminant analysis, factor 1 correlations tell that X-ray, dyspnea and auscultation are clinical signs that better contribute to the separation of pneumonia cases, fuzzy relations add the information that dyspnea does also play a role in cases of `non-pneumonia disease'. Likewise, even though fuzzy relations do not challenge the information of function 2, which suggests that heart rate, body temperature, toxemia, and respiratory rate are important clinical signs to separate `non-pneumonia disease' from healthy subjects, fuzzy relations complementarily inform that these clinical signs do also have a strong relationship with the diagnosis of pneumonia. Moreover, while in multi-discriminant analysis the importance of toxemia and respiratory rate is belittled since their variations account less than the other clinical signs for the chances of one diagnosis or another, in fuzzy relations their intermingling with both diagnoses is revealed. By the same token, were it not for fuzzy relations showing overlaps between healthy cases and heart rate, those six cases of disputable healthy diagnosis would remain undisclosed.
Focusing on relations rather than on predictions might better serve not only scientific knowledge but also medical practice. Indeed, as to devising actions to take, the practitioner is much better advised by information on the relations his patient has with different diagnoses, like those provided by the vectors of membership grade for different diagnoses, than he is with guesses of diagnosis, no matter whether they are the product of mathematical functions or of logical defuzzification rules.
From the present results, the clinical investigator concerned with diagnosis, be it pneumonia in children or any other, can certainly get a glimpse into the opportunities that fuzzy sets theory provides to help him in the study of clinical signs and diagnoses. Allowing for uncertainty both in metrics and data processing as done here, one can apply fuzzy sets theory not necessarily to supersede stochastic methods, but surely as a method to obtain information that might be overlooked by stochastic methods. Having used a simple clinical problem such as pneumonia diagnosis, the present results can be easily appreciated by clinical investigators in any fields. Indeed, anyone can appreciate that fuzzy relations were more perceptive than correlations in evaluating clinical signs such as toxemia and respiratory rate. These, though major signs in pneumonia, are also present in other diseases but certainly not to a greater extent than they are in pneumonia, and this is what fuzzy relations capture (compare Tables 1 and 3). In regard to temperature, as a further example, correlations were also less keen than fuzzy relations, the latter detecting that fever (membership in high temperature as defined in item 5 of clinical signs measurement) relates to pneumonia at a grade of 0.67 while the former suggests that temperature is very mildly related to pneumonia (r = -0.07)
In conclusion, from the present study one can learn that relations between clinical signs and medical diagnoses should themselves have precedence over predictions of diagnoses drawn from such relations, and one can also learn that it is worth using fuzzy sets theory to better know these relations.
Address for correspondence: J.C.R. Pereira, Departamento de Epidemiologia, FSP, USP, Av. Dr. Arnaldo, 715, 01246-904 São Paulo, SP, Brasil. E-mail: juliocrp@usp.br
Research supported by FAPESP (No. 01/04905-0). Received July 15, 2003. Accepted January 5, 2004.
- 1. Poincaré H (1952). Science and Hypothesis Dover Publications, New York, xxiv.
- 2. Wallace WA (1974). Causality and Scientific Explanation Vol. 2. The University of Michigan Press, Ann Arbor, MI, USA, 38-51.
- 3. Susser M (1973). Casual Thinking in the Health Sciences Oxford University Press, New York, 43.
- 4. Klir GJ & Yuan BO (1995). Fuzzy Sets and Fuzzy Logic - Theory and Applications Prentice Hall PTR, Upper Saddle River, NJ, USA, 1.
- 5. Rouvray DH (1997). The treatment of uncertainty in the sciences. Endeavour, 21: 154-158.
- 6. Reznik L (1997). Fuzzy Controllers Newnes, Oxford, Oxfordshire, UK, 5-8.
- 7. Zadeh LA (1965). Fuzzy sets. Information and Control, 8: 338-353.
- 8. Pereira JCR & Escuder MML (1998). The importance of clinical symptoms and signs in the diagnosis of community-acquired pneumonia. Journal of Tropical Pediatrics, 44: 18-24.
- 9. Pedrycs W & Gomide F (1998). An Introduction to Fuzzy Sets Analysis and Design The MIT Press, Cambridge, MA, USA, 165-180.
- 10. Hair JF, Anderson RE, Tatham RL & Black WC (1998). Multivariate Data Analysis 5th edn. Prentice Hall, Upper Saddle River, NJ, USA, 239-325.
- 11. Nguyen HT & Walker EA (1999). A First Course in Fuzzy Logic 2nd edn. Chapman & Hall/CRC, New York, 182-184.
- 12. Vandenbroucke JP (1988). Clinical investigation in the 20th century: the ascendancy of numerical reasoning. Lancet, 352 (Suppl 2): 2-6.
- 13. Special relativity and modern physics. Prof. Scott Menary homepage. Experimental High Energy Physics, York University, Canada, 2001. (http://www.stcloudstate.edu/~lesikar/einstein/E2.html).
Correspondence and Footnotes
Publication Dates
-
Publication in this collection
22 Apr 2004 -
Date of issue
May 2004
History
-
Accepted
05 Jan 2004 -
Received
15 July 2003









