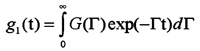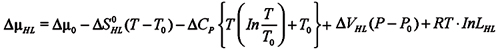Abstract
Pressure-induced dissociation of a turbid solution of casein micelles was studied in situ in static and dynamic light scattering experiments. We show that at high pressure casein micelles decompose into small fragments comparable in size to casein monomers. At intermediate pressure we observe particles measuring 15 to 20 nm in diameter. The stability against pressure dissociation increased with temperature, suggesting enhanced hydrophobic contacts. The pressure transition curves are biphasic, compatible with a temperature (but not pressure)-dependent conformational equilibrium of two micelle species. Our thermodynamic model predicts an increase in structural entropy with temperature.
Casein micelles; High-pressure light scattering; Pressure dissociation
Braz J Med Biol Res, August 2005, Volume 38(8) 1209-1214
Pressure-induced dissociation of casein micelles: size distribution and effect of temperature
R. Gebhardt1,  W. Doster1 and U. Kulozik2
W. Doster1 and U. Kulozik2
1Physics Department E13, Technical University Munich, Garching, Germany
2Department for Food and Nutrition, Freising-Weihenstephan, Germany
 References
References
 Correspondence and Footnotes
Correspondence and Footnotes
Correspondence and Footnotes
Correspondence and Footnotes
Correspondence and Footnotes
Correspondence and Footnotes
Abstract
Pressure-induced dissociation of a turbid solution of casein micelles was studied in situ in static and dynamic light scattering experiments. We show that at high pressure casein micelles decompose into small fragments comparable in size to casein monomers. At intermediate pressure we observe particles measuring 15 to 20 nm in diameter. The stability against pressure dissociation increased with temperature, suggesting enhanced hydrophobic contacts. The pressure transition curves are biphasic, compatible with a temperature (but not pressure)-dependent conformational equilibrium of two micelle species. Our thermodynamic model predicts an increase in structural entropy with temperature.
Key words: Casein micelles, High-pressure light scattering, Pressure dissociation
Introduction
Casein micelles are poly-disperse, roughly spherical aggregates in milk with a mean radius of 150 nm. Their main physiological task is to transport calcium, proteins and phosphorus to neonates. The micelles are composed of four different phospho-proteins aS1-, aS2-, ß-, k-casein and calcium phosphate (1). The structure of casein micelles is still a matter of debate (2-4). Casein sub-micelle models propose smaller units consisting mainly of caseins, which are linked by small calcium phosphate clusters (5), while other models deny casein sub-micelles and consider calcium phosphate cluster as growing centers for caseins (6). The dual binding model of Horne (7,8) is based on primary structures of caseins, which show distinct hydrophilic and hydrophobic regions along the protein chain. According to this model, caseins can be described as block copolymers. The hydrophilic regions in aS1-, aS2-, and ß-casein are rich in phospo-serines, to which the colloidal calcium phosphate particles become attached. The casein micelle is stabilized by a hydrophobic core and hydrophilic fringes on the surface and by electrostatic coupling to calcium phosphate particles.
Both hydrophobic and electrostatic interactions decrease with pressure, which generally leads to dissociation and unfolding of proteins. Casein micelles disintegrate irreversibly under pressure.
As demonstrated by ex-situ measurements using static and dynamic light scattering (3,9) and imaging techniques such as electron microscopy (10,11) or atomic force microscopy (12), high pressure reduces the hydrophobic interactions between the caseins inside the micelle. Increased exposure of hydrophobic groups was observed after pressure treatment of milk proteins (13). Moreover, pressure affects the mineral equilibrium of calcium, phosphorus and other components. Conflicting data from ex-situ measurements related to the calcium equilibrium have been presented: no effect of pressure on the free calcium concentration was found by Shibauchi et al. (14) while Anema et al. (9) found an increased calcium concentration after a pressure treatment of 200 MPa.
Material and Methods
Casein micelles were extracted from commercial-grade skim milk by combined uniform transmembrane pressure micro-filtration (mean pore diameter: 0.1 µm) and ultra-filtration, concentrated by five washing steps and dried in a spraying tower. The fractionation procedure has been described in detail by Tolkach and Kulozik (15). Casein powder was dissolved in filtered 0.1 M Mes/Tris-HCl solution at a concentration of 40 mg/ml and the pH was adjusted to 7.3 with HCl. All solutions were equilibrated by thoroughly stirring for 5 h at 20ºC.
Turbid casein solutions (3%) were studied by photon correlation spectroscopy in a back-scattering geometry to reduce multiple scattering of light. An He-Ne-laser light source (l = 632.4 nm) from an ALV-NIBS System (ALV-Laser GmbH, Langen) was focused on an optical SITEC high-pressure cell. In dilute solutions the single-scattered intensity of light is proportional to the square of the molecular weight, the concentration and the molecular form factor. The scattered intensity is thus heavily biased by high-molecular weight particles.
We employed dynamic light scattering to analyze the molecular size distribution. These experiments showed that the pressure-induced dissociation process essentially involves a high-molecular weight species, the intact micelle and low-molecular weight fragments. For the present purpose, we thus used the average light intensity as an empirical indicator of the degree of dissociation of the intact micelle since the fragments do not contribute significantly to the scattering signal. After subtraction of a background intensity I (P = 400 MPa) at high pressure we defined a dissociated fraction by normalizing the measured intensity I(P) by I(P = 1 bar):
The size distribution was derived by expanding the measured scattered field autocorrelation function, g1(t) in terms of exponentials:
where G(G) is the distribution of relaxation rates, G(q) = q2D(R), where q denotes the scattering vector. D(R) is the diffusion coefficient depending on the effective hydrodynamic radius according to the Stokes-Einstein relation: D = KT/(6phR), h is the viscosity of the solvent.
G(G) was derived using the Laplace-inversion program CONTIN. For a particular value of R the distribution is given by Pz(R) = n(R) . M(R)2, where n is the number density of particles with radius R and M is their molecular mass. Assuming spherical, compact particles, M µ R3, one can derive an estimate of the number distribution n(R).
Results
Dynamic and static light scattering experiments were performed at 177º with turbid casein solutions at various pressures. Figure 1 displays the distribution Pz(R) at 0.1 MPa, which is dominated by micelles with diameters near 300 nm. The micelles were rather poly-disperse, with the half width of the distribution corresponding to 100 nm. At 100 MPa the turbidity had nearly vanished, but the z-average of R was still dominated by 300-nm particles. At low turbidity it became possible to determine the number average, which is shown in Figure 1. Now the dominant particle size was 15-20 nm. At 300 MPa most fragments were reduced to the monomer level with diameters close to 3 nm.
Figure 2 displays pressure-temperature dissociation plots derived from the average light scattering intensity in 177º back-scattering geometry. The dissociation of casein into small fragments, M ® F, was complete at 350 MPa at all temperatures. The location of the midpoint of the transition on the pressure scale increased with increasing temperature. The forces that stabilize the micelle, thus increased with temperature. Moreover, the transition curves were not as smooth as expected for a simple two-state mechanism. In the temperature range between 30 and 60ºC, a plateau emerged, suggesting the existence of an intermediate state.
Since the fragments differed in size and molecular weight from the intact micelle at least by a factor of ten, they contributed only weakly to the average light scattering intensity. The measured dissociated fraction a (Equation 1) is thus dominated by the high-molecular weight micelle fraction. This means that the plateau in a at the 50% level in Figure 2 cannot be attributed to a partially dissociated intermediate state with two fragments of approximately equal size. Since we do not observe fragments of the appropriate size (100 nm), a purely sequential dissociation process is not compatible with the data. Instead we suggest a parallel model, which assumes two types of casein micelles, which differ in stability.
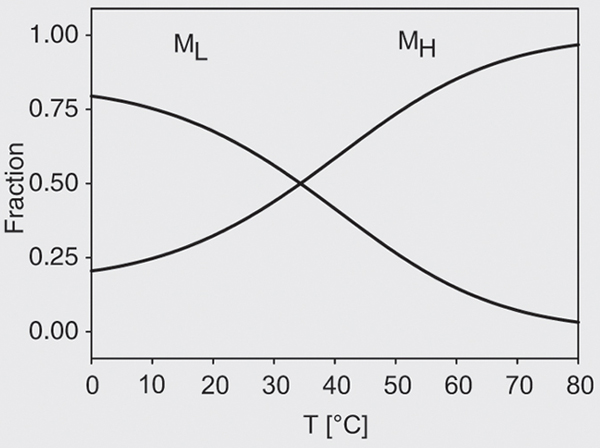
At low temperatures the dominant form was the pressure-unstable state ML, while with increasing temperature a high-temperature form, MH, was increasingly present and was more stable.
Thermodynamic analysis of pressure-temperature dissociation of casein micelles
Pressure-induced dissociation of casein micelles is not fully reversible due to dissociation between colloidal calcium and phosphate particles (11). This process, which is associated with the formation of 15- to 20-nm particles (Figure 1), is slow. Thus, on a time scale of 30 min one can determine stable, time-independent values of scattered light. With this restriction, we performed a thermodynamic analysis of the transition curves. Next we consider an equilibrium of two types of micelles, ML and MH, which dissociated under pressure into fragments FL and FH:
The difference in chemical potential between ML and MH follows from the Gibbs-Duhem relation:
Dµ0 is the potential of the reference state, DSHL denotes the difference in molar entropy and DVHL denotes the respective volume difference. DCP is the difference heat capacity at constant pressure between the H and L forms. The difference in chemical potential vanishes in equilibrium, DµHL = 0. Thus, at the reference temperature and pressure one has:
Dµ0 = -RT ln LHL
The equilibrium constant, LHL, is defined by the ratio of the molar concentrations if the solution is diluted: LHL = NH/NL. If the reference temperature and pressure, T0 and P0, are chosen at the midpoint of the HL equilibrium, NH = NL, and the reference potential vanishes: Dµ0 = 0.
The equilibrium is controlled by the entropy difference DSHL(T), which decreases with increasing temperature. This implies a finite difference in the heat capacities, DCHL ¹ 0.
We can fit the data ignoring the pressure dependence of the conformational equilibrium; thus DVHK » 0.
The fraction of the dissociated conformer aH/L H or L is controlled by the pressure-dependent constants KL and KH(P):
and
ln KL/H,F(P) = ln KL/H,F(P = 0) - 1/(RT) × P × DVH/L,F + DSH/L,F/R
DVH/L,F and DSH/L,F are the volume and entropy differences between the H or L form and its fragments F. The combined dissociation fraction is then given by:

(Eq. 8)
In its present form the model is over-determined with 8 parameters. The simplest model fitting the data was based on the assumption that the H « L equilibrium is only temperature dependent, DVHL» 0 and that the dissociation of H or L into fragments is only pressure but not temperature dependent. This implies DSH/L,F» 0. Global fits to all transition curves were performed, and are represented by the full lines in Figure 2. The correlation coefficient of the fit was 0.98 and the residuals did not exhibit any systematic deviations. The resulting parameters are listed in Table 1. The dissociation constant KL(0) = 0.09 of the low temperature form is small, favoring intact micelles at ambient pressure. The dissociation volume, DVLF= -61 ± 7 ml/mol, is negative and surprisingly small. The dissociation constant of the high temperature form H, KH(0) = 9.5 x 10-10, is negligible at ambient pressure, while the dissociation volume, DVHF = -204 ± 3 ml/mol, is again negative and significantly larger in comparison with the L form. The positive DSHL = 150 ± 10 J/(mol . K) implies that the H form is more stable than the L form at high temperature and vice versa. Introducing a finite heat capacity change noticeably improves the quality of the fits. The resulting difference, DCHL» -0.5 kJ/(mol . K), is smaller than heat capacity changes found in denaturation experiments with small proteins. However, the sign of DCHL is negative, implying that the H-form exhibits a lower heat capacity than the L-form in spite of its larger entropy. Figure 3 shows the resulting temperature-dependent populations of H and L. The pressure-induced dissociation transition is monophasic at high temperatures since only the high-temperature form H is present. At low temperatures both species, L and H, contribute. The midpoint temperature is T0 = 307 ± 2 K, independent of the pressure.
In conclusion, in situ light scattering measurements demonstrate that casein micelles (d » 200 nm) disintegrate at pressures above 300 MPa into 3-nm particles, most likely casein monomers or small oligomers. We also observe particles of intermediate size near 15 nm, which represent either intermediate states or aggregates of casein monomers, which evolve a posteriori to pressure dissociation. The pressure required to dissociate the micelles increases with temperature in accordance with hydrophobic stabilization. A continuous enhancement of hydrophobic interactions would simply shift the midpoint of the transition on the pressure scale. Instead we observe two discrete steps with a temperature-dependent partition: with increasing temperature the fraction of a low temperature form (L) decreases in favor of a high temperature form (H), which is more pressure stable.
The thermodynamic analysis based on Equation 3 indicates that the H-form is more disordered, T0 . DSHL = 46 kJ/mol (T0 = 307 K), and exhibits a larger dissociation volume, 204 versus 61 ml/mol, than the L-micelle (Table 1). This could suggest that the high-temperature form has an open structure, while the L-form is more compact. However, the H « L equilibrium is approximately pressure independent, and thus the volume difference DVHL must be small. This implies that the fragments of H and L, FL and FH differ in volume. However, due to the small size of the fragments they contribute very little to the observed scattering intensity. Thus, no information about the FL « FH equilibrium is obtained from the light scattering data. The apparent volume difference is derived from the width of the pressure transition. It is likely that the apparent difference in the dissociation volumes, DVHF, DVLF, reflects a difference in heterogeneity of the size and stability of the L and H micelles, which will broaden the transition. The dissociation constants of H and L, KH(P) and KL(P), depend only on the pressure but not on the temperature. This implies that the entropic difference between micelle and fragments must be small, DSH/L,F» 0. Since H and L differ in entropy, one must conclude that DSHL is stored in the respective fragments DSHL» DSF,H/L. We observe indeed two distinct fragments corresponding to particle sizes near 3 nm and 15 nm. But the arguments concerning the fragments given above apply again. Moreover, the pressure-induced dissociation process is only partially reversible. The main result of this in situ pressure work is the finding of two states of native-like casein micelles, which differ in sensitivity to pressure dissociation. The H form is dominant at high temperatures. We are presently investigating whether the two states differ in the manner how calcium phosphate particles are bound. The model should be considered as rather preliminary, and further extensions for explicit inclusion of heterogeneity and size distribution are in progress.
In situ size distribution of casein particles at three pressures derived from the intensity correlation function, z-distribution at 0.1 MPa and number distribution at 100 and 300 MPa (see text).
Temperature-pressure profile of the dissociated fraction of casein micelles (pH 7.3) and simultaneous fit according to the model of Equations 4-8.
Temperature-dependent population the low (L) and high (H) temperature conformer of casein micelles at ambient pressure according to the model of Equation 3.
Figure 3. Temperature-dependent population the low (L) and high (H) temperature conformer of casein micelles at ambient pressure according to the model of Equation 3.
Address for correspondence: W. Doster, Physikdepartment E13, Technische Universität München, D-85748 Garching, Germany. Fax: +49-89-289-12473. E-mail: wdoster@ph.tum.de
Presented at the 3rd International Conference on High Pressure Bioscience and Biotechnology, Rio de Janeiro, RJ, Brazil, September 26-30, 2004. Reesearch supported by the Deutsche Forschungsgemeinschaft, Research Project "High Pressure Treatment of Food". Received January 21, 2005. Accepted May 10, 2005.
- 1. Walstra P & Jenness R (1984). On the stability of casein micelles. Journal of Dairy Science, 73: 1965-1979.
- 2. Dalgleish DG, Spagnuolo PA & Goff HD (2004). A possible structure of the casein micelle based on high-resolution field-emission scanning electron microscopy. International Dairy Journal, 14: 1013-1089.
- 3. Desobry-Banon S, Richard F & Hardy J (1994). Study of acid and rennet coagulation of high pressurized milk. Journal of Dairy Science, 77: 3267-3274.
- 4. McMahon DJ & McManus WR (1998). Rethinking casein micelle structure using electron microscopy. Journal of Dairy Science, 81: 2985-2993.
- 5. Walstra P (1999). Casein sub-micelles: do they exist? International Dairy Journal, 9: 189-192.
- 6. Holt C, de Kruif CG, Tuinier R et al. (2003). Substructure of bovine casein micelles by small-angle X-ray and neutron scattering. Colloids and Surfaces A, 213: 275-284.
- 7. Horne DS (1998). Casein interactions: casting light on the black boxes, the structure in dairy products. International Dairy Journal, 8: 171-177.
- 8. Horne DS (2003). Casein micelles as hard spheres: limitations of the model in acidified gel formation. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 213: 255-263.
- 9. Anema SG, Lee SK, Schrader K et al. (1997). Effect of pH on the turbidity of pressure-treated calcium caseinate suspensions and skim milk. Milchwissenschaft, 52: 141-146.
- 10. Needs EC, Stenning RA, Gill AL et al. (2000). High pressure treatment of milk: Effects on casein micelle structure and on enzyme coagulation. Journal of Dairy Research, 67: 31-42.
- 11. Keenan RD, Hubbard CD, Mayes DM et al. (2003). Role of Calcium Phosphate in High Pressure-Induced Gelation of Milk. Food Colloids-Biopolymers and Materials, Royal Society of Chemistry, Cambridge, UK, 109-118.
- 12. Regnault S, Thiebaud M, Dumay E et al. (2004). Pressurisation of raw skim milk and of a dispersion of phosphocaseinate at 9ºC or 20ºC: effects on casein micelle size distribution. International Dairy Journal, 14: 55-68.
- 13. Gaucheron F, Famelart M, Mariette F et al. (1997). Combined effects of temperature and high pressure on physicochemical characteristics of skim milk. Food Chemistry, 59: 439-447.
- 14. Shibauchi Y, Yamamoto H, Sagara Y et al. (1992). Pressure-induced conformational changes of casein micelles. In: Heremans K & Masson P (Editors), High Pressure and Biotechnology. Colloque INSERM Vol. 224. John Libbey Eurotext Ltd., London, UK.
- 15. Tolkach A & Kulozik U (2005). Fractionation of whey proteins and caseino-macropeptide by means of enzymatic cross-linking and membrane separation techniques. Journal of Food Engineering, 67: 13-20.
Publication Dates
-
Publication in this collection
30 July 2005 -
Date of issue
Aug 2005
History
-
Accepted
10 May 2005 -
Received
21 Jan 2005