Abstract
This study was designed to evaluate the effect of drag reducer polymers (DRP) on arteries from normotensive (Wistar) and spontaneously hypertensive rats (SHR). Polyethylene glycol (PEG 4000 at 5000 ppm) was perfused in the tail arterial bed with (E+) and without endothelium (E-) from male, adult Wistar (N = 14) and SHR (N = 13) animals under basal conditions (constant flow at 2.5 mL/min). In these preparations, flow-pressure curves (1.5 to 10 mL/min) were constructed before and 1 h after PEG 4000 perfusion. Afterwards, the tail arterial bed was fixed and the internal diameters of the arteries were then measured by microscopy and drag reduction was assessed based on the values of wall shear stress (WSS) by computational simulation. In Wistar and SHR groups, perfusion of PEG 4000 significantly reduced pulsatile pressure (Wistar/E+: 17.5 ± 2.8; SHR/E+: 16.3 ± 2.7%), WSS (Wistar/E+: 36; SHR/E+: 40%) and the flow-pressure response. The E- reduced the effects of PEG 4000 on arteries from both groups, suggesting that endothelial damage decreased the effect of PEG 4000 as a DRP. Moreover, the effects of PEG 4000 were more pronounced in the tail arterial bed from SHR compared to Wistar rats. In conclusion, these data demonstrated for the first time that PEG 4000 was more effective in reducing the pressure-flow response as well as WSS in the tail arterial bed of hypertensive than of normotensive rats and these effects were amplified by, but not dependent on, endothelial integrity. Thus, these results show an additional mechanism of action of this polymer besides its mechanical effect through the release and/or bioavailability of endothelial factors.
Shear stress; Flow-pressure response; Drag reduction; Endothelium; Polyethylene glycol; Hypertension
Abstract
Introduction
Material and Methods
Results
Discussion
References
Acknowledgments
Braz J Med Biol Res, August 2011, Volume 44(8) 767-777
Drag reduction by polyethylene glycol in the tail arterial bed of normotensive and hypertensive rats
 Correspondence and Footnotes
Correspondence and Footnotes
 K.L. Bessa1,4, J.F. Belletati2, L. dos Santos3, L.V. Rossoni2 and J.P. Ortiz4,5
K.L. Bessa1,4, J.F. Belletati2, L. dos Santos3, L.V. Rossoni2 and J.P. Ortiz4,5
1Departamento de Ciências Ambientais e Tecnológicas, Universidade Federal Rural do Semi-Árido, Mossoró, RN, Brasil
2Departamento de Fisiologia e Biofísica, Instituto de Ciências Biomédicas, Universidade de São Paulo, São Paulo, SP, Brasil
3Departamento de Ciências Fisiológicas, Universidade Federal do Espírito Santo, Vitória, ES, Brasil
4Departamento de Engenharia Mecânica, Escola Politécnica, Universidade de São Paulo, São Paulo, SP, Brasil
5Instituto Mauá de Tecnologia, Escola de Engenharia, São Caetano do Sul, SP, Brasil
 Correspondence and Footnotes
Correspondence and Footnotes
Correspondence and Footnotes
Correspondence and Footnotes
Correspondence and Footnotes
Correspondence and Footnotes
This study was designed to evaluate the effect of drag reducer polymers (DRP) on arteries from normotensive (Wistar) and spontaneously hypertensive rats (SHR). Polyethylene glycol (PEG 4000 at 5000 ppm) was perfused in the tail arterial bed with (E+) and without endothelium (E-) from male, adult Wistar (N = 14) and SHR (N = 13) animals under basal conditions (constant flow at 2.5 mL/min). In these preparations, flow-pressure curves (1.5 to 10 mL/min) were constructed before and 1 h after PEG 4000 perfusion. Afterwards, the tail arterial bed was fixed and the internal diameters of the arteries were then measured by microscopy and drag reduction was assessed based on the values of wall shear stress (WSS) by computational simulation. In Wistar and SHR groups, perfusion of PEG 4000 significantly reduced pulsatile pressure (Wistar/E+: 17.5 ± 2.8; SHR/E+: 16.3 ± 2.7%), WSS (Wistar/E+: 36; SHR/E+: 40%) and the flow-pressure response. The E- reduced the effects of PEG 4000 on arteries from both groups, suggesting that endothelial damage decreased the effect of PEG 4000 as a DRP. Moreover, the effects of PEG 4000 were more pronounced in the tail arterial bed from SHR compared to Wistar rats. In conclusion, these data demonstrated for the first time that PEG 4000 was more effective in reducing the pressure-flow response as well as WSS in the tail arterial bed of hypertensive than of normotensive rats and these effects were amplified by, but not dependent on, endothelial integrity. Thus, these results show an additional mechanism of action of this polymer besides its mechanical effect through the release and/or bioavailability of endothelial factors.
Key words: Shear stress; Flow-pressure response; Drag reduction; Endothelium; Polyethylene glycol; Hypertension
Hypertension is a common disease that affects more than 40% of the adult population in developed countries and about 25% in emerging countries such as Brazil, and is associated with risk of cardiovascular morbidity and mortality (1). Although hypertension is of multifactorial origin, an increased peripheral resistance is observed in hypertensive patients and animal models (2). In addition, it is well known that drag reducer polymers (DRP) can reduce flow resistance (3).
The drag reduction phenomenon occurs in turbulent flows when friction drag is diminished by the addition of a few parts per million of long chain polymers, reaching up to 80% reduction (3,4). This phenomenon has been studied since 1949 (5), when Toms first published his study showing the drag reduction phenomenon. For this phenomenon to occur, the polymer molecule should have specific characteristics such as high molecular weight, long chains and a relatively linear structure. Classically, the polymer-induced drag-reducing effect occurs in turbulent flows, even though some studies have also described this effect on pulsatile flows in straight and spiral pipes or in Couette flows with Taylor vortices at low Reynolds numbers (6,7).
There are results showing that atherosclerotic plaque formation in aortas from rabbits submitted to a high cholesterol diet was reduced by using the polymer Separan AP-30 (8). In addition, the administration of small amounts of DRP may decrease atherosclerosis by increasing shear stress in areas normally exposed to low shear stress (9). Moreover, it has been demonstrated that infusion of DRP solutions significantly improved tissue perfusion and oxygenation, as well as survival rate of fluid resuscitation after acute hemorrhagic shock (10). Furthermore, intravenous injection of poly-N-vinylformamide reduced vascular resistance in healthy Sprague-Dawley rats (11).
It is well known that hypertension amplifies vascular reactivity due, in part, to endothelium dysfunction leading to an increase in vascular resistance (12,13). Furthermore, in arterial vessels obtained from spontaneously hypertensive rats (SHR), there is also an increase in inflammatory markers (14). Associated with other factors such as oxidative stress and dyslipidemia, these vascular alterations might contribute to a high probability of the occurrence of atherosclerotic plaque in this disease (13). On the basis of these effects of DRP, we hypothesize that the use of DRP would reduce flow resistance in arteries of normotensive and hypertensive rats. Thus, the objective of the present study was to determine the drag reduction effect of polyethylene glycol (PEG 4000), molecular mass 4000 Da, on the hydrodynamic or physiological mechanisms of the tail arterial bed of normotensive and hypertensive rats.
Viscosity
Viscosity was determined according to the Standard Specifications and Operating Instructions for Glass Capillary Kinematic Viscometers - American Society for Testing and Materials (ASTM D446). To measure viscosity, we used the Ubbelohde viscometer with the following characteristics: size number of 0C and an approximate constant of 0.003 (mm2/s2). The measurements were performed using a Krebs-Hanseleit nutrient solution in the presence of 5000 ppm of PEG 4000 (Synth, Brazil) at 37 ± 0.02°C.
Kinematic viscosity was determined as follows: the viscometer was loaded with PEG 4000 (5000 ppm) diluted in Krebs Hanseleit solution until the liquid meniscus located between the minimum and maximum filled lines marked on the reservoir. The viscometer was then inserted into a constant temperature bath for 20 min for the sample to reach the bath temperature. Suction was applied until the liquid reached the center of the bulb. Next, suction was removed and the liquid sample was allowed to flow freely and the time for the meniscus to pass between two markers was measured. Thus, kinematic viscosity can be calculated by multiplying efflux time by the viscometer constant. This procedure was repeated six times.
Experimental animals
Four-month-old male Wistar rats (N = 14) and SHR (N = 13) weighing 250-300 g were obtained from colonies maintained in the animal facilities of Departamento de Fisiologia e Biofísica, Instituto de Ciências Biomédicas, Universidade de São Paulo. Rats were housed at constant room temperature, humidity, and light cycles (12/12-h light-dark), had free access to tap water, and were fed standard chow ad libitum. The investigation conformed to the Guide for the Care and Use of Laboratory Animals published by the US National Institutes of Health (NIH Publication #85-23, revised 1996) and to the guidelines of the Committee on Care and Use of Laboratory Animal Resources of Instituto de Ciências Biomédicas, Universidade de São Paulo.
Perfusion of the tail arterial bed
The isolated and perfused tail arterial bed of normotensive and hypertensive rats was used to study the effects of DRP as described by França et al. (15). The rats were anesthetized intraperitoneally (ip) with a mixture of ketamine, xylazine, and acepromazine (64.9, 3.2, and 0.78 mg/kg, respectively), and received 500 U heparin ip. After 10 min, a 1-cm strip of the tail artery was dissected and cannulated near the base of the tail using a 24G catheter filled with Krebs-Hanseleit solution. The tail was then severed from the body, placed in a tissue bath, and perfused with Krebs-Hanseleit bicarbonate buffer (KHB) containing 27.2 mM NaHCO3, 119 mM NaCl, 1 mM NaH2PO4, 1.2 mM MgSO4, 5 mM KCl, 1.25 mM CaCl2, 11 mM glucose, and 30 µM EDTA, pH 7.4, bubbled with 5% CO2-95% O2 at 37 ± 0.5°C. The tail was cut approximately 1 cm from the tip to avoid microcirculation and venous return. The flow was provided by a peristaltic pump (Milan, Brazil) at 2.5 mL/min. The perfusion pressure was measured using a Utah pressure transducer (Utah Medical Products, USA) connected to the peristaltic pump and to the arterial cannula. The data were recorded by an interface software for computer data acquisition with a Windaq™ Waveform Browser (DATAQ Instruments, USA) at sample acquisition rate of 70 Hz. Because the flow rate was the same in the presence and absence of PEG 4000, changes in perfusion pressure represented changes in vascular resistance according to the Poiseuille equation:
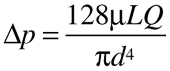
(Eq. 1)
where Δp is the differential pressure between the extremities of the vessel, µ is the dynamic viscosity, L is the vessel length, Q is the volumetric flow rate, and d is the vessel diameter.
Experimental protocols
Two protocols were used to study the drag reduction effect of the polymer on the tail arterial beds and flow-response curves were constructed for physiological and non-physiological flow rates. To establish the baseline conditions, the preparation was initially perfused with KHB solution for 1 h at a constant flow of 2.5 mL/min (15). The flow rates used were 1.5, 2.5, 5.0, 7.5, and 10.0 mL/min for 10 min each, and the steady-state perfusion pressure was obtained for all flow rates. The flow rate was then returned to 2.5 mL/min, and the KHB solution was changed to KHB containing 5000 ppm of PEG 4000. After 1 h, a new pressure-flow relationship was obtained as described above but now in the presence of PEG 4000.
To assess the role of the vascular endothelium in the PEG 4000 effect, endothelial damage was achieved by perfusing the membrane detergent CHAPS (3-[(3-cholamidopropyl) dimethylammonio]-1-propane sulfonate; 9 µg, 90 µL, in bolus) (Sigma, USA) at a flow rate of 2.5 mL/min. Endothelial damage and vascular reactivity to a nitric oxide (NO) donor were assessed by comparing the responses to a bolus injection of acetylcholine (5 µg in 100 µL; Sigma) and sodium nitroprusside (5 µg in 100 µL; Sigma), respectively, administered before and after endothelial damage. The endothelium was considered to be intact if the tail artery bed relaxed more than 70% in response to acetylcholine, while endothelial damage was indicated by less than 10% relaxation. After a new stabilization with KHB solution at a constant flow of 2.5 mL/min for 45 min, pressure-flow curves were determined using KHB solution and KHB plus PEG 4000 as described above.
At the end of the protocols, tail arteries were fixed for the measurement of internal diameter under the experimental conditions use, with appropriate calculations by computational analysis. Because the geometry and grid constructions should be performed using diameters equivalent to those at the time of perfusion, pressure data were acquired. Thus, the tail arterial bed from Wistar rats and SHR was fixed by perfusion with Bouin’s solution at the same flow rate as used in in vitro protocols (2.5 mL/min) for 8 h. Next, the tail artery was totally dissected and cut into three segments, embedded in paraffin and transversely cut at 5 µm. The sections were stained with hematoxylin-eosin and examined by bright field microscopy (Carl Zeiss, Germany) for the determination of the luminal diameters.
Computational analysis - geometry and grid
Because hemodynamic wall shear stress (WSS) has been reported to affect endothelial function and vascular tone, it was important to quantify it in the arteries used in the present study. However, a simple Poiseuille flow model could not be used because of the tapered geometry and therefore the WSS distribution was determined by computational fluid dynamic simulation. The artery geometry was obtained from the average proximal and distal diameters of 4-5 tail samples of each group as described above, together with measurements of the length of these vessels. The average length was approximately 110 mm. The geometry and the grid were generated by the preprocessor (Gambit 2.3.16, Fluent Inc., USA) and three boundary layer meshes having a total thickness of 0.3 mm were created in the vicinity of the wall to better resolve the shear gradients. The total number of nodes used for the generated mesh was 78,166, giving rise to 331,077 computational tetrahedron volumes (Figure 1).
Computational parameters and flow equations
The assumptions made about the nature of the flow were that it is 3-dimensional, unsteady, isothermal (37°C), with no external forces applied. For the computational analysis, the arterial wall was considered to be rigid and impermeable. The perfusing solution was considered to be a Newtonian liquid with constant density, with ρ assumed to be 1000 kg/m3. The inlet and outlet discharge was assumed to be equal. The mean pulsatile pressure curves obtained by the average of 10 complete pulsatile cycles from each group and experimental condition (Figure 2) were used as the inlet pressures in the numerical model for calculating WSS distribution. The distribution of WSS along the vessel length was plotted for the mean maximum value of pulsatile perfusion pressure representative of each group and experimental condition. A fundamental consequence of the viscous property of fluids is that in fluid flow there can be no step change in velocity at any point within the flow field. The reason for this is that the velocity gradient at a point is a measure of the rate of deformation of the fluid element at that point, which is resisted by the viscosity of the fluid. In particular, at the interface between a fluid and a solid boundary, such as the inner wall of a tube, the velocity of the fluid in contact with the wall must be the same as the velocity of the wall, otherwise there would be a step change in velocity at that point. This so-called no-slip condition is a fundamental condition that must be satisfied in any analysis of viscous flow. Thus, the no slip condition was applied to all walls. All the computational parameters defined in the preprocessor were exported to the solver Fluent 6.2.16. The mathematical equations governing the flow are:

(Eq. 2)
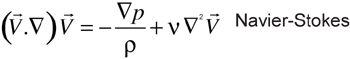
(Eq. 3)
where  is the velocity vector, ρ is the density, and p is the pressure. Discretization of these equations at each control volume involved an upwind scheme. The set of algebraic equations was solved iteratively using a procedure based on the semi-implicit SIMPLE algorithm. Convergence was achieved when the changes of the mass and of all velocity components, from iteration to iteration, were less than 10-4. Preliminary simulations were performed for all artery models under investigation in order to obtain information in terms of grid independence, which means that all models were independent of size of the control volume.
is the velocity vector, ρ is the density, and p is the pressure. Discretization of these equations at each control volume involved an upwind scheme. The set of algebraic equations was solved iteratively using a procedure based on the semi-implicit SIMPLE algorithm. Convergence was achieved when the changes of the mass and of all velocity components, from iteration to iteration, were less than 10-4. Preliminary simulations were performed for all artery models under investigation in order to obtain information in terms of grid independence, which means that all models were independent of size of the control volume.
Calculation of wall shear stress distribution
WSS is determined from the velocity gradient at the wall as follows:
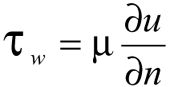
(Eq. 4)
where µ is the dynamic viscosity, u is the tangential velocity at the wall, and n is the unit vector perpendicular to the wall. The unit used for shear stress is Pascal (Pa) from the International System of Units. Pascal is defined as one Newton per square meter (1 Pa = 1 N/m2) and one Pascal is equivalent to ten dynes/cm2 (1 Pa = 10 dyn/cm2).
Drag reduction
Reynolds numbers (Re) were calculated based on the following volumetric flow rates: 1.5, 2.5, 5.0, 7.5, and 10 mL/min (Re = 100, 173, 346, 520, and 694, respectively). Drag reduction was calculated using the WSS along the vessel according to Equation 5:
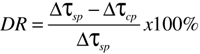
(Eq. 5)
where DR is the percentage of drag reduction, and Δτsp and Δτcp are the shear stress without and with the polymer, respectively. Re was calculated using Equation 6:
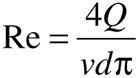
(Eq. 6)
where Q is the volumetric flow rate, ν is the kinematic viscosity, and d is the mean tube diameter.
Statistical analysis
Data are reported as means ± SEM, with N indicating the number of observations. Values were analyzed by one- or two-way analysis of variance (ANOVA). When ANOVA revealed significant difference, the Bonferroni post hoc test was applied. The level of significance was set at 0.05.
Viscosity measurements
Viscosity was measured with Glass Capillary Kinematic Viscometers. The value of kinematic viscosity (ν) was obtained by multiplying the instrument constant (C) by efflux time (Δt):
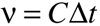
(Eq. 7)
whose value was 0.75 x 10-6 ± 0.0006 m2/s.
Internal arterial diameters
Active diameters obtained from tail arteries under the pulsatile volumetric flow rate of 2.5 mL/min were considered to contain intact structural and functional endothelium, as detected by microscopic visualization of endothelial cells and by functional experiments where the tail arterial bed was able to relax under acetylcholine infusion (data not shown). As shown in Figure 3A, the internal diameter of the proximal portion of the tail artery (base of tail) did not differ between Wistar rats and SHR (Wistar: 535 ± 13 vs SHR: 531 ± 19 µm, P > 0.05), whereas the diameter of the intermediate and distal portions of SHR tail arteries were significant smaller than those of normotensive rats (intermediary - Wistar: 424 ± 33 vs SHR: 305 ± 16 µm, P < 0.05, and distal - Wistar: 348 ± 12 vs SHR: 228 ± 10 µm, P < 0.05). It is important to state that in both groups there was a continuing reduction in internal diameter from the base to the tip of the tail (Figure 3A), which was associated with an increase in vessel media layer/lumen ratio in the distal portion (Figure 3B). In addition, it is important to emphasize that these changes were more expressive in tail arteries from SHR than from Wistar rats (Figure 3B).
Perfusion pressure and flow-response curves
Perfusion with PEG 4000 was able to decrease the main parameters of pulsatile pressure in all groups and experimental conditions (with (E+) or without (E-) endothelium), as shown Figure 2. Statistical analysis showed a significant decrease in minimum and maximum peak pressures, as well as in the delta of pulsatile pressure (Figure 2).
Figure 4A shows the pressure-flow relationship in isolated and perfused tail arterial beds obtained by plotting mean perfusion pressure (MPP) in response to increasing flow rates of KHB solution perfusion before and after endothelial damage. MPP levels increased with increasing perfusion flow rate (from 1.5 to 10 mL/min) in both experimental groups and in all conditions evaluated (Figure 4A). However, the pressure-flow relationship in the tail arterial bed with intact endothelium from SHR exhibited higher rises in MPP in response to increasing flow rates compared the tail arterial bed of normotensive rats (Figure 4A). Interestingly, endothelial damage by CHAPS caused the tail arterial bed from Wistar rats to present higher flow-induced MPP increments, reaching the behavior of the tail arterial bed from the hypertensive group (Figure 4A). In contrast, when the endothelium was damaged in SHR preparations, no changes were noted in pressure-flow relationship (Figure 4A).
One-hour perfusion with PEG 4000 in KHB solution (Figure 4B) was able to decrease MPP levels in pressure-flow response in the tail arterial bed with intact endothelium from both groups. However, SHR preparations presented a greater reduction than Wistar preparations (Figure 4B). Two-way ANOVA showed a significant interaction in flow-response curves between SHR/E+ and SHR/E+/PEG 4000 conditions. Figure 4C shows the effect of PEG 4000 in the absence of endothelium. After endothelial damage, as described above, similar increases in MPP induced by increasing flow rates were noted in both Wistar and SHR groups, and PEG 4000 perfusion similarly reduced these responses in both groups (Figure 4C).
Wall shear stress
Figure 5 shows the WSS distribution calculated along the length of the tail artery from Wistar and SHR rats under all experimental conditions at a flow of 2.5 mL/min. Computational simulation estimated that WSS values increased along the vessel wall due to diameter reduction, as demonstrated in Figure 3. In Wistar rats, WSS increased from 2.30 to 23.60 Pa (from the beginning to the end of the vessel; Figure 5A) but, after endothelium removal, WSS levels increased along the tail artery length (from 2.84 to 29.52 Pa; Figure 5C). As shown in Figure 5B and D, simulation of WSS data acquired in experiments on SHR vessels with and without endothelium also showed a similar behavior. However, in contrast to what was observed for Wistar rats, in tail arterial beds from SHR, these levels were closely similar both in the presence and in the absence of endothelial cells, ranging from 3.23 to 32.91 and from 3.22 to 33.24 Pa, respectively (Figure 5B and D).
Figure 5A and B show the WSS in the presence and absence of PEG 4000 in the tail arterial bed with intact endothelium from Wistar rats and SHR. Interestingly, WSS was lower in the presence of PEG 4000 in both groups, but a more expressive reduction was found in SHR (compare Figure 5A and B). Figure 5C and D graphically present the behavior of WSS in the presence and absence of PEG 4000 in simulations of data acquired from experiments with damaged endothelium. In these situations, PEG 4000 was also able to reduce the shear stress along the vessel wall in both Wistar rats and SHR. Although this modulating effect of PEG 4000 occurred in both groups and in both conditions (before and after endothelial damage), this effect was more significant in the presence of endothelial cells.
Drag reduction
The relative drag reduction calculated from WSS along the vessel length caused by PEG 4000 perfusion is illustrated in Figure 6 (data calculated from computational simulation results reported in Figure 5). The addition of PEG 4000 to the perfusion solution produced a marked reduction in the resistance to flow, which was constant along the length of the vessel for all groups and experimental conditions. The effect of PEG 4000 on percent drag reduction was slightly higher in the tail arterial bed with endothelium from SHR (40%) compared to Wistar rats (36%). Furthermore, the drag reduction effect was reduced by endothelial damage in both groups (Figure 6). In the absence of endothelial cells, PEG 4000 induced a 28% drag reduction in the tail arterial bed of Wistar rats and a 24% reduction in the tail arterial bed of SHR according to computational simulations.
Effect of PEG 4000 perfused at the flow rate of 2.5 mL/min on the pulsatile pressure acquired from tail arterial beds with intact endothelium (E+) (A and B, respectively) and after endothelial damage (E-) of Wistar rats and spontaneously hypertensive rats (SHR) (C and D, respectively). KHB = Krebs-Hanseleit-buffered solution. Relative time was calculated as actual time (t1) divided by total time (tt). N = 4-6 animals in each group. *P < 0.05 for KHB vs KHB + PEG (paired Student t-test). Differences were analyzed concerning peak pressure, delta of pulsatile pressure, and area under the pressure curve.
A, Active internal diameters of tail arteries from Wistar rats (N = 4 animals) and spontaneously hypertensive rats (SHR, N = 5 animals) fixed at a volumetric flow rate of 2.5 mL/min. *P < 0.05 vs proximal portion; #P < 0.05 vs Wistar rats (two-way ANOVA followed by the Bonferroni post hoc test). B, Photomicrograph of transverse sections of proximal and distal tail artery from Wistar rats and SHR. Magnification: 10X. Inset panels in the proximal tail artery photomicrographs of Wistar and SHR are amplified images showing the endothelial (E), medium (M) and adventitial (A) layers of the artery.
Flow-pressure relationship in tail arterial beds. A, Before (E+) and after (E-) endothelial damage on tail arterial beds from SHR (N = 7 animals) and Wistar rats (N = 6 animals); B, in the absence and presence of PEG 4000 in tail arterial beds with intact endothelium (E+) from SHR (N = 5 animals) and Wistar rats (N = 7 animals); C, effect of PEG 4000 after endothelial damage (E-) on tail arterial beds from SHR (N = 7 animals) and Wistar rats (N = 6 animals). MPP = mean perfusion pressure. #P < 0.05 vs Wistar; *P < 0.05 vs PEG effectiveness; §P < 0.05 interaction between PEG effect on Wistar rats and SHR (two-way ANOVA followed by the Bonferroni post hoc test).
Distribution of wall shear stress along the vessel wall from the base (0 mm) to the end (110 mm) simulated for the mean of the maximum value of pulsatile cycle represented in Figure 2 at a flow of 2.5 mL/min. N = 4-6 animals in each group. A and B, Effect of PEG 4000 on the wall shear stress (Pa = Pascal) along the wall of the tail arterial bed with intact endothelium (E+) from Wistar rats and spontaneously hypertensive rats (SHR), respectively; C and D, effect of endothelial damage (E-) on PEG-induced changes in wall shear stress in the tail arterial beds from Wistar rats and SHR, respectively.
Percent drag reduction by PEG 4000 (derived from the computer simulated graphs in Figure 5) along the vessel length in Wistar rats (circles) and spontaneously hypertensive rats (SHR, triangles), before (open symbols) and after endothelium damage (filled symbols). Drag reduction values along the vessel length were higher in the presence of endothelium than after damage, and in the tail arterial bed from SHR compared to Wistar rats.
In the present investigation, the effects of PEG 4000 on the tail arterial beds of normotensive and spontaneously hypertensive rats were studied both in the presence and in the absence of endothelial cells, and computational analysis of shear stress and drag reduction along the vessel wall was carried out. The data suggest that PEG 4000 acts differently in the two rat strains, with its effects on vascular perfusion pressure or pressure-flow response being more pronounced in the tail arterial bed from hypertensive rats. In addition, the effect of PEG 4000 on drag reduction was amplified in the presence of endothelial cells. To the best of our knowledge, this is the first time that these phenomena are shown for PEG 4000.
It is well known that DRP, like PEG 4000, can effectively decrease resistance to flow without affecting fluid viscosity or density (5). These polymers have been investigated and used for various industrial and engineering applications including crude oil transport through pipelines, firefighting, and reducing drag on ships and submarines (16). When applied to animal models of atherosclerotic plaque these polymers showed beneficial hemodynamic effects including delay/prevention of the development of atherosclerosis in animals kept on an atherogenic diet (8). The literature has reported that DRP are described as long-chain polymers with a molecular weight above 1,000,000 Da (10). However, almost all tests reported were performed in an in vitro circulating system using rigid glass tubes. A previous study by our group using an in vitro circulating system (silicon tubes) showed no drag reduction concerning laminar and turbulent flows with PEG 4000 (5000 ppm) (17). On the other hand, the present results showed drag reduction also using PEG 4000 (5000 ppm) in an in vitro circulating system of isolated tail arterial beds. Thus, the drag reduction phenomenon may be based on hydrodynamic as well as physiological mechanisms.
In the present study, perfusion pressure was altered in the perfused vascular bed, with a consequent increased vascular resistance in experiments conducted on hypertensive rats compared to control Wistar rats. These characteristics are suggestive of the well-known pathological changes that occur in the arterial wall of SHR (18,19). Thus, the high intra-arterial pressure per se is sufficient to induce the lack of NO-mediated vasodilatation present in hypertension, contributing to the intensification of WSS and vascular resistance (20,21). Notably, in the presence of PEG 4000, the perfusion pressure of isolated tail arteries from both normal and hypertensive animals was decreased, reflecting a reduction in vascular flow resistance. This result agrees with the hypothesis of Huang et al. (22) that a reduction in pressure can contribute to improving the vessel response.
Our protocol evaluating the effect of endothelial cells on vascular reactivity to flow rate demonstrated higher values of perfusion pressure after endothelial damage with CHAPS only in the tail arterial bed from Wistar rats. Specifically, the tail arterial bed from Wistar rats without endothelial cells behaved as the tail arterial bed from SHR in the presence or absence of endothelial cells. This can explain why the negative endothelial modulation of the flow-induced response in the tail arterial bed was lower in SHR than in Wistar rats (20,23). In fact, the concept of endothelial dysfunction in hypertension has been well established, and plays an important role in impaired or blunted physiological vascular responses (13,24). Interestingly, the presence of intact endothelium may also be very significant for the effects of PEG. Although PEG 4000 perfusion was able to reduce the pressure-flow response even in the absence of endothelial cells, as seen in Figure 4C, this modulation was significantly less expressive than that obtained with intact endothelium (Figure 4B), suggesting that endothelial cells have an important role in the PEG-induced reduction of the pressure-flow relationship. These results support the importance of endothelial cells in pressure and flow regulation, which play a critical role in vascular homeostasis by acting as vasoactive, antithrombotic and anti-inflammatory modulators (12,13), as well as specialized sensors of local changes in blood flow (25-27).
In vivo studies have demonstrated that, in the presence of intact functional endothelium, the circumference of vessels increases under high-flow conditions and decreases under low-flow conditions, demonstrating the vasodilator effect of flow (25). This control is lost, at least in part, when the endothelium is intentionally damaged or in pathological conditions involving endothelial dysfunction, as seen in SHR preparations. In addition, in these situations, increases in flow rate were not accompanied by significant vasodilatation and the perfusion pressure was markedly increased (28). In fact, the present results support this hypothesis, showing that the flow-pressure relationship in the tail arterial bed was shifted upwards and its slope was enhanced in SHR compared to Wistar rats. Moreover, the computational simulation study concluded that WSS increased with diameter reduction along the vessel length. This generated an exponential relationship and also showed that WSS levels were higher in the tail arterial bed from SHR than from Wistar rats. Several studies using hypertensive animals have revealed morphological changes in the vascular wall suggesting that structural modifications added to altered endothelial function are not only a consequence, but also a cause of the development or maintenance of increased resistance in hypertension (18,29).
In hypertension, as well as in other pathologic conditions, increases in WSS can be observed during increases in blood flow because higher blood pressure and reduced vessel diameter occur concomitantly (30). Therefore, the higher WSS observed in the present study for the tail arterial bed from SHR occurs due to the reduction in diameter contributing to an increase in flow resistance, possibly due to excessive endothelial synthesis and release of constrictor factors, and/or a decrease in the synthesis, release or bioavailability of dilator factors such as NO, that are altered in hypertension (21,31,32). It is also important to mention that at the end of the tail arterial conduit, the WSS calculated by the simulation software was markedly increased up to uncommon levels. This was due to the fact that the computational domain does not consider collateral vessels arising from the main tail artery, which probably forced the volumetric flow rate to be exactly equal at inlet and outlet of the conduit.
Perfusion with PEG 4000 reduced WSS in both groups. Some studies have shown that other PEGs, such as PEG 5000 or PEG 10000 were able to reduce the vasoconstriction, lack of capillary perfusion, vascular permeability, leukocyte adhesion, and the increase in von Willebrand factor in post-ischemic reperfusion. Moreover, following PEG 5000 or PEG 10000 injection, there was a significant vasodilatation associated with an increased flow during early reperfusion, which might have increased membrane fluidity in endothelial cells as a response to the increased shear stress (33). Other studies have reported that PEG repairs neuronal membranes and inhibits free radical production in in vitro and in vivo models of spinal cord injury (34,35). Accordingly, a possible explanation for the reduction in WSS in the presence of PEG 4000 is that this polymer makes the endothelium more responsive to shear stress and more resistant to oxidative stress, leading to a reduction in vasoconstriction. It is known that in human and experimental model of hypertension there is an increased oxidative stress in the endothelium (24,36,37) and this fact can negatively interfere with the NO-mediated shear stress-induced dilation (38). On this basis, the fact that PEG 4000 decreased WSS along the vessel supports the hypothesis that these polymers act favorably on vascular homeostasis by improving the action or the bioavailability of vasodilators such as NO or even decreasing the actions of free radicals with deleterious and vasoconstrictor effects.
The drag reduction caused by PEG 4000 differed between the two experimental groups and was also modulated by the presence of endothelium since in the absence of endothelial cells the drag reduction phenomenon decreased significantly. The exact in vivo mechanism of action of DRPs is unknown because of their complex fluid dynamic behavior in conjunction with the non-Newtonian physics of blood flow (39). Some hypotheses have been raised in the literature to explain the action of DRPs on the vascular system. A commonly accepted explanation is that DRPs could carry the red blood cells very close to the wall vessel, contributing to an increase local viscosity and stimulating NO release, with consequent vasodilatation (10). This assumption will be valid if the endothelial cells do not show endothelial dysfunction. In our experiments, PEG 4000 induced drag reduction in preparations perfused with a KHB solution without cells. As a result, this drag reduction phenomenon cannot be attributed to increased local viscosity due to any special red blood cell arrangement. Although drag reduction induced by DRPs may be intensified by endothelial cells, the effect of PEG 4000 was even higher in SHR preparations, which typically exhibit an important endothelial dysfunction, refuting the idea of NO release-dependent drag reduction by DRPs as a key mechanism.
The present study demonstrated that PEG 4000 was more effective in reducing the pressure-flow response and WSS in the tail arterial bed of hypertensive than normotensive rats. In addition, the drag reduction was greater in the presence of intact endothelium, indicating the further necessity of a better understanding of the interaction between PEG 4000 and endothelial cells in this biological milieu. With this knowledge, it may be possible to consider the usefulness of PEG solutions to reduce the unfavorable effects of endothelial dysfunction and vasculopathies present in hypertension.
1. Mulvany MJ. Small artery remodeling and significance in the development of hypertension. News Physiol Sci 2002; 17: 105-109.
2. Mulvany MJ. Small artery remodelling in hypertension: causes, consequences and therapeutic implications. Med Biol Eng Comput 2008; 46: 461-467.
3. Virk PS. Drag reduction fundamentals. AIChE Journal 1975; 21: 625-656.
4. Vlachogiannis M, Liberatore MW, McHugh AJ, Hanratty TJ. Effectiveness of a drag reducing polymer: relation to molecular weight distribution and structuring. Phys Fluids 2003; 15: 3786-3794.
5. Toms BA. Some observations on the flow of linear polymer solutions through straight tubes at large Reynolds numbers. Proceedings of the 1st International Congress on Rheology. Amsterdam: North Holland; 1949. p 135-141.
6. Keller A, Kiss G, Mackley MR. Polymer drag reduction in Taylor vortices. Nature 1975; 257: 304-305.
7. Driels MR, Ayyash S. Drag reduction in laminar flow. Nature 1976; 259: 389-390.
8. Faruqui FI, Otten MD, Polimeni PI. Protection against atherogenesis with the polymer drag-reducing agent Separan AP-30. Circulation 1987; 75: 627-635.
9. Sawchuk AP, Unthank JL, Dalsing MC. Drag reducing polymers may decrease atherosclerosis by increasing shear in areas normally exposed to low shear stress. J Vasc Surg 1999; 30: 761-764.
10. Kameneva MV, Wu ZJ, Uraysh A, Repko B, Litwak KN, Billiar TR, et al. Blood soluble drag-reducing polymers prevent lethality from hemorrhagic shock in acute animal experiments. Biorheology 2004; 41: 53-64.
11. Marhefka JN, Marascalco PJ, Chapman TM, Russell AJ, Kameneva MV. Poly(N-vinylformamide)-A drag-reducing polymer for biomedical applications. Biomacromolecules 2006; 7: 1597-1603.
12. Michel T, Vanhoutte PM. Cellular signaling and NO production.Pfluggers Arch-Eur J Physiol 2010; 459: 807-816.
13. Félétou M, Köhler R, Vanhoutte PM. Endothelium-derived vasoactive factors and hypertension: Possible roles in pathogenesis and as treatment targets. Curr Hypertens Rep 2010; 12: 267-275.
14. Sanz-Rosa D, Oubina MP, Cediel E, de Las Heras N, Vegazo O, Jimenez J, et al. Effect of AT1 receptor antagonism on vascular and circulating inflammatory mediators in SHR: role of NF-kappaB/IkappaB system. Am J Physiol Heart Circ Physiol 2005; 288: H111-H115.
15. França AS, Rossoni LV, Amaral SM, Vassallo DV. Reactivity of the isolated perfused rat tail vascular bed. Braz J Med Biol Res 1997; 30: 891-895.
16. Hoyt JW. The effect of additives on fluid friction. J Basic Engineering 1972; 94: 28.
17. Bessa KL, Ortiz JP. Efeito de polímeros redutores de arrasto em escoamento pulsátil laminar. 1° Encontro Nacional de Engenharia Biomecânica. Petrópolis: 2007.
18. Mulvany MJ, Aalkjaer C. Structure and function of small arteries. Physiol Rev 1990; 70: 921-961.
19. Safar M, Chamiot-Clerc P, Dagher G, Renaud JF. Pulse pressure, endothelium function, and arterial stiffness in spontaneously hypertensive rats. Hypertension 2001; 38: 1416-1421.
20. Qiu HY, Henrion D, Levy BI. Alterations in flow-dependent vasomotor tone in spontaneously hypertensive rats. Hypertension 1994; 24: 474-479.
21. Matrougui K, Maclouf J, Levy BI, Henrion D. Impaired nitric oxide- and prostaglandin-mediated responses to flow in resistance arteries of hypertensive rats. Hypertension 1997; 30: 942-947.
22. Huang A, Sun D, Kaley G, Koller A. Superoxide released to high intra-arteriolar pressure reduces nitric oxide-mediated shear stress- and agonist-induced dilations. Circ Res 1998; 83: 960-965.
23. Koller A, Huang A. Shear stress-induced dilation is attenuated in skeletal muscle arterioles of hypertensive rats. Hypertension 1995; 25: 758-763.
24. Landmesser U, Drexler H. Endothelial function and hypertension. Curr Opin Cardiol 2007; 22: 316-320.
25. Davies PF. Flow-mediated endothelial mechanotransduction. Physiol Rev 1995; 75: 519-560.
26. Ishida T, Takahashi M, Corson MA, Berk BC. Fluid shear stress-mediated signal transduction: how do endothelial cells transduce mechanical force into biological responses? Ann N Y Acad Sci 1997; 811: 12-23.
27. Chien S. Mechanotransduction and endothelial cell homeostasis: the wisdom of the cell. Am J Physiol Heart Circ Physiol 2007; 292: H1209-H1224.
28. Koller A, Huang A. Impaired nitric oxide-mediated flow-induced dilation in arterioles of spontaneously hypertensive rats. Circ Res 1994; 74: 416-421.
29. Folkow B. "Structural factor" in primary and secondary hypertension. Hypertension 1990; 16: 89-101.
30. Koller A, Kaley G. Endothelial regulation of wall shear stress and blood flow in skeletal muscle microcirculation. Am J Physiol 1991; 260: H862-H868.
31. Lemne CE, Lundeberg T, Theodorsson E, de FU. Increased basal concentrations of plasma endothelin in borderline hypertension. J Hypertens 1994; 12: 1069-1074.
32. Ge T, Hughes H, Junquero DC, Wu KK, Vanhoutte PM, Boulanger CM. Endothelium-dependent contractions are associated with both augmented expression of prostaglandin H synthase-1 and hypersensitivity to prostaglandin H2 in the SHR aorta. Circ Res 1995; 76: 1003-1010.
33. Bertuglia S, Veronese FM, Pasut G. Polyethylene glycol and a novel developed polyethylene glycol-nitric oxide normalize arteriolar response and oxidative stress in ischemia-reperfusion. Am J Physiol Heart Circ Physiol 2006; 291: H1536-H1544.
34. Luo J, Borgens R, Shi R. Polyethylene glycol immediately repairs neuronal membranes and inhibits free radical production after acute spinal cord injury. J Neurochem 2002; 83: 471-480.
35. Shi R, Borgens RB. Anatomical repair of nerve membranes in crushed mammalian spinal cord with polyethylene glycol. J Neurocytol 2000; 29: 633-643.
36. Nabha L, Garbern JC, Buller CL, Charpie JR. Vascular oxidative stress precedes high blood pressure in spontaneously hypertensive rats. Clin Exp Hypertens 2005; 27: 71-82.
37. Wu R, Millette E, Wu L, de Champlain J. Enhanced superoxide anion formation in vascular tissues from spontaneously hypertensive and desoxycorticosterone acetate-salt hypertensive rats. J Hypertens 2001; 19: 741-748.
38. Payne JA, Reckelhoff JF, Khalil RA. Role of oxidative stress in age-related reduction of NO-cGMP-mediated vascular relaxation in SHR. Am J Physiol Regul Integr Comp Physiol 2003; 285: R542-R551.
39. Pacella JJ, Kameneva MV, Csikari M, Lu E, Villanueva FS. A novel hydrodynamic approach to the treatment of coronary artery disease. Eur Heart J 2006; 27: 2362-2369.
We would like to thank Dr. C.F.M. Menck, Instituto de Ciências Biomédicas, Universidade de São Paulo, for providing the microscope for the measurement of tail artery diameter. Research supported by CNPq and FAPESP. K.L. Bessa and L. dos Santos were supported by PhD fellowships from CNPq and J.F. Belletati was supported by an undergraduate fellowship from FAPESP. L.V. Rossoni is the recipient of a CNPq research fellowship.
 Address for correspondence: K.L. Bessa, DCAT, UFERSA, BR 110, km 47, Costa e Silva, 59625-900 Mossoró, RN, Brasil. Fax: +55-84-3315-1778. E-mail: klbessa@ufersa.edu.br
Address for correspondence: K.L. Bessa, DCAT, UFERSA, BR 110, km 47, Costa e Silva, 59625-900 Mossoró, RN, Brasil. Fax: +55-84-3315-1778. E-mail: klbessa@ufersa.edu.br
Received January 15, 2011. Accepted May 26, 2011. Available online June 10, 2011. Published August 19, 2011.
The Brazilian Journal of Medical and Biological Research is partially financed by
All the contents of this journal, except where otherwise noted, is licensed under a Creative Commons Attribution License
- 1. Mulvany MJ. Small artery remodeling and significance in the development of hypertension. News Physiol Sci 2002; 17: 105-109.
- 2. Mulvany MJ. Small artery remodelling in hypertension: causes, consequences and therapeutic implications. Med Biol Eng Comput 2008; 46: 461-467.
- 3. Virk PS. Drag reduction fundamentals. AIChE Journal 1975; 21: 625-656.
- 4. Vlachogiannis M, Liberatore MW, McHugh AJ, Hanratty TJ. Effectiveness of a drag reducing polymer: relation to molecular weight distribution and structuring. Phys Fluids 2003; 15: 3786-3794.
- 5. Toms BA. Some observations on the flow of linear polymer solutions through straight tubes at large Reynolds numbers. Proceedings of the 1st International Congress on Rheology Amsterdam: North Holland; 1949. p 135-141.
- 6. Keller A, Kiss G, Mackley MR. Polymer drag reduction in Taylor vortices. Nature 1975; 257: 304-305.
- 7. Driels MR, Ayyash S. Drag reduction in laminar flow. Nature 1976; 259: 389-390.
- 8. Faruqui FI, Otten MD, Polimeni PI. Protection against atherogenesis with the polymer drag-reducing agent Separan AP-30. Circulation 1987; 75: 627-635.
- 9. Sawchuk AP, Unthank JL, Dalsing MC. Drag reducing polymers may decrease atherosclerosis by increasing shear in areas normally exposed to low shear stress. J Vasc Surg 1999; 30: 761-764.
- 10. Kameneva MV, Wu ZJ, Uraysh A, Repko B, Litwak KN, Billiar TR, et al. Blood soluble drag-reducing polymers prevent lethality from hemorrhagic shock in acute animal experiments. Biorheology 2004; 41: 53-64.
- 11. Marhefka JN, Marascalco PJ, Chapman TM, Russell AJ, Kameneva MV. Poly(N-vinylformamide)-A drag-reducing polymer for biomedical applications. Biomacromolecules 2006; 7: 1597-1603.
- 12. Michel T, Vanhoutte PM. Cellular signaling and NO production.Pfluggers Arch-Eur J Physiol 2010; 459: 807-816.
- 13. Félétou M, Köhler R, Vanhoutte PM. Endothelium-derived vasoactive factors and hypertension: Possible roles in pathogenesis and as treatment targets. Curr Hypertens Rep 2010; 12: 267-275.
- 14. Sanz-Rosa D, Oubina MP, Cediel E, de Las Heras N, Vegazo O, Jimenez J, et al. Effect of AT1 receptor antagonism on vascular and circulating inflammatory mediators in SHR: role of NF-kappaB/IkappaB system. Am J Physiol Heart Circ Physiol 2005; 288: H111-H115.
- 15. França AS, Rossoni LV, Amaral SM, Vassallo DV. Reactivity of the isolated perfused rat tail vascular bed. Braz J Med Biol Res 1997; 30: 891-895.
- 16. Hoyt JW. The effect of additives on fluid friction. J Basic Engineering 1972; 94: 28.
- 17. Bessa KL, Ortiz JP. Efeito de polímeros redutores de arrasto em escoamento pulsátil laminar. 1° Encontro Nacional de Engenharia Biomecânica Petrópolis: 2007.
- 18. Mulvany MJ, Aalkjaer C. Structure and function of small arteries. Physiol Rev 1990; 70: 921-961.
- 19. Safar M, Chamiot-Clerc P, Dagher G, Renaud JF. Pulse pressure, endothelium function, and arterial stiffness in spontaneously hypertensive rats. Hypertension 2001; 38: 1416-1421.
- 20. Qiu HY, Henrion D, Levy BI. Alterations in flow-dependent vasomotor tone in spontaneously hypertensive rats. Hypertension 1994; 24: 474-479.
- 21. Matrougui K, Maclouf J, Levy BI, Henrion D. Impaired nitric oxide- and prostaglandin-mediated responses to flow in resistance arteries of hypertensive rats. Hypertension 1997; 30: 942-947.
- 22. Huang A, Sun D, Kaley G, Koller A. Superoxide released to high intra-arteriolar pressure reduces nitric oxide-mediated shear stress- and agonist-induced dilations. Circ Res 1998; 83: 960-965.
- 23. Koller A, Huang A. Shear stress-induced dilation is attenuated in skeletal muscle arterioles of hypertensive rats. Hypertension 1995; 25: 758-763.
- 24. Landmesser U, Drexler H. Endothelial function and hypertension. Curr Opin Cardiol 2007; 22: 316-320.
- 25. Davies PF. Flow-mediated endothelial mechanotransduction. Physiol Rev 1995; 75: 519-560.
- 26. Ishida T, Takahashi M, Corson MA, Berk BC. Fluid shear stress-mediated signal transduction: how do endothelial cells transduce mechanical force into biological responses? Ann N Y Acad Sci 1997; 811: 12-23.
- 27. Chien S. Mechanotransduction and endothelial cell homeostasis: the wisdom of the cell. Am J Physiol Heart Circ Physiol 2007; 292: H1209-H1224.
- 28. Koller A, Huang A. Impaired nitric oxide-mediated flow-induced dilation in arterioles of spontaneously hypertensive rats. Circ Res 1994; 74: 416-421.
- 29. Folkow B. "Structural factor" in primary and secondary hypertension. Hypertension 1990; 16: 89-101.
- 30. Koller A, Kaley G. Endothelial regulation of wall shear stress and blood flow in skeletal muscle microcirculation. Am J Physiol 1991; 260: H862-H868.
- 31. Lemne CE, Lundeberg T, Theodorsson E, de FU. Increased basal concentrations of plasma endothelin in borderline hypertension. J Hypertens 1994; 12: 1069-1074.
- 32. Ge T, Hughes H, Junquero DC, Wu KK, Vanhoutte PM, Boulanger CM. Endothelium-dependent contractions are associated with both augmented expression of prostaglandin H synthase-1 and hypersensitivity to prostaglandin H2 in the SHR aorta. Circ Res 1995; 76: 1003-1010.
- 33. Bertuglia S, Veronese FM, Pasut G. Polyethylene glycol and a novel developed polyethylene glycol-nitric oxide normalize arteriolar response and oxidative stress in ischemia-reperfusion. Am J Physiol Heart Circ Physiol 2006; 291: H1536-H1544.
- 34. Luo J, Borgens R, Shi R. Polyethylene glycol immediately repairs neuronal membranes and inhibits free radical production after acute spinal cord injury. J Neurochem 2002; 83: 471-480.
- 35. Shi R, Borgens RB. Anatomical repair of nerve membranes in crushed mammalian spinal cord with polyethylene glycol. J Neurocytol 2000; 29: 633-643.
- 36. Nabha L, Garbern JC, Buller CL, Charpie JR. Vascular oxidative stress precedes high blood pressure in spontaneously hypertensive rats. Clin Exp Hypertens 2005; 27: 71-82.
- 37. Wu R, Millette E, Wu L, de Champlain J. Enhanced superoxide anion formation in vascular tissues from spontaneously hypertensive and desoxycorticosterone acetate-salt hypertensive rats. J Hypertens 2001; 19: 741-748.
- 38. Payne JA, Reckelhoff JF, Khalil RA. Role of oxidative stress in age-related reduction of NO-cGMP-mediated vascular relaxation in SHR. Am J Physiol Regul Integr Comp Physiol 2003; 285: R542-R551.
- 39. Pacella JJ, Kameneva MV, Csikari M, Lu E, Villanueva FS. A novel hydrodynamic approach to the treatment of coronary artery disease. Eur Heart J 2006; 27: 2362-2369.
Correspondence and Footnotes
Publication Dates
-
Publication in this collection
27 Sept 2011 -
Date of issue
Aug 2011
History
-
Received
15 Jan 2011 -
Accepted
26 May 2011














