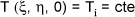ESTUDO TEÓRICO DO RESFRIAMENTO COM AR FORÇADO DE FRUTAS DE GEOMETRIAS DIFERENTES

THEORETICAL STUDY OF FRUITS COOLING WITH DIFFERENT FORMS GEOMETRICAL IN THE FORCED-AIR SYSTEM

Resumos

Neste trabalho apresenta-se um estudo numérico para a obtenção das curvas de resfriamento de laranja Valência, (Citrus sinensis O.) e banana prata (Mussa balbisiana Colla), em posições diferentes ao longo do leito e acondicionadas em embalagens com 40% de área efetiva de abertura. Os frutos foram resfriados num sistema de circulação com ar forçado (1.933m³/h), à temperatura de 1°C e 7°C, umidade relativa de 88,4 ± 2,0% e velocidade do ar em torno de 1m/s. Um modelo matemático bidimensional, em coordenadas esferoidais prolato, foi aplicado para predizer a condução de calor transiente dentro das frutas, assumindo-se condição de contorno convectiva na superfície do corpo. As equações geradas foram resolvidas numericamente pelo método de volumes finitos e o coeficiente convectivo de transferência de calor foi obtido aplicando o método de ajuste do erro quadrático mínimo, entre os dados experimentais e numéricos. A análise comparativa das curvas teóricas e experimentais mostrou uma concordância satisfatória, com valores de erro entre 5% e 7%. Notou-se que o coeficiente de transferência de calor varia com a posição dos frutos no leito e que o tempo de resfriamento apresenta uma variação de aproximadamente 38% entre os diferentes pontos. A distribuição espacial de temperatura no interior dos frutos, para três instantes de tempo, demonstrou a existência de um diferencial de temperatura entre o centro e a superfície de aproximadamente 30%. O modelo matemático prediz que a taxa de resfriamento nas bananas é muito mais alta nas pontas que nas outras regiões do fruto. O número de Bi e de Fo mostraram-se adequados e representativos do processo estudado, caracterizando adequadamente o resfriamento de corpos em qualquer relação de área/volume diferente.

laranja; banana; numérico; volumes finitos; refrigeração

This paper presents a numerical study for obtaining cooling curves of orange Valência (Citrus sinensis O.) and banana Prata (Mussa Balbisiana Colla), in different positions along the bed and conditioned in package with 40% of effective opening area. The fruits were pre-cooled in a forced-air system (1.933m³/h), at 1°C and 7°C, RH= 88,4 ± 2,0% and air velocity around 1m/s. A two-dimensional mathematical model was applied, assuming prolate spheroid coordinate, to characterize the transient heat transfer process inside the fruits considering convective profile conditions at the surface of the body. The generated equations were numerically solved by finite-volume method. The convective heat transfer coefficients were obtained using the least square method by comparison between experimental and numerical data. The comparative analysis of the theoretical and experimental curves presented a satisfactory agreement, with error between 5% and 7%. It was noted that the convective heat transfer coefficient changes with the fruits position in the bed and cooling time present a variation of approximately 38% among the different points. The spatial distributions of temperature inside the fruits, for three times, demonstrate the existence of a temperature differential between the center and the surface of 30%, approximately. The model predicts that the cooling rate is in the extremes of the banana. The Bi and Fo numbers obtained represent very well the heat transfer process in the fruits under different relationships of volume/area.

orange; banana; numerical; finite-volume

¹

Bárbara TERUEL²,^*, Luís A. CORTEZ³, Paulo LEAL³, Antonio G. B. LIMA⁴

RESUMO

Neste trabalho apresenta-se um estudo numérico para a obtenção das curvas de resfriamento de laranja Valência, (Citrus sinensis O.) e banana prata (Mussa balbisiana Colla), em posições diferentes ao longo do leito e acondicionadas em embalagens com 40% de área efetiva de abertura. Os frutos foram resfriados num sistema de circulação com ar forçado (1.933m³/h), à temperatura de 1°C e 7°C, umidade relativa de 88,4 ± 2,0% e velocidade do ar em torno de 1m/s. Um modelo matemático bidimensional, em coordenadas esferoidais prolato, foi aplicado para predizer a condução de calor transiente dentro das frutas, assumindo-se condição de contorno convectiva na superfície do corpo. As equações geradas foram resolvidas numericamente pelo método de volumes finitos e o coeficiente convectivo de transferência de calor foi obtido aplicando o método de ajuste do erro quadrático mínimo, entre os dados experimentais e numéricos. A análise comparativa das curvas teóricas e experimentais mostrou uma concordância satisfatória, com valores de erro entre 5% e 7%. Notou-se que o coeficiente de transferência de calor varia com a posição dos frutos no leito e que o tempo de resfriamento apresenta uma variação de aproximadamente 38% entre os diferentes pontos. A distribuição espacial de temperatura no interior dos frutos, para três instantes de tempo, demonstrou a existência de um diferencial de temperatura entre o centro e a superfície de aproximadamente 30%. O modelo matemático prediz que a taxa de resfriamento nas bananas é muito mais alta nas pontas que nas outras regiões do fruto. O número de Bi e de Fo mostraram-se adequados e representativos do processo estudado, caracterizando adequadamente o resfriamento de corpos em qualquer relação de área/volume diferente.

Palavras-chave: laranja; banana; numérico; volumes finitos; refrigeração.

SUMMARY

THEORETICAL STUDY OF FRUITS COOLING WITH DIFFERENT FORMS GEOMETRICAL IN THE FORCED-AIR SYSTEM. This paper presents a numerical study for obtaining cooling curves of orange Valência (Citrus sinensis O.) and banana Prata (Mussa Balbisiana Colla), in different positions along the bed and conditioned in package with 40% of effective opening area. The fruits were pre-cooled in a forced-air system (1.933m³/h), at 1°C and 7°C, RH= 88,4 ± 2,0% and air velocity around 1m/s. A two-dimensional mathematical model was applied, assuming prolate spheroid coordinate, to characterize the transient heat transfer process inside the fruits considering convective profile conditions at the surface of the body. The generated equations were numerically solved by finite-volume method. The convective heat transfer coefficients were obtained using the least square method by comparison between experimental and numerical data. The comparative analysis of the theoretical and experimental curves presented a satisfactory agreement, with error between 5% and 7%. It was noted that the convective heat transfer coefficient changes with the fruits position in the bed and cooling time present a variation of approximately 38% among the different points. The spatial distributions of temperature inside the fruits, for three times, demonstrate the existence of a temperature differential between the center and the surface of 30%, approximately. The model predicts that the cooling rate is in the extremes of the banana. The Bi and Fo numbers obtained represent very well the heat transfer process in the fruits under different relationships of volume/area.

Keywords: orange; banana; numerical; finite-volume.

1 ¾ INTRODUÇÃO

O resfriamento de produtos agrícolas, dentre eles as frutas, é um processo de transferência de calor, no qual estão envolvidos, geralmente, os três mecanismos de transmissão de calor: condução, convecção e radiação.

Em particular o problema da predição do tempo de resfriamento dos produtos e a caracterização de parâmetros do processo de transferência de calor têm sido estudados ao longo de muitos anos. O objetivo comum desses estudos é desenvolver um método simples de predição, que requeira uma quantidade mínima de dados e um programa computacional adequado.

Por outro lado, o coeficiente convectivo de transferência de calor (hc), tem um papel muito importante nos processos que envolvem a convecção. Uma das causas mais comuns de erro no cálculo da temperatura dentro do sólido é originada pela avaliação deste coeficiente, o qual, em muitos trabalhos, é assumido por sugestões da literatura. As equações mais precisas encontradas na literatura apresentam uma margem de incerteza considerável. Além disso, a medição experimental da distribuição de temperatura na superfície dos corpos, de forma precisa e direta, torna-se complexa [5], o que dificulta a determinação correta deste parâmetro.

Diversos modelos são apresentados na literatura, na forma numérica ou analítica, desde os mais simples até os mais complexos, para a avaliação de processos envolvendo refrigeração de frutas, resolvidos por vários métodos (diferenças finitas, volumes finitos), e com diferentes restrições e condições de contorno, para geometrias cilíndricas, esféricas ou planas [6, 7, 8, 11, 12, 13, 23, 26].

Apesar das vantagens da aplicação de modelos matemáticos, existem alguns problemas físicos em que a simulação de alguns parâmetros torna-se muito complexa, e onde os métodos numéricos não garantem uma adequada precisão, afastando-se das condições reais [18, 20].

O objetivo deste trabalho foi apresentar um estudo teórico aplicando um modelo matemático bidimensional, que considera o fruto como um elipsóide de revolução, permitindo avaliar a cinética de resfriamento, o coeficiente convectivo de transferência de calor (ajustado a partir dos dados experimentais) e a distribuição de temperatura em todo o fruto para distintos instantes de tempo, para frutas com formas geométricas diferentes.

2 ¾ MATERIAL E MÉTODOS

2.1 ¾ Dados experimentais

Os dados de temperatura que foram utilizados neste trabalho foram obtidos de forma experimental em pesquisas precedentes [24, 25]. Os frutos foram resfriados num sistema com ar forçado, utilizando um fluxo de ar de 1.933m³/h, e acondicionados em embalagens com 40% de área de abertura efetiva para a passagem do ar. A velocidade do ar no interior do túnel foi em torno de 1m/s.

Os experimentos foram conduzidos em duas partes, que contemplou experimentos com laranja Valência (Citrus sinensis O.) e com banana prata (Mussa balbisiana Colla). Estas duas frutas destacam-se dentre a grande variedade de frutas produzidas no país, entre as mais consumidas e, com um mercado de exportações promissor. Além disto, tornaram-se interessantes para a validação do modelo matemático, por possuir forma geométrica completamente diferente. Neste trabalho será apresentado o comportamento da taxa de resfriamento em três posições diferentes ao longo do leito, para os experimentos com laranja, e em duas posições nos experimentos com banana.

O tempo de resfriamento foi determinado a partir dos dados experimentais de temperatura e do cálculo da Taxa Adimensional de Temperatura (TAT). O tempo de meio resfriamento e de ⁷/₈ do resfriamento foram determinados a partir da equação 1. Quando o valor da TAT for de 0,5 o fruto teria atingido o tempo de meio resfriamento e quando esta relação for de 0,125, o tempo de ⁷/₈ do resfriamento [2, 19] :

Onde T_c é a temperatura no centro do fruto, T_i é a temperatura inicial do fruto e T_a é a temperatura do ar de resfriamento (°C).

A temperatura média inicial nos experimentos com laranja foi de 25,22 ± 0,19°C (T_i) e o sistema de resfriamento foi programado para trabalhar a 1°C (T_a). Nos experimentos com banana a temperatura do ar de resfriamento foi de 7°C e a temperatura inicial dos frutos foi de 26,5 ± 0,3°C. A umidade relativa média em todos os experimentos foi de 88,4 ± 2,0%.

Para as condições experimentais apresentadas, o tempo de meio resfriamento foi atingido quando a temperatura no centro das laranjas (T_c) foi de aproximadamente 13°C (TAT_1/2=0,5). O tempo de ⁷/₈ do resfriamento foi atingido quando nesse mesmo ponto, a temperatura T_c foi de aproximadamente 3°C (TAT_7/8=0,125). Nos experimentos com banana, o tempo de meio resfriamento foi atingido para uma temperatura de 17,5°C (TAT_1/2=0,5), e o tempo de ⁷/₈ do resfriamento quando T_c foi de 9,5°C (TAT_7/8=0,125).

2.2 ¾ Modelagem matemática

A equação da transferência de calor para um meio sólido pode ser expressa como:

Onde r é a densidade (kg/m³), C_p é o calor específico (J/kg°C), k é a condutividade térmica (W/m°C), é a taxa de geração interna de energia, ou calor (W/m³), T é a temperatura (°C) e t é o tempo (s).

O modelo utilizado neste trabalho define o processo de transferência de calor em regime transiente, usando o sistema de coordenadas esferoidais prolato, e incorpora os parâmetros adimensionais comumente usados na literatura. Este sistema de coordenadas é muito flexível, e permite sua aplicação em geometrias que vão desde uma esfera até um cilindro [16, 25]. Na Figura 1 mostra-se a caracterização geométrica de um corpo esferoidal prolato, os quais são elipsóides de revolução que tem L₂ >L₁ (semi-eixos maior e menor do corpo).

Para a simplificação do problema de transferência de calor, foram feitas as seguintes considerações: sólido homogêneo e isotrópico; propriedades termofísicas dos produtos constantes e independentes da temperatura e do teor de umidade do corpo; variação da temperatura simétrica ao redor do eixo z; a condução de calor partícula-partícula pode ser desprezada; considerando que a transferência de calor é fundamentalmente por convecção; os efeitos da respiração e da transpiração do produto sobre a transferência de calor são desprezíveis; as perdas de calor para o meio ambiente são desprezíveis, e na superfície do sólido o processo de transferência de calor é convectivo.

Com as considerações feitas, definindo as variáveis x = coshm, h = cosf e z = cosw, e considerando a existência de simetria em w (¶/¶w=0, ¶/¶z=0), pode-se escrever a equação da transferência de calor em regime transiente como segue:

Onde a é a difusividade térmica do corpo, em m²/s.

Para a análise do problema foram propostas as seguintes condições de contorno.

• Superfície: fluxo de calor difusivo é igual ao fluxo de calor convectivo.

Os termos desta equação representam o fluxo de calor por unidade de área que atravessa a superfície do corpo.

• Condição inicial: a temperatura do corpo tem uma distribuição uniforme.

• Condição de simetria: os gradientes angulares e radiais de posição são nulos nos planos de simetria.

Para a adimensionalização da equação de transferência de calor, foram considerados os seguintes parâmetros adimensionais:

Onde T* é o valor de TAT para cada instante de tempo, e t* o número de Fo. A equação de difusão foi discretizada usando o método de volumes finitos e um programa computacional codificado em linguagem FORTRAN foi implementado para resolver o sistema de equações lineares, utilizando uma malha uniforme de 20x20 pontos e o método interativo de Gauss-Seidel [16, 17, 25].

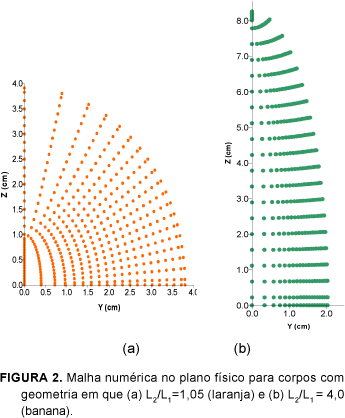
As Figuras 2 (a)e (b) ilustram a forma que adota a malha para as dimensões das laranjas e para as dimensões da banana, respectivamente. Como pode ser observado, o sistema de coordenadas esferoidais prolato caracteriza muito bem a geometria de corpos de aspecto diferente, com valores que vão de L₂/L₁=1 até L₂/L₁=µ.

Os cálculos foram iniciados partindo de uma condição inicial, e a solução numérica é obtida quando os seguintes critérios de convergência foram satisfeitos, em cada ponto do domínio computacional:

Nestas equações, k representa a k-ésima interação em cada instante de tempo e A_k os pontos nodais vizinhos do ponto nodal P, onde está sendo determinada a temperatura no interior do sólido.

O ajuste do coeficiente convectivo de transferência de calor (hc)_, foi feito através do cálculo do erro médio quadrado entre o valor teórico e o valor experimental, da temperatura no centro da laranja. O desvio relativo entre os valores experimentais e os valores teóricos calculados (E), assim como a variância (S²), foram definidas como:

A variável n representa o número de pontos experimentais. O valor ajustado de hc será aquele para o qual o valor do erro seja o mínimo. Neste ponto considera-se interessante ressaltar que devido à complexidade na determinação do hc, assim como pela quantidade de fatores que influenciam este coeficiente, e tomando em consideração que neste trabalho foi feita uma série de simplificações, considera-se que os valores do hc obtidos e apresentados podem ser considerados aparentes. Portanto o coeficiente convectivo de transferência de calor obtido será denominado coeficiente aparente.

Os valores de L₁ e L₂ foram calculados a partir dos dados experimentais de diâmetro, como L₁ = d₁/2 e L₂ = d₂/2. Nos experimentos com laranja, o valor do diâmetro equatorial e longitudinal, d₁ e d₂, foram de 7,60 ± 0,015cm e 7,82 ±0,024cm.

O comprimento em média das bananas L₁ foi de 4,06 ± 0,07cm (metade do fruto) e o diâmetro médio equatorial, L₂, = 16,5 ± 0,48cm. O valor de L é calculado como L = (L₂²-L₁² )^0,5.

O coeficiente de difusividade térmica usado para a validação do modelo matemático foi de 1,06x10^-7 m²/s [21]. O valor da condutividade térmica foi assumido como uma média entre o valor da casca e o valor do suco, ou seja, 0,58W/m°C [26].

Para a validação dos resultados com banana foi utilizado o valor de 1,25 x 10^-7 m²/s, para o coeficiente de difusividade térmica [1] e 0,48w/m°C para a condutividade térmica [22].

3 ¾ RESULTADOS E DISCUSSÃO

Na Figura 3 observa-se o comportamento da TAT nos experimentos com laranja, para os três pontos (1, 2 e 3) onde foi monitorada a temperatura Tc. As siglas TATn representam os valores numéricos, obtidos da validação do software Spherodiff-Transf. Os valores experimentais estão nomeados na legenda como TATe.

Pode-se observar que existe uma diferença na taxa de resfriamento entre os três pontos, situação que evidencia a existência de um diferencial de temperatura. Isto é provocado pelo fato das frutas ficarem expostas de forma diferente ao contato com o fluxo de ar resfriado.

O fruto da posição 1 (entrada da caixa) fica em contato imediato com o fluxo de ar, já os frutos das posições 2 e 3 encontram-se no meio do leito e na saída do ar da embalagem, respectivamente. Como pode ser observado na Figura 3, existe uma diferença na taxa de temperatura entre os três pontos, na ordem de 2 a 5°C, ao longo do leito na direção transversal, o que se reflete no tempo de resfriamento dos frutos (Tabela 1).

O tempo meio de resfriamento oscilou, em média, entre 40min. a 65min. entre os três pontos. Já o tempo dos ⁷/₈ do resfriamento variou entre 105min. a 180min. O tempo de resfriamento é diferente para cada ponto monitorado, existindo uma diferença de aproximadamente 38% entre o ponto 1 e o ponto 3, tanto para o tempo meio de resfriamento, como para o tempo de ⁷/₈ do resfriamento.

Observando-se a Figura 3 (experimentos com laranja), pode-se apreciar que existe um adequado ajuste das curvas teóricas aos pontos experimentais, e isto se reflete nos baixos valores do erro (Equação 8), e de variância (Equação 9). O valor do erro por ponto esteve entre 0,13% e 0,08%, para os pontos 1, 2 e 3 respectivamente (60 pontos experimentais para cada curva). No ponto em que TAT_1/2 = 0,5; a diferença de temperatura entre o valor experimental e o numérico foi de 0,13%; 0,08% e 0,05% (posições 1, 2 e 3, respectivamente). No instante em que é atingido o tempo de ⁷/₈ do resfriamento (TAT_7/8 = 0,125), a diferença da temperatura entre o ponto teórico e experimental, para as posições 1, 2 e 3, foi de 0,17%; 1,15% e 0,09%, respectivamente.

Os valores do erro e do desvio padrão são baixos, em média 3,62x10^-2 e 2,44x10^-2. Estes valores permitem afirmar que o ajuste do coeficiente convectivo de transferência de calor, hc, apresenta uma concordância adequada com o fenômeno em estudo. O decréscimo do valor do hc entre o ponto 1 e 2 é aproximadamente de 40% (Tabela 1).

Verificou-se a diminuição do hc ao longo do leito, na ordem de aproximadamente 30%, o que se deve ao decréscimo do fluxo de ar produzido pela perda de carga. Esta redução de velocidade provoca uma diminuição mais lenta da temperatura no interior dos frutos, o que é muito bem caraterizada pelo modelo (Tabela 1).

BAIRD & GAFFNEY [3], resfriaram laranjas a granel, a 5°C, e com velocidade do ar variando de 0,05m/s a 2,1m/s, e obtiveram, usando um método de ajuste, valores do hc entre 8,15W/m²°C e 55W/m²°C. Outros valores de hc são apresentados na literatura oscilando nesta mesma ordem [8, 9, 19].

Na Figura 4 apresenta-se a distribuição da temperatura adimensional (TAT), nos experimentos com laranja, na posição 1 e na posição 3, em três instantes de tempo diferentes. A Figura 4 (a) e (c) correspondem ao tempo de meio resfriamento e de ⁷/₈ do resfriamento, respectivamente.

Como se pode observar, no início do resfriamento a temperatura na superfície do corpo apresenta um TAT de aproximadamente 0,70; que corresponde a uma temperatura de aproximadamente 18°C. Já na dimensão em que Y= 3cm, o valor de TAT é de 0,85; ou seja, a temperatura é de aproximadamente 22°C, sendo que nas regiões mais próximas do centro a temperatura é ainda invariável e igual à temperatura inicial.

Observa-se também na Figura 4 (b), que aos 40min. (tempo de meio resfriamento), o fruto já se apresentava resfriado a aproximadamente 7°C, nas regiões mais próximas da superfície, sendo que no centro a temperatura era de aproximadamente 13°C. Na superfície, a temperatura já era de aproximadamente de 2°C (T_a=1°C). Aos 105min, o fruto encontrava-se no tempo de ⁷/₈ do resfriamento, instante em que se encontra praticamente resfriado. No centro apresenta uma temperatura em torno de 3°C, e na superfície de 1,5°C. Deve-se lembrar que o tempo de meio resfriamento está relacionado com a temperatura no centro do fruto.

A aplicação do modelo proposto permite, a partir dos resultados gerados, obter a distribuição da temperatura no interior do fruto, podendo assim obter o que se pode chamar de uma ¨radiografia¨ do processo de resfriamento em diferentes instantes de tempo. De forma experimental seria muito complicado poder obter esta distribuição.

Estes resultados confirmam a análise das curvas de resfriamento apresentadas, ou seja, o resfriamento dos frutos depende da localização destes no leito, sendo que o processo de transferência de calor é mais intenso nos frutos que tem um maior contato com o ar, a velocidades mais elevadas, refletindo-se em maiores valores do coeficiente convectivo de transferência de calor.

É valido ressaltar que durante o resfriamento, existiu um diferencial de temperatura entre a superfície e o centro dos frutos em torno de 30%, sendo comprovado tanto de forma teórica com a geração dos gráficos de perfil de temperatura, como de forma experimental. Com estes resultados demonstra-se que na superfície dos frutos atinge-se a condição de equilíbrio com o meio de resfriamento rapidamente.

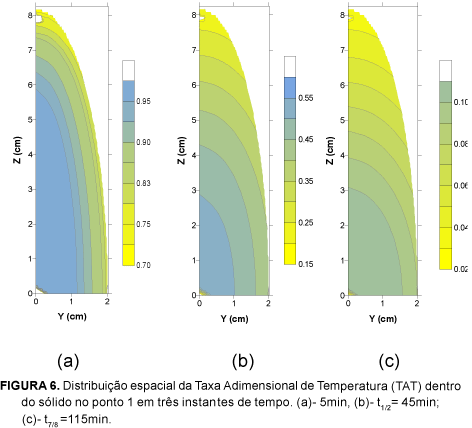
As curvas teóricas e experimentais quando feito o resfriamento de banana são mostradas na Figura 5. Notou-se o fato do resfriamento das bananas não ser homogêneo, ou seja, observando-se a Figura 6 (a), na região superior, no extremo (ponta) da banana, o valor da TAT está em torno de 0,70; o que em termos de temperatura significa que nessa parte da fruta, a temperatura na superfície e nas camadas mais próximas é da ordem de 19°C.

No entanto, nas outras regiões da fruta (Z = 7,5cm), o valor da TAT está na ordem de 0,83 o que representa temperaturas na ordem de 22°C, incluindo a superfície. Este fato pode ser explicado pela quantidade de massa que apresenta a fruta na região superior, ou seja, na ponta, o que se deduz que as pontas resfriam-se num menor tempo que o restante do fruto. Observa-se que este fenômeno está muito bem representado por este tipo de mapeamento. Esta mesma tendência apresenta-se nas Figuras 6 (b) e (c), observando-se que à medida que o fruto resfria-se a escala de cores passa a ser amarela intensa.

Observa-se também que quando no centro é atingido o valor de TAT de 0,5, na ponta o valor de TAT é de 0,15 (Ts » 9°C), e nas outras regiões perto da superfície, a TAT está na ordem de 0,45 a 0,35 (temperaturas na faixa de 12°C a 14°C). No entanto no centro a temperatura encontra-se na ordem dos 17°C.

A diferença entre o tempo de resfriamento obtido de forma experimental e teórica em termos de temperatura oscilou na faixa de 0,10°C a 0,97°C, o que demonstra a adequada concordância entre os valores experimentais e os obtidos de forma numérica.

Assim sendo, os resultados obtidos permitem afirmar que o modelo e a metodologia usada neste trabalho são consistentes para predizer o processo de resfriamento de laranja e para determinar o coeficiente convectivo de transferência de calor, com satisfatória exatidão.

3.1 ¾ Comparação dos resultados em função do número de Fourier e de Biot

O valor dos números de Fourier (Fo) e de Biot (Bi) para os experimentos com laranja e com banana, foi calculado a partir dos dados experimentais, pelo modelo matemático. Como pode ser observado na Figura 7, os valores de Bi estão entre 3,5 e 0,5, numa faixa de Fo entre 0 e 1, para os experimentos com laranja. Observando a Figura 7, verifica-se que os valores de Bi estão numa faixa entre 0,2 e 0,10, e uma faixa de Fo entre 0 e 2, nos experimentos com banana.

Valores muitos baixos do Bi indicam que a resistência interna de condução é desprezível se comparada com a resistência superficial por convecção. O número de Fo, por sua parte, relaciona a dimensão do corpo com os efeitos da penetração dos efeitos térmicos, sendo usado para determinar o tempo de resfriamento, e vice-versa [14, 19].

Corpos esféricos resfriam em menor tempo que corpos cilíndricos, em função da relação área/volume (A/V). A área superficial das esferas é menor que a área superficial dos cilindros, como pode ser constatado nos experimentos com laranja e banana, onde a relação A/V para laranja é aproximadamente 50 vezes menor que para a banana.

Verificou-se a diferença existente entre os valores de Fo para os experimentos com laranja, onde a relação A/V é menor, os tempos de resfriamento são menores e o valor de Fo é baixo. Já o comportamento nos experimentos com banana é diferente, a relação A/V é maior, obteve-se em média tempos de resfriamento maiores, e o valor de Fo é maior que para os corpos esféricos.

CLELAND & EARLE [7], determinaram, aplicando soluções numéricas, o valor do Fo, para cilindros, esferas e placas. Os autores comprovaram que para números de Bi entre 0,01 e 100, o valor de Fo para cilindros esteve na faixa de 34,9 a 0,120 e para esferas o valor de Fo comportou valores entre 23,3 e 0,072.

Para uma mesma condição convectiva, uma duplicação do diâmetro dos produtos, leva um aumento do tempo de resfriamento de até quatro vezes maior [4, 15].

Se corpos esféricos esfriam em menor tempo que corpos cilíndricos, então, explica-se o porquê o valor de Bi está entre 3,5 e 0,5 (laranja), e entre 0,2 e 0,1 (banana). Valores baixos de Bi refletem uma baixa intensidade no processo de transferência de calor, o que foi muito bem caracterizado nos valores de hc que foram obtidos por ajuste, os quais oscilaram entre 13,62 W/m²°C a 2,68W/m²°C. Por outro lado, valores mais altos de Bi, indicam uma maior intensidade no processo de transferência de calor, o que se reflete em altos coeficientes de transferência de calor. Os valores obtidos com a aplicação do modelo matemático para o resfriamento de laranja oscilaram entre 56,48W/m²°C a 5,39W/m²°C. Gráficos semelhantes aos obtidos neste trabalho são apresentados na literatura consultada.

Valores de Bi entre 0,85 e 1,7 foram obtidos por DINCER & GENCELI [10], durante o resfriamento com ar forçado de pepino, a uma temperatura de 4°C.

4 ¾ CONCLUSÕES

O modelo matemático aplicado mostrou-se adequado para a caracterização do fenômeno de transferência de calor estudado, apresentando como vantagens: o grau de aproximação razoável, permitindo obter ajustes adequados, aplicável em diversos produtos hortifrutícolas (com geometria desde esferas até cilindros e semelhantes, e com propriedades termofísicas diferentes), alta estabilidade numérica e baixo custo computacional.

Comprovou-se com a aplicação do modelo resultados muito próximos dos obtidos na medição experimental da temperatura na superfície. Esta temperatura apresenta uma diferença com respeito ao centro em torno de 7°C a 2°C, o que representou diferenças da ordem de 50% a 30%, aproximadamente.

O modelo apresentado prediz que a taxa de resfriamento nos experimentos com banana é muito mais alta nas pontas que nas outras regiões do fruto.

A diferença entre o tempo de resfriamento obtido de forma experimental e teórica em termos de temperatura oscilou na faixa de 0,10°C a 0,97°C, o que demonstra a adequada concordância entre os valores experimentais e os obtidos de forma numérica.

Os valores do coeficiente convectivo de transferência de calor são representativos do processo estudado, tendo sido obtidos a partir de dados experimentais e com razoáveis valores do erro.

O número de Bi e de Fo mostrou-se adequado e representativo do processo estudado, caracterizando adequadamente o resfriamento de corpos com a relação de área/volume diferente.

5 ¾ REFERÊNCIAS BIBLIOGRÁFICAS

6 ¾ AGRADECIMENTOS

Os autores agradecem à FAPESP pelo apoio financeiro da pesquisa e ao Laboratório de Refrigeração da Faculdade de Engenharia de Alimentos, da UNICAMP.

² Universidade Estadual de Campinas, UNICAMP. Faculdade de Engenharia Mecânica. Cx. P. 6122 ¾ CEP 13081-970 ¾ Campinas, SP, Brasil. Fone: (0xx19) 3788-8435/Fax: (0xx19) 289-3722. [e-mail]

³ Universidade Estadual de Campinas (UNICAMP). Faculdade de Engenharia Agrícola. Cx. P. 6120 ¾ CEP 13081-970. E-mail: [e-mail]

⁴ Universidade Federal da Paraíba,UFPb. Departamento de Engenharia Mecânica, Cx. P. 10069, CEP 58109-970, Campina Grande, PB, Brasil. [e-mail]

* A quem a correspondência deve ser enviada.

• [1] ANSARI, F. A, AFAQ, A. A new method of measuring thermal diffusivity of spherical produts. International Journal of Refrigeration, v. 9, n.3, p.158-160, 1986.
• [2] ASHRAE. Systems and Applications. Methods of precooling of fruits, vegetables and flowers Atlanta: American Society of Heating, Refrigerating and Air-Conditioning Engineers, 1994. Chapter 10, p, 1-10.
• [3] BAIRD, C. D., GAFFNEY, J. J. An numerical procedure for calculating heat transfer in bulk loads of fruits or vegetables. ASHRAE Transactions, v. 82, n. 2, p. 525. 1976.
• [4] BAIRD, C. D., GAFFNEY, J. J., TALBOT, M. T. Design criteria for efficient and cost effective forced-air cooling systems for fruits and vegetables. ASHRAE Transactions v. 94, p. 1434-1453, 1988.
• [5] BENAVIDES, M. N. & AVENDAÑO, G. O. Curvas de congelación y descongelación de fresas y frambuesas calculadas con el método de diferencias finitas. IV Congreso Iberoamericano de Aire Acondicionado y Refrigeración, v. 1, pp. 154-159. 1997.
• [6] CHAU, K. V.; GAFFNEY, J. J.; BAIRD, C. D.; CHURCH, G. A. Resistance to air flow of oranges in bulk and in cartons. Transactions of ASAE v. 28, n. 6, p. 2083-2088. 1985.
• [7] CLELAND, D.J., EARLE, R. L. Freezing time prediction foi foodsža simplified procedure. Revue Internationale du Froid, v. 5, n. 3, p. 134- 140, 1982.
• [8] DINCER, I. An effective method for analysing of precooling process parameters. International Journal of Energy Research, v. 19, p. 95-102, 1995.
• [9] DINCER, I., GENCELI, O. F. Cooling process and heat transfer parameters of cylindrical products cooled both in water and air. International Journal Heat Transfer, v. 37, n. 4, p. 625-633, 1994.
• [10] DINCER, I., GENCELI, F. Determination of surface heat transfer coefficients from measured temperature data for spherical and cylindrical bodies during cooling. Heat and Mass Transfer, v. 30, p. 215-220, 1995.
• [11] FRASER H., OTTEN, L. Predicting ⁷/₈ cooling times for peaches by comparing heat transfer modelling and field measurement methods. American Society of Agricultural Engineers. ASAE Paper no. 92-6016. 10 p. 1992.
• [12] HAYAKAWA, K. Computarized simulation for heat transfer and moisture loss from an idealized fresh produce. Transactions of the ASAE, v. 21, p. 4-6, 1978.
• [13] HAYAKAWA, K., SUCCAR, J. Heat transfer and moisture loss of spherical fresh produce. Journal of Food Science, v. 47, p. 596- 605, 1982.
• [14] HOLMAN, J. P. Heat transfer Toronto: Mc. Graw-Hill Book Company. 1986. 675 p.
• [15] KOPELMAN, I., BLAISDELL, J. L., PFLUG, I. J. Influence of fruit size and coolant velocity on the cooling of Jonathan apples in water and air. ASHRAE Transactions, v. 72, part. I, p. 209-216, 1966.
• [16] LIMA, A. G. B., NEBRA, S. A. Influência de parâmetros geométricos na cinética de secagem de elipsóides sólidos. In: Congresso Brasileiro de Sistemas Particulados (ENEMP), 26, vol. 1, pp. 195-202, 1997.
• [17] LIMA, A. G. B., NEBRA, S. A. Formulação utilizando o método de volumes finitos para problemas de difusão de massa transiente em corpos elipsoidais axi-simétricos. In: Congresso Brasileiro de Sistemas Particulados (ENEMP), 26, 1998.
• [18] MALISKA, C. R. Transferência de calor e mecânica dos fluidos computacional Rio de Janeiro: LTC. 1995. 424p.
• [19] MOHSENIN, N. N. Thermal properties of foods and agricultural materials New York. USA. 1980. 405 p.
• [20] PATANKAR, S. V. Numerical heat transfer and fluid flow New York: Hemisphere Publishing Coorporation, 1980. 197p.
• [21] RAMOS, A. L., PALMISANO, E., DOMBEY, A., PIMENTEL, J. A., FAYÉS, D., GONZÁLEZ, D. Thermal properties of tropical fruits and vegetables. Revista Española de Ciencia e Tecnología de los Alimentos, v. 33, n. 3, p. 271-283, 1993.
• [22] SWEAT, V. E. Experimental values of the thermal conductivity of select fruits and vegetables. Journal of Food Science, v. 39, p. 1080-1083, 1974.
• [23] TALBOT, M. T., CHAU, K. V. Precooling strawberries. Institute of Food and Agricultural Sciencies. University of Florida. Circular 942. 1991. 8 p.
• [24] TERUEL, M. B. J. Estudo teórico-experimental do resfriamento com ar forçado de laranja e banana. Campinas, 2000. 300 p. Faculdade de Engenharia Mecânica. Tese (Doutorado). Universidade Estadual de Campinas (Unicamp).
• [25] TERUEL M. B. J; CORTEZ, L. A. B.; LEAL, P. M.; LIMA, G. A B. Obtenção numérico/experimental das curvas de resfriamento de laranja (variedade Valência). In: Congresso Brasileiro de Engenharia Mecânica (COBEM), 12, 1999.
• [26] TRELEA, I. C., ALVAREZ, G., TRYSTRAM, G. Nonlinear predictive optimal control of a batch refrigeration process. Journal of Food Process Engineering, v. 21, p. 1-32, 1998.

¹

Recebido para publicação em 19/03/01. Aceito para publicação em 03/08/01.

Datas de Publicação

• Publicação nesta coleção
  25 Abr 2002
• Data do Fascículo
  Ago 2001

Histórico

• Recebido
  19 Mar 2001
• Aceito
  03 Ago 2001