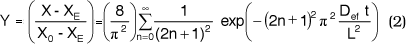Resumos
Neste trabalho estudou-se a cinética de secagem da cebola em camada delgada, comparando os valores da difusividade efetiva média baseados nas espessuras inicial e média das amostras. Estes resultados foram utilizados para a estimativa da temperatura das amostras através de um modelo térmico simplificado. Foram analisadas também as propriedades físicas e de transporte das amostras em função da umidade ao longo da operação. Os ensaios de secagem foram realizados em um secador com escoamento de ar perpendicular à área de seção transversal do leito de amostras de cebola, operando com Tar=60ºC e v ar=1,5m/s. A determinação da umidade de equilíbrio foi obtida através das isotermas de dessorção e a temperatura das amostras foi determinada por meio de um termopar inserido no centro da partícula. As massas específicas das amostras aparente e absoluta foram determinadas através dos métodos indireto e destrutivo, respectivamente. Os valores da difusividade efetiva variável de umidade foram obtidos através do método das tangentes. O modelo térmico simplificado apresentou melhor ajuste com os valores da difusividade efetiva média de secagem, baseados na espessura média. Os valores das massas específicas das amostras de cebola aparente e absoluta foram ajustados em função da umidade através da equação de LOZANO, ROTSTEIN & URBICAIN [10], apresentando coeficientes de correlação maiores que 96%. A redução de espessura do material foi de 80% em relação a da amostra inicial. Os resultados da difusividade efetiva média de umidade, baseados na espessura média das amostras, foram semelhantes aos valores médios da difusividade efetiva variável de umidade para a primeira etapa de secagem.
cebola; secagem em camada delgada; difusividade efetiva de umidade
In this work it was studied the onion drying kinetics in thin layer comparing the values of the drying difusivity effective average based on the initial and average thickness of the samples. These results were fitted to a simplified thermal model. It was also analyzed the physical and transport properties of the samples in function of the moisture along the operation. The drying experiments were realized in a dryer with air flowing perpendicular to the cross section area of the bed of samples with Tair=60ºC and v air=1,5m/s. The equilibrium moisture was obtained through the sorption isotherms and the temperature was verified through a termocouple inserted into the particle center. The density apparent and true were obtained through the indirect and destructive methods, respectively. The values of the moisture difusivity effective variable were obtained through the method of the tangents. The simplified thermal model presented better correlation with the values of the moisture difusivity effective average, based on the medium thickness. The values of the density apparent and true of the samples were fitted in function of the moisture using LOZANO, ROTSTEIN and URBICAIN [10] equation, presenting correlation coefficients greater that 96%. The reduction of thickness of the samples was of 80% in relation to initial. The results of the moisture difusivity effective average based on the medium thickness of the samples were similar to the medium values of the moisture difusivity effective variable for the first period drying.
onion; thin layer drying; moisture difusivity effective
Estudo das propriedades físicas e de transporte na secagem de cebola (Allium cepa L.) em camada delgada
Study of the physical and transport properties in the onion (Allium cepa L.) drying in thin layer
Pierre Corrêa MartinsI; Paulo Sérgio da Silva PortoII; Luiz Antonio de Almeida PintoIII,* * A quem a correspondência deve ser enviada.
IParte da Dissertação de Mestrado em Engenharia de Alimentos Fundação Universidade Federal do Rio Grande RS. E-mail: pierremartins@bol.com.br
IIE-mail: paulosergioporto@bol.com.br
III Departamento de Química Laboratório de Secagem/NUPEN/Fundação Universidade Federal do Rio Grande FURG, Rua Alfredo Huch, 475. CEP 96201-900, Rio Grande/RS Brasil. E-mail: dqmpinto@super.furg.br
RESUMO
Neste trabalho estudou-se a cinética de secagem da cebola em camada delgada, comparando os valores da difusividade efetiva média baseados nas espessuras inicial e média das amostras. Estes resultados foram utilizados para a estimativa da temperatura das amostras através de um modelo térmico simplificado. Foram analisadas também as propriedades físicas e de transporte das amostras em função da umidade ao longo da operação. Os ensaios de secagem foram realizados em um secador com escoamento de ar perpendicular à área de seção transversal do leito de amostras de cebola, operando com Tar=60ºC e var=1,5m/s. A determinação da umidade de equilíbrio foi obtida através das isotermas de dessorção e a temperatura das amostras foi determinada por meio de um termopar inserido no centro da partícula. As massas específicas das amostras aparente e absoluta foram determinadas através dos métodos indireto e destrutivo, respectivamente. Os valores da difusividade efetiva variável de umidade foram obtidos através do método das tangentes. O modelo térmico simplificado apresentou melhor ajuste com os valores da difusividade efetiva média de secagem, baseados na espessura média. Os valores das massas específicas das amostras de cebola aparente e absoluta foram ajustados em função da umidade através da equação de LOZANO, ROTSTEIN & URBICAIN [10], apresentando coeficientes de correlação maiores que 96%. A redução de espessura do material foi de 80% em relação a da amostra inicial. Os resultados da difusividade efetiva média de umidade, baseados na espessura média das amostras, foram semelhantes aos valores médios da difusividade efetiva variável de umidade para a primeira etapa de secagem.
Palavras-chave: cebola; secagem em camada delgada; difusividade efetiva de umidade.
SUMMARY
In this work it was studied the onion drying kinetics in thin layer comparing the values of the drying difusivity effective average based on the initial and average thickness of the samples. These results were fitted to a simplified thermal model. It was also analyzed the physical and transport properties of the samples in function of the moisture along the operation. The drying experiments were realized in a dryer with air flowing perpendicular to the cross section area of the bed of samples with Tair=60ºC and vair=1,5m/s. The equilibrium moisture was obtained through the sorption isotherms and the temperature was verified through a termocouple inserted into the particle center. The density apparent and true were obtained through the indirect and destructive methods, respectively. The values of the moisture difusivity effective variable were obtained through the method of the tangents. The simplified thermal model presented better correlation with the values of the moisture difusivity effective average, based on the medium thickness. The values of the density apparent and true of the samples were fitted in function of the moisture using LOZANO, ROTSTEIN and URBICAIN [10] equation, presenting correlation coefficients greater that 96%. The reduction of thickness of the samples was of 80% in relation to initial. The results of the moisture difusivity effective average based on the medium thickness of the samples were similar to the medium values of the moisture difusivity effective variable for the first period drying.
Keywords: onion; thin layer drying; moisture difusivity effective.
1 INTRODUÇÃO
A isoterma de equilíbrio relacionando a umidade do alimento e a umidade relativa do ar ambiente em que este se insere, sob determinada temperatura, possibilita a obtenção do teor de água presente no material. Assim, a umidade de equilíbrio do alimento em função da umidade relativa do meio, fornece informações muito úteis para os processos de secagem, preservação e acondicionamento do material. Para correlacionar umidades de equilíbrio de alimentos fibrosos com alto teor de umidade inicial, como a cebola, a correlação de Guggenheim, Anderson e De Boer (GAB) é muito utilizada, por apresentar bom ajuste frente aos valores experimentais [8].
A determinação da difusividade efetiva de umidade de um alimento é muito importante para formulação dos modelos físico-matemáticos que explicam o comportamento do alimento durante a secagem. Geralmente se utiliza a lei de Fick da difusão, para a estimativa do valor médio da difusividade efetiva de água em um sólido [15].
PARK [12] estudou a influência do encolhimento de filés de tubarão salgado na difusividade efetiva de umidade e concluiu que se obtinha valores mais corretos deste parâmetro de transporte quando se utilizava a espessura média do filé na estimativa. Durante a secagem a variação da espessura do filé apresentava uma relação linear com a umidade.
Segundo VACCAREZA & CHIRIFE [18], o número de Biot de calor (BiC) calculado para a secagem de vários vegetais se situa na faixa de 0,2 a 0,5. Nesta situação, a temperatura interna do material pode ser considerada aproximadamente uniforme, devido aos baixos gradientes internos, assim a temperatura da amostra varia apenas no tempo, assumindo-se então o processo como quase-isotérmico.
SUZUKI et al. [17] estudaram o encolhimento volumétrico de vegetais e suas raízes, e observaram que o mesmo ocorreu de maneira uniforme nas diferentes dimensões do material, consideraram assim o fenômeno de encolhimento em vegetais como isotrópico. Por outro lado, BALABAN & PIGOTT [2] constataram diferenças quanto ao efeito da variação volumétrica nas três dimensões das fibras de pescado, sendo que tal anisotropia também pode ser observada em vários alimentos fibrosos. FELIPE & PINTO [5] analisaram o encolhimento volumétrico de batatas e maçãs e constataram que a variação na espessura foi mais acentuada do que nas outras dimensões, devido ao fato da espessura estudada ter sido disposta transversal ao sentido das fibras do material. LOZANO, ROTSTEIN & URBICAIN [10] relacionaram a variação da massa específica de diversos vegetais, entre estes o alho, com o teor de umidade e obtiveram uma correlação para esta propriedade física.
Segundo VAGENAS & KARATHANOS [19] e PORTER et al. [15], uma maneira de determinar a variação da difusividade efetiva ao longo da operação de secagem é com a aplicação do método das tangentes, utilizando os valores do adimensional de água livre em função do tempo, obtidos da curva experimental de secagem, com os valores do adimensional de água livre em função do número de Fourier (Fo), da curva teórica da difusão de água.
O presente trabalho teve como objetivo estudar a cinética de secagem de cebola em camada delgada, comparando os valores da difusividade efetiva média de umidade, baseada nas espessuras inicial e média do material, utilizando estes resultados para o ajuste de um modelo térmico simplificado. Estudou-se também as relações das propriedades físicas e de transporte das amostras de cebolas em função da umidade do material durante a operação.
2 MATERIAL E MÉTODOS
2.1 Material
-
Matéria-prima: utilizou-se a cebola (Allium cepa L.) de diferentes cultivares (safra 2001), obtida no mercado varejista local.
-
Equipamentos: os ensaios experimentais foram realizados em um secador descontínuo, conforme o esquema apresentado pela Figura 1.
2.2 Metodologia
2.2.1 Metodologia experimental
A matéria-prima foi selecionada, descascada, lavada, fatiada em espessura constante de 3mm e picada em fatias de comprimento de 30mm, após colocada em bandeja de tela perfurada (mesh 10), sendo a mesma inserida no secador.
A carga de sólidos utilizada nos ensaios experimentais foi de 6kg/m2 de fatias de cebola, cujo sentido de escoamento do ar de secagem foi descendente (Ensaio 1) e ascendente (Ensaio 2).
A monitoração dos ensaios experimentais foi efetuada através da determinação da variação de massa das amostras com o tempo, em intervalos de 2 minutos para os 50 minutos iniciais e de 5 minutos até o final da secagem, estando o ar escoando na velocidade de 1,5m/s e temperatura de 60°C.
Determinou-se os constituintes da cebola utilizando métodos analíticos: proteínas, cinzas e umidade segundo as normas oficiais da A.O.A.C. [1], e de carboidratos, conforme método do 3,5-DNS [11].
A umidade de equilíbrio das amostras foi determinada por isoterma de dessorção, a temperatura de 60°C. Para obter a isoterma, foi utilizado o método gravimétrico estático, com o uso de soluções de ácido sulfúrico em diferentes concentrações. As amostras permaneceram em ambiente hermético, com temperatura controlada, por 14 dias, cujas massas foram quantificadas no primeiro, sétimo, décimo e décimo quarto dias.
Realizou-se a medida da temperatura do sólido utilizando um termopar (Cu-Constantan, diâmetro do fio de 1mm), com resolução de 0,1°C inserido no centro da partícula, registrando-se a temperatura em função do tempo da operação.
A determinação da massa específica e do volume das amostras de cebola ao longo da operação foi realizada pelos métodos indireto e destrutivo.
O método indireto foi utilizado para a determinação da massa específica do sólido (rs), a qual representa a massa específica absoluta sem considerar os poros do material, e está baseado na composição química de seus constituintes em relação as suas respectivas massas específicas, dos quais a água foi a única que apresentou variação de massa durante a secagem. Os valores das densidades específicas de cada componente, proteína, cinzas (como sal de potássio), carboidratos e lipídios, foram obtidos na literatura [10, 15].
A determinação da massa específica aparente das amostras de cebola, que considera os poros do material, foi realizada segundo o método destrutivo [5], no qual retirou-se periodicamente, no decorrer da secagem, uma amostra do material para as análises de massa específica e umidade. Após sua coleta, as amostras foram envolvidas em filme de polietileno e acondicionadas em temperatura de refrigeração (T=5-10°C) por 24h para a uniformização da umidade do material. A massa específica das amostras foi determinada através de picnometria de sólido, utilizando um picnômetro de 50mL com hexano como solvente [5], e a umidade das amostras foi realizada segundo normas da A.O.A.C.[1].
As dimensões das amostras de cebola in natura e do produto final foram medidas utilizando um paquímetro digital MITUTOYO, modelo CD-6 CS, com resolução de 0,01mm.
2.2.2 Metodologia de cálculo
Os resultados da umidade de equilíbrio das amostras de cebola em função da umidade relativa do meio em que permaneceram acondicionadas, obtidos através das curvas experimentais da isoterma de dessorção, foram ajustados com o uso correlação de GAB, a qual apresenta a seguinte forma:
Onde:
XE é a umidade de equilíbrio (kg água/kg sólido seco); Xm é a umidade da monocamada de água do material (kg água/kg sólido seco); UR é a umidade relativa do meio em valores decimais; A e B são parâmetros de ajuste.
Os valores da difusividade efetiva média de umidade foram determinados através da solução analítica da lei de Fick para a difusão de água líquida em um sólido, com as seguintes considerações: lâmina infinita, espessura e difusividade efetiva de umidade constantes para um dado conteúdo de umidade de fatias de cebola, secagem por ambos os lados da fatia de cebola e condição de equilíbrio na superfície do material sendo var>1,0m/s. Assim, com os valores experimentais das curvas de secagem em termos do adimensional de água livre em função do tempo e utilizando as espessuras inicial, média e final das amostras, determinou-se os valores da difusividade efetiva média de umidade das amostras, resolvendo a seguinte equação [3, 4]:
Onde:
Y é o adimensional de água livre; Def é a difusividade efetiva média de umidade (m2/s); X é o teor umidade média da amostra (kg água/kg sólido seco), XE é a umidade de equilíbrio da amostra (kg água/kg sólido seco); X0 é a umidade inicial da amostra (kg água/kg sólido seco); L é a espessura da amostra (m); t é o tempo de secagem (s).
Para a determinação da temperatura teórica das amostras (Ts), foi utilizado um modelo térmico simplificado, proposto por VACCAREZZA & CHIRIFE [18] e apresentado pela Equação (3), baseado no balanço geral de calor com as seguintes considerações: transferência de calor em meio sólido, homogêneo e isotrópico, lâmina infinita e o material apresentando temperatura uniforme na posição ao longo do processo.
Onde:
Ts é a temperatura da amostra (°C); Tbs é a temperatura de bulbo seco do ar de secagem (°C); DHvap é o calor latente de vaporização da água (J/kg); Def é a difusividade efetiva média de umidade da amostra (m2/s); rb0 é a massa específica aparente da amostra (kg/m3); hC é o coeficiente convectivo de transferência de calor (W/m2°C); X é a umidade média da amostra (kg água/kg sólido seco); X0 é a umidade inicial da amostra (kg água/kg sólido seco); L é a espessura da amostra (m).
Para a determinação do coeficiente convectivo de transferência de calor (hC), utilizou-se uma correlação clássica da literatura, descrita por GEANKOPLIS [6], indicada para a secagem com escoamento de ar perpendicular a superfície do material, a qual é expressa pela Equação (4):
Onde:
G é a vazão mássica do ar por unidade de área da seção transversal (kg/h.m2), sendo igual a (r.v)ar, onde rar é dado em kg/m3 e var em m/s.
Para determinação da massa específica do sólido das amostras (rs) foi tomada a seguinte relação com a sua composição química, cuja variação da composição de água foi obtida através das curvas de secagem.
Onde:
r s é a densidade absoluta da amostra (g/cm3); X é a umidade da amostra (base seca); Xi é a composição de cada constituinte (base seca); ri é a massa específica de cada constituinte da cebola (g/cm3). Sendo para proteína de 1,45g/cm3, para cinzas (como sal de potássio) de 2,00g/cm3, para carboidratos de 1,55g/cm3, para lipídios 0,92g/cm3; ni é o número de cada constituinte da cebola.
Os resultados das determinações das massas específicas foram ajustados em função da umidade das amostras, através da correlação indicada pela Equação (6), conforme apresentado por LOZANO, ROTSTEIN & URBICAIN [10]:
Onde:
r é a massa específica da amostra (g/cm3), X é a umidade da amostra (base seca); X0 é a umidade inicial da amostra (base seca); a, b, c e d são parâmetros de ajuste.
A espessura das amostras foi obtida pela razão entre o volume e a área apresentadas por estas. O volume das amostras foi calculado através da razão entre a massa e a massa específica aparente das mesmas.
Os valores da difusividade efetiva variável de umidade foram determinados através do método das tangentes, segundo VAGENAS & KARATANOS [19], utilizando-se a Equação (7).
Onde:
DefVAR é a difusividade efetiva variável de umidade (m2/s); (dY/dt)Exp. é a variação do adimensional de água livre das amostras em função do tempo, obtida pelos ensaios experimentais de secagem (kg água/kg sólido seco*s), (dY/dFo)teo. é a variação do adimensional de água livre em função do número de Fourier, obtida pela curva da teórica da difusão (kg água/kg sólido seco); Y é o adimensional de água livre; Fo é o número de Fourier (adimensional); Def é a difusividade efetiva média de umidade (m2/s); L é a espessura da amostra (m); t é o tempo de secagem (s).
Os resultados obtidos da difusividade efetiva variável de umidade foram ajustados em função dos valores experimentais da umidade e da temperatura das amostras, por meio da Equação (8), [14].
Onde:
Def VAR é a difusividade efetiva variável de umidade da amostra (m2/s); X é a umidade da amostra (kg água/kg sólido seco); Ts é a temperatura da amostra (°C); e, f e g são parâmetros de ajuste.
3 RESULTADOS E DISCUSSÕES
3.1 Composição química
A caracterização química da matéria-prima indicou os resultados expressos na Tabela 1.
3.2 Umidade de equilíbrio e caracterização da secagem
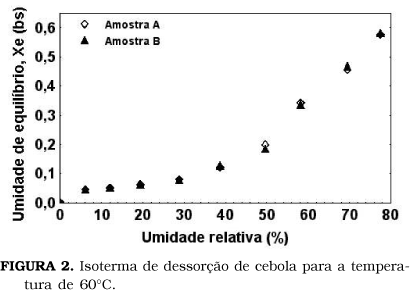
Os resultados das determinações das umidades de equilíbrio das amostras em função da umidade relativa do meio, estão representados pelas curvas de dessorção da Figura 2.
Com os valores experimentais obtidos da isoterma de dessorção (Figura 2) determinou-se os parâmetros de ajuste da Equação (1), apresentados na Tabela 2.
Utilizando a equação de GAB, com os parâmetros da Tabela 2, para o valor da umidade relativa do interior do secador em torno de 7,5%, determinada através das medidas das temperaturas de bulbo seco e úmido do ar de secagem, obteve-se o valor para a umidade de equilíbrio das amostras igual a 0,052kg água/kg sólido seco (base seca).
A taxa de secagem das amostras em função do tempo, foi obtida derivando a curva de secagem expressa por umidade em base seca (X) em função do tempo, e está apresentada na Figura 3.
A inclinação mais acentuada das curvas de secagem, apresentada na Figura 3, ocorreu à umidades superiores as do intervalo em torno de 5,0-5,5 de umidade em base seca (bs), provavelmente correspondente ao período de evaporação superficial de umidade. A partir desta faixa de umidade das amostras, nota-se um comportamento de menor intensidade da variação da taxa de secagem em função da umidade das amostras, devido ao processo passar a ser controlado pelo mecanismo de migração interna de umidade do material. Este período está representado pela primeira e segunda fases da taxa decrescente de umidade.
Os parâmetros que caracterizam a secagem estão apresentados na Tabela 3, cuja umidade final do produto desidratado foi fixada em 7,6±0,2 em base seca, o qual corresponde ao valor de umidade comercial da cebola desidratada.
Os valores da umidade em base seca da cebola (Xc) e do tempo de duração desta fase (tc) apresentados na Tabela 3, correspondem ao término do período inicial de secagem, que representa o período de evaporação superficial do material. Pode-se verificar nesta tabela, através dos valores da umidade de transição (Xtrans), que ocorreram dois períodos da taxa decrescente de secagem, com controle interno de migração de umidade, antes da cebola alcançar a umidade comercial. O tempo da primeira etapa de secagem (t1°etapa) corresponde aos períodos de evaporação superficial e o da primeira fase da taxa decrescente com controle interno de migração de umidade. Já o tempo da segunda etapa de secagem (t2°etapa) representa a duração da segunda fase do controle interno.
Observa-se na Tabela 3 que as amostras que foram processadas com escoamento descendente do ar atingiram a faixa de umidade final desejada mais rapidamente que no escoamento ascendente.
Os valores da difusividade efetiva média de umidade das etapas de secagem, foram obtidos através da Equação (2), utilizando-se os valores do adimensional de água livre em função do tempo, apresentados nas curvas da Figura 4.
in natura e do produto final apresentaram como espessura L
0 igual a 3,0mm e L
S igual a 0,6mm, respectivamente. Foi observado que praticamente toda a contração de espessura do material ocorreu na primeira etapa de secagem, e, considerando que seu comportamento foi de forma linear, determinou-se os valores das difusividades efetivas médias de umidade com a Equação (2), baseados na espessura média (L
m=1,8mm) e final do material (L
s), para a caracterização da primeira e segunda etapas de secagem. Paralelamente a esta análise, determinou-se os valores das difusividades efetivas médias de umidade, para tais etapas, baseados na espessura inicial (L
0) das amostras.
Utilizando-se a solução da Equação (2), foi observado que os resultados da difusividade efetiva média de umidade não apresentavam diferença quanto ao desvio padrão, a partir do quarto termo expresso pela Equação (2), conforme verificado por PINTO, PENEIREIRO & TOBINAGA [13]. Os valores das difusividades efetivas de umidade estão apresentados na Tabela 4.
A relação entre os valores das difusividades efetivas médias de umidade da primeira e da segunda etapas de secagem, baseados em Lm e Ls, ficou acima da apresentada por CHIRIFE [4], cuja faixa era de 4 a 8 vezes. Por outro lado, esta relação é estabelecida quando utiliza-se a comparação dos valores do parâmetro de transporte baseado na espessura inicial das amostras, conforme os valores apresentados na Tabela 4.
Para a determinação da temperatura teórica das amostras utilizando o modelo térmico simplificado apresentado na Equação (3), verificou-se inicialmente o valor do número de Biot para a transferência de calor [Bic=(hcL/Ks)]. O cálculo de hC foi realizado utilizando a Equação (4), com os valores de rar=1,062kg/m3 e var=1,5m/s, a Tar= 60°C e Par =1,0atm abs, obtendo-se o valor de hC=28,8W/m2 K. O valor da condutividade térmica (KS) para cebola foi obtido da literatura [7], sendo igual a 0,57W/m K. Através dos valores encontrados para hC, KS e L0, obteve-se o valor de BiC=0,15; validando a condição da temperatura do material uniforme espacialmente. Foi considerada a condição inicial de evaporação superficial de umidade para o cálculo de hC, devido esta apresentar o maior valor para o coeficiente convectivo de transferência de calor.
Estimou-se a temperatura das amostras (TS) em função da umidade da cebola, utilizando a Equação (3), com os valores constantes de rb0, L0, hC, DHvap., variando-se somente o valor da difusividade efetiva média de umidade (Def). O valor da entalpia de vaporização da água foi obtida através da literatura [8], sendo igual a 2358,50kJ/kg. O resultado do ajuste do modelo térmico simplificado com os valores da Def, baseados nas espessuras média e inicial, comparados com as determinações experimentais, estão apresentados na Figura 5.
Observa-se na Figura 5, que o modelo térmico simplificado utilizando o valor da difusividade efetiva média de umidade, baseada na espessura média Lm, apresentou melhor ajuste em relação aos resultados experimentais da temperatura do sólido. O modelo não ajustou bem no início da secagem, durante o período de evaporação superficial de umidade (10min iniciais), pois segundo VACCAREZA & CHIRIFE [18], este foi proposto para a taxa decrescente de secagem com controle interno de migração de umidade. O modelo térmico simplificado que utilizou o valor da difusividade efetiva média de umidade, baseada na espessura inicial L0, não apresentou ajuste adequado com os resultados experimentais, devido ao alto valor apresentado pelo parâmetro de transporte utilizado.
3.3 Propriedades físicas e de transporte em função da umidade das amostras
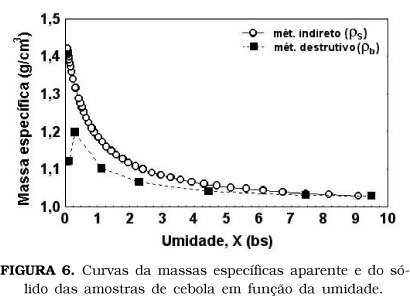
Os resultados das determinações de massa específica, realizadas através dos métodos indireto e destrutivo, estão apresentados nas curvas da Figura 6.
Observa-se na Figura 6 que, a partir do final do primeiro período de taxa decrescente, de evaporação superficial (X=5,5bs), a massa específica aparente da cebola (rb), determinada pelo método destrutivo que considera os poros do material, apresenta valores inferiores aos da massa específica do sólido (rs), que representa a massa específica absoluta não considerando os vazios, determinada pela Equação (5) e com os valores da composição química apresentados na Tabela 1. Este fato pode ser explicado pelo aparecimento de zonas secas na matriz estrutural do alimento, em virtude da configuração porosa das células dos tecidos vegetais (grandes vacúolos).
O material apresentou uma variação volumétrica relacionada com o seu encolhimento, para ambas as massas específicas até a transição das etapas de secagem (X=0,15bs), conforme observado na Figura 6. Neste valor de umidade, que corresponde a segunda etapa do período de taxa decrescente, a massa específica aparente do material tende a diminuir seu valor, já que a variação de volume do mesmo é desconsiderável em relação a sua variação de umidade. Este efeito foi observado por LOZANO, ROTSTEIN & URBICAIN [10] na secagem de amostras de alho.
Os valores das massas específicas das amostras em função da umidade foram ajustados através da Equação (6), cujos resultados estão apresentados na Tabela 5.
Observa-se na Tabela 5 que, a massa específica do sólido (rs) por apresentar um alto coeficiente de ajuste, pode ser considerada como uma curva padrão. Para os resultados da determinação de massa específica aparente (rb) das amostras, a correlação de LOZANO, ROTSTEIN & URBICAIN [10] apresentou ajuste somente para a primeira etapa de secagem. A faixa de valores de 1,38 a 1,40g/cm3 para rs e de 1,14 a 1,20g/cm3 para rb, com as amostras de cebolas apresentando um teor de umidade entre 7,0 a 15,0%, estão de acordo com os resultados encontrados por RAPUSAS & DRISCOLL [16].
A determinação da espessura das amostras de cebola foi obtida com os valores de seu volume, o qual apresentou um comportamento linear com a umidade do material, e da sua área. Como a área do produto final apresentou uma redução de 50% em relação a amostra inicial, ajustou-se um fator de correção para a mesma. A variação da espessura das amostras ao longo da secagem com ar escoando no sentido descendente está apresentada na Figura 7.
Observa-se na Figura 7, que a espessura da cebola diminuiu aproximadamente 80% em relação ao seu valor inicial ao final da secagem. Este comportamento foi similar ao ocorrido com a umidade das amostras em base úmida, que reduziu de 90% até 6%.
A primeira etapa de taxa da secagem, que corresponde a evaporação superficial e a primeira fase da taxa decrescente com controle interno de migração de umidade, foi a responsável por praticamente toda a redução da espessura inicial das amostras, pois a partir dos 80 minutos, onde inicia-se a segunda etapa de taxa decrescente, o material não apresentou variação na espessura. O volume de encolhimento da cebola foi próximo ao volume de água evaporada até a faixa de 20-25% de umidade do material, conforme observado por KILPATRICK, LOWE & VAN ARSDEL [9]. O valor médio da espessura, segundo os resultados do método destrutivo, foi de 1,55mm, o qual aproximou-se do valor médio considerado anteriormente.
Os valores da difusividade efetiva variável de umidade, obtidos através do método das tangentes, Equação (7), e baseados na espessura média experimental (1,55mm) e final, estão apresentados na Figura 8.
Observa-se na Figura 8 que os valores dos pontos iniciais das curvas da difusividade efetiva variável de umidade estão situados em torno de 8,5x10-10m2/s, próximos aos valores calculados com a espessura inicial das amostras para a primeira etapa da secagem (Tabela 4). Como a umidade de transição das etapas de secagem se situa em 0,15bs, a média dos valores da difusividade efetiva variável de umidade para a primeira etapa foi igual a 2,8x10-10m2/s, apresentando-se assim semelhante ao valor da difusividade efetiva média de umidade, baseada na espessura média das amostras considerada anteriormente. Constata-se assim, que o mecanismo de difusão para a água líquida, segundo a lei de Fick, é bastante representativo para a transferência de massa durante a primeira etapa do processo de secagem no período decrescente.
R ealizou-se o ajuste dos resultados da difusividade efetiva em função da umidade e da temperatura das amostras, através da Equação (8), cujos resultados estão apresentados na Tabela 6.
Observa-se que a correlação do tipo linear-exponencial apresentou um bom ajuste para a estimativa da difusividade efetiva de umidade, conforme observado por PINTO et al. [14] na secagem de cebola em pasta. Isto deve-se ao fato de que as curvas da taxa de secagem (Figura 3) e difusividade efetiva variável (Figura 8) em função da umidade apresentam um comportamento linear similar, durante a primeira etapa de secagem. Como a difusividade efetiva de umidade varia com a temperatura de forma exponencial, segundo a equação de Arrhenius, na segunda etapa de secagem a sua variação é mais pronunciada, devido a maior temperatura do sólido.
4 CONCLUSÕES
-
A correlação de Guggenheim, Anderson e De Boer (GAB) apresentou um bom coeficiente de ajuste (R2=98,7%) para os resultados das isotermas de dessorção de cebola, sendo a umidade da monocamada das amostras de 0,045kg água/kg sólido seco para a temperatura do ar de 60°C.
-
Na caracterização da secagem os valores da difusividade efetiva média de umidade, baseada na espessura inicial das amostras, apresentaram-se três vezes maiores do que os valores médios deste parâmetro, baseado na espessura média das amostras, para a primeira etapa de secagem.
-
O modelo térmico simplificado, utilizando o valor da difusividade efetiva média de umidade, baseado na espessura média das amostras, apresentou ajuste em relação aos resultados obtidos experimentalmente.
-
Os valores das massas específicas das amostras, aparente e do sólido, apresentaram bons coeficientes de ajuste (R2>96,8%) para a correlação de LOZANO, ROTSTEIN & URBICAN [10], em função da umidade das amostras.
-
A espessura do material apresentou uma redução de aproximadamente 80% em relação as amostras iniciais, sendo que praticamente toda variação desta dimensão ocorreu durante a primeira etapa de secagem, que considera o período de evaporação superficial e o da primeira fase de taxa decrescente com controle interno de migração de umidade.
-
O valor da difusividade efetiva média de umidade, baseado na espessura média das amostras de cebola, apresentou-se similar ao valor médio da difusividade efetiva variável de umidade, para a primeira etapa de secagem. Os valores obtidos para a difusividade efetiva variável em função da umidade das amostras apresentaram bom ajuste com uso de uma equação do tipo linear exponencial (R2=96,7%).
5 REFERÊNCIAS BIBLIOGRÁFICAS
6 AGRADECIMENTOS
Os autores agradecem o apoio recebido da CAPES para elaboração deste trabalho.
Recebido para publicação em 20/01/2002. Aceito para publicação em 28/06/2004 (000819)
- [1] ASSOCIATION OF OFFICIAL ANALYTICAL CHEMISTS A.O.A.C. Official Methods of Analysis, ed. 14, 1995, v. 1.
- [2] BALABAN, M.; PIGOTT, G.M.. Shrinkage in Fish Muscle During Drying. Journal of Food Science, v. 51, n. 2, p. 510-511, 1986.
- [3] CRANK, J. The Mathematics of Difusion. Great Britain, 2ed. Claredon Press, Oxford, 1975. 414p.
- [4] CHIRIFE, J. Fundamentals of the drying mechanism during air dehydration of foods. In: MUJUMDAR. Arum S. (ed). Advances in drying Washington Hemisphere Publishing Corporation, v. 1, p. 73-102. 1983.
- [5] FELIPE, C.A.S.; PINTO, L.A.A. Análise do encolhimento na secagem de alimentos fibrosos. Rio Grande, 1997. 30 p. Relatório final PIBIC/CNPq Fundação Universidade do Rio Grande (FURG).
- [6] GEANKOPLIS, C. Transport and Unit Operations 2nd Ed. Prentice-Hall International Inc. New Jersey, USA. 1983. 921p.
- [7] HAYES, G. D. Manual de Indústrias dos Alimentos, editora ACRIBIA, 1992. 182 p.
- [8] KARATHANOS, V.T. Determination of water content of dried fruits by drying kinetics. Journal of Food Engineering, n. 39, p. 337-334, 1999.
- [9] KILPATRICK, P.W.; LOWE, E.; VAN ARSDEL, W.B. Tunnel dehydration for fruits and vegetables. In: Van Arsdel, W. B. Advances in Food Research Academic Press. New York. v. 4. p.313-371, 1955.
- [10] LOZANO, J.E.; ROTSTEIN, E.; URBICAN, M.J. Shrinkage, porosity and bulk density of foodstuffus at changing moisture contents. Journal of Food Science v. 48, n. 5, p. 1497-1553, 1983.
- [11] MILLER, G.L. Use of Dinitrosalicylic acid reagent for determination of sugar, Analytical Chemistry, v. 31, n. 3, p. 326-428, 1959.
- [12] PARK, K. J. Estudo comparativo do coeficiente de difusão sem e com encolhimento durante a secagem Campinas, 1986. 163 p. Tese Livre do Docência- Faculdade de Engenharia de Alimentos. Universidade Estadual de Campinas (UNICAMP).
- [13] PINTO, L.A.A.; PENEIREIRO, J.B.; TOBINAGA, S. Difusão líquida na secagem de músculos de peixes. In: XX ENCONTRO SOBRE ESCOAMENTO EM MEIOS POROSOS (ENEMP), v. 2, p. 555-562, São Carlos/SP, 1992.
- [14] PINTO, M.L.M.; SILVA, J.D.; BACELO, L.R.; PINTO, L.A.A. Influências da umidade e da temperatura na difusividade efetiva de umidade na secagem de cebola, In: XXVI ENCONTRO SOBRE ESCOAMENTO EM MEIOS POROSOS (ENEMP), v. 2, p. 462-469, Teresópolis/RJ, 1998.
- [15] PORTER, H.F.; SCHURR, G.A.; WELLS, D.F.; SEMRAU, T.K. Solids drying and gas-solid In: Perry, R.H. and Chilton, C.H., Chemical Engineer's Handbook. McGraw-Hill Co. 6 ed. Sec. 20-4, 1984.
- [16] RAPUSAS, R.S.; DRISCOLL; R.H. Termophysical properties of fresh and dried white onion slices. Journal of Food Engineering, 24, p. 149-164, 1995.
- [17] SUZUKI, K.; KUBOTA, K.; HASEGAWA, T.; HOSAKA, H. Shrinkage in dehydration of root vegetables. Journal of Food Science v. 41, n. 5, p. 1189-1193, 1976.
- [18] VACCAREZZA, L.M.; CHIRIFE, J. On the application of Fick's law for the kinetics analysis of air drying of foods. Journal of Food Science v. 3, p. 236-238, 1978.
- [19] VAGENAS, G.K.; KARATHANOS, C.; Predistion of the effective moisture diffusivity in gelatinized food systems. Journal of Food Engineering, n. 18, p. 159-179, 1993.
Datas de Publicação
-
Publicação nesta coleção
30 Nov 2005 -
Data do Fascículo
Set 2004
Histórico
-
Recebido
20 Jan 2002 -
Aceito
28 Jun 2004