Resumos
O objetivo do presente trabalho foi ajustar o modelo da difusão líquida às curvas de secagem do trigo considerando a contração volumétrica do grão e determinar os coeficientes de difusão para diversas condições controladas de temperatura e umidade relativa. Foram utilizados grãos de trigo, com teor de água inicial de 0,32 b.s. A secagem do produto foi realizada para diferentes condições controladas de temperatura, entre 25 e 55 °C, e umidade relativa de 55 ± 1%. A contração volumétrica do grão foi determinada pela relação entre o volume para cada teor de água e o volume inicial. Com base nos resultados obtidos, conclui-se que o modelo da difusão líquida representa satisfatoriamente a cinética de secagem do trigo para as diversas condições de ar experimentadas, não tendo sido considerado o efeito da contração volumétrica dos grãos. O coeficiente de difusão aumenta com a elevação da temperatura do ar, apresentando valores de 8,6775 x 10-11 e 42,8743 x 10-11 m².s-1 para a faixa de temperatura estudada e considerando a contração volumétrica. A relação entre o coeficiente de difusão e a temperatura pode ser descrita pela expressão de Arrhenius, que apresenta uma energia de ativação para a difusão líquida nos grãos de trigo de 42,00 kJ.mol-1.
coeficiente de difusão; contração volumétrica; modelagem; grãos de trigo
The aim of this work was to adjust the liquid diffusion model to the wheat drying curves considering the shrinkage of the grains and to determine the diffusion coefficients under different air conditions. Rough rice with 0.32 (d.b.) moisture content was used in this experiment. The drying procedure was done under different controlled temperatures of 25 to 55 °C with the drying air relative humidity of 55 ± 1%. The shrinkage of the grains was determined by the ratio between the volume of each moisture content and the initial volume. Based on the results, it can be concluded that the liquid diffusion model represents the wheat drying kinetics satisfactorily for experimental conditions in this test, however, the shrinkage of grains was not considered. The diffusion coefficient increases with the increase of the air temperature, with values ranging between 8.6775 x 10-11 and 41.0977 x 10-11 m².s-1 for the strip of studied temperature. The variation of the diffusion coefficient with the temperature may be described by the Arrhenius expression, presenting an activation energy of liquid diffusion wheat of 42.00 kJ.mol-1.
diffusion coefficient; shrinkage; modeling; wheat grains
Estudo da difusão de umidade em grãos de trigo durante a secagem
Study of moisture diffusion in wheat grain drying
André Luís Duarte Gonelli, * * A quem a correspondência deve ser enviada ; Paulo Cesar Corrêa; Osvaldo Resende; Stelito Assis dos Reis Neto
Centro Nacional de Treinamento em Armazenagem CENTREINAR, Universidade Federal de Viçosa, Campus da Universidade Federal de Viçosa, CP 270, CEP 36570-000, Viçosa - MG, Brasil, E-mail: andregoneli@yahoo.com.br
RESUMO
O objetivo do presente trabalho foi ajustar o modelo da difusão líquida às curvas de secagem do trigo considerando a contração volumétrica do grão e determinar os coeficientes de difusão para diversas condições controladas de temperatura e umidade relativa. Foram utilizados grãos de trigo, com teor de água inicial de 0,32 b.s. A secagem do produto foi realizada para diferentes condições controladas de temperatura, entre 25 e 55 °C, e umidade relativa de 55 ± 1%. A contração volumétrica do grão foi determinada pela relação entre o volume para cada teor de água e o volume inicial. Com base nos resultados obtidos, conclui-se que o modelo da difusão líquida representa satisfatoriamente a cinética de secagem do trigo para as diversas condições de ar experimentadas, não tendo sido considerado o efeito da contração volumétrica dos grãos. O coeficiente de difusão aumenta com a elevação da temperatura do ar, apresentando valores de 8,6775 x 10-11 e 42,8743 x 10-11 m2.s-1 para a faixa de temperatura estudada e considerando a contração volumétrica. A relação entre o coeficiente de difusão e a temperatura pode ser descrita pela expressão de Arrhenius, que apresenta uma energia de ativação para a difusão líquida nos grãos de trigo de 42,00 kJ.mol-1.
Palavras-chave: coeficiente de difusão; contração volumétrica; modelagem; grãos de trigo.
ABSTRACT
The aim of this work was to adjust the liquid diffusion model to the wheat drying curves considering the shrinkage of the grains and to determine the diffusion coefficients under different air conditions. Rough rice with 0.32 (d.b.) moisture content was used in this experiment. The drying procedure was done under different controlled temperatures of 25 to 55 °C with the drying air relative humidity of 55 ± 1%. The shrinkage of the grains was determined by the ratio between the volume of each moisture content and the initial volume. Based on the results, it can be concluded that the liquid diffusion model represents the wheat drying kinetics satisfactorily for experimental conditions in this test, however, the shrinkage of grains was not considered. The diffusion coefficient increases with the increase of the air temperature, with values ranging between 8.6775 x 10-11 and 41.0977 x 10-11 m2.s-1 for the strip of studied temperature. The variation of the diffusion coefficient with the temperature may be described by the Arrhenius expression, presenting an activation energy of liquid diffusion wheat of 42.00 kJ.mol-1.
Keywords: diffusion coefficient; shrinkage; modeling; wheat grains.
1 Introdução
A secagem dos produtos agrícolas é o processo mais utilizado para assegurar sua qualidade e estabilidade durante o armazenamento. A diminuição da quantidade de água do material reduz a atividade biológica e as mudanças químicas e físicas que ocorrem durante o período de pós-colheita. A conservação pela secagem baseia-se no fato de que tanto os microrganismos como as enzimas e todo o mecanismo metabólico necessitam de água para suas atividades. Com a redução da quantidade de água disponível até níveis seguros para armazenagem, serão reduzidos a atividade de água, a velocidade das reações químicas no produto e o desenvolvimento de microrganismos8.
O fenômeno de redução do teor de água envolve o movimento hidráulico do interior para a superfície do grão através de mecanismos distintos de transferência de calor e massa, que podem alterar de forma substancial a qualidade e as propriedades físicas do produto, dependendo do método e das condições de secagem12.
No estudo de sistemas de secagem, desenvolvimento e aperfeiçoamento de equipamentos utilizados para a secagem de grãos, dimensionamento, otimização e determinação da viabilidade da aplicação comercial, é de fundamental importância a simulação e a obtenção de informações teóricas a respeito do comportamento de cada produto durante a remoção de água. Para a simulação, cujo princípio se fundamenta na secagem de sucessivas camadas delgadas do produto, utiliza-se um modelo matemático que representa, satisfatoriamente, sua perda de água durante o período de secagem4. As curvas de secagem em camada delgada variam com a espécie, variedade, condições ambientais, métodos de preparo pós-colheita, entre outros fatores.
BROOKER et al.5 relatam que a maioria dos modelos empregados para representar a secagem dos produtos agrícolas foi desenvolvida, negligenciando-se a importância da contração volumétrica do produto durante o processo de desidratação. Segundo PRADO et al.19, a remoção de água durante a secagem dos produtos biológicos gera a redução da tensão existente no interior das células promovendo, assim, a sua contração volumétrica. Para RAMOS et al.21, estas modificações também devem ser incluídas nos modelos para uma completa descrição e análise do fenômeno.
Os modelos de secagem baseados na teoria da difusão líquida têm merecido atenção especial por parte dos pesquisadores. Estes modelos assumem que não há influência da capilaridade, desprezam os efeitos da transferência de energia e massa de um corpo para outro, dada a dificuldade de se quantificarem esses múltiplos efeitos na massa de produto e, também, por considerarem que os corpos entram em equilíbrio térmico com o ar instantaneamente, o que pode induzir a discrepâncias entre os resultados encontrados.
O mecanismo pelo qual ocorre a difusão da água nos produtos agrícolas é muito complexo devido à diversidade da composição química e estrutura física dos produtos. Na literatura sobre secagem envolvendo o fenômeno da difusão de água, são encontradas grandes variações nos valores do coeficiente de difusividade, não só devido à complexidade dos produtos, como também em função dos diferentes métodos de predição, tipo de material, teor de água, processo de secagem e a metodologia utilizada para sua obtenção22.
Segundo BROOKER et al.5, na teoria da difusão líquida, a segunda lei de Fick tem sido utilizada para estabelecer a difusão da água em função do gradiente de concentração, de acordo com a seguinte expressão:
em que, U*: teor de água do produto, decimal (b.s.); D: coeficiente de difusão líquida, m2.s-1; t: tempo, s; e x: distância em relação a um ponto de referência no corpo, m.
A variação do teor de água em função do tempo de secagem, considerando materiais homogêneos com coeficiente de difusão constante, é representada pela seguinte equação:
em que, r: distância radial ou espessura, m; c = 0 para corpos planos; c = 1 para corpos cilíndricos; e c = 2 para corpos esféricos.
BROOKER et al.5 apresentam a solução analítica da Equação 2 para a forma geométrica cilíndrica:
em que, RU: razão de umidade do produto, adimensional; n: número de termos; ln: raízes da equação de Bessel de ordem zero; e r: raio de esfera equivalente.
Alguns pesquisadores, ao analisarem o modelo da difusão líquida para a representação do processo de secagem, consideraram em seus trabalhos o efeito da contração volumétrica no melhor ajuste do modelo7,21.
A solução analítica dessa equação apresenta-se na forma de uma série infinita, podendo o número finito de termos (n) no truncamento determinar a precisão dos resultados. Durante a modelagem e simulação dos processos de secagem de produtos agrícolas, diversos autores correlacionaram satisfatoriamente o coeficiente de difusão com os parâmetros de secagem1,9,14,15,17. O coeficiente de difusão, geralmente, aumenta com a elevação da temperatura do ar de secagem20 e esta relação pode ser descrita por meio da equação de Arrhenius:
em que, Do: fator pré-exponencial; Ea: energia de ativação, kJ.mol-1; R: constante universal dos gases, 8,134 kJ.kmol-1.K-1; e Ta: temperatura absoluta, K.
Assim, considerando a importância do estudo teórico do processo de secagem dos produtos agrícolas tropicais de variedades locais, o presente trabalho foi realizado com o objetivo de ajustar o modelo da difusão líquida acrescentando a análise do efeito da contração volumétrica do grão durante a secagem de trigo, bem como determinar e avaliar o coeficiente de difusão para diversas condições do ar.
2 Material e métodos
O presente trabalho foi realizado no Laboratório de Propriedades Físicas e Qualidade de Produtos Agrícolas pertencente ao Centro Nacional de Treinamento em Armazenagem (-CENTREINAR), localizado na Universidade Federal de Viçosa.
Foram utilizados grãos de trigo, cultivar Aliança, com teor de água inicial de 0,32 b.s. A secagem do produto foi realizada para diferentes condições controladas de temperatura (25, 35, 45, e 55 °C), com umidade relativa de 55 ± 1%. O trigo foi seco até que o produto atingisse seu teor de água de equilíbrio com a condição do ar especificada. Os teores de água do produto foram determinados por gravimetria utilizando-se estufa a 105 ± 3 °C, durante 24 horas, em três repetições.
As condições ambientais para realização dos testes foram fornecidas por meio de uma unidade condicionadora de atmosfera de fabricação da empresa Aminco, modelo Aminco-Aire 150/300 CFM. Foram colocadas no interior do equipamento duas bandejas removíveis com fundo telado para permitir a passagem do ar através da amostra, contendo cada uma, 50 g de produto. O fluxo de ar foi monitorado com o auxílio de um anemômetro de lâminas rotativas e mantido em torno de 4 m3.s-1.m-2. A temperatura e a umidade relativa do ar foram monitoradas por meio de psicrômetro instalado próximo às bandejas, contendo as amostras.
Durante o processo de secagem as bandejas com o produto foram removidas, periodicamente, da câmara e pesadas, sendo o equilíbrio higroscópio atingido quando a variação da massa dos recipientes permaneceu, aproximadamente, invariável durante três pesagens consecutivas.
Para a determinação das razões de umidade do trigo durante a secagem, nas diferentes condições de ar, utilizou-se a seguinte expressão:
em que, U*e: teor de água de equilíbrio do produto, decimal (b.s.); e U*i: teor de água inicial do produto, decimal (b.s.).
No interior de cada bandeja contendo o produto, uma pequena amostra foi devidamente individualizada, por meio do envolvimento de um tecido permeável ao ar. Durante as pesagens do produto, estes grãos foram retirados das bandejas e encaminhados para medição do volume.
Considerando a forma do grão de trigo um esferóide prolato, o volume de cada grão foi obtido por meio da medição dos três eixos ortogonais (comprimento, largura e espessura, conforme apresentado na Figura 1), em oito grãos ao longo do processo de secagem, com auxílio de um paquímetro digital, de acordo com a expressão proposta por MOHSENIN16:
em que: Vg: volume do grão, m3; a: maior eixo do grão, m; b: eixo médio do grão, m; e c: menor eixo do grão, m.
O raio da esfera equivalente (R) foi calculado pela seguinte expressão:
O índice de contração volumétrica do grão durante a secagem foi determinado pela relação:
em que, yg: índice de contração volumétrica dos grãos, %; V: volume dos grãos para cada teor de água, m3; e Vo: volume inicial dos grãos, m3.
O modelo matemático da difusão líquida, com a solução analítica para a forma geométrica cilíndrica, com aproximação de oito termos (Equação 3), foi ajustado aos dados experimentais de secagem do trigo em casca considerando-se a contração volumétrica unitária dos grãos e desprezando-se este fenômeno.
Para o ajuste do modelo, foi realizada análise de regressão não linear, pelo método Quasi-Newton, utilizando-se o programa computacional STATISTICA 5.0®. O grau de ajuste para cada condição considerou a significância do coeficiente de regressão pelo teste t, adotando o nível de 5% de probabilidade e as magnitudes do coeficiente de determinação (R2) e do erro médio estimado (SE), calculado conforme a seguinte expressão:
em que: SE: erro médio estimado, decimal; Y: valor observado experimentalmente;  : valor calculado pelo modelo; e GLR: graus de liberdade do modelo.
: valor calculado pelo modelo; e GLR: graus de liberdade do modelo.
Para comparar os modelos da difusão líquida com e sem a contração volumétrica dos grãos, para cada uma das condições de secagem, os valores estimados pelos modelos foram plotados, procedendo-se à análise de regressão linear, com a reta passando pela origem, sendo a consistência do modelo avaliada pelo coeficiente de determinação (R2) e pela concordância expressa pelo índice "d" proposto por WILLMOTT et al.25. O índice "d" indica o grau de exatidão entre os valores estimados pelos modelos. Quanto mais próximo de 1 este valor, menor a diferença entre os modelos. O índice "d" é representado pela seguinte expressão:
em que, d: índice de concordância; Y: i-ésimo valor estimado pelo modelo 1; Yo: i-ésimo valor estimado pelo modelo 2; e  : média dos valores estimados pelo modelo 2.
: média dos valores estimados pelo modelo 2.
3 Resultados e discussão
Na Tabela 1, estão apresentados os valores experimentais da contração volumétrica dos grãos de trigo (yg) durante a secagem em diversas condições de temperatura, com seus respectivos valores de teor de água e tempo de secagem.
Na Tabela 1, pode-se observar que, para a umidade relativa constante de 55 ± 1%, os valores do teor de água de equilíbrio diminuíram com o aumento da temperatura, seguindo a mesma tendência da maioria dos produtos agrícolas2,24,.
Ainda na Tabela 1, verifica-se a redução do volume inicial dos grãos de trigo entre 10,79 e 17,60 %, para as diversas condições de secagem, com o teor de água do produto variando de, aproximadamente, 0,32 (b.s.) até o teor de água de equilíbrio específico para cada condição de temperatura. RESENDE et al.22 verificaram diminuição do volume inicial dos grãos de arroz em casca, sob diferentes condições de temperatura e umidade relativa do ar, entre 7,4 e 17,9%. O produto continha teor de água inicial de 0,272 b.s., sendo seco até o equilíbrio higroscópico do produto com as diferentes condições do ar de secagem impostas. Já RAMOS et al.21 observaram uma redução de 35% do raio de uvas durante o processo de secagem e ressaltam que esta variação significativa na contração volumétrica do produto deve ser incluída nos modelos de transferência de massa.
Na Tabela 1, também é possível observar que, à exceção da temperatura de 25 °C, o aumento da temperatura promoveu maiores valores de contração volumétrica dos grãos de trigo, concordando com os resultados encontrados por RESENDE et al.22, trabalhando com grãos de arroz em casca. Os maiores valores de contração volumétrica encontrados para a temperatura de 25 °C deve-se, provavelmente, ao elevado tempo de exposição ao processo de secagem.
Na Tabela 2, estão apresentados os valores médios dos coeficientes de difusão, erros médios estimados e coeficientes de determinação (R2) para o modelo da difusão líquida, considerando a contração volumétrica (r variável) e desconsiderando este fenômeno (r constante) durante a secagem do trigo nas diversas temperaturas do ar de secagem.
De acordo com a Tabela 2, observa-se que o modelo da difusão líquida ajustado para os grãos de trigo apresentou, para todas as condições de ar estudadas, significância do coeficiente de regressão ao nível de 5% de probabilidade pelo teste t, e coeficiente de determinação superior a 99%. Os valores do erro médio estimado, também apresentaram magnitudes reduzidas (menor que 0,04), confirmando o ajuste satisfatório do modelo aos dados experimentais.
Analisando os resultados encontrados, pôde-se observar que o coeficiente de difusão aumentou com a elevação da temperatura do ar de secagem, o que sugere que, para menores temperaturas, os grãos de trigo oferecem maiores resistências internas ao transporte de água, resultando em menores coeficientes de difusão. Dessa forma, a elevação da temperatura do ar de secagem indica uma maior intensidade do fenômeno de transporte de água do interior para a periferia do grão, estando de acordo com outros resultados encontrados na literatura especializada3,22,23.
Para a faixa de temperatura estudada, os coeficientes de difusão dos grãos de trigo apresentaram magnitudes entre 8,3306 x 10-11 e 41,0977 x 10-11 m2.s-1 considerando a contração volumétrica do grão, e entre 9,0244 x 10-11 e 44,6509 x 10-11 m2 .s-1 utilizando-se o raio equivalente inicial dos grãos, ou seja, desprezando-se a redução de volume do produto ao longo da secagem. Estes valores estão coerentes aos relatados na literatura sobre secagem de produtos agrícolas que, de acordo com MADAMBA et al.14, apresentam-se na ordem de 10-9 a 10-11 m2.s-1.
Na Tabela 3, estão apresentados os valores dos índices "d" propostos por WILLMOTT et al.25 para comparação dos modelos da difusão líquida com e sem a contração volumétrica dos grãos de trigo, durante a secagem nas diferentes temperaturas do ar.
De acordo com a Tabela 3, verificam-se elevados valores do índice de Willmott para todas as temperaturas do ar, indicando uma excelente concordância entre os valores estimados pelos dois modelos testados. Quanto mais próximos de 1 forem estes índices, menores serão as diferenças existentes entre os valores estimados por duas equações. As regressões lineares simples para a razão de umidade estimada pelos modelos (x: razão de umidade estimada pelo modelo com a contração volumétrica; y: razão de umidade estimada pelo modelo sem a contração volumétrica), com a reta passando pela origem, também obtiveram elevados valores dos coeficientes de determinação ajustado, comprovando a acentuada semelhança e correlação entre os modelos da difusão líquida considerando ou não a contração volumétrica dos grãos.
Baseando-se nestes parâmetros estatísticos, verifica-se que a inclusão da contração volumétrica dos grãos de trigo no modelo da difusão líquida não forneceu um melhor ajuste do modelo aos dados experimentais, podendo ser considerado, para fins de avaliação, o valor médio (r variável e constante) do coeficiente de difusividade para as condições experimentadas (Tabela 2).
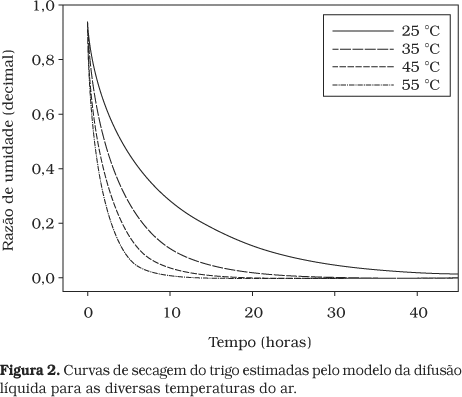
Os valores da razão de umidade estimados pelo modelo da difusão líquida para a secagem dos grãos de trigo para as diversas condições de temperatura estão apresentados na Figura 2.
Na Figura 3, é mostrado o gráfico de correspondência entre os valores observados e estimados de razão de umidade para as diversas condições testadas. Nesta figura, pode-se observar o adequado ajuste do modelo da difusão de umidade para a descrição da cinética de secagem dos grãos de trigo da variedade Aliança.
A dependência do coeficiente de difusão em relação à temperatura do ar de secagem pode ser descrita pela relação de Arrhenius, como ilustrado na Figura 4 e pela Equação 10.
A inclinação da curva da representação de Arrhenius fornece a relação Ea/R, enquanto a sua interseção com o eixo y indica o valor de Do. A Equação 11 apresenta os coeficientes da expressão ajustada para o coeficiente de difusão dos grãos de trigo, calculados de acordo com a Equação 4.
Considerando R = 8,134 kJ.kmol-1, a energia de ativação para a difusão líquida do trigo foi de 42,00 kJ.mol-1. Segundo SHARMA e PRASAD23, termodinamicamente, energia da ativação representa a energia necessária para o rompimento da barreira que as moléculas de água encontram, durante o processo de secagem, ao migrarem do interior para a superfície do produto, sendo que energia de ativação mais baixa traduz-se em maior difusividade de água no produto. A redução na energia de ativação de um processo resulta de um aumento na energia média das moléculas, que fazem parte do processo. Segundo KAYACIER e SINGH13, a energia de ativação diminui com a elevação do teor de água inicial do produto durante o processo de secagem.
O valor da energia de ativação encontrado no presente estudo foi ligeiramente superior ao encontrado por MOHAPATRA e RAO15 que, trabalhando com trigo parbolizado, encontraram valores da ordem de 37,01 kJ.mol-1. Isto se deve provavelmente ao fato de que, neste trabalho foi estudado o intervalo de temperatura de 25 a 55 °C, diferente do usado por aqueles autores (40 a 60 °C), além do fato do material experimentado ser pré-processado. Na literatura pesquisada, foram encontrados valores da energia de ativação para diversos produtos agrícolas: para soja de 28,8 a 30 kJ.mol-1, gel de amido 18,8 a 50 kJ.mol-1, cebolinha 29,05 a 42,05 kJ.mol-1, champignon em conserva 23,89 a 31,45 kJ.mol-1 e milho da espécie Zea mays indentata 29,56 kJ.mol-16,10,11,18. ZOGZAS et al.26 ressaltam que a energia de ativação para produtos agrícolas varia entre 12,7 a 110 kJ.mol-1.
4 Conclusão
Com base nos resultados obtidos conclui-se que o modelo da difusão líquida representa satisfatoriamente a cinética de secagem dos grãos de trigo para as diversas condições de ar experimentadas. A inclusão da contração volumétrica dos grãos de trigo no modelo da difusão líquida foi insuficiente para melhorar o ajuste do modelo. O coeficiente de difusão aumenta com a elevação da temperatura do ar, apresentando valores médios de 8,6775 x 10-11 e 42,8743 x 10-11 m2.s-1 para a faixa de temperatura estudada. A relação entre o coeficiente de difusão e a temperatura pode ser descrita pela expressão de Arrhenius, que apresenta uma energia de ativação para a difusão líquida nos grãos de trigo de 42,00 kJ.mol-1.
Recebido para publicação em 2/4/2006
Aceito para publicação em 24/1/2007 (001722)
- 1. AFONSO JÚNIOR, P. C.; CORRÊA, P. C. Comparação de modelos matemáticos para descrição da cinética de secagem em camada fina de sementes de feijão. Revista Brasileira de Engenharia agrícola e ambiental, Campina Grande, v. 3, n. 3, p. 349-353, 1999.
- 2. AYRANCI, E.; DUMAN, O. Moisture sorption isotherms of cowpea (Vigna unguiculata L. Walp) and its protein isotate at 10, 20 and 30°C. Journal of Food Engineering, Davis, v. 70, n. 1, p. 83-91, 2005.
- 3. BABALIS, S. J.; BELESSIOTIS, V. G. Influence of the drying conditions on the drying constants and moisture diffusivity during the thin-layer drying of figs. Journal of Food Engineering, Davis, v. 65, n. 3, p. 449-458, 2004.
- 4. BERBERT, P. A.; QUEIROZ, D. M.; SILVA, J. S.; PINHEIRO FILHO, J. B. Simulation of coffe drying in a fixed bed with periodic airflow reversal. Journal of Agricultural Engineering Research, London, v. 60, n. 3, p. 167-173, 1995.
- 5. BROOKER, D. B.; BAKKER-ARKEMA, F. W.; HALL, C. W. Drying and storage of grains and oilseeds. New Cork: Van Nostrand Reinhold, 1992. 450 p.
- 6. BRÓVIA, P. M. N.; BROD, F. P. R.; PARK, K. J. Estudio de secado de champiñón en conserva (Agaricus bisporus) utilizando un secador vertical. Alimentaria: revista de tecnología e higiene de los alimentos, Madrid, v. 286, p. 119-122, 1997.
-
7CARMO, J. E. F.; LIMA, A. G. B. Drying of lentils including shrinkage: a numerical simulation. In: 14th INTERNATIONAL DRYING SYMPOSIUM, 2004, São Paulo. Proceeding of the 14th International Drying Symposium, Ourograf, São Paulo, 2004, v. A, p. 510-517.
- 8. CHRISTENSEN, C. M.; KAUFMANN, H. H. Microflora. In: CHRISTENSEN, C. M. Storage of cereal grain and their products. St. Paul: American Association of Cereal Chemists, 1974, p. 158-192.
- 9. DOYMAZ, I. Drying characteristics and kinetics of ockra. Journal of Food Engineering, Davis, v. 69, n. 3, p. 275-279, 2005.
- 10. DOYMAZ, I.; PALA, M. The thin-layer drying characteristics of corn. Journal of Food Engineering, Davis, v. 60, n. 2, p. 125130, 2003.
- 11. FISH, B. P. Diffusion and thermodynamics of water in potato starch gel. Fundamental aspects of the dehydration of foodstuffs [s.I.]: Society of Chemical Industry, p. 143-157, 1975.
- 12. HALL, C. W. Drying and storage of agricultural crops. Westport: AVI Publishing Company, 1980, 381.
- 13. KAYACIER, A.; SINGH, R. K. Application of effetive diffusivity approach for the moisture content prediction of tortilla chips during baking. Lebensmittel-Wissenschaft und-Technologie, London, v. 37, n. 2, p. 275-281, 2004.
- 14. MADAMBA, P. S.; DRISCOLL, R. H.; BUCKLE, K. A. Thin-layer drying characteristcs of garlic slices. Journal of Food Engineering, Davis, v. 29, n. 1, p. 75-97, 1996.
- 15. MOHAPATRA, D.; RAO, P.S. A thin layer drying model of parboiled wheat. Journal of Food Engineering, v. 66, n. 4, p. 513-518, 2005.
- 16. MOHSENIN, N. N. Physical properties of plant and animal materials. 2. ed. New York: Gordon and Breach Publishers, 1986. 841p.
- 17. OZDEMIR, M.; DEVRES, Y. O. The thin layer drying characteristics of hazelnuts during roasting. Journal of Food Engineering, Davis, v. 42, n. 4, p. 225-233, 1999.
- 18. PARK, K. J.; BROD, F. P. R.; SILVA, J. E. A. R. Estudo comparativo de secagem de cebolinha (Allium sp. Cv. Galega) utilizando secadores vertical e horizontal. Revista Ciência e Tecnologia de Alimentos, Campinas, v. 16, n. 2, p. 143-145, 1996.
- 19. PRADO, M. E. T.; ALONSO, L. F. T.; PARK, K. J. Shrinkage of dates (Phoenix Dacyilyfera L.) during drying. Drying Technology, New York, v. 18, n. 1 e 2, p. 295-310, 2000.
- 20. RAMESH, M. N. Moisture transfer properties of cooked rice during drying. Lebensmittel-Wissenschaft und-Technologie, London, v. 36, n. 2, p. 245-255, 2003.
- 21. RAMOS, I. N.; BRANDÃO, T. R. S.; SILVA, C. L. M. Integrated approach on solar drying, pilot convective drying and microstructural changes. Journal of Food Engineering, Davis, v. 67, n. 1-2, p.195-203, 2005.
- 22. RESENDE, O.; CORRÊA, P. C.; GONELI, A. L. D.; MARTINAZZO, A. P.; RIBEIRO, R.M. Contração volumétrica na difusão líquida durante o processo de secagem do arroz em casca. Revista Brasileira de Armazenamento, Viçosa, v. 30, n. 2, p. 163-171, 2005.
- 23. SHARMA, G. P.; PRASAD, S. Effetive moisture diffusivity of garlic cloves undergoing microwave- convective drying. Journal of Food Engineering, Davis, v. 65, n. 4, p. 609-617, 2004.
- 24. TOLABA, M. P.; PELTZER, M.; ENRIQUEZ, N.; POLLIO, M. L. Grain sorption equilibria of quinoa grains. Journal of Food Engineering, Davis, v. 61, n. 3, p. 365-371, 2004.
- 25. WILLMOTT, C. J.; ACKLESON, S. G.; DAVIS, R. E.; FEDDEMA, J. J.; KLINK, K. M.; LEGATES, D. R.; O'DONNELL, J.; ROWE, C. M. Statistics for the evaluation and comparison of models. Journal of Geophysical Research, Washington DC, v. 90, n.C5, p. 8995-9005, 1985.
- 26. ZOGZAS, N. P.; MAROULIS, Z. B.; MARINOS-KOURIS, D. Moisture diffusivity data compilation in foodstuffs. Drying Technology, New York, v. 14, n. 10, p. 2225-2253, 1996.
Datas de Publicação
-
Publicação nesta coleção
09 Maio 2007 -
Data do Fascículo
Mar 2007
Histórico
-
Recebido
02 Abr 2006 -
Aceito
24 Jan 2007