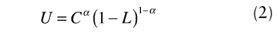Resumo
This paper presents the two major hypotheses explaining the relatively higher GDP growth of Northeast, when compared to the one for the whole country. These hypotheses are that governmental transferences towards the poorest and the rises in minimum wages are responsible for such relative performance. They are formally presented theoretically and a method to test their relative role is developed, relying on county data for the period 2000 to 2006. The results indicate that the Bolsa Familia Program had a higher positive impact in the GDP growth rate of the region than the rises in Minimum wage.
minimum wage; transference policies; Northeastern growth
minimum wage; transference policies; Northeastern growth
Salário mínimo, Bolsa Família e desempenho relativo recente da economia do Nordeste
Minimum wages, poverty alleviation income policies, and the relative performance of the Northeastern economy in Brazil
Alexandre Rands BarrosI; Diloá AthiasII
IDepartamento de Economia, Universidade Federal de Pernambuco. E-mail: acrbarros@gmail.com
IIDepartment of Economics, University of Illinois. E-mail: diloaj@gmail.com
ABSTRACT
This paper presents the two major hypotheses explaining the relatively higher GDP growth of Northeast, when compared to the one for the whole country. These hypotheses are that governmental transferences towards the poorest and the rises in minimum wages are responsible for such relative performance. They are formally presented theoretically and a method to test their relative role is developed, relying on county data for the period 2000 to 2006. The results indicate that the Bolsa Familia Program had a higher positive impact in the GDP growth rate of the region than the rises in Minimum wage.
Keywords: minimum wage; transference policies; Northeastern growth.
JEL Classification: R11.
INTRODUÇÃO
Desde 2002 que o crescimento do PIB per capita do Nordeste tem sido superior à média nacional. Essa superioridade tem sido particularmente relevante quando a comparação é feita com o Sudeste, região mais populosa do país. Enquanto o crescimento médio em nossa região foi de 3,2% entre 2002 e 2008, ele atingiu apenas 2,85% no Brasil. Outras regiões, como o Centro-Oeste e o Norte, até cresceram tanto ou mais que o Nordeste no mesmo período, mas, tendo elas populações inferiores, ainda assim o desempenho dessa última foi superior ao encontrado para todo o país.
Esse maior desempenho relativo tem gerado duas questões para as pessoas que são preocupadas com o desenvolvimento regional brasileiro. Em primeiro lugar, busca-se explicar por que ele foi superior. Em seguida, questiona-se se tal comportamento é apenas temporário e será revertido no futuro, ou deixará a região em um novo patamar de desenvolvimento relativo no país, superior ao que se encontrou nos últimos 30 anos. Obviamente, uma consequência que permeia as buscas de respostas às duas questões apresentadas é a tentativa de se saber até quando a região continuará crescendo mais que o Brasil e qual será o novo patamar de equilíbrio da renda per capita dessa região em relação à média nacional e à encontrada no Sudeste.
Essas questões estão longe de ser preocupações apenas acadêmicas. Conhecer as respostas a elas pode influenciar os investimentos que as empresas de vários setores deverão fazer para posicionar-se no mercado regional e, de forma mais genérica, distribuir espacialmente sua produção e estruturas mercadológicas. O desempenho relativo recente, inclusive, já gerou maior direcionamento de preocupações de grandes empresas para a região. As incertezas quanto a sua extensão e duração, contudo, ainda limita essas ações.
As discussões até então sobre essas questões têm apontado duas principais hipóteses para explicar o desempenho econômico relativo recente do Nordeste. A primeira delas é que a expansão das políticas de transferência de renda após 2002, principalmente os Programas Bolsa Escola e Bolsa Família, por serem relativamente mais direcionados para o Nordeste, região com maior percentual de pobres, estaria elevando a demanda na região e isso estaria gerando esse maior crescimento econômico.
A segunda hipótese é que o aumento real do salário mínimo desde 2003 gerou maior ajuste tecnológico e demanda na região, que tem uma maior participação de trabalhadores cuja renda é influenciada pelo salário mínimo. Apesar de ter tido menor apelo tanto em meios acadêmicos como não acadêmicos, ela tem sido sempre respeitada como plausível e provavelmente com impacto efetivo, quando apresentada.
Dadas essas questões sobre o desempenho recente do Nordeste, este artigo tem dois focos principais. Em primeiro lugar, ele discute os possíveis fundamentos da capacidade de explicação do maior crescimento do Nordeste advindos das duas hipóteses brevemente apresentadas. O segundo foco será em uma estimação do papel relativo dessas duas causas do maior crescimento do Nordeste. Obviamente essas estimações partem do pressuposto de que as duas hipóteses não são excludentes e que ambas podem ter tido algum papel na geração do maior desempenho da região.
O artigo está organizado como segue. Na próxima seção se discutem os fundamentos teóricos das duas hipóteses. Na terceira seção o método de estimação dos impactos de cada um dos possíveis determinantes é apresentado. A quarta seção apresenta e discute os principais resultados empíricos das estimações e a quinta seção traz uma discussão das consequências dos resultados empíricos para posicionamentos empresariais e possíveis políticas de desenvolvimento regional.
FUNDAMENTOS TEÓRICOS DAS PRINCIPAIS EXPLICAÇÕES PARA O MAIOR CRESCIMENTO RECENTE DO NORDESTE
Como argumentado anteriormente, há duas hipóteses fundamentais para explicar o maior crescimento do Nordeste nos últimos anos. A primeira o faz através do impacto dos programas sociais de transferência de renda. A segunda recorre ao maior papel do salário mínimo na região Nordeste e sua elevação em termos reais nos últimos anos para explicar esse dinamismo. Essas hipóteses são apresentadas em maiores detalhes nas subseções que seguem.
1. O papel dos programas de transferência de renda
Essa hipótese parte do pressuposto inicial de que o Nordeste tem mais beneficiários dos programas de transferência de renda do Governo Federal, cujo objetivo é o combate à pobreza. Obviamente isso ocorre porque ao longo do período em análise a região sempre teve maior proporção de sua população vivendo abaixo da linha de pobreza. Nenhum desses dois pressupostos são objetos de disputa entre estudiosos do problema e ambos são confirmados pelos dados apresentados na Tabela 1.
Nos programas de transferência de renda podem ter duas consequências importantes que possibiletem um maior crescimento relativo do Nordeste. A primeira delas é o aumento da demanda local, que eleva a produção realizada próxima a ela por causa dos custos de transporte e informação. A segunda é certa escassez relativa de mão de obra na região a baixas remunerações, o que eleva o desenvolvimento tecnológico.1 1 Acemoglu (2009) apresenta argumentação rigorosa mostrando em que condições essa relação é verdadeira. A seguir essas duas visões são um pouco mais detalhadas.
1.1. Efeito demanda
A ideia de que a maior demanda pode elevar o PIB per capita dos municípios que são beneficiados pelas transferências do Governo Federal, como o Bolsa Família, parte do pressuposto de que o funcionamento da economia é mais apropriadamente representado pela competição monopolística e retornos crescentes de escala em setores significativos dela. Isso significa que na oferta de cada bem existe um número finito de ofertantes e que eles não são perfeitamente substitutos entre si, seja por diferenciações dos seus produtos ou, mais importante no problema em questão, pela conveniência de suas localizações espaciais. Além disso, pode se supor que os retornos crescentes de escala advêm da existência de custos de gestão que não crescem proporcionalmente à produção.
Assim, as firmas se defrontam com uma demanda negativamente inclinada, como a representada pela reta "demanda antes das transferências" na figura 1. Por consequência, essas firmas, tendo as funções custo marginal (CMg) e custo médio (CMédio) também negativamente inclinadas, como apresentadas na Figura 1, maximizam o seu lucro igualando o custo marginal à receita marginal e definindo o preço no nível que a quantidade definida dessa forma iguala a demanda. Ou seja, elas produziriam Q0 na Figura 1 e teriam preço igual a P0 nessa mesma figura. O lucro dessas firmas nesse caso seria como definido na Figura 1 pelo retângulo cujos vértices são A0, A1, A2, P0. Quando há um aumento da demanda por causa da renda maior dos consumidores, cada firma terá sua curva de demanda deslocada para a direita, como representado na Figura 1, a partir do deslocamento de "demanda antes das transferências" para "demanda após transferências". Vale observar que não haveria razão para haver choque de produtividade após o início das transferências. Assim, as curvas de custos marginal e médio das empresas manter-se-iam nos mesmos patamares anteriores. Consequentemente, o novo equilíbrio seria no ponto (Q1, P1), onde a nova demanda encontra-se com a quantidade Q1, definida a partir da igualação do custo marginal à nova receita marginal.
Nesse segundo equilíbrio o lucro das empresas locais é maior. Isso pode ser concluído porque o novo lucro, definido pela área do retângulo definido pelos vértices B0, B1, B2, P1, inclui o lucro antes do choque como apenas uma parte de sua área.
Assim, a renda gerada na região que recebe mais transferências se eleva pelo componente lucro e pelo componente emprego, já que ele será maior no novo equilíbrio. Em uma versão de equilíbrio geral, em que os salários também possam reagir ao maior emprego, também pode se concluir que haverá um aumento da renda por causa deles. Nesse caso, as curvas de custos marginal e médio girariam um pouco para cima, fazendo com que os salários adicionais corroessem parte dos lucros, mas tal aumento não seria suficiente para eliminar o aumento de produção, se for praticado dentro de certos limites plausíveis. Com curvas de custo marginal decrescente, e aumentos dos salários dentro de certos limites, o aumento de demanda não corroeria a competitividade das empresas locais, que permitiria que elas aumentassem a produção.
Numa visão de contabilidade regional, a renda que entra no município em forma de transferências poderia até sair toda por maior importação de bens do resto da economia. Todavia, deixaria a produção interna mais eficiente e complexa, o que faria com que o consumo total dos agentes internos venha a ser maior não só pela maior importação, mas também por maior produção interna.2 2 A existência de retorno crescente de escala e os limites impostos para o aumento dos salários nessa visão eliminam a possibilidade de haver o problema de " Dutch disease".
Apesar de o modelo em que a ideia foi exposta ser essencialmente de estática comparativa, pode se pensar em um modelo dinâmico em que a taxa de crescimento a cada momento seja definida como:
onde Y é o PIB per capita, g é a taxa de crescimento de equilíbrio gerada por outras relações da economia e Ye é o PIB per capita de equilíbrio a cada momento. Sendo 0 < γ < 1 um parâmetro positivo, obviamente a taxa de crescimento dessa área geográfica converge para a taxa de crescimento g de equilíbrio em que Y segue um caminho de equilíbrio traçado por outros fatores da economia. Entretanto, quando há o choque de demanda causado pelo início das transferências, essa taxa de crescimento passa um tempo sendo superior à taxa de equilíbrio, enquanto não houver convergência. Nesse intervalo, a taxa de crescimento das áreas geográficas que recebem mais transferências tenderá a ser maior que a média nacional.
A partir dessa visão, as maiores transferências para o Nordeste seriam responsáveis pela maior taxa de crescimento dessa região nos últimos anos. Vale salientar, contudo, que dentro dessa concepção a taxa de crescimento da economia convergiria para sua taxa de equilíbrio e não necessariamente haveria maior crescimento da região Nordeste a partir de então. Isso ocorre porque, quando as transferências pararem de aumentar, a demanda para de se deslocar para cima e o emprego e a produção local em equilíbrio já não têm mais motivos para se deslocarem mais rápido do que o resto da economia (nas demais regiões). Ou seja, esse maior crescimento é transitório e não necessariamente levaria a uma convergência absoluta das rendas per capita regionais no país.3 3 Ver Barros (2011, cap. 7) para uma discussão dessa dinâmica de resposta a tal política.
1.2. Efeito desenvolvimento tecnológico
O efeito desenvolvimento tecnológico ocorre porque as pessoas preferem não trabalhar a salários baixos e ficar aptas a receber as transferências sem ter de realizar o esforço relacionado com o trabalho. Isso muda a relação de custo entre o fator trabalho e o investimento em tecnologia, o que eleva o investimento em desenvolvimento tecnológico. Como no Nordeste há maior contingente de pobres com potencial acesso aos programas de transferência, essa retração da oferta de mão de obra é relativamente maior, o que elevou o desenvolvimento tecnológico relativo na região.
O efeito no desenvolvimento tecnológico de programas de transferência de renda é similar ao que ocorre quando há aumento de salário mínimo, pois na prática há uma aceleração no desenvolvimento tecnológico por causa da elevação do salário de equilíbrio na área geográfica em que residem os beneficiários de tal política.4 4 Acemoglu (2009) traz uma discussão mais rigorosa das condições em que o impacto da escassez de trabalho e da elevação dos salários no desenvolvimento tecnológico são similares. Assim, esse efeito será mais bem explicado na subseção a seguir. A discussão aqui será apenas de (i) como um programa de transferência de renda como o Bolsa Família eleva o salário de equilíbrio nos municípios e (ii) como esse impacto é maior em municípios mais pobres.
i. Impacto de programas de transferência no salário de equilíbrio dos municípios
Quando as pessoas ofertam seu trabalho, elas o fazem considerando uma função utilidade em que pesa a utilidade negativa do trabalho e a positiva do que se pode adquirir com a remuneração e a experiência obtida. De forma simplificada, dentro de um padrão teórico comum, pode se dizer que o consumidor maximiza uma função utilidade tipo Cobb-Douglas como a expressa na equação (2).
onde U é a utilidade total, C é o consumo, medido em unidades de uma cesta de bens, L é a quantidade de trabalho que ele despende, medida em tempo em um determinado intervalo, e α é um parâmetro, tal que 0 < α < 1. Ele maximiza essa função sujeita a uma restrição orçamentária, que de forma simplificada pode ser expressa como segue:
onde T são as transferências recebidas, w é o salário nominal e P é o índice de preços. As demais variáveis são como previamente definidas. A condição de primeira ordem para a solução desse problema gera:
Ou seja, quanto maiores as transferências, maior o salário que terá de ser pago para que haja um dado patamar de oferta de trabalho. Isso faz com que se gere uma escassez relativa de mão de obra a cada nível salarial. Para uma mesma demanda por trabalho, o salário de equilíbrio tende a se elevar, quando T sobe.
É importante enfatizar que apesar das transferências recebidas pelo agente representativo na equação (4) estarem definidas como constantes, esse não é o caso na realidade. Programas de transferência como o Bolsa Família são dirigidos apenas para os mais pobres. Sendo assim, pode se definir uma função tal que T = T(w), onde a primeira derivada T'(w) é negativa, ou T'(w) < 0.5 5 Mais rigorosamente, deve-se acrescentar que T'( w) = 0 e T'( w) = 0 quando w > , onde é um valor qualquer de salário definido por política pública tal que ∈ + e w < ∞. Ou seja, quando aumenta o salário recebido pelos indivíduos, cai as transferências que eles recebem. Além disso, a partir de certo patamar de salário, os indivíduos não recebem mais transferências.
Sendo assim, a oferta de trabalho definida pela equação (4) pode ser representada como na Figura 2, onde aparece a oferta antes e depois das transferências serem estabelecidas. Nessa mesma figura colocou-se uma demanda por mão de obra e dois equilíbrios foram apresentados, um em (L0,w0) e o outro em (L1,w1). O primeiro é antes das transferências serem estabelecidas e o outro é após a introdução delas. Como pode se ver, as transferências elevam os salários de equilíbrio de w0 para w1, quando elas são introduzidas. Isso decorre da retração da oferta de trabalho promovida pelas transferências.
ii. Maior impacto relativo nos municípios mais pobres
Nem todos os indivíduos em uma sociedade integram o mesmo mercado de trabalho. Indivíduos menos qualificados não são perfeitos substitutos para indivíduos mais qualificados. Assim, para simplificar o raciocínio pode se trabalhar com dois mercados de trabalho, um para indivíduos mais qualificados e outro para indivíduos menos qualificados. Nesse caso, o mercado de trabalho teria duas ofertas e duas demandas, como as apresentadas na Figura 3. Somente salários que compõem o intervalo coberto pela oferta de trabalho menos qualificado, oferta de trabalho II na Figura 3, qualificam para receber transferências. Todo o intervalo da oferta de trabalho I está fora dos valores passíveis de qualificar para transferências.
Essa economia teria dois salários após a introdução das transferências, w1 e w2. Eles prevalecem nos mercados de mão de obra menos qualificada e mais qualificada, respectivamente. Apenas o segundo mercado possui trabalhadores que podem qualificar para receber transferências. Assim, somente o salário nesse mercado é afetado pelas transferências, como mostra a Figura 3.
As diversas regiões geográficas brasileiras têm quantidades de pessoas diferentes com os diversos níveis de formação e expectativas salariais. O Nordeste e o Norte particularmente são as regiões com maior participação de pessoas de baixa formação e qualificação.
A Tabela 2 traz dados que mostram que há um contingente proporcional maior de pessoas trabalhando com rendimento até um salário mínimo nessas regiões, assim como pessoas com nível de instrução até quatro anos de estudo.
O raciocínio sistematizado na Figura 3 implica que quanto maior a participação de trabalhadores no mercado de trabalho II, maior será a proporção deles afetada por transferências governamentais. Assim, pelos dados apresentados, é de supor que o Norte e o Nordeste são as regiões cujos mercados de trabalho são mais afetados pela introdução das transferências. Mais precisamente, nessas regiões deve ter havido maior aumento de salários em vários setores por causa da introdução ou expansão de programas de transferências do Governo Federal. Suas consequências para o crescimento são objeto da próxima subseção, já que o impacto é de aumento de salário nos segmentos de menor remuneração, assim como ocorre com a elevação do salário mínimo.
2.1. O papel das elevações do salário mínimo
Há toda uma literatura que enfatiza o papel de imposição de salários mínimos elevados ou escassez de trabalho como indutores de desenvolvimento tecnológico.6 6 Ver, por exemplo, Acemoglu (2009) para um modelo que define as condições em que tal relação é verdadeira e uma revisão de ideias sobre o assunto. Marx (1887) já enfatizava essa ideia na composição de suas concepções sobre a dinâmica do exército industrial de reserva. Hicks (1932) também incorporou tal ideia já dentro de um escopo teórico neoclássico. Barros (1993a, 1993b) a introduziu dentro de modelos tradicionais da nova teoria do crescimento, mais especificamente os modelos de Lucas (1988) e Romer (1990). Alesina e Zeira (2006), Acemoglu (2009) e Cahuc e Michel (1996) trazem modelos recentes que incorporam essa hipótese. Diante de toda essa literatura, não será preocupação aqui apresentar ou mesmo desenvolver qualquer modelo que incorpore essa hipótese. A sua intuição, contudo, será discutida.
A ideia é simples. Suponha um mercado de trabalho em equilíbrio, como o da figura 4 com salário e emprego determinados como w0 e L0, respectivamente. De repente alguma legislação eleva o salário para w1. Imediatamente haverá desemprego, pois o novo equilíbrio será em (L1, w1), onde o novo salário encontra a demanda D0 por trabalho. Essa elevação dos salários, contudo, eleva o incentivo às firmas investirem em tecnologia e aos trabalhadores investirem em capital humano. No segundo caso, o efeito é óbvio, pois o custo de oportunidade do tempo expendido passa a ser bem menor, já que muitos trabalhadores estarão desempregados (Barros, 1993a; Cahuc e Michel, 1996). No caso de investimento em tecnologia parece menos óbvio, mas essa relação decorre do fato de que os setores que produzem novas tecnologias são menos intensivos em trabalho não qualificado. Assim, o aumento de salário mínimo leva à elevação de custo de sua produção proporcionalmente menor do que ocorre em outros setores produtores de bens finais. Assim, há um deslocamento de fatores de produção para o primeiro setor e com isso acelera-se o processo de desenvolvimento tecnológico. Ele induz ao deslocamento da demanda para cima, movendo-se na Figura 4 de D0 para D1.
Vale adicionar a esse mecanismo de desenvolvimento tecnológico o próprio investimento dentro de cada empresa em aperfeiçoamentos e controle dos processos produtivos, que são realizados com mão de obra de maior qualificação e que por tal não tem sua remuneração afetada pelo salário mínimo. Quando há elevação dos salários de mão de obra menos qualificada, passa a ser lucrativo para as empresas gastar mais dinheiro com essas atividades de aperfeiçoamentos e controle dos processos produtivos, pois os gastos adicionais com mão de obra mais qualificada podem se tornar menores que os salários a serem gastos com "desperdícios", dados os preços relativos anteriores. Além disso, os preços relativos dos bens e serviços produzidos são tal que esses "desperdícios" agora terão valor mais elevado e por tal poderão contribuir para compensar os investimentos mencionados, que requerem mão de obra mais qualificada.
Ou seja, todos esses mecanismos mostram que haverá uma aceleração do desenvolvimento de produtividade que deslocará a demanda para cima e com isso restaurará o pleno emprego no longo prazo, mas com taxas de crescimento maiores na transição, para que o novo patamar de renda mais elevado seja atingido. A Figura 5, extraída de Barros (1993b), bem representa esse movimento do logaritmo da renda (Ln Y) entre dois equilíbrios (E0 e E1) a partir de um aumento do salário mínimo em t0 e mostra por que a taxa de crescimento na transição (entre t0 e t1) será maior. Para que a economia alcance E1, ela terá de crescer mais rápido do que as inclinações de E0 e E1 definem.7 7 Obviamente, se o choque no salário mínimo não for previsível, a renda terá um recuo e passará a crescer mais rápido até que o novo equilíbrio seja atingido em t 1. A linha tracejada na Figura 5 mostra esse caminho de Ln Y. Entretanto, esse detalhe não é relevante para a análise aqui.
Numa região em que mais pessoas têm seus salários afetados por esses choques positivos de salário, seja ele um mínimo institucional ou determinado por elevação da escassez relativa de mão de obra, haverá uma tendência a proporcionalmente maiores ajustes tecnológicos e de produtividade. Isso decorre do fato de que mais setores produtivos terão seus custos mais afetados por tal choque. A consequência é que essa região deverá ter seu crescimento proporcionalmente mais afetado pelo choque. Como visto anteriormente, o Nordeste tem mais pessoas com rendimentos próximos ao salário mínimo e por tal tendem a ser mais afetados por mudanças no salário mínimo. Assim, ele tenderá a crescer mais após elevações do salário mínimo ou da remuneração do trabalho por consequência de maior escassez de mão de obra causada pelas transferências.
MÉTODO DE ESTIMAÇÃO DOS EFEITOS DO SALÁRIO MÍNIMO E DO PROGRAMA BOLSA FAMÍLIA NO CRESCIMENTO DO NORDESTE
O método empírico utilizado inicia com uma equação de regressão de crescimento com dados longitudinais, como a apresentada por Barro e Sala-i-Martin (1992), que pode ser representada como:
em que yi é a taxa de crescimento do PIB do município i entre 2000 e 2006; Y0i é o logaritmo natural do nível inicial do PIB per capita em um município i; Xj são outras variáveis que a literatura aponta como relevantes para explicar a taxa de crescimento e ei é o termo de erro, com média zero e variância finita. As letras gregas αj e βj, para qualquer que seja o j, são parâmetros tomados como constantes entre os municípios.
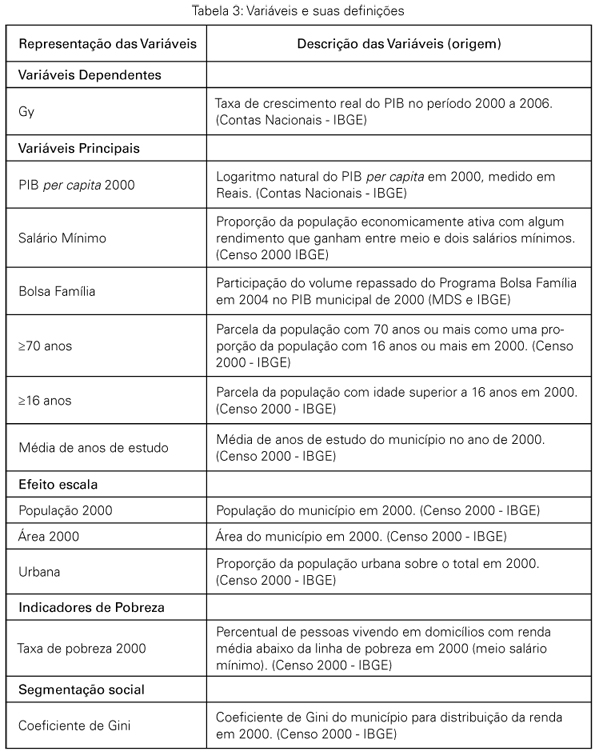
As variáveis incluídas no vetor X aparecem especificadas na Tabela 3, junto com suas fontes. Elas podem ser divididas em dois grupos. O primeiro inclui aquelas que são consideradas como determinantes do crescimento na maioria dos estudos, como é o caso do PIB per capita em 2000 e da média dos anos de estudo. Também foram incluídas entre as variáveis principais duas parcelas da população que possuem comportamentos distintos no mercado de trabalho e programas sociais. São elas: a parcela da população com idade superior a 16 anos e a parcela da população com idade superior a 70 anos. Juntas essas duas variáveis dão uma proxy para a oferta de trabalho mais produtiva. Apesar de dados do IBGE já incluírem, na população economicamente ativa (PEA) pessoas com mais de 10 anos, após 16 anos é que a população realmente ganha um perfil mais produtivo e tem uma propensão maior a se integrar à PEA. Após 70 anos muito pouca gente está ainda ativa no mercado de trabalho. Assim, a inclusão de uma variável que define a proporção desse segmento na população também ajuda a delinear a oferta de trabalho.
Ainda entre as variáveis principais, incluiu-se aquelas que são relevantes para testar as principais hipóteses desse artigo, que são (i) a proporção de pessoas na população economicamente ativa com rendimento entre meio e dois salários mínimos, e (ii) a participação do Bolsa Família no PIB municipal em 2004. A partir dessas duas variáveis poder-se-á testar as principais hipóteses deste trabalho, que podem ser assim apresentadas:
Hipótese I: Os aumentos do salário mínimo desempenharam papel relevante na determinação do maior crescimento relativo da região Nordeste nessa década.
Hipótese II: As transferências do Governo Federal tendo como objetivo aliviar a pobreza também tiveram papel relevante na determinação do maior crescimento relativo do Nordeste nessa década.
Hipótese III: É possível mensurar o impacto relativo desses dois efeitos na determinação do crescimento relativo do Nordeste e compará-los.
A primeira hipótese será testada utilizando-se como proxy para o impacto do salário mínimo no crescimento do PIB municipal o impacto nessa variável capturado pela participação das pessoas com rendimento entre meio e dois salários mínimos na população economicamente ativa total que tem algum rendimento. Para que tal proxy possa capturar o impacto desejado, será necessário que o impacto dos aumentos do salário mínimo seja mais sentido nos municípios que têm população com rendimentos mais afetados pelo salário mínimo e que essa seja exatamente aquela que tenha rendimento mais próximo dele.
Considerou-se que o segmento da PEA com rendimentos mais afetados pelo salário mínimo diretamente é aquele cujo rendimento está mais próximo dele, conforme tem sido sugerido em vários estudos sobre o efeito farol.8 8 Ver, por exemplo, Néri, Gonzaga e Camargo (2001), Giambiagi e Franco (2007), e Barros, Carvalho e Franco (2006). Para a escolha desse intervalo utilizou-se um método simples, que tinha dois princípios básicos. O primeiro é que quanto mais afastado do salário mínimo, menor o efeito dele sobre os rendimentos dos indivíduos nesse segmento. O segundo é que a própria hipótese inicial supõe que o efeito do mínimo é maior no Nordeste do que nas demais regiões brasileiras, com possível exceção do Norte. Assim, somente intervalos de rendimento em que o Nordeste tivesse maior participação na PEA deveriam ser incluídos.
A partir desses princípios básicos, inicialmente identificaram-se os intervalos de renda para os quais os dados do Censo de 2000 estavam disponíveis e organizados pelo IBGE. O salário mínimo é um divisor nesses intervalos. Assim, os dois mais próximos do salário mínimo foram tomados como ponto de partida. Eles incluíam a PEA que recebia entre ½ e 1 salário mínimo e um segundo incluindo indivíduos com rendimento entre 1 e 2 salários mínimos. Antes de proceder calcularam-se essas participações para as diversas regiões e confirmou-se que no Nordeste elas eram maiores.
A partir dessa primeira etapa, calcularam-se as participações dos intervalos adjacentes, que eram de ¼ a ½ e de 2 a 3 salários mínimos. No caso do intervalo entre 2 e 3 salários mínimos, o Nordeste já não era a região com maior participação. Além disso, quando esses intervalos somavam-se aos outros, o Nordeste permanecia não sendo a região com maior participação. Ou seja, esse intervalo entre 2 e 3 salários mínimos teria ser descartado para manter a coerência da proxy cujo propósito era capturar o impacto dele no crescimento.
O intervalo entre ¼ e ½ salário mínimo também foi dispensado porque a análise de dados de PNADs revelou que esse intervalo inclui muita mão de obra que não tem plena ocupação no dia. Ou seja, muitos desses indivíduos não são efetivamente ativos, mas fazem parte de um grupo da população em transição entre a atividade e a inatividade. Esse grupo também já estaria muito afastado do salário mínimo e por tal já teria suas rendas bem menos afetadas por ele. Assim, ficou-se com intervalo entre ½ e 2 salários mínimos. A participação dos indivíduos com rendimento dentro desse intervalo na PEA com rendimento positivo foi a variável incluída para servir de proxy para a relevância do salário mínimo no município.
No caso da proxy para as transferências, utilizou-se a participação do Programa Bolsa Família no PIB dos municípios como a proxy para elas. Esses dados só estavam disponíveis a partir de 2004. Assim, a participação incluída foi exatamente nesse ano. A inclusão de anos posteriores causaria causalidade inversa. Ou seja, menos crescimento elevaria a participação do Bolsa Família na renda e poderia viesar para baixo o coeficiente estimado. Obviamente o fato de a série de crescimento começar em 2000 e essa variável só ser definida para 2004 permite que haja tal efeito reverso. Consequentemente, a interpretação dos resultados deve considerar que os efeitos das transferências encontrados podem estar um pouco subdimensionados.
O segundo grupo de variáveis contém aquelas que não são sempre incluídas nas regressões de crescimento, mas que também aparecem em algumas delas.9 9 Essa inclusão que se considerou no texto é conceitual, não sendo as variáveis concretamente definidas necessariamente na forma que aparece a seguir. Essas variáveis são subdivididas em outros grupos. São eles: efeito escala, indicadores de pobreza e segmentação social. Dentro do subgrupo classificado como de efeito escala, todas capturam a função do efeito escala na taxa de crescimento dos municípios. São elas: população, área e parcela da população urbana, todas calculadas para o ano 2000. Quanto maior for a participação da população urbana, maior será o efeito escala dos negócios do município. Quanto maior a sua área, maior é o negócio rural atendido pelos serviços urbanos e, consequentemente, maior serão os benefícios de escala. Quanto maior é a população, maiores também tendem a ser os benefícios de escala.10 10 Vale salientar que a população já é incluída como uma variável com efeito positivo a partir de sua participação na definição do PIB per capita. Consequentemente, em algumas regressões, quando utilizada sozinha, além da inclusão do PIB per capita, seu efeito pode aparecer negativo. O logaritmo natural do PIB per capita em 2000 é também uma variável de efeito escala, mas ela foi incluída entre as variáveis principais, com o objetivo de capturar a convergência dos PIBs per capita.
O segundo subgrupo de variáveis inclui também um indicador de pobreza, que é o percentual de pessoas vivendo em domicílios cuja renda per capita é inferior ou igual a meio salário mínimo. Quanto maior for a parcela da população pobre, maior será a parcela de recursos públicos alocados para aliviar a pobreza; então uma menor proporção desses recursos serão investidos produtivamente. Por conta disso, menor tende a ser a taxa de crescimento do PIB per capita do município, recursos dos Governos Estaduais e Federal tendem a ser proporcionalmente mais direcionados para aliviar a pobreza, quanto mais pobre for o município. Como investimentos públicos e privados são complementares,11 11 Ver, por exemplo, Aschauer (1989), Erenburg (1993) e Erenburg e Wohar (1995). isso tende a reduzir a taxa de crescimento nos municípios com maiores indicadores de pobreza.
Há um terceiro subgrupo de variáveis, chamadas de variáveis de segmentação social, no qual apenas o coeficiente de Gini foi incluído. Muitos estudos argumentam que distribuição de renda causa algum efeito no crescimento econômico,12 12 Ver, por exemplo, Tabellini e Persson (1994) e Benabou (1996). ainda que os argumentos que o justifiquem sejam não só variados, como muitas vezes até contraditórios entre eles. Existem os argumentos políticos que ressaltam que a concentração de renda tende a conduzir ao poder políticos que não são muito pró-investimentos e são mais propensos a implementar políticas distributivas, além de não terem também foco no apoio aos investimentos privados.13 13 Ver, por exemplo, Alesina e Rodrik (1994). Assim haveria uma relação inversa entre o coeficiente de Gini e o crescimento econômico. Há também o argumento do efeito escala, que defende a ideia de que uma melhor distribuição de renda aumenta o tamanho do mercado e cria mais incentivos para a introdução de novas tecnologias. Assim, também nesse caso haveria uma relação inversa entre coeficiente de Gini e crescimento econômico. Outro argumento que aparece na literatura defende a existência de efeito contrário aos anteriores. Ele baseia-se na hipótese de que a maior concentração de renda geraria maior poder de investimento, pois aumentaria a proporção de renda nas mãos de pessoas com maior propensão a poupar e que teriam mais facilidade em investir. Assim, a economia tenderia a crescer mais rápido por causa da maior disponibilidade de recursos para tal.14 14 Entre municípios pode haver migração de poupança com muita facilidade. Assim, essa hipótese só torna-se válida caso algumas outras hipóteses quanto ao comportamento do fluxo de informação sejam verdadeiras. Como consequência dessas visões contraditórias, o sinal esperado do coeficiente de Gini é incerto.15 15 Ver Benabou (1996) para uma pesquisa com diferentes resultados de estudos empíricos e teóricos referentes a esta relação. Bjørnskov (2008) possui uma abordagem diferente a este problema.
A inclusão das variáveis segue uma regra simples: primeiro, estima-se o modelo apenas com a inclusão das variáveis principais; segundo, promove-se uma nova rodada de estimações, na qual serão incluídas as variáveis explicativas de efeito escala, todas de uma vez; numa terceira rodada de estimações serão incluídas as variáveis de segmentação social; ou seja, o coeficiente de Gini. Por fim, uma quarta e última rodada de estimações incluirá o coeficiente de pobreza, além de todas as demais variáveis previamente incluídas. Esse método de inclusão progressiva de conjunto de variáveis visa gerar informações sobre a estabilidade dos coeficientes relevantes para o presente estudo. Com ele será possível se perceber, em algumas circunstâncias, se as variáveis salário mínimo e Bolsa Família estão gerando resultados espúrios por consequência de sua correlação com outras relevantes para explicar o crescimento do PIB. Mesmo que o método não exclua a possibilidade de tal problema existir e não ser percebido, principalmente quando essas outras variáveis não são incluídas no modelo, ainda assim ele pode dar alguma indicação e evitar erros grosseiros na interpretação dos resultados.
As estimações foram feitas, para cada conjunto de equações, utilizando o método dos Mínimos Quadrados Ordinários (MQO), com correção para heterocedasticidade pelo método de White (1980), e o método dos Mínimos Desvios Absolutos. A amostra incluirá todos os municípios listados no ano 2000 para a região Nordeste do Brasil que não tiveram suas áreas alteradas por desmembramentos. Essa restrição permite que se mantenha coerência em várias dessas variáveis, como PIB per capita, área e população, por exemplo.
RESULTADOS EMPÍRICOS
Os resultados dos diversos modelos estimados foram omitidos por problema de espaço. Entretanto, eles encontram-se disponíveis com os autores e podem ser enviados a partir de demanda. Eles foram utilizados para fazer duas simulações importantes. Em cada uma delas foram criados valores simulados para as duas variáveis relevantes para a estimação do impacto das transferências e do salário mínimo no crescimento do PIB. Esses valores foram criados a partir de uma lógica simples, que foi tornar a média da região Nordeste para essas variáveis como sendo igual à média nacional. Para isso recorreu-se a um artifício matemático simples, que foi multiplicar o valor dessa variável em cada um dos municípios pela sua média para todo o país e dividir pela média do Nordeste. Assim, obtiveram-se valores artificiais para as duas variáveis, que poderiam ser entendidos como aqueles que deveriam prevalecer caso o Nordeste não tivesse tido condições melhores para se beneficiar das duas políticas.
Essas duas séries de valores artificialmente criados foram utilizadas para substituir as originais numa recomposição das taxas de crescimento. Assim procedeu-se às seguintes operações, criando novas séries simuladas das taxas de crescimento do PIB dos municípios nordestinos:
onde
Bi e Si são as taxas de crescimento do PIB do município i quando os valores das variáveis referentes ao Bolsa Família e ao salário mínimo, respectivamente, são os simulados pela lógica descrita acima. Bi e
Si são as taxas de crescimento do PIB do município i quando os valores das variáveis referentes ao Bolsa Família e ao salário mínimo, respectivamente, são os simulados pela lógica descrita acima. Bi e  i são os valores observados e simulados da proporção dos recursos distribuídos pelo Programa Bolsa Família no PIB do município i, respectivamente. Si e
i são os valores observados e simulados da proporção dos recursos distribuídos pelo Programa Bolsa Família no PIB do município i, respectivamente. Si e  i são os valores observados e simulados da participação da população recebendo de ½ a 2 salários mínimos na PEA com remuneração do município i, respectivamente.
i são os valores observados e simulados da participação da população recebendo de ½ a 2 salários mínimos na PEA com remuneração do município i, respectivamente.
Os valores simulados das taxas de crescimento,
Bi e Si, foram utilizados para recompor valores simulados do PIB de 2006 nos diversos municípios. Esses valores foram agregados para toda a região e assim gerou-se uma taxa de crescimento do PIB na região para cada uma das duas hipóteses alternativas. A primeira, de que não houve maior proporção de transferências via Programa Bolsa Família para o Nordeste e a segunda, de que não houve maior benefício da região com o aumento do salário mínimo. Essas taxas aparecem na Tabela 4 na sexta e sétima colunas, respectivamente.
Si, foram utilizados para recompor valores simulados do PIB de 2006 nos diversos municípios. Esses valores foram agregados para toda a região e assim gerou-se uma taxa de crescimento do PIB na região para cada uma das duas hipóteses alternativas. A primeira, de que não houve maior proporção de transferências via Programa Bolsa Família para o Nordeste e a segunda, de que não houve maior benefício da região com o aumento do salário mínimo. Essas taxas aparecem na Tabela 4 na sexta e sétima colunas, respectivamente.
Essas simulações mostram que é possível mensurar o impacto relativo dos efeitos das transferências e do salário mínimo na determinação do crescimento relativo do Nordeste e compará-los. Os dados da tabela 4 mostram que as transferências via Bolsa Família tiveram impacto bem maior que os aumentos do salário mínimo. Tendo como base de comparação uma taxa de crescimento anual média efetiva para o conjunto dos municípios incluídos na amostra de 4,2%, vê-se que, se não houvesse maior proporção de transferências via Programa Bolsa Família no PIB, a região teria tido seu crescimento reduzido para algo entre 3,0% e 3,4% apenas, variando de acordo com o modelo estimado.
Caso não houvesse condições melhores do Nordeste para se beneficiar dos aumentos do salário mínimo, a região também teria amargado quedas na sua taxa de crescimento, porém menores do que no caso anterior. Essa queda teria sido para algo em torno de 4,0% a 4,1%, dependendo do modelo. Ou seja, o PIB teria tido sua taxa de crescimento reduzida de 4,22% para algo entre 4,0% e 4,1%, se não fosse pela sua situação privilegiada para se beneficiar dos aumentos do salário mínimo. Isso significa que a queda na taxa de crescimento teria sido menor do que teria ocorrido caso as transferências não tivessem sido proporcionalmente maiores na região.
As quarta e quinta colunas trazem resultados cuja intuição é mais fácil de ser percebida. Nessas colunas utilizaram-se as taxas de crescimento para simular os PIBs municipais em 2006 e comparou-se seu agregado para toda a região com os valores efetivamente observados. Caso não houvesse o maior benefício do Programa Bolsa Família, o PIB do Nordeste em 2006 teria sido algo em torno de 93% e 95,1% do que foi efetivamente observado naquele ano. Da mesma forma, sem as condições privilegiadas para se beneficiar dos aumentos do salário mínimo, o Nordeste teria tido em 2006 um PIB que seria algo em torno de 99% do efetivamente observado.
CONCLUSÕES
Este artigo insere-se na discussão existente sobre os determinantes do maior crescimento do PIB nordestino nos últimos anos, quando se compara à média nacional, utilizando para tal uma abordagem econométrica. Inicialmente fez-se uma síntese dos fundamentos teóricos principais das duas hipóteses que têm sido mais comumente apresentadas como potenciais fontes de explicação. Em seguida, desenvolveu-se um método para confrontar a magnitude relativa dessas duas principais hipóteses e, por fim, estimou-se o impacto relativo de cada uma delas.
As hipóteses confrontadas foram: (i) a região tem se beneficiado relativamente mais dos programas de transferência de renda do Governo Federal, como o Bolsa Família; e (ii) os aumentos do salário mínimo têm tido impacto positivo maior na renda local porque a região tem um percentual maior de pessoas cujo rendimento é influenciado por ele. Apesar de dentro da teoria ortodoxa o impacto de ambas as políticas no crescimento econômico ser negativo, mostrou-se que sob algumas hipóteses plausíveis, como concorrência monopolística, retornos crescentes de escala e maior densidade de capital humano no setor gerador de inovações tecnológicas, elas podem acelerar o crescimento, como geralmente suposto nas discussões.
O teste empírico baseou-se em regressões de crescimento com dados longitudinais, que são padrão na literatura. A amostra incluiu dados por município da região Nordeste. A taxa de crescimento foi calculada entre 2000 e 2006, último ano para o qual havia dados disponíveis na época da elaboração das estimações. Algumas simulações de crescimento contrafactuais, sob hipóteses alternativas, serviram de base para a comparação dos efeitos relativos das duas políticas.
Os resultados indicaram que, conforme previsto pelas teorias apresentadas, o impacto das duas políticas na taxa de crescimento dos municípios nordestinos é positiva e significativamente diferente de zero. Tanto os aumentos do salário mínimo como as transferências via Programa Bolsa Família tiveram impactos positivos no crescimento da região no período analisado. As simulações, por sua vez, indicaram que o efeito do Programa Bolsa Família foi superior ao dos aumentos do salário mínimo. Ou seja, apesar de ambas as políticas terem contribuído para o maior crescimento da região, o Programa Bolsa Família contribuiu mais que o salário mínimo.
As discussões teóricas indicaram que o maior crescimento do PIB da região por decorrência dessas duas políticas é um fenômeno transitório. Ambas estão mudando o patamar de equilíbrio da relação entre o PIB per capita do Nordeste e o do resto do Brasil. Não há razão, contudo, para acreditar que esse novo patamar atingido será muito superior ao que já existe hoje ou que as disparidades serão eliminadas a partir de um movimento de convergência recentemente desencadeado. Se os argumentos teóricos apresentados forem corretos, essa nova relação de equilíbrio entre regiões deverá depender de quanto o salário mínimo e os programas de transferência poderão continuar aumentando. No caso das transferências, elas parecem ter já atingido níveis a partir dos quais a participação delas no PIB não mais se elevará. O salário mínimo, contudo, ainda não deu sinais de que terá uma estabilidade em termos reais, apesar de já começarem a aparecer os primeiros questionamentos sobre sua capacidade de continuar se elevando.16 16 Ver, por exemplo, Giambiagi e Franco (2007).
Submetido: 29/setembro/2009
Aprovado: 13/dezembro/2011.
- ACEMOGLU, D., (2009) "When does labor scarcity encourage innovation?", NBER Working Paper # 14809, NBER, Cambridge MA, Março.
- ALESINA, A. E D. RODRIK, (1994) "Distributive politics and economic growth", Quarterly Journal of Economics, 109(2), 465-490.
- ALESINA, ALBERTO F. E JOSEPH ZEIRA, (2006) "Technology and labor regulations", Harvard Institute of Economic Research Discussion Paper, # 2123, October.
- ASCHAUER, D., (1989) "Does public capital crowd out private capital?", Journal of Monetary Economics, 24, 171-188.
- BARRO, R. E X. SALA-I-MARTIN, (1992) "Convergence", Journal of Political Economy, 100, 223-251.
- BARROS, A., (1993) "Real wages and economic growth: a structuralist hypothesis in an endogenous growth model", Anais do XV Encontro Brasileiro de Econometria, Rio de Janeiro.
- BARROS, A., (1993) "The role of wage stickiness in economic growth", Anais do XXI Encontro Nacional de Economia, Belo Horizonte.
- BARROS, R. P. DE; M. CARVALHO E S. FRANCO, (2006) "A efetividade do salário mínimo como um instrumento para reduzir a pobreza no Brasil". Boletim de Conjuntura, Rio de Janeiro, Ipea, n. 74, Nota Técnica.
- BENABOU, R., (1996) "Inequality and growth", in B. Bernanke and J. Rotemberg (eds.), NBER Macroeconomics Annual 1996, 11-73, Cambridge, MA: MIT Press.
- BJØRNSKOV, C., (2008) "Inequality, tolerance and growth," Working Paper 04-8, Department of Economics, Aarhus School of Business.
- CAHUC, P. , E P. MICHEL, (1996) "Minimum wage unemployment and growth". European Economic Review, p. 1463-1482.
- ERENBURG, S., (1993) "The relationship between public and private investment," The Jerome Levy Economics Institute of Bard College and Eastern Michigan University Working Paper # 85.
- ERENBURG, S. M. WOHAR, (1995) "Public and private investment: are there causal linkages?", Journal of Macroeconomics, 17(1): 1-30.
- GIAMBIAGI, F E S. FRANCO, (2007) "O esgotamento do papel do salário mínimo como mecanismo de combate à pobreza extrema", IPEA, Texto para Discussão nº 1290.
- HICKS, J., (1932) The Theory of Wages, London: Macmillan.
- LUCAS, R., (1988) "On the mechanics of economic development", Journal of Monetary Economics, 22(1): 3-42.
- MARX, K., (1887) Capital, London: Swan Sonnenschein, Lowry & Co.
- NÉRI, G., G. GONZAGA E J. M. CAMARGO, (2001) "Salário mínimo, 'efeito farol' e pobreza", Revista de Economia Política, 21(2): 78-90.
- ROMER, P. , (1990) "Endogenous technological change", Journal of Political Economy, 98(5): 71-102.
- TABELLINI, G. E T. PERSSON, (1994) "Is inequality harmful for growth?", American Economic Review, 84(3), 600-621.
- WHITE, H., (1980) "A heteroscedasticity-consistent covariance matrix estimator and a direct test for heteroscedasticity", Econometrica, 48: 817-838.
 , onde
, onde  é um valor qualquer de salário definido por política pública tal que
é um valor qualquer de salário definido por política pública tal que  ∈
∈ Datas de Publicação
-
Publicação nesta coleção
10 Abr 2013 -
Data do Fascículo
Mar 2013
Histórico
-
Recebido
29 Set 2009 -
Aceito
13 Dez 2011