Abstracts
Though there is widespread agreement that the logarithmic spot and forward rates are both integrated of order one (I(1)) variables, so that their corresponding returns are I(0) stationary, it has been recently claimed that they may be long memory. In this article, we examine this hypothesis by means of fractional integration techniques. The results based on parametric and semiparametric tests show that though fractional degrees of integration are plausible alternatives, the confidence intervals include the unit root case in both series. In addition, the hypothesis of unbiasedness of the forward rate as a forecaster for the future spot rate cannot be rejected for the Australian daily exchange rate market.
spot and forward exchange rates; fractional integration; long memory
Embora haja um acordo difundido de que o ponto logarítmico e as taxas para frente são ambas integradas de variáveis da ordem um (I(1)), de modo que seus retornos correspondentes sejam I(0) estacionário, tem-se reivindicado recentemente que elas podem ser memória longa. Neste artigo, examinamos esta hipótese por meio do uso de técnicas fracionárias de integração. Os resultados baseados em testes paramétricos e semiparametricos mostram que embora os graus fracionários de integração sejam alternativas plausíveis, os intervalos de confiança incluem o caso da raiz unitária em ambas as séries. Além disso, a hipótese de não viés da taxa para frente como um preditor para a taxa a vista futura não pode ser rejeitada para o caso australiano.
taxa a vista e taxa futura; integração fracionária; memória longa
Empirical evidence against the exchange rate anomaly: the Australian case* * The author gratefully acknowledges financial support from the Ministerio de Ciencia y Tecnologia (SEC2005-07657, Spain). Comments of an anonymous referee are also acknowledged. He also thanks Susan Cabo for all her constant support.
Luis A. Gil-Alana** ** Correspondence author: University of Navarre Faculty of Economics, Edificio Biblioteca, Entrada Este, E-31080 Pamplona SPAIN. Phone: 00 34 948 425 625 - Fax: 00 34 948 425 626. Email: alana@unav.es
University of Navarre, Department of Economics, Pamplona, Spain
ABSTRACT
Though there is widespread agreement that the logarithmic spot and forward rates are both integrated of order one (I(1)) variables, so that their corresponding returns are I(0) stationary, it has been recently claimed that they may be long memory. In this article, we examine this hypothesis by means of fractional integration techniques. The results based on parametric and semiparametric tests show that though fractional degrees of integration are plausible alternatives, the confidence intervals include the unit root case in both series. In addition, the hypothesis of unbiasedness of the forward rate as a forecaster for the future spot rate cannot be rejected for the Australian daily exchange rate market.
Key words: spot and forward exchange rates, fractional integration, long memory
JEL Classification: C22
RESUMO
Embora haja um acordo difundido de que o ponto logarítmico e as taxas para frente são ambas integradas de variáveis da ordem um (I(1)), de modo que seus retornos correspondentes sejam I(0) estacionário, tem-se reivindicado recentemente que elas podem ser memória longa. Neste artigo, examinamos esta hipótese por meio do uso de técnicas fracionárias de integração. Os resultados baseados em testes paramétricos e semiparametricos mostram que embora os graus fracionários de integração sejam alternativas plausíveis, os intervalos de confiança incluem o caso da raiz unitária em ambas as séries. Além disso, a hipótese de não viés da taxa para frente como um preditor para a taxa a vista futura não pode ser rejeitada para o caso australiano.
Palavras-chave: taxa a vista e taxa futura, integração fracionária, memória longa
INTRODUCTION
For nearly two decades, the failure of forward exchange rates to forecast future spot rates has posed one of the central puzzles in international finance. Most of the empirical models presume short memory stationarity in both the spot return and the forward premium. However, the current evidence from unit root and cointegration tests appears to lead to conflicting conclusions and, in the last few years, the short memory property of the forward premium has been questioned by many authors (e.g., Baillie and Bollerslev, 1994, Maynard and Phillips, 2001, etc.). They argue that the forward premium is long memory, implying a strong degree of association between the observations. Then, the difference in persistence between the short memory spot return and the long memory forward premium does not admit a valid regression relation in returns, and the slope coefficient in the Fama (1984) regression is found to converge to zero.
In this article we examine the above mentioned issue by using both parametric and semiparametric techniques of long memory processes. Firstly, we use a testing procedure due to Robinson (1994a) that permits us to test the order of integration in raw time series and apply it to the nominal spot and forward daily exchange rates in Australia. This method has several distinguishing features compared with other procedures for testing unit (or fractional) roots. In particular, it has standard null and local limit distributions and this standard (normal) distribution holds independently of the inclusion or not of deterministic regressors and of the different types of I(0) disturbances underlying the process. A semiparametric procedure (Robinson, 1995a) will also be implemented at the end of the article.
The structure of the paper is as follows: section 1 briefly presents the economic foundations. In section 2, we describe the testing procedures. Section 3 contains the empirical application and last section concludes.
1. ECONOMIC FOUNDATIONS
In the following, St denotes the spot exchange rate at time t, while Ft,l refers to the forward exchange rate at time t, for delivery at time t+l. Corresponding logarithmic values are denoted by the lower case variables, st and ft,l respectively. Tests of forward rate unbiasedness provided the original motivation for much of the empirical work behind the forward discount anomaly. The hypothesis of interest states that the forward rate should act as an unbiased forecaster for the future spot rate, i.e.  , which is generally interpreted as a joint test of market efficiency, rational expectations and risk neutrality. Some of the earliest tests of unbiasedness (e.g. Frenkel, 1976) were conducted in exchange rate levels by regressing the future spot rate on the forward rate, i.e.,
, which is generally interpreted as a joint test of market efficiency, rational expectations and risk neutrality. Some of the earliest tests of unbiasedness (e.g. Frenkel, 1976) were conducted in exchange rate levels by regressing the future spot rate on the forward rate, i.e.,
and though the results were promising in terms of the estimate of the slope coefficient, due to the nonstationarity of the series, the results are now interpreted in terms of cointegrating relationships, assuming that both variables are I(1). Thus, following Fama (1984), the most influential tests have been conducted using a regression in returns, in which the spot return (st+l st) is regressed against the forward premium (ft+l st):
Under the null hypothesis of unbiasedness, one would expect an estimate of a close to 0 and b close to 1, but the empirical evidence suggests that the estimate of the slope coefficient is typically negative and significantly different from zero. This result forms the central stylized fact underlying the forward discount anomaly. A large number of studies have tried to explain this anomaly. Engle (1996) proposed four explanations: i) the existence of a foreign exchange risk premium; ii) the peso problem; iii) irrational expectations, and iv) international financial market inefficiency from various frictions, and he focuses mainly on a time varying rational expectations risk premium.1 1 The traditional explanation for the forward discount anomaly emphasizes the behaviour of the expected excess nominal forward foreign exchange payoff: pt = ft Et(st+1). The expected excess nominal forward foreign exchange payoff maybe interpreted as a risk premium and its characteristics are able to determine the sign of the slope coefficient. An alternative explanation is suggested by Baillie and Bollerslev (1994, 2000). They focus on the time series properties of the spot and forward exchange rates and is based on the fact that (2) assumes short memory for the returns, implying that the levels are I(1) when they may be in fact fractionally integrated. In the following section, we propose various procedures for testing I(d) statistical models in raw time series.
2. THE TESTING PROCEDURES
Robinson (1994a) considers a very general testing procedure for testing unit roots and other nonstationary hypotheses in raw time series. Unlike most of unit root tests, which are embedded in autoregressive alternatives, Robinson's (1994a) tests are nested in a fractionally integrated model,
where d is a given real number; ut is an I(0) process, with parametric density function f of form:
where the scalar s2 and the (qx1) vector t are unknown, but g is of known form; and xt is the time series we observe from t=1,2, n. Thus, under the null hypothesis:
xt in (1) is I(d) and the residuals are 
Unless g is a completely known function (e.g., g º 1, as when ut is white noise) we have to estimate the nuisance parameter t, for example by  , where T* is a suitable subset of Rq and
, where T* is a suitable subset of Rq and
The test statistic, (denoted by ), is fully described in Appendix A APPENDIX A . Robinson (1994a) established that under certain regularity conditions:2 2 These conditions are very mild and they are satisfied by the model in (3) and (4).
 ®d N(1,0) as n ® ¥,
®d N(1,0) as n ® ¥,
and thus, an approximate one-sided 100a% test of (4) against the alternative q > 0 rejects Ho if  > za where the probability that a standard normal variate exceeds za is a. Conversely, a test of (4) against q < 0 rejects Ho if
> za where the probability that a standard normal variate exceeds za is a. Conversely, a test of (4) against q < 0 rejects Ho if  < - za. He also showed that the test is efficient in the Pitman sense, i.e., that when directed against local alternatives: Ha: q = d n-1/2 for d ¹ 0, the limit distribution is normal with variance 1 and mean which cannot (when ut is Gaussian) be exceeded in absolute value by that of any rival regular statistic. Thus, we are under standard situations, unlike most of the tests for unit roots, where a nonstandard limit distribution and lack of efficiency theory is obtained.
< - za. He also showed that the test is efficient in the Pitman sense, i.e., that when directed against local alternatives: Ha: q = d n-1/2 for d ¹ 0, the limit distribution is normal with variance 1 and mean which cannot (when ut is Gaussian) be exceeded in absolute value by that of any rival regular statistic. Thus, we are under standard situations, unlike most of the tests for unit roots, where a nonstandard limit distribution and lack of efficiency theory is obtained.
A problem with the parametric procedures is that the model must be correctly specified. Otherwise, the estimates are liable to be inconsistent.3 3 Note, however, that the method described just above has nothing to do with the estimation of the fractional differencing parameter. It merely computes diagnostic departures from the null which may be any real number. In fact, misspecification of the short run components of the process may invalidate the estimation of the long run parameter d. This is the main reason for using also a semiparametric approach.
There are several methods for estimating the fractional differencing parameter in a semiparametric way. Examples are the log-periodogram regression estimate (LPE), initially proposed by Geweke and Porter-Hudak (GPH, 1983) and later modified by Künsch (1986) and Robinson (1995b); the average periodogram estimate of Robinson (APE, 1994b); and a Gaussian semiparametric estimate. (Robinson, 1995a).
Robinson's (1995a) Gaussian semiparametric estimate is basically a local "Whittle estimate" in the frequency domain, using a band of frequencies that degenerates to zero. The estimate ( ) is described in Appendix B
APPENDIX B
.
) is described in Appendix B
APPENDIX B
.
Under finiteness of the fourth moment and other mild conditions, Robinson (1995a) proved that:
where do is the true value of d and with the only additional requirement that m ® ¥ slower than n.4 4 The exact requirement is that (1/m) + ((m 1+2a(log m) 2)/(n 2a)) ® 0 as n ® ¥, where a is determined by the smoothness of the spectral density of the short run component. In case of a stationary and invertible ARMA, a may be set equal to 2 and the condition is (1/m) + ((m 5(log m) 2)/(n 4)) ® 0 as n ® ¥. Robinson (1995a) showed that m must be smaller than n/2 to avoid aliasing effects. We use the Gaussian Whittle estimate because of its computational simplicity. Note that the Gaussian method requires no additional user-chosen numbers in the estimation (as is the case with the LPE and the APE). Also, the estimate is more efficient than the LPE, and we do not assume Gaussianity to obtain an asymptotic normal distribution. A diskette containing the FORTRAN codes for the tests is available from the author on request.
3. THE EMPIRICAL EVIDENCE
The time series data analysed in this section corresponds to the daily nominal spot and forward exchange rates in Australia, obtained from the Midlands Bank for the time period 9.m10.86 10.m3.98. Figure 1 contains plots of the logged series as well as their corresponding correlograms and periodograms. The nonstationary nature of the series becomes apparent in view of the correlograms, (with values decaying very slowly), and also throughout the periodogram, (with a large peak around the smallest frequency).
Figure 2 contains similar plots but based on the first differenced data. We see that the series have now an appearance of stationary, though we still observe significant values in the correlogram even at some lags far away from zero, which may be an indication that some type of differencing greater than or smaller than one in the original series may be more adequate than first differences.
Table 1 resumes the results of  in Appendix A
APPENDIX A
for values d = 0, (0.25), 2 and different types of I(0) ut. In particular, we use white noise, AR and Bloomfield (1973) disturbances. The latter is a nonparametric approach of modelling the I(0) disturbances in which ut is exclusively specified in terms of its spectral density function, which is given by:
in Appendix A
APPENDIX A
for values d = 0, (0.25), 2 and different types of I(0) ut. In particular, we use white noise, AR and Bloomfield (1973) disturbances. The latter is a nonparametric approach of modelling the I(0) disturbances in which ut is exclusively specified in terms of its spectral density function, which is given by:
Like the stationary AR(p) case, this model has exponentially decaying autocorrelations and thus, using this specification, we do not need to rely on so many parameters as in the ARMA processes, which always results tedious in terms of estimation, testing and model specification.
The most noticeable feature observed across Table 1 is that the only value of d where Ho (4) cannot be rejected corresponds to d = 1. Assuming white noise or Bloomfield disturbances, the values of the test statistic monotonically decrease with d. This is something to be expected given that it is a one-sided test statistic. Thus, for example, we would with that if Ho is rejected with d = 0.75 against Ha: q > 0, an even more significant result in this direction should be expected when d = 0.50 or 0.25 are tested. We also observe that if ut is AR, there is a lack of this property for small values of d. This lack of monotonicity could be explained in terms of model misspecification as is argued, for example, in Gil-Alana and Robinson (1997). However, it may also be due to the fact that the AR coefficients are Yule-Walker estimates and thus, though they are smaller than one in absolute value, they can be arbitrarily close to 1. A problem then may occur in that they may be capturing the order of integration by means, for example, of a coefficient of 0.99 in case of using AR(1) disturbances. The last column of the table reports the 95%-confidence intervals of those values of d where Ho cannot be rejected. We see that these intervals are very narrow in both series in case of white noise ut, however, if the disturbances are autocorrelated, they are wider especially for the forward rate. In case of the spot rate, the intervals seem to be centered around 1, while for the forward rate there is an asymmetry in favour of values of d higher than 1, which may be consistent with the results reported in Baillie and Bollerslev (1994) of long memory behaviour in the forward premium.5 5 Other parametric approaches like Sowell's (1992) maximum likelihood estimation in the time domain were also performed and the results were very similar to those based on Robinson's (1994a) approach. This is not surprising if we take into account that Robinson (1994a) is based on the Whittle function, which is an approximation to the likelihood function.
Figure 3 displays the estimates of d based on the Whittle semiparametric approach (Robinson, 1995a). Since the two series are nonstationary, the analysis is carried out based on the first differenced data, adding then 1 to obtain the proper orders of integration of the series. We present the results for the whole range of values of the bandwidth number m, along with the 95% confidence interval corresponding to the I(1) hypothesis.6 6 Some attempts to calculate the optimal bandwidth numbers have been examined in Delgado and Robinson (1996) and Robinson and Henry (1996). However, in the case of the Whittle estimator, the use of optimal values has not been theoretically justified. Other authors, such as Lobato and Savin (1998) use an interval of values for m but we have preferred to report the results for the whole range of values of m. We observe that for the spot rate practically all values are within the I(1) interval, implying thus the existence of a unit root; for the forward rate, however, some values are slightly below 1, though in most cases the unit root null cannot be rejected. In any case, we can conclude the analysis of this section by saying that unit roots are plausible models for these series, and though other fractional orders of integration may also be credible alternatives, the fact that the unit root cannot statistically be rejected suggest that regressions of form as in (2) still remain valid in this context. Thus, performing OLS in (2), the resulting estimates for the intercept and the slope coefficients were respectively 0.0024 and 0.814, and the null hypotheses of a = 0 and b = 1 were not rejected, implying that the hypothesis of unbiasedness cannot be rejected for the Australian economy.
CONCLUSIONS
In this article we have examined the stochastic behaviour of the spot and forward exchange rates in Australia by means of fractional integration techniques. Using both parametric and semiparametric techniques, the results show that the two series contain unit roots. This result is consistent with other empirical works on the exchange rates in other countries. Thus, for example, Gil-Alana (2004) showed that the spot and forward exchange rates in Japan were close to an I(1) process, though fractional alternatives were also plausible in some cases. On the other hand, Gil-Alana (2002) found evidence of I(d) with d < 1 in the forward rate in Canada implying mean reverting behaviour. We finally performed the OLS regression of the spot returns on the forward premium, the results showing that the forward rate may act as a forecaster for the future spot rate in the Australian economy. This result is in apparent contradiction with the forward discount anomaly found in most of the countries. Two arguments can be employed to justify this result: the first one is the daily structure of the data. In a recent study, Hodgson, Linton and Vorkink (2004) use a semiparametric procedure for a seemingly unrelated regression model using weekly and daily exchange rates for Japan, the UK and Canada. Their data strongly reject the unbiasedness hypothesis at a weekly horizon but fail to reject it on the daily data. The second argument is the time period employed in the article. In another recent work, Radalj (2002) finds a negative coefficient for the slope coefficient in the Australian exchange market for the time period 1986-1998, though he was unable to reject the null of a coefficient equal to 1. However, for the time period 1992-1997, the estimated coefficient was about 0.837, being very close to the one obtained in the present paper.
Recebido em junho de 2004. Aceito para publicação em outubro de 2005.
The test statistic proposed by Robinson (1994a) is based on the Lagrange Multiplier (LM) principle, and is given by:
where n is the sample size and
where T* is a compact subset of the Rq Euclidean space. I(lj) is the periodogram of ut evaluated under the null, and g is a known function related to the spectral density of ut, f = (s2/2p)g. Note that these tests are purely parametric and therefore, they require specific modelling assumptions regarding the short memory specification of ut. Thus, if ut is white noise, g º 1, (and thus,  (lj) = 0), and if ut is an AR process of form f(L)ut = et, g = |f(eil)|-2, with s2 = V(et), so that the AR coefficients are a function of t.
(lj) = 0), and if ut is an AR process of form f(L)ut = et, g = |f(eil)|-2, with s2 = V(et), so that the AR coefficients are a function of t.
The estimate of Robinson (1995a) is implicitly defined by:
where m is a bandwidth parameter number.
- Baillie, R. T.; Bollerslev, T. Cointegration, fractional cointegration and exchange rate dynamics. Journal of Finance, 49, p. 737-745, 1994.
- _______. The forward premium anomaly is not as bad as you think. Journal of International Money and Finance, 19, p. 471-488, 2000.
- Bloomfield, P. An exponential model in the spectrum of a scalar time series. Biometrika, 60, p. 217-226, 1973.
- Delgado, Miguel; Robinson, Peter M. Optimal spectral bandwidth for long memory. Statistica Seneca, 6, p. 97-112, 1996.
- Engle, C. The forward discount anomaly and the risk premium. A survey of recent evidence. Journal of Empirical Finance, 3, p. 123-192, 1996.
- Fama, E. Forward and spot exchange rates. Journal of Monetary Economics, 14, p. 319-338, 1984.
- Frenkel, J. A. A monetary approach to the exchange rate: doctrinal aspects and empirical evidence. Scandinavian Journal of Economics, 78, p. 200-224, 1976.
- Geweke, J.; Porter-Hudak, S. The estimation and application of long memory time series models. Journal of Time Series Analysis, 4, p. 221-238, 1983.
- Hodgson, D. J.; Linton, O.; Vorkink, K. Testing forward exchange rate unbiasedness efficiently. A semiparametric approach. Journal of Applied Economics, 7, p. 325-353, 2004.
- Künsch, H. Discrimination between monotonic trends and long-range dependence. Journal of Applied Probability, 23, p. 1025-1030.417, 1986.
- Gil-Alana, L. A. Empirical evidence of the spot and the forward exchange rates in Canada. Economics Letters, 77, p. 405-410, 2002.
- _______. Fractional integration and cointegration in the Japanese exchange rates. Japanese Economy, 32, p. 12-35, 2004.
- Gil-Alana, L. A.; Robinson, P. M. Testing of unit roots and other nonstationary hypotheses in macroeconomic time series. Journal of Econometrics, 80, p. 241-268, 1997.
- Lobato, Ignacio; Savin, N. E. Real and spurious long memory properties of stock market data. Journal of Business and Economics and Statistics, 16, p. 261-283, 1998.
- Maynard, A.; Phillips, P. C. B. Rethinking an old empirical puzzle: econometric evidence of the forward discount anomaly. Journal of Applied Econometrics, 16, p. 671-708, 2001.
- Radalj, K. Systematic risks, speculators and the forward rate puzzle. In: Rizzoli, A.; Jakeman, J. (eds.), Proceedings of the International Conference on Enviromental Modelling and Software, V. 2, Lugano, Switzerland, 2002, p. 556-561.
- Robinson, P. M., Efficient tests of nonstationary hypotheses. Journal of the American Statistical Association, 89, p. 1420-1437, 1994a.
- _______. Semiparametric analysis of long memory time series. Annals of Statistics, 22, p. 515-539, 1994b.
- _______. Gaussian semiparametric estimation of long range dependence. Annals of Statistics, 23, p. 1630-1661, 1995a.
- _______. Log-periodogram regression of time series with long range dependence. Annals of Statistics, 23, p. 1048-1072, 1995b.
- Robinson, Peter M.; Marc Henry. Bandwidth choice in Gaussian semi-parametric estimation of long range dependence. In: Robinson, P. M.; M. Rosenblatt, M. (eds.), Athens Conference on Applied Probability in Time Series Analysis, V. II, New York, 1996, p. 220-232.
- Sowell, F. Maximum likelihood estimation of stationary univariate fractionally integrated time series models. Journal of Econometrics, 53, p. 165-188, 1992.
APPENDIX A
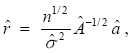
APPENDIX B
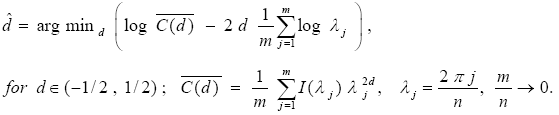
Publication Dates
-
Publication in this collection
29 Aug 2006 -
Date of issue
June 2006
History
-
Received
June 2004 -
Accepted
Oct 2005














