Resumos
O artigo identifica os custos de oportunidade da alocação de efluentes nas áreas plantadas de cana, distantes mais de 2 Km da agroindústria JB, nos meses de safra em que isso não ocorre. Esses custos são obtidos por meio dos valores marginais das variáveis de decisão, provenientes do problema de maximização de benefícios econômicos, resolvido por meio do General Algebraic Modeling System (GAMS) e da análise do dual do problema linearizado. Além disso, simulam-se diferentes coeficientes para os custos de transporte e de tratamento de efluentes para verificação dos efeitos sobre sua alocação e os benefícios associados à mesma. Desta forma, pode-se subsidiar a identificação de taxas e/ou subsídios que favoreçam a alocação dos efluentes em áreas plantadas de cana mais distantes das agroindústrias, proporcionando não só ganhos de produtividade mais disseminados, como também o respeito aos limites de qualidade do rio.
efluentes; fertirrigação; custo de oportunidade
This paper identifies the opportunity costs in effluent allocation over sugarcane crop acres located more than 2Km away from the agroindustry plant JB, during the harvest season. The optimization problem described herein explains why these opportunity costs are usually missed. Actually, these costs derive from the marginal values associated to the decision-making variables concerning an economic benefit maximization problem resolved using the General Algebraic Modeling System (GAMS) and from the dual analysis of the linearized problem therein. Besides, different effluent transportation and effluent treatment cost coefficients were considered in simulating possible impacts and benefits regarding effluent allocation. This approach supports the optimal definition of charging and/or subsidizing schemes best suited to allocate effluents over sugarcane crops located farther away from hub agroindustry plants, not just for more disseminated productivity gains, but also for best compliance with river water quality constraints.
effluents; fertirrigation; opportunity cost
Custos de oportunidade para alocação de efluentes nas áreas plantadas de cana na bacia do rio Pirapama
Bruna da Nóbrega GermanoI; Márcia Maria Guedes Alcoforado de MoraesII; Francisco de Sousa RamosIII
IDepartamento de Economia, Universidade Federal de Pernambuco (UFPE). E-mail: nobrega.bruna@gmail.com
IIDepartamento de Economia, Universidade Federal de Pernambuco (UFPE). E-mail: marciagamoraes@yahoo.com.br
IIIDepartamento de Economia, Universidade Federal de Pernambuco (UFPE). E-mail: ramosfs@gmail.com
Endereço para contato Endereço para contato: DECON - Departamento de Economia - Centro de Ciências Sociais Aplicadas - UFPE Av. dos Economistas, s/n, Cidade Universitária Recife - PE. CEP: 50740-590
RESUMO
O artigo identifica os custos de oportunidade da alocação de efluentes nas áreas plantadas de cana, distantes mais de 2 Km da agroindústria JB, nos meses de safra em que isso não ocorre. Esses custos são obtidos por meio dos valores marginais das variáveis de decisão, provenientes do problema de maximização de benefícios econômicos, resolvido por meio do General Algebraic Modeling System (GAMS) e da análise do dual do problema linearizado. Além disso, simulam-se diferentes coeficientes para os custos de transporte e de tratamento de efluentes para verificação dos efeitos sobre sua alocação e os benefícios associados à mesma. Desta forma, pode-se subsidiar a identificação de taxas e/ou subsídios que favoreçam a alocação dos efluentes em áreas plantadas de cana mais distantes das agroindústrias, proporcionando não só ganhos de produtividade mais disseminados, como também o respeito aos limites de qualidade do rio.
Palavras-Chave: efluentes, fertirrigação, custo de oportunidade
ABSTRACT
This paper identifies the opportunity costs in effluent allocation over sugarcane crop acres located more than 2Km away from the agroindustry plant JB, during the harvest season. The optimization problem described herein explains why these opportunity costs are usually missed. Actually, these costs derive from the marginal values associated to the decision-making variables concerning an economic benefit maximization problem resolved using the General Algebraic Modeling System (GAMS) and from the dual analysis of the linearized problem therein. Besides, different effluent transportation and effluent treatment cost coefficients were considered in simulating possible impacts and benefits regarding effluent allocation. This approach supports the optimal definition of charging and/or subsidizing schemes best suited to allocate effluents over sugarcane crops located farther away from hub agroindustry plants, not just for more disseminated productivity gains, but also for best compliance with river water quality constraints.
Keywords: effluents, fertirrigation, opportunity cost
JEL Classification: C60, C61, O12, O13, O21, L95, Q20, Q21, Q25, Q28
1 Introdução
A modelagem econômico-hidrológica integrada, aplicada na bacia do Rio Pirapama e utilizada neste trabalho, representa a bacia hidrográfica como um todo por meio de uma rede de nós. O objetivo é maximizar os benefícios econômicos para os múltiplos usuários da bacia hidrográfica do rio Pirapama, sujeito às restrições hidrológicas (quantidade e qualidade de água) e institucionais (MORAES; SAMPAIO; CIRILO, 2008a).
Este modelo considera as seguintes categorias de uso: abastecimento humano (AH), abastecimento agroindustrial (AI), geração de energia (GE) e fertirrigação1 1 Fertirrigação é a aplicação de efluentes do processo de produção de açúcar, álcool e aguardente nas lavouras de cana-de-açúcar com o objetivo de fertilização. Esta técnica proporciona um aumento de produtividade médio de 30 ton/ha, economia com fertilizantes, além de possibilitar o descarte de um efluente com alto teor orgânico. (O vinhoto possui uma concentração de 16.400mg/l). Para se ter uma ideia de quão prejudicial é o grau de concentração do vinhoto, basta compará-lo ao do esgoto doméstico, que é de 350 mg/l (VON SPERLING, 1996). (FIR). No entanto, apenas a fertirrigação será aqui tratada, uma vez que busca-se encontrar algumas soluções que visem minimizar o problema da poluição no trecho modelado da bacia do Pirapama, e essa categoria de uso não emprega e nem compromete a água no que se refere ao volume de captação (dado que se utiliza na fertirrigação o vinhoto,2 2 O vinhoto é responsável por um custo social, devido ao alto consumo de oxigênio no seu processo de decomposição. A sua coloração escura dificulta a penetração dos raios solares quando descartado nos recursos hídricos, prejudicando a flora e a fauna aquática (NASCIMENTO, 2003). efluente resultante da produção das destilarias), impactando apenas na qualidade da mesma (idem, 2008b). É importante salientar que se localizam no trecho modelado três destilarias de álcool: a JB, a Sibéria e a Liberdade. Entretanto, serão consideradas apenas as áreas plantadas de cana fertirrigadas pela agroindústria JB, pois é a que apresenta a maior produção de vinhoto e fertirriga um maior número de áreas plantadas de cana.
Pretende-se identificar, com este estudo, os valores dos custos de oportunidade na alocação de efluentes em áreas plantadas de cana, a partir de uma análise de sensibilidade realizada através da solução ótima do problema de maximização (MORAES, 2003).
Ademais, através da simulação de novos valores para os coeficientes de custos de transporte, bem como para os valores dos custos de tratamento e de aspersão de efluentes, pode-se apoiar a adoção de subsídios ou taxas que incentivem a alocação de efluentes nas áreas de cana mais afastadas, favorecendo a manutenção dos índices de qualidade do rio em níveis admissíveis pela legislação.
2 Área de Estudo
Localizada na porção centro-sul da Zona da Mata Pernambucana, a bacia hidrográfica do rio Pirapama ocupa uma área de cerca de 600 km2, abrangendo parte dos municípios de Jaboatão dos Guararapes, Cabo de Santo Agostinho, Ipojuca, Moreno, Escada, Vitória de Santo Antão e Pombos (os quatro primeiros situados na Região Metropolitana do Recife - RMR), sendo o manancial para suprimento de água mais importante em um raio de 40 km da cidade do Recife. É formada por vários afluentes, dos quais se destacam o rio Gurjaú, os riachos dos Macacos, Cajabuçu e Arandu, na margem esquerda, e os riachos Santa Amélia, Utinga de Cima e Camaçari, na margem direita.
Nessa bacia existem 24 grandes indústrias, incluindo o setor agroindustrial (álcool e açúcar), o setor químico, de bebidas, de alimentos, de papéis, têxtil, minerais não metálicos e mecânico. Na sua zona rural, a economia é baseada na monocultura canavieira.
Os principais problemas encontrados no setor de recursos hídricos dessa região são: insuficiente produção de água tratada, elevadas perdas e altos desperdícios, precário atendimento dos sistemas de esgotamento sanitário e de limpeza pública e altos índices de poluentes (RIBEIRO, 2000).
Uma das consequências desses problemas é que os serviços de abastecimento urbano de água da região da bacia do rio Pirapama, feito pela Companhia Pernambucana de Saneamento (COMPESA), vêm passando por racionamento nos últimos anos, implicando um comprometimento da regularidade do atendimento à população, tanto da RMR quanto dos demais municípios, principalmente em épocas de prolongada estiagem (MORAES; CIRILO; SAMPAIO, 2006).
A questão da qualidade da água no rio Pirapama é crítica. Todo o trecho do rio atualmente monitorado apresenta-se em desacordo com os critérios de qualidade da água, ou seja, a maioria dos parâmetros utilizados na classificação do rio está fora dos padrões estabelecidos pela legislação. O reservatório Pirapama, manancial estratégico para o complemento da oferta de água tratada para a RMR, antes de iniciar sua operação, pela inexistência de adutoras, já está em situação de risco com relação a uma possível eutrofização.4 4 Eutrofização é o enriquecimento das águas superficiais por alguns nutrientes, em particular fósforo e nitrogênio, que levam a um grande crescimento de algas e outras espécies vegetais aquáticas. A morte e apodrecimento desta flora aquática provocam um grande consumo do oxigênio dissolvido no corpo d'água, levando os animais à morte por asfixia. O principal fator de estímulo é um nível excessivo de nutrientes no corpo d'água, principalmente nitrogênio e fósforo.
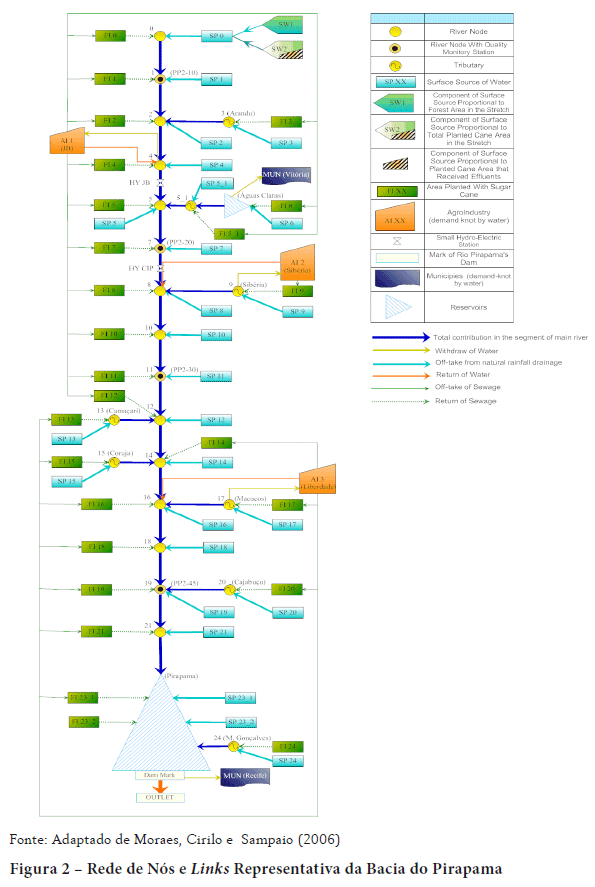
O primeiro trecho da bacia (ver Figura 1), onde o modelo é aplicado, vai da nascente até o reservatório Pirapama, ou seja, se constitui em todo o trecho a montante da barragem.5 5 Este é um trecho de crucial importância, pois nele está concentrada a maioria das agroindústrias localizadas na bacia, cuja produção de efluentes é a principal fonte de carga orgânica nesta área. Além disso, o segmento é responsável por todo o aporte de água afluente ao reservatório Pirapama. Dentre os fatores que levam à ocorrência de poluição no trecho modelado por este estudo, os mais significativos provêm da presença do vinhoto. Ele se constitui num sistema em que são agregados os seguintes elementos: oito principais afluentes, dois reservatórios,6 6 Os dois reservatórios considerados no modelo são Pirapama e Águas Claras. O primeiro já está construído e o sistema de adução está em obras. Já o segundo está na fase de projeto. duas Pequenas Centrais Hidroelétricas -PCH's (PCHJB e PCHCIP), 25 fontes superficiais de água e 25 áreas plantadas de cana (denominadas FIR0 a FIR24),7 7 Áreas plantadas de cana fertirrigadas pelas agroindústrias Sibéria, JB e Liberdade, numeradas de 0 a 24. que demandam lançamentos de efluentes agroindustriais (vinhoto ou vinhaça) para fertilização e consequente aumento da produtividade. Localizam-se, no trecho modelado, três destilarias de álcool: a JB, a Sibéria e a Liberdade. A produção das mesmas, à época da elaboração do Diagnóstico Integrado (DFID, 1999), equivalia a um contingente populacional de 4.2 milhões de habitantes (MORAES; CIRILO; SAMPAIO, 2006).
A única prática atualmente adotada para disposição final do efluente da produção das destilarias (vinhoto) é o aproveitamento na fertirrigação. A questão que vem sendo colocada decorre das observações feitas em campo e principalmente da avaliação dos dados de monitoramento da qualidade da água do rio Pirapama: é que parte deste vinhoto lançado no solo atinge os cursos d'água.
Assim, o modelo não só trata a questão da alocação da água como também a questão da qualidade - crítica para o Pirapama, especialmente depois que foi construído o reservatório -, considerando o uso da fertirrigação. Portanto, busca-se definir a alocação ideal do vinhoto nas áreas plantadas de cana ao longo da bacia, de forma a garantir níveis de qualidade adequados aos usos.8 8 Ao mesmo tempo, na medida em que se inclui o benefício da fertirrigação na função objetivo e as questões da qualidade e quantidade de água tratadas como restrições, o processo está considerando diluição de cargas orgânicas como outro uso, e a disponibilidade será certamente afetada. Em síntese, outros usos deverão ser restringidos para que o rio possa se recuperar através do processo de autodepuração.
A Figura 2 apresenta a rede de nós e links, representativa da configuração atual da oferta e da demanda por água na bacia do Pirapama ao longo do rio no trecho modelado.
3 Fundamentação Teórica do Modelo
A teoria microeconômica clássica prevê um resultado eficiente, dados certos pressupostos sobre formação de preços, definição do produto, condições de custos e barreiras à entrada no mercado. Se um desses pressupostos não for válido, as forças de mercado não poderão operar livremente. Dependendo do pressuposto violado, o resultado poderá ser qualquer uma das inúmeras condições de ineficiência de mercado, denominadas coletivamente como falhas de mercado. Estas incluem concorrência imperfeita, assimetria de informação, bens públicos e externalidades (THOMAS; CALLAN, 2009).
A alocação da água como insumo para a produção de um determinado bem não contabiliza os custos externos impostos à sociedade pela diminuição dessa oferta ou pela sua contaminação. Quando um usuário que está situado a montante de um rio lança poluente ou usa a água de forma inadequada, diz-se que ele impõe ao usuário a jusante uma externalidade negativa.9 9 Se o efeito externo gerar custos (benefícios) a um terceiro será uma externalidade negativa (positiva).
Há, portanto, um efeito de propagação fora da transação de mercado, que não é capturado pelo preço do bem que está sendo negociado. Se o preço não refletir todos os benefícios e custos decorrentes da produção e do consumo não será confiável como mecanismo de sinalização e o mercado falhará. Uma consequência importante é que os recursos escassos serão ineficientemente alocados (idem, 2009). Particularmente, no caso de uma externalidade negativa haverá uma sobrealocação.
Se o mercado for definido em um sentido mais lato, considerando tanto o aspecto de quantidade como o de qualidade das águas, a fonte de falha é o fato de a água, em seus diversos usos, ter características de um bem público.10 10 Um bem público puro é aquele que é não rival no consumo e seus benefícios são não excludentes. Para os diversos usos da água, há diferentes graus de rivalidade e exclusão, e a maioria deles leva à tragédia do uso comum, que surge quando os direitos de propriedade não estão devidamente estabelecidos, resultando, assim, em interações econômicas ineficientes.
A modelagem econômico-hidrológica integrada identifica a alocação ótima através da maximização do benefício agregado líquido, que é a diferença entre o benefício agregado e o custo total, ambos sob a ótica privada (e não social), sujeito às restrições de quantidade e qualidade de águas, agronômicas e institucionais, incorporando nestas últimas a preocupação com os possíveis danos ao bem público. Assim, simula-se uma situação em que os agentes econômicos poderiam atuar livremente em busca de seus interesses privados, pois as restrições para evitar custos externos teriam o cumprimento assegurado.
Alguns autores11 11 Esta ideia foi aplicada por Rosegrant et al. (2000), na bacia do rio Maipo, por Ringler (2001), na bacia do rio Mekong e, posteriormente, por Moraes, Cirilo e Sampaio (2006), na bacia do rio Pirapama. vêm utilizando essa ideia para obter o valor alocativamente eficiente, com os custos externos já devidamente internalizados, na medida em que as restrições necessariamente estariam atendidas.
A partir desta referência (valores ótimos de alocação), poderão ser avaliadas as diversas alternativas de políticas públicas, a saber, as soluções convencionais, por meio do estabelecimento de padrões, bem como as econômicas, por meio dos diversos instrumentos de mercado. Como exemplos, têm-se: através da modelagem, pode-se mensurar impactos econômicos de restrições mais ou menos tolerantes (estabelecimento de padrões) com os diversos resultados de valores dos custos e benefícios de cada um dos agentes; pode-se também simular metodologias de cobrança diferentes e comparar os valores ótimos resultantes, para avaliar a eficiência de cada uma delas, tanto no que se refere à eficiência alocativa como a custo-efetividade (MENDES, 2007).
Deve-se ressaltar que os resultados do problema de otimização não se constituem unicamente nos valores ótimos de alocação de água e efluentes entre os usuários, e seus respectivos benefícios e custos associados. O referido problema, a partir dos seus relatórios de saída, fornece informações adicionais como preços sombra12 12 O preço sombra indica a variação no valor da função objetivo, decorrente da alteração de uma unidade no fator de restrição indicado, mantendo todos os demais coeficientes constantes. e custos de oportunidade. Estes últimos serão avaliados, neste trabalho, no que se refere à questão da alocação dos efluentes nos diversos sites (FIR) de demanda por fertirrigação.
4 Modelagem Econômico-Hidrológica Integrada
O modelo expressa matematicamente a função objetivo do problema de otimização como a diferença entre os benefícios e os custos incorridos pelos múltiplos usuários da água e efluentes da bacia do Pirapama no trecho estudado (MORAES; SAMPAIO; CIRILO, 2008a). Os benefícios brutos são mensurados através da integração das áreas abaixo da curva de demanda (ver seção 5), que correspondem à definição de excedente bruto do consumidor (VARIAN, 2003) na teoria econômica, por usuário/uso, até o valor alocado de água ou efluentes, dependendo do uso. No caso dos efluentes, a alocação é feita em termos de área fertirrigada, ou seja, como a dosagem de efluentes aplicada é fixa (300m3/ha) (ITEP/SUDENE, 1986); a variável de decisão é a quantidade de hectares fertirrigados.
A modelagem obtida para resolver o problema de alocação na bacia do Pirapama pode ser considerada dentro da categoria de sistemas não lineares grandes e complexos, tendo em vista que possui mais de 10.000 variáveis e restrições. O problema foi resolvido (MORAES; CIRILO; SAMPAIO, 2006) utilizando a "modelagem holística" com método de decomposição a partir de temas - usada para integrar modelagem de quantidade e de qualidade -, através de dois submodelos (quantidade e qualidade de água). Para implementar esta abordagem, utilizou-se o método pieceby-piece apresentado em Cai, MCkinney e Landson (2001). Esta abordagem utiliza o General Algebraic Modeling System (GAMS), software de alto nível utilizado para resolução de problemas de programação matemática. A solução de um submodelo é escrita num arquivo e usada como ponto de partida para o próximo submodelo. Isto favorece a identificação de uma solução ótima, pois o problema de Programação Não Linear tem sua performance dependente dos valores iniciais dados às variáveis.
5 Obtenção das Funções de Demanda Inversa e Benefício na Bacia do Pirapama
A estratégia utilizada para obtenção das funções de demanda inversa para cada um dos usuários foi usar valores de elasticidade-preço da demanda por água/efluentes, obtidas em Carrera-Fernandez (1999). Estes valores foram utilizados nos respectivos pontos previstos de demanda, na bacia do Pirapama, para cada modalidade de uso. A partir desses valores e do pressuposto de que eles são constantes,13 13 Embora não acurada, esta premissa é bastante razoável. Há relatos na literatura de que, embora se esperem mudanças na elasticidade à medida que os preços aumentem, não há base confiável para a realização destes ajustes (MORAES; CIRILO; SAMPAIO, 2006). ao longo da curva de demanda, foi obtida a expressão da função de demanda inversa através da resolução de uma equação diferencial simples. Integrando as áreas abaixo das mesmas, obteve-se a função benefício de cada um dos usos. A seguir, descreve-se em detalhes o procedimento desenvolvido por Moraes, Cirilo e Sampaio (2006).
A elasticidade-preço da demanda η é definida por:
onde P é o preço no qual a quantidade observada Q é demandada. Assumida a elasticidade constante, a equação acima foi rearranjada e integrada,
resultando na seguinte função de demanda inversa:
Esta função, dado que as elasticidades-preço são negativas, é uma função exponencial no primeiro quadrante do eixo (P, Q), que é assíntota aos eixos P e Q em direção ao infinito (ver Figura 3). Assim, quando Q tende a zero, o valor de P tende a infinito, e tende a zero quando Q aumenta indefinidamente. Isto representa a realidade teoricamente.
Como tal função demanda impossibilitaria o cálculo dos benefícios brutos associados a uma determinada quantidade, foi necessário adaptar a curva teórica a valores práticos. Para isto, considerou-se um valor não nulo para a quantidade alocada zero, além de considerar os valores absolutos das elasticidades, resultando na expressão:
Esta função traz para valores finitos o valor da água para quantidades alocadas nulas, além de definir uma quantidade alocada na qual o preço tende a zero (consumo autônomo) - observe-se que este é um ponto de indefinição na função, ou seja, é aberto (ver Figura 4). Observe-se também que, para valores maiores que C2, a função volta a ser definida e, como é uma função módulo, volta a ter valores positivos. Na verdade, alocações a partir deste valor não trariam benefícios e sim prejuízos. Como será visto a seguir, o excedente calculado, resultante de uma determinada alocação, será a área abaixo desta curva até o valor alocado. No caso de alocações maiores que o consumo autônomo, a área associada a partir deste ponto será computada como negativa (representando redução no excedente total bruto).
O excedente bruto calculado foi obtido com a integração da função de demanda inversa (equação 3) para valores de Qaloc menores e maiores do que C2, ou seja, a área sob esta curva de demanda de Q = 0 até Q= Qaloc.
Como se trata de uma função módulo, é necessário fazer a seguinte observação:
Assumiu-se, inicialmente, o caso (4). Portanto, para o cálculo do excedente bruto, substituiu-se o módulo da função por (-Qaloc + C2 ), obtendo o seguinte resultado:
Benefício(R$ / seg) =

Benefício(R$ / seg) =

Benefício(R$ / seg) =

Benefício(R$ / seg) =

O excedente bruto está representado pela área hachurada (Figura 5).
Quando se trata de quantidades alocadas acima de C2 ( Qaloc> C2), tem-se que:
Então, de (5) obtém-se:
Benefício(R$ / seg) =

Benefício(R$ / seg) =

Benefício(R$ / seg) =

Benefício(R$ / seg) =

O valor do excedente bruto para valores de Qaloc > C2 está apresentado na Figura 6. Ele foi obtido com a subtração da área sob a curva hachurada em tom mais claro da área que aparece mais escura.14 14 O valor de C2, o chamado consumo autônomo, representa a quantidade alocada a partir da qual a disposição a pagar do usuário tende a zero. Por exemplo, no caso de uma PCH, uma quantidade de água maior do que a capacidade da planta de gerar eletricidade ou, no caso de efluentes (a quantidade alocada aqui seria de terra para fertirrigar), o consumo autônomo seria a área total do site de demanda. A curva de demanda P (q) foi dada em módulo, o que implica que, a partir deste valor, teríamos prejuízo, ou benefício negativo. Isto significa que, se o modelo aloca mais do que o consumo autônomo a um dado usuário, o resultado será prejuízo. Ele estará, por exemplo, jogando uma dosagem maior de efluentes na sua área plantada de cana.
Dessa forma, pode-se perceber que, tanto para valores de Qaloc> C2, como para valores de Qaloc < C2, a função de benefício bruto resultante é a mesma, podendo ser expressa colocando-se um módulo na diferença (C2 -Qaloc), o que a torna:
Para determinar completamente estas funções de demanda inversa dos usuários, é necessária ainda a determinação das duas condições de contorno (C1 e C2). A primeira condição de contorno foi definida como sendo o ponto de operação de cada usuário em valores atuais. Este ponto foi aquele associado às demandas requeridas no ponto de operação atual, cuja ordenada correspondente é o custo médio para a captação (Qreq, Cméd) (ver Figura 7). Dessa forma, os usuários estariam requerendo água até o ponto a partir do qual qualquer acréscimo na quantidade faria o benefício marginal menor do que o custo marginal para obtenção desse adicional.
A segunda condição de contorno veio de estimativas do excedente bruto obtido com as demandas requeridas no ponto de operação atual, que correspondem à área sob a curva que aparece hachurada na Figura 7. Estas estimativas foram obtidas calculando-se os excedentes brutos com a água requerida.
Com essas condições de contorno definidas, foram estimadas as constantes C1e C2 para cada usuário, através das equações (3) e (4) e, consequentemente, determinadas as funções de demanda e as funções de benefício bruto para os usuários da bacia do Pirapama. A função de benefício líquido, também conhecida como excedente líquido do consumidor (VARIAN, 2003), resulta da subtração dos custos incorridos por cada usuário do benefício bruto:
No caso do abastecimento industrial, além desse custo médio, será debitado também um custo adicional, se houver sobras de efluentes. Isto ocorre porque o modelo considera que, caso não seja alocado todo o efluente nas áreas plantadas de cana fertirrigadas pela agroindústria, a mesma deverá arcar com os custos de tratamento dessas sobras. Já para a fertirrigação, além de custos de aspersão do vinhoto, há também economia com os fertilizantes que não precisam ser utilizados e, dependendo do site de demanda a ser fertirrigado, haverá ou não custos com transporte por carros-pipas (ver equação 9 na próxima seção).
5.1 usuários de Fertirrigação
Os usuários de fertirrigação da bacia do Pirapama maximizam sua função de benefício líquido (MORAES; CIRILO; SAMPAIO, 2006), dada por:
As restrições associadas a este problema se referem ao quantitativo de efluentes disponível e à qualidade de águas. As constantes ec1 e C2 assumem valores para cada nó de demanda por efluentes, ao passo que a elasticidade é a mesma (η) . A Áreafirrig (usuário t,) é a área de cana a ser fertirrigada, e deve atender as restrições de quantitativo de efluentes15 15 Quantidade de vinhoto disponível, quantidade de cana plantada e dose de aplicação utilizada. e de qualidade de água.16 16 Níveis de Oxigênio Dissolvido (OD) ao longo do rio, resultantes da decisão de alocar vinhoto. O Cmédio é o custo com aspersão por hectare fertirrigado e o ganho médio, Gmédio, representa a economia com os fertilizantes, relativa à mesma área onde se utilizou o vinhoto, ao invés destes.
O último termo da função de benefício líquido em questão é o custo de transporte do vinhoto. Estes custos incidirão apenas nos nós de demanda, situados mais de 2 km da agroindústria, cuja produção de vinhoto se utiliza no processo. O custo de transporte é dado por:
onde Ccarro_pipa é o custo do carro-pipa17 17 O custo do carro-pipa foi considerado como sendo R$ 6,00/m3, de acordo com dados da COMPESA (MORAES; CIRILO; SAMPAIO, 2006). em R$/m3; Qaloc_vinh (usuário t,) é a quantidade de vinhoto alocada pela agroindústria no nó de demanda no mês de produção, em milhões de m3; o fator 0,25 é o custo por quilômetro (R$/Km), obtido através do produto entre o custo de combustível (R$ 2,00/litro) e o consumo esperado (1/8 litro/km) (MORAES; CIRILO; SAMPAIO, 2006), e dist _ Km usuário() é a distância (Km) do nó de demanda para a agroindústria, cujo efluente se utiliza.
O problema de maximização de benefícios descrito, sujeito às restrições hidrológicas e institucionais, é um problema de Programação Não Linear, que, se for linearizado em torno de um determinado ponto candidato a ótimo, poderia ser representado por:
Max ∑ Bx
Sujeito a: Ax < Q
onde B representa a matriz das derivadas das funções benefício num determinado ponto por quantidade alocada de água/efluentes. No caso da função benefício associada à fertirrigação, a quantidade alocada é de efluentes, e estaria em milhões de reais por unidade de área, sendo a variável de decisão x a área fertirrigada ( Áreafirrig (usuário t ,) em milhares de ha). A é a matriz das derivadas das funçõesrestrição no ponto, associadas a este problema, que, no caso das áreas fertirrigadas, referem-se à qualidade de águas e estará em unidade de concentração de carga orgânica por unidade de área, e Q é o vetor que representa os limites que, no caso das restrições de qualidade de águas, representam limites admissíveis, em unidades de concentração de carga orgânica (mg/l). Este é o problema original (primal).
O dual deste problema linearizado é obtido através de um problema de minimização:
Min ∑QT y
Sujeito a: ATy > BT
onde AT é a matriz transposta de A, em unidades de concentração de carga orgânica por unidade de área, y é o vetor das variáveis de decisão, que, no caso das alocações de área, serão os custos unitários de alocação para cada nó de demanda, em milhões de reais por unidade de concentração de carga orgânica, e BT é o vetor transposto de B, em milhões de reais por unidade de área. Dessa forma, o dual do problema linearizado determinaria os valores mínimos dos custos unitários de alocação de cargas orgânicas incorridos pelos usuários, sujeito às restrições de benefício mínimo.
A descrição deste problema linearizado serve para entender o conceito dos custos de oportunidade para os usuários da fertirrigação. Os mesmos, para as áreas de cana onde não se alocam efluentes, serão estritamente maiores que os valores de B associados (haverá variável de excesso na restrição acima). Portanto, para que essas áreas passem a receber efluentes, será necessário o aumento do benefício associado exatamente do valor da variável de excesso (o chamado custo reduzido ou, no caso não linear, o gradiente reduzido).
O custo de oportunidade dos usuários de fertirrigação, portanto, será a soma do benefício real (no caso não linear da taxa de benefício associado) ao gradiente reduzido (ver equação 11). Os mesmos podem ser obtidos através do relatório de resposta (.lst) fornecido pelo General Algebraic Modeling System (GAMS). Neste relatório,18 18 Para maiores informações acerca do relatório gerado pelo GAMS, consultar Moraes (2003), capítulo 5. os valores ótimos das variáveis de decisão vêm acompanhados de seus valores marginais, que são os gradientes reduzidos ou as variáveis de folga/excesso do dual do problema linearizado descrito anteriormente.
No caso em pauta, o gradiente reduzido, para a variável de decisão (x) do problema primal, é a variável de excesso da restrição do dual do problema linearizado e, portanto, se constituiu no valor a se acrescentar à taxa de variação de benefícios reais, para que uma área passe à condição de fertirrigada. Vale destacar que, quando uma variável apresenta valor nulo na solução ótima, ela apresenta gradiente reduzido diferente de zero, ao passo que, se seu valor ótimo for diferente de zero, a mesma apresenta valores marginais nulos (COLIN, 2007). A partir do valor do gradiente reduzido (a rigor benefício aumentado), somando o mesmo à taxa de variação de benefícios reais por unidade de área alocada, pode-se obter o custo de oportunidade (a rigor benefício de oportunidade), em milhares de reais por ha:
Para obter a taxa de variação de benefícios reais, calcula-se a inclinação da curva de benefício líquido dos usuários que incorrem em custos de transporte no ponto de alocação nula.
6 Resultados
Os resultados obtidos são relativos apenas à questão da alocação dos efluentes produzidos pela agroindústria JB e colocados em áreas plantadas de cana que a abastecem. Ao todo, essa agroindústria fertirriga 13 áreas plantadas de cana (FIR0 a FIR8, FIR10 a FIR12, e FIR5_1). Destas, apenas FIR3, FIR4, FIR5, FIR6, FIR7 e FIR5_1 não incorrem em custos de transporte, pois ficam mais próximas da JB.
O resultado do modelo original mostra que, das áreas que incorrem em custos de transporte, FIR0, FIR1 e FIR2 são as únicas que não recebem efluentes em todos os meses de safra. Já o mês em que não ocorre alocação de vinhoto é o mesmo para estes três nós de demanda - mês 1 (ver 3 (ver Quadro 1).
Em seguida, foram feitas algumas simulações, procedendo assim a uma análise de sensibilidade. É importante salientar que essas simulações foram realizadas considerando-se apenas o submodelo2 (modelo de qualidade), pois com relação ao sub-modelo1 (modelo de quantidade), o efluente é alocado sem considerar restrições de qualidade de águas, e o que se observa é que não há sobras de efluentes a serem tratadas pelas agroindústrias, mesmo sendo fertirrigados apenas os nós de demanda que não incorrem em custos de transporte.
Um ponto relevante, levantado por Moraes, Cirilo e Sampaio (2006), é que o modelo foi concebido como se cada um dos nós de demanda pertencesse a um proprietário diferente, pois, na realidade, não foi levantado nenhum cadastro de propriedade destas áreas e o que se tem informação é de que grande parte das mesmas pertence às próprias agroindústrias.
É importante destacar que as simulações apresentadas no Quadro 1 foram selecionadas dentre as que deram resultados mais significativos. Além disso, considerou-se o objetivo de simular mecanismos de incentivo para reduzir as sobras de efluentes a serem tratadas pela JB, bem como aumentar/proporcionar a alocação de efluentes para os nós de demanda que incorrem em custos de transporte.19 19 Ver resultado da nova alocação de área fertirrigada para os sites de demanda que arcam com custos de transporte, para as simulações 1, 2, 3, 4, 6 e 9, no Anexo A. O resultado das simulações 5, 7 e 8, bem como os resultados para os nós de demanda que ficam próximos da JB, não foram colocados no anexo, pois, nestes casos, o vinhoto é alocado para todos os nós de demanda em todos os meses de safra.
Analisando os resultados das simulações (Tabela 1), verificamos que todas atenderam o objetivo de reduzir as sobras de efluentes a serem tratadas pela JB.
Na simulação 1, apesar de haver redução na sobra de efluentes, o excedente líquido da JB teve uma redução de R$ 50.000,00, pois o aumento no custo de tratamento das sobras mais que compensou a redução das mesmas. A JB continua a não fertirrigar todos os nós de demanda distantes da mesma em todos os meses de safra. Comparado ao modelo original, FIR1 e FIR2 passam a receber vinhoto em todos os meses de safra. Já FIR0 passa a não receber vinhoto também no mês 11. No caso dos nós de demanda FIR11 e FIR12, estes passam a não receber efluentes no mês 1 e no mês 12, respectivamente, ao contrário do resultado do modelo original em que ambos recebiam vinhoto em todos os meses de safra. Na verdade, este aumento no custo de tratamento das sobras, pago pela JB (modifica os valores da função benefício dos agroindustriais), não altera o valor do benefício (real) associado para fertirrigar cada uma das áreas distantes e, portanto, não leva a uma alocação de vinhoto em todas elas, pois o "benefício de oportunidade" de não alocar continua maior que o real.
Com relação à segunda simulação, pode-se mostrar que FIR0 conseguiu cobrir os custos de oportunidade no mês 1, comparado ao modelo original, mas passou a não alcançá-los no mês 12. Já FIR8, que recebia vinhoto em todos os meses de safra, passou a não recebê-los no mês de safra 1. Os custos de oportunidade são, para FIR0 no mês 12 e FIR8 no mês 1, 41,251 e 15,001 milhões de reais por ha, respectivamente.
Observe-se que esses valores refletem pouca informação, pois mensuram o quanto se deveria aumentar a taxa de benefícios apenas daquele mês e daquele nó de demanda, com tudo mais constante, para que a alocação fosse realizada.
Os valores das inclinações (Tabela 2) foram obtidos por meio da taxa de variação da função de benefício líquido, no ponto de alocação nula. Isto foi feito para cada nó de demanda que incorre em custos de transporte, em quaisquer dos meses, para os valores de ganhos médios, custos de aspersão e custos de transporte originais, como está ilustrado a seguir.20 20 O gráfico apresentado mostra apenas o caso de FIR0. Os gráficos para os demais FIR's que incorrem em custos de transporte podem ser encontrados em Germano (2008).
Gráfico 1 - Clique para ampliar
Pode-se verificar que, ainda com relação à simulação 2, a sobra de efluentes a ser tratada pela JB reduz-se relativamente pouco (0,005), mas ainda assim eleva seu benefício líquido em R$ 5.000,00. O benefício social líquido apresenta um aumento de R$ 125.000,00, devido também ao aumento no ganho de economia com fertilizantes dos fertirrigadores.
A simulação 3 mostra que a elevação da taxa de benefícios dos fertirrigantes não é suficiente para que os efluentes sejam alocados em todos os meses de safra: não se aloca em FIR0 (meses 11 e 12), FIR11 (mês 12), nem FIR12 (mês 1). Neste caso, verificamos que tanto FIR1 como FIR2 conseguem cobrir os custos de oportunidade para o mês 1 (modelo original). Já FIR0 consegue cobrir esse custo no mês 1, mas não nos meses 11 e 12 (custo de oportunidade de R$ 41,251 milhões de reais por ha, para cada mês). Com relação a FIR11 e FIR 12, estes não conseguiram cobrir os custos de oportunidade (28,751 e 33,751 milhões de reais por ha, respectivamente) nos meses de safra em questão, diferentemente do resultado original em que ambos recebiam efluentes em todos os meses de safra.
Na simulação seguinte, observamos que há um aumento no excedente líquido da JB de R$ 2.000,00, comparado ao resultado original, devido à redução na sobra de efluente a ser tratada pela empresa. No entanto, o benefício social líquido se reduz (R$ 5.000,00), pois FIR0 não recebe vinhoto nos meses de safra 11 e 12, sendo o único nó de demanda a não se beneficiar em todos os meses de safra da redução no valor do carro-pipa. Os custos de oportunidade associados a esses meses são de 41,251 milhões de reais por ha.
Na quinta simulação, os benefícios líquidos, social e da JB apresentaram variações positivas. Houve uma redução na sobra de efluentes (0,011) e todos os nós de demanda receberam vinhoto em todos os meses de safra. Assim, a combinação de maior economia com fertilizantes e menores custos de transporte consegue elevar os benefícios de todos os fertirrigantes de forma que todas as áreas recebam efluentes, o que garantirá menores custos de tratamento para a JB e uma melhor distribuição da carga orgânica ao longo do rio.
A simulação 6 mostra que os excedentes líquidos se elevam bastante. No caso da JB, esse aumento pode ser explicado pela redução de mais de 50% na quantidade de vinhoto a ser tratada. Já o aumento no excedente social líquido é decorrente, além da melhora no excedente líquido da JB, do aumento no benefício líquido dos fertirrigadores. Apesar disso, não há alocação de vinhoto em todos os meses de safra nos nós de demanda FIR0, FIR1 e FIR12. Assim como no resultado original, FIR0 e FIR1 não recebem vinhoto no mês de safra 1, e FIR12 passa a não cobrir os custos de oportunidade também para este mês. Os custos de oportunidade foram, respectivamente, de 41,251, 20,001 e 33,751 milhões de reais por ha.
A sétima simulação apresenta bastante semelhança com a simulação 5, pois ambas proporcionam mudanças nas mesmas variáveis. Porém, enquanto a simulação 5 varia mais o ganho médio, esta modifica mais o custo do carro-pipa. A única diferença entre estas simulações é que os excedentes líquidos (JB e social) apresentam maiores elevações. Ou seja, essa simulação, além de reduzir a sobra de vinhoto, alocando para todos os nós de demanda em todos os meses de safra, também faz com que o benefício social líquido aumente.
A simulação 8 é semelhante à sexta, mas reduz-se mais o valor do carro-pipa e menos os custos com aspersão. Pode-se verificar que os excedentes líquidos, social e da JB apresentaram elevações mais significativas do que na simulação 6. A redução na sobra de efluentes também foi mais representativa com esta simulação (0,070). Assim, todos os nós de demanda passam a receber efluentes em todos os meses de safra, indicando que todos os fertirrigadores passam a cobrir seus custos de oportunidade nesses meses.
A última simulação mostra que há um aumento no benefício líquido da JB, mesmo com um custo a mais (custo de transporte), o que revela que a queda na sobra de efluentes a ser tratada por essa agroindústria proporciona ganhos maiores do que o prejuízo obtido com o pagamento de 50% do custo de transporte dos fertirrigadores. O benefício social líquido, no entanto, se reduz, pois nem todos os nós de demanda podem se beneficiar em todos os meses de safra da redução no custo de transporte. Os custos de oportunidade são de: 61,881 milhões de R$ por ha, para FIR0 no mês 12, e de 22,501 milhões de R$ por ha, para FIR8 no mês 10.
7 Considerações Finais
Observa-se que variações combinadas de aumentos na economia com fertilizantes e redução nos custos de transporte (simulações 5 e 7) levam à alocação de efluentes em todas as áreas, assim como àquelas em que se conjugam reduções nos custos de transporte e nos custos com aspersão (simulação 8). Comparando as mesmas, verifica-se que a simulação 8 é a melhor delas, pois, além de reduzir significativamente as sobras de efluentes a serem tratadas pela JB, proporciona ganhos de excedentes líquidos mais elevados, tanto para JB como para o social (respectivamente, R$ 59.000,00 e R$ 559.000,00).
Sendo assim, um subsídio de 50% no valor do carro-pipa, juntamente com subsídio no custo de aspersão (simulação 8), apesar de ainda resultar em sobra de efluentes, leva a uma melhor distribuição na alocação de efluentes nas áreas plantadas de cana consideradas no trabalho, sendo feita tanto nas que incorrem em custos de transporte quanto nas que se encontram próximas da JB, além de uma melhora nos excedentes líquidos, social e da JB.
A economia da JB com a redução na sobra de efluentes é da ordem de R$ 59.200,00. Já a economia realizada pelos fertirrigadores, devido à redução no custo de aspersão, é de R$ 63.400,00 e, com relação ao custo de transporte, no resultado original, a maioria dos nós de demanda que incorriam nestes custos, ou não, recebia efluentes em todos os meses de safra ou recebia muito pouco (quase zero), o que não compensaria o pagamento do carro-pipa para fazer o transporte dos mesmos. Com essa simulação, o vinhoto passa a ser alocado em todos os meses de safra para todos os nós de demanda em questão e, portanto, há um aumento nos custos dos fertirrigadores, pois agora eles passam a pagar o custo de transporte, que é de R$ 26.100,00. Dessa forma, os fertirrigadores apresentam uma economia total de R$ 37.300,00 (diferença entre R$ 63.400,00 e R$ 26.100,00), que é menor do que a economia obtida pela JB.
Portanto, sugere-se que, como política ótima, a JB subsidie os fertirrigantes com o pagamento de 50% no valor do carro-pipa, bem como incorra em uma parte dos custos de aspersão para uma melhor distribuição dos efluentes nas áreas estudadas, uma vez que essa medida acarretará um benefício maior para ambos os usuários e ainda levará a condições melhores neste trecho do rio.
(Recebido em dezembro de 2008. Revisões requeridas em agosto de 2009. Aceito para publicação em novembro de 2009).
O autor agradece a bolsa de produtividade do CNPq.
Clique para ampliar

Clique para ampliar

Clique para ampliar

Clique para ampliar

Clique para ampliar

Clique para ampliar

Clique para ampliar

- CAI, X.; MCKINNEY, D. C.; LANDSON, L.S. Piece-by-piece approach to solving large nonlinear water resources management models. Jornal of Water Resources Planning and Management, v. 127, n. 6, p. 363-368, 2001.
- CARRERA-FERNANDEZ, J. Estudo de cobrança pelo uso da água na bacia hidrográfica do Rio Pirapama. Cidade: CPRH, ago. 1999. (Relatório de Consultoria).
- COLIN, E. C. Pesquisa Operacional. 170 aplicações em estratégia, finanças, logística, produção, marketing e vendas Rio de Janeiro: Editora Eletrônica - ARTE & IDÉIA, 2007.
- DFID (Departament for Internacional Development) and CPRH (Companhia Pernambucana do MeioAmbiente). Diagnóstico ambiental integrado da bacia do Pirapama Recife: CPRH, 1999.
- GERMANO, B. N. Identificação do custo de oportunidade para alocação de efluentes nas áreas plantadas de cana na bacia do Pirapama com vistas ao atendimento das restrições de qualidade do rio, através do Modelo Econômico-Hidrológico Integrado Monografia - UFPE, Recife, jul. 2008.
- ITEP; SUDENE. Vinhoto: alternativas de aproveitamento e aspectos sócio-econômicos. Recife: Governo do Estado de Pernambuco, 1986.
- MENDES, B. G. Avaliação da cobrança como mecanismo econômico alocativo na gestão de bacias hidrográficas: o caso da bacia do rio Pirapama. Dissertação (Mestrado) - UFPE, ago. 2007.
- MORAES, M. M. G. A. Modelo Econômico-Hidrológico Integrado para alocação ótima de água em diferentes usos e vinhoto em áreas plantadas de cana na bacia do rio Pirapama. Tese (Doutorado) - UFPE, Recife, jul. 2003.
- MORAES, M. M. G. A. et al. Sistema de Apoio a Decisão Espacial para Gestão de Bacias Hidrográficas Incorporando Modelagem Econômico-Hidrológica Integrada para Alocação de Água: SADEGBHidro. In: SIMPÓSIO DE RECURSOS HÍDRICOS DO NORDESTE, 8, 2006, Gravatá. Anais.. Gravatá: ABRH, 2006b.
- MORAES, M. M. G. A.; CIRILO, J. A.; SAMPAIO, Y. Integração dos componentes econômico e hidrológico na modelagem de alocação ótima de água para apoio a gestão de recursos: uma aplicação na bacia do Pirapama. Revista Economia, v. 7, n. 2, p. 332-364, maio/ago. 2006.
- ______. Apoio a decisão na gestão de recursos hídricos usando modelo econômicohidrológico integrado para alocação ótima de água: uma aplicação na bacia do rio Pirapama. Revista Brasileira de Recursos Hídricos, v. 13, p. 29-42, 2008a.
- ______. Modelo econômico-hidrológico integrado para gestão de bacias hidrográficas: abordagem piece-by-piece para incorporar a capacidade de autodepuração dos rios e limites de trofia dos reservatórios. Revista Brasileira de Recursos Hídricos, v. 13, p. 43-56, 2008b.
- NASCIMENTO, C. L. Avaliação econômica do aproveitamento do vinhoto concentrado como fertilizante. Disponível em: <http://www.uenf.br/Uenf/Downloads/POSENGPRODUCAO_2397_1213390120.pdf>. Acesso em: 07 nov. 2007.
- RIBEIRO, M. M. R. Alternativas para a outorga e a cobrança pelo uso da água Tese (Doutorado) - UFRS, Porto Alegre, jan. 2000.
- ROSEGRANT, M. W. et al. Integrated Economic-Hydrologic Water Modeling at the basin scale: the Maipo River Basin. Agricultural Economics, v. 24, n. 1, p. 33-46, 2000.
- THOMAS, J. M.; CALLAN, S. J. Economia ambiental: fundamentos, políticas e aplicações. São Paulo: Cengage Learning, 2009.
- VARIAN, H. R. Microeconomia - princípios básicos. Rio de Janeiro: Campus, 2003.
- VON SPERLING, M. Introdução à qualidade das águas e ao tratamento de esgotos Belo Horizonte: Editora da UFMG, 1996. v. 1.
Anexo A
ANEXO A
Endereço para contato:
Datas de Publicação
-
Publicação nesta coleção
20 Set 2010 -
Data do Fascículo
Set 2010
Histórico
-
Revisado
Ago 2009 -
Recebido
Dez 2008 -
Aceito
Nov 2009