Abstracts
Consumers surveys are conducted very often by many companies with the main objective of obtaining information about the opinions the consumers have about a specific prototype, product or service. In many situations the goal is to identify the characteristics that are considered important by the consumers when taking the decision of buying or using the products or services. When the survey is performed some characteristics that are present in the consumers population might not be reported by those consumers in the observed sample. Therefore, some important characteristics of the product according to the consumers opinions could be missing in the observed sample. The main objective of this paper is to show how the amount of characteristics missing in the observed sample could be easily estimated by using some Bayesian estimators proposed by Mingoti & Meeden (1992) and Mingoti (1999). An example of application related to an automobile survey is presented.
species problem; Bayesian estimators; maximum likelihood; consumers survey
Pesquisas de mercado são conduzidas freqüentemente com o propósito de obter informações sobre a opinião dos consumidores em relação a produtos já existentes no mercado, protótipos, ou determinados tipos de serviços prestados pela empresa. Em muitas situações deseja-se identificar as características que são consideradas importantes pelos consumidores no que se refere à tomada de decisão de compra do produto ou de opção pelo serviço prestado pela empresa. Como as pesquisas são feitas com amostras de consumidores do mercado potencial, algumas características consideradas importantes pela população podem não estar representadas nas amostras. O objetivo deste artigo é mostrar como a quantidade de características presentes na população e que não estão representadas nas amostras, pode ser facilmente estimada através de estimadores Bayesianos propostos por Mingoti & Meeden (1992) e Mingoti (1999). Como ilustração apresentamos um exemplo de uma pesquisa de mercado sobre um modelo de automóvel.
estimação de espécies; estimadores Bayesianos; máxima verossimilhança; pesquisas de mercado
HOW TO ESTIMATE THE AMOUNT OF IMPORTANT CHARACTERISTICS MISSING IN A CONSUMERS SAMPLE BY USING BAYESIAN ESTIMATORS
Sueli A. Mingoti
Department of Statistics
Universidade Federal de Minas Gerais
e-mail: sueli@est.ufmg.br
Abstract
Consumers surveys are conducted very often by many companies with the main objective of obtaining information about the opinions the consumers have about a specific prototype, product or service. In many situations the goal is to identify the characteristics that are considered important by the consumers when taking the decision of buying or using the products or services. When the survey is performed some characteristics that are present in the consumers population might not be reported by those consumers in the observed sample. Therefore, some important characteristics of the product according to the consumers opinions could be missing in the observed sample. The main objective of this paper is to show how the amount of characteristics missing in the observed sample could be easily estimated by using some Bayesian estimators proposed by Mingoti & Meeden (1992) and Mingoti (1999). An example of application related to an automobile survey is presented.
Keywords: species problem; Bayesian estimators; maximum likelihood; consumers survey.
Resumo
Pesquisas de mercado são conduzidas freqüentemente com o propósito de obter informações sobre a opinião dos consumidores em relação a produtos já existentes no mercado, protótipos, ou determinados tipos de serviços prestados pela empresa. Em muitas situações deseja-se identificar as características que são consideradas importantes pelos consumidores no que se refere à tomada de decisão de compra do produto ou de opção pelo serviço prestado pela empresa. Como as pesquisas são feitas com amostras de consumidores do mercado potencial, algumas características consideradas importantes pela população podem não estar representadas nas amostras. O objetivo deste artigo é mostrar como a quantidade de características presentes na população e que não estão representadas nas amostras, pode ser facilmente estimada através de estimadores Bayesianos propostos por Mingoti & Meeden (1992) e Mingoti (1999). Como ilustração apresentamos um exemplo de uma pesquisa de mercado sobre um modelo de automóvel.
Palavras-chave: estimação de espécies; estimadores Bayesianos; máxima verossimilhança; pesquisas de mercado.
1. Introduction
The new vision about quality control and the increasing competition among the companies have required a constant monitoring of the consumers market. The clients opinions have taken a fundamental part in the decisions about the type of new products that should be introduced into the market in order to satisfy their present or future needs or about some changes the product should suffer in order to be more attractive to the consumer. The word "product" here is used in a very general sense and it could mean a manufactured item or a service offered by a company, a person or a device.
Many surveys are conducted with the main objective of identifying the important characteristics that the product should have in order to fulfil the expectations of the potential consumers. Usually, the product (a prototype, an initial conception or the product unit) is presented to the clients and they are asked to give their opinion about the characteristics of the product they would consider more important for taking a decision of buying it or using it. The typical result of this kind of survey is a certain number of distinct characteristics reported as important by the consumers. Because of the fact that only a portion of the universe of consumers is interviewed some important characteristics may not appear in the observed sample. Therefore, one point of interest is to estimate the total number of distinct characteristics that are missing in the observed sample of clients. If this number is large, it means that a new sample should be taken from the universe of clients in order to improve the quality of the information about the opinion the consumers have about the specific product.
In this article we present a possible solution for this kind of estimation. The situation will be treated as a particular case of the well-known "species-problem" in Statistics (Bunge, Fitzpatrick & Handley, 1993). The word "species" can be taken as a general terminology and does not have to mean exactly an animal or plant species for example. It describes basically the possible categories of the population. Therefore, any distinct characteristic mentioned by a client can be considered as a "species". The estimators considered in this paper are those proposed by Mingoti & Meeden (1992) and Mingoti (1999).
2. Basic Estimators
In this section we present the estimators proposed as a solution for the problem addressed in the previous section. Let's suppose that the sample consists of n consumers randomly chosen from the universe of N consumers. Each individual of the sample would report a certain number of distinct characteristics that he or she believes is important in the product that is being evaluated. In the end of the study there will be a total of s' different characteristics mentioned by a number of different people. Every characteristic could be mention more than once. Let ni be the number of characteristics that were mentioned exactly by i individuals of the sample, i=1,2, ,n. Therefore,  ni = s'. Let S be the true number of distinct characteristics that the universe of clients would consider as important in the product. The true value of S is unknown and has to be estimated. The number s' observed in the sample is an estimate for S. However, it has been proved that S is usually underestimated by s'. Some estimators have been proposed to correct the bias of s' and to obtain better results. Mingoti & Meeden (1992) and Mingoti (1999) proposed some Bayesian estimators which in general give better results than s', and other classical estimators such as Jackknife (Heltshe & Forrester, 1983) and Bootstrap (Smith & van Belle, 1984). They are very simple to use and will be defined next.
ni = s'. Let S be the true number of distinct characteristics that the universe of clients would consider as important in the product. The true value of S is unknown and has to be estimated. The number s' observed in the sample is an estimate for S. However, it has been proved that S is usually underestimated by s'. Some estimators have been proposed to correct the bias of s' and to obtain better results. Mingoti & Meeden (1992) and Mingoti (1999) proposed some Bayesian estimators which in general give better results than s', and other classical estimators such as Jackknife (Heltshe & Forrester, 1983) and Bootstrap (Smith & van Belle, 1984). They are very simple to use and will be defined next.
2.1 The Empirical Bayesian Estimators (Mingoti & Meeden, 1992)
Let n1 be the number of distinct characteristics that were mentioned by only one person in the sample. Then, the Empirical Bayes estimator for the true value of S is given by  which is defined as
which is defined as
where G (.) is the Gamma function and the constants a > 0, b > 0, are the parameters of a Beta distribution used in the technical construction of the estimator  to describe the probabilistic behavior of the unknown value of pi , which is defined as the probability that the characteristic si will be mentioned by a person who belongs to the universe of clients, i = 1, 2, , S. Given S, the probabilities p1 , p2 , , pS are assumed to be independent and identically distributed random variables from the Beta density function.
to describe the probabilistic behavior of the unknown value of pi , which is defined as the probability that the characteristic si will be mentioned by a person who belongs to the universe of clients, i = 1, 2, , S. Given S, the probabilities p1 , p2 , , pS are assumed to be independent and identically distributed random variables from the Beta density function.
It can be proved that when a approaches to zero the estimator  approaches to the estimator
approaches to the estimator  * given by
* given by
where  is the Digamma function. By using well-known properties of the Digamma function the estimator
is the Digamma function. By using well-known properties of the Digamma function the estimator  * can also be expressed as
* can also be expressed as
The value of a close to zero is related to populations that have many characteristics that are more difficult to be observed in the sample. In the species terminology they are the so-called "rare species". The meaning of "rare" here is the same as that used by Mingoti & Meeden (1992) and Mingoti (1999) and basically it represents the difficulty of observing the species (characteristic) when a sampling procedure is used, not necessarily caused by the rarity of the characteristics in the spatial or abundance sense but also caused by the limitations of the operational procedure used to collect the sample of the population. In the business terminology these characteristics would be representing a part of the consumer's population that has more particular kind of opinion or taste about the product, or in other words it could be represent the part of the market that have an opinion more different than the majority of the population.
To make the estimators  and
and  * more appealing for the practical users Mingoti & Meeden (1992) had shown that the parameters a, b of the Beta distribution can be estimated by using the following procedure: considering that given the value of s' the random vector (n1 , n2 ,¼ , nn) has a multinomial distribution with parameter vector (q1 , q2 ,¼ , qn),
* more appealing for the practical users Mingoti & Meeden (1992) had shown that the parameters a, b of the Beta distribution can be estimated by using the following procedure: considering that given the value of s' the random vector (n1 , n2 ,¼ , nn) has a multinomial distribution with parameter vector (q1 , q2 ,¼ , qn), , where
, where
then the maximum likelihood estimators of the parameters (a , b) could be achieved by maximizing the likelihood function (n1 , n2 ,¼ , nn / s') with respect to a and b, where
which is also well-defined for a ® 0 (Mingoti & Meeden, 1992).
It is interesting to notice that both estimators depend upon the value of n1 which is clearly related to the amount of "rare" characteristics presented in the universe of clients. If n1 is large there is an indication that the population has a large number of rare characteristics, or in other words a large amount of characteristics present in the population is expected to be missing in the observed sample.
More technical details about the construction of these two estimators and their performance in general situations can be found in Mingoti & Meeden (1992).
2.2 The Bayesian Estimators (Mingoti, 1999)
An admissible estimator for the true value of S is given by Sp which is defined as
where
The estimator Sp is derived under the assumption that given the value of S the probabilities p1 , p2 ,¼ , pS are independent and identically distributed according to a Beta distribution with parameters (a, b), a > 0, b > 0, where pi is defined as in the Empirical Bayesian estimators, i=1,2, ,S. The constants (R > 0, 0 < q < 1) are related to a Negative Binomial distribution (Taylor, Woiwod & Perry, 1979) used as a prior distribution for the true value of S in the steps of construction of the estimator Sp. The parameter q represents the prior probability that any distinct characteristic will be mentioned by a typical person of the population or in other words, is the proportion of distinct characteristics in the population. The constant g0 represents the difficulty of observing any characteristic of the population when a sampling procedure is used. Values of g0 close to one describe populations where a large number of distinct characteristics are expected and they are difficult to be observed in the sample or in other words, probably many of them would not be mentioned by any person in the sample. For this kind of population the value of s' will be much lower than the true value of S. Mathematically speaking, g0 is expressed as
For fixed values of R and q the estimator Sp is an increasing function of g0 and when g0 ® 1 this estimator converges to:
The parameters a and b have the same meaning as in the Empirical Bayesian estimators and they can be estimated by maximizing the likelihood function in equation (2.5) as described before. Therefore, an estimator of g0 is easily obtained. According to a "ad-hoc" procedure suggested by Mingoti (1999) the parameters (R,q) can be easily estimated by using the sample quantities Rs=[n/s'], qs=n1/s', respectively, where [w] denotes the largest integer less than or equal to w. If w is less than 1 then RS is taken as equal to 1. When the value of qS is large the researcher should expect a large number of spatially "rare" characteristics in the population. In this case the choice of the parameter R would be related to the expected number of "rare" characteristics that would be found if the whole (N n) unsampled individuals were interviewed.
It is interesting to notice that the estimators Sp and 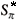 do not depend upon the value of N and therefore they can be used even in situations where N is unknown or very large. The estimator
do not depend upon the value of N and therefore they can be used even in situations where N is unknown or very large. The estimator  * also has this property. However, the fact that it is unbounded gives an advantage to Sp and
* also has this property. However, the fact that it is unbounded gives an advantage to Sp and  * estimators which are always bounded for 0 £ q < 1.
* estimators which are always bounded for 0 £ q < 1.
The Bayesian estimators presented in this paper are very well discussed in the given references and the steps used to derive them will not be shown in this paper. Our main purpose is to show how they can be easily applied in the industrial field.
3. Example
An automobile model was shown to a total of n = 274 different individuals which were asked to identify the characteristics of the car that they felt to be more important in the decision process of buying a car. A total of s' = 108 different characteristics were mentioned by the consumers. Table 1 presents the distribution of the characteristics observed in the sample, according to the values of the number of people who had mentioned them. About 54% of the distinct characteristics were mentioned only by one person and 19% were mentioned by only two people. By using the methodology described in section 2 to estimate the parameters (a , b) we obtain the estimated value  0 = 0.5802. Since the value of population size of consumers N is unknown in this case the estimators described in equations (2.6) and (2.9) would be appropriated. The estimated values of the parameters (R,q) are:
0 = 0.5802. Since the value of population size of consumers N is unknown in this case the estimators described in equations (2.6) and (2.9) would be appropriated. The estimated values of the parameters (R,q) are:
Therefore, the estimated values of the total amount of distinct characteristics of the automobile that would be mentioned by the whole population of clients are given by:
Because of the fact that the estimated probability
0 is not close to one, the more appropriated estimate for this data set would be Sp = 158 and the estimated amount of characteristics missing in the sample would be 50. Therefore, the sample of n=274 people had showed about 68% of the distinct characteristics of the automobile which were important for the investigated consumers population. The value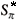 would work as an upper bound.
would work as an upper bound.
As another illustration of the procedures described in this paper and also to motivate their practical use we have selected 30 random samples of sizes n=10, 20 and 55, from the group of 274 individuals. Therefore, in this application we are considering the 274 individuals as our population of consumers (N=274). For each sample we used the estimators  ,
,  *, Sp,
*, Sp, 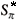 to estimate the true value of S = 108 characteristics. Tables 2 and 3 show the observed average results from the selected samples as well the mean error (ME) and the square root of the mean square error (SRMSE). The methods used to estimate the parameters a , b , R and q were the likelihood and the "ad-hoc" procedures described in section 2.0. It can be seen that the estimators
to estimate the true value of S = 108 characteristics. Tables 2 and 3 show the observed average results from the selected samples as well the mean error (ME) and the square root of the mean square error (SRMSE). The methods used to estimate the parameters a , b , R and q were the likelihood and the "ad-hoc" procedures described in section 2.0. It can be seen that the estimators  , Sp ,
, Sp , 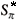 performed very well to estimate the true value of S even for a small sample fraction. The worst result was obtained by
performed very well to estimate the true value of S even for a small sample fraction. The worst result was obtained by  * which was expected because this estimator is strongly dependent upon the assumption of g0® 1 what might be appropriated for many ecological populations but not necessarily for human populations, specially in opinion polls or consumers research. The values of the Mean Error show that all four estimators are biased. For the 3.65% sample fraction the estimators
* which was expected because this estimator is strongly dependent upon the assumption of g0® 1 what might be appropriated for many ecological populations but not necessarily for human populations, specially in opinion polls or consumers research. The values of the Mean Error show that all four estimators are biased. For the 3.65% sample fraction the estimators  , Sp underestimated the true value of S and
, Sp underestimated the true value of S and  *,
*, 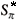 , overestimated. For the others sample fractions the true value of S was overestimated for all estimators except Sp . For all the sample fractions considered, the SRMSE values were not too high. Finally, this illustration shows that probably the estimators
, overestimated. For the others sample fractions the true value of S was overestimated for all estimators except Sp . For all the sample fractions considered, the SRMSE values were not too high. Finally, this illustration shows that probably the estimators  , Sp ,
, Sp , 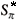 will be more appropriated for the estimation of S in consumer's research than the estimator
will be more appropriated for the estimation of S in consumer's research than the estimator  *
*
In Mingoti's paper (1999) a more general simulation study was performed considering several data sets and the estimators  ,
,  *, Sp ,
*, Sp , 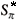 were compared. It was shown that in general these four estimators had a very good performance for many different types of sample fraction, being good alternatives to estimate S.
were compared. It was shown that in general these four estimators had a very good performance for many different types of sample fraction, being good alternatives to estimate S.
4. Final Remarks
The purpose of this article was to show how the estimators that are usually used in ecological situations can also be used to solve a problem in the industrial field. A simple adaptation of the terminology and the concepts involved are necessary. It is important to point out that the proposed estimators give only information about the expected number of missing characteristics in the sample that can be present in the universe of clients. However, they do not tell us the nature of these characteristics. Therefore, in practical situations if the estimated number of unobserved characteristics is too high, two main decisions can be taken: the first one refers to a careful analysis of the quality of the sampling procedure used to obtain the sample. It may happen that the sample was not very representative of the population of consumers or some other problems had occurred in collecting the data. If that is not the case, the second decision would be to take a new sample of clients of the same population with the purpose of investigating the nature of the missing characteristics (new characteristics) because they might be representing an important and distinct part of the target market of the product.
Finally, in Mingoti's paper (1999) a more general estimator for S was presented which enables the researcher to use other prior distributions than the Beta and the Negative Binomial. Therefore, if there is some previous information about S or g0 , then the researcher could use other distributions to describe their probabilistic behavior. We suggest the reader to take a look in Mingoti's paper for more details.
5. Acknowledgement
The author was partially supported by the Brazilian Institution CNPq.
Bibliography
- (1) Bunge, J.; Fitzpatrick, M. & Handley, J. (1993). Estimating the number of species: a review. Journal of the American Statistical Association, 88, 364-373.
- (2) Heltshe, J.F. & Forrester, N.E. (1983). Estimating species richness using the jackknife procedure. Biometrics, 39, 1-12.
- (3) Mingoti, S.A. & Meeden, G. (1992). Estimating the total number of distinct species using presence and absense data. Biometrics, 48, 863-75.
- (4) Mingoti, S.A. (1999). Bayesian estimator for the total number of distinct species when quadrat sampling is used. Journal of Applied Statistics, 26(4), 463-477.
- (5) Smith, E.P. & van Belle, G.V. (1984). Nonparametric estimation of species richness. Biometrics, 40, 119-29.
- (6) Taylor, L.R.; Woiwod, I.P. & Perry, J.N. (1979). The negative binomial as a dynamic ecological model for aggregation and the density dependence of k. Journal of Animal Ecology, 48, 289-304.
Publication Dates
-
Publication in this collection
24 Apr 2002 -
Date of issue
June 2001















