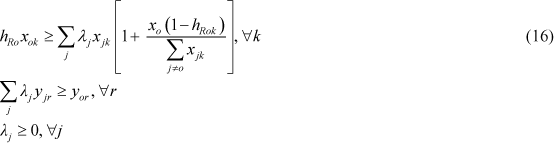Uniformização da fronteira eficiente em modelos de análise de envoltória de dados com ganhos de soma zero e retornos constantes de escala

Uniformização da fronteira eficiente em modelos de análise de envoltória de dados com ganhos de soma zero e retornos constantes de escala

Eliane Gonçalves GomesI, ^*; João Carlos Correia Baptista Soares de Mello^II; Marcos Pereira Estellita Lins^III

^IEmpresa Brasileira de Pesquisa Agropecuária (Embrapa) – SGE; Brasília – DF; [e-mail]

^IIDepartamento de Engenharia de Produção; Universidade Federal Fluminense (UFF); Niterói – RJ; [e-mail]

^IIIPrograma de Engenharia de Produção; Universidade Federal do Rio de Janeiro (UFRJ); Rio de Janeiro – RJ; [e-mail]

RESUMO

Nos modelos DEA com Ganhos de Soma Zero (DEA-GSZ) a restrição dos modelos DEA clássicos de total liberdade de produção ou de uso dos recursos é substituída pela restrição de soma total constante de inputs ou outputs. Neste artigo são apresentados o modelo DEA-GSZ com retornos constantes de escala (DEA-GSZ CCR) e um estudo de caso sobre a realocação do número de aprovados em um concurso vestibular.

Palavras-chave: DEA; ganhos de soma zero; retornos constantes de escala; realocação da produção.

ABSTRACT

When using Zero Sum Gains DEA models (ZSG-DEA), classical DEA models restriction of total freedom of production or resources use is replaced by the constant sum of inputs or outputs restriction. In this paper we develop ZSG-DEA models with constant returns to scale (ZSG-DEA CCR) and employ it in the reallocation of the quantity of approved students in the "vestibular".

Keywords: DEA; zero sum gains; constant returns to scale; production reallocation.

1. Introdução

Uma suposição existente nos modelos de Análise de Envoltória de Dados (Data Envelopment Analysis – DEA) clássicos (Cooper et al., 2000; Estellita Lins & Angulo Meza, 2000; Coelli et al., 1998; Charnes et al., 1994) é a total liberdade de produção ou de uso dos recursos, ou seja, a produção ou o uso dos recursos de uma unidade de tomada de decisão (Decision Making Unit – DMU) não interfere na produção ou no uso dos recursos das demais. Em alguns casos, porém, essa liberdade não existe.

Nos modelos DEA chamados de Modelos DEA com Ganhos de Soma Zero (DEA-GSZ) (Gomes, 2003), uma DMU ineficiente que busque a fronteira pelo aumento de outputs (redução de inputs) imputará às demais a redução do valor de seus outputs (ou aumento de seus inputs) de modo a manter a soma total constante. Assim, os modelos DEA-GSZ têm aplicação direta nos estudos de alocação ou (re)alocação de recursos (ou de produção), em que a restrição de soma constante seja uma necessidade da modelagem. A solução desses modelos depende da estratégia de redistribuição adotada (redistribuição igual, proporcional etc.). Por exemplo, na estratégia de redução proporcional, para que a DMU que busca eficiência ganhe determinada quantidade de output (perca quantidade de input), todas as demais DMUs devem perder quantidade de output (ganhar quantidade de input) proporcionalmente ao seu valor original, de modo que a soma das perdas seja igual ao ganho para que a soma seja mantida constante. Dessa forma, quem tem menos output (input) perde (ganha) menos; quem tem mais output (input) perde (ganha) mais.

Em Gomes (2003), Estellita Lins et al. (2003), Gomes et al. (2003a, 2003b, 2001), Gomes & Soares de Mello (2002) são formulados os modelos DEA-GSZ com retornos variáveis de escala (DEA-GSZ BCC), inspirado no modelo DEA BCC clássico (Banker et al., 1984). Nestas referências são apresentadas as formulações gerais para o caso de uma única DMU ou de várias (em cooperação) em busca de eficiência, ou seja, alcance da fronteira pela redução de inputs ou incremento de outputs. Para o caso do uso de estratégia proporcional, são demonstrados teoremas que permitem a simplificação do modelo geral de Programação Não Linear Multiobjetivo, reduzindo-o a um problema de programação linear clássico, acrescido da resolução de uma equação algébrica linear.

Estes modelos têm sua aplicação prática em qualquer estudo de caso que envolva a necessidade de (re)alocação dos recursos ou da produção, de modo que o total existente não possa ser alterado. No caso do modelo orientado a recursos, um exemplo é aquele em que o input é a quantidade de servidores públicos (médicos, professores, policiais etc.) alocados a uma determinada atividade. Se para atingir eficiência uma DMU tiver que reduzir a quantidade de pessoal, esses servidores deverão ser realocados a outras unidades, já que possuem estabilidade no emprego.

No caso de competições, por exemplo, se for considerado como output um índice que agrega seus resultados (Soares de Mello et al., 2001a; Gomes et al., 2001), a melhora de posição de qualquer competidor implica na perda de posição de um ou mais de seus adversários. Nesse caso, um modelo DEA-GSZ (CCR ou BCC) orientado a outputs teria aplicação imediata.

Em Gomes (2003) é apresentado o emprego do modelo DEA-GSZ para realocar as emissões de CO₂ entre os países do mundo, com base nos mecanismos do Protocolo de Kyoto. Esse é um caso de análise de eficiência com a presença de outputs indesejáveis, em que os modelos DEA-GSZ tornam-se bastante úteis na determinação de diretrizes para as unidades em avaliação, já que a soma das quantidades produzidas por todas as DMUs deveria ser o limite máximo permitido. Logo, qualquer DMU que busque a fronteira aumentando a quantidade desse output deverá impor a perda dessa quantidade pelas demais.

Neste artigo é apresentado o modelo DEA-GSZ com retornos constantes de escala (DEA-GSZ CCR), que toma como o base o modelo DEA CCR clássico (Charnes et al., 1978). São apresentadas as formulações gerais para os casos de orientação a inputs e outputs, com e sem restrições aos pesos dos multiplicadores, para situações de uma única DMU em busca de eficiência, ou de várias DMUs atuando em cooperação.

É ainda mostrado que para o caso CCR, a estratégia de alcance da fronteira não é livre; é determinada pelas equações da fronteira. Desta forma, mostra-se que no modelo DEA-GSZ CCR, para que seja mantida a composição da fronteira eficiente, a menos da DMU que busca eficiência, o uso da estratégia proporcional é obrigatório.

Para ilustrar a aplicação prática destes modelos é apresentado o estudo de caso sobre a realocação/redistribuição do número de aprovados em um concurso vestibular. As DMUs do modelo DEA são os municípios do Estado do Rio de Janeiro que tiveram alunos aprovados no vestibular da Universidade Federal Fluminense: o número total de aprovados é igual ao número de vagas, que é constante. Como resultado do modelo DEA-GSZ CCR será obtida a distribuição justa de aprovados por município, de modo que todos os municípios sejam 100% eficientes. Os dados utilizados são os mesmos de Soares de Mello et al. (2001b).

Deve-se destacar que os modelos de Avellar et al. (2005), Avellar (2004), Lozano & Villa (2004) e Villa & Lozano (2004) são empregados quando da presença da restrição de soma constante de variáveis. Os primeiros propõem modelos tipo DEA CCR baseados em inputs/outputs limitados, nos quais a distribuição dos recursos/produtos pode ser influenciada tanto pelos inputs como pelos outputs envolvidos. A construção dos modelos tomou como base o perfil geométrico da fronteira CCR tridimensional, que é substituída por uma fronteira hiperbólica ou esférica, função da natureza da variável a distribuir.

Já o modelo de Lozano & Villa (2004) e Villa & Lozano (2004), chamado de Constant Sum of Outputs (CSO), refere-se à tomada de decisão centralizada em relação à alocação de recursos. Os autores propõem um modelo DEA BCC, em duas fases, no qual a maximização de eficiência de cada DMU individual é feita simultaneamente à minimização do total de recursos ou maximização da produção total. Em Villa & Lozano (2004) o modelo proposto é aplicado ao mesmo estudo de caso usado por Estellita Lins et al. (2003) e os resultados de ambos os modelos (CSO e DEA-GSZ) são comparados.

2. Modelo DEA-GSZ CCR

2.1 Formulação geral

Tal como foram desenvolvidos modelos DEA-GSZ BCC (Gomes, 2003; Estellita Lins et al., 2003; Gomes et al., 2003a, 2003b), é possível derivar modelos DEA com a restrição de ganhos de soma zero com base nos modelos DEA CCR clássicos. A formulação clássica do modelo do envelope DEA CCR com orientação a outputs usa para cada DMU o PPL apresentado em (1). Nesse PPL, para a DMU o em análise, a eficiência é dada por , x_j representam os inputs, y_j representam os outputs, l_j representam a contribuição da DMU j para a projeção (alvo) da DMU o na fronteira.

Max h₀

sujeito a

Em casos em que não haja total independência entre as DMUs e que a soma dos outputs deva ser constante, o modelo é descrito em (2) e chamado de Modelo DEA CCR com Ganhos de Soma Zero (DEA-GSZ CCR).

Max h_Ro

Em (2), a unidade em análise é a DMU o. h_Ro é o inverso da eficiência da DMU o sob a condição de soma de outputs constante; x_j e y_j são valores originais dos inputs e dos outputs, respectivamente; x_o e y_o são os valores de inputs e outputs para a DMU o; l_j são as contribuições das DMUs na projeção eficiente; y_j' são os novos outputs das DMUs restantes e incorporam a perda de output devido ao ganho da DMU o, de forma que a soma seja mantida constante. Assim como no caso do modelo BCC, as variáveis de decisão são l_j, h_Ro,y_j'=f_j(h_Ro).

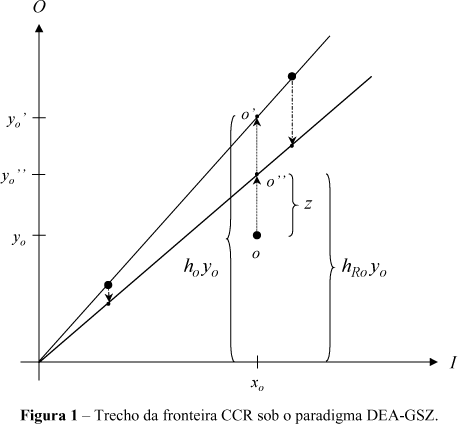
A Figura 1 representa um trecho da fronteira CCR para o caso bidimensional. Analogamente ao caso BCC, a DMU o receberá uma determinada quantidade de output para pertencer à fronteira. O ganho z pode ser definido por , ou seja, é o quanto a DMU o deverá ganhar para atingir a fronteira eficiente, que corresponde à perda das demais DMUs.

A definição do modelo DEA CCR assume proporcionalidade entre inputs e outputs na fronteira, ou seja, se uma atividade (x,y) é viável, para um escalar t positivo, a atividade (tx,ty) também o será. Assim, impõe-se que os hiperplanos suporte que formam a fronteira eficiente passem pela origem dos planos coordenados.

Para o caso bidimensional representado na Figura 2, A e B são DMUs de referência (perdem quantidade de output) para a DMU o que busca a fronteira (ganha quantidade de output).

Da Figura 2 derivam-se as relações (3) e (4), que combinadas resultam na relação (5).

A relação (5) expressa que o alvo da DMU o na fronteira original, y_0', desloca-se como as DMUs reais da fronteira. Desta forma, a estratégia de alcance da fronteira, e conseqüente deslocamento, não é livre. Em outras palavras, a adoção de uma estratégia livre (qualquer) para o modelo DEA-GSZ CCR pode alterar a fronteira. Como a hipótese adotada é a de não alteração da composição da fronteira, a menos da DMU (ou DMUs) que busca(m) a eficiência, a estratégia deve ser determinada pelas equações da fronteira (para que não sejam retiradas DMUs eficientes da fronteira).

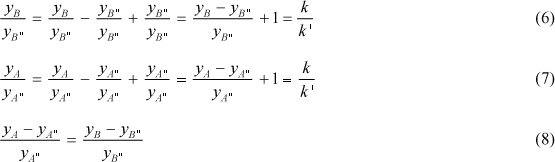
Das relações (3) e (4), para as DMUs A e B obtêm-se (6) e (7), que combinadas resultam em (8), que expressa que a perda de output é proporcional ao novo valor de output.

Ainda das relações (3) e (4) é possível derivar as relações (9) e (10) que, ao serem substituídas em (8), resultam na expressão (11).

Da expressão (11) afirma-se que a perda de output de cada DMU j, j¹0, sendo o a DMU que busca a eficiência, é proporcional ao seu valor original. Esse é o enunciado da estratégia de redução proporcional (Gomes, 2003), ou seja, no modelo DEA-GSZ CCR, para que seja mantida a composição da fronteira eficiente, a menos da DMU que busca eficiência, o uso da estratégia proporcional é obrigatório.

A demonstração acima é válida para o caso de um input e um output. Para casos multidimensionais, a demonstração pode ser generalizada apenas se todas as DMUs estiverem na mesma face. Para tal, basta substituir as retas por hiperplanos.

No entanto, é extremamente raro todas as DMUs eficientes estarem na mesma face. Portanto, é necessário generalizar a demonstração. Pode-se, sem perda de generalidade, considerar duas DMUs A e B eficientes em faces adjacentes. Neste caso, existe pelo menos uma DMU C eficiente que pertence simultaneamente às duas faces (caso contrário, as duas DMUs consideradas estariam na mesma face). Então, A e C pertencem à mesma face e a demonstração aplica-se às duas. Ou seja, a retirada de output tem que ser proporcional ao output das duas. Por outro lado, as DMUs B e C também estão em uma face comum, e a retirada de output tem que ser proporcional ao output de cada uma. Portanto, se a retirada de output de A e C é proporcional aos seus outputs e a de B e C também o é, então, a retirada de outputs de A e B é proporcional aos seus respectivos outputs.

2.2 Modelagem

Analogamente aos desenvolvimentos feitos para o modelo DEA-GSZ BCC de redução de outputs por estratégia proporcional (Gomes, 2003; Estellita Lins et al., 2003; Gomes et al., 2003a, 2003b), para o modelo DEA-GSZ CCR orientado a outputs (Gomes, 2003; Gomes et al., 2004), a DMU o precisa ganhar z unidades de output e a perda das outras DMUs é, obrigatoriamente, proporcional aos seus níveis de output, mantendo-se a restrição de que a soma dos outputs é constante.

Da Figura 1, tem-se que o ganho ' e a perda de output de cada DMU j, (o é a DMU que busca a fronteira) vale (Gomes, 2003).

Aplicando-se este resultado ao modelo geral (2), obtém-se o modelo (12) para o modelo DEA-GSZ CCR orientado a output (output único), no qual o termo é denotado de Coeficiente de Redução (CR). Assim como no caso de DEA-GSZ BCC, esse modelo é um Problema de Programação Não Linear.

Max h_Ro

sujeito a

Não há dificuldades em provar-se que os teoremas da Igualdade das Contribuições das DMUs de Referência ("No modelo DEA-GSZ em que seja adotada uma estratégia que não altere a composição da fronteira eficiente (exceto pela DMU que busca o alvo), o valor da contribuição das DMUs j (l_j), j ¹ o, é igual ao seu valor no modelo DEA clássico") e de Determinação do Alvo ("O alvo da DMU em análise no DEA-GSZ de estratégia proporcional é igual ao alvo no caso clássico multiplicado pelo coeficiente de redução"), demonstrados em Gomes (2003) e Gomes et al. (2003a, 2003b), são válidos também para o caso DEA-GSZ CCR. Dessa forma, o modelo deve ser resolvido em duas etapas:

1. Correr o modelo DEA CCR clássico, orientado a

   outputs. Obter os valores dos

   outputs das DMUs de referência e os valores das contribuições

   ou da eficiência

   .

2. Com os valores anteriores, resolver a equação (13), resultante dos dois teoremas anteriores, na qual

   h_Ro é o valor da eficiência segundo o modelo DEA-GSZ CCR.

Tal como o análogo BCC, o modelo DEA-GSZ CCR também admite a orientação a inputs com input único, bem como presença de múltiplos outputs ou inputs de soma constante. Em (14) é apresentado o modelo DEA-GSZ CCR orientado a outputs, com outputs múltiplos de soma constante. Em (15) e (16) estão os modelos DEA-GSZ CCR orientados a inputs, com input único e múltiplos de soma constante, respectivamente.

Max h_Ro

sujeito a

Min h_Ro

sujeito a

Min h_Ro

sujeito a

É possível, ainda, derivar modelos DEA-GSZ CCR com restrições aos pesos. Tomando como base os modelos apresentados por Cooper et al. (2000), que incorporam restrições do tipo Regiões de Segurança ao modelo DEA CCR do envelope, apresenta-se em (17) e (18), os modelos DEA-GSZ CCR com restrições aos pesos, orientados a inputs e a outputs, respectivamente, nos quais J_i e g_i são as variáveis duais que representam as restrições aos pesos no modelo dos multiplicadores, conforme proposto por Estellita Lins & Silva (2001, 2002). Em (17) e (18), B^TJ e A^Tg representam as matrizes dos coeficientes das restrições aos pesos de inputs e outputs, Bv< 0 e Au< 0, respectivamente.

Min h_Ro

sujeito a

Max h_Ro

sujeito a

2.3 Cooperação entre DMUs

A situação até aqui modelada representa o caso em que uma única DMU busca a fronteira eficiente. Entretanto, há a possibilidade de mais de uma DMU procurar maximizar a eficiência, o que pode ser feito em competição ou cooperação. Neste artigo trata-se apenas do caso de um número de DMUs que formam um grupo de cooperação. No paradigma do DEA-GSZ, a busca em cooperação significa que as DMUs deste grupo tentam retirar determinada quantidade de output apenas das DMUs não pertencentes ao grupo.

Para o caso de duas DMUs atuando em cooperação para a busca de eficiência, o modelo DEA-GSZ é expresso por um Problema Bi-objetivo Não Linear; no caso geral, de múltiplas DMUs atuarem em regime de cooperação, o modelo DEA-GSZ é um problema de programação não linear multiobjetivo (Gomes, 2003; Gomes et al., 2003a, 2003b).

Para o caso de uma estratégia qualquer de redução, o modelo multiobjetivo deve ser resolvido com o uso de técnicas de Programação Não Linear Multiobjetivo. Problemas deste tipo conduzem freqüentemente ao uso de metaheurísticas. No entanto, para a estratégia de redução proporcional, em especial para o modelo CCR, Gomes (2003) e Gomes et al. (2004) provam que o modelo é reduzido a um modelo de Programação Não Linear Mono-objetivo, segundo o Teorema da Proporcionalidade das Eficiências em Estratégia Proporcional (Gomes, 2003; Gomes et al., 2003a), cujo enunciado diz: "Considere-se o problema de várias DMUs em cooperação na busca de alvos com estratégia proporcional. As eficiências das DMUs no modelo DEA-GSZ são diretamente proporcionais às suas eficiências no modelo DEA clássico".

Como conseqüência deste teorema, ao considerar-se o caso em que várias DMUs atuam em cooperação na busca de alvos com estratégia proporcional, o Problema de Programação Não Linear Multiobjetivo é reduzido a um Problema de Programação Não Linear Mono-objetivo.

2.4 Uniformização da fronteira DEA

No caso em que todas as DMUs ineficientes formam um único grupo de cooperação e buscam eficiência na fronteira de eficiência DEA clássica, a aplicação do modelo DEA-GSZ fará com que ocorra a redistribuição do input ou do output de soma constante. Após essa redistribuição, todas as DMUs pertencerão à fronteira eficiente, ou seja todas serão 100% eficientes. A resolução deste problema conduz a uma fronteira uniformizada e supõe a existência de um decisor que promove os ajustes necessários a tal fim. Este decisor é designado em Lozano e Villa (2004) por DM, ou seja, um ente acima das DMUs.

A fronteira DEA uniformizada estará localizada em níveis inferiores aos da fronteira DEA do modelo clássico, já que as DMUs eficientes perdem unidades de output (ou ganham unidades de input) para compensar o ganho (ou perda) das unidades ineficientes, de modo a manter a soma constante. Esta situação de eficientização máxima pode ser vista como "ideal" por órgãos reguladores, já que será apresentada ao decisor a distribuição de recursos (ou produtos) que faz com que todas as unidades sejam 100% eficientes.

Para a construção da fronteira uniformizada de forma direta, em que as DMUs ineficientes formam um grupo de cooperação W, segundo o modelo DEA CCR tem-se as equações (19), para orientação a inputs, e (20), para orientação a outputs, que representam o Teorema da Determinação do Alvo ("o alvo da DMU em análise no DEA-GSZ de estratégia proporcional é igual ao alvo no caso clássico multiplicado pelo coeficiente de redução"). Nessas equações, h_Ri e h_i são, respectivamente, as eficiências nos modelos DEA-GSZ CCR e DEA CCR clássico; W é o grupo de DMUs em cooperação; r_ij=h_i-I/h_j-I é o fator de proporcionalidade resultante do emprego da estratégia proporcional, na orientação a inputs; q_ij=h_i-O/h_j-O é o fator de proporcionalidade na orientação a outputs. Para os modelos DEA BCC orientados a outputs e a inputs são derivadas expressões análogas (Gomes, 2003).

3. Estudo de Caso: Realocação de Outputs

3.1 Antecedentes

A Universidade Federal Fluminense (UFF) foi criada a partir da fusão de várias faculdades isoladas do município de Niterói, sua sede, e da agregação de outras unidades de ensino, localizadas em outros municípios do estado do Rio de Janeiro.

A partir de 1984, a UFF começou um projeto de interiorização de cursos de graduação que, à época da coleta dos dados usados contemplava os municípios de Angra dos Reis, Cabo Frio, Itaperuna, Macaé, Miracema e Santo Antônio de Pádua. Um histórico desse processo de interiorização e do concurso vestibular da UFF pode ser visto em Soares de Mello et al. (2002, 2001b), Vaz et al. (2002) e Rangel et al. (2003). A Figura 3 mostra a distribuição espacial da presença e atuação da UFF no Estado do Rio de Janeiro (Soares de Mello et al., 2001b).

Devido a esse processo de interiorização, a UFF realiza a inscrição e as provas de seu vestibular em vários municípios do estado do Rio de Janeiro. A eficiência da UFF e dos municípios em relação ao vestibular foi avaliada em Soares de Mello et al. (2001b, 2000). Em Soares de Mello et al. (2001b) foram utilizados dois modelos DEA CCR parciais, cujos resultados foram agregados posteriormente. A justificativa para o uso do modelo DEA CCR pode ser vista em Soares de Mello et al. (2001b).

O primeiro modelo de eficiência parcial, denominado de modelo de eficiência segundo a ótica da UFF, avalia a capacidade da universidade em atrair inscritos dos diversos municípios. O segundo modelo, modelo de eficiência segundo a ótica dos municípios, analisa o poder dos municípios em aprovar alunos no vestibular da instituição.

Em ambos os modelos, as DMUs são os municípios do estado do Rio de Janeiro. Os inputs são a população de cada município e um parâmetro denominado influência de vagas, ou vagas equivalentes, cuja construção é explicitada em Soares de Mello et al. (2001b). Para o modelo de eficiência segundo a ótica da UFF, o output é o número de inscritos no vestibular. Já no modelo que avalia a eficiência segundo a ótica dos municípios, o output é o número de aprovados.

3.2 Modelagem proposta para o modelo DEA-GSZ CCR

No modelo de avaliação de eficiência segundo a ótica dos municípios, o output número de aprovados tem soma constante. Com efeito, a soma do número de aprovados é igual ao número total de vagas, que é determinado no edital do concurso. Destaca-se que foram desprezados dois efeitos: o não total preenchimento das vagas oferecidas e vagas ocupadas por candidatos não residentes no estado.

Com a aplicação do modelo DEA-GSZ CCR de busca da fronteira uniformizada a este modelo é possível determinar uma configuração de alocação dos aprovados com a qual todos os municípios teriam máxima eficiência.

Para este fim, foram utilizados os mesmos dados usados em Soares de Mello et al. (2001b, 2000) para o modelo segundo a ótica dos municípios. Foi utilizado o modelo DEA-GSZ CCR, orientado a output, com dois inputs (população e vagas equivalentes) e um output de soma constante (número de aprovados). As DMUs do modelo DEA são todos os municípios do estado do Rio de Janeiro que inscreveram alunos no vestibular. Esses dados referem-se ao ano de 2000.

3.3 Resultados

Na aplicação do modelo DEA-GSZ CCR, com orientação a outputs, foi utilizada a estratégia de busca direta da fronteira uniformizada, conforme apresentado em Gomes (2003). Nesta estratégia, as DMUs ineficientes no modelo DEA CCR clássico formam o grupo de cooperação, que retiram quantidade de output das DMUs eficientes de modo a alcançarem a fronteira e manterem a restrição de ganhos de soma zero. A Tabela 1 apresenta os resultados da aplicação do modelo DEA-GSZ CCR. Traz ainda os valores originais do output "número de aprovados" e da eficiência DEA CCR antes e após a redistribuição do output.

No modelo DEA CCR clássico, as DMUs com 100% de eficiência são Rio de Janeiro e Niterói. As demais DMUs formam o grupo de cooperação. Conforme pode ser verificado, alguma DMUs do grupo de cooperação têm seu valor de output reduzido, assim como ocorre com as DMUs inicialmente eficientes. Isto ocorre porque não foram usadas camadas de iso-eficiência (Gomes, 2003) e a designação de cooperação apenas representa o modelo matemático a ser adotado, já que há efetiva competição ente algumas das DMUs. Ou seja, como explicado em Gomes (2003), o grupo das DMUs ineficientes atua em cooperação para retirar quantidades de output das DMUs da fronteira, mas estão em competição entre si na busca da eficiência individual.

Os resultados da aplicação deste modelo podem servir como subsídio ao fomento de políticas públicas de incentivo ao ingresso à educação superior e de melhoria do ensino, de modo a aumentar o número de aprovados no vestibular.

Verifica-se na Tabela 1 que o valor do output após a redistribuição para todas as DMUs não é um número inteiro. Isto ocorre porque os resultados obtidos são uma primeira aproximação para a solução do problema. Para que o valor do output fosse obtido como um número inteiro, deveriam ser utilizados algoritmos mais precisos, como, por exemplo, o empregado por Leta et al. (2003). Verifica-se ainda que alguns erros de aproximação, introduzidos pelo algoritmo utilizado no programa computacional SIAD (Angulo Meza et al., 2004) para calcular os PPLs de DEA, conduzem a valores das eficiências, após a redistribuição, ligeiramente abaixo de 100% (99, 997%, por exemplo).

Lembrando que no caso do modelo DEA-GSZ CCR a redistribuição segue obrigatoriamente uma estratégia proporcional, uma outra forma de redistribuir o output é aplicar o conceito de proporcionalidade. Dessa forma, o novo output pode ser calculado conforme a expressão (21), na qual o alvo de cada DMU é calculado pela multiplicação entre o seu output original e sua eficiência. Esta proposta de cálculo do valor do output após a redistribuição gera os mesmos resultados da Tabela 1.

4. Conclusões

Os modelos DEA com Ganhos de Soma Zero (DEA-GSZ), tanto com retornos constantes (CCR) ou variáveis de escala (BCC), com orientação a inputs ou a outputs, com ou sem restrições aos pesos, preenchem uma lacuna na atual literatura em modelagem DEA, qual seja, a da inserção da restrição de soma constante para inputs ou outputs (únicos ou múltiplos).

A proposição de modelos DEA-GSZ CCR complementa os modelos já propostos na literatura. Nesses modelos, a adoção de uma estratégia livre (qualquer) pode alterar a fronteira. Prova-se, neste artigo, que com base na geometria da fronteira DEA CCR, a estratégia que não altera a composição da fronteira, a menos da DMU (ou DMUs) que busca(m) a eficiência, é a estratégia proporcional, o que simplifica bastante o modelo.

As estratégias de busca da fronteira por várias DMUs atuando em cooperação pode ser levada ao ponto em que se obtenha a fronteira de eficientização máxima, ou fronteira uniformizada. Essa situação pode ser vista como "ideal" por órgãos reguladores ou agências de controle central, já que representa a alocação ótima de recursos ou de produção entre todas as DMUs da amostra em avaliação.

A aplicação do modelo DEA-GSZ CCR ao estudo de caso da redistribuição do número de aprovados entre os municípios que inscreveram alunos no vestibular mostra-se bastante útil no apoio a políticas educacionais. Resultados mais abrangentes poderiam ser obtidos se fosse usado um modelo que incluísse também o output número de inscritos. Modelos que contemplem a modelagem conjunta de outputs de soma constante com outputs não restritos encontram-se em fase de desenvolvimento.

Recebido em 10/2004; aceito em 04/2005

Received October 2004; accepted April 2005

• (1) Angulo Meza, L.; Biondi Neto, L.; Soares de Mello, J.C.C.B.; Gomes, E.G. & Coelho, P.H.G. (2004). FSDA Free Software for Decision Analysis (SLAD Software Livre de Apoio à Decisão): a software package for data envelopment analysis models. Memorias del XII Congreso Latino-Iberoamericano de Investigación Operativa CLAIO, La Habana, Cuba.
• (2) Avellar, J.V.G. (2004). Modelos DEA com soma constante de inputs/outputs. Tese de Mestrado, Instituto Tecnológico de Aeronáutica, São José dos Campos.
• (3) Avellar, J.V.G.; Milioni, A.Z. & Rabello, T.N. (2005). Modelos DEA com variáveis limitadas ou soma constante. Pesquisa Operacional, 25(1), 135-150.
• (4) Banker, R.D.; Charnes, A. & Cooper, W.W. (1984). Some models for estimating technical scale inefficiencies in Data Envelopment Analysis. Management Science, 30(9), 1078-1092.
• (5) Charnes, A.; Cooper, W.W. & Rhodes, E. (1978). Measuring the efficiency of decision-making units. European Journal of Operational Research, 2, 429-444.
• (6) Charnes, A.; Cooper, W.W.; Lewin, a.y. & Seiford, l.m. (1994). Data envelopment analysis: Theory, methodology and applications Kluwer Academic Publishers, Boston, USA.
• (7) Coelli, T.J.; Rao, D.S.P. & Battese, G.E. (1998). An Introduction to Efficiency and Productivity Analysis Kluwer Academic Publishers.
• (8) Cooper, W.W.; Seiford, L.M. & Tone, K. (2000). Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software Kluwer Academic Publishers, USA.
• (9) Estellita Lins, M.P. & Angulo Meza, L. (2000). Análise Envoltória de Dados e perspectivas de integração no ambiente de Apoio à Decisão Editora da COPPE/UFRJ, Rio de Janeiro.
• (10) Estellita Lins, M.P. & Silva, A.C.M. (2001). Evitando a inviabilidade em modelos DEA com restrições aos pesos. Relatório Técnico EP03/01-PO, Programa de Engenharia de Produção, COPPE/UFRJ, Rio de Janeiro.
• (11) Estellita Lins, M.P. & Silva, A.C.M. (2002). Avoiding unfeasibility in DEA models with weight restrictions. Anais do XI Congreso Latino-Iberoamericano de Investigación Operativa, Concepción, Chile. Disponível em: <http://www.udec.cl/~claioxi/english/ comprog.htm>.
• (12) Estellita Lins, M.P.; Gomes, E.G.; Soares de Mello, J.C.C.B. & Soares de Mello, A.J.R. (2003). Olympic ranking based on a Zero Sum Gains DEA model. European Journal of Operational Research, 148(2), 312-322.
• (13) Gomes, E.G. (2003). Modelos de Análise de Envoltória de Dados com Ganhos de Soma Zero. Tese de Doutorado em Engenharia de Produção, COPPE/Universidade Federal do Rio de Janeiro, Rio de Janeiro, Dezembro.
• (14) Gomes, E.G. & Soares de Mello, J.C.C.B. (2002). Determinação de alvos em modelos DEA com ganhos de soma zero. Anais do XXXIV Simpósio Brasileiro de Pesquisa Operacional, Rio de Janeiro, RJ, Novembro.
• (15) Gomes, E.G.; Soares de Mello, J.C.C.B. & Estellita Lins, M.P. (2001). Modelos DEA com soma de outputs constante. Anais do XXXIII Simpósio Brasileiro de Pesquisa Operacional, Campos do Jordão, SP, Novembro.
• (16) Gomes, E.G.; Soares de Mello, J.C.C.B. & Estellita Lins, M.P. (2003a). Busca seqüencial de alvos intermediários em modelos DEA com soma de outputs constante. Investigação Operacional, 23(2), 163-178.
• (17) Gomes, E.G.; Soares de Mello, J.C.C.B. & Estellita Lins, M.P. (2003b) Deslocamento de DMUs pela fronteira de eficiência em modelos de Análise de Envoltória de Dados com Ganhos de Soma Zero. Anais do XXXV Simpósio Brasileiro de Pesquisa Operacional, Natal, RN, Novembro.
• (18) Gomes, E.G.; Soares de Mello, J.C.C.B. & Estellita Lins, M.P. (2004). Modelos de Análise de Envoltória de Dados com Ganhos de Soma Zero e Retornos Constantes de Escala. Actas do 11ş Congresso da Associação Portuguesa de Investigação Operacional, Porto, Portugal, Abril.
• (19) Leta, F.R.; Gomes, E.G.; Soares de Mello, M.H.C. & Soares de Mello, J.C.C.B. (2003). Análise de Envoltória de Dados para Alocação de Recursos: Uma Proposta de Algoritmo Seqüencial. Anais do XXXV Simpósio Brasileiro de Pesquisa Operacional, Natal.
• (20) Lozano, S.N. & Villa, G. (2004). Centralized Resource Allocation Using Data Envelopment Analysis. Journal of Productivity Analysis, 22, 143-161.
• (21) Rangel, L.A.D.; Soares de Mello, J.C.C.B.; Gomes, E.G. & Gomes, L.F.A.M. (2003). Avaliação da interiorização dos cursos da Universidade Federal Fluminense com o uso conjugado dos métodos UTA e Macbeth. Investigação Operacional, 23(1), 49-69.
• (22) Soares de Mello, J.C.C.B.; Gomes, E.G. & Estellita Lins, M.P. (2002). Análise Multicritério da presença da Universidade Federal Fluminense com o uso do Método Macbeth. Revista Produção, 11(2), 53-67.
• (23) Soares de Mello, J.C.C.B.; Gomes, E.G.; Estellita Lins, M.P. & Soares de Mello, A.J.R. (2001a). Uso da Pesquisa Operacional em esportes: o caso das Olimpíadas. Boletim da Sociedade Brasileira de Pesquisa Operacional, 19, 5-6.
• (24) Soares de Mello, J.C.C.B.; Gomes, E.G.; Estellita Lins, M.P. & Vieira, L.A.M. (2001b). Um caso de estudo de integração SIG-DEA-MCDA: a influência de uma instituição de ensino superior em vários municípios do Estado do Rio de Janeiro. Investigação Operacional, 21(2), 171-190.
• (25) Soares de Mello, J.C.C.B.; Gomes, E.G.; Estellita Lins, M.P. & Vieira, L.A.M. (2000). Mapeamento da Interiorização da Universidade Federal Fluminense, Fazendo Uso Integrado de Sistemas de Informação Geográfica, Análise de Envoltória de Dados e Análise Multicritério. Anais do GISBrasil 2000, Salvador.
• (26) Vaz, M.R.; Soares de Mello, J.C.C.B.; Soares de Mello, M.H.C. & Moura, H.L.S. (2002). Participação das Engenharias na Interiorização dos Cursos da UFF. Anais do XXX COBENGE Congresso Brasileiro de Ensino de Engenharia, Piracicaba.
• (27) Villa, G. & Lozano, S.A. (2004). Constant Sum of Outputs DEA model for Olympic Games target setting. In: 4th International Symposium on DEA. Proceedings of the 4th International Symposium on DEA, Aston University, US, p.36.

*

Corresponding author / autor para quem as correspondências devem ser encaminhadas

Datas de Publicação

• Publicação nesta coleção
  13 Set 2005
• Data do Fascículo
  Ago 2005

Histórico

• Aceito
  Abr 2005
• Recebido
  Out 2004