Abstracts
This article concerns the application of the Mixture of Local Expert Models (MLEM) to predict the daily and monthly price of the Sugar No. 14 contract in the New York Board of Trade. This technique can be seen as a forecasting method that performs data exploratory analysis and mathematical modeling simultaneously. Given a set of data points, the basic idea is as follows: 1) a Kohonen Neural Network is used to divide the data into clusters of points, 2) several modeling techniques are then used to construct competing models for each cluster, 3) the best model for each cluster is then selected and called the Local Expert Model. Finally, a so-called Gating Network combines the outputs of all Local Expert Models. For comparison purposes, the same modeling techniques are also evaluated when acting as Global Experts, i. e., when the technique uses the entire data set without any clustering.
mixture of local expert models; forecasting time series; neural networks
Este artigo aborda a aplicação de Modelos da Composição de Especialistas Locais (MCEL) para previsão de preços diários e mensais da comodity açúcar da bolsa de valores de Nova York. Esta técnica pode ser vista como método de previsão que realiza simultaneamente análise exploratória de dados assim como modelagem matemática. Dado um conjunto de dados, a idéia básica é a seguinte: 1) uma Rede Neural de Kohonen é utilizada para dividir o conjunto de dados em clusters, 2) várias técnicas de modelagem são utilizadas para calibrar modelos para cada cluster, 3) o melhor modelo para cada cluster é selecionado e denominado Modelo de Especialista Local. Finalmente, uma Rede Supervisora combina as saídas de cada um dos Modelos de Especialista Local. Com a finalidade de comparação, as mesmas técnicas de modelagem são também avaliadas atuando como Especialistas Globais, ou seja, quando as técnicas usam o conjunto de dados único, sem clusters.
modelos da composição de especialistas locais; previsão de séries temporais; redes neurais
Daily and monthly sugar price forecasting using the mixture of local expert models
Brício de MeloI; Armando Zeferino MilioniI,* * Corresponding author / autor para quem as correspondências devem ser encaminhadas ; Cairo Lucio Nascimento JúniorII
IDivision of Mechanical & Aeronautical Engineering - Instituto Tecnológico de Aeronáutica (ITA) - São José dos
Campos SP, Brazil - bricio@bb.com.br; milioni@ita.br
IIElectronic Engineering Division - Instituto Tecnológico de Aeronáutica (ITA) - São José dos Campos SP, Brazil
ABSTRACT
This article concerns the application of the Mixture of Local Expert Models (MLEM) to predict the daily and monthly price of the Sugar No. 14 contract in the New York Board of Trade. This technique can be seen as a forecasting method that performs data exploratory analysis and mathematical modeling simultaneously. Given a set of data points, the basic idea is as follows: 1) a Kohonen Neural Network is used to divide the data into clusters of points, 2) several modeling techniques are then used to construct competing models for each cluster, 3) the best model for each cluster is then selected and called the Local Expert Model. Finally, a so-called Gating Network combines the outputs of all Local Expert Models. For comparison purposes, the same modeling techniques are also evaluated when acting as Global Experts, i. e., when the technique uses the entire data set without any clustering.
Keywords: mixture of local expert models; forecasting time series; neural networks.
RESUMO
Este artigo aborda a aplicação de Modelos da Composição de Especialistas Locais (MCEL) para previsão de preços diários e mensais da comodity açúcar da bolsa de valores de Nova York. Esta técnica pode ser vista como método de previsão que realiza simultaneamente análise exploratória de dados assim como modelagem matemática. Dado um conjunto de dados, a idéia básica é a seguinte: 1) uma Rede Neural de Kohonen é utilizada para dividir o conjunto de dados em clusters, 2) várias técnicas de modelagem são utilizadas para calibrar modelos para cada cluster, 3) o melhor modelo para cada cluster é selecionado e denominado Modelo de Especialista Local. Finalmente, uma Rede Supervisora combina as saídas de cada um dos Modelos de Especialista Local. Com a finalidade de comparação, as mesmas técnicas de modelagem são também avaliadas atuando como Especialistas Globais, ou seja, quando as técnicas usam o conjunto de dados único, sem clusters.
Palavras-chave: modelos da composição de especialistas locais; previsão de séries temporais; redes neurais.
1. Introduction
It is well known that in general no modeling technique is complete. Some techniques exhibit fast convergence but might fail when submitted to cross validation tests. Other techniques perform well regarding cross validation but have poor convergence properties, as in Nascimento Júnior & Yoneyama (2000).
In this paper we propose a modeling technique designed to combine the results of different experts (time series forecasting techniques, in our case) where each expert model (called Local Expert) is developed using only part of the data set. Many expert models are developed for the same part of the data set and only the best expert for each part is then used.
Several of the traditional time series forecasting techniques use linear models which, by their nature, are not capable of capturing non-linear behavior that is often present in real world situations. Artificial neural networks and other techniques allow the development of non-linear time series forecasting models, which, however, do not necessarily imply better results when compared to traditional linear techniques, as in Makridakis et al. (1998).
Our purpose is to combine linear and non-linear techniques in the task of time series forecasting, capturing the best characteristics of each technique.
2. Mixture of local expert system as a forecasting approach
The mixture of local expert system presented in this article follows the idea proposed by Jacobs et al. (1991) and has the following procedure: a) divide the data set into regions or clusters, b) for each cluster train all expert models, c) find the best expert for each cluster, and d) implement a composition of the best local experts using a gating network which will decide how to weight each local expert output for a given input point.
The major hypothesis of the proposed Mixture of Local Experts Model (MLEM) is that, when the data set can be divided into a set of clusters, one can develop a local model (a local expert) for each data cluster. However, one has to define a procedure to calculate the output when an input point x does not belong exactly to any of the data clusters used to construct the local models. The structure of MLEM can be seen in Figure 1.
The steps in order to construct the desired models have the following phases:
-
Firstly we cluster the input data set (X) in several regions (Xi).
-
For each one of the regions, considering only the data points in the training set of that region, all experts are used to construct the local models.
-
The best local expert for each of the regions is found, considering the smallest RMSE (Root Mean Squared Error) measured using only the data points in the training set of the region:
where NT = number of data points in the training set of the region, Yt is the observed output and Yt is the local model output.
-
The best local expert for each of the regions is found, considering the smallest RMSE (Root Mean Squared Error) measured using the data points in the
test set of the region, as in eqn. (1), but changing NT by NE = number of data points in the
test set of the region.
In our proposal, after the local expert has been developed, the MLEM structure can be used to yield a forecast for a given input point x in the following manner:
-
The input point x is delivered to the best expert elected for each cluster i who computes its output yi.
-
Next the gating network is used to compute the weight coefficients gi which will depend on the distance of the input point x to the center of each cluster as well as the size of the region of the input space taken by each cluster of training data points.
-
The final output y will be computed as the weighted average of the outputs yi using the coefficients gi as weight factors, i.e.:
where k represents the number of local experts.
3. Data set clustering and weight coefficients computation
3.1 Data set clustering
The data set is clustered using a Kohonen neural network trained by a SOM (Self-Organizing Map) algorithm applied to available data, as in Kohonen (1989). The Kohonen neural network training aims at finding similarities on the input data set. It is possible to show that a Kohonen neural network divides the input data set in such a way that input points that are close to each other (by a given measure) will be assigned to the same cluster (see, for example, Nascimento Júnior & Yoneyama, 2000; Haykin, 1994).
Each cluster defines a region on the input data set space and each input data used during training belongs to one and only one of these clusters. It is possible to show, as in Nascimento Júnior & Yoneyama (2000) that, after training, the weights of the Kohonen neural network units indicate the center of each cluster (denoted by ctri).
3.2 Weight coefficients computation
According to Bishop (1995) and Mitchell (1997) the weight coefficients gi can be computed using a Radial Basis Function RBF. Firstly the center of the clusters and their variances are used to compute the coefficients di:
where:
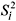
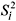 , i. e., S2 = max (
, i. e., S2 = max (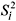 ) for i = 1, 2, ..., k.
) for i = 1, 2, ..., k.
The coefficients gi can then simply be computed by normalizing the coefficients di:
The parameter di could also be computed by using the Mahalanobis distance (see Kohonen, 1989; Bishop, 1995):
where Mi is the covariance matrix computed considering only the training input vectors xj assigned to the ith cluster:
Eqn. (6) adjusts the form of the radial basis function to an elliptical one. However, such procedure is computational intensive and in this article the simpler eqn. (3) was used.
4. Choosing the experts
The expert candidates should be chosen in such a way that the collection of experts represents different types of modeling techniques. In this article the Artificial Neural Networks (ANN) model was chosen for its non-linear properties and the Multiple Regression Analysis (MRA) model was chosen for its linear properties.
Regarding the ANN model, a multi-layer perceptron (MLP) neural network can be seen as a non-linear regression model when used as a time series forecasting technique. The MLP neural network was chosen because several time series forecasting problems can be addressed by it. There are many training algorithms that can be used to develop MLP models. Among these algorithms we selected the Back-Propagation, a gradient-type algorithm which aims at minimizing the root mean squared error (RMSE) between observed values and model outputs as in Nascimento Júnior & Yoneyama (2000). Then, were adopted two types of ANN: a) ANNI a Multi Layer Perceptrons without Input - Output direct connection and b) ANNII a Multi Layer Perceptrons with linear Input - Output direct connection. The main difference between the two types of ANN is the direct input-output connections. According to Weigend & Gershenfeld (1994) the direct linear connections between each input and the output units can help the training algorithm to quickly find the linear input-output relationship (if it exists) and then the hidden nonlinear units can be used to find the nonlinear part of the desired input-output mapping.
The MRA model uses ordinary least squares in order to find the best linear function that fits the given input-output data. When using MRA, several hypotheses are of fundamental importance for the good quality of the results. Pindyck & Rubinfeld (1998) and Gujarati (2000) recommend checking the normal distribution of the output error, homoscedasticity and the absence of multicolinearity in the data, serial correlation of the output error and the presence of outliers.
Finally, the Carbon Copy (CRB) model, which is considered a very naïve and simple technique, was used as a reference model. The CRB model simply states that the observation at time t becomes the model value at time t+1, that is:
5. MLEM to forecast the prices of a commodity
5.1 Daily sugar price
5.1.1 Methodology
This section presents a case study where the goal is to predict the deflated daily price of Sugar No. 14 contracts in the New York Board of Trade (NYBOT) using a Mixture of Local Experts Models (MLEM). The time series used in this case has 3,521 consecutive daily prices (around 14 years, from 03/Jan/1989 to 03/Feb/2003). The first 3231 points of the time series were used as data to construct the models (training set: 2,996 first points, test set: 235 last points). The last 260 points were used only to validate the models (validation data set) and were not used during the construction of the MLEM phase. The real price commodity was obtained using the CPI (Consumer Price Index) as a deflator. Since CPI is presented in a monthly basis, we computed a linear adjustment among sequence values in order to have it too in a daily basis, as the commodity price. The reference date to obtain daily real price was 1-january-2003. The behavior of the time series (training and test data sets) can be seen in Figure 2 that shows both nominal price as the real price (in bold).
A window size of 10 points was used for all experts, that is, the points Yt9, Yt8, ..., Yt were used as model inputs in order to predict the model output Yt+1. This window size was chosen in order to capture at least the past 2 weeks of this commodity trading. This 10 days time window was a suggestion of experts on daily sugar price forecast from Copersucar, a Brazilian sugar producer co-operative. Their long time experience upholds the claim that this choice should be considered best practice
The first step was to use a Kohonen neural network as described in section 3.1 over the 3,231 data points (training and test sets). The data set was then divided into 6 regions. Furthermore, the specifications described in greater detail can be seen in Melo (2003).
Table 1 summarizes how the data points used to construct the models were distributed:
Four modeling techniques were used to develop the local experts for each one of the 6 regions, considering only the data points in the training set of the region:
-
ANN I (Artificial Neural Network I): Multi Layer Perceptrons without Input - Output direct connection and a [10, Nh, 1] topology, which means 10 input units, Nh hidden units and 1 output unit.
-
ANN II (Artificial Neural Network II): Multi Layer Perceptrons with linear Input - Output direct connection and a [10, Nh, 1] topology II.
-
MRA (Multiple Regression Analysis): the model used to predict
Yt+
1 was a linear combination of
Yt,
Yt
1,
..., Yt
9 and their inverse and logarithmic transformations.
-
CRB (Carbon Copy):
 = Yt.
= Yt.
The second step in order to construct the desired models is to find the best local expert for each of the 6 regions. The best local expert for a region is the expert that has the smallest RMSE (Root Mean Squared Error) measured using only the data points in the test set of that region. However, if there are no test data points in a region, the RMSE is measured considering the training data points assigned to that region.
Finally, in the validation phase, a one-step ahead forecast is performed for the 260 points in the validation set using the mixture of the best local experts, as described by eqns. (3) and (4).
For comparison purposes, the same 4 modeling techniques (ANN I, ANN II, MRA and CRB) were used to develop the so-called global experts, that is, considering that the training data set (2,996 points) formed just one region.
5.1.2 Analysis of the experimental results Daily prices
For regions I, II and IV the best local expert was the ANN I model, while for region III the best local expert was the ANN II model, considering the RMSE measured on the training data set for those regions (since these regions have no test data set). For regions V and VI the best local expert was the MRA considering the RMSE measured on the test data set (if the RMSE was measured on the training data set the best local expert for region V would be the ANN I model and for region VI would be the ANN II).
So, the one-step ahead forecast for the 260 points in the validation data set was calculated by eqn. (8) as follows:
Figure 3 shows the forecast for the validation data set made by the MLEM technique. From this figure one can see that, although the validation data set points have a little variation (@3.5 US$ cents/pound), the proposed mixture of local experts technique follows the time series volatility.
Table 2 shows the RMSE and MAPE measures (considering the validation data set) for different expert models. Mean Absolute Percentage Error (MAPE) was computed as eqn. (9):
where NV = number of data points in the validation set, Yt is the observed output and  is the model output.
is the model output.
Given the high volatility of this time series, it is no surprise that the best global model is the Carbon-Copy model. However, the MLEM technique produced a model that is better (even though only marginally better) than the Carbon-Copy model, which is a considerable achievement.
Finally, from the point of the ultimate user of forecasting, knowing that the MAPE of a method is 1.91% means a great deal more than simply knowing that the RMSE is 0.08982.
5.2 Monthly sugar price
5.2.1 Methodology
This section presents a case where the goal is to predict the deflated monthly price of a commodity from the agribusiness sector using a Mixture of Local Expert Models (MLEM). The time series used in this case has 505 consecutive monthly prices (around 42 years). The first 492 points of the time series where used as data to construct the models (training and test data sets). The last 13 points were used only to validate the models (validation data set) and never where used during the construction of the MLEM phase.
A window size of 12 points was used for all experts, that is, the points Yt11, Yt10, ..., Yt where used as model inputs in order to predict the model output Yt+1. Therefore 480 points were used to construct the models and 13 points were used to validate the models. In this case 12 as chosen as the window size since its believed that the commodity price exhibits annual seasonal behavior.
The behavior of the first 480 points of the time series (training and test data sets), including the clustering performed by the Kohonen neural network, can be seen in Figure 4. This time series exhibits a typical behavior of many economic time series with stationary phases alternating with high volatility periods therefore resulting in a variable mean as in Enders (1995).
The first step in order to construct the desired models was to divide the first 480 data points as follows: 1) the training set was composed of the first 468 data points. 2) the test set was composed of the last 12 data points. Then, by using a Kohonen neural network, as described in section 3.1, the 480 data points were divided into 2 regions (shown in Figure 4), where region I contained 402 data points and region II contained 78 data points. Table 3 summarizes how the data points used to construct the models were distributed:
From Figure 4 and Table 3 can see that, since the 78 training data set points belong to region II, the signals denoted by these data points seem to be increase/decrease sections of the time series, specially the major expansion/retraction observed between 150 180 time period and other low retractions near 30 and 240 time periods.
Four techniques were used to develop the local experts for each one of the 2 regions, considering only the data points in the training set of the region:
-
ANN I (Artificial Neural Network I): Multi Layer Perceptrons without Input - Output direct connection and a [12, Nh, 1] topology, which means 12 input units, Nh hidden units and 1 output unit.
-
ANN II (Artificial Neural Network II): Multi Layer Perceptrons with linear Input - Output direct connection and a [12, Nh, 1] topology II.
-
MRA (Multiple Regression Analysis): the model used to predict Yt+1 was a linear combination of Yt, Yt1, ..., Yt11 and their inverse and logarithmic transforms.
-
CRB (Carbon Copy): Yt+1 = Yt, this technique was included only for comparison purposes.
The second step follows the very same pattern presented in our first case study as in section 5.1.1.
Finally, in the validation phase, a one-step ahead forecast is performed for the 13 points in the validation set using the mixture of the best local experts, as described by eqns. (3) and (4).
For comparison purposes, the same 4 techniques (ANN I, ANN II, MRA e CRB) were used to develop the so-called global experts, that is, considering all available data as belonging to just one region.
5.2.2 Analysis of the experimental results Monthly prices
For the region I the best local expert was the ANN I model, considering the RMSE measured on the test set data points. Besides that, the ANN I model was the best local expert as well if one had considered the smallest RMSE measured on the training data set. For region II the best local expert was the ANN II model, considering the RMSE measured on the training set data points, since this region has no test data set.
So, the one-step ahead forecast for the 13 points in the validation set was calculated as follows:
Table 4 shows the RMSE and MAPE (calculated as showed in our first case study as in section 5.1.1.) for the global experts and for mixture of local experts (measured on the 13 points in the validation data set):
From Table 4 we can see that the mixture of local expert models technique obtained the best result. Furthermore, this result was obtained by combining the two worst global experts (among the 4 global experts investigated). Finally, from the point of the ultimate user of forecasting, knowing that the MAPE of a method is 4.74% means a great deal more than simply knowing that the RMSE is 0.39686.
Figure 5 shows the forecast for the 13 validation data set points made by the 2 best local experts (ANN I for region I and ANN II for region II) and by the mixture of local experts technique.
From Figure 5 can see that, since the 13 validation data set points belong to region I, the proposed mixture of local experts technique automatically considers that the prediction done by the local expert for region I (ANN I) is more important than the prediction done by the other local expert (ANN II).
6. Conclusions and future work
The proposed system for the implementation of the mixture of local expert technique can be applied to a large number of modeling problems, including the forecast of time series, a fundamental part of most decision-making processes that continues to be a challenge for researchers from all over the world.
It is important to note that, when using any modeling technique, the benefits must be large enough to outweigh the costs. Therefore any improvement obtained by the application of the technique proposed in this article should be weighted against the increased complexity and extra burden needed to implement the technique. The costs and results when one uses global experts based on single techniques should also be considered in this comparison, as mentioned by Khotanzad et al. (2000).
Future research will investigate other clustering procedures, more modelling techniques to develop the local expert models, and different strategies to combine the local expert models.
Acknowledgements
We wish to express our appreciation to those whose publications have assisted us with our research. We would also like to thank the referees for their comments which helped the improvement of this paper. A first version of this article was presented at the 5th International Conference on Data Mining, Text Mining and Their Business Applications in Malaga, Spain, September 15 17, 2004.
(2) Enders, W. (1995). Applied Econometric Time Series. John Wiley & Sons, New York.
(3) Gujarati, D.N. (2000). Econometria Básica. Makron Books, São Paulo (in Portuguese).
(4) Haykin, S. (1994). Neural Networks: A Comprehensive Foundation. 2nd edn. Prentice Hall, New York.
(5) Jacobs, R.A., Jordan, M.I., Nowlan, S.J. & Hinton, G.E. (1991). Adaptive Mixture of Local Experts. Neural Computation, MIT Press, 3(1), 79-87.
(6) Khotanzad, A.; Elragal, H. & Lu, T.L. (2000). Combination of Artificial Neural Network Forecasters for Prediction of Natural Gas Consumption. IEEE Transactions on Neural Networks, 11(2), 464-473.
(7) Kohonen, T. (1989). Self-Organization and Associative Memory. 3rd edn. Springer-Verlag, Berlin.
(8) Makridakis, S.; Wheelwright, S. & Hyndman, R.J. (1998). Forecasting Methods and Applications. 3rd edn. John Wiley & Sons, New York.
(9) Melo, Brício (2003). Previsão de Séries Temporais Usando Modelos da Composição de Especialistas locais. MSc Thesis, Instituto Tecnológico de Aeronáutica ITA, São José dos Campos (SP) (in Portuguese).
(10) Mitchell, T.M. (1997). Machine Learning. McGraw-Hill, Singapore.
(11) Nascimento Júnior, C.L. & Yoneyama, T. (2000). Inteligência Artificial em Controle e Automação. Editora Edgard Blücher, São Paulo (in Portuguese).
(12) Pindyck, R.S. & Rubinfeld, D.L. (1998). Econometric models and economic forecasts. 4th edn., McGraw-Hill, New York.
(13) Weigend, A.S. & Gershenfeld, N.A. (1994). Time Series Prediction: Forecasting the Future and Understanding the Past. Addison Wesley, Reading.
Recebido em 03/2006; aceito em 06/2007 após 1 revisão
Received March 2006; accepted June 2007 after 1 revision
- (1) Bishop, C.M. (1995). Neural Networks for Pattern Recognition Oxford University Press Inc., New York.
Publication Dates
-
Publication in this collection
25 Sept 2007 -
Date of issue
Aug 2007
History
-
Received
Mar 2006 -
Accepted
Mar 2007




















