Resumos
O presente trabalho apresenta um Algoritmo Transgenético para a solução do Problema do Caixeiro Comprador Capacitado Simétrico. O algoritmo é baseado em endossimbiose e outras transformações do fluxo intracelular. O algoritmo é descrito e experimentos computacionais são relatados no sentido de validar a eficiência da abordagem. São também apresentadas novas melhores soluções para 17 instâncias de um conhecido banco de instâncias para o problema.
problema do caixeiro comprador capacitado simétrico; algoritmos evolucionários; algoritmos transgenéticos
This paper presents a Transgenetic Algorithm to solve the Symmetric Capacitated Traveling Purchaser Problem. The biological inspiration of the proposed algorithm comes from the endosymbiotic theory of evolution. The algorithm is described and the results of computational experiments are reported. The performance of the algorithm is compared with other recent work presented in the literature. New best solutions for 17 instances of a known benchmark are reported.
symmetric capacitated traveling purchaser problem; evolutionary algorithms; transgenetic algorithms
Algoritmo transgenético aplicado ao problema do caixeiro comprador capacitado simétrico
Marco César Goldbarg* * Corresponding author / autor para quem as correspondências devem ser encaminhadas ; Ligia Bariani Bagi; Elizabeth Ferreira Gouvêa Goldbarg
Universidade Federal do Rio Grande do Norte (UFRN) Natal RN, Brasil gold@dimap.ufrn.br; ligiabagi@yahoo.com.br; beth@dimap.ufrn.br
RESUMO
O presente trabalho apresenta um Algoritmo Transgenético para a solução do Problema do Caixeiro Comprador Capacitado Simétrico. O algoritmo é baseado em endossimbiose e outras transformações do fluxo intracelular. O algoritmo é descrito e experimentos computacionais são relatados no sentido de validar a eficiência da abordagem. São também apresentadas novas melhores soluções para 17 instâncias de um conhecido banco de instâncias para o problema.
Palavras-chave: problema do caixeiro comprador capacitado simétrico; algoritmos evolucionários; algoritmos transgenéticos.
ABSTRACT
This paper presents a Transgenetic Algorithm to solve the Symmetric Capacitated Traveling Purchaser Problem. The biological inspiration of the proposed algorithm comes from the endosymbiotic theory of evolution. The algorithm is described and the results of computational experiments are reported. The performance of the algorithm is compared with other recent work presented in the literature. New best solutions for 17 instances of a known benchmark are reported.
Keywords: symmetric capacitated traveling purchaser problem; evolutionary algorithms; transgenetic algorithms.
1. Introdução
Os Algoritmos Transgenéticos pertencem à classe dos algoritmos evolucionários e apóiam sua metáfora na endossimbiose e propriedades do fluxo intracelular (Goldbarg & Goldbarg, 2002). A endossimbiose é uma teoria evolucionária que baseia sua formulação na união de indivíduos de naturezas distintas de diferentes espécies para a constituição de saltos adaptativos ou a formação de espécies híbridas ou novas (Morowitz, 1992). A endossimbiose enfatiza a evolução por cooperação. Os algoritmos transgenéticos, adaptando os conceitos da endossimbiose ao contexto computacional, propõem a execução da evolução através de um processo de troca de informações entre uma população de cromossomos simbiontes e um hospedeiro. A troca é intermediada e influenciada por vetores transgenéticos que, mimetizando os verdadeiros atuadores microbiais e celulares, operacionalizam a obtenção e compartilhamento de informações genéticas. As informações de manipulação são no processo evolucionário ou de fontes externas.
No presente trabalho a abordagem é aplicada a um problema NP-Árduo denominado Traveling Purchaser Problem (TPP) ou Problema do Caixeiro Comprador (PCCo), uma generalização do Problema do Caixeiro Viajante. Nessa variante um comprador deve programar uma rota sobre os vértices de um grafo G de modo a, visitando as cidades-mercado, adquirir da forma mais barata possível um conjunto de itens que são necessários ao comprador e ofertados segundo diferentes custos e quantidades nas cidades representadas pelos vértices de G.
Considerando um domicílio v0 , um conjunto de mercados M={v1, v2,..., vm} e um conjunto de produtos K={f1, f2,..., fn}, o problema pode ser representado em um grafo G = (V,E) simples e não direcionado em que V = {v0}ÈM é o conjunto de vértices e E = {(vi, vj): vi, vj ÎV, i<j} é o conjunto de arestas. Cada produto fk está associado a uma demanda dk disponível em um subconjunto de mercados Mk Í M, sendo bki o preço do produto fk no mercado vie cij o custo da viagem entre vi e vj.
O PCCo consiste em determinar uma rota em G iniciando e terminando em v0 , passando pelos vértices necessários de modo a adquirir os produtos fk , k=1,..,n, necessários ao atendimento das demandas dk minimizando-se o custo de aquisição dos produtos somado ao custo do deslocamento no grafo. Denotando-se por qki o número de unidades do produto fk disponível no mercado vi , o presente estudo vai abordar a situação em que dk> qki >0, sendo dk > 1, "fk Î K e "vi Î Mk e  qki > dk, também denominado Problema do Caixeiro Comprador Capacitado (PCCC). O PCCC pode ser reduzido ao Problema do Caixeiro Viajante no caso particular de m = n, |Mk| = 1 para todo fkÎ K e dk= 1.
qki > dk, também denominado Problema do Caixeiro Comprador Capacitado (PCCC). O PCCC pode ser reduzido ao Problema do Caixeiro Viajante no caso particular de m = n, |Mk| = 1 para todo fkÎ K e dk= 1.
O presente trabalho apresenta um breve histórico dos algoritmos desenvolvidos para o Problema Caixeiro Comprador na seção 2. Na seção 3 são introduzidos conceitos da metáfora endossimbiótica empregada no algoritmo proposto. Também, é apresentado na seção 3 um pequeno levantamento bibliográfico sobre algoritmos baseados no conceito de simbiose e endossimbiose. Os conceitos básicos do algoritmo proposto e sua aplicação ao PCCC são apresentados na seção 4. Os resultados de experimentos computacionais são relatados na seção 5. Finalmente, a seção 6 apresenta as conclusões do trabalho, bem como tece considerações sobre futuras melhorias do algoritmo.
2. Revisão Bibliográfica dos Algoritmos de Solução do Caixeiro Comprador
Burstall (1966) descreveu um problema real com estrutura similar ao PCCo em uma firma de produção de tubos, no entanto seu modelo foi descrito como um problema de scheduling. O método de solução apresentado por Burstall (1966) foi heurístico e baseado no trabalho de Lomnicki (1966). Buzacott & Dutta (1971) desenvolveram um procedimento exato para a solução do modelo de Burstall via programação dinâmica. O primeiro trabalho da literatura abordando o problema em sua forma atual deve-se a Ramesh (1981), onde um algoritmo exato e uma heurística são apresentados para o problema. O algoritmo exato se baseia em uma busca lexicográfica, onde cada solução é representada como uma seqüência de símbolos. A estratégia de solução se faz análoga à busca por uma palavra específica de um dicionário. A partir de uma palavra inicial, as soluções são geradas de acordo com uma hierarquia que reflete seus valores. Cada palavra parcial define um bloco de soluções, e para cada bloco de soluções um limite inferior é calculado. Se o limite inferior excede o valor da solução conhecida (solução experimental), o bloco de palavras é rejeitado, pois não contem soluções com valores melhores que a solução experimental, desta forma o próximo bloco de soluções é explorado. No entanto, o limite inferior depende somente do custo da viagem de diferentes mercados para o mercado inicial e é independente do preço de compra das mercadorias. Devido a conseguir resolver apenas problemas pequenos, uma heurística foi desenvolvida baseada no mesmo procedimento de busca do algoritmo exato. O algoritmo executa a busca até que uma solução viável seja encontrada. Essa solução vai sendo modificada examinando-se a inclusão de cada mercado até que todos os mercados sejam examinados ou até que o valor da solução exceda o valor da melhor solução corrente.
Singh & van Oudheusden (1997) desenvolveram um algoritmo branch-and-bound para o PCCo baseado na idéia de quebrar o conjunto de todos os possíveis caminhos em subconjuntos cada vez menores e então calcular para cada um deles os limites inferiores incluindo a soma da viagem e a soma da compra dos produtos. O limite inferior é calculado resolvendo uma relaxação do problema baseada na formulação via o Problema de Localização de Facilidades não Capacitado (Uncapacitated Facility Location Problem). O trabalho testa o algoritmo em 65 problemas assimétricos com o número de mercados variando entre 10 e 25, e o de produtos entre 10 e 100. Um algoritmo branch-and-cut foi recentemente proposto por Laporte et al. (2003).
Na abordagem heurística um dos primeiros trabalhos deve-se a Golden et al. (1981) que propõem a Heurística de Economias Generalizadas (Generalized Savings Heuristic). A heurística inicia com um ciclo contendo o mercado inicial e o mercado que oferece o maior número de produtos do que qualquer outro mercado com o menor custo. Se existir empate, escolhe-se o mercado com o menor preço total. No passo de economia o ciclo é alterado pela introdução de um mercado que produza uma menor soma nos custos dos produtos na solução. A heurística termina quando nenhuma economia pode ser alcançada pela introdução de novos mercados. Esta heurística foi modificada por Ong (1982) que propôs a Heurística de Redução de Rota (Tour Reduction Heuristic). A heurística começa com um subconjunto de mercados oferecendo os n produtos e, iterativamente, retira os mercados que oferecem o maior custo até que nenhuma melhoria adicional possa ser obtida.
Pearn & Chien (1998) sugeriram modificações das heurísticas propostas nos trabalhos de Ramesh (1981), Golden et al. (1981) e Ong (1982). No trabalho de Pearn & Chien (1998) são, ainda, apresentadas duas versões da Heurística de Adição de Comodidades (Commodity Adding Heuristic) apresentada em trabalho anterior dos autores.
Vob (1996) apresentou uma metaheurística baseada em busca tabu e simulated annealing para (PCCo). No trabalho de Vob são apresentadas duas estratégias dinâmicas para o controle da lista tabu: o método da eliminação reversa (reverse elimination method) e o método da seqüência de cancelamento (cancellation sequence method). Dois procedimentos heurísticos, acréscimo (ADD-procedure) e decréscimo (DROP-procedure), também foram construídos para gerar a solução inicial. O primeiro é um procedimento iterativo que constrói um possível caminho adicionando novos mercados de acordo com um critério de economia. Assim que um ciclo aceitável for criado, os mercados restantes são adicionados até que nenhuma melhoria na função objetivo seja possível. O procedimento de decréscimo é o inverso do de acréscimo. Inicia-se com uma solução viável que contém todos os mercados. O procedimento remove em cada passo o mercado que irá gerar a maior redução na função objetivo. Se não existir nenhuma redução possível, é terminado com uma solução praticável. Este último procedimento é também descrito por Ong (1982) na Heurística de Redução de Rota.
Boctor et al. (2003) propõem algoritmos baseados em busca tabu para o problema capacitado e não capacitado. Estes algoritmos foram testados segundo várias combinações em instâncias de maior porte e comparados com as duas versões da Heurística de Adição de Comodidades descritas por Pearn & Chien (1998).
Teeninga & Volgenant (2004) desenvolveram sub-rotinas que foram incorporadas aos algoritmos de Golden et al. (1981), Ong (1982) e Singh & van Oudheusden (1997).
Riera-Ledesma & Salazar-González (2005) apresentaram uma heurística aplicada ao problema simétrico, presentemente denominada de RL-SG, baseada em um esquema que desenvolve uma busca local segundo duas estruturas de vizinhança e uma estratégia de diversificação denominada shaking. A vizinhança proposta pelo algoritmo realiza um procedimento de l -troca, em substituição aos procedimentos clássicos de 1-troca, l>1. A solução do comprador é obtida removendo-se trechos do ciclo vários mercados visitados em seqüência na rota, e inserindo-se outros mercados em seu lugar. O novo conjunto de mercados proposto pelos procedimentos de inserção e troca é submetido a uma busca local baseada no procedimento de Lin & Kernighan (1973) para o Problema do Caixeiro Viajante, com o objetivo de obter uma rota de boa qualidade. O procedimento shaking diversifica a solução quando uma melhoria não é mais encontrada no passo de busca local. Um experimento computacional compara o desempenho da heurística proposta com o algoritmo de Boctor et al. (2003). Recentemente, Bontoux & Feillet (2008) apresentaram um algoritmo em colônia de formigas aplicado ao problema não capacitado simétrico que, conclusivamente, supera em desempenho o algoritmo de Riera-Ledesma & Salazar-González (2005).
3. Abordagem Endossimbiótica
A teoria da evolução endossimbiótica representa um aperfeiçoamento na teoria da Simbiogenese proposta por Ivan Wallin em seu livro "Symbiogenesis and the Origin of Species" publicado em 1926. A Teoria Serial Endossimbiótica, desenvolvida por diversos autores (McFadden, 2001; Witzany, 2006), foi popularizada por Margulis (1991) e diz que um novo organismo pode surgir pela fusão de dois ou mais organismos independentes. Mais precisamente, afirma que organismos que evoluíram de forma independente são capazes de se unir em um sistema simbiótico e, eventualmente, constituir um só organismo. A proposta sugere, portanto, que a competição não representa a única via promotora do aperfeiçoamento genético. O aprofundamento teórico da abordagem propõe, inclusive, que a reprodução sexual teve origem em uma variação da endossimbiose e que tal modalidade de reprodução primordialmente representou uma forma de prevenir a perpetuação de alterações genéticas provocados pelas transcrições microbiais (Margulis & Sagan, 1986). Segundo Margulis, a reprodução sexual teria emergido devido à necessidade de preservação da continuidade da identidade genética dos organismos eucarióticos mais complexos frente à permeabilidade genética típica do contexto celular. Tal permeabilidade que facilitaria a evolução de células procarióticas, igualmente poderia ser nociva no contexto de complexos tecidos eucarióticos.
A comprovação da proposta de Margulis tem sido corroborada por sucessivas descobertas de mecanismos evolucionários naturais voltados para o compartilhamento direto de DNA entre microorganismos / células (Hadfield & Axton, 1999). Tais mecanismos são muito primitivos e foram constituídos no sentido de permitirem a ocorrência de alterações permanentes no código genético de células e microorganismos, facilitando a emergência de saltos de adequação. Um conhecido conjunto desses processos é apresentado pela literatura sob o nome de "transferência horizontal". A transferência horizontal de genes é definida como o movimento de material genético entre bactérias de modo distinto da transferência vertical. A transferência vertical de genes se dá através da reprodução, onde uma bactéria herda material genético de seu ancestral. Portanto, a transferência horizontal de genes se dá entre microorganismos de modo distinto ao da reprodução. Dois dos conhecidos veículos de transferência horizontal que serviram de inspiração para o algoritmo proposto neste trabalho são os plasmídios e os transposons. Os plasmídios são partículas genéticas móveis, anéis de DNA, que podem ser inter-cambiadas entre certas células e que podem se replicar independente de um cromossomo. Os transposons, ou genes saltadores, são elementos genéticos que podem se mover espontaneamente de uma posição para outra dentro do DNA.
Na Computação Evolucionária existem diversos trabalhos cuja inspiração biológica é a simbiose. O primeiro desses trabalhos deve-se a Hillis (1990). Trabalhos que mimetizam a endossimbiose surgiram com Bull & Fogarty (1995). Kim et al. (2001) se baseiam no trabalho de Bull & Fogarty (1995) e propõem um algoritmo co-evolucionário que introduz o conceito de indivíduos endossimbiontes formados pela união de dois outros indivíduos. Outros algoritmos abordando a metáfora são apresentados na literatura dando mais ênfase à co-evolução ou à simbiose (não propriamente a endossimbiose). Nessa linha destacam-se os trabalhos de Tsujimura et al. (2001), Pagie & Mitchell (2002), Rosin & Belew (1997), Husbands (1994), De La Cal Marín et al. (2004), Kim et al. (2003), e Michaelian (1998). Os mecanismos de transferência horizontal igualmente inspiraram operadores para algoritmos genéticos, dentre eles os trabalhos de Kubota et al. (1996), Nawa et al. (1999), Mühlenbein & Voigt, (1995), Simões & Costa (2001a e 2001b) e Chan et al. (2005).
O presente trabalho apresenta um tipo de algoritmo evolucionário que possui sua inspiração baseada na teoria da evolução endossimbiótica. O contexto da evolução dos Algoritmos Transgenéticos, diferentemente dos anteriormente citados, ocorre no interior de uma célula. Sob tal perspectiva, uma população de endossimbiontes co-evolve com uma célula hospedeira, de modo que a adequação do sistema simbionte/hospedeiro seja melhorada. O Algoritmo Computacional copia o fenômeno natural de troca das informações genéticas contidas no DNA dos endossimbiontes com as informações contidas na célula hospedeira. O processo de evolução da população de endossimbiontes e a integração de sua informação às informações do hospedeiro são intermediados por agentes igualmente inspirados em veículos naturais de transferência horizontal de genes. Tais agentes são denominados vetores transgenéticos. Neste trabalho, os vetores transgenéticos recebem o mesmo nome dos veículos naturais nos quais foram inspirados, sendo eles: plasmídios e transposons. Os Algoritmos Transgenéticos são descritos na seção seguinte.
4. Algoritmo Transgenético
A evolução biológica natural tem sido uma fonte de inspiração para o desenvolvimento de métodos de otimização. Alguns desses métodos são denominados de algoritmos evolucionários. Segundo a definição de Michalewicz & Fogel (2000), os algoritmos evolucionários são métodos estocásticos de busca que operam em uma população de soluções candidatas. A população evolui iterativamente por meio de variações e seleção até que um critério de parada seja satisfeito. Nesta família de técnicas encontram-se os Algoritmos Transgenéticos que são constituídos em três contextos e da seguinte forma:
-
Uma população de soluções candidatas (correspondendo aos cromossomos endossimbiontes que vivem no interior da célula).
-
Uma base de dados com informações sobre o problema e sobre o processo evolucionário (correspondendo ao DNA do hospedeiro). No hospedeiro encontram-se abrigadas informações sobre o problema (obtidas
a priori) e informações obtidas no processo evolucionário (obtidas
a posteriori). O contexto da célula contém ainda as regras que coordenam e realimentam o processo evolucionário (Goldbarg & Goldbarg, 2002).
-
Uma população de vetores que modificam as soluções candidatas, transportando informação da base de dados do hospedeiro para os cromossomos e realizando o rearranjo do código genético dos cromossomos (correspondendo aos agentes do fluxo intra-extracelular). Os vetores operacionalizam a intensificação e diversificação da busca.
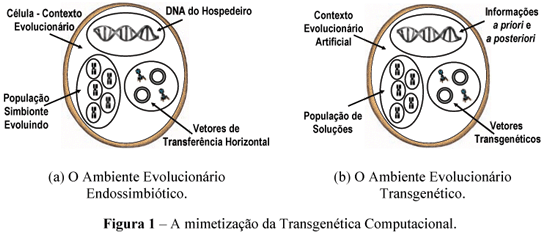
A Figura 1 exemplifica a mimetização realizada pela abordagem. Os três contextos da endossimbiose são ressaltados dentro das elipses.
O processo de endossimbiose artificial acontece mediante a troca de informações entre os três contextos anteriormente descritos. Os dados obtidos a priori podem, por exemplo, estarem associados a limites do problema (inferiores ou superiores), soluções heurísticas ou informações decorrentes de análise estatística da estrutura de casos específicos do problema. Soluções de elite, informações sobre a análise da amostra do espaço de busca contida na população ou estatísticas do processo evolucionário são exemplos de informações obtidas durante a busca, ditas informações a posteriori. As informações pertencentes ao contexto do hospedeiro podem ser codificadas no formato genético como, por exemplo, uma solução parcial, ou em um formato abstrato, como o representado por procedimentos ou regras de rearranjo genético.
Um vetor transgenético, l , é uma dupla l = (I, F), onde I é uma cadeia de informação e Fé um método de manipulação, F = (p1,...,ps), pj, j=1,...,s, são procedimentos que definem a atuação do vetor. Ao infiltrarem sua cadeia de informação I em um cromossomo S, os vetores transgenéticos provavelmente alterarão o código genético de S e, por conseguinte, sua adequação. A Tabela 1 resume os procedimentos que compõem o método de manipulação dos dois vetores transgenéticos que serão utilizados no algoritmo proposto.
Um vetor lé dito um plasmídio quando sua cadeia de informação I é traduzida no formato genético uma subcadeia de DNA e seu método utiliza somente os procedimentos p1 e p2. Um vetor lé dito transposon quando sua cadeia de informação corresponde a uma regra ou método e seu método utiliza os procedimentos p1, p2 e p3. A fim de ilustrar esses conceitos, um breve exemplo será dado para o Problema do Caixeiro Viajante.
Dado um conjunto de n cidades e distâncias entre cada par de cidades, o Problema do Caixeiro Viajante, PCV, consiste em encontrar um ciclo de comprimento mínimo que passe por todas as cidades, sendo que cada uma delas é visitada uma única vez. Uma representação usual de cromossomos de algoritmos evolucionários para este problema é através de permutações. Uma permutação das n cidades descreve uma seqüência de visitas a todas as cidades do problema considerado. Assim, como a cadeia de informação de um plasmídio é definida como uma subcadeia de DNA, esta informação pode ser entendida como parte de uma solução para o problema, ou seja, uma seqüência com r cidades, r < n. A seqüência que define a cadeia de informações do plasmídio é obtida da base de dados. Na base de dados pode-se ter, por exemplo, uma árvore geradora mínima do grafo que representa o PCV. A árvore geradora mínima é um limite inferior para a solução do problema e pode ser utilizada como uma fonte de informação para obtenção das cadeias dos plasmídios. Desse modo, a cadeia de informação do plasmídio pode ser uma seqüência de r cidades que formem um caminho na árvore geradora mínima. Um outro exemplo de fonte de informação para cadeias de plasmídios para o PCV é dada no trabalho de Goldbarg et al. (2003), onde se utiliza análise estatística da estrutura do problema através da análise de grupamentos. Um exemplo de procedimentos para o plasmídio para o PCV é mostrado na Tabela 2. No procedimento p1, é estabelecido que se a adequação do cromossomo manipulado, a(S), for melhor que a adequação do cromossomo original, a(S), então o cromossomo é suscetível à manipulação. O procedimento p2, estabelece que a cadeia de informação, I, do plasmídio é inserida no cromossomo S a partir da posição em S correspondente ao primeiro alelo de I. Como as cidades constantes na seqüência de I ficam repetidas no cromossomo, é necessário removê-las. A remoção é feita nas cidades que estão em locais que não correspondem à cadeia inserida.
No caso do transposon para o PCV a cadeia de informação pode corresponder a uma regra para remover r arestas. O transposon fará isso em uma parte pré-especificada do cromossomo estabelecida no procedimento p3. A Tabela 3 mostra um exemplo de procedimentos de um transposon para o PCV. Considere que a regra da cadeia I seja remover as r arestas do trecho especificado com o maior peso w(ei), i = 1, ..., r. O procedimento de ataque, p1, verifica se a diferença entre o peso das k arestas removidas e o peso de r arestas aleatórias, w(ei), i = 1, ..., r, que podem ser utilizadas para refazer o ciclo é maior que 0. No procedimento p2 as novas r arestas são escolhidas e incluídas no ciclo.
Três classes de regras controlam o processo evolucionário de um algoritmo transgenético. As regras do tipo 1 dirigem a construção da cadeia de informação I que será transportada por um vetor transgenético l. Estas regras podem estabelecer a utilização de qualquer conhecimento armazenado na base de dados do hospedeiro. No exemplo descrito anteriormente para o PCV, pode-se criar uma regra do tipo 1 que estabeleça que a cadeia de informação do plasmídio é retirada de uma fonte de informação escolhida aleatoriamente na base de dados. As regras do tipo 2 definem como a informação I será transcrita no cromossomo S, isto é o operador que será utilizado por l. As regras de transcrição podem evoluir em conformidade com a resistência à manipulação demonstrada pelos cromossomos. Em um algoritmo poderão existir várias regras do tipo 1 e 2. As regras tipo 3 direcionam o processo evolucionário estabelecendo, por exemplo, quantos e quais vetores são criados a cada iteração, quantos cromossomos são manipulados por um vetor específico (ou conjunto de vetores), quando e como a base de dados do hospedeiro é atualizada. A Figura 1 ilustra as etapas principais reguladas pelas três classes de regras no processo evolucionário de um algoritmo transgenético. É mostrado que regras do tipo 1 definem a formação da cadeia dos vetores transgenéticos obtidas a partir da base de dados do hospedeiro, regras do tipo 2 definem como o vetor atua sobre o cromossomos e as regras do tipo 3 controlam o processo de interação entre os vetores, cromossomos e a base de dados do hospedeiro. Por ocasião da descrição do algoritmo tais regras não serão formalmente destacadas para evitar sobrecarregar o texto, todavia elas são presentemente sumarizadas visando fornecer uma visão panorâmica da abordagem. A Figura 2 ressalta como os três contextos cooperativos da Transgenética Computacional interagem.
O Quadro 1 apresenta o pseudo-código de um algoritmo transgenético genérico. No início é gerada uma população de cromossomos. O algoritmo então carrega as regras que serão utilizadas por ele e constrói a base de informações a priori e a posteriori. Os passos de 5 a 8 são então repetidos até que um critério de parada seja satisfeito. Em cada iteração, são gerados os vetores transgenéticos e selecionados os cromossomos que serão manipulados. Depois da atuação dos vetores sobre os cromossomos, se necessário, as regras e a base de dados são atualizadas.
Tendo em vista a Transgenética Computacional compartilhar vários conceitos com a Computação Evolucionária tradicional e ser ainda uma abordagem pouco difundida, convém ressaltar algumas de suas peculiaridades:
-
Na evolução endossimbiótica vários tipos de informações se combinam livremente. A informação é organizada em contextos interdependentes, contudo autônomos. Os contextos se ligam em rede e são equivalentes em importância. Um comportamento complexo é criado através do aninhamento de contextos de fácil configuração. A transgenética, ao mimetizar a evolução endossimbiótica, se diferencia dos Algoritmos Genéticos que consideram apenas a informação contida no contexto genético. Por outro lado, os Algoritmos Meméticos (Merz & Freisleben, 1999) e Culturais (Coello & Becerra, 2004) mesmo permitindo a consideração de um contexto adicional o contexto cultural, entendem a estruturação da informação de modo hierarquizado. A dimensão cultural evolui mais rapidamente, sendo ainda hierarquicamente superior à dimensão genética, cabe-lhe o papel de guiar a última introduzir viés na busca.
-
A população de cromossomos endossimbiontes possui um papel evolucionário distinto da população de cromossomos dos algoritmos genéticos. Representa uma memória de curto prazo codificada exclusivamente no formato genético o que torna possível sua alteração ser algoritmicamente eficiente. Ela sofre a pressão evolucionária imposta pelas tentativas de transcrição dos vetores transgenéticos. Tão pouco ocorre qualquer forma de recombinação direta entre o material genético dessa população.
-
As mutações não desempenham papel significativo na evolução endossimbiótica. A mistura das informações do contexto do hospedeiro com as existentes na população de cromossomos produz a diversificação necessária. Assim, a transgenética desenvolve sua evolução dispensando completamente o mecanismo de mutações para promover a alteração de conteúdo genético seja no reservatório representado pelos endossimbiontes, seja no reservatório do hospedeiro. As manipulações dos vetores nunca visam exclusivamente diversificar a busca. Ressalte-se que as duas últimas características (reprodução e mutação do material genético) são aspectos tão marcantes para os Algoritmos Genéticos e algoritmos derivados que alguns autores definem Algoritmos Genéticos simplesmente como os algoritmos baseados em uma população de cromossomos e dotada das duas propriedades referidas (Goldberg, 1989).
-
O hospedeiro representa, com simplicidade, uma memória de longo prazo repleta de boas informações genéticas e não genéticas mimetizando o papel do citoplasma de uma célula.
-
Os vetores transgenéticos podem sofrer várias formas de pressão seletiva. Uma primeira forma associada à escolha de suas cadeias de informação, o que pode ser realizado através de avaliação direta da cadeia na ocasião de sua obtenção. Uma segunda forma é relativa à eficácia de sua transcrição. Caso mais de um agente ataque simultaneamente um cromossomo, a pressão de seleção se dará no sentido da escolha daquele que executar a melhor transcrição.
-
Os vetores transgenéticos possuem características que não encontram paralelo em outros algoritmos evolucionários:
Vetores do mesmo tipo podem se recombinar (por exemplo, plasmídios que, combinando suas cadeias, formem novo tipo de vetor) na busca de uma melhor eficiência de manipulação. Aqui recombinar não significa reproduzir, e sim alterar método ou conteúdo (o que permite a constituição de um processo de evolução do vetor).
Vetores de diferentes tipos podem ser empregados simultaneamente de modo que a composição de diferentes habilidades de manipulação resulte em uma evolução mais eficiente. Nesse caso a própria composição pode ser regulada pela evolução (o que permite a evolução da estratégia de manipulação (Goldbarg et al., 2007)).
O aspecto volátil dos vetores permite que a informação transportada seja passível de avaliação per si independentemente de influências dos endossimbiontes ou do hospedeiro (o que permite considerar a evolução da informação de manipulação tanto sob a ótica da eficácia, como da eficiência).
A seção 4.1 exemplifica a aplicação de um algoritmo transgenético ao PCCC.
4.1 Algoritmo Transgenético para o PCCC
Com o objetivo de ilustrar cada parte do algoritmo transgenético para o PCCC, nesta seção apresenta-se um exemplo com seis mercados e quatro produtos (e um domicílio). A instância exemplo é mostrada na Figura 3(a), onde se exibe a distribuição da quantidade e do custo de cada produto em cada mercado do grafo, bem como o valor do vetor de demanda dk.
Inicialmente, será descrita a constituição de cada um dos três contextos do algoritmo transgenético proposto: os cromossomos, a base de dados do hospedeiro e os vetores transgenéticos.
As soluções do PCCC são representadas através de cromossomos que definem uma seqüência de visitas aos mercados, iniciando e terminando no vértice zero, o domicílio. A Figura 3(b) exemplifica uma solução válida para o problema. Os produtos ressaltados pelas células escurecidas estão sendo adquiridos no mercado associado. Observa-se que a solução não passa por todos os mercados grafo, não compra produtos em todos os mercados da rota e divide a compra do produto três nas cidades seis e cinco, em virtude do mercado seis, o mais barato, não oferecer a quantidade demandada.
A adequação do cromossomo é calculada somando-se o custo da rota com os custos de aquisição de cada produto nos mercados da rota. O custo de aquisição dos produtos corresponde ao preço mais barato pago por unidade adquirida. O quadro inferior direito da Figura 3(b) mostra o cálculo da adequação da solução proposta, separando a parcela relativa à compra dos produtos em relação à rota. Ao se dispor de uma seqüência de mercados visitados, o custo de aquisição dos produtos é fixado pela lógica da obrigação de comprar a maior quantidade possível de um produto no mercado mais barato. Assim, um cromossomo representado pela seqüência de visitas é suficiente para determinar completamente a solução do problema. No caso da Figura 3(b) o cromossomo possui adequação igual a 69.
A base de dados do hospedeiro é constituída com informações obtidas a priori e a posteriori. Apenas um tipo de informação a priori é utilizado no algoritmo proposto. A informação a priori é constituída por um ciclo Hamiltoniano em G obtido pela versão do algoritmo de Lin & Kernighan (1973) implementada por Applegate et al. (1999). Como informação a posteriori utiliza-se os quatro melhores cromossomos obtidos durante o processo de busca.
A evolução transgenética foi organizada de modo a utilizar simultaneamente dois tipos de vetores: plasmídios e transposons.
Uma regra do tipo 1 estabelece que a fonte de informação para a formação da cadeia do plasmídio é escolhida aleatoriamente com probabilidade uniforme dentre as cinco fontes constantes na base de dados do hospedeiro. As características do plasmídio para o PCCC são mostradas na Tabela 4. A cadeia de informação é formada por uma seqüência de r mercados. O procedimento p1 estabelece que o cromossomo é suscetível à manipulação caso a adequação do cromossomo manipulado, a(S) seja maior que a adequação do cromossomo original, a(S). A adequação é dada pelo inverso do custo da solução representada no cromossomo.
As características do transposon para o PCCC são mostradas na Tabela 5. A cadeia de informações estabelece a remoção de cada mercado do trecho definido em p3. A suscetibilidade ao ataque é definida da mesma forma do plasmídio. A operacionalização da remoção dos mercados é definida em p2 e realizada de forma iterativa. Inicialmente, o primeiro mercado do trecho definido em p3 é removido. Caso a remoção do mercado torne a solução representada no cromossomo inviável devido a impossibilidade de adquirir toda a demanda de algum(ns) produto(s), então novos mercados são inseridos no cromossomo até que a viabilidade seja atingida. Após a remoção de cada mercado testa-se se houve melhoria de adequação do cromossomo. É mantida a configuração que resulte na melhor adequação. Caso as tentativas de remoção de um mercado não resultem em qualquer melhoria do cromossomo, então o processo é repetido com a remoção de dois mercados. Os detalhes de implementação desse procedimento são descritos adiante na apresentação do algoritmo.
O pseudo-código do algoritmo proposto para o PCCC é mostrado no Quadro 2. Inicialmente, é gerada uma população de cromossomos. Um procedimento iterativo faz a inclusão aleatória de mercados em cada cromossomo até que se alcance uma solução viável. A rota gerada aleatoriamente no primeiro passo é submetida a um procedimento de busca local com a versão do algoritmo de Lin e Kernighan segundo Applegate et al. (1999). O banco de informações do hospedeiro é iniciado no passo 2.
O laço principal do algoritmo, descrito entre os passos 4-28, realiza o processo de busca em etapas. Em cada etapa é fixada uma probabilidade para o sorteio de um dos dois tipos de vetor transgenético, o qual será utilizado para manipular os cromossomos. Nos estágios iniciais, o algoritmo transgenético emprega mais intensamente o vetor plasmídio. Na medida em que a população de cromossomos evolui, as manipulações por transposons passam a ser mais freqüentes. A razão para isso é que no início as soluções geradas aleatoriamente, provavelmente, encontram-se distantes de ótimos locais. Portanto, trechos de informação obtidas das fontes do banco podem contribuir para melhorar as soluções aproximando-as de ótimos locais. Os rearranjos genéticos produzidos pelo transposons realizam procedimentos de intensificação em partes do cromossomo. Portanto, à medida que as soluções tornam-se melhores, o emprego dos transposons torna-se cada vez mais interessante. Uma das vantagens do emprego dos transposons é a possibilidade de empregar procedimentos de intensificação rápidos, uma vez que apenas parte da solução é considerada.
Os patamares de evolução são controlados pelos parâmetros h e b. São executadas, ao todo, h iterações do algoritmo, sendo que em cada conjunto de h/b iterações, a probabilidade de sorteio dos vetores se mantém fixa. A cada iteração, um tipo de vetor, plasmídio ou transposon, é sorteado. O contador j controla a mudança da probabilidade nos passos 3 e 27. No passo 7 a variável u recebe um inteiro aleatório no intervalo [1, h]. A comparação feita no passo 8 entre as variáveis u e j determina o tipo de vetor gerado na iteração.
Caso seja escolhido o vetor tipo plasmídio, são geradas e avaliadas k cadeias de informação. Na formação de cada cadeia, um cromossomo do banco de informações é escolhido aleatoriamente de acordo com uma distribuição uniforme, como fonte de informação. O comprimento da cadeia é sorteado aleatoriamente entre 3 e ën/8û posições. Um sumário experimento computacional envolvendo 4 instâncias 200x200 sorteadas aleatoriamente do banco teste fixou o intervalo entre as opções de 3 e ën/5û , ën/8û , ou ën/10û . O início da cadeia é também sorteado aleatoriamente na fonte selecionada (ciclo hamiltoniano ou cromossomos).
Cada cadeia representa uma seqüência de visitas, com os respectivos produtos e preços associados aos seus mercados. Atribui-se um valor a cada uma das k cadeias o qual é calculado através do somatório de três parcelas:
1. A soma do peso das arestas da cadeia
2. A soma dos menores valores dos produtos disponíveis em algum mercado da cadeia
3. A soma dos maiores valores dos produtos não disponíveis em algum mercado da cadeia.
A cadeia que tiver o menor valor associado é utilizada para formar o plasmídio que ataca toda a população de cromossomos. O operador de transcrição do vetor testa a inserção da cadeia de informação entre cada par de cidades do ciclo representado no cromossomo, preservando a melhor inserção possível. A Figura 4 ilustra o processo de infiltração descrito algoritmo do Quadro 3. Na figura os retângulos representam os mercados e a seqüência dos retângulos mapeia a seqüência de visitas da rota. As setas pontilhadas mostram as possíveis posições de infiltração da cadeia do plasmídio. O operador de infiltração elimina repetições de mercados na rota, com base na seqüência de mercados infiltrados.
No algoritmo do Quadro 3, inicialmente faz-se uma cópia do cromossomo C em C. No passo 2 todos os mercados que estão simultaneamente na cadeia do vetor e no cromossomo considerado são removidos.
A variável c_best que guarda o valor da melhor solução gerada no procedimento e a variável índice que guarda a melhor posição para inserção da cadeia do plasmídio são iniciadas no passo 3. Entre os passos 4 e 8 todas as posições de infiltração da cadeia são testadas. No passo 5, a cadeia do plasmídio é inserida na posição q de C e o cromossomo resultante é guardado em C". Caso o custo da solução em C" seja menor que o melhor custo corrente, então a posição de infiltração é copiada para a variável índice. No passo 9 a cadeia é finalmente transcrita em C na posição definida em índice. Caso existam mercados onde nenhum produto é adquirido em C, eles são removidos no passo 10. No passo 11, a solução representada no cromossomo é submetida a um procedimento de busca local no procedimento LK(). Este procedimento implementa a versão de Applegate et al. (1999) do algoritmo de busca de Lin & Kernighan (1973). Finalmente, se houve melhoria o algoritmo retorna C no passo 12, caso contrário o algoritmo retorna o cromossomo original no passo 13. Caso o vetor escolhido seja o transposon, o algoritmo transgenético executa os passos 16 e 17 do Quadro 2.
No algoritmo descrito no Quadro 4, inicialmente o cromossomo original é copiado para C". São criados dois conjuntos de vértices no passo 2: Y e X. No conjunto Y estão os mercados que não estão no cromossomo considerado. No conjunto X estão os mercados do cromossomo que estão entre as posições definidas no procedimento p3 do vetor transgenético. No laço entre os passos 4 e 16, os mercados de X são removidos do cromossomo. No passo 4, o cromossomo C recebe o resultado da remoção do mercado definido por q do cromossomo original. Pode ser que após a remoção do mercado a solução torne-se inviável. Nesse caso, é necessário incluir novos mercados em C até que o mesmo corresponda a uma solução viável. No procedimento inclui_novos_mercados(), um valor é atribuído a cada mercado de Y. Esse valor é calculado pelo menor aumento que a adição daquele mercado trará à rota definida em C mais os preços mais altos dos produtos que ainda continuam sem ser adquiridos caso esse mercado seja incluído em C. O menor aumento da rota é calculado pelo critério utilizado na heurística de inserção para o Problema do Caixeiro Viajante de Rosenkrantz et al. (1977). O vértice com o menor valor dentre todos os demais é incluído em C. No passo 6, o procedimento de busca local é chamado para C. Caso a solução em C seja melhor que a solução em C", C é copiado para C". Caso contrário, é tentada a remoção de dois vértices entre os passos 9 e 13. Remove-se o vértice q e o vértice seguinte q+1. Os vértices em X são implementados como uma lista circular, portanto no caso de q representar o último vértice de X, q+1 representa o primeiro vértice. Verifica-se no passo 15 se existem mercados onde produtos não são adquiridos em C" e em caso positivo, os mesmos são removidos.
A Figura 5 ilustra a remoção de mercados que é possível de ser realizada por um vetor transposon, considerando o ciclo 0-4-3-2-1-6-5-0 (o vértice 0 é omitido no ciclo do cromossomo por ser uma posição previamente conhecida). Na figura o transposon sorteia o trecho de atuação 3-2-1-6. Um transposon poderia remover até r-1 mercados, sendo r o comprimento da cadeia definida pelo procedimento p3.
Finalmente, a melhor solução obtida no procedimento é retornada no passo 17. No passo 19 do Quadro 2 verifica-se a suscetibilidade do cromossomo ao ataque. Caso o procedimento procedimento_p1() retorne o valor verdadeiro, o cromossomo original é substituído pelo cromossomo resultante do ataque no passo 20. No passo 21 verifica-se se o novo cromossomo representa uma solução melhor que todas as encontradas até o momento no procedimento campeão(). Em caso positivo, o banco de informações BIH é atualizado com a sua inclusão e a remoção do cromossomo de pior adequação no passo 22 do Quadro 2.
5. Resultados dos Experimentos Computacionais
Os testes foram realizados tendo por base 487 instâncias simétricas da classe 4 do banco TPPLib (disponíveis em http://webpages.ull.es/users/jriera/TPP.htm) que possuem alguma solução conhecida e que é considerada a classe de mais difícil solução do banco (Laport et al., 2003). Destas, 440 instâncias possuem soluções ótimas obtidas pelo método descrito no trabalho de Laporte et al. (2003). Os resultados para os dois grupos de instâncias são apresentados separadamente. Cada instância é identificada pelo número de produtos, n, variando entre 50 e 200, pelo número de mercados, m, variando entre 50 e 200, por uma constante a utilizada na formação da instância e pelo identificador ID que varia de 1 a 5. Conseqüentemente, o banco de instâncias apresenta cinco instâncias geradas para cada valor de n, m e a . A cada produto fj , j = 1, ..., n, está associado um conjunto de mercados Mj , selecionados aleatoriamente no intervalo [1,m]. O custo do produto j no mercado i, bji é gerado aleatoriamente no intervalo [1,500] de acordo com uma distribuição uniforme. O número de unidades cada produto fj em cada mercado vi , qji foi gerado de forma aleatória e uniforme no intervalo [1,15], j = 1, ..., n, i = 1, ..., m . O valor da demanda dj é obtido conforme a seguinte fórmula:
para a = 0,1; 0,3; 0,5; 0,7; 0,9; 0,95 e 0,99.
As tabelas de comparação dos resultados para as 440 instâncias com ótimo conhecido possuem o formato sugerido nos trabalhos de Boctor et al. (2003) e Riera-Ledesma & Salazar-González (2005). O formato empregado na literatura tem a vantagem de permitir examinar o desempenho do algoritmo em uma tabela compacta, especialmente considerando o grande número de instâncias do banco. Nesse formato calcula-se a média dos melhores valores obtidos nas execuções de um algoritmo e compara-se este valor com a média das soluções ótimas das instâncias examinadas. Nas tabelas de comparação de resultados, a coluna "%gap" descreve o afastamento percentual entre essas duas medidas. A coluna T(s) relata o tempo médio em segundos de processamento nas instâncias examinadas. As demais colunas mostram a identificação do algoritmo a ser comparado. As linhas estão associadas às instâncias conforme especificado em cada tabela. Infelizmente, no formato de comparação adotado pela literatura algumas informações relevantes não são relatadas como, por exemplo, a percentagem de ótimos alcançados pelas execuções do algoritmo.
Ao testes computacionais foram executados em uma plataforma Pentium IV 1.8GHz, com 512 Mb de RAM, sistema operacional Ubuntu Linux e compilador g++.
O experimento computacional foi dividido em três partes. A primeira delas, apresentada na seção 5.1, visou determinar o desempenho dos vetores transgenéticos e sua contribuição ao processo de busca. A primeira parte do experimento concentra-se principalmente em obter dados que permitam concluir se existem vantagens no combinado de diferentes vetores transgenéticos. Os parâmetros do algoritmo proposto foram ajustados em testes preliminares. Na seção 5.2 é feita uma análise dos parâmetros k, h e b, visando avaliar seu potencial de melhoria e guiar futuros aperfeiçoamentos no algoritmo. Finalmente, a seção 5.3 apresenta uma comparação do desempenho do algoritmo proposto com o melhor algoritmo apresentado na literatura para o problema considerado de modo a concluir sobre a exeqüibilidade prática da proposta, bem como avaliar sua eficiência em relação à literatura.
5.1 Desempenho dos Vetores Transgenéticos
A evolução proposta pelos algoritmos transgenéticos não exige a participação simultânea de mais de um tipo de vetor de manipulação. Como demonstrado em Goldbarg & Goldbarg (2002), uma evolução eficiente pode se dar exclusivamente pela troca de informações operacionalizadas através de plasmídios. O tipo de algoritmo transgenético cuja evolução considera exclusivamente a transcrição característica dos plasmídios foi denominado de ProtoG (Gouvêa, 2001). Pretendendo examinar as vantagens da utilização simultânea de mais de um vetor na solução do problema abordado, a Tabela 6 exibe uma comparação do algoritmo transgenético, AT, proposto no Quadro 2, executado considerando h = 40 e b = 4 em quatro diferentes versões. A tabela relata a média de 30 execuções para as 440 instâncias com valor ótimo conhecido.
O algoritmo "plasmídio" corresponde a um algoritmo do tipo ProtoG, sendo o mesmo algoritmo mostrado no Quadro 2 com probabilidade nula de utilização de transposons. O algoritmo "transposon" corresponde ao algoritmo AT sem o uso de plasmídios. O algoritmo "Plas/Trans 50%" corresponde a uma versão de AT em que existe a utilização simultânea de ambos os vetores com probabilidade fixada em 50% na escolha do vetor transgenético, portanto sem a graduação de probabilidade computada pelo parâmetro b. Finalmente, a coluna AT exibe os resultados do algoritmo implementado conforme descrito no Quadro 2.
Da análise da Tabela 6 verifica-se que, considerados os efeitos isolados, o vetor de transposição é significativamente mais eficiente que o vetor plasmídio no que tange à qualidade de solução do problema considerado. Por outro lado, o desempenho do plasmídio se mostra mais eficiente do que o transposon em tempo de processamento. O emprego conjunto e equiprovável dos vetores, todavia, revela uma solução de compromisso que tende produzir menor consumo de tempo computacional do que o associado ao uso exclusivo do transposon, e melhor qualidade de solução do que a obtida pelo uso exclusivo dos plasmídios. A Tabela 6 ainda demonstra que a estratégia de realizar a evolução em patamares, cujos resultados são mostrados na coluna AT, é mais vantajosa que o sorteio equiprovável resultando em ganhos quantitativos ou qualitativos, ou em ambos.
5.2 Análise de Sensibilidade de k, h , b
O valor de k
A Tabela 7 exibe a variação de desempenho verificada no algoritmo AT quando o número de cadeias de informação consideradas na formação de um plasmídio (passo 13 do Quadro 2) varia para os valores 10, 30 e 40. A tabela relata a média de 30 execuções para cada valor de k nas 440 instâncias com valor ótimo conhecido.
Observa-se que nas classes de instâncias onde m = 50, a = 0,1, a = 0,5 e a = 0,7, os resultados não se mostraram sensíveis à variação do parâmetro. Embora, os resultados não sejam conclusivamente favoráveis a um determinado valor de k, a coluna k = 30 deixa de exibir o melhor valor somente para a classe de instâncias onde a = 0,8. Comparando os algoritmos com k = 10 e k = 30, observa-se que o último encontra melhores resultados para 9 classes de instâncias, o primeiro encontra o melhor resultado apenas para 1 classe de instâncias e as duas versões obtêm os mesmos resultados nas demais 5 classes. Dentre as 15 classes de instâncias o algoritmo com k = 30 encontra melhores soluções médias que o algoritmo com k=40 em 8 classes e mostra o mesmo desempenho para 7 classes. Pode-se, também, observar que mesmo em relação aos piores desempenhos verificados na Tabela 7, os valores ainda permanecem competitivos em relação aos constantes da Tabela 9 em relação ao algoritmo RL-SG (Riera-Ledesma & Salazar-Gonzalez, 2005) que corresponde ao melhor resultado da literatura.
Analisando o desempenho através do percentual de soluções ótimas alcançadas nas execuções é possível elaborar a Tabela 8. A coluna "% Acertos" exibe o percentual médio de execuções que logrou alcançar o ótimo dentre as 30 execuções efetuadas. Dentre as 15 classes de instâncias consideradas o algoritmo que utiliza k = 30 exibe performance superior ao que possui k = 40, em relação à qualidade de solução, em 7 classes. O segundo é melhor que o primeiro em 8 classes. O algoritmo com k = 30, também, exibe melhor desempenho que o algoritmo com k = 10 em 9 classes, enquanto o último exibe melhor desempenho para 6 classes. A composição dos resultados não permite decidir conclusivamente sobre qual dos algoritmos apresenta melhor qualidade de solução.
Entretanto, analisando-se o tempo de processamento, nota-se que o algoritmo com k = 40 gasta, no mínimo, o mesmo tempo que o algoritmo com k = 30, chegando a gastar até 79% mais tempo, sendo em média 24,36% mais lento que a versão com k = 30. Por outro lado, comparando-se os tempos das versões com k = 10 e k = 30, verifica-se que apesar de, em geral, o primeiro exibir melhores tempos que o segundo, essa diferença é em média de 11%.
Destarte, pode-se concluir um desempenho robusto do algoritmo em relação a esse parâmetro e à qualidade de solução. Apesar dos resultados serem muito aproximados, escolheu-se o valor k=30 uma vez que o mesmo equilibra o ganho em tempo computacional com a qualidade da solução alcançada.
Os valores de h , b e tamanho de população
Foram testados para h os valores 40, 50 e 60, para b os valores 4, 5 e 6, e para tamanho da população os valores 40, 50 e 60. Da mesma forma que para k, os resultados não mostraram um resultado significativamente superior para qualquer conjunto de parâmetros, sendo que o algoritmo que mostrou também a melhor relação entre esforço computacional e qualidade de solução apresentava os seguintes parâmetros: h = 40, b = 4 e uma população com 50 cromossomos.
Para ilustrar o comportamento do algoritmo, a Figura 6 exibe o gráfico de evolução da melhor solução ao longo das iterações de AT para algumas instâncias selecionadas aleatoriamente do banco TPPLib. Nesses casos o algoritmo encontra sempre a solução ótima. Os gráficos reportam o desempenho de AT com h = 60 e b = 6. As abscissas dos gráficos representam as iterações enquanto as ordenadas o valor da melhor solução encontrada pelo algoritmo. Os valores constantes do gráfico são obtidos de uma média de 30 execuções para a instância analisada.
Da análise da Figura 6 é possível perceber que existe uma variação significativa entre o número de iterações necessárias para que um valor ótimo seja alcançado, como mostram os gráficos relativos às instâncias 100.50.5.4, 100.100.5.3, 150.50.5.4 e 200.100.7.2 (a identificação da instância é feita por m.n.a .ID). Também é possível notar que, em alguns casos, ocorrem melhoria em manipulações que ocorreriam além das 50 iterações, como mostram as instâncias 50.15095.4, 50.100.1.4 e 50.100.9.4.
Considerando os resultados da Tabela 6, é possível fazer a conjectura de que um segundo critério de parada associado ao número máximo de iterações sem melhoria poderia beneficiar o tempo de processamento do algoritmo em instâncias cujo comportamento seguisse os padrões das instâncias 50.50.5.5, 100.50.5.4, 100.100.5.3, 100.150.5.4 e 200.100.7.2 poderia diminuir.
Por outro lado, para algumas instâncias, um aumento do número máximo de iterações poderia melhorar a qualidade de solução.
5.3 Desempenho Comparativo do Algoritmo Transgenético
Inicialmente, o algoritmo AT é comparado ao RL-SG (Riera-Ledesma & Salazar-González, 2005), tendo em vista este último reportar os melhores resultados heurísticos da literatura para o PCCC. O algoritmo RL-SG é executado exclusivamente sobre instâncias que possuem o ótimo conhecido. Como o algoritmo RL-SG pode ser entendido como um procedimento de Iterated Local Search mobiliado com um procedimento de shaking perturbação, foi implementado por Riera-Ledesma & Salazar-González com controle de parada via tempo de processamento. Como as perturbações produzem um efeito semelhante ao reinício dos algoritmos evolucionários, os autores dispensaram execuções independentes. O tempo máximo de processamento para cada conjunto de instâncias cada linha da tabela, foi fixado, no referido trabalho, em duas horas. O equipamento empregado no teste foi um Celeron 500MHz. Destaque-se que o desempenho do algoritmo RL-SG foi otimizado com o auxílio de aplicativos proprietários e um solver, o CPLEX.
A comparação do desempenho do algoritmo RL-SG com os demais algoritmos da literatura consta do trabalho referido, sendo conclusivamente favorável a esse último. A coluna melhoria exibe a diferença percentual entre os resultados obtidos por cada algoritmo dada pela fórmula:
onde solRL-SG e solAT correspondem, respectivamente aos valores exibidos nas colunas "%gap" relativas aos algoritmos RL-SG e AT, respectivamente.
Como o experimento do algoritmo RL-SG segue a mesma metodologia do trabalho de Boctor et al. (2003), efetua o relato do comportamento médio do algoritmo por conjuntos de instâncias teste. Para aumentar a confiabilidade de que o desempenho verificado no algoritmo transgenético realmente representasse um comportamento médio, o algoritmo foi rodado 100 vezes de forma independente para cada instância teste, anotando-se o comportamento médio dessas 100 execuções como o valor a ser considerado em cada instância.
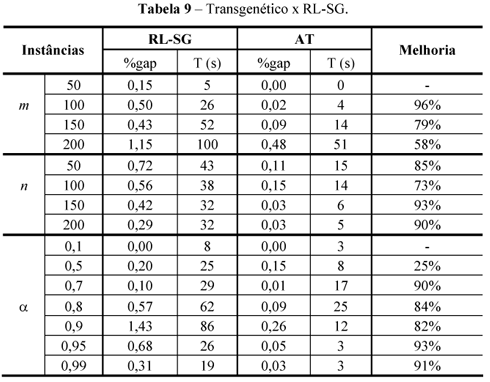
A Tabela 9 apresenta uma comparação qualitativa entre os resultados do algoritmo AT e os do algoritmo RL-SG. Ela mostra os resultados encontrados nas 440 instâncias com solução ótima conhecida. Observa-se que o AT apresenta médias de resultados qualitativamente superiores ao algoritmo RL-SG. Embora para m = 50 e a = 0,1, a fórmula não possa calcular valores de melhoria devido a divisão por zero, a diferença percentual não pode ser calculada porque o AT encontra o ótimo em todas as instâncias, pode-se considerar que o AT melhora em 100% e em 0%, respectivamente, os resultado do outro algoritmo. Em média, a melhoria do AT em relação ao RL-SG é de aproximadamente 76% em relação à qualidade da solução obtida.
Em relação ao tempo de processamento as colunas T(s) da Tabela 9 mostram que o algoritmo AT é de 1,5 a 7 vezes mais rápido que o RL_SG. Tal resultado, todavia, não comprova uma superioridade em desempenho em virtude da influência de dois fatos que distorcem os valores absolutos dos tempos, um atuando contra o AT, outro em sentido favorável de seu melhor desempenho, como se segue: o algoritmo AT não foi aparelhado por softwares específicos de apoio à solução em programação matemática para aumentar a performance do código como o foi o algoritmo RL_SG. O algoritmo AT foi executado em plataforma superior ao do teste de RL-SG.
Tendo em vista complementar o experimento computacional, o algoritmo AT também foi aplicado às demais 44 instâncias simétricas da classe 4 que possuem um valor relatado na literatura. Para esse conjunto de instâncias o trabalho de Laporte et al. (2003) reporta os melhores resultados da literatura. Por se tratar de um algoritmo exato, os autores param o algoritmo quando a solução ótima é encontrada ou quando o tempo de processamento ultrapassa 5 horas. O algoritmo Laporte et al. (2003) de foi implementado em um Pentium III 500 Mhz, Linux, C++, abacus 2.2 com ceplex 2.0.
Dentre as 44 instâncias testadas o algoritmo AT foi capaz de produzir uma solução melhor que a melhor existente na literatura para 17 instâncias. A Tabela 10 esclarece os resultados obtidos para citadas 17. Nas colunas da tabela são visíveis os parâmetros de identificação das instâncias (m, n, a e ID), o melhor valor reportado na literatura encontrado no trabalho de Laporte et al. (2003) (Melhor da Literatura), O tempo de processamento do algoritmo de Laporte et al. (2003) (T(s)), o valor da melhor solução encontrada pelo algoritmo proposto (AT), o tempo médio em segundos de 30 execuções independentes do algoritmo AT (T(s)) e o número de mercados na melhor solução (Nº de Mercados).
Como se observa nas colunas T(s), o maior tempo de solução gasto por AT é de cerca de 1 hora e 48 minutos, enquanto seu menor tempo é de 1 minuto e 45 segundos. No caso do algoritmo exato, são utilizadas completamente as cinco horas de processamento em todos os casos. Os valores de tempo do algoritmo de Laporte et al. (2003) flutuam um pouco mais que 5 horas uma vez que, esgotado o tempo de processamento, os autores permitiram que seu algoritmo completasse o seu último passo Branch-and-Cut. A Tabela 10 mostra também que para as 17 instâncias relatadas, o AT encontra valores médios de 0,022 a 14,80% melhores que os do trabalho de Laporte et al. (2003), encontrando, em média, uma melhoria de 1,24% para esse conjunto de instâncias. Pelos mesmos motivos descritos no primeiro teste, o resultado do desempenho computacional em tempo não pode ser considerado conclusivo, contudo evidencia o fato que pode ser executado em tempo bastante competitivo com o estado-da-arte.
6. Conclusões
O presente trabalho propõe um novo algoritmo evolucionário para a solução do Problema do Caixeiro Comprador Capacitado. Para testar a viabilidade computacional dessa metáfora desenvolve-se um experimento computacional objetivando responder principalmente os seguintes pontos:A mimetização de veículos naturais de transferência de genes poderiam proporcionar um processo de evolução computacional competitivo para o problema proposto, se comparado ao de outros eficientes algoritmos da literatura?
1. Um uso conjunto de dois tipos de vetores transgenéticos poderia resultar em desempenho superior ao de apenas um?
2. Qual seria a dependência do processo de evolução proposto pelo algoritmo transgenético em relação aos parâmetros livres permitidos pela metáfora?
Dos resultados experimentais conclui-se:
1. A mimetização do comportamento dos veículos naturais de transferência genética pode inspirar algoritmos computacionais eficientes.
2. O uso conjunto de diferentes vetores de manipulação pode resultar em vantagens qualitativas para os algoritmos evolucionários.
3. O processo é dependente dos parâmetros da abordagem, mas nada leva supor que tal fato represente um fenômeno particularmente diferente do que ocorre com as demais abordagens clássicas, pelo contrário. No experimento realizado os parâmetros empregados possuem, claramente, razoáveis intervalos de estabilidade, o que facilitaria o projeto de algoritmos semelhantes.
4. O algoritmo proposto mostrou-se de eficiente adaptação à solução do PCCC segundo o banco de instâncias proposto no TPPLIB. O algoritmo transgenético obteve os melhores resultados qualitativos dentre os reportados na literatura segundo a metodologia de comparação adotada por Boctor et al. (2003) e Riera-Ledesma & Salazar-González (2005), determinando também novas "melhores soluções" para 17 instâncias do TPPLib que não possuem solução ótima conhecida.
5. O tempo computacional do algoritmo AT, em termos absolutos, é menor que os tempos reportados nos experimentos de referência, todavia ressalte-se que foi executado em plataforma superior a dos trabalhos examinados, o que impede uma comparação conclusiva nesse aspecto.
6. Vislumbra-se uma via de melhoria do algoritmo AT caso seja considerada uma regra de parada composta por um limite de iterações sem melhoria conjugada com um limite maior que 50 para o número máximo de iterações.
Agradecimentos
Ao professor Jorge Riera Ledesma por ter disponibilizado detalhes dos resultados computacionais de seu artigo. A presente pesquisa foi parcialmente apoiada pelo CNPq e CAPES.
Referências Bibliográficas
(1) Applegate, D.; Bixby, R.; Chvatal, V. & Cook, W. (1999). Finding Tours in the TSP. Technical Report TR99-05, Department of Computational and Applied Mathematics, Rice University.
(2) Boctor, F.F.; Laporte G. & Renaud, J. (2003). Heuristics for the traveling purchaser problem. Computers & Operations Research, 30, 491-504.
(3) Bontoux, B. & Feillet, D. (2008). Ant colony optimization for the traveling purchaser problem. Computers & Operations Research, 35, 628-637.
(4) Bull, L. & Fogarty, T.C. (1995). Artificial symbiogenesis. Artificial Life, 2, 269-292.
(5) Burstall, R.M. (1966). A heuristic method for a job sequencing problem. Operational Research Quarterly, 17, 291-04.
(6) Buzacott, J.A. & Dutta, S.K. (1971). Sequencing many jobs on a multipurpose facility. Naval Research Logistics Quarterly, 18, 75-82.
(7) Chan, T-M.; Man, K-F.; Tang, K-S. & Kwong, S.A. (2005). Jumping gene algorithm for multiobjective resource management in wideband CDMA. Computer Journal, 48(6), 749-768.
(8) Coello, C.A.C. & Becerra, R.L. (2004). Efficient Evolutionary Optimization through the use of a Cultural Algorithm. Engineering Optimization, 36(2), 219-236.
(9) De La Cal Marín, E.A. & Ramos, L.S. (2004). Supply estimation using coevolutionary genetic algorithms in the Spanish electrical market. Applied Intelligence, 21, 7-24.
(10) Goldbarg, M.C. & Goldbarg, E.F.G. (2002). Transgenética computacional: Uma aplicação ao problema quadrático de alocação. Pesquisa Operacional, 22(3), 359-386.
(11) Goldbarg, M.C.; Goldbarg, E.F.G. & Ramos, I.C.O. (2003). A ProtoG Algorithm Applied to the traveling salesman problem. WSEAS Transactions on Computers, 2, 299-304.
(12) Goldbarg, E.F.G.; Goldbarg, M.C. & Bagi, L.B. (2007). Transgenetic algorithm: A new evolutionary perspective for heuristics design. GECCO 2007 Genetic and Evolutionary Computation Conference, Workshop The Evolution of Natural and Artificial Systems Metaphors and Analogies in Single and Multi-objective Problems, 2701-2708.
(13) Goldberg, D.E. (1989). Genetic Algorithms in Search, Optimization and Machine Learning. Kluwer Academic Publishers, Boston, MA.
(14) Golden, B.L.; Levy, L. & Dahl, R. (1981). Two generalizations of the traveling salesman problem. Omega, 9, 439-445.
(15) Gouvêa, E.F. (2001). Transgenética Computacional: Um estudo Algorítmico. Tese de doutorado, COPPE-UFRJ, Programa de Engenharia da Produção.
(16) Hadfield, S.J. & Axton, J.M. (1999). Germ cells colonized by endosymbiotic bacteria. Nature, 402, 482.
(17) Hillis, D.W. (1990). Co-evolving parasites improve simulated evolution in an optimization procedure. Physica D, 42, 228-234.
(18) Husbands, P. (1994). Distributed coevolutionary genetic algorithms for multi-criteria and multi-constraint optimisation. In: Evolutionary Computing [edited by T. Fogarty], AISB Workshop Selected Papers. Lecture Notes in Computer Science, 865, 150-165.
(19) Kim, J.Y.; Kim, Y. & Kim, Y.K. (2001). An endosymbiotic evolutionary algorithm for optimization. Applied Intelligence, 15, 117-130.
(20) Kim, Y.K.; Park, K. & Ko. J. (2003). A symbiotic evolutionary algorithm for the integration of process planning and job shop scheduling. Computers & Operations Research, 30(8), 1151-1171.
(21) Kubota, N.; Fukuda, T.; Arakawa, T. & Shimojima, K. (1997). Evolutionary transition on Virus-Evolutionary Genetic Algorithm. Proceedings of 1997 IEEE International Conference on Evolutionary Computation, 291-296.
(22) Kubota, N.; Shimojima, K. & Fukuda, T. (1996). Virus-evolutionary genetic algorithm coevolution of planar grid model. Proceedings of the Fifth IEEE International Conference on Fuzzy Systems (FUZZIEEE96), 1, 232-238.
(23) Laporte, G.; Rieira-Ledesma, J. & Salazar-González, J.J. (2003). A branch-and-cut algorithm for the undirected traveling purchase. Operations Research, 51(6), 142-152.
(24) Lin, S. & Kernighan, B.W. (1973). An effective heuristic algorithm for the traveling salesman problem. Operations Research, 21, 498-516.
(25) Lomnicki, Z.A. (1966). Job scheduling. Operational Research Quarterly, 17, 314-316.
(26) Margulis, L. (1991). Symbiosis as a Source of Evolutionary Innovation: Speciation and Morphogenesis. The MIT Press.
(27) Margulis, L. & Sagan, D. (1986). Origins of Sex: Three Billion Years of Genetic Recombination. Yale University Press.
(28) McFadden, G.I. (2001). Primary and secondary endosymbiosis and the origin of plastids. Journal of Physiology, 37(6), 951-959.
(29) Merz, P. & Freisleben, B. (1999), A comparison of memetic algorithms, tabu search, and ant colonies for the quadratic assignment problem. In: Proceedings of the 1999 International Congress of Evolutionary Computation (CEC99).
(30) Michaelian, K. (1998). A symbiotic algorithm for finding the lowest energy isomers of large clusters and molecules. Chemical Physics Letters, 293, 202-215.
(31) Michalewicz, Z. & Fogel, D.B. (2000). How to solve it: Modern heuristics. Springer.
(32) Morowitz, H.J. (1992). Beginning of Cellular Life. Yale University Press, New Haven, Conn.
(33) Mühlenbein, H. & Voigt, H-M.(1995). Gene pool recombination in genetic algorithms. In: Proceedings of the Sixth International Conference on Genetic Algorithms [edited by L. Eshelman], Morgan Kaufmann, San Mateo, 104-113.
(34) Nawa, N.; Furuhashi, T.; Hashiyama, T. & Uchikawa, Y. (1999). A study of the discovery of relevant fuzzy rules using pseudo-bacterial genetic algorithm. IEEE Transactions on Industrial Electronics, 46(6), 1080-1089.
(35) Ong, H.L. (1982). Approximate algorithms for the traveling purchaser problem. Operations Research Letters, 1, 201-205.
(36) Pagie, L. & Mitchell, M. (2002). A comparison of evolutionary and co-evolutionary search. International Journal of Computational Intelligence and Applications, 2(1), 53-69.
(37) Pearn, W.L. & Chien, R.C. (1998). Improved solutions for the traveling purchaser problem. Computers & Operations Research, 25(11), 879-885.
(38) Ramesh, T. (1981). Traveling purchaser problem. Opsearch, 18, 78-91.
(39) Riera-Ledesma, J. & Salazar-González, J.J. (2005). A heuristic approach for the Traveling Purchaser Problem. European Journal of Operational Research, 162, 142-152.
(40) Rosenkrantz, D.J.; Stearns, R.E. & Lewis II, P.M. (1977). An analysis of several heuristics for the traveling salesman problem. SIAM Journal on Computing, 6, 563-581.
(41) Rosin, C.D. & Belew, R.K. (1997). New methods for competitive coevolution. Evolutionary Computation, 5(1), 1-29.
(42) Simões, A. & Costa, E. (2001a). On biologically inspired genetic operators: Transformation in the standard genetic algorithm. Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-2001), 584-591.
(43) Simões, A. & Costa, E. (2001b). An evolutionary approach to the zero/one knapsack problem: Testing ideas from biology. Proceedings of the Fifth International Conference on Neural Networks and Genetic Algorithms (ICANNGA 2001), Springer-Verlag, 22-25.
(44) Singh, K.N. & van Oudheusden, D.L. (1997). A branch and bound algorithm for the traveling purchaser problem. European Journal of Operational Research, 97, 571-579.
(45) Teeninga, A. & Volgenant, A. (2004). Improved heuristics for the traveling purchase problem. Computers & Operations Research, 31, 139-150.
(46) Tsujimura, Y.; Mafune, Y. & Gen, M. (2001). Effects of symbiotic evolution in genetic algorithms for the job-shop scheduling. Proceedings of the 34 Hawaii International Conference on Systems Science, 1-7.
(47) Witzany, G. (2006). Serial endosymbiotic theory (SET): The biosemiotic update. Acta Biotheoretica, 54(1), 103-117.
(48) Vob, S. (1996). Dynamic tabu search strategies for the traveling purchaser problem. Annals of Operations Research, 63, 253-275.
Recebido em 08/2006; aceito em 11/2007 após 1 revisão
Received August 2006; accepted November 2007 after one revision
- (1) Applegate, D.; Bixby, R.; Chvatal, V. & Cook, W. (1999). Finding Tours in the TSP. Technical Report TR99-05, Department of Computational and Applied Mathematics, Rice University.
- (2) Boctor, F.F.; Laporte G. & Renaud, J. (2003). Heuristics for the traveling purchaser problem. Computers & Operations Research, 30, 491-504.
- (3) Bontoux, B. & Feillet, D. (2008). Ant colony optimization for the traveling purchaser problem. Computers & Operations Research, 35, 628-637.
- (4) Bull, L. & Fogarty, T.C. (1995). Artificial symbiogenesis. Artificial Life, 2, 269-292.
- (5) Burstall, R.M. (1966). A heuristic method for a job sequencing problem. Operational Research Quarterly, 17, 291-04.
- (6) Buzacott, J.A. & Dutta, S.K. (1971). Sequencing many jobs on a multipurpose facility. Naval Research Logistics Quarterly, 18, 75-82.
- (7) Chan, T-M.; Man, K-F.; Tang, K-S. & Kwong, S.A. (2005). Jumping gene algorithm for multiobjective resource management in wideband CDMA. Computer Journal, 48(6), 749-768.
- (8) Coello, C.A.C. & Becerra, R.L. (2004). Efficient Evolutionary Optimization through the use of a Cultural Algorithm. Engineering Optimization, 36(2), 219-236.
- (9) De La Cal Marín, E.A. & Ramos, L.S. (2004). Supply estimation using coevolutionary genetic algorithms in the Spanish electrical market. Applied Intelligence, 21, 7-24.
- (10) Goldbarg, M.C. & Goldbarg, E.F.G. (2002). Transgenética computacional: Uma aplicação ao problema quadrático de alocação. Pesquisa Operacional, 22(3), 359-386.
- (11) Goldbarg, M.C.; Goldbarg, E.F.G. & Ramos, I.C.O. (2003). A ProtoG Algorithm Applied to the traveling salesman problem. WSEAS Transactions on Computers, 2, 299-304.
- (12) Goldbarg, E.F.G.; Goldbarg, M.C. & Bagi, L.B. (2007). Transgenetic algorithm: A new evolutionary perspective for heuristics design. GECCO 2007 Genetic and Evolutionary Computation Conference, Workshop The Evolution of Natural and Artificial Systems Metaphors and Analogies in Single and Multi-objective Problems, 2701-2708.
- (13) Goldberg, D.E. (1989). Genetic Algorithms in Search, Optimization and Machine Learning. Kluwer Academic Publishers, Boston, MA.
- (14) Golden, B.L.; Levy, L. & Dahl, R. (1981). Two generalizations of the traveling salesman problem. Omega, 9, 439-445.
- (15) Gouvêa, E.F. (2001). Transgenética Computacional: Um estudo Algorítmico. Tese de doutorado, COPPE-UFRJ, Programa de Engenharia da Produção.
- (16) Hadfield, S.J. & Axton, J.M. (1999). Germ cells colonized by endosymbiotic bacteria. Nature, 402, 482.
- (17) Hillis, D.W. (1990). Co-evolving parasites improve simulated evolution in an optimization procedure. Physica D, 42, 228-234.
- (18) Husbands, P. (1994). Distributed coevolutionary genetic algorithms for multi-criteria and multi-constraint optimisation. In: Evolutionary Computing [edited by T. Fogarty], AISB Workshop Selected Papers.
- Lecture Notes in Computer Science, 865, 150-165.
- (19) Kim, J.Y.; Kim, Y. & Kim, Y.K. (2001). An endosymbiotic evolutionary algorithm for optimization. Applied Intelligence, 15, 117-130.
- (20) Kim, Y.K.; Park, K. & Ko. J. (2003). A symbiotic evolutionary algorithm for the integration of process planning and job shop scheduling. Computers & Operations Research, 30(8), 1151-1171.
- (21) Kubota, N.; Fukuda, T.; Arakawa, T. & Shimojima, K. (1997). Evolutionary transition on Virus-Evolutionary Genetic Algorithm. Proceedings of 1997 IEEE International Conference on Evolutionary Computation, 291-296.
- (22) Kubota, N.; Shimojima, K. & Fukuda, T. (1996). Virus-evolutionary genetic algorithm coevolution of planar grid model. Proceedings of the Fifth IEEE International Conference on Fuzzy Systems (FUZZIEEE96), 1, 232-238.
- (23) Laporte, G.; Rieira-Ledesma, J. & Salazar-González, J.J. (2003). A branch-and-cut algorithm for the undirected traveling purchase. Operations Research, 51(6), 142-152.
- (24) Lin, S. & Kernighan, B.W. (1973). An effective heuristic algorithm for the traveling salesman problem. Operations Research, 21, 498-516.
- (25) Lomnicki, Z.A. (1966). Job scheduling. Operational Research Quarterly, 17, 314-316.
- (26) Margulis, L. (1991). Symbiosis as a Source of Evolutionary Innovation: Speciation and Morphogenesis The MIT Press.
- (27) Margulis, L. & Sagan, D. (1986). Origins of Sex: Three Billion Years of Genetic Recombination Yale University Press.
- (28) McFadden, G.I. (2001). Primary and secondary endosymbiosis and the origin of plastids. Journal of Physiology, 37(6), 951-959.
- (29) Merz, P. & Freisleben, B. (1999), A comparison of memetic algorithms, tabu search, and ant colonies for the quadratic assignment problem. In: Proceedings of the 1999 International Congress of Evolutionary Computation (CEC99).
- (30) Michaelian, K. (1998). A symbiotic algorithm for finding the lowest energy isomers of large clusters and molecules. Chemical Physics Letters, 293, 202-215.
- (31) Michalewicz, Z. & Fogel, D.B. (2000). How to solve it: Modern heuristics Springer.
- (32) Morowitz, H.J. (1992). Beginning of Cellular Life Yale University Press, New Haven, Conn.
- (33) Mühlenbein, H. & Voigt, H-M.(1995). Gene pool recombination in genetic algorithms. In: Proceedings of the Sixth International Conference on Genetic Algorithms [edited by L. Eshelman], Morgan Kaufmann, San Mateo, 104-113.
- (34) Nawa, N.; Furuhashi, T.; Hashiyama, T. & Uchikawa, Y. (1999). A study of the discovery of relevant fuzzy rules using pseudo-bacterial genetic algorithm. IEEE Transactions on Industrial Electronics, 46(6), 1080-1089.
- (35) Ong, H.L. (1982). Approximate algorithms for the traveling purchaser problem. Operations Research Letters, 1, 201-205.
- (36) Pagie, L. & Mitchell, M. (2002). A comparison of evolutionary and co-evolutionary search. International Journal of Computational Intelligence and Applications, 2(1), 53-69.
- (37) Pearn, W.L. & Chien, R.C. (1998). Improved solutions for the traveling purchaser problem. Computers & Operations Research, 25(11), 879-885.
- (38) Ramesh, T. (1981). Traveling purchaser problem. Opsearch, 18, 78-91.
- (39) Riera-Ledesma, J. & Salazar-González, J.J. (2005). A heuristic approach for the Traveling Purchaser Problem. European Journal of Operational Research, 162, 142-152.
- (40) Rosenkrantz, D.J.; Stearns, R.E. & Lewis II, P.M. (1977). An analysis of several heuristics for the traveling salesman problem. SIAM Journal on Computing, 6, 563-581.
- (41) Rosin, C.D. & Belew, R.K. (1997). New methods for competitive coevolution. Evolutionary Computation, 5(1), 1-29.
- (42) Simões, A. & Costa, E. (2001a). On biologically inspired genetic operators: Transformation in the standard genetic algorithm. Proceedings of the Genetic and Evolutionary Computation Conference (GECCO-2001), 584-591.
- (43) Simões, A. & Costa, E. (2001b). An evolutionary approach to the zero/one knapsack problem: Testing ideas from biology. Proceedings of the Fifth International Conference on Neural Networks and Genetic Algorithms (ICANNGA 2001), Springer-Verlag, 22-25.
- (44) Singh, K.N. & van Oudheusden, D.L. (1997). A branch and bound algorithm for the traveling purchaser problem. European Journal of Operational Research, 97, 571-579.
- (45) Teeninga, A. & Volgenant, A. (2004). Improved heuristics for the traveling purchase problem. Computers & Operations Research, 31, 139-150.
- (46) Tsujimura, Y.; Mafune, Y. & Gen, M. (2001). Effects of symbiotic evolution in genetic algorithms for the job-shop scheduling. Proceedings of the 34 Hawaii International Conference on Systems Science, 1-7.
- (47) Witzany, G. (2006). Serial endosymbiotic theory (SET): The biosemiotic update. Acta Biotheoretica, 54(1), 103-117.
- (48) Vob, S. (1996). Dynamic tabu search strategies for the traveling purchaser problem. Annals of Operations Research, 63, 253-275.
Datas de Publicação
-
Publicação nesta coleção
23 Jun 2008 -
Data do Fascículo
Abr 2008
Histórico
-
Aceito
Nov 2007 -
Recebido
Ago 2006