Abstract
The aim of multicriteria decision aiding is to give the decision maker a recommendation concerning a set of objects evaluated from multiple points of view called criteria. Since a rational decision maker acts with respect to his/her value system, in order to recommend the most-preferred decision, one must identify decision maker's preferences. In this paper, we focus on preference discovery from data concerning some past decisions of the decision maker. We consider the preference model in the form of a set of "if..., then..." decision rules discovered from the data by inductive learning. To structure the data prior to induction of rules, we use the Dominance-based Rough Set Approach (DRSA). DRSA is a methodology for reasoning about data, which handles ordinal evaluations of objects on considered criteria and monotonic relationships between these evaluations and the decision. We review applications of DRSA to a large variety of multicriteria decision problems.
multicriteria decision aiding; ordinal classification; choice; ranking; Dominance-based Rough Set Approach; preference modeling; decision rules
Rough set and rule-based multicriteria decision aiding* * Invited paper
Roman SlowinskiI, ** ** Corresponding author ; Salvatore GrecoII; Benedetto MatarazzoII
IInstitute of Computing Science, Poznan University of Technology, 60-965 Poznan, and Systems Research Institute, Polish Academy of Sciences, 01-447 Warsaw, Poland. E-mail: Roman.Slowinski@cs.put.poznan.pl
IIDepartment of Economics and Business, University of Catania, Corso Italia, 55, 95129 Catania, Italy. E-mails: salgreco@unict.it, matarazz@unict.it
ABSTRACT
The aim of multicriteria decision aiding is to give the decision maker a recommendation concerning a set of objects evaluated from multiple points of view called criteria. Since a rational decision maker acts with respect to his/her value system, in order to recommend the most-preferred decision, one must identify decision maker's preferences. In this paper, we focus on preference discovery from data concerning some past decisions of the decision maker. We consider the preference model in the form of a set of "if..., then..." decision rules discovered from the data by inductive learning. To structure the data prior to induction of rules, we use the Dominance-based Rough Set Approach (DRSA). DRSA is a methodology for reasoning about data, which handles ordinal evaluations of objects on considered criteria and monotonic relationships between these evaluations and the decision. We review applications of DRSA to a large variety of multicriteria decision problems.
Keywords: multicriteria decision aiding, ordinal classification, choice, ranking, Dominance-based Rough Set Approach, preference modeling, decision rules.
1 INTRODUCTION
In this paper, we review a multicriteria decision aiding methodology which employs decision maker's (DM's) preference model in form of a set of decision rules discovered from some preference data. Multicriteria decision problems concern a finite set of objects (also called alternatives, actions, acts, solutions, etc.) evaluated by a finite set of criteria (also called attributes, features, variables, etc.), and raise one of the following questions: (i) how to assign the objects to some ordered classes (ordinal classification), (ii) how to choose the best subset of objects (choice or optimization), or (iii) how to rank the objects from the best to the worst (ranking). The answer to everyone of these questions involves an aggregation of the multicriteria evaluations of objects, which takes into account preferences of the DM. In consequence, the aggregation formula is at the same time the DM's preference model. Thus, any recommendation referring to one of the above questions must be based on the DM's preference model. The preference data used for building this model, as well as the way of building and using it in the decision process, are main factors distinguishing various multicriteria decision aiding methodologies.
In our case, we assume that the preference data includes either observations of DM's past decisions in the same decision problem, or examples of decisions consciously elicited by the DM on demand of an analyst. This way of preference data elicitation is called indirect, by opposition to direct elicitation when the DM is supposed to provide information leading directly to definition of all preference model parameters, like weights and discrimination thresholds of criteria, trade-off rates, etc. (see, e.g., Roy, 1996).
Past decisions or decision examples may be, however, inconsistent with the dominance principle commonly accepted for multicriteria decision problems. Decisions are inconsistent with the dominance principle if:
-
in case of ordinal classification: object
a has been assigned to a worse decision class than object
b, although
a is at least as good as
b on all the considered criteria,
i.e. a dominates
b;
-
in case of choice and ranking: pair of objects (
a,
b) has been assigned a degree of preference worse than pair (
c,
d), although differences of evaluations between
a and
b on all the considered criteria is at least as good as respective differences of evaluations between
c and
d,
i.e. pair (
a,
b) dominates pair (
c,
d)s.
Thus, in order to build a preference model from partly inconsistent preference data, we had an idea to structure this data using the concept of a rough set introduced by Pawlak (1982, 1991). Since its conception, rough set theory has often proved to be an excellent mathematical tool for the analysis of inconsistent description of objects. Originally, its understanding of inconsistency was different, however, than the above inconsistency with the dominance principle. The original rough set philosophy is based on the assumption that with every object of the universe U there is associated a certain amount of information (data, knowledge). This information can be expressed by means of a number of attributes. The attributes describe the objects. Objects which have the same description are said to be indiscernible (or similar) with respect to the available information. The indiscernibility relation thus generated constitutes the mathematical basis of rough set theory. It induces a partition of the universe into blocks of indiscernible objects, called elementary sets, which can be used to build knowledge about a real or abstract world. The use of the indiscernibility relation results in information granulation.
Any subset X of the universe may be expressed in terms of these blocks either precisely (as a union of elementary sets) or approximately. In the latter case, the subset X may be characterized by two ordinary sets, called the lower and upper approximations. A rough set is defined by means of these two approximations, which coincide in the case of an ordinary set. The lower approximation of X is composed of all the elementary sets included in X (whose elements, therefore, certainly belong to X), while the upper approximation of X consists of all the elementary sets which have a non-empty intersection with X (whose elements, therefore, may belong to X). The difference between the upper and lower approximation constitutes the boundary region of the rough set, whose elements cannot be characterized with certainty as belonging or not to X (by using the available information). The information about objects from the boundary region is, therefore, inconsistent or ambiguous. The cardinality of the boundary region states, moreover, the extent to which it is possible to express X in exact terms, on the basis of the available information. For this reason, this cardinality may be used as a measure of vagueness of the information about X.
Some important characteristics of the rough set approach makes it a particularly interesting tool in a variety of problems and concrete applications. For example, it is possible to deal with both quantitative and qualitative input data and inconsistencies need not to be removed prior to the analysis. In terms of the output information, it is possible to acquire a posteriori information regarding the relevance of particular attributes and their subsets to the quality of approximation considered within the problem at hand. Moreover, the lower and upper approximations of a partition of U into decision classes, prepare the ground for inducing certain and possible knowledge patterns in the form of "if... then..." decision rules.
Several attempts have been made to employ rough set theory for decision aiding (Slowinski, 1993; Pawlak & Slowinski, 1994). The Indiscernibility-based Rough Set Approach (IRSA) is not able, however, to deal with preference ordered attribute scales and preference ordered decision classes. In multicriteria decision analysis, an attribute with a preference ordered scale (value set) is called a criterion.
An extension of the IRSA which deals with inconsistencies with respect to dominance principle, typical for preference data, was proposed by Greco, Matarazzo & Slowinski (1998a, 1999a,b). This extension, called the Dominance-based Rough Set Approach (DRSA) is mainly based on the substitution of the indiscernibility relation by a dominance relation in the rough approximation of decision classes. An important consequence of this fact is the possibility of inferring (from observations of past decisions or from exemplary decisions) the DM's preference model in terms of decision rules which are logical statements of the type "if..., then...". The separation of certain and uncertain knowledge about the DM's preferences is carried out by the distinction of different kinds of decision rules, depending upon whether they are induced from lower approximations of decision classes or from the difference between upper and lower approximations (composed of inconsistent examples). Such a preference model is more general than the classical functional models considered within multi-attribute utility theory or the relational models considered, for example, in outranking methods (Greco et al., 2002c, 2004; Slowinski et al., 2002b).
This paper is a review based on previous publications. In the next section, we present some basics on the Indiscernibility-based Rough Set Approach (IRSA) as well as on its extension to similarity relation. In Section 3, we explain the need of replacing indiscernibility or similarity relation by dominance relation in the definition of rough sets, when considering preference data. This leads us to Section 4, where Dominace-based Rough Set Approach (DRSA) is presented with respect to multicriteria ordinal classification. This section also includes two special versions of DRSA: Variable Consistency DRSA (VC-DRSA) and Stochastic DRSA. Section 5 presents DRSA with respect to multicriteria choice and ranking. In Sections 4 and 5, application of DRSA to all three categories of multicriteria decision problems is explained by the way of examples. Section 6 groups conclusions and characterizes other relevant extensions and applications of DRSA to decision problems. Finally, Section 7 provides information about additional sources of information about rough set theory and applications.
2 SOME BASICS ON INDISCERNIBILITY-BASED ROUGH SET APPROACH (IRSA)
2.1 Definition of rough approximations by IRSA
For algorithmic reasons, we supply the information regarding the objects in the form of a data table, whose separate rows refer to distinct objects and whose columns refer to the different attributes considered. Each cell of this table indicates an evaluation (quantitative or qualitative) of the object placed in that row by means of the attribute in the corresponding column.
Formally, a data table is the 4-tuple S  , where U is a finite set of objects (universe),
, where U is a finite set of objects (universe),  is a finite set of attributes, Vq is the value set of the attribute q,
is a finite set of attributes, Vq is the value set of the attribute q,  and
and  is a total function such that
is a total function such that  for each
for each  ,
,  , called the information function.
, called the information function.
Each object x of U is described by a vector (string)
called the description of x in terms of the evaluations of the attributes from Q. It represents the available information about x.
To every (non-empty) subset of attributes P we associate an indiscernibility relation on U, denoted by Ip and defined as follows:
If  , we say that the objects x and y are P-indiscernible. Clearly, the indiscernibility relation thus defined is an equivalence relation (reflexive, symmetric and transitive). The family of all the equivalence classes of the relation Ip is denoted by
, we say that the objects x and y are P-indiscernible. Clearly, the indiscernibility relation thus defined is an equivalence relation (reflexive, symmetric and transitive). The family of all the equivalence classes of the relation Ip is denoted by  and the equivalence class containing an object
and the equivalence class containing an object  is denoted by
is denoted by  . The equivalence classes of the relation Ip are called the P-elementary sets or granules of knowledge encoded by P.
. The equivalence classes of the relation Ip are called the P-elementary sets or granules of knowledge encoded by P.
Let S be a data table, X be a non-empty subset of U and Æ  . The set X may be characterized by two ordinary sets, called the P-lower approximation of X (denoted by
. The set X may be characterized by two ordinary sets, called the P-lower approximation of X (denoted by  ) and the P-upper approximation of X (denoted by
) and the P-upper approximation of X (denoted by  ) in S. They can be defined, respectively, as:
) in S. They can be defined, respectively, as:
The family of all the sets  having the same P-lower and P-upper approximations is called a P-rough set. The elements of
having the same P-lower and P-upper approximations is called a P-rough set. The elements of  are all and only those objects
are all and only those objects  which belong to the equivalence classes generated by the indiscernibility relation Ip contained in X. The elements of
which belong to the equivalence classes generated by the indiscernibility relation Ip contained in X. The elements of  are all and only those objects
are all and only those objects  which belong to the equivalence classes generated by the indiscernibility relation Ip containing at least one object X belonging to X. In other words,
which belong to the equivalence classes generated by the indiscernibility relation Ip containing at least one object X belonging to X. In other words,  is the largest union of the P-elementary sets included in X, while
is the largest union of the P-elementary sets included in X, while  is the smallest union of the P-elementary sets containing X.
is the smallest union of the P-elementary sets containing X.
The lower and upper approximations can be written in an equivalent form, in terms of unions of elementary sets as follows:
The P-boundary of X in S, denoted by  , is defined as:
, is defined as:
The term rough approximation is a general term used to express the operation of the P-lower and P-upper approximation of a set or of a union of sets. The rough approximations obey the following basic laws (cf. Pawlak, 1991):
-
the inclusion property:
 ,
, -
the complementarity property:
Directly from the definitions, we can also get the following properties of the P-lower and P-upper approximations (Pawlak, 1982, 1991):
Therefore, if an object x belongs to  , it is also certainly contained in X, while if x belongsto
, it is also certainly contained in X, while if x belongsto  , it is only possibly contained in X.
, it is only possibly contained in X.  constitutes the doubtful region of X: using the knowledge encoded by P nothing can be said with certainty about the inclusion of its elements in set X.
constitutes the doubtful region of X: using the knowledge encoded by P nothing can be said with certainty about the inclusion of its elements in set X.
If the P-boundary of X is empty (i.e.  Æ) then the set X is an ordinary set, called the P-exact set. By this, we mean that it may be expressed as the union of some P-elementary sets. Otherwise, if
Æ) then the set X is an ordinary set, called the P-exact set. By this, we mean that it may be expressed as the union of some P-elementary sets. Otherwise, if  Æ, then the set X is a P-rough set and may be characterized by means of
Æ, then the set X is a P-rough set and may be characterized by means of  and
and  .
.
The following ratio defines an accuracy measure of the approximation of  by means of the attributes from P:
by means of the attributes from P:  , where
, where  denotes the cardinality of a (finite) set Y. Obviously,
denotes the cardinality of a (finite) set Y. Obviously,  . If
. If  , then X is a P-exact set. If
, then X is a P-exact set. If  , then X is a P-rough set.
, then X is a P-rough set.
Another ratio defines a quality measure of the approximation of  by means of the attributes from P:
by means of the attributes from P:  . The quality
. The quality  represents the relative frequency of the objects correctly assigned by means of the attributes from P. Moreover,
represents the relative frequency of the objects correctly assigned by means of the attributes from P. Moreover,  , and
, and  iff
iff  , while
, while  iff
iff  .
.
The definition of approximations of a subset  can be extended to a classification, i.e. a partition
can be extended to a classification, i.e. a partition  of U. The subsets
of U. The subsets  ,
,  , are disjunctive classes of Y. By the P-lower and P-upper approximations of Y in S we mean the sets
, are disjunctive classes of Y. By the P-lower and P-upper approximations of Y in S we mean the sets  and
and  , respectively. The coefficient
, respectively. The coefficient  is called the quality of approximation of classification Y by the set of attributes P, or in short, the quality of classification. It expresses the ratio of all P-correctly classified objects to all objects in the data table.
is called the quality of approximation of classification Y by the set of attributes P, or in short, the quality of classification. It expresses the ratio of all P-correctly classified objects to all objects in the data table.
The main issue in rough set theory is the approximation of subsets or partitions of U, representing knowledge about U, with other sets or partitions that have been built up using available information about U. From the perspective of a particular object  , it may be interesting, however, to use the available information to assess the degree of its membership to a subset X of U. The subset X can be identified with the knowledge to be approximated. Using the rough set approach one can calculate the membership function
, it may be interesting, however, to use the available information to assess the degree of its membership to a subset X of U. The subset X can be identified with the knowledge to be approximated. Using the rough set approach one can calculate the membership function  (rough membership function) as
(rough membership function) as
The value of  may be interpreted analogously as conditional probability and may be understood as the degree of certainty (credibility) to which x belongs to X. Observe that the value of the membership function is calculated from the available data, and not subjectively assumed, as it is in the case of membership functions of fuzzy sets.
may be interpreted analogously as conditional probability and may be understood as the degree of certainty (credibility) to which x belongs to X. Observe that the value of the membership function is calculated from the available data, and not subjectively assumed, as it is in the case of membership functions of fuzzy sets.
Between the rough membership function and the rough approximations of X the following relationships hold:
In rough set theory there is, therefore, a close link between the granularity connected with the rough approximation of sets and the uncertainty connected with the rough membership of objects to sets.
A very important concept for concrete applications is that of the dependence of attributes. Intuitively, a set of attributes
totally depends upon a set of attributes if all the values of the attributes from T are uniquely determined by the values of the attributes from P. In other words, this is the case if a functional dependence exists between evaluations by the attributes from P and by the attributes from T. This means that the partition (granularity) generated by the attributes from P is at least as "fine" as that generated by the attributes from T, so that it is sufficient to use the attributes from P to build the partition
if all the values of the attributes from T are uniquely determined by the values of the attributes from P. In other words, this is the case if a functional dependence exists between evaluations by the attributes from P and by the attributes from T. This means that the partition (granularity) generated by the attributes from P is at least as "fine" as that generated by the attributes from T, so that it is sufficient to use the attributes from P to build the partition  . Formally, T totally depends on
. Formally, T totally depends on  iff
iff  .
.
Therefore, T is totally (partially) dependent on P if all (some) objects of the universe U may be univocally assigned to granules of the partition  , using only the attributes from P.
, using only the attributes from P.
Another issue of great practical importance is that of knowledge reduction. This concerns the elimination of superfluous data from the data table, without deteriorating the information contained in the original table.
Let  and
and  . It is said that attribute p is superfluous in P if
. It is said that attribute p is superfluous in P if  ; otherwise, p is indispensable in P.
; otherwise, p is indispensable in P.
The set P is independent if all its attributes are indispensable. The subset P' of P is a reduct of P (denoted by  ) if P' is independent and
) if P' is independent and  .
.
A reduct of P may also be defined with respect to an approximation of the classification Y of objects from U. It is then called a Y-reduct of P (denoted by  ) and it specifies a minimal (with respect to inclusion) subset P' of P which keeps the quality of the classification unchanged, i.e.
) and it specifies a minimal (with respect to inclusion) subset P' of P which keeps the quality of the classification unchanged, i.e.  . In other words, the attributes that do not belong to a Y-reduct of P are superfluous with respect to the classification Y of objects from U.
. In other words, the attributes that do not belong to a Y-reduct of P are superfluous with respect to the classification Y of objects from U.
More than one Y-reduct (or reduct) of P may exist in a data table. The set containing all the indispensable attributes of P is known as the Y-core (denoted by  ). In formal terms,
). In formal terms,  . Obviously, since the Y-core is the intersection of all the Y-reducts of P, it is included in every Y-reduct of P. It is the most important subset of attributes of Q, because none of its elements can be removed without deteriorating the quality ofthe classification.
. Obviously, since the Y-core is the intersection of all the Y-reducts of P, it is included in every Y-reduct of P. It is the most important subset of attributes of Q, because none of its elements can be removed without deteriorating the quality ofthe classification.
2.2 Decision rules induced from rough approximations
In a data table the attributes of the set Q are often divided into condition attributes (set  Æ) and decision attributes (set
Æ) and decision attributes (set  Æ). Note that
Æ). Note that  and
and  Æ. Such a table is called a decision table. The decision attributes induce a partition of U deduced from the indiscernibility relation ID in a way that is independent of the condition attributes. D-elementary sets are called decision classes. There is a tendency to reduce the set C while keeping all important relationships between C and D, in order to make decisions on the basis of a smaller amount of information. When the set of condition attributes is replaced by one of its reducts, the quality of approximation of the classification induced by the decision attributes does not deteriorate.
Æ. Such a table is called a decision table. The decision attributes induce a partition of U deduced from the indiscernibility relation ID in a way that is independent of the condition attributes. D-elementary sets are called decision classes. There is a tendency to reduce the set C while keeping all important relationships between C and D, in order to make decisions on the basis of a smaller amount of information. When the set of condition attributes is replaced by one of its reducts, the quality of approximation of the classification induced by the decision attributes does not deteriorate.
Since the tendency is to underline the functional dependencies between condition and decision attributes, a decision table may also be seen as a set of decision rules. These are logical statements of the type " if..., then...", where the antecedent (condition part) specifies values assumed by one or more condition attributes (describing C-elementary sets) and the consequence (decision part) specifies an assignment to one or more decision classes (describing D-elementary sets). Therefore, the syntax of a rule can be outlined as follows:
if f(x, q1) is equal to rq1 and
is equal to rq2 and... f(x, qp) is equal to rqp, then x belongs to Yj1 or Yj2 or ...Yjk,
where  and Yj1, Yj2,..., Yjk are some decision classes of the considered classification (D-elementary sets). If there is only one possible consequence, i.e. k = 1, then the rule is said to be certain, otherwise it is said to be approximate or ambiguous.
and Yj1, Yj2,..., Yjk are some decision classes of the considered classification (D-elementary sets). If there is only one possible consequence, i.e. k = 1, then the rule is said to be certain, otherwise it is said to be approximate or ambiguous.
An object
supports decision rule r if its description is matching both the condition part and the decision part of the rule. We also say that decision rule r covers object x if it matches at least the condition part of the rule. Each decision rule is characterized by its strength defined as the number of objects supporting the rule. In the case of approximate rules, the strength is calculated for each possible decision class separately.Let us observe that certain rules are supported only by objects from the lower approximation of the corresponding decision class. Approximate rules are supported, in turn, only by objects from the boundaries of the corresponding decision classes.
Procedures for the generation of decision rules from a decision table use an inductive learning principle. The objects are considered as examples of decisions. In order to induce decision rules with a unique consequent assignment to a D-elementary set, the examples belonging to the D-elementary set are called positive and all the others negative. A decision rule is discriminant if it is consistent (i.e. if it distinguishes positive examples from negative ones) and minimal (i.e. if removing any attribute from a condition part gives a rule covering negative objects). It may be also interesting to look for partly discriminant rules. These are rules that, besides positive examples, could cover a limited number of negative ones. They are characterized by a coefficient, called the level of confidence, which is the ratio of the number of positive examples (supporting the rule) to the number of all examples covered by the rule.
The generation of decision rules from decision tables is a complex task and a number of procedures have been proposed to solve it (see, for example, Grzymala-Busse, 1992, 1997; Skowron, 1993; Ziarko & Shan, 1994; Skowron & Polkowski, 1997; Stefanowski, 1998; Slowinski, Stefanowski, Greco & Matarazzo, 2000). The existing induction algorithms use one of the following strategies:
(a) The generation of a minimal set of rules covering all objects from a decision table.
(b) The generation of an exhaustive set of rules consisting of all possible rules for a decision table.
(c) The generation of a set of 'strong' decision rules, even partly discriminant, covering relatively many objects from the decision table (but not necessarily all of them).
To summarize the above description of IRSA, let us list particular benefits one can get when applying the rough set approach to analysis of data presented in decision tables:
-
a characterization of decision classes in terms of chosen attributes through lower and upper approximation,
-
a measure of the quality of approximation which indicates how good the chosen set of attributes is for approximation of the classification,
-
a reduction of the knowledge contained in the table to a description by relevant attributes
i.e. those belonging to reducts; at the same time, exchangeable and superfluous attributes are also identified,
-
a core of attributes, being an intersection of all reducts, indicates indispensable attributes,
-
a set of decision rules which is induced from the lower and upper approximations of the decision classes; this shows classification patterns which exist in the data set.
A tutorial example illustrating all these benefits has been given in (Slowinski et al., 2005). For more details about IRSA and its extensions, the reader is referred to Pawlak (1991), Polkowski (2002), Slowinski (1992b) and many others (see Section 7). Internet addresses to freely available software implementations of these algorithms can also be found in the last section of this paper.
2.3 From indiscernibility to similarity
As mentioned above, the classical definitions of lower and upper approximations are based on the use of the binary indiscernibility relation which is an equivalence relation. The indiscernibility implies the impossibility of distinguishing between two objects of U having the same description in terms of the attributes from Q. This relation induces equivalence classes on U, which constitute the basic granules of knowledge. In reality, due to the imprecision of data describing the objects, small differences are often not considered significant for the purpose of discrimination. This situation may be formally modeled by considering similarity or tolerance relations (see e.g. Nieminen, 1988; Marcus, 1994; Slowinski, 1992a; Polkowski, Skowron & Zytkow, 1995; Skowron & Stepaniuk, 1995; Slowinski & Vanderpooten, 1995, 2000; Stepaniuk, 2000; Yao & Wong, 1995).
Replacing the indiscernibility relation by a weaker binary similarity relation has considerably extended the capacity of the rough set approach. This is because, in the least demanding case, the similarity relation requires reflexivity only, relaxing the assumptions of symmetry and transitivity of the indiscernibility relation.
In general, a similarity relation R does not generate a partition but a cover of U. The information regarding similarity may be represented using similarity classes for each object  . More precisely, the similarity class of x, denoted by R(x), consists of the set of objects which are similar to x:
. More precisely, the similarity class of x, denoted by R(x), consists of the set of objects which are similar to x:
It is obvious that an object y may be similar to both x and z, while z is not similar to x, i.e.  and
and  , but
, but  ,
,  . The similarity relation is of course reflexive (each object is similar to itself). Slowinski & Vanderpooten (1995, 2000) have proposed a similarity relation which is only reflexive. The abandonment of the transitivity requirement is easily justifiable. For example, see Luce's paradox of the cups of tea (Luce, 1956). As for the symmetry, one should notice that yRx, which means "y is similar to x", is directional. There is a subject y and a referent x, and in general this is not equivalent to the proposition "x is similar to y", as maintained by Tversky (1977). This is quite immediate when the similarity relation is defined in terms of a percentage difference between evaluations of the objects compared on a numerical attribute in hand, calculated with respect to evaluation of the referent object. Therefore, the symmetry of the similarity relation should not be imposed. It then makes sense to consider the inverse relation of R, denoted by R-1, where xR-1y means again "y is similar to x". R-1(x),
. The similarity relation is of course reflexive (each object is similar to itself). Slowinski & Vanderpooten (1995, 2000) have proposed a similarity relation which is only reflexive. The abandonment of the transitivity requirement is easily justifiable. For example, see Luce's paradox of the cups of tea (Luce, 1956). As for the symmetry, one should notice that yRx, which means "y is similar to x", is directional. There is a subject y and a referent x, and in general this is not equivalent to the proposition "x is similar to y", as maintained by Tversky (1977). This is quite immediate when the similarity relation is defined in terms of a percentage difference between evaluations of the objects compared on a numerical attribute in hand, calculated with respect to evaluation of the referent object. Therefore, the symmetry of the similarity relation should not be imposed. It then makes sense to consider the inverse relation of R, denoted by R-1, where xR-1y means again "y is similar to x". R-1(x),  , is the class of referent objects to which x is similar:
, is the class of referent objects to which x is similar:
Given a subset  and a similarity relation R on U, an object
and a similarity relation R on U, an object  is said to be non-ambiguous in each of the two following cases:
is said to be non-ambiguous in each of the two following cases:
-
x belongs to
X without ambiguity, that is
 and
and  ; such objects are also called
; such objects are also called positive;
-
x does not belong to
X without ambiguity (
x clearly does not belong to
X), that is
 and
and  (or
(or  Æ); such objects are also called
Æ); such objects are also called negative.
The objects which are neither positive nor negative are said to be ambiguous. A more general definition of lower and upper approximation may thus be offered (see Slowinski & Vanderpooten, 2000). Let  and let R be a reflexive binary relation defined on U. The lower approximation of X, denoted by
and let R be a reflexive binary relation defined on U. The lower approximation of X, denoted by  , and the upper approximation of X, denoted by
, and the upper approximation of X, denoted by  , are defined, respectively, as:
, are defined, respectively, as:
It may be demonstrated that the key properties - inclusion and complementarity - still hold and that
Moreover, the above definition of rough approximation is the only one that correctly characterizes the set of positive objects (lower approximation) and the set of positive or ambiguous objects (upper approximation) when a similarity relation is reflexive, but not necessarily symmetric nor transitive.
Using a similarity relation, we are able to induce decision rules from a decision table. The syntax of a rule is represented as follows:
If f(x, q1) is similar to rq1 and f(x, q2) is similar to rq2 and... f(x, qp) is similar to rqp, then x belongs to Yj1 or Yj2 or... Yjk,
where  and Yj1, Yj2,..., Yjk are some classes of the considered classification (D-elementary sets). As mentioned above, if k = 1 then the rule is certain, otherwise it is approximate or ambiguous. Procedures for generation of decision rules follow the induction principle described in point 2.2. One such procedure has been proposed by Krawiec, Slowinski & Vanderpooten (1998) - it involves a similarity relation that is learned from data. We would also like to point out that Greco, Matarazzo & Slowinski (1998b, 2000b) proposed a fuzzy extension of the similarity, that is, rough approximation of fuzzy sets (decision classes) by means of fuzzy similarity relations (reflexive only).
and Yj1, Yj2,..., Yjk are some classes of the considered classification (D-elementary sets). As mentioned above, if k = 1 then the rule is certain, otherwise it is approximate or ambiguous. Procedures for generation of decision rules follow the induction principle described in point 2.2. One such procedure has been proposed by Krawiec, Slowinski & Vanderpooten (1998) - it involves a similarity relation that is learned from data. We would also like to point out that Greco, Matarazzo & Slowinski (1998b, 2000b) proposed a fuzzy extension of the similarity, that is, rough approximation of fuzzy sets (decision classes) by means of fuzzy similarity relations (reflexive only).
3 THE NEED OF REPLACING INDISCERNIBILITY RELATION BY DOMINANCE RELATION WHEN REASONING ABOUT PREFERENCE DATA
When trying to apply the rough set concept based on indisceribility or similarity to reasoning about preference ordered data, it has been noted that IRSA ignores not only the preference order in the value sets of attributes but also the monotonic relationship between evaluations of objects on such attributes (called criteria) and the preference ordered value of decision (classification decision or degree of preference) (see Greco, Matarazzo & Slowinski, 1998a, 1999b, 2001a; Slowinski, Greco & Matarazzo, 2000a).
In order to explain how important is the above monotonic relationship for data describing multicriteria decision problems, let us consider an example of a data set concerning pupils' achievements in a high school. Suppose that among the attributes describing the pupils there are results in Mathematics (Math) and Physics (Ph). There is also a General Achievement (GA) result, which is considered as a classification decision. The domains of all three attributes are composed of three values: bad, medium and good. The preference order of the attribute values is obvious: good is better than medium and bad, and medium is better than bad. Such attributes are called criteria because they involve an evaluation. One can also notice a semantic correlation between the two criteria and the classification decision, which means that an improvement on one criterion should not worsen the classification decision, while the other criterion is unchanged. Precisely, an improvement of a pupil's score in Math or Ph, with other criterion value unchanged, should not worsen the pupil's general achievement (GA), but rather improve it. In general terms, this requirement is concordant with the dominance principle definedin the Introduction.
This semantic correlation is also called monotonicity constraint, and thus, an alternative name of the classification problem with semantic correlation between evaluation criteria and classification decision is ordinal classification with monotonicity constraints.
Two questions naturally follow consideration of this example:
-
What classification rules can be drawn from the pupils' data set?
-
How does the semantic correlation influences the classification rules?
The answer to the first question is: monotonic "if..., then..." decision rules. Each decision rule is characterized by a condition profile and a decision profile, corresponding to vectors of threshold values on evaluation criteria and on classification decision, respectively. The answer to the second question is that condition and decision profiles of a decision rule should observe the dominance principle (monotonicity constraint) if the rule has at least one pair of semantically correlated criteria spanned over the condition and decision part. We say that one profile dominates another if the values of criteria of the first profile are not worse than the values of criteria of the second profile.
Let us explain the dominance principle with respect to decision rules on the pupils' example. Suppose that two rules induced from the pupils' data set relate Math and Ph on the condition side, with GA on the decision side:
rule#1: if Math=medium and Ph=medium, then GA=good,
rule#2: if Math=good and Ph=medium, then GA=medium.
The two rules do not observe the dominance principle because the condition profile of rule #2 dominates the condition profile of rule #1, while the decision profile of rule #2 is dominated by the decision profile of rule #1. Thus, in the sense of the dominance principle, the two rules are inconsistent, i.e. they are wrong.
One could say that the above rules are true because they are supported by examples of pupils from the analyzed data set, but this would mean that the examples are also inconsistent. The inconsistency may come from many sources. Examples include:
-
Missing attributes (regular ones or criteria) in the description of objects. Maybe the data set does not include such attributes as the
opinion of the pupil's tutor expressed only verbally during an assessment of the pupil's
GA by a school assessment committee.
-
Unstable preferences of decision makers. Maybe the members of the school assessment committee changed their view on the influence of
Math on
GA during the assessment.
Handling these inconsistencies is of crucial importance for knowledge discovery about preferences. They cannot be simply considered as noise or error to be eliminated from data, or amalgamated with consistent data by some averaging operators. They should be identified and presented as uncertain rules.
If the semantic correlation was ignored in prior knowledge, then the handling of the above mentioned inconsistencies would be impossible. Indeed, there would be nothing wrong with rules #1 and #2. They would be supported by different examples discerned by considered attributes.
It has been acknowledged by many authors that rough set theory provides an excellent framework for dealing with inconsistencies in knowledge discovery (Grzymala-Busse, 1992; Pawlak, 1991; Pawlak, Grzymala-Busse, Slowinski & Ziarko, 1995; Polkowski, 2002; Polkowski & Skowron, 1999; Slowinski, 1992b; Slowinski & Zopounidis, 1995; Ziarko, 1998). As we have shown in Section 2, the paradigm of rough set theory is that of granular computing, because the main concept of the theory (rough approximation of a set) is built up of blocks of objects which are indiscernible by a given set of attributes, called granules of knowledge. In the space of regular attributes, the indiscernibility granules are bounded sets. Decision rules induced from rough approximation of a classification are also built up of such granules.
The authors have proposed an extension of the granular computing paradigm that enables us to take into account prior knowledge, either about evaluation of objects on multiple criteria only (Greco, Matarazzo, Slowinski & Stefanowski, 2002), or about multicriteria evaluation with monotonicity constraints (Greco, Matarazzo & Slowinski, 1998a, 1999b, 2000d, 2001a, 2002a, 2002b; Slowinski, Greco & Matarazzo, 2002a, 2009). The combination of the new granules with the idea of rough approximation is called the Dominance-based Rough Set Approach (DRSA).
In the following, we present the concept of granules which permit us to handle prior knowledge about multicriteria evaluation with monotonicity constraints when inducing decision rules.
Let U be a finite set of objects (universe) and let Q be a finite set of attributes divided into a set C of condition attributes and a set D of decision attributes, where  Æ. Also, let
Æ. Also, let
be attribute spaces corresponding to sets of condition and decision attributes, respectively. The elements of XC and XD can be interpreted as possible evaluations of objects on attributes from set  and from set
and from set  , respectively. Therefore, Xq is the set of possible evaluations of considered objects with respect to attribute q. The value of object x on attribute
, respectively. Therefore, Xq is the set of possible evaluations of considered objects with respect to attribute q. The value of object x on attribute  is denoted by Xq. Objects x and y are indiscernible by
is denoted by Xq. Objects x and y are indiscernible by  if
if  for all
for all  and, analogously, objects x and y are indiscernible by
and, analogously, objects x and y are indiscernible by  if
if  for all
for all  . The sets of indiscernible objects are equivalence classes of the corresponding indiscernibility relation Ip or IR. Moreover, Ip(x) and IR(x) denote equivalence classes including object x. ID generates a partition of U into a finite number of decision classes
. The sets of indiscernible objects are equivalence classes of the corresponding indiscernibility relation Ip or IR. Moreover, Ip(x) and IR(x) denote equivalence classes including object x. ID generates a partition of U into a finite number of decision classes  . Each
. Each  belongs to one and only one class
belongs to one and only one class  .
.
The above definitions are valid for regular attributes, not involving monotonicity relationships between values of condition and decision attributes. In this case, the granules of knowledge are bounded sets in XP and XR ( and
and  ), defined by partitions of U induced by the indiscernibility relations Ip and IR, respectively. Then, classification rules to be discovered are functions representing granules IR(x) by granules Ip(x) in the condition attribute space Xp, for any
), defined by partitions of U induced by the indiscernibility relations Ip and IR, respectively. Then, classification rules to be discovered are functions representing granules IR(x) by granules Ip(x) in the condition attribute space Xp, for any  and for any
and for any  .
.
If value sets of some condition and decision attributes are preference ordered (i.e. they are evaluation criteria), and there are known monotonic relationships between value sets of these condition and decision attributes, then the indiscernibility relation is unable to produce granules in XC and XD that would take into account the preference order. To do so, the indiscernibility relation has to be substituted by a dominance relation in  and
and  (
( and
and  ). Suppose, for simplicity, that all condition attributes in C and all decision attributes in D are criteria, and that C and D are semantically correlated.
). Suppose, for simplicity, that all condition attributes in C and all decision attributes in D are criteria, and that C and D are semantically correlated.
Let  be a weak preference relation on U (often called outranking) representing a preference on the set of objects with respect to criterion
be a weak preference relation on U (often called outranking) representing a preference on the set of objects with respect to criterion  . Now,
. Now,  means "xq is at least as good as yq with respect to criterion q". On the one hand, we say that x dominates y with respect to
means "xq is at least as good as yq with respect to criterion q". On the one hand, we say that x dominates y with respect to  (shortly, xP-dominates y) in the condition attribute space XP (denoted by
(shortly, xP-dominates y) in the condition attribute space XP (denoted by  ) if
) if  for all
for all  . Assuming, without loss of generality, that the domains of the criteria are numerical (i.e.
. Assuming, without loss of generality, that the domains of the criteria are numerical (i.e.  for any
for any  ) and that they are ordered so that the preference increases with the value, we can say that
) and that they are ordered so that the preference increases with the value, we can say that  is equivalent to
is equivalent to  for all
for all  ,
,  . Observe that for each
. Observe that for each  , xDpx, i.e. P-dominance is reflexive. On the other hand, the analogous definition holds in the decision attribute space XR (denoted by xDRy), where
, xDpx, i.e. P-dominance is reflexive. On the other hand, the analogous definition holds in the decision attribute space XR (denoted by xDRy), where  .
.
The dominance relations xDpy and xDRx ( and
and  ) are directional statements where x is a subject and y is a referent.
) are directional statements where x is a subject and y is a referent.
If  is the referent, then one can define a set of objects
is the referent, then one can define a set of objects  dominating x, called the P-dominating set (denoted by
dominating x, called the P-dominating set (denoted by  ) and defined as
) and defined as  .
.
If  is the subject, then one can define a set of objects
is the subject, then one can define a set of objects  dominated by x, called the P-dominated set (denoted by
dominated by x, called the P-dominated set (denoted by  ) and defined as
) and defined as  .
.
P-dominating sets  and P-dominated sets
and P-dominated sets  correspond to positive and negative dominance cones in XP, with the origin x.
correspond to positive and negative dominance cones in XP, with the origin x.
With respect to the decision attribute space XR (where  ), the R-dominance relation enables us to define the following sets:
), the R-dominance relation enables us to define the following sets:
 is a decision class with respect to
is a decision class with respect to  .
.  is called the upward union of classes, and
is called the upward union of classes, and  is the downward union of classes. If
is the downward union of classes. If  , then
, then  belongs to class
belongs to class  ,
,  , or better, on each decision attribute
, or better, on each decision attribute  . On the other hand, if
. On the other hand, if  , then x belongs to class
, then x belongs to class  ,
,  , or worse, on each decision attribute
, or worse, on each decision attribute  . The downward and upward unions of classes correspond to the positive and negative dominance cones in XR, respectively.
. The downward and upward unions of classes correspond to the positive and negative dominance cones in XR, respectively.
In this case, the granules of knowledge are open sets in XP and XR defined by dominance cones  ,
, 
 and
and  ,
, 
 , respectively. Then, classification rules to be discovered are functions representing granules
, respectively. Then, classification rules to be discovered are functions representing granules  ,
,  by granules
by granules  ,
,  , respectively, in the condition attribute space XP, for any
, respectively, in the condition attribute space XP, for any  and
and  and for any
and for any  .
.
4 THE DOMINANCE-BASED ROUGH SET APPROACH (DRSA) TO MULTICRITERIA ORDINAL CLASSIFICATION
4.1 Granular computing with dominance cones
When discovering classification rules, a set D of decision attributes is, usually, a singleton,  . Let us take this assumption for further presentation, although it is not necessary for the Dominance-based Rough Set Approach. The decision attribute d makes a partition of U into a finite number of classes,
. Let us take this assumption for further presentation, although it is not necessary for the Dominance-based Rough Set Approach. The decision attribute d makes a partition of U into a finite number of classes,  . Each object
. Each object  belongs to one and only one class,
belongs to one and only one class,  . The upward and downward unions of classes boil down, respectively, to:
. The upward and downward unions of classes boil down, respectively, to:
where  . Notice that for
. Notice that for  we have
we have  , i.e. all the objects not belonging to class Clt or better, belong to class
, i.e. all the objects not belonging to class Clt or better, belong to class  or worse.
or worse.
Let us explain how the rough set concept has been generalized to the Dominance-based Rough Set Approach in order to enable granular computing with dominance cones (for more details, see Greco, Matarazzo & Slowinski (1998a, 1999b, 2000d, 2001a, 2002a), Slowinski, Greco & Matarazzo (2009), Slowinski, Stefanowski, Greco & Matarazzo (2000)).
Given a set of criteria,  , the inclusion of an object
, the inclusion of an object  to the upward union of classes
to the upward union of classes  , = 2,..., n, is inconsistent with the dominance principle if one of the following conditions holds:
, = 2,..., n, is inconsistent with the dominance principle if one of the following conditions holds:
-
x belongs to class
 or better but it is
or better but it is P-dominated by an object
y belonging to a class worse than
 ,
, i.e.
 but
but  Æ,
Æ, -
x belongs to a worse class than
 but it
but it P-dominates an object
y belonging to class
 or better,
or better, i.e.
 but
but  Æ.
Æ.
If, given a set of criteria  , the inclusion of
, the inclusion of  to
to  , where
, where  , is inconsistent with the dominance principle, we say that
, is inconsistent with the dominance principle, we say that  belongs to
belongs to  with some ambiguity. Thus,
with some ambiguity. Thus,  belongs to
belongs to  without any ambiguity with respect to
without any ambiguity with respect to  , if
, if  and there is no inconsistency with the dominance principle. This means that all objects P-dominating
and there is no inconsistency with the dominance principle. This means that all objects P-dominating  belong to
belong to  , i.e.
, i.e.  . Geometrically, this corresponds to the inclusion of the complete set of objects contained in the positive dominance cone originating in
. Geometrically, this corresponds to the inclusion of the complete set of objects contained in the positive dominance cone originating in  , in the positive dominance cone
, in the positive dominance cone  originating in
originating in  .
.
Furthermore,  possibly belongs to
possibly belongs to  with respect to
with respect to  if one of the following conditions holds:
if one of the following conditions holds:
-
according to decision attribute
d,
x belongs to
-
according to decision attribute
d,
x does not belong to
y belonging to
In terms of ambiguity, x possibly belongs to  with respect to
with respect to  , if x belongs to
, if x belongs to  with or without any ambiguity. Due to the reflexivity of the
with or without any ambiguity. Due to the reflexivity of the  -dominance relation
-dominance relation  , the above conditions can be summarized as follows: xpossibly belongs to class
, the above conditions can be summarized as follows: xpossibly belongs to class  or better, with respect to
or better, with respect to  , if among the objects
, if among the objects  -dominated by xthere is an object
-dominated by xthere is an object  belonging to class
belonging to class  or better, i.e.
or better, i.e.
Geometrically, this corresponds to the non-empty intersection of the set of objects contained in the negative dominance cone originating in  , with the positive dominance cone
, with the positive dominance cone  originating in
originating in  .
.
For  , the set of all objects belonging to
, the set of all objects belonging to  without any ambiguity constitutes the P-lower approximation of
without any ambiguity constitutes the P-lower approximation of  , denoted by
, denoted by  , and the set of all objects that possibly belong to
, and the set of all objects that possibly belong to  constitutes the P-upper approximation of
constitutes the P-upper approximation of  , denoted by
, denoted by  . More formally:
. More formally:
where  . Analogously, one can define the P-lower approximation and the P-upper approximation of
. Analogously, one can define the P-lower approximation and the P-upper approximation of  :
:
where  .
.
The P-lower and P-upper approximations of  ,
,  , can also be expressed in terms of unions of positive dominance cones as follows:
, can also be expressed in terms of unions of positive dominance cones as follows:
Analogously, the P-lower and P-upper approximations of  ,
,  , can be expressed in terms of unions of negative dominance cones as follows:
, can be expressed in terms of unions of negative dominance cones as follows:
The P-lower and P-upper approximations so defined satisfy the following inclusion properties for each  and for all
and for all  :
:
All the objects belonging to  and
and  with some ambiguity constitute the P-boundary of
with some ambiguity constitute the P-boundary of  and
and  , denoted by
, denoted by  and
and  , respectively. They can be represented, in terms of upper and lower approximations, as follows:
, respectively. They can be represented, in terms of upper and lower approximations, as follows:
where  . The P-lower and P-upper approximations of the unions of classes
. The P-lower and P-upper approximations of the unions of classes  and
and  have an important complementarity property. It says that if object
have an important complementarity property. It says that if object  belongs without any ambiguity to class
belongs without any ambiguity to class  or better, then it is impossible that it could belong to class
or better, then it is impossible that it could belong to class  or worse, i.e.
or worse, i.e.
Due to the complementarity property,  , for
, for  , which means that if x belongs with ambiguity to class
, which means that if x belongs with ambiguity to class  or better, then it also belongs with ambiguity to class
or better, then it also belongs with ambiguity to class  or worse.
or worse.
Considering application of the lower and the upper approximations based on dominance  ,
,  , to any set
, to any set  , instead of the unions of classes
, instead of the unions of classes  and
and  , one gets upward lower and upper approximations
, one gets upward lower and upper approximations  and
and  , as well as downward lower and upper approximations
, as well as downward lower and upper approximations  and
and  , as follows:
, as follows:
From the definition of rough approximations  ,
,  ,
,  and
and  , we can get also the following properties of the P-lower and P-upper approximations (see Greco, Matarazzo & Slowinski, 2007, 2012):
, we can get also the following properties of the P-lower and P-upper approximations (see Greco, Matarazzo & Slowinski, 2007, 2012):
From the knowledge discovery point of view, P-lower approximations of unions of classes represent certain knowledge provided by criteria from  , while P-upper approximations represent possible knowledge and the P-boundaries contain doubtful knowledge provided by the criteria from
, while P-upper approximations represent possible knowledge and the P-boundaries contain doubtful knowledge provided by the criteria from  .
.
4.2 Variable Consistency Dominance-based Rough set Approach
The above definitions of rough approximations are based on a strict application of the dominance principle. However, when defining non-ambiguous objects, it is reasonable to accept a limited proportion of negative examples, particularly for large data tables. This extended version of the Dominance-based Rough Set Approach is called the Variable Consistency Dominance-based Rough Set Approach (VC-DRSA) model (Greco, Matarazzo, Slowinski & Stefanowski, 2001a).
For any  , we say that
, we say that  belongs to
belongs to  with no ambiguity at consistency level
with no ambiguity at consistency level  , if
, if  and at least
and at least  of all objects
of all objects  dominating x with respect to P also belong to
dominating x with respect to P also belong to  , i.e.
, i.e.
The term  is called rough membership and can be interpreted as conditional probability
is called rough membership and can be interpreted as conditional probability  . The level l is called the consistency level because it controls the degree of consistency between objects qualified as belonging to
. The level l is called the consistency level because it controls the degree of consistency between objects qualified as belonging to  without any ambiguity. In other words, if
without any ambiguity. In other words, if  , then at most
, then at most  of all objects
of all objects  dominating x with respect to P do not belong to
dominating x with respect to P do not belong to  and thus contradict the inclusion of x in
and thus contradict the inclusion of x in  .
.
Analogously, for any  we say that
we say that  belongs to
belongs to  with no ambiguity at consistency level
with no ambiguity at consistency level  , if
, if  and at least
and at least  of all the objects
of all the objects  dominated by x with respect to P also belong to
dominated by x with respect to P also belong to  , i.e.
, i.e.
The rough membership  can be interpreted as conditional probability
can be interpreted as conditional probability  . Thus, for any
. Thus, for any  , each object
, each object  is either ambiguous or non-ambiguous at consistency level
is either ambiguous or non-ambiguous at consistency level  with respect to the upward union
with respect to the upward union  or with respect to the downward union
or with respect to the downward union  .
.
The concept of non-ambiguous objects at some consistency level  leads naturally to the definition of
leads naturally to the definition of  -lower approximations of the unions of classes
-lower approximations of the unions of classes  and
and  which can be formally presented as follows:
which can be formally presented as follows:
Given  and consistency level
and consistency level  , we can define the
, we can define the  -upper approximations of
-upper approximations of  and
and  , denoted by
, denoted by  and
and  , respectively, by complementation of
, respectively, by complementation of  and
and  with respect to
with respect to  as follows:
as follows:
 can be interpreted as the set of all the objects belonging to
can be interpreted as the set of all the objects belonging to  , which are possibly ambiguous at consistency level
, which are possibly ambiguous at consistency level  . Analogously,
. Analogously,  can be interpreted as the set of all the objects belonging to
can be interpreted as the set of all the objects belonging to  , which are possibly ambiguous at consistency level
, which are possibly ambiguous at consistency level  . The
. The  -boundaries (
-boundaries ( -doubtful regions) of
-doubtful regions) of  and
and  are defined as:
are defined as:
where  . The VC-DRSA model provides some degree of flexibility in assigning objects to lower and upper approximations of the unions of decision classes. It can easily be demonstrated that for
. The VC-DRSA model provides some degree of flexibility in assigning objects to lower and upper approximations of the unions of decision classes. It can easily be demonstrated that for  and
and  ,
,
The VC-DRSA model is inspired by Ziarko's model of the variable precision rough set approach (Ziarko, 1993, 1998). However, there is a significant difference in the definition of rough approximations because  and
and  are composed of non-ambiguous and ambiguous objects at the consistency level
are composed of non-ambiguous and ambiguous objects at the consistency level  , respectively, while Ziarko's
, respectively, while Ziarko's  and
and  are composed of
are composed of  -indiscernibility sets such that at least
-indiscernibility sets such that at least  of these sets are included in
of these sets are included in  or have an non-empty intersection with
or have an non-empty intersection with  , respectively. If one would like to use Ziarko's definition of variable precision rough approximations in the context of multiple-criteria classification, then the
, respectively. If one would like to use Ziarko's definition of variable precision rough approximations in the context of multiple-criteria classification, then the  -indiscernibility sets should be substituted by
-indiscernibility sets should be substituted by  -dominating sets
-dominating sets  . However, then the notion of ambiguity that naturally leads to the general definition of rough approximations (see Slowinski & Vanderpooten (2000)) loses its meaning. Moreover, a bad side effect of the direct use of Ziarko's definition is that a lower approximation
. However, then the notion of ambiguity that naturally leads to the general definition of rough approximations (see Slowinski & Vanderpooten (2000)) loses its meaning. Moreover, a bad side effect of the direct use of Ziarko's definition is that a lower approximation  may include objects
may include objects  assigned to
assigned to  , where
, where 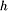 is much less than
is much less than  , if
, if  belongs to
belongs to  , which was included in
, which was included in  . When the decision classes are preference ordered, it is reasonable to expect that objects assigned to far worse classes than the considered union are not counted to the lower approximation of this union.
. When the decision classes are preference ordered, it is reasonable to expect that objects assigned to far worse classes than the considered union are not counted to the lower approximation of this union.
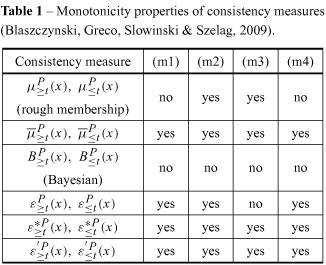
The VC-DRSA model presented above has been generalized in (Greco, Matarazzo & Slowinski, 2008b; Blaszczynski, Greco, Slowinski & Szelag, 2009). The generalized model applies two types of consistency measures in the definition of lower approximations:
-
gain-type consistency measures
-
cost-type consistency measures
 :
:
where  ,
,  ,
,  ,
,  , are threshold values on the consistency measures which are conditioning the inclusion of object
, are threshold values on the consistency measures which are conditioning the inclusion of object  in the
in the  -lower approximation of
-lower approximation of  , or
, or  . Here are the consistency measures considered in (Blaszczynski, Greco, Slowinski & Szelag, 2009): for all
. Here are the consistency measures considered in (Blaszczynski, Greco, Slowinski & Szelag, 2009): for all  and
and 
with
being cost-type consistency measures and
being cost-type consistency measures.
To be concordant with the rough set philosophy, consistency measures should enjoy some monotonicity properties (see Table 1). A consistency measure is monotonic if it does not decrease (or does not increase) when:
(m1) the set of attributes is growing,
(m2) the set of objects is growing,
(m3) the union of ordered classes is growing,
(m4)
As to the consistency measures  and
and  which enjoy all four monotonicity properties, they can be interpreted as estimates of conditional probability, respectively:
which enjoy all four monotonicity properties, they can be interpreted as estimates of conditional probability, respectively:
They say how far the implications
are not supported by the data.
For every  , the objects being consistent in the sense of the dominance principle with all upward and downward unions of classes are called
, the objects being consistent in the sense of the dominance principle with all upward and downward unions of classes are called  -correctly classified. For every
-correctly classified. For every  , the quality of approximation of classification
, the quality of approximation of classification  by the set of criteria
by the set of criteria  is defined as the ratio between the number of
is defined as the ratio between the number of  -correctly classified objects and the number of all the objects in the decision table. Since the objects which are
-correctly classified objects and the number of all the objects in the decision table. Since the objects which are  -correctly classified are those that do not belong to any
-correctly classified are those that do not belong to any  -boundary of unions
-boundary of unions  and
and  ,
,  , the quality of approximation of classification
, the quality of approximation of classification  by set of criteria
by set of criteria  , can be written as
, can be written as
 can be seen as a measure of the quality of knowledge that can be extracted from the decision table, where
can be seen as a measure of the quality of knowledge that can be extracted from the decision table, where  is the set of criteria and
is the set of criteria and  is the considered classification.
is the considered classification.
Each minimal subset  , such that
, such that  , is called a reduct of
, is called a reduct of  and is denoted by
and is denoted by  . Note that a decision table can have more than one reduct. The intersection of all reducts is called the core and is denoted by
. Note that a decision table can have more than one reduct. The intersection of all reducts is called the core and is denoted by  . Criteria from
. Criteria from  cannot be removed from the decision table without deteriorating the knowledge to be discovered. This means that in set
cannot be removed from the decision table without deteriorating the knowledge to be discovered. This means that in set  there are three categories of criteria:
there are three categories of criteria:
-
indispensable criteria included in the core,
-
exchangeable criteria included in some reducts but not in the core,
-
redundant criteria being neither indispensable nor exchangeable, thus not included in any reduct.
Note that reducts are minimal subsets of criteria conveying the relevant knowledge contained in the decision table. This knowledge is relevant for the explanation of patterns in a given decision table but not necessarily for prediction.
It has been shown in (Greco, Matarazzo & Slowinski, 2001d) that the quality of classification satisfies properties of set functions which are called fuzzy measures. For this reason, we can use the quality of classification for the calculation of indices which measure the relevance of particular attributes and/or criteria, in addition to the strength of interactions between them. The useful indices are: the value index and interaction indices of Shapley and Banzhaf; the interaction indices of Murofushi-Soneda and Roubens; and the Möbius representation. All these indices can help to assess the interaction between the considered criteria, and can help to choose the best reduct.
4.3 Stochastic dominance-based rough set approach
From a probabilistic point of view, the assignment of object  to "at least" class
to "at least" class  can be made with probability
can be made with probability  , where
, where  is classification decision for
is classification decision for  . This probability is supposed to satisfy the usual axioms of probability:
. This probability is supposed to satisfy the usual axioms of probability:
These probabilities are unknown but can be estimated from data.
For each class  , we have a binary problem of estimating the conditional probabilities
, we have a binary problem of estimating the conditional probabilities  ,
,  . It can be solved by isotonic regression (Kotlowski, Dembczynski, Greco & Slowinski, 2008). Let
. It can be solved by isotonic regression (Kotlowski, Dembczynski, Greco & Slowinski, 2008). Let  if
if  , otherwise
, otherwise  . Let also
. Let also  be the estimate of the probability
be the estimate of the probability  . Then, choose estimates
. Then, choose estimates  which minimize the squared distance to the class assignment
which minimize the squared distance to the class assignment  , subject to the monotonicity constraints:
, subject to the monotonicity constraints:
where  means that
means that  dominates
dominates  .
.
Then, stochastic  -lower approximations for classes "at least
-lower approximations for classes "at least  " and "at most
" and "at most  " can be defined as:
" can be defined as:
Replacing the unknown probabilities  ,
,  , by their estimates
, by their estimates  obtained from isotonic regression, we get:
obtained from isotonic regression, we get:
where parameter
Solving isotonic regression requires  time, but a good heuristic needs only
time, but a good heuristic needs only  .
.
In fact, as shown in (Kotlowski, Dembczynski, Greco & Slowinski, 2008), we don't really need to know the probability estimates to obtain stochastic lower approximations. We only need to know for which object  ,
,  and for which
and for which  ,
,  . This can be found by solving a linear programming (reassignment) problem.
. This can be found by solving a linear programming (reassignment) problem.
As before,  if
if  , otherwise
, otherwise  . Let
. Let  be the decision variable which determines a new class assignment for object
be the decision variable which determines a new class assignment for object  . Then, reassign objects from union of classes indicated by
. Then, reassign objects from union of classes indicated by  to union of classes indicated by
to union of classes indicated by  , such that the new class assignments are consistent with the dominance principle, where
, such that the new class assignments are consistent with the dominance principle, where  results from solving the following linear programming problem:
results from solving the following linear programming problem:
where  are arbitrary positive weights and
are arbitrary positive weights and  means that
means that  dominates
dominates  .
.
Due to unimodularity of the constraint matrix, the optimal solution of this linear programming problem is always integer, i.e.  . For all objects consistent with the dominance principle,
. For all objects consistent with the dominance principle,  . If we set
. If we set  and
and  , then the optimal solution
, then the optimal solution  satisfies:
satisfies:  . If we set
. If we set  and
and  , then the optimal solution
, then the optimal solution  satisfies:
satisfies:  .
.
For each  , solving the reassignment problem twice, we can obtain the lower approximations
, solving the reassignment problem twice, we can obtain the lower approximations  ,
,  , without knowing the probability estimates!
, without knowing the probability estimates!
4.4 Induction of decision rules
Using the terms of knowledge discovery, the dominance-based rough approximations of upward and downward unions of classes are applied on the data set in the pre-processing stage. In result of this stage, the data are structured in a way facilitating induction of "if..., then..." decision rules with a guaranteed consistency level. For a given upward or downward union of classes,  or
or  , the decision rules induced under a hypothesis that objects belonging to
, the decision rules induced under a hypothesis that objects belonging to  or
or  are positive and all the others are negative, suggests an assignment to "class
are positive and all the others are negative, suggests an assignment to "class  or better", or to "class
or better", or to "class  or worse", respectively. On the other hand, the decision rules induced under a hypothesis that objects belonging to the intersection
or worse", respectively. On the other hand, the decision rules induced under a hypothesis that objects belonging to the intersection  are positive and all the others are negative, are suggesting an assignment to some classes between
are positive and all the others are negative, are suggesting an assignment to some classes between  and
and  .
.
In the case of preference ordered data it is meaningful to consider the following five types of decision rules:
1) Certain
-decision rules. These provide lower profile descriptions for objects belonging to
without ambiguity: if
and
and...
, then
, where for each
, "
" means "
is at least as good as
";
2) Possible
-decision rules. Such rules provide lower profile descriptions for objectsbelonging to
with or without any ambiguity: if
and
and...
, then
possibly belongs to
;
3) Certain
-decision rules. These give upper profile descriptions for objects belonging to
without ambiguity: if
and
and...
, then
, where for each
, "
, means "
is at most as good as
";
4) Possible
-decision rules. These provide upper profile descriptions for objects belonging to
with or without any ambiguity: if
and
and...
, then
possibly belongs to
;
5) Approximate
-decision rules. These represent simultaneously lower and upper profile descriptions for objects belonging to
without the possibility of discerning the actual class: if
and...
and
and...
, then
.
In the left hand side of a  -decision rule we can have "
-decision rule we can have " " and "
" and " ", where
", where  , for the same
, for the same  . Moreover, if
. Moreover, if  , the two conditions boil down to "
, the two conditions boil down to " ", where for each
", where for each  , "
, " " means "
" means " is indifferent to
is indifferent to  ".
".
A minimal rule is an implication where we understand that there is no other implication with a left hand side which has at least the same weakness (which means that it uses a subset of elementary conditions and/or weaker elementary conditions) and which has a right hand side that has at least the same strength (which means, a  - or a
- or a  -decision rule assigning objects to the same union or sub-union of classes, or a
-decision rule assigning objects to the same union or sub-union of classes, or a  -decision rule assigning objects to the same or larger set of classes).
-decision rule assigning objects to the same or larger set of classes).
The rules of type 1) and 3) represent certain knowledge extracted from the decision table, while the rules of type 2) and 4) represent possible knowledge. Rules of type 5) represent doubtful knowledge.
The rules of type 1) and 3) are exact if they do not cover negative examples; they are probabilistic, otherwise. In the latter case, each rule is characterized by a confidence ratio, representing the probability that an object matching left hand side of the rule matches also its right hand side. Probabilistic rules concord with the Variable-Consistency Dominance-based Rough Set Approach model mentioned above.
4.5 Rule-based classification algorithms
We will now comment upon the application of decision rules to some objects described by criteria from  . When applying
. When applying 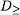 -decision rules to an object
-decision rules to an object  , it is possible that
, it is possible that  either matches the left hand side of at least one decision rule or it does not. In the case of at least one such match, it is reasonable to conclude that
either matches the left hand side of at least one decision rule or it does not. In the case of at least one such match, it is reasonable to conclude that  belongs to class
belongs to class  , because it is the lowest class of the upward union
, because it is the lowest class of the upward union  which results from intersection of all the right hand sides of the rules covering
which results from intersection of all the right hand sides of the rules covering  . More precisely, if
. More precisely, if  matches the left hand side of rules
matches the left hand side of rules  , having right hand sides
, having right hand sides  ,
,  , then
, then  is assigned to class
is assigned to class  , where
, where  . In the case of no matching, we can conclude that
. In the case of no matching, we can conclude that  belongs to
belongs to  , i.e. to the worst class, since no rule with a right hand side suggesting a better classification of
, i.e. to the worst class, since no rule with a right hand side suggesting a better classification of  is covering this object.
is covering this object.
Analogously, when applying  -decision rules to the object
-decision rules to the object  , we can conclude that
, we can conclude that  belongs either to class
belongs either to class  (because it is the highest class of the downward union
(because it is the highest class of the downward union  resulting from the intersection of all the right hand sides of the rules covering
resulting from the intersection of all the right hand sides of the rules covering  ), or to class
), or to class  , i.e. to the best class, when
, i.e. to the best class, when  is not covered by any rule. More precisely, if
is not covered by any rule. More precisely, if  matches the left hand side of rules
matches the left hand side of rules  , having right hand sides
, having right hand sides  ,
,  , then
, then  is assigned to class
is assigned to class  , where
, where  . In the case of no matching, it is concluded that
. In the case of no matching, it is concluded that  belongs to the best class
belongs to the best class  because no rule with a right hand side suggesting a worse classification of
because no rule with a right hand side suggesting a worse classification of  is covering this object. Finally, when applying D
is covering this object. Finally, when applying D -decision rules to
-decision rules to  , it is possible to conclude that
, it is possible to conclude that  belongs to the union of all the classes suggested in the right hand side of the rules covering
belongs to the union of all the classes suggested in the right hand side of the rules covering  .
.
A new classification algorithm has been proposed in (Blaszczynski, Greco & Slowinski, 2007). Let  , be the rules matching object
, be the rules matching object  . Then,
. Then,  denotes the set of rules matching
denotes the set of rules matching  , which are recommending assignment of object
, which are recommending assignment of object  to a union including class
to a union including class  , and
, and  denotes the set of rules matching
denotes the set of rules matching  , which are not recommending assignment of object
, which are not recommending assignment of object  to a union including class
to a union including class  .
.  ,
,  are sets of objects with property
are sets of objects with property  and
and  , respectively,
, respectively,  . For a classified object
. For a classified object  , one has to calculate the score for each candidate class:
, one has to calculate the score for each candidate class:
where
and
 and
and  can be interpreted in terms of conditional probability as a product of confidence and coverage of the matching rules:
can be interpreted in terms of conditional probability as a product of confidence and coverage of the matching rules:
The recommendation of the univocal classification  is such that:
is such that:
A set of decision rules is complete if it is able to cover all objects from the decision table in such a way that consistent objects are re-classified to their original classes and inconsistent objects are classified to clusters of classes which refer to this inconsistency. Each set of decision rules that is complete and non-redundant is called minimal. Note that an exclusion of any rule from this set makes it non-complete.
In the case of the Variable-Consistency Dominance-based Rough Set Approach, the decision rules are induced from the  -lower approximations whose composition is controlled by the user-specified consistency level
-lower approximations whose composition is controlled by the user-specified consistency level  . Consequently, the value of confidence
. Consequently, the value of confidence  for the rule should be constrained from the bottom. It is reasonable to require that the smallest accepted confidence level of the rule should not be lower than the currently used consistency level
for the rule should be constrained from the bottom. It is reasonable to require that the smallest accepted confidence level of the rule should not be lower than the currently used consistency level  . Indeed, in the worst case, some objects from the
. Indeed, in the worst case, some objects from the  -lower approximation may create a rule using all the criteria from
-lower approximation may create a rule using all the criteria from  thus giving a confidence
thus giving a confidence  .
.
Observe that the syntax of decision rules induced from dominance-based rough approximations uses the concept of dominance cones: each condition profile is a dominance cone in  , and each decision profile is a dominance cone in
, and each decision profile is a dominance cone in  . In both cases the cone is positive for
. In both cases the cone is positive for 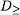 -rules and negative for
-rules and negative for  -rules.
-rules.
Also note that dominance cones which correspond to condition profiles can originate in any point of  , without the risk of being too specific. Thus, in contrast to granular computing based on indiscernibility (or similarity) relation, in case of granular computing based on dominance, the condition attribute space
, without the risk of being too specific. Thus, in contrast to granular computing based on indiscernibility (or similarity) relation, in case of granular computing based on dominance, the condition attribute space  need not be discretized (Greco, Matarazzo & Slowinski, 2007, 2008a, 2009).
need not be discretized (Greco, Matarazzo & Slowinski, 2007, 2008a, 2009).
Procedures for induction of rules from dominance-based rough approximations have beenproposed in (Greco, Matarazzo, Slowinski & Stefanowski, 2001b; Blaszczynski, Slowinski & Szelag, 2011).
The utility of decision rules is threefold: they explain (summarize) decisions made on objects from the dataset, they can be used to make decisions with respect to new (unseen) objects which are matching conditions of some rules, and they permit to build up a strategy of intervention (Greco, Matarazzo, Pappalardo & Slowinski, 2005). Attractiveness of particular decision rules can be measured in many different ways, however, the most convincing measures are Bayesian confirmation measures enjoying a special monotonicity property, as reported in (Greco, Pawlak & Slowinski, 2004).
In Giove, Greco, Matarazzo & Slowinski (2002), a new methodology for the induction of monotonic decision trees from dominance-based rough approximations of preference-ordered decision classes has been proposed.
It is finally worth noting that several algebraic models have been proposed for Dominance-based Rough Set Approach (Greco, Matarazzo & Slowinski, 2010a, 2010g, 2012) - the algebraic structures are based on bipolar disjoint representation (positive and negative) of interior and exterior of a concept. These algebra models give elegant representations of basic properties of Dominance-based Rough Sets. Moreover, a topology for Dominance-based Rough Set Approach in a bitopological space has been proposed in (Greco, Matarazzo & Slowinski, 2010b).
4.6 An illustrative example
To illustrate the application of the Dominanced Based Rough Set Approach to multicriteria classification, we will use a part of some data provided by a Greek industrial bank ETEVA which finances industrial and commercial firms in Greece (Slowinski & Zopounidis, 1995; Slowinski et al., 2005). A sample composed of 39 firms has been chosen for the study in co-operation with the ETEVA's financial manager. The manager has classified the selected firms into three classes of bankruptcy risk. The classification decision is represented by decision attribute  making a trichotomic partition of the 39 firms:
making a trichotomic partition of the 39 firms:
 means "acceptable",
means "acceptable",  means "uncertain",
means "uncertain",  means "non-acceptable".
means "non-acceptable".
The partition is denoted by  and, obviously, class
and, obviously, class  is better than
is better than  which is better than
which is better than  .
.
The firms were evaluated using the following twelve criteria ( means preference increasing with value and
means preference increasing with value and  means preference decreasing with value):
means preference decreasing with value):
-
 earnings before interests and taxes/total assets,
earnings before interests and taxes/total assets, -
 net income/net worth,
net income/net worth, -
-
 total liabilities/cash flow,
total liabilities/cash flow, -
 interest expenses/sales,
interest expenses/sales, -
-
 (very low
(very low  1, low
1, low  2, medium
2, medium  3, high
3, high  4, very high
4, very high  5)
5) -
 firm's market niche/position,
firm's market niche/position,  (bad
(bad  1, rather bad
1, rather bad  2, medium
2, medium  3, good
3, good  4, very good
4, very good  5)
5) -
 technical structure-facilities,
technical structure-facilities,  (bad
(bad  1, rather bad
1, rather bad  2, medium
2, medium  3, good
3, good  4, very good
4, very good  5)
5) -
 (bad
(bad 1, rather bad
1, rather bad  2, medium
2, medium  3, good
3, good  4, very good
4, very good  5)
5) -
 special competitive advantage of firms,
special competitive advantage of firms,  (low
(low  1, medium
1, medium  2, high
2, high  3, very high
3, very high  4)
4) -
 market flexibility,
market flexibility,  (very low
(very low  1, low
1, low  2, medium
2, medium  3, high
3, high  4, veryhigh
4, veryhigh  5)
5)
The first six criteria are cardinal (financial ratios) and the last six are ordinal. The data table is presented in Table 2.
The main questions to be answered by the knowledge discovery process were the following:
-
Is the information contained in
Table 2 consistent?
-
What are the reducts of criteria ensuring the same quality of approximation of the multicriteria classification as the whole set of criteria?
-
What decision rules can be extracted from
-
What are the minimal sets of decision rules?
We will answer these questions using the Dominance-based Rough Set Approach. The first result from this approach is a discovery that the financial data table is consistent for the complete set of criteria  . Therefore, the
. Therefore, the  -lower and C-upper approximations of
-lower and C-upper approximations of  ,
,  and
and  ,
,  are the same. In other words, the quality of approximation of all upward and downward unions of classes, as well as the quality of classification, is equal to 1.
are the same. In other words, the quality of approximation of all upward and downward unions of classes, as well as the quality of classification, is equal to 1.
The second discovery is a set of 18 reducts of criteria ensuring the same quality of classification as the whole set of 12 criteria:
All the eighteen subsets of criteria are equally good and sufficient for the perfect approximation of the classification performed by ETEVA's financial manager on the 39 firms. The core of  is empty
is empty  which means that no criterion is indispensable for the approximation. Moreover, all the criteria are exchangeable and no criterion is redundant.
which means that no criterion is indispensable for the approximation. Moreover, all the criteria are exchangeable and no criterion is redundant.
The third discovery is the set of all decision rules. We obtained 74 rules describing  , 51 rules describing
, 51 rules describing  , 75 rules describing
, 75 rules describing  and 79 rules describing
and 79 rules describing  .
.
The fourth discovery is the finding of minimal sets of decision rules. Several minimal sets were found. One of them is shown below. The number in parenthesis indicates the number of objects which support the corresponding rule, i.e. the rule strength:
1. if
and
and
, then
,(4),
2. if
and
, then
, (5),
3. if
and
and
, then
, (4),
4. if
and
, then
, (14),
5. if
, then
, (18),
6. if
and
, then
, (26),
7. if
, then
, (21),
8. if
and
, then
, (27),
9. if
and
, then
, (20).
As the minimal set of rules is complete and composed of 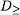 -decision rules and
-decision rules and  -decision rules only, application of these rules to the 39 firms will result in their exact re-classification to classes of risk.
-decision rules only, application of these rules to the 39 firms will result in their exact re-classification to classes of risk.
Minimal sets of decision rules represent the most concise and non-redundant knowledge representations. The above minimal set of 9 decision rules uses 8 criteria and 18 elementary conditions, i.e. 3.85% of descriptors from the data table.
The well-known machine discovery methods cannot deal with multicriteria classification because they do not consider preference orders in the domains of attributes and among the classes. There are multicriteria decision analysis methods for such classification. However, they are not discovering classification rules from data. They simply apply a preference model, like the utility function in scoring methods (see, e.g., (Thomas, Crook & Edelman, 1992)), to a set of objects to be classified. In this sense, they are not knowledge discovery methods at all.
Comparing the Dominance-based Rough Set Approach to the Indiscernibility-based Rough Set Approach, we can notice the following differences between the two approaches. The Indiscern-ibility-based Rough Set Approach extracts knowledge about a partition of  into classes which are not preference-ordered. The granules used for knowledge representation are sets of objects which are indiscernible by a set of condition attributes.
into classes which are not preference-ordered. The granules used for knowledge representation are sets of objects which are indiscernible by a set of condition attributes.
In the case of the Dominance-based Rough Set Approach and multicriteria classification, the condition attributes are criteria and the classes are preference-ordered. The extracted knowledge concerns a collection of upward and downward unions of classes and the granules used for knowledge representation are sets of objects defined using the dominance relation. This is the main difference between the Indiscernibility-based Rough Set Approach and the Dominance-based Rough Set Approach.
There are three notable advantages of the Dominance-based Rough Set Approach over theIndiscernibility-based Rough Set Approach. The first one is the ability to handle criteria, pref-erence-ordered classes and inconsistencies in the set of decision examples that the Indiscern-ibility-based Rough Set Approach is simply not able to discover. Consequently, the rough approximations separate the certain information from the doubtful, which is taken into account in rule induction. The second advantage is the ability to analyze a data table without any preprocessing of data. The third advantage lies in the richer syntax of decision rules that are induced from rough approximations. The elementary conditions of decision rules resulting from Dominance-based Rough Set Approach use relations from  , while those resulting from the Indiscernibility-based Rough Set Approach only use =. The Dominance-based Rough Set Approach syntax is more understandable to practitioners. The minimal sets of decision rules are smaller than the minimal sets which result from the Indiscernibility-based Rough Set Approach.
, while those resulting from the Indiscernibility-based Rough Set Approach only use =. The Dominance-based Rough Set Approach syntax is more understandable to practitioners. The minimal sets of decision rules are smaller than the minimal sets which result from the Indiscernibility-based Rough Set Approach.
5 THE DOMINANCE-BASED ROUGH SET APPROACH TO MULTICRITERIA CHOICE AND RANKING
One of the very first extensions of the Dominance-based Rough Set Approach concerned pref-erence-ordered data representing pairwise comparisons (i.e. binary relations) between objects on both, condition and decision attributes (Greco, Matarazzo & Slowinski, 1999a, 1999b, 2000d, 2001c). Note that while classification is based on the absolute evaluation of objects, choice and ranking refer to pairwise comparisons of objects. In this case, the decision rules to be discovered from the data characterize a comprehensive binary relation on the set of objects. If this relation is a preference relation and if, among the condition attributes, there are some criteria which are semantically correlated with the comprehensive preference relation, then the data set (serving as the learning sample) can be considered to be preference information for a decision maker in a multicriteria choice or ranking problem. In consequence, the comprehensive preference relation characterized by the decision rules discovered from this data set can be considered as a preference model for the decision maker. It may be used to explain the decision policy of the decision maker and to recommend a good choice or preference ranking with respect to new objects.
Let us consider a finite set  of objects evaluated by a finite set
of objects evaluated by a finite set  of criteria. The best choice (or the preference ranking) in set
of criteria. The best choice (or the preference ranking) in set  is semantically correlated with the criteria from set
is semantically correlated with the criteria from set  . The preference information concerning the multicriteria choice or ranking problem is a data set in the form of a pairwise comparison table which includes pairs of some reference objects from a subset
. The preference information concerning the multicriteria choice or ranking problem is a data set in the form of a pairwise comparison table which includes pairs of some reference objects from a subset  . This is described by preference relations on particular criteria and a comprehensive preference relation. One such example is a weak preference relation called the outranking relation. By using the Dominance-based Rough Set Approach for the analysis of the pairwise comparison table, we can obtain a rough approximation of the outranking relation by a dominance relation. The decision rules induced from the rough approximation are then applied to the complete set
. This is described by preference relations on particular criteria and a comprehensive preference relation. One such example is a weak preference relation called the outranking relation. By using the Dominance-based Rough Set Approach for the analysis of the pairwise comparison table, we can obtain a rough approximation of the outranking relation by a dominance relation. The decision rules induced from the rough approximation are then applied to the complete set  of the objects associated with the choice or ranking. As a result, one obtains a four-valued outranking relation on this set. In order to obtain a recommendation, it is advisable to use an exploitation procedure based on the net flow score of the objects. We present this methodology in more detail below.
of the objects associated with the choice or ranking. As a result, one obtains a four-valued outranking relation on this set. In order to obtain a recommendation, it is advisable to use an exploitation procedure based on the net flow score of the objects. We present this methodology in more detail below.
5.1 The pairwise comparison table as input preference information
Given a multicriteria choice or ranking problem, a decision maker can express the preferences by pairwise comparisons of the reference objects. In the following,  will denote the presence, while
will denote the presence, while  denotes the absence of the outranking relation for a pair of objects
denotes the absence of the outranking relation for a pair of objects  .
.
For each pair of reference objects  , the decision maker can select one of the three following possibilities:
, the decision maker can select one of the three following possibilities:
1) object
is as good as
, i.e.
,
2) object
is worse than
, i.e.
,
3) the two objects are incomparable at the present stage.
A pairwise comparison table, denoted by  , is then created on the basis of this information. The first
, is then created on the basis of this information. The first  columns correspond to the criteria from set
columns correspond to the criteria from set  . The last, i.e. the
. The last, i.e. the  -th column, represents the comprehensive binary preference relation
-th column, represents the comprehensive binary preference relation 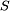 or
or  . The rows correspond to the pairs from
. The rows correspond to the pairs from  . For each pair in
. For each pair in  , a difference between criterion values is put in the corresponding column. If the decision maker judges that two objects are incomparable, then the corresponding pair does not appear in
, a difference between criterion values is put in the corresponding column. If the decision maker judges that two objects are incomparable, then the corresponding pair does not appear in  .
.
We will define  more formally. For any criterion
more formally. For any criterion  , let
, let  be a finite set of binary relations defined on
be a finite set of binary relations defined on  on the basis of the evaluations of objects from
on the basis of the evaluations of objects from  with respect to the considered criterion
with respect to the considered criterion  , such that for every
, such that for every  exactly one binary relation
exactly one binary relation  is verified. More precisely, given the domain
is verified. More precisely, given the domain  of
of  , if
, if  ,
,  are the respective evaluations of
are the respective evaluations of  by means of
by means of  and
and  , with
, with  , then for each
, then for each  having the same evaluations
having the same evaluations  ,
,  by means of
by means of  ,
,  . Furthermore, let
. Furthermore, let  be a set of binary relations defined on set
be a set of binary relations defined on set  (comprehensive pairwise comparisons) such that at most one binary relation
(comprehensive pairwise comparisons) such that at most one binary relation  is verified for every
is verified for every  .
.
The pairwise comparison table is defined as data table  , where
, where  is a non-empty set of exemplary pairwise comparisons of reference objects,
is a non-empty set of exemplary pairwise comparisons of reference objects,  ,
,  is a decision corresponding to the comprehensive pairwise comparison (comprehensive preference relation), and
is a decision corresponding to the comprehensive pairwise comparison (comprehensive preference relation), and  is a total function such that
is a total function such that  for every
for every  and for each
and for each  , and
, and  for every
for every  . It follows that for any pair of reference objects
. It follows that for any pair of reference objects  there is verified one and only one binary relation
there is verified one and only one binary relation  . Thus,
. Thus,  induces a partition of
induces a partition of  . In fact, the data table
. In fact, the data table  can be seen as decision table, since the set of considered criteria
can be seen as decision table, since the set of considered criteria  and the decision
and the decision  are distinguished.
are distinguished.
We are considering a pairwise comparison table where the set  is composed of two binary relations defined on
is composed of two binary relations defined on  :
:
-
 or
or  ), where
), where -
 or
or  ), where
), where
Observe that the binary relation
5.2 Rough approximation of preference relations specified in the pairwise comparison table
In the following we will distinguish between two types of evaluation scales of criteria: cardinal and ordinal. Let  be the set of criteria expressing preferences on a cardinal scale, and let
be the set of criteria expressing preferences on a cardinal scale, and let  , be the set of criteria expressing preferences on an ordinal scale, such that
, be the set of criteria expressing preferences on an ordinal scale, such that  and
and  Æ. Moreover, for each
Æ. Moreover, for each  , we denote by
, we denote by  the subset of
the subset of  composed of criteria expressing preferences on an ordinal scale, i.e.
composed of criteria expressing preferences on an ordinal scale, i.e.  , and by
, and by  we denote the subset of
we denote the subset of  composed of criteria expressing preferences on a cardinal scale, i.e.
composed of criteria expressing preferences on a cardinal scale, i.e.  . Of course, for each
. Of course, for each  , we have
, we have  and
and  Æ.
Æ.
The meaning of the two scales is such that in the case of the cardinal scale we can specify the intensity of preference for a given difference of evaluations, while in the case of the ordinal scale, this is not possible and we can only establish an order of evaluations.
5.2.1 Multigraded dominance
We assume that the pairwise comparisons of reference objects on cardinal criteria from set  can be represented in terms of graded preference relations (for example "very weak preference", "weak preference", "strict preference", "strong preference" and "very strong preference"), denoted by
can be represented in terms of graded preference relations (for example "very weak preference", "weak preference", "strict preference", "strong preference" and "very strong preference"), denoted by  : for each
: for each  and for every
and for every  ,
,  , where
, where  is a particular subset of the relative integers and
is a particular subset of the relative integers and
-
-
-
 means that object
means that object
Within the preference context, the similarity relation  , even if not symmetric, resembles the indifference relation. Thus, in this case, we call this similarity relation "asymmetric indifference". Of course, for each
, even if not symmetric, resembles the indifference relation. Thus, in this case, we call this similarity relation "asymmetric indifference". Of course, for each  and for every
and for every  ,
,
Let  and
and  º = Æ. Given
º = Æ. Given  ,
,  , the pair of objects
, the pair of objects  is said to dominate
is said to dominate  with respect to criteria from
with respect to criteria from  (denoted by
(denoted by  ), if
), if  is preferred to
is preferred to  at least as strongly as
at least as strongly as  is preferred to
is preferred to  with respect to each
with respect to each  . More precisely, "at least as strongly as" means "by at least the same degree", i.e.
. More precisely, "at least as strongly as" means "by at least the same degree", i.e.  , where
, where  ,
,  and
and  , for each
, for each  .
.
Let  be the dominance relation confined to the single criterion
be the dominance relation confined to the single criterion  . The binary relation
. The binary relation  is reflexive (
is reflexive ( , for every
, for every  ), transitive (
), transitive ( and
and  imply
imply  , for every
, for every  ), and complete (
), and complete ( and/or
and/or  , for all
, for all  ). Therefore,
). Therefore,  is a complete preorder on
is a complete preorder on  . Since the intersection of complete preorders is a partial preorder and
. Since the intersection of complete preorders is a partial preorder and  ,
,  , then the dominance relation
, then the dominance relation  is a partial preorder on
is a partial preorder on  .
.
Let  and
and  ; then the following implication holds:
; then the following implication holds:
Given  and
and  , we define the following:
, we define the following:
-
A set of pairs of objects dominating
 , called the
, called the  -
-dominating set, denoted by
 and defined to be
and defined to be  ;
; -
A set of pairs of objects dominated by
 , called the
, called the  -
-dominated set, denoted by
 and defined as
and defined as  .
.
The  -dominating sets and the
-dominating sets and the  -dominated sets defined on
-dominated sets defined on  for all pairs of reference objects from
for all pairs of reference objects from  are "granules of knowledge" that can be used to express
are "granules of knowledge" that can be used to express  -lower and
-lower and  -upper approximations of the comprehensive outranking relations
-upper approximations of the comprehensive outranking relations  and
and  , respectively:
, respectively:
It has been proved in (Greco, Matarazzo & Slowinski, 1999a) that
Furthermore, the following complementarity properties hold:
The  -boundaries (
-boundaries ( -doubtful regions) of
-doubtful regions) of  and
and  are defined as
are defined as
From the above it follows that  .
.
The concepts of the quality of approximation, reducts and core can be extended also to the approximation of the outranking relation by multigraded dominance relations.
In particular, the coefficient
defines the quality of approximation of  and
and  by
by  . It expresses the ratio of all pairs of reference objects
. It expresses the ratio of all pairs of reference objects  correctly assigned to
correctly assigned to  and
and  by the set
by the set  of criteria to all the pairs of objects contained in
of criteria to all the pairs of objects contained in  . Each minimal subset
. Each minimal subset  , such that
, such that  , is called a reduct of
, is called a reduct of  (denoted by
(denoted by  ). Note that
). Note that  can have more than one reduct. The intersection of all
can have more than one reduct. The intersection of all  -reducts is called the core (denoted by
-reducts is called the core (denoted by  ).
).
It is also possible to use the Variable Consistency Model on  (Slowinski, Greco & Mata-razzo, 2002b), being aware that some of the pairs in the positive or negative dominance sets belong to the opposite relation, while at least
(Slowinski, Greco & Mata-razzo, 2002b), being aware that some of the pairs in the positive or negative dominance sets belong to the opposite relation, while at least  of pairs belong to the correct one. Then the definition of the lower approximations of
of pairs belong to the correct one. Then the definition of the lower approximations of  and
and  boils down to:
boils down to:
5.2.2 Dominance without degrees of preference
The degree of graded preference considered above is defined on a cardinal scale of the strength of preference. However, in many real world problems, the existence of such a quantitative scale is rather questionable. This is the case with ordinal scales of criteria. In this case, the dominance relation is defined directly on evaluations  for all objects
for all objects  . Let us explain this latter case in more detail.
. Let us explain this latter case in more detail.
Let  and
and  Æ, then, given
Æ, then, given  , the pair (x, y) is said to dominate the pair (w, z) with respect to criteria from
, the pair (x, y) is said to dominate the pair (w, z) with respect to criteria from  (denoted by
(denoted by  ), if for each
), if for each  ,
,  and
and  .
.
Let  be the dominance relation confined to the single criterion
be the dominance relation confined to the single criterion  . The binary relation
. The binary relation  is reflexive, transitive, but non-complete (it is possible that not
is reflexive, transitive, but non-complete (it is possible that not  and not
and not  for some
for some  ). Therefore,
). Therefore,  is a partial preorder. Since the intersection of partial preorders is also a partial preorder and
is a partial preorder. Since the intersection of partial preorders is also a partial preorder and  ,
,  , then the dominance relation
, then the dominance relation  is a partial preorder.
is a partial preorder.
If some criteria from  express preferences on a quantitative or a numerical non-quantitative scale and others on an ordinal scale, i.e. if
express preferences on a quantitative or a numerical non-quantitative scale and others on an ordinal scale, i.e. if  Æ and
Æ and  Æ, then, given
Æ, then, given  , the pair
, the pair  is said to dominate the pair
is said to dominate the pair  with respect to criteria from
with respect to criteria from  , if
, if  dominates
dominates  with respect to both
with respect to both  and
and  . Since the dominance relation with respect to
. Since the dominance relation with respect to  is a partial preorder on
is a partial preorder on  (because it is a multigraded dominance) and the dominance with respect to
(because it is a multigraded dominance) and the dominance with respect to  is also a partial preorder on
is also a partial preorder on  (as explained above), then the dominance
(as explained above), then the dominance  , being the intersection of these two dominance relations, is a partial preorder. In consequence, all the concepts introduced in the previous section can be restored using this specific definition of dominance.
, being the intersection of these two dominance relations, is a partial preorder. In consequence, all the concepts introduced in the previous section can be restored using this specific definition of dominance.
5.3 Induction of decision rules from rough approximations of preference relations
Using the rough approximations of preference relations  and
and  defined in 5.2.1 and 5.2.2, it is possible to induce a generalized description of the preference information contained in a given
defined in 5.2.1 and 5.2.2, it is possible to induce a generalized description of the preference information contained in a given  in terms of suitable decision rules. The syntax of these rules involves the concept of upward cumulated preferences (denoted by
in terms of suitable decision rules. The syntax of these rules involves the concept of upward cumulated preferences (denoted by  ) and downward cumulated preferences (denoted by
) and downward cumulated preferences (denoted by  ), having the following interpretation:
), having the following interpretation:
-
 means "
means " -
 means "
means "
Exact definition of the cumulated preferences, for each  ,
,  and
and  , can be represented as follows:
, can be represented as follows:
-
 if
if  , where
, where  and
and  ;
; -
 if
if  , where
, where  and
and
Let also  ,
,  ,
,  . The decision rules have then the following syntax:
. The decision rules have then the following syntax:
1)
If and...
and... and
and and
and and...
and... and
and , then
, then ,
,
where  ,
,  ,
,  ,
, 
 and
and  ,
,  . These rules are supported by pairs of objects from the
. These rules are supported by pairs of objects from the  -lower approximation of
-lower approximation of  only;
only;
2)  -decision rules:
-decision rules:
If and...
and... and
and and
and and...
and... and
and , then
, then ,
,
where  ,
,  ,
,  ,
, 
 and
and  ,
,  . These rules are supported by pairs of objects from the
. These rules are supported by pairs of objects from the  -lower approximation of
-lower approximation of  only;
only;
3)  -decision rules:
-decision rules:
If and...
and... and
and and
and and
and and...
and... and
and and
and and
and and...
and... and
and , then
, then or
or ,
,
where  ,
,  ,
,  ,
,  and
and  are not necessarily disjoint,
are not necessarily disjoint,  ,
,  ,
,  . These rules are supported by pairs of objects from the
. These rules are supported by pairs of objects from the  -boundary of
-boundary of  and
and  only.
only.
5.4 Use of decision rules for multicriteria choice and ranking
The decision rules induced from a given  describe the comprehensive preference relations
describe the comprehensive preference relations  and
and  either exactly (
either exactly (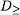 - and
- and  -decision rules) or approximately (
-decision rules) or approximately ( -decision rules). A set of these rules covering all pairs of
-decision rules). A set of these rules covering all pairs of  represents a preference model of the decision maker who gave the pairwise comparison of reference objects. The application of these decision rules on a new subset
represents a preference model of the decision maker who gave the pairwise comparison of reference objects. The application of these decision rules on a new subset  of objects induces a specific preference structure on
of objects induces a specific preference structure on  .
.
In fact, any pair of objects
-
At least one
-
At least one
-
At least one
-
No decision rule.
These four ways correspond to the following four situations of outranking, respectively:
-
not
 ,
, i.e. true outranking (denoted by
 );
); -
 and
and not
i.e. false outranking (denoted by
 );
); -
i.e. contradictory outranking (denoted by
 );
); -
not
not
i.e. unknown outranking (denoted by
 ).
).
The four above situations, which together constitute the so-called four-valued outranking (Greco, Matarazzo, Slowinski & Tsoukias, 1998), have been introduced to underline the presence and absence of positive and negative reasons for the outranking. Moreover, they make it possible to distinguish contradictory situations from unknown ones.
A final recommendation (choice or ranking) can be obtained upon a suitable exploitation of this structure, i.e. of the presence and the absence of outranking  and
and  on
on  . A possible exploitation procedure consists of calculating a specific score, called the Net Flow Score, for each object
. A possible exploitation procedure consists of calculating a specific score, called the Net Flow Score, for each object  :
:
where
card
: there is at least one decision rule which affirms
;
card
: there is at least one decision rule which affirms
;
card
: there is at least one decision rule which affirms
;
card
: there is at least one decision rule which affirms
.
The recommendation in ranking problems consists of the total preorder determined by  on
on  . In choice problems, it consists of the object(s)
. In choice problems, it consists of the object(s)  such that
such that  .
.
The above procedure has been characterized with reference to a number of desirable properties in (Greco, Matarazzo, Slowinski & Tsoukias, 1998; Szelag, Greco & Slowinski, 2012).
Recently, Fortemps, Greco & Slowinski (2008) extended the Dominance-based Rough Set Approach to multicriteria choice and ranking on multi-graded preference relations, instead of uni-graded relations  and
and  .
.
It is also worth mentioning a machine learning approach to multicriteria choice and ranking using ensembles of decision rules. The approach presented by Dembczynski, Kotlowski, Slowinski & Szelag (2010) makes a bridge between stochastic methods of preference learning and DRSA for choice and ranking.
5.5 An illustrative example
Let us suppose that a company managing a chain of warehouses wants to buy some new warehouses. To choose the best proposals or to rank them all, the managers of the company decide to analyze first the characteristics of eight warehouses already owned by the company (reference objects). This analysis should give some indications for the choice and ranking of the new proposals. Eight warehouses belonging to the company have been evaluated by the following three criteria: capacity of the sales staff  , perceived quality of goods
, perceived quality of goods  and high traffic location
and high traffic location  . The domains (scales) of these attributes are presently composed of three preference-ordered echelons: V1 = V2 = V3
. The domains (scales) of these attributes are presently composed of three preference-ordered echelons: V1 = V2 = V3 sufficient, medium, good
sufficient, medium, good . The decision attribute
. The decision attribute  indicates the profitability of warehouses, expressed by the Return On Equity ( ROE) ratio (in %). Table 3 presents a decision table which represents this situation.
indicates the profitability of warehouses, expressed by the Return On Equity ( ROE) ratio (in %). Table 3 presents a decision table which represents this situation.
With respect to the set of criteria  , the following multigraded preference relations
, the following multigraded preference relations  ,
,  , are defined:
, are defined:
-
 (and
(and  ), meaning that
), meaning that indifferent to
-
 (and
(and  ), meaning that
), meaning that preferred to
-
 (and
(and  ), meaning that
), meaning that strongly preferred to
Using the decision attribute, the comprehensive outranking relation was built as follows: warehouse  is at least as good as warehouse
is at least as good as warehouse  with respect to profitability
with respect to profitability  if
if
Otherwise, i.e. if ROE , warehouse
, warehouse  is not at least as good as warehouse
is not at least as good as warehouse  with respect to profitability
with respect to profitability  .
.
The pairwise comparisons of the reference objects result in  . The rough set analysis of the
. The rough set analysis of the  leads to the conclusion that the set of decision examples on the reference objects is inconsistent. The quality of approximation of
leads to the conclusion that the set of decision examples on the reference objects is inconsistent. The quality of approximation of  and
and  by all criteria from set
by all criteria from set  is equal to 0.44. Moreover,
is equal to 0.44. Moreover,  . This means that no criterion is superfluous.
. This means that no criterion is superfluous.
The  -lower approximations and the
-lower approximations and the  -upper approximations of
-upper approximations of 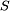 and
and  , obtained by means of multigraded dominance relations, are:
, obtained by means of multigraded dominance relations, are:
All the remaining 36 pairs of reference objects belong to the  -boundaries of
-boundaries of 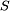 and
and  , i.e.
, i.e.  .
.
The following minimal 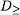 -decision rules and
-decision rules and  -decision rules can be induced from lower approximations of
-decision rules can be induced from lower approximations of 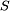 and
and  , respectively (the figures within parentheses represent the pairs of objects supporting the corresponding rules):
, respectively (the figures within parentheses represent the pairs of objects supporting the corresponding rules):
If and
and , then
, then ;((1,6),(3,6),(7,6))
;((1,6),(3,6),(7,6))
If and
and , then
, then ; ((1,2),(1,6),(1,8),(3,2),(3,6),(3,8),(7,2),(7,6),(7,8))
; ((1,2),(1,6),(1,8),(3,2),(3,6),(3,8),(7,2),(7,6),(7,8))
If If and
and , then
, then ; ((1,4),(1,5),(3,4),(3,5),(7,4),(7,5))
; ((1,4),(1,5),(3,4),(3,5),(7,4),(7,5))
If and
and , then
, then ;((6,1),(6,3),(6,7))
;((6,1),(6,3),(6,7))
If and
and , then
, then ; ((4,1),(4,3),(4,7),(5,1),(5,3),(5,7))
; ((4,1),(4,3),(4,7),(5,1),(5,3),(5,7))
If and
and and
and , then
, then ;((2,1),(2,7),(6,1),(6,3),(6,7),(8,1),(8,7))
;((2,1),(2,7),(6,1),(6,3),(6,7),(8,1),(8,7))
Moreover, it is possible to induce five minimal D -decision rules from the boundary of approximation of
-decision rules from the boundary of approximation of 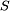 and
and  :
:
If and
and and
and and
and , then
, then or
or ; ((1,1),(1,3),(1,7),(2,2),(2,6),
; ((1,1),(1,3),(1,7),(2,2),(2,6),
(2,8),(3,1),(3,3),(3,7),(4,4),(4,5),(5,4),(5,5),(6,2),(6,6),(6,8),(7,1),(7,3),(7,7),(8,2),(8,6),(8,8))
If and
and , then
, then or
or ; ((2,4),(2,5),(6,4),(6,5),(8,4),(8,5))
; ((2,4),(2,5),(6,4),(6,5),(8,4),(8,5))
If and
and , then
, then or
or ; ((4,2),(4,6),(4,8),(5,2),(5,6),(5,8))
; ((4,2),(4,6),(4,8),(5,2),(5,6),(5,8))
If and
and and
and , then
, then or
or ; ((1,3),(2,3),(2,6),(7,3),(8,3),(8,6))
; ((1,3),(2,3),(2,6),(7,3),(8,3),(8,6))
If and
and , then
, then or
or ; ((2,3),(2,4),(2,5),(8,3),(8,4),(8,5))
; ((2,3),(2,4),(2,5),(8,3),(8,4),(8,5))
Using all the above decision rules and the Net Flow Score exploitation procedure on ten other warehouses proposed for purchase, the managers can obtain the result presented in Table 4. The dominance-based rough set approach gives a clear recommendation:
-
For the
choice problem it suggests the selection of warehouse 2
-
For the
ranking problem it suggests the
ranking presented in the last column of
Table 4, as follows:
5.6 Summary
We briefly presented the contribution of the Dominance-based Rough Set Approach to multi-criteria choice and ranking problems. Let us point out the main features of the describedmethodology:
-
The decision maker is asked for the preference information necessary to deal with a multicriteria decision problem in terms of exemplary decisions.
-
The rough set analysis of preference information supplies some useful elements of knowledge about the decision situation. These are: the relevance of particular attributes and/or criteria, information about their interaction, minimal subsets of attributes or criteria (re-ducts) conveying important knowledge contained in the exemplary decisions and the set of the non-reducible attributes or criteria (core).
-
The preference model induced from the preference information is expressed in a natural and comprehensible language of "
if..., then..." decision rules. The decision rules concern pairs of objects and from them we can determine either the presence or the absence of a comprehensive preference relation. The conditions for the presence are expressed in "at least" terms, and for the absence in "at most" terms, on particular criteria.
-
The decision rules do not convert ordinal information into numeric but keep the ordinal character of input data due to the syntax proposed.
-
Heterogeneous information (qualitative and quantitative, ordered and non-ordered) and scales of preference (ordinal, cardinal) can be processed within the Dominance-based Rough Set Approach, while classical methods consider only quantitative ordered evaluations (with rare exceptions).
-
No prior discretization of the quantitative domains of criteria is necessary.
6 RELEVANT EXTENSIONS OF DRSA
We introduced a knowledge discovery paradigm for multiattribute and multicriteria decision support, based on the concept of rough sets. Rough set theory provides mathematical tools for dealing with granularity of information and possible inconsistencies in the description of objects. Considering this description as an input data about a decision problem, the knowledge discovery paradigm consists of searching for rules in the data that facilitate an understanding of the decision maker's preferences and that enable us to recommend a decision which is in line with these preferences. An original component of this paradigm is that it takes into account prior knowledge about preference semantics in the rules to be discovered.
Knowledge discovery from preference ordered data differs from usual knowledge discovery since the former involves preference orders in domains of attributes and in the set of decision classes. This requires that a knowledge discovery method applied to preference ordered data respects the dominance principle. As this is not the case for the well-known methods of data mining and knowledge discovery, they are not able to discover all relevant knowledge contained in the analyzed data sample and, even worse, they may yield unreasonable discoveries, because of inconsistency with the dominance principle. These deficiencies are addressed in the Dominance-based Rough Set Approach (DRSA). Moreover, this approach enables us to apply a rough set approach to multicriteria decision making. We showed how the approach could be used for multicriteria classification, choice and ranking. In more advanced papers, we have presented many extensions of the approach that make it a useful tool for other practical applications. These extensions are:
-
DRSA to decision under risk and uncertainty (Greco, Matarazzo & Slowinski, 2001e);
-
DRSA to decision under uncertainty and time preference (Greco, Matarazzo & Slowinski, 2010c);
-
DRSA handling missing data (Greco, Matarazzo & Slowinski, 1999c, 2000a);
-
DRSA for imprecise object evaluations and assignments (Dembczynski, Greco & Slowinski, 2009);
-
Dominance-based approach to induction of association rules (Greco, Matarazzo, Slowinski & Stefanowski, 2002);
-
Fuzzy-rough hybridization of DRSA (Greco, Matarazzo & Slowinski, 1999b, 2000b,2000c; Greco, Inuiguchi & Slowinski, 2002, 2003);
-
DRSA as a way of operator-free fuzzy-rough hybridization (Greco, Inuiguchi & Slowinski, 2003, 2005, Greco, Matarazzo & Slowinski, 2007);
-
DRSA to granular computing (Greco, Matarazzo & Slowinski, 2008a, 2009);
-
DRSA to case-based reasoning (Greco, Matarazzo & Slowinski, 2008d);
-
DRSA for hierarchical structure of evaluation criteria (Dembczynski, Greco, Slowinski, 2002);
-
DRSA to decision involving multiple decision makers (Greco, Matarazzo & Slowinski, 2006, 2011);
-
DRSA to interactive multiobjective optimization (Greco, Matarazzo & Slowinski, 2008c);
-
DRSA to interactive evolutionary multiobjective optimization under risk and uncertainty (Greco, Matarazzo & Slowinski, 2010d).
The Dominance-based Rough Set Approach leads to a preference model of a decision maker in terms of decision rules. The decision rules have a special syntax which involves partial evaluation profiles and dominance relations on these profiles. The clarity of the rule representation of preferences enables us to see the limits of other traditional aggregation functions: the utility function and the outranking relation. In several studies (Greco, Matarazzo & Slowinski, 2001b, 2002c, 2003; Slowinski, Greco & Matarazzo, 2002b), we proposed an axiomatic characterization of these aggregation functions in terms of conjoint measurement theory and in terms of a set of decision rules. In comparison to other studies on the characterization of aggregation functions, our axioms do not require any preliminary assumptions about the scales of criteria. A side-result of these investigations is that the decision rule aggregation (preference model) is the most general among the known aggregation functions. The decision rule preference model fulfils, moreover, the postulate of transparency and interpretability of preference models in decision support.
Dealing with ordered data and monotonicity constraints makes also sense in general classification problems, where the notion of preference has no meaning. Even when the ordering seems irrelevant, the presence or the absence of a property have an ordinal interpretation. If two properties are related, one of the two: the presence or the absence of one property should make more (or less) probable the presence of the other property. A formal proof showing that the Indiscernibility-based Rough Set Approach is a particular case of the Dominance-based Rough Set Appraoch has been given in (Greco, Matarazzo & Slowinski, 2007). Having this in mind, DRSA can be seen as a general framework for analysis of classification data. Although it has been designed for ordinal classification problems with monotonicity constraints, DRSA can be used to solve a general classification problem where no additional information about ordering is taken into account.
The idea which stands behind this claim is the following (Blaszczynski, Greco & Slowinski, 2012). We assume, without loss of generality, that the value sets of all regular attributes are number-coded. While this is natural for numerical attributes, categorical attributes must get numerical codes for categories. In this way, the value sets of all regular attributes get ordered (as all sets of numbers are ordered). Now, to analyze a non-ordinal classification problem using DRSA, we transform decision table such that each regular attribute is cloned (doubled). It is assumed that the value set of each original attribute is ordered with respect to increasing preference (gain type), and the value set of its clone is ordered with respect to decreasing preference (cost type). Using DRSA, for each  , we approximate two sets of objects from the decision table: class
, we approximate two sets of objects from the decision table: class  and its complement
and its complement  . Obviously, we can calculate dominance-based rough approximations of the two sets. Moreover, they can serve to induce "if..., then..." decision rules recommending assignment to class
. Obviously, we can calculate dominance-based rough approximations of the two sets. Moreover, they can serve to induce "if..., then..." decision rules recommending assignment to class  or to its complement
or to its complement  . In this way, we reformulated the original non-ordinal classification problem to an ordinal classification problem with monotonicity constraints. Due to cloning of attributes with opposite preference orders, we can have rules that cover a subspace in the condition space, which is bounded from the top and from the bottom - this leads (without discretization) to more synthetic rules than those resulting from the Indiscernibility-based Rough Set Approach.
. In this way, we reformulated the original non-ordinal classification problem to an ordinal classification problem with monotonicity constraints. Due to cloning of attributes with opposite preference orders, we can have rules that cover a subspace in the condition space, which is bounded from the top and from the bottom - this leads (without discretization) to more synthetic rules than those resulting from the Indiscernibility-based Rough Set Approach.
7 DRSA AND OPERATIONS RESEARCH PROBLEMS
DRSA is also a useful instrument in the toolbox of Operations Research (OR). DRSA has been applied to the following OR problems:
1) interactive multiobjective optimization (IMO-DRSA) (Greco, Matarazzo & Slowinski, 2008c);
2) interactive evolutionary multiobjective optimization under risk and uncertainty (Greco, Matarazzo & Slowinski, 2010d);
3) decision under uncertainty and time preference (Greco, Matarazzo & Slowinski, 2010c).
7.1 DRSA to interactive multiobjective optimization (IMO-DRSA)
DRSA to interactive multiobjective optimization (IMO-DRSA) (Greco, Matarazzo & Slowinski, 2008c) permits to deal with many optimization problems considered within OR (ranging from inventory management to scheduling, passing through portfolio management) in a way which is very much oriented towards interaction with the users. In fact, in IMO-DRSA a sample of representative solutions to a multiobjective optimization problem is presented to the DM who is asked to indicate a subset of relatively "good" solutions in the sample. Applying DRSA to the sample of representative solutions classified into "good" and "others" by the DM, a set of decision rules is induced in the form: "if objective  and...
and...  , then
, then  is a good solution". The DM selects the rule that in his opinion is the most representative of his preference and the constraints coming from that rule are adjoined to the set of constraints imposed on the Pareto optimal set, in order to focus on a part interesting from the point of view of DM's preferences in the next iteration. For example, if the DM selects the rule "if
is a good solution". The DM selects the rule that in his opinion is the most representative of his preference and the constraints coming from that rule are adjoined to the set of constraints imposed on the Pareto optimal set, in order to focus on a part interesting from the point of view of DM's preferences in the next iteration. For example, if the DM selects the rule "if  and...
and...  , then
, then  is a good solution", then the constraints
is a good solution", then the constraints  and...
and...  are adjoined to the set of constraints of the multiobjective optimization problem, such that the new set of constraints implies a Pareto optimal set being the subset of the original Pareto optimal set. This subset satisfies the requirements of the selected rule, so that it is composed of solutions that are considered relatively good by the DM. The procedure continues iteratively until the DM is satisfied with one solution from the current sample - this is the most preferred solution.
are adjoined to the set of constraints of the multiobjective optimization problem, such that the new set of constraints implies a Pareto optimal set being the subset of the original Pareto optimal set. This subset satisfies the requirements of the selected rule, so that it is composed of solutions that are considered relatively good by the DM. The procedure continues iteratively until the DM is satisfied with one solution from the current sample - this is the most preferred solution.
The IMO-DRSA procedure can be analyzed from the point of view of input and output information. As to the input, the DM gives preference information by answering easy questions related to ordinal classification of some representative solutions into two classes ("good" and "others"). Very often, in multiple criteria decision analysis in general, and in interactive multiobjective optimization in particular, the preference information has to be given in terms of preference model parameters, such as importance weights, substitution rates and various thresholds. This information is specified in (Fishburn, 1967) with respect to Multiple Attribute Utility Theory, and in (Roy & Bouyssou, 1993; Figueira, Mousseau & Roy, 2005; Brans & Mareschal, 2005; Martel & Matarazzo, 2005) with respect to outranking methods. In case of multiobjective optimization, the preference information depends on the method; e.g., the Geoffrion-Dyer-Feinberg method (Geoffrion-Dyer-Feinberg, 1972), the method of Zionts & Wallenius (Zionts & Wallenius, 1976, 1983) and the Interactive Surrogate Worth Tradeoff method (Chankong & Haimes, 1978, 1983) require information in terms of marginal rates of substitution; the reference point method (Wierzbicki, 1980) requiries a reference point and weights to formulate an achievement scalarizing function; the Light Beam Search method (Jaszkiewicz & Slowinski, 1999) requires information in terms of weights and indifference, preference and veto thresholds, being typical parameters of ELECTRE methods. Eliciting such information requires a significant cognitive effort on the part of the DM. It is generally acknowledged that people rather prefer to make exemplary decisions than to explain them in terms of specific parameters. For this reason, the idea of inferring preference models from exemplary decisions provided by theDM is very attractive.
The output result of the analysis is the model of preferences in terms of "if..., then..." decision rules which is used to reduce the Pareto optimal set iteratively, until the DM selects a satisfactory solution. The decision rule preference model is very convenient for decision support, because it gives argumentation for preferences in a logical form, which is intelligible for the DM, and identifies the Pareto optimal solutions supporting each particular decision rule. This is very useful for a critical revision of the original ordinal classification of representative solutions into the two classes of "good" and "others". Indeed, decision rule preference model speaks the same language of the DM without any recourse to technical terms, like utility, tradeoffs, scalarizing functions and so on.
All this implies that IMO-DRSA has a transparent feedback organized in a learning oriented perspective, which permits to consider this procedure as a "glass box", contrary to the "black box" characteristic of many procedures giving final result without any clear explanation. The information given by the decision rules is particularly intelligible for the DM, since they speak the language of the DM and permit him/her to identify the Pareto optimal solutions supporting each decision rule. Thus, decision rules give an explanation and a justification of the final decision, that does not result from a mechanical application of a certain technical method, but rather from a mature conclusion of a decision process based on active intervention of the DM.
Observe, finally, that the decision rules representing preferences are based on ordinal properties of objective functions only. Differently from methods involving some scalarization (almost all existing interactive methods), in any step the proposed procedure does not aggregate the objectives into a single value, avoiding operations (such as averaging, weighted sum, different types of distance, achievement scalarization) which are always arbitrary to some extent. Observe that one could use a method based on scalarization to generate the representative set of Pareto optimal solutions, nevertheless, the decision rule approach would continue to be based on ordinal properties of objective functions only, because the dialogue stage of the method operates on ordinal comparisons only. In the proposed method, the DM gets clear arguments for his/her decision in terms of "if..., then..." decision rules and the verification if a proposed solution satisfies these decision rules is particularly easy. This is not the case of interactive multiobjective optimization methods based on scalarization. For example, in the methods using an achievement scalarizing function, it is not evident what does it mean for a solution to be "close" to the reference point. How to justify the choice of the weights used in the achievement function? What is their interpretation? Observe, instead, that IMO-DRSA operates on data using ordinal comparisons which would not be affected by any increasing monotonic transformation of scales, and this ensures the meaningfulness of results from the point of view of measurement theory (see, e.g.,Roberts, 1979).
With respect to computational aspects of the method, notice that the decision rules can be calculated efficiently in few seconds only using the algorithms presented in (Greco, Matarazzo, Slowinski & Stefanowski, 2001, 2002; Blaszczynski, Slowinski & Szelag, 2011). When the number of objective functions is not too large to be effectively controlled by the DM (say, seven plus or minus two, as suggested by Miller (1956)), then the decision rules can be calculated in a fraction of one second. In any case, the computational effort grows exponentially with the number of objective functions, but not with respect to the number of considered Pareto optimal solutions, which can increase with no particularly negative consequence on calculation time.
7.2 DRSA to interactive evolutionary multiobjective optimization
Very often real life optimization problems are so complex that exact methods fail to find an optimal solution. In these cases some heuristics are to be applied. Within multiobjective optimization, Evolutionary Multiobjective Optimization (EMO) appeared to be particularly efficient; see, e.g., (Coello Coello, Van Veldhuizen & Lamont, 2002; Deb, 2001).
The underlying reasoning behind the EMO search of an approximation of the Pareto-optimal frontier is that, in the absence of any preference information, all Pareto-optimal solutions have to be considered equivalent. On the other hand, if the DM (alternatively called user) is involved in the multiobjective optimization process, then the preference information provided by the DM can be used to focus the search on the most preferred part of the Pareto-optimal frontier. This idea stands behind Interactive Multiobjective Optimization (IMO) methods proposed long time before EMO has emerged.
Recently, it became clear that merging the IMO and EMO methodologies should be beneficial for the multiobjective optimization process (Branke, Deb, Miettinen & Slowinski, 2008). Several approaches have been presented in this context; see, e.g., (Fonseca & Fleming, 1993; Deb, Sundar, Rao & Chaudhuri, 2006; Deb & Chaudhuri, 2010; Coello, Van Veldhuizen & Lamont, 2002; Branke, Kaußler & Schmeck, 2001; Greenwood, Hu & D'Ambrosio, 1997; Jaszkiewicz, 2007; Phelps & Koksalan, 2003; Branke, Greco, Slowinski & Zielniewicz, 2009).
The methodology of interactive EMO based on DRSA (Greco, Matarazzo & Slowinski, 2010d, 2010e) involves application of decision rules in EMO, which are induced from easily elicited preference information by DRSA, proposing two general schemes, called DRSA-EMO and DRSA-EMO-PCT. This results in focusing the search of the Pareto-optimal frontier on the most preferred region. More specifically, DRSA is used for structuring preference information obtained through interaction with the user, and then a set of decision rules representing user's preferences is induced from this information. These rules are used to rank solutions in the current population of EMO, which has an impact on the selection and crossover.
Within interactive EMO, one can also apply DRSA for decision under uncertainty. This permits to take into account robustness concerns in the multiobjective optimization. In fact, two methods of robust optimization methods combining DRSA and interactive EMO have been proposed: DARWIN (Dominance-based rough set Approach to handling Robust Winning solutions in IN teractive multiobjective optimization) and DARWIN-PCT (DARWIN using Pairwise Comparison Tables). DARWIN and DARWIN-PCT can be considered as two specific instances of DRSA-EMO and DRSA-EMO-PCT, respectively.
The integration of DRSA and EMO is particularly promising for two reasons:
1. The preference information required by DRSA is very basic and easy to be elicited by the DM. All that the DM is asked for is to assign solutions to preference ordered classes, such as "good", "medium" and "bad", or compare pairs of non-dominated solutions from a current population in order to reveal whether one is preferred over the other. The preference information is provided every
iterations (
depends on the problem and the willingness of the user to interact with the system. In our studies,
ranges from 10 to 30).
2. The decision rules are transparent and easy to interpret for the DM. As explained in the previous subsection, the preference model supplied by decision rules is a "glass box", while many other competitive multiple criteria decision methodologies involve preference models that are "black boxes" for the user. The "glass box" model improves the quality of the interaction and makes that the DM accepts well the resulting recommendation.
The integration of DRSA and EMO provides very general interactive EMO schemes which can be customized to a large variety of OR problems, from location and routing to scheduling and supply chain management.
7.3 DRSA to decision under uncertainty and time preference
DRSA can also be applied to preference modeling for decision under uncertainty with consequences distributed over time, using the idea of time-stochastic dominance, i.e. putting together the concept of time dominance and stochastic dominance (Greco, Matarazzo & Slowinski, 2010c). Preference information provided by the DM is a set of decision examples specifying the quality of some chosen acts, i.e. assigning these acts to preference-ordered classes. The resulting preference model expressed in terms of "if..., then..." decision rules is much more intelligible than any utility function. Moreover, it permits to handle inconsistent preference information. Let us observe that the approach handles an additive probability distribution as well as a non-additive probability, and even a qualitative ordinal probability. Furthermore, in case the elements of sets of possible probability values and of time epochs were very numerous (like in real life applications in which very often they are infinite), it would be enough to consider a subset of the most significant probability values (e.g.,  ) and a subset of the most significant epochs (e.g., each month).
) and a subset of the most significant epochs (e.g., each month).
Applying DRSA to decision under uncertainty and time preference we get decision rules of the type:
"if the cumulated outcome at
is at least -50 , and the cumulated outcome at
is at least 300, then act
is (at least) good"
or
"if the cumulated outcome at
is at most -100 and the cumulated outcome at
is at most 150, then act
is (at least) good".
This method can be extended on the case of pairwise comparisons (Greco, Matarazzo & Slowinski, 2010e) obtaining rules whose syntax is:
"if the difference between the cumulated outcome of act a and act b is not smaller than
at
, and not smaller than
at
, then act a is at least weakly preferred to act b".
The above methodology can be very useful for dealing with many OR problems where uncertainty of outcomes and their distribution over the time play a fundamental role, such as portfolio selection, scheduling with time-resource interactions and inventory management. Indeed, putting together the decision rules produced by this methodology with IMO-DRSA and DRSA applied to EMO, provides an important tool for dealing with even more OR problems. An example of a recent application of this methodology to a typical OR problem, which is inventory control, can be found in (Greco, Matarazzo, Slowinski & Vaccarella, 2012).
8 SOURCES OF ADDITIONAL INFORMATION ABOUT ROUGH SET THEORY AND APPLICATIONS
The community of researchers and practitioners interested in rough set theory and applications is organized in the International Rough Set Society (http://roughsets.home.pl/www/). The society's web page includes information about rough set conferences, about Transactions on Rough Sets published in a journal series of LNCS by Springer, and about International Journal of Granular Computing, Rough Sets and Intelligent Systems. This page also includes slides of tutorial presentations on rough sets. A database of rough set references can be found at http://rsds.univ.rzeszow.pl.
The following software is available free in the Internet:
RSES - Rough Set Exploration System http://logic.mimuw.edu.pl/~rses,
ROSE - ROugh Set data Explorer http://idss.cs.put.poznan.pl/site/rose.html,
jMAF - java Multi-criteria and Multi-attribute Analysis Framework http://www.cs.put.poznan.pl/jblaszczynski/Site/jRS.html, and
jRank - ranking generator using Dominance-based Rough Set Approach http://www.cs.put.poznan.pl/mszelag/Software/jRank/jRank.html.
ACKNOWLEDGEMENTS
The first author wishes to acknowledge financial support from the Polish National ScienceCentre, grant no. NN519 441939.
- [1] Blaszczynski J, Greco S & Slowinski R. 2007. Multi-criteria classification - a new scheme for application of dominance-based decision rules. European J. Operational Research, 181(3): 1030-1044.
- [2] Blaszczynski J, Greco S & Slowinski R. 2012. Inductive discovery of laws using monotonic rules. Engineering Applications of Artificial Intelligence, 25(2): 284-294.
- [3] Blaszczynski J, Greco S, Slowinski R & Szelag M. 2009. Monotonic variable consistency rough set approaches. International Journal of Approximate Reasoning, 50(7): 979-999.
- [4] Blaszczynski J, Slowinski R & Szelag M. 2011. Sequential covering rule induction algorithm for variable consistency rough set approaches. Information Sciences, 181: 987-1002.
- [5] Branke J, Deb K, Miettinen K & Slowinski R.(Eds.). 2008. Multiobjective Optimization: Interactive and Evolutionary Approaches, LNCS 5252, Springer, Berlin.
- [6] Branke J, Kaußler T & Schmeck H. 2001. Guidance in evolutionary multi-objective optimization. Advances in Engineering Software, 32: 499-507.
- [7] Branke J, Greco S, Slowinski R & Zielniewicz P. 2009. Interactive evolutionary multiobjective optimization using robust ordinal regression. In: Ehrgott M, Fonseca CM, Gandi-bleux X, Hao J-K & Sevaux M.(Eds.), Evolutionary Multi-Criterion Optimization (EMO'09), LNCS 5467, Springer, Berlin, 554-568.
- [8] Brans JP & Mareschal B. 2005. PROMETHEE Methods. Chapter 5. In: Figueira J, Greco S & Ehrgott M.(Eds.), Multiple Criteria Decision Analysis: State of the Art Surveys, Springer, Berlin, 163-195.
- [9] Chankong V & Haimes YY. 1978. The interactive surrogate worth trade-off (ISWT) method for multiobjective decision-making. In: Zionts S. (Ed.), Multiple Criteria Problem Solving, Springer-Verlag, Berlin, New York, pp. 42-67.
- [10] Chankong V & Haimes YY. 1983. Multiobjective Decision Making Theory and Methodology, Elsiever Science Publishing Co., New York.
- [11] Coello Coello CA, Van Veldhuizen DA & Lamont GB. 2002. Evolutionary Algorithms for Solving Multi-Objective Problems, Kluwer, Dordrecht.
- [12] Deb K. 2001. Multi-Objective Optimization using Evolutionary Algorithms, Wiley, Chichester, UK.
- [13] Deb K & Chaudhuri S. 2010. I-MODE: An interactive multi-objective op-timization and decision-making using evolutionary methods. Applied Soft Computing, 10: 496-511.
- [14] Deb K, Sundar J, Rao NUB & Chaudhuri S. 2006. Reference point based multi-objective optimization using evolutionary algorithms. International Journal of Computational Intelligence Research, 2(3): 273-286.
- [15] Dembczynski K, Greco S & Slowinski R. 2002. Methodology of rough-set-based classification and sorting with hierarchical structure of attributes and criteria. Control & Cybernetics, 31: 891-920.
- [16] Dembczynski K, Greco S & Slowinski R. 2009. Rough set approach to multiple criteria classification with imprecise evaluations and assignments. European J. Operational Research, 198(2): 626-636.
- [17] Dembczynski K, Kotlowski W, Slowinski R & M Szelag. 2010. Learning of rule Ensembles for multiple attribute ranking problems. In: Fürnkranz J & Hüllermeier E.(Eds.), Preference Learning, Springer, Berlin, pp. 217-247.
- [18] Figueira J, Mousseau V & Roy B. 2005. ELECTRE Methods. Chapter 4. In: Figueira J, Greco S & Ehrgott M.(Eds.), Multiple Criteria Decision Analysis: State of the Art Surveys, Springer, Berlin, pp. 133-162.
- [19] Figueira J, Greco S & Ehrgott M.(Eds.). 2005. Multiple Criteria Decision Analysis: State of the Art Surveys. Springer, Berlin.
- [20] Fishburn PC. 1967. Methods of estimating additive utilities. Management Science, 13(7): 435-453.
- [21] Fonseca CM & Fleming PJ. 1993. Genetic algorithms for multiobjective optimization: Formulation, discussion, and generalization. In: Proceedings of the Fifth International Conference on Genetic Algorithms, pp. 416-423.
- [22] Fortemps Ph, Greco S & Slowinski R. 2008. Multicriteria decision support using rules that represent rough-graded preference relations. European J. Operational Research, 188(1): 206-223.
- [23] Geoffrion A, Dyer J & Feinberg A.1972. An interactive approach for multi-criterion optimization, with an application to the operation of an academic department. Management Science, 19(4): 357-368.
- [24] Giove S, Greco S, Matarazzo B & Slowinski R. 2002. Variable consistency monotonic decision trees. In: Alpigini JJ, Peters JF, Skowron A & Zhong N.(Eds.), Rough Sets and Current Trends in Computing. Springer LNAI 2475, Berlin, pp. 247-254.
- [25] Greco S, Inuiguchi M & Slowinski R. 2002. Dominance-based rough set approach using possibility and necessity measures. In: Alpigini JJ, Peters JF, Skowron A & Zhong N.(Eds.), Rough Sets and Current Trends in Computing. Springer LNAI 2475, Berlin, pp. 85-92.
- [26] Greco S, Inuiguchi M & Slowinski R. 2003. A new proposal for fuzzy rough approximations and gradual decision rule representation. Transactions on Rough Sets II Springer LNCS 3135, Berlin, pp. 319-342.
- [27] Greco S, Inuiguchi M & Slowinski R. 2005. Fuzzy rough sets and multiple-premise gradual decision rules. International Journal of Approximate Reasoning, 41: 179-211.
- [28] Greco S, Matarazzo B, Pappalardo N & Slowinski R. 2005. Measuring expected effects of interventions based on decision rules. Journal of Experimental and Theoretical Artificial Intelligence, 17(1-2): 103-118.
- [29] Greco S, Matarazzo B & Slowinski R.1998a. A new rough set approach to evaluation of bankruptcy risk. In: Zopounidis C.(Ed.), Operational Tools in the Management of Financial Risk. Kluwer, Dordrecht, pp. 121-136.
- [30] Greco S, Matarazzo B & Slowinski R.1998b. Fuzzy similarity relation as a basis for rough approximation. In: Polkowski L & Skowron A. (Eds.), Rough sets and Current Trends in Computing. Springer LNAI 1424, Berlin, pp. 283-289.
- [31] Greco S, Matarazzo B & Slowinski R.1999a. Rough approximation of a preference relation by dominance relations. European J. Operational Research, 117: 63-83.
- [32] Greco S, Matarazzo B & Slowinski R.1999b. The use of rough sets and fuzzy sets in MCDM. Chapter 14. In: Gal T, Stewart T & Hanne T. (Eds.), Advances in Multiple Criteria Decision Making. Kluwer, Dordrecht, pp. 14.1-14.59.
- [33] Greco S, Matarazzo B & Slowinski R.1999c. Handling missing values in rough set analysis of multi-attribute and multi-criteria decision problems. In: Zhong N, Skowron A & Ohsuga S.(Eds.), New Directions in Rough Sets, Data Mining and Granular-Soft Computing. Springer LNAI 1711, 146-157.
- [34] Greco S, Matarazzo B & Slowinski R. 2000a. Dealing with missing data in rough set ana-lysis of multi-attribute and multi-criteria decision problems. In: Zanakis SH, Doukidis G &Zopounidis C.(Eds.), Decision Making: Recent Developments and Worldwide Applications. Kluwer, Dordrecht, pp. 295-316.
- [35] Greco S, Matarazzo B & Slowinski R. 2000b. Rough set processing of vague information using fuzzy similarity relations. In: Calude CS & Paun G. (Eds.), Finite Versus Infinite - Contributions to an Eternal Dilemma. Springer, Berlin, pp. 149-173.
- [36] Greco S, Matarazzo B & Slowinski R. 2000c. Fuzzy extension of the rough set approach to multicriteria and multiattribute sorting. In: Fodor J, De Baets B & Perny P.(Eds.), Preferences and Decisions under Incomplete Knowledge. Physica-Verlag, Heidelberg, pp. 131-151.
- [37] Greco S, Matarazzo B & Slowinski R. 2000d. Extension of the rough set approach to multicriteria decision support. INFOR, 38: 161-196.
- [38] Greco S, Matarazzo B & Slowinski R. 2001a. Rough sets theory for multicriteria decision analysis. European J. of Operational Research, 129: 1-47.
- [39] Greco S, Matarazzo B & Slowinski R. 2001b. Conjoint measurement and rough set approach for multicriteria sorting problems in presence of ordinal criteria. In: Colorni A, Paruccini M & Roy B.(Eds.), A-MCD-A: Aide Multi-Critère la Décision - Multiple Criteria Decision Aiding. European Commission Report, EUR 19808 EN, Ispra, 2001b, pp. 117-144.
- [40] Greco S, Matarazzo B & Slowinski R. 2001c. Rule-based decision support in multicriteria choice & ranking. In: Benferhat S & Besnard P. (Eds.), Symbolic & Quantitative Approaches to Reasoning with Uncertainty. Springer LNAI 2143, Berlin, pp. 29-47.
- [41] Greco S, Matarazzo B & Slowinski R. 2001d. Assessment of a value of information using rough sets and fuzzy measures. In: Chocjan J & Leski J. (Eds.), Fuzzy Sets and their Applications. Silesian University of Technology Press, pp. 185-193.
- [42] Greco S, Matarazzo B & Slowinski R. 2001e. Rough set approach to decisions under risk. In: Ziarko W & Yao Y. (Eds.), Rough Sets and Current Trends in Computing. Springer LNAI 2005, Berlin, pp. 160-169.
- [43] Greco S, Matarazzo B & Slowinski R. 2002a. Rough sets methodology for sorting problems in presence of multiple attributes and criteria. European J. of Operational Research, 138: 247-259.
- [44] Greco S, Matarazzo B & Slowinski R. 2002b. Multicriteria classification. In: Kloesgen W & Zytkow J. (Eds.), Handbook of Data Mining and Knowledge Discovery. Oxford University Press, chapter 16.1.9, pp. 318-328.
- [45] Greco S, Matarazzo B & Slowinski R. 2002c. Preference representation by means of conjoint measurement & decision rule model. In: Bouyssou D, Jacquet-Lagrèze E, Perny P, Slowinski R, Vanderpooten D & Vincke P. (Eds.), Aiding Decisions with Multiple Criteria-Essays in Honor of Bernard Roy. Kluwer, Dordrecht, pp. 263-313.
- [46] Greco S, Matarazzo B & Slowinski R. 2004. Axiomatic characterization of a general utility function and its particular cases in terms of conjoint measurement and rough-set decision rules. European J. Operational Research, 158: 271-292.
- [47] Greco S, Matarazzo B & Slowinski R. 2006. Dominance-based rough set approach todecision involving multiple decision makers. In: Greco S, Hata Y, Hirano S, Inuiguchi M, Miyamoto S, Nguyen HS & Slowinski R. (Eds.), Rough Sets and Current Trends in Computing (RSCTC 2006). Springer LNCS 4259, Berlin, pp. 306-317.
- [48] Greco S, Matarazzo B & Slowinski R. 2007. Dominance-based Rough Set Approach as a proper way of handling graduality in rough set theory. Transactions on Rough Sets VII, Springer LNCS 4400, Berlin, pp. 36-52.
- [49] Greco S, Matarazzo B & Slowinski R. 2008a. Granular computing for reasoning aboutordered data: the dominance-based rough set approach. Chapter 15. In: Pedrycz W, Skowron A & Kreinovich V.(Eds.), Handbook of Granular Computing. Wiley, Chichester, pp. 347-373.
- [50] Greco S, Matarazzo B & Slowinski R. 2008b. Parameterized rough set model using rough membership and Bayesian confirmation measures. International Journal of Approximate Reasoning, 49: 285-300.
- [51] Greco S, Matarazzo B & Slowinski R. 2008c. Dominance-based Rough Set Approach to Interactive Multiobjective Optimization. Chapter 5. In: Branke J, Deb K, Miettinen K & Slowinski R.(Eds.), Multiobjective Optimization: Interactive and Evolutionary Approaches. Springer LNCS 5252, Berlin, pp. 121-156.
- [52] Greco S, Matarazzo B & Slowinski R. 2008d. Case-based reasoning using gradual rules induced from dominance-based rough approximations. In: Wang G, Li T, Grzymala-Busse JW, Miao D, Skowron A & Yao Y.(Eds.), Rough Sets and Knowledge Technology (RSKT 2008). Springer LNAI 5009, Berlin, pp. 268-275.
- [53] Greco S, Matarazzo B & Slowinski R. 2009. Granular Computing and Data Mining for Ordered Data - the Dominance-based RoughSet Approach. In: Meyers RA. (Ed.), Encyclopedia of Complexity and Systems Science, Springer, New York, pp. 4283-4305.
- [54] Greco S, Matarazzo B & Slowinski R. 2010a. Algebra and Topology for Dominance-basedRough Set Approach. In: Ras ZW & Tsay L-S.(Eds.), Advances in Intelligent InformationSystems, Studies in Computational Intelligence, vol. 265, Springer, Berlin, pp. 43-78.
- [55] Greco S, Matarazzo B & Slowinski R. 2010b. On Topological Dominance-based RoughSet Approach. Transactions on Rough Sets XII, Springer LNCS 6190, Berlin, pp. 21-45.
- [56] Greco S, Matarazzo B & Slowinski R. 2010c. Dominance-based rough set approach todecision under uncertainty and time preference. Annals of Operations Research, 176: 41-75.
- [57] Greco S, Matarazzo B & Slowinski R. 2010d. Dominance-based Rough Set Approach to Interactive Evolutionary Multiobjective Optimization. In: Greco S, Marques Pereira RA, Squillante M, Yager RR & Kacprzyk J.(Eds.), Preferences and Decisions: Models and Applications, Springer, Studies in Fuzziness 257, Berlin, pp. 225-260.
- [58] Greco S, Matarazzo B & Slowinski R. 2010e. Interactive Evolutionary Multiobjective Optimization using Dominance-based Rough Set Approach. In: Proc. of WCCI 2010, IEEE World Congress on Computational Intelligence, July 18-23, 2010, Barcelona, Spain,pp. 3026-3033.
- [59] Greco S, Matarazzo B & Slowinski R. 2010g. Dominance-based Rough Set Approach to Granular Computing. In: Yao J.(Ed.), Novel Developments in Granular Computing, Hershey,New York, pp. 439-527.
- [60] Greco S, Matarazzo B & Slowinski R. 2012. The Bipolar Complemented de Morgan Brouwer-Zadeh Distributive Lattice as an Algebraic Structure for the Dominance-based Rough Set Approach. Fundamenta Informaticae, 115: 25-56.
- [61] Greco S, Matarazzo B, Slowinski R & Stefanowski J. 2001a. Variable consistency model of dominance-based rough set approach. In: Ziarko W & Yao Y. (Eds.), Rough Sets and Current Trends in Computing. Springer LNAI 2005, Berlin, pp. 170-181.
- [62] Greco S, Matarazzo B, Slowinski R & Stefanowski J. 2001b. An algorithm for induction of decision rules consistent with dominance principle. In: Ziarko W & Yao Y. (Eds.), Rough Sets & Current Trends in Computing. Springer LNAI 2005, Berlin, pp. 304-313.
- [63] Greco S, Matarazzo B, Slowinski R & Stefanowski J. 2002. Mining association rules in preference-ordered data. In: Hacid M-S, Ras ZW, Zighed DA & Kodratoff Y.(Eds.), Foundations of Intelligent Systems. Springer LNAI 2366, Berlin, pp. 442-450.
- [64] Greco S, Matarazzo B, Slowinski R & Tsoukias A.1998. Exploitation of a rough approximation of the outranking relation in multicriteria choice and ranking. In: Stewart TJ & van den Honert RC.(Eds.), Trends in Multicriteria Decision Making. Springer LNEMS 465, Berlin, pp. 45-60.
- [65] Greco S, Matarazzo B, Slowinski R & Vaccarella G. 2012. Inventory Control usingInteractive Multiobjective Optimization guided by Dominance-based Rough Set Approach, submitted for publication.
- [66] Greco S, Pawlak Z & Slowinski R. 2004. Can Bayesian confirmation measures be useful for rough set decision rules? Engineering Applications of Artificial Intelligence, 17(4): 345-361.
- [67] Greenwood GW, Hu XS & D'Ambrosio JG.1997. Fitness functions for multiple objective optimization problems: combining preferences with Pareto rankings. In: Belew RK & Vose MD. (Eds.), Foundations of Genetic Algorithms, Morgan Kaufmann, pp. 437-455.
- [68] Goldstein WM. 1991. Decomposable threshold models. Journal of Mathematical Psychology, 35: 64-79.
- [69] Grzymala-Busse JW. 1992. LERS - a system for learning from examples based on rough sets. In: Slowinski R. (Ed.), Intelligent Decision Support. Handbook of Applications and Advances of the Rough Sets Theory. Kluwer, Dordrecht, pp. 3-18.
- [70] Grzymala-Busse JW. 1997. A new version of the rule induction system LERS. Fundamenta Informaticae, 31: 27-39.
- [71] Jaszkiewicz A & Slowinski R. 1999. The "Light Beam Search" approach - an overview of methodology and applications. European Journal of Operational Research, 113: 300-314.
- [72] Jaszkiewicz A. 2007. Interactive multiobjective optimization with the Pareto memetic algorithm. Foundations of Computing and Decision Sciences, 32(1): 15-32.
- [73] Kotlowski W, Dembczynski K, Greco S & Slowinski R. 2008. Stochastic dominance-based rough set model for ordinal classification. Information Sciences, 178(21): 4019-4037.
- [74] Krawiec K, Slowinski R & Vanderpooten D.1998. Learning of decision rules from similarity based rough approximations. In: Polkowski L & Skowron A. (Eds.), Rough Sets in Knowledge Discovery. Vol. 2, Physica-Verlag, pp. 37-54.
- [75] Luce RD. 1956. Semi-orders and a theory of utility discrimination. Econometrica, 24: 178-191.
- [76] Marcus S. 1994. Tolerance rough sets, Cech topologies, learning processes. Bull. of the Polish Academy of Sciences, ser. Technical Sciences, 42(3): 471-487.
- [77] Martel JM & Matarazzo B. 2005. Other outranking approaches. Chapter 6. In: Figueira J, Greco S & Ehrgott M.(Eds.), Multiple Criteria Decision Analysis: State of the Art Surveys, Springer, Berlin, pp. 197-262.
- [78] Miller GA. 1956. The magical number seven, plus or minus two: some limits in our capacity for processing information. The Psychological Review, 63: 81-97.
- [79] Nieminen J. 1988. Rough tolerance equality. Fundamenta Informaticae, 11: 289-296.
- [80] Pawlak Z. 1982. Rough sets. Int. J. Information & Computer Sciences, 11: 341-356.
- [81] Pawlak Z. 1991. Rough Sets. Theoretical Aspects of Reasoning about Data. Kluwer.
- [82] Pawlak Z, Grzymala-Busse JW, Slowinski R & Ziarko W.1995. Rough sets. Communications of the ACM, 38: 89-95.
- [83] Pawlak Z & Slowinski R. 1994. Rough set approach to multi-attribute decision analysis. European J. of Operational Research, 72: 443-459.
- [84] Polkowski L. 2002. Rough Sets: Mathematical Foundations. Physica-Verlag.
- [85] Polkowski L & Skowron A. 1999. Calculi of granules based on rough set theory: approximate distributed synthesis and granular semantics for computing with words. In: Zhong N, Skowron A & Ohsuga S.(Eds.), New Directions in Rough sets, Data Mining and Soft-Granular Computing. Springer LNAI 1711, pp. 20-28.
- [86] Polkowski L, Skowron A & Zytkow J.1995. Rough foundations for rough sets. In: Lin TY & Wildberger A.(Eds.), Soft Computing. Simulation Councils, Inc., San Diego, CA,pp. 142-149.
- [87] Phelps S & Koksalan M. 2003. An interactive evolutionary metaheuristic for multiobjective combinatorial optimization. Management Science, 49(12): 1726-1738.
- [88] Roberts F. 1979. Measurement Theory, with Applications to Decision Making, Utility and the Social Sciences, Addison-Wesley, Boston.
- [89] Roy B. 1996. Multicriteria Methodology for Decision Aiding. Kluwer Academic Publishers,Dordrecht.
- [90] Roy B & Bouyssou D. 1993. Aide Multicritère la Décision: Méthodes et Cas, Economica, Paris.
- [91] Skowron A. 1993. Boolean reasoning for decision rules generation. In: Komorowski J & Ras ZW. (Eds.), Methodologies for Intelligent Systems. Springer LNAI 689, Berlin, pp. 295-305.
- [92] Skowron A & Polkowski L. 1997. Decision algorithms: a survey of rough set-theoretic methods. Fundamenta Informaticae, 27: 345-358.
- [93] Skowron A & Stepaniuk J. 1995. Generalized approximation spaces. In: Lin TY & Wildberger A.(Eds.), Soft Computing. Simulation Councils, Inc., San Diego, CA, pp. 18-21.
- [94] Slowinski R. 1992a. A generalization of the indiscernibility relation for rough set analysis of quantitative information. Rivista di matematica per le scienze economiche e sociali, 15: 65-78.
- [95] Slowinski R. (Ed.) 1992b. Intelligent Decision Support. Handbook of Applications and Advances of the Rough Sets Theory. Kluwer, Dordrecht.
- [96] Slowinski R. 1993. Rough set learning of preferential attitude in multi-criteria decision making. In: Komorowski J & Ras ZW. (Eds.), Methodologies for Intelligent Systems. Springer LNAI 689, Berlin, pp. 642-651.
- [97] Slowinski R, Greco S & Matarazzo B. 2002a. Rough set analysis of preference-ordered data. In: Alpigini JJ, Peters JF, Skowron A & Zhong N.(Eds.), Rough Sets and Current Trends in Computing. Springer LNAI 2475, Berlin, pp. 44-59.
- [98] Slowinski R, Greco S & Matarazzo B. 2002b. Mining decision-rule preference model from rough approximation of preference relation. In: Proc. 26th IEEE Annual Int. Conf. on Computer Software & Applications, Oxford, UK, pp. 1129-1134.
- [99] Slowinski R, Greco S & Matarazzo B. 2002b. Axiomatization of utility, outranking and decision-rule preference models for multiple-criteria classification problems under partial inconsistency with the dominance principle. Control and Cybernetics, 31: 1005-1035.
- [100] Slowinski R, Greco S & Matarazzo B. 2005. Rough set based decision support. Chapter 16. In: Burke EK & Kendall G.(Eds.), Search Methodologies: Introductory Tutorials in Optimization and Decision Support Techniques, Springer, New York, pp. 475-527.
- [101] Slowinski R, Greco S & Matarazzo B. 2009. Rough Sets in Decision Making. In: Meyers RA. (Ed.), Encyclopedia of Complexity and Systems Science, Springer, New York, pp. 7753-7786.
- [102] Slowinski R, Stefanowski J, Greco S & Matarazzo B. 2000. Rough sets based processing of inconsistent information in decision analysis. Control and Cybernetics, 29: 379-404.
- [103] Slowinski R & Vanderpooten D.1997. Similarity relation as a basis for rough approximations. In: Wang PP.(Ed.), Advances in Machine Intelligence & Soft-Computing, vol. IV, Duke University Press, Durham, NC, pp. 17-33.
- [104] Slowinski R & Vanderpooten D. 2000. A generalised definition of rough approximations. IEEE Transactions on Data and Knowledge Engineering, 12: 331-336.
- [105] Slowinski R & Zopounidis C.1995. Application of the rough set approach to evaluation of bankruptcy risk. Intelligent Systems in Accounting, Finance & Management, 4: 27-41.
- [106] Stefanowski J. 1998. On rough set based approaches to induction of decision rules. In: Polkowski L & Skowron A. (Eds.), Rough Sets in Data Mining and Knowledge Discovery. Vol. 1, Physica-Verlag, pp. 500-529.
- [107] Stepaniuk J. 2000. Knowledge Discovery by Application of Rough Set Models. In: Polkowski L, Tsumoto S & Lin TY.(Eds.), Rough Set Methods and Application, Physica-Verlag, Heidelberg, pp. 137-231.
- [108] Szelag M, Greco S & Slowinski R. 2012. Variable Consistency Dominance-based Rough Set Approach to Preference Learning in Multicriteria Ranking. Submitted for publication.
- [109] Thomas LC, Crook JN & Edelman DB.(Eds.). 1992. Credit Scoring and Credit Control. Clarendon Press, Oxford.
- [110] Tversky A. 1977. Features of similarity. Psychological Review, 84: 327-352.
- [111] Yao Y & Wong S. 1995. Generalization of rough sets using relationships between attribute values. In: Proc. 2nd Annual Joint Conference on Information Sciences, Wrightsville Beach, NC, pp. 30-33.
- [112] Wierzbicki AP. 1980. The use of reference objectives in multiobjective optimization. In: Fandel G & Gal T. (Eds.), Multiple Criteria Decision Making, Theory and Applications, Springer, Berlin, pp. 468-486.
- [113] Ziarko W. 1993. Variable precision rough sets model. Journal of Computer and Systems Sciences, 46: 39-59.
- [114] Ziarko W. 1998. Rough sets as a methodology for data mining. In: Polkowski L & Skowron A.(Eds.), Rough Sets in Knowledge Discovery. Vol. 1, Physica-Verlag, pp. 554-576.
- [115] Ziarko W & Shan N. 1994. An incremental learning algorithm for constructing decision rules. In: Ziarko WP.(Ed.), Rough Sets, Fuzzy Sets and Knowledge Discovery. Springer, Berlin,pp. 326-334.
- [116] Zionts S & Wallenius J. 1976. An interactive programming method for solving the multiple criteria problem. Management Science, 22: 652-663.
- [117] Zionts S & Wallenius J. 1983. An interactive multiple objective linear programming method for a class of underlying nonlinear utility functions. Management Science, 29: 519-523.
Publication Dates
-
Publication in this collection
04 Sept 2012 -
Date of issue
Aug 2012






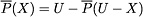 .
.
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, .
.
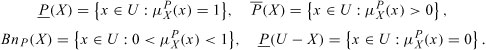

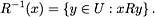
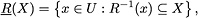







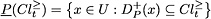

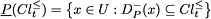
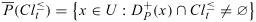
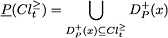


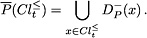




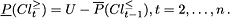
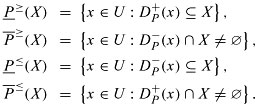

 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 ,
,
 ,
,
 ,
,
 ,
,

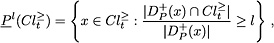

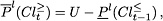
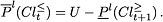
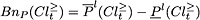
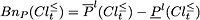
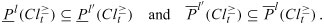
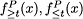 :
:






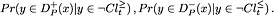


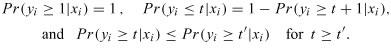


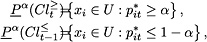
 controls the allowed amount of inconsistency.
controls the allowed amount of inconsistency.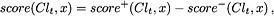



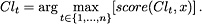
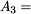 total liabilities/total assets,
total liabilities/total assets,  general and administrative expense/sales,
general and administrative expense/sales, 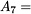 managers' work experience,
managers' work experience,  organization-personnel,
organization-personnel, 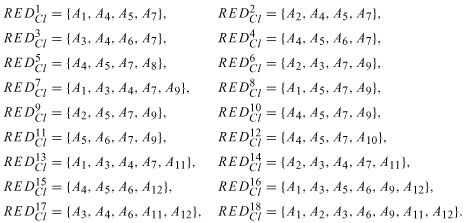
 .
. , means that object
, means that object  , means that object
, means that object 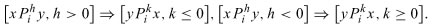



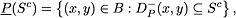







 .
. can match the decision rules in one of four ways:
can match the decision rules in one of four ways: -decision rule, or at least one D
-decision rule, or at least one D and
and 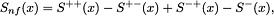
 , if
, if  ;
; good and
good and  medium, or if
medium, or if 

 and 6
and 6