ABSTRACT
The survival analysis was originally proposed for data analysis related to time before the occurrence of a specific event of interest and has been widely used in studies of biomedical data (survival analysis), industrial research (reliability analysis) and financial data (credit scoring). In this study, we presented a new approach to modeling the market value of urban lots based on survival analysis considering the left censoring mechanism, which allows estimating the probability for sale and the hazard associated with sales at the lot market value. The modeling is made from the survival analysis that introduces greater flexibility when compared to the usual linear models as it allows including the effectively traded lots (not censored) and lots in negotiation (censored) into the process, however, it is not enough to affirm the effective improvement of models based on the survival analysis.
Keywords:
urban lots; survival analysis; left censoring
1 INTRODUCTION
Location is one of the main components in the formation of use-values and market value of a property. Land Value Maps (LVM), one of the most important elements to determine values for taxation, consists of generalizations inferred from individual sampling of observable events in local real estate markets.
In drafting LVM based on a scientific methodology, in this case, the statistical methodology, the manager (assessor) should comply with the principle of impartiality, which should guide any decision involving the interests of citizens. Impartiality is directly associated to fundaments for the statistical methodology, that is, in the end, by questioning LVM, we indirectly question the rationale of the statistical methodology used, ranging from the sampling plan to the inference of values.
In Brazil, real state mass evaluation is of great importance to municipal governments. In addition to taxation issues, especially LVM, its applicability widens with the advent of the "Statute of Cities", a federal law that also rules the adoption of tax instruments by municipal urban policies. Therefore, LVM enhance efficiency of instruments for urban policy induction, such as progressive real estate taxes, as well as grants of land use and occupation and acquisition of land by municipalities.
Location is the main explanatory variable of market value of urban lots, however, its modeling for mass evaluation in routine of cities is rather divergent, according to a note published by the (Brazilian Ministry of Cities, 200522 MINISTÉRIO DAS CIDADES. 2005. Cadastro Multifinalitário como instrumento de política fiscal e urbana. Organizadores: Diego Alfonso Erba et al. Rio de Janeiro.). As part of Assessments Engineering, some studies, such as (Dantas, 19988 DANTAS RA. 1998. Engenharia de Avaliações, Uma Introdução à Metodologia Científica. São Paulo: PINI. Vol. 1.), location is treated as a variable of the qualitative type of various stages. In (Hermann & Haddad, 200511 HERMANN BM & HADDAD EA. 2005. Mercado imobiliário e amenidades urbanas: a view through the window. Estudos Econômicos, 35(2): 237-269.), location is a quantitative variable, representing the distance to certain centers of influence in the city. In (Zancan, 199632 ZANCAN EC. 1996. Avaliações de Imóveis em Massa para Efeitos de Tributos Municipais. Florianópolis: Rocha.), for example, location is treated as a series of dichotomous variables. These are examples of different encodings of distinct variables aiming to represent the same feature.
Despite the different ways in treating location, a statistical model can introduce increasing levels of complexity given by the type and number of variables involved. To estimate the market value of a vacant lot, for example, it is possible to compile a list of dozens of explanatory variables from bibliography. This creates numerous possibilities of representation, posing a problem for the researcher about which model to specify. There is a considerable amount of mathematical, statistical and computational approaches in parallel to the issue of relative partial approaches concerning urban location, analyzing this issue by critics of urban theories. In general, it is evident in LVM preparation certain remnants of the actual economicism in the speeches, the reductively economic vision of world (Souza, 200929 SOUZA J. 2009. A ralé brasileira - quem é e como vive. Belo Horizonte: Editora UFMG.), promoted largely by the quantitative lines of sociology and geography, characterized by the sophistication of the instruments, but with very low ability to elucidate the reality comprehensively (Abreu, 19942 ABREU MA. 1994. O estudo geográfico da cidade no Brasil: Evolução e avaliação. In: CARLOS AFA (Ed.) Os caminhos da reflexão sobre a cidade e o urbano. São Paulo: Editora da Universidade de São Paulo.).
The sampling also becomes relevant. The process of mass evaluation of real estate and LVM creation requires a duration in which it is not always possible to obtain a satisfactory amount and spatial balance in sample collections. When this occurs, the assessor is faced with the problem to infer land values in sites where it is difficult to obtain samples, based on comparison with similar sites. The question is: what are the comparison parameters among two different locations?
There is need to build boundary conditions to apply indicator variables from the location to inferential models for real estate assessment. These boundary conditions may be applicable to the universe of Brazilian urban contexts, especially non-metropolitan sites.
According to data from the (Brazilian Institute of Geography and Statistics - IBGE, 200213 INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA - IBGE. 2002. Base de Informações Municipais [CD-ROM]. (3rd ed.). Rio de Janeiro: IBGE.), between 2000 and 2007, the population of São Carlos increased from 160,000 to 210,000 inhabitants, a population growth higher than the average in the state and the country. São Carlos is a medium-sized city whose spatial patterns of real estate valuation are not so simple, as in small municipalities, but they outline factors whose effects have maximum expression in the metropolitan environment. One of the most powerful processes in urban structure is segregation. It is no longer possible to explain the urban patterns of residential segregation by the model center versus periphery, as it was the situation until the mid of decade of 1980 in Brazilian cities.
This article is part of some innovative studies linking two apparently distinct knowledge fields - inferential methodologies of mass evaluation and intra-urban location studies of sociological, geographical and historical nature. The potentially common theme is the prospect of application in urban and taxation planning, which means for the municipal government the use of scientific methods to consider the city as it is, ensuring not only success in assessment formulations, but also respecting to impartiality principles that should characterize its policies.
Urban agglomerations are systems composed of several locations that have accessibility as one of their major attributes with great influence on land valuation. Intra-urban locations with feature to minimize the time required for people's daily locomotion, such as home-to-work trips, leisure, home-to-school, home-to-commerce trips, among others, are more valued. Use-values and prices are closely related categories. According to (Santos, 200326 SANTOS M. 2003. Economia Espacial. Críticas e Alternativas. Trad. MARIA IRENE DE Q.F. SZMRECSÁNYI. (2a ed.). São Paulo: Editora da Universidade de São Paulo. (Coleção Milton Santos).), and (Santos, 200527 SANTOS M. 2005. Da Totalidade ao Lugar. São Paulo: Editora da Universidade de São Paulo. (Coleção Milton Santos).), the urban economy can be split into the poor and the rich, which constitute separate circuits. Thus, the most valued sites are those located near commerce centers and work places of the social strata in its various socioeconomic conditions. In this context, barriers are relevant as they devalue certain locations compared to others. These barriers are of natural order, such as conformation of relief and hydrography, and often, railroads, roads, highways and bridges are designed under the influence of these factors.
Focusing our attention on the vacant lot as an object of study in this article, it is worth to mention the subset of not urbanized inner lands, for instance. In the proposed model whose modeling is characterized by homogeneous regions in terms of location, the assessment of this subset can achieve contextualized dimensions in which common variables used for urbanized lots are considered. It will therefore be possible to quantifying the location value implicit in these areas more clearly and evaluating more comprehensively aspects of land under-use, property speculation in connection with its social function, because these areas usually form urban voids.
This study presents a new perspective based on survival analysis models (Louzada-Neto et al., 200219 LOUZADA-NETO F, MAZUCHELI J & ACHCAR JA. 2002. Análise de Sobrevivência e Confiabilidade. Lima, Peru: Instituto de Matematicas y Ciencias Afines, IMCA. Vol. 1.; Andreeva et al., 20073 ANDREEVA G, ANSELL J & CROOK J. 2007. Modelling profitability using survival combination scores. European Journal of Operational Research, 183(3): 1537-1549.; Hosmer et al., 200812 HOSMER D, LEMESHOW S & MAY S. 2008. Applied Survival Analysis: Regression Modeling of Time to Event Data. (2nd ed.). Wiley-Interscience. ), considering the left censoring mechanism to determine the market value of urban lots. This perspective uses all available information on the modeling process: (i) effectively traded lots (not censored) and (ii) lots under negotiation (censored). The survival analysis according to (Colosimo & Giolo, 20065 COLOSIMO EA & GIOLO SR. 2006. Análise de Sobrevivência Aplicada. São Paulo: Edgard Blücher.) "is one of the areas of statistics that most developed in the last decades of the last century". (Ryan & Woodall, 200525 RYAN TP & WOODALL WH. 2005. The Most-Cited Statistical Papers. Journal of Applied Statistics, 32(5): 461-474.) identified 25 most cited statistical papers and the first two studies in their list were: (i) first, with 25,869 citations (currently cited 1,984 times per year), is (Kaplan & Meier, 195816 KAPLAN EL & MEIER P. 1958. Nonparametric estimation from incomplete observations. Journal of the American Statistical Association, 53: 457-481.) and (ii) second, with 18,193 citations (cited 1,342 times per year), (Cox, 19727 COX DR. 1972. Regression models and life tables. Journal of the Royal Statistical Society, Series B, 34: 187-220.). Both studies refer to the survival analysis and its relevance. The survival analysis, in addition to allowing the construction of a model to predict the market value of lots, as the usual linear regression model does, it allows estimating the likelihood and hazard associated with the sales price of a particular lot.
The paper is organized as follows. Section 2 refers to the description of materials and methods, such as data collection, covariates, survival analysis considering left censoring divided into two sub-sections, a sub-section for the non-parametric estimator of Kaplan-Meier and another sub-section for the Weibull linear model. Section 3 refers to the discussion of the results and is subdivided into three sub-sections (descriptive and exploratory analysis and Weibull linear model). Some final comments and conclusion are presented in Section 4.
2 MATERIALS AND METHODS
2.1 Data collection
In the context of this study, the term "lot" means a real estate property consisting of a land parcel, resulting from an urban developing program, parcelment or condominium fractionation. Strictly speaking, this concept is not restricted to a legal definition, but purely to the morphological aspect of the vacant lot. The universe (population in a statistical standpoint) comprised 24,975 vacant lots, almost a quarter of all real estate properties in the municipality of São Carlos (São Carlos, 200628 SÃO CARLOS. 2006. Prefeitura Municipal - Divisão de Cadastro Imobiliário. Base de dados cadastrais.), São Paulo State, Brazil. In this property type, the value of the location is explicit, whereas in built-up lots, the land value is implicit, due to the construction characteristics and its conservation. Although there are many interference on values of vacant lots, there are not as many as those for built-up lots.
(Ferreira, 200710 FERREIRA JF. 2007. Proposta de tratamento da variável localização em modelos inferenciais de avaliação imobiliária para municípios médios. Dissertação (Mestrado em Engenharia Urbana)- Departamento de Engenharia Civil, Universidade Federal de São Carlos. Exame de defesa rea li za do em 18/12/2007.) characterized the spatial distribution of the different households of São Carlos City based on education and income data in the 2000 census (IBGE, 200213 INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA - IBGE. 2002. Base de Informações Municipais [CD-ROM]. (3rd ed.). Rio de Janeiro: IBGE.). The method used in this analysis consists in determining a statistical distance between the 241 census sectors based on the method of the multivariate analysis described in (Johnson & Wichern, 199814 JOHNSON RA & WICHERN DW. 1998. Applied Multivariate Statistical Analysis. (4th ed.). Upper Saddle River, NJ: Prentice-Hall Inc.). Figure 1 shows a comprehensive configuration of the spatial distribution patterns of the residential neighborhoods of social strata with higher and lower purchasing power. Each one composes a pole.
Non-colored sectors do not belong to any of the poles and the common feature observed in its residents is the popular profile, considered a sector of average purchasing power. In blue regions, there are the residents of above-average purchasing power, while residents with below-average income are represented in orange. It reveals the occurrence of a basic pattern, characterized by the arrangement of high-income residential neighborhoods in a predominantly east-west axis, from the city center. The underprivileged neighborhoods tend to be located in the extreme north and south of the built-up area, separated from the city center by urban barriers and located next to them. The major barriers are the railway, highway SP-310 (Washington Luiz Highway) and southern slopes. Efforts were directed to obtain the largest possible number of samples related to real estate transactions effectively carried out whose information is harder to be obtained. Therefore, this research concentrates on asking prices of lots obtained at the local real estate agencies. The choice for this value is justified for being faithful, synthetic and easy to obtain by the researcher. Although somewhat biased, for expressing purely seller's interests, this value represents the maximum possible value on a particular parcel of land. Associated with this asking price are the advantages offered by acquiring the property: neighborhood, accessibility, natural attractions, infrastructures accumulation, among others.
In the higher income strata, in terms of valuation, there is a strong dependence on the land value with the blue areas in Figure 1. The most valued areas, according to the samples collected coincide with the blue areas with the exception of parcels that were created after the 2000 census (Parque Faber II, Residential Condominiums Dahma and Montreal, for example).
Classification map of census sectors according to the value of the statistic distance to one of the social strata poles. Indication of the largest intra-urban barriers. Source: (Ferreira, 200710 FERREIRA JF. 2007. Proposta de tratamento da variável localização em modelos inferenciais de avaliação imobiliária para municípios médios. Dissertação (Mestrado em Engenharia Urbana)- Departamento de Engenharia Civil, Universidade Federal de São Carlos. Exame de defesa rea li za do em 18/12/2007.).
Housing standards show two distinct profiles. The richer pole (Parque Faber I) characterized as a parcelment with formal appearance of a condominium, in terms of common spaces and services, including walls and caretaker services. This pole has a set of building codes more stringent that the municipal law for site buildings and constructions. On the other hand, the opposite pole (Jardim Gonzaga) shows extreme informality in land use, lack of infrastructure and predominance of "subnormal" standard housings. Exclusion levels are evident to justify the deployment of Programa Habitar Brasil/BID, a project funded by the Brazilian Federal Government around the year 2001.
2.2 Covariates
To treat the location concept of urban lots, the urban space was subdivided according to the criteria described above. Each hypothesis is an explanatory variable to be included in this model, in other words, in the language of regression models, each hypothesis corresponds to a covariate. The concept and the label (between parenthesis) used throughout the modeling process of each covariate are described below:
-
Central Hill (PLN_CENTRAL) - the relevance to these areas is a valuation factor.
-
Railway (FERROVIA) - the dichotomy of this variable is useful to estimate depreciation averages resulting from the influence of the railway.
-
Highway (RODOVIA) - areas with accessibility unaffected by Highway SP-310 are most valued.
-
Southern Slope (ENCOSTA) - areas situated before the barrier of southern slopes are most valued.
-
Closed (FECHADO) - the closing of these installments is a valuation factor.
-
Condominium (CONDO) - the institution is a condominium is a valuation factor.
-
Residential Use (ESTRIT_RESID) - the characteristic of the allotment for strictly residential use or any restrictions in this regard contribute to valuation of lots.
-
City Center (NUC_PRINC) - the relatively remote locations with respect to the city center separated by several watersheds are more devalued.
In the model proposed, the subdivision of urban lot location is expressed by eight dichotomous variables as shown below in Table 1. The unity of the response variable, Total Value of the Property (Vi ), is in Real per square meter (R$/m ).
2.3 Analysis of survival considering the left censoring mechanism
In medical, financial or industrial studies, in general, the event of interest is the time elapsed until the failure time. In the first case, failure can be the death of the patient. In the second, failureof a certain artifact, usually a system or a part of it. In the third, failure is when the customer (payer) becomes a defaulter. However, the term has been extended beyond this limit in order to apply it to various types of events, including non-fatal ones. In this study, the event of interest (failure) is treated as the sale in Reais (R$) of the lot. In other words, through this approach, for example, we may be interested in knowing the probable sale price (V), but it was offered by a price (Z), being that V ≤ Z (a condition imposed by the left censoring mechanism). Note that the sale price (V) is non-observable (latent), requiring the use of the survival analysis to describe and interpret it.
The survival and reliability analysis becomes peculiar due to the special features inherent to data types that are typically available for the analysis. Here, we discuss only two main characteristics of the survival and reliability data: presence of censoring and presence of covariates (similar to the usual linear model).
In the databases for the survival analysis, the main feature is the presence of censoring, which is the partial observation of the response. This refers to situations where, for some reason, the unit monitoring (urban lot) was interrupted. Without censoring, the classical statistical techniques such as the regression analysis and experiment designs could be used in the analysis of this data type, probably using a transformation for the answer. Therefore, the use of survival analysis methods allows incorporating in the statistical analysis the information contained in the censored data (Colosimo & Giolo, 20065 COLOSIMO EA & GIOLO SR. 2006. Análise de Sobrevivência Aplicada. São Paulo: Edgard Blücher.). This means that there is need to introduce an extra variable to the survival analysis, indicating whether the response of interest was observed. In this study, whether the sale of a given lot was carried out. This variable is known in the literature for the survival and reliability analysis as the indicator variable of censoring, or simply censoring.
(Louzada-Neto et al., 2006) highlight the fact that though censored, all the results from a data set should be used in the statistical analysis. Two reasons justify this procedure:
-
even incomplete, censored observations provide information on the response variable, for example, the actual value of the lot;
-
the omission of censoring in calculating the statistics of interest could lead to flawed conclusions.
Censoring can occur in several ways, according to various mechanisms such as right censoring, left censoring, censoring type I, censoring type II and random censoring (Lawless, 198217 LAWLESS JF. 1982. Statistical Models and Methods for Lifetime Data. New York: John Wiley and Sons.).
The survival analysis usually uses the right censoring mechanism, because the occurrence time of the event of interest is to the right of the time, that is, until the end of the study, the experimental unit did not fail. The mechanisms related to censoring type I (when the study ends in a preset time and some of the survival times are not observed) and random (when a patient leaves the study without having experienced the event of interest) are observed more frequently in biomedical studies. However, in industrial experiments, censoring type II (when the study ends after a certain number of pre-established failures within the items under study) are predominant (Colosimo & Giolo, 20065 COLOSIMO EA & GIOLO SR. 2006. Análise de Sobrevivência Aplicada. São Paulo: Edgard Blücher.).
In this study, we adopted the left censoring concept. This censoring type occurs when, for example, the time registered is greater than the failure time, meaning that the event of interest happened when the individual was observed (Colosimo & Giolo, 20065 COLOSIMO EA & GIOLO SR. 2006. Análise de Sobrevivência Aplicada. São Paulo: Edgard Blücher.). In other words, the price of the lot offered on the market is the upper limit that the owner accepts to sell it. For example, a given lot is offered for R$ 50,000.00. It will be sold (event of interest or failure) for a maximum of R$ 50,000.00, given that it is unlikely for anyone to pay any amount above the price offered. The left censoring mechanism is shown in Figure 2.
In the survival analysis, as well as in the usual linear regression models, in addition to the survival time (represented by the Total Value of the Property (R$/m2)) and the indicator variable, we can also observe in the data, variables that represent the existing heterogeneity in the population, that is, the covariates presented in Table 1.
2.3.1 Kaplan-Meier nonparametric estimator
The following describes how the survival and hazard functions can be estimated by using the Kaplan-Meier nonparametric estimator (Kaplan & Meier, 195816 KAPLAN EL & MEIER P. 1958. Nonparametric estimation from incomplete observations. Journal of the American Statistical Association, 53: 457-481.), which allows the presence of censoring observations. Consider a study involving n lots and that the values of permanence for sale, including censorship, are ordered, that is, v 1 ≤ v 2 K ≤ vn . The empirical function of permanence for sale is estimated by:
where vr is the greatest value of permanence for sale smaller than or equal to v, ni is the number of lots not sold until value vi (which represents the value of lot for sale ordered i) and di represents the number of lots sold at value vi (di = 0 for censored values of permanence for sale), where i can be any round value between 1 and r. In the absence of censoring, the Kaplan-Meier estimator of the function of permanence for sale reduces to,
The Kaplan-Meier estimator of the cumulative hazard function within the range value (0, v] is given by
where 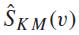 cannot be equal to zero.
cannot be equal to zero.
2.3.2 Weibull linear model
The Weibull distribution (195131 WEIBULL WA. 1951. A statistical distribution of wide applicability. Journal of Applied Mechanics, 18: 293-297.), mostly due to its simplicity, has been one of the most commonly used probability distributions in biomedical and industrial data modeling. Here, its use is evaluated to model the total value of the lot in Reais (R$). Its density can be described as:
where γ > 0 and α > 0 are the shape and scale parameters, respectively.
When γ = 1 in (1), we obtain the exponential distribution as a special case. The Weibulldistribution is commonly described in the literature under different parameterizations (Droguett & Mosleh, 20079 DROGUETT EL & MOSLEH A. 2007. Time to failure assessment of products at service conditions from accelerated lifetime tests with stress-dependent spread in life. Pesqui. Oper., 27(2): 209-233.; Hosmer et al., 200812 HOSMER D, LEMESHOW S & MAY S. 2008. Applied Survival Analysis: Regression Modeling of Time to Event Data. (2nd ed.). Wiley-Interscience. ).
The hazard and survival functions of (permanence for sale) and Weibull distribution percentages are given, respectively, by
The hazard function in (5) is the ratio of the probability density function and the survival function (complement to the distribution function). The function is expressed as
describing, therefore, the relationship between the three functions that are usually used to represent the behavior of the survival time or the value of permanence for sale. Expression (8) shows that the functions of survival (permanence for sale) and hazard are inversely proportional.
The accumulated hazard function of the Weibull distribution is given by
Due to its interpretation, the hazard function (8) has been preferred by many authors to describe the behavior of the survival time, in this case, the value of permanence for sale. The hazard function describes how the instant probability of failure (failure rate) changes over time (Colosimo & Giolo, 20065 COLOSIMO EA & GIOLO SR. 2006. Análise de Sobrevivência Aplicada. São Paulo: Edgard Blücher.; Hosmer et al., 200812 HOSMER D, LEMESHOW S & MAY S. 2008. Applied Survival Analysis: Regression Modeling of Time to Event Data. (2nd ed.). Wiley-Interscience. ). It is also known as instantaneous failure rate, mortality force and conditional mortality rate (Cox & Oakes, 19846 COX DR & OAKES D. 1984. Analysis of Survival Data. London: Chapman and Hall.).
Moreover, the hazard function allows to characterize special classes of distributions of survival time (value of permanence for sale), according to its behavior as a function of the sale value. The hazard function can be constant, increasing, decreasing or even monotic. Some usual distributions of survival time are, for example, exponential, Weibull, lognormal, log-logistic (Colosimo & Giolo, 20065 COLOSIMO EA & GIOLO SR. 2006. Análise de Sobrevivência Aplicada. São Paulo: Edgard Blücher.).
The exponential distribution accommodates hazard functions, whereas if the hazard function is monotonically ascending or descending in v, we have a Weibull distribution (Lawless, 198217 LAWLESS JF. 1982. Statistical Models and Methods for Lifetime Data. New York: John Wiley and Sons.). The log-logistic and lognormal distributions accommodate unimodal hazard functions (Kalbfleisch & Prentice, 198015 KALBFLEISCH JD & PRENTICE RL. 1980. The Statistical Analysis of Failure Time Data. New York: John Wiley and Sons.). In addition, although not very common, multimodal and hazard functions in "U" shape can also be observed. (Louzada-Neto, 199918 LOUZADA-NETO F. 1999. Polyhazard regression models for lifetime data. Biometrics, 55: 1281-1285.) proposed a multiple hazard function that accommodates these forms of hazard functions.
One of the important features of the Weibull distribution in survival time modeling is related to its flexibility in accommodating different forms of hazard functions. For the parameter γ < 1,we have functions monotonically decreasing, for γ > 1, hazard functions are monotonically increasing and for γ = 1, we have exponential distribution with constant hazard function (Louzada-Neto et al, 2006).
According to (Colosimo & Giolo, 20065 COLOSIMO EA & GIOLO SR. 2006. Análise de Sobrevivência Aplicada. São Paulo: Edgard Blücher.) and (Hosmer et al., 200812 HOSMER D, LEMESHOW S & MAY S. 2008. Applied Survival Analysis: Regression Modeling of Time to Event Data. (2nd ed.). Wiley-Interscience. ), in the survival analysis, the models cited above are competing with one another. To adjust a given set of sale values of real estate (they may have different forms of hazard functions), it becomes necessary to use a methodology to select the most appropriate model, even before any adjustment.
In many applications, there is qualitative and, in many cases, structural information about the phenomenon in question, which can be used in the empirical determination of the form of the hazard function. Structural information is directly linked to the researcher's knowledge about the phenomenon, while qualitative information can be extracted by means of a graphical analysis.In this context, a graph known as the chart of total time on test (TTT-plot) is very useful. This chart was originally proposed by (Aarset, 19871 AARSET MV. 1987. How to identify a bathtub hazard rate. IEEE Transactions on Reliability, 36: 106-108.) and is built from the quantities:
where r = 1, K, n and Ti : n , i = 1, K, n are the statistics of the sample order (Mudholkar et al., 199623 MUDHOLKAR GS, SRIVASTAVA DK & KOLLIA GD. 1996. A generalization of the Weibulldistribution with application to the analysis of survival data. Journal of the American Statistical Association, 91(436): 1575-1583.).
If there is information on covariates for each individual and a significant number of individuals in each level or combination of these covariates, the TTT-plot (10) can be constructed considering each covariate level or combination separately.
In a practical context, the survival data modeling is linked to the shape of the hazard function. At this point, justification about the choice for the Weibull distribution and the whole presentation of the concepts in order to model the sale value of the lots in this study is necessary. In Figure 3(a), the TTT-plot presents concavity on the curve, indicating that the shape of the hazard function is monotonically increasing. Thus, a candidate distribution for the adjustment is the Weibull with the shape parameter greater than one. Finding a suitable probability distribution for the data in the study is the most important step of modeling, only after finding this distribution allows to estimate and test quantities of interest (Colosimo & Giolo, 20065 COLOSIMO EA & GIOLO SR. 2006. Análise de Sobrevivência Aplicada. São Paulo: Edgard Blücher.). In Figure 3(b) the Weibull can be confirmed such as an adequate model since there is no substantial deviation from a straight line. Since the Weibull model assumes a proportionality of hazards, in Figures 3(c), 3(d) and 3(e) this proportionality was graphically checked out stratified by covariates. Therefore, all of the three covariates ("NUC_PRINC", "PLN_CENTRAL" and "RODOVIA") present proportionality along the unitary value of urban lot (R$/m2).
The next step is the construction of the likelihood function of the linear model Weibull. We consider the situation in which we have available a random sample v 1, K, vn of survival times and the values of the indicator variable δi , δi = 1, if vi is exactly observed or δi = 0 if vi is left censored.
Based on the information (v 1, δ1), K(vn , δn ) that the censoring mechanism is not informative and that vi is from the same probability distribution indexed by parameter θ, the likelihood function is generally written as:
For the Weibull distribution with parameters α and γ, considering a random sample v 1, K, vn and the indicator variable of censoring δi , δi = 1 if vi is exactly observed or left censored, the likelihood function, in the presence of covariates, is written as:
where xi is the vector of covariates for the i-th lot and the indicator variable of censoring is set as,
Applying the natural logarithm in the likelihood function and after a few steps, we obtain the following function,
where l(α; γ|vi ; δi ; xi = log[L(α; γ|vi ; δi ; xi )].
Here, we opted to use a selection strategy of models derived from the proposal of (Collett, 19944 COLLETT D. 1994. Modelling Survival Data in Medical Research. New York: Chapman and Hall.). The steps used in the selection process are described in (Colosimo & Giolo, 20065 COLOSIMO EA & GIOLO SR. 2006. Análise de Sobrevivência Aplicada. São Paulo: Edgard Blücher.). Similar to the usual linear model, the model proposed by the strategy of (Collett, 19944 COLLETT D. 1994. Modelling Survival Data in Medical Research. New York: Chapman and Hall.) began our modeling process, never leaving aside the opinions of specialists in this field.
(a) TTT-plot for the unitary value of urban lots (R$/m2) in São Carlos City, SP, in the year 2005; (b) Plot of the empirical log{-log[2)], and its estimated curve; (c) Plot of the empirical log{-log[2)], and its estimated curve stratified by covariate "NUC_PRINC"; (d) Plot of the empirical log{-log[2)], and its estimated curve stratified by covariate "PLN_CENTRAL"; (e) Plot of the empirical log{-log[2)], and its estimated curve stratified by covariate "RODOVIA".
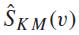 ]} against log [Unitary value of urban lots (R$/m
]} against log [Unitary value of urban lots (R$/m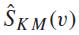 ]} against log [Unitary value of urban lots (R$/m
]} against log [Unitary value of urban lots (R$/m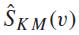 ]} against log [Unitary value of urban lots (R$/m
]} against log [Unitary value of urban lots (R$/m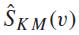 ]} against log [Unitary value of urban lots (R$/m
]} against log [Unitary value of urban lots (R$/m
All data analyses and simulation studies were conducted in the computing environment R version 3.1.1 (R Core Team, 201424 R CORE TEAM. 2014. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. http://www.R-project.org.
http://www.R-project.org...
). We used the basic distribution packages besides the functions "survreg" and "Surv" of the "survival" package (Therneau, 201430 THERNEAU T. 2014. Survival: A Package for Survival Analysis in S. R package version 2.37-7. http://CRAN.R-project.org/package=survival (acesso em 12 out. 2015).
http://CRAN.R-project.org/package=surviv...
), intrinsic to the computing environment R. "Surv" allows specifying the censoring type, in this case, left censoring and the "survreg" function allows specifying the distribution of interest, in this case, the Weibulldistribution.
For the model construction, the database was divided into two parts: 70% for model adjustment and 30% for model validation.
3 RESULTS AND DISCUSSION
3.1 Descriptive and exploratory analysis
The first step of any statistical data analysis consists of descriptive analyses of the variables under study. In the survival analysis, this step means to use non-parametric methods presented in (1), (2) and (3). In Figure 4(a), empirical function of permanence for sale is presented, estimated using the non-parametric method of Kaplan-Meier and in Figure 4(b), the cumulative empirical hazard function is shown. In Figure 4(a), we observe that as the lot value increases, the probability for the lot remain for sale decreases, that is, when the value is high, there is little probability of a lot to become available for sale. The probability of a lot to remain for sale for the minimum value 200 (R$/m2) is 0.05. Figure 4(b) presents the empirical cumulative hazard. The cumulative hazard is a non-decreasing function, if the cumulative hazard is increasing it means that the hazard is larger than zero but it not means that the hazard is increasing. Moreover, from approximately 310 (R$/m2) the cumulative hazard is constant, meaning that from this value onwardthe hazard is null. When the hazard increases, the likelihood of permanence for sale decreases and vice versa.
(a) Curve of permanence for sale estimated by the Kaplan-Meier method; (b) empirical cumulative sale hazard and confidence intervals at 95%.
3.2 Weibull linear model
We considered only lots with an area smaller than or equal to 800 m2 while the lots not sold in 2005 were considered censored since they did not experience the event of interest (sale), that is, they remained for sale. In this study, we used the left censoring mechanism. It began with the selection of the covariates that best explain the sale value of the lot. We decided to use a selection strategy of models derived from the strategy proposed by (Collett, 19944 COLLETT D. 1994. Modelling Survival Data in Medical Research. New York: Chapman and Hall.). It is based on the ratio test of likelihood.
At the end of the selection strategy of covariates (Table 2), the final model is obtained:
The estimates of parameters and respective sale hazards considering the Weibull model with left censoring are shown in Table 2.
Estimation of parameters of coefficients
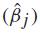 and the sale hazard associated with each covariate given by exp
and the sale hazard associated with each covariate given by exp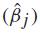 , j = 0, ..., 3.
, j = 0, ..., 3.
The estimated shape parameter of our final model is 2.57, greater than one, showing that the sale hazard function increases according to the information obtained through Figures 3(a), 3(b), 3(c), 3(d) and 3(e) that showed the Weibull distribution with shape parameter greater than one, a plausible distribution for the adjustment.
We observe that for the Weibull regression, the three covariates that comprise the final model increased the sale hazard of lots and can be considered valuation factors during the sale of the lots. For example, the sale hazard of a lot located adjacent to the agglomeration of the CityCenter was exp(0.82) = 2.27 times higher compared to a lot located in rural installments. The hazard sale of a lot located within the Central Hill was, exp(0.41) = 1.51 that is, for a lot inside the Central Hill there was a 51% increase in the sale hazard in relation to a lot located outside of the Central Hill. For a lot whose accessibility to the City Center is not affected by Highway SP-310 (Washington Luiz Highway), the sale hazard was around 2 times higher in relation to a lot whose accessibility to the City Center is affected by Highway SP-310. Another interesting interpretation is to compare the sale hazard of lots contiguous to the agglomeration of City Center ("NUC_PRINC") with the lots located within the Central Hill ("PLN_CENTRAL"). To estimate this hazard, exp[-(-0.82 + 0.41)] = 1.51 is calculated. Thus, there was an increase of sale hazard of 51% for lots contiguous to agglomeration of City Center compared to lots located within the Central Hill. In other words, the lots located in the agglomeration of the City Center had an appreciation of 51% compared to lots located in within the Central Hill. More details about the discussion on implications from the perspective of urban planning are presented in (Ferreira, 200710 FERREIRA JF. 2007. Proposta de tratamento da variável localização em modelos inferenciais de avaliação imobiliária para municípios médios. Dissertação (Mestrado em Engenharia Urbana)- Departamento de Engenharia Civil, Universidade Federal de São Carlos. Exame de defesa rea li za do em 18/12/2007.).
Figure 5 shows the functions of permanence for sale for each stratum (hypotheses concerning location of urban lots - subdivision of urban space), which describe the probability of the lot not to be sold and remain for sale. We highlight that the unitary value of urban lot, in R$/m2, is higher for the curves to the right. For example, the dashed blue curve ("PLN_CENTRAL + RODOVIA") referring to the lots located simultaneously within the Central Hill whose accessibility to the City Center is not affected by Highway SP-310 presents the highest unitary lot value compared to other curves. Lots located exclusively within the Central Hill (red curve) had the lowest unitary lot price, in R$/m2, among the curves. For lots located within the Central Hill ("PLN_CENTRAL"), the value at which about 50% (median value) of these lots are sold is R$36.00/m2, while for lots whose accessibility to the City Center is not affected by Highway SP-310, this value hovers around R$50.00/m2.
Curves of permanence for sale estimated from each stratum and combinations of interest for the Weibull linear model considering the left censoring mechanism. The horizontal dotted gray lines refer to 90% and 50% (median value). The vertical dotted black line refers to the value of R$36.00/m2.
Also, Figure 5 shows the percentage of lots that were not sold and remained for sale, up to a certain value of interest. For example, for lots located simultaneously within the Central Hill whose accessibility to the city center is not affected by Highway SP-310, about 90% of the lots remained for sale above R$36.00 R$/m2. This point refers to the vertical dotted black curve in Figure 5. While, for lots located within the Central Hill ("PLN_CENTRAL"), only 50% remained for sale at that value (median value). About 90% of lots located within the Central Hill ("PLN_CENTRAL") are still available for sale above R$18.00/m2. Therefore, for lots located within the Central Hill whose accessibility to the City Center is not affected by Highway SP-310, there is a greater likelihood of a lot to remain for sale for the minimum value of R$36.00/m2 in relation to lots located within the Central Hill. For all strata and combinations, the probability is zero for a lot to remain for sale at a value greater than R$150.00/m2, according to theWeibull model.
Figure 6 shows that the hazard or instant sale rate is increasing, that is, as the lot value increases, the hazard of selling it for this exact value also increases. For example, lots located within the Central Hill ("PLN_CENTRAL") show greater hazard of instant sale. While lots located simultaneously in the Central Hill whose accessibility to the City Center is not affected by Highway SP-310, represented by the dashed blue curve, had lower hazard of instant sale.
Hazard curves (instant sale rate) estimated from each stratum and combinations of interest for the Weibull linear model considering the left censoring mechanism.
Finally, Figure 7 shows the hazard or cumulative sales rate, that is, as the lot value increases, the hazard of selling it for this value at most also increases. The interpretation is rather similar to instant hazard (Fig. 6) and the only subtle difference lies in the hazard interpretation. For example, for lots located within the Central Hill ("PLN_CENTRAL"), the hazard for these lots to be sold for the exact value of R$50.00/m2 is 0.08 (instant hazard), while the hazard of these lots be sold at most R$50.00/m2 is 1.70 (cumulative hazard).
Cumulative hazard curves (cumulative sales rate) estimated from each stratum and combinations of interest for the Weibull linear model considering the left censoring mechanism.
4 CONCLUSION AND FURTHER STUDIES
The survival analysis is more flexible and uses all the information available in the database of real estate evaluation, because it allows including the effectively traded lots (not censored) and lots in negotiation (censored) in the modeling process. The same does not occur when the usual linear models are considered. The survival analysis allowed estimating the likelihood of a lot to remain for sale and the sale hazards associated with the market value of the lot. Moreover, it allowed the construction of a model to predict the market value of the lot.
We highlight that although the sample size is moderate (275 lots), the prediction power of the model is considerable. This statement is especially valid when we consider that there are "micro" variables of significant importance that were not considered, such as the lot shape, its position in the block, its proximity to shopping and service sub-centers, among other features. The influence of these "micro" variables, within homogeneous regions, and the use of statistical and computational approaches, such as Generalized Linear Models and Artificial Neural Networks, could be considered in future studies.
REFERENCES
-
1AARSET MV. 1987. How to identify a bathtub hazard rate. IEEE Transactions on Reliability, 36: 106-108.
-
2ABREU MA. 1994. O estudo geográfico da cidade no Brasil: Evolução e avaliação. In: CARLOS AFA (Ed.) Os caminhos da reflexão sobre a cidade e o urbano. São Paulo: Editora da Universidade de São Paulo.
-
3ANDREEVA G, ANSELL J & CROOK J. 2007. Modelling profitability using survival combination scores. European Journal of Operational Research, 183(3): 1537-1549.
-
4COLLETT D. 1994. Modelling Survival Data in Medical Research. New York: Chapman and Hall.
-
5COLOSIMO EA & GIOLO SR. 2006. Análise de Sobrevivência Aplicada. São Paulo: Edgard Blücher.
-
6COX DR & OAKES D. 1984. Analysis of Survival Data. London: Chapman and Hall.
-
7COX DR. 1972. Regression models and life tables. Journal of the Royal Statistical Society, Series B, 34: 187-220.
-
8DANTAS RA. 1998. Engenharia de Avaliações, Uma Introdução à Metodologia Científica. São Paulo: PINI. Vol. 1.
-
9DROGUETT EL & MOSLEH A. 2007. Time to failure assessment of products at service conditions from accelerated lifetime tests with stress-dependent spread in life. Pesqui. Oper., 27(2): 209-233.
-
10FERREIRA JF. 2007. Proposta de tratamento da variável localização em modelos inferenciais de avaliação imobiliária para municípios médios. Dissertação (Mestrado em Engenharia Urbana)- Departamento de Engenharia Civil, Universidade Federal de São Carlos. Exame de defesa rea li za do em 18/12/2007.
-
11HERMANN BM & HADDAD EA. 2005. Mercado imobiliário e amenidades urbanas: a view through the window. Estudos Econômicos, 35(2): 237-269.
-
12HOSMER D, LEMESHOW S & MAY S. 2008. Applied Survival Analysis: Regression Modeling of Time to Event Data. (2nd ed.). Wiley-Interscience.
-
13INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA - IBGE. 2002. Base de Informações Municipais [CD-ROM]. (3rd ed.). Rio de Janeiro: IBGE.
-
14JOHNSON RA & WICHERN DW. 1998. Applied Multivariate Statistical Analysis. (4th ed.). Upper Saddle River, NJ: Prentice-Hall Inc.
-
15KALBFLEISCH JD & PRENTICE RL. 1980. The Statistical Analysis of Failure Time Data. New York: John Wiley and Sons.
-
16KAPLAN EL & MEIER P. 1958. Nonparametric estimation from incomplete observations. Journal of the American Statistical Association, 53: 457-481.
-
17LAWLESS JF. 1982. Statistical Models and Methods for Lifetime Data. New York: John Wiley and Sons.
-
18LOUZADA-NETO F. 1999. Polyhazard regression models for lifetime data. Biometrics, 55: 1281-1285.
-
19LOUZADA-NETO F, MAZUCHELI J & ACHCAR JA. 2002. Análise de Sobrevivência e Confiabilidade. Lima, Peru: Instituto de Matematicas y Ciencias Afines, IMCA. Vol. 1.
-
20MANTEL N. 1966. Evaluation of survival data and two new rank order statistics arising in its consideration. Cancer Chemotherapy Reports, 50: 163-170.
-
21MANTEL NE & HAENSZEL W. 1959. Statistical aspects of the analysis of data from retrospective studies of disease. Journal of the National Cancer Institute, 22: 719-748.
-
22MINISTÉRIO DAS CIDADES. 2005. Cadastro Multifinalitário como instrumento de política fiscal e urbana. Organizadores: Diego Alfonso Erba et al. Rio de Janeiro.
-
23MUDHOLKAR GS, SRIVASTAVA DK & KOLLIA GD. 1996. A generalization of the Weibulldistribution with application to the analysis of survival data. Journal of the American Statistical Association, 91(436): 1575-1583.
-
24R CORE TEAM. 2014. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. http://www.R-project.org
» http://www.R-project.org -
25RYAN TP & WOODALL WH. 2005. The Most-Cited Statistical Papers. Journal of Applied Statistics, 32(5): 461-474.
-
26SANTOS M. 2003. Economia Espacial. Críticas e Alternativas. Trad. MARIA IRENE DE Q.F. SZMRECSÁNYI. (2a ed.). São Paulo: Editora da Universidade de São Paulo. (Coleção Milton Santos).
-
27SANTOS M. 2005. Da Totalidade ao Lugar. São Paulo: Editora da Universidade de São Paulo. (Coleção Milton Santos).
-
28SÃO CARLOS. 2006. Prefeitura Municipal - Divisão de Cadastro Imobiliário. Base de dados cadastrais.
-
29SOUZA J. 2009. A ralé brasileira - quem é e como vive. Belo Horizonte: Editora UFMG.
-
30THERNEAU T. 2014. Survival: A Package for Survival Analysis in S. R package version 2.37-7. http://CRAN.R-project.org/package=survival (acesso em 12 out. 2015).
» http://CRAN.R-project.org/package=survival -
31WEIBULL WA. 1951. A statistical distribution of wide applicability. Journal of Applied Mechanics, 18: 293-297.
-
32ZANCAN EC. 1996. Avaliações de Imóveis em Massa para Efeitos de Tributos Municipais. Florianópolis: Rocha.
Publication Dates
-
Publication in this collection
May-Aug 2016
History
-
Received
04 Dec 2015 -
Accepted
13 July 2016
























