Abstract
Berkovitz's notion of strategy and payoff for differential games is extended to study two player zero-sum infinite dimensional differential games on the infinite horizon with discounted payoff. After proving dynamic programming inequalities in this framework, we establish the existence and characterization of value. We also construct a saddle point for the game.
differential game; strategy; value; viscosity solution; saddle point
Infinite horizon differential games for abstract evolution equations
A.J. Shaiju* * The author is a CSIR research fellow and the financial support from CSIR is gratefully acknowledged.
Department of Mathematics, Indian Institute of Science, Bangalore, 560 012, India, E-mail: shaiju@math.iisc.ernet.in
ABSTRACT
Berkovitz's notion of strategy and payoff for differential games is extended to study two player zero-sum infinite dimensional differential games on the infinite horizon with discounted payoff. After proving dynamic programming inequalities in this framework, we establish the existence and characterization of value. We also construct a saddle point for the game.
Mathematical subject classification: 91A23, 49N70, 49L20, 49L25.
Key words: differential game, strategy, value, viscosity solution, saddle point.
1 Introduction
In [1], Berkovitz has introduced a novel approach to differential games of fixed duration. He has extended this framework to cover games of generalized pursuit-evasion [2] and games of survival [3] in finite dimensional spaces. Motivated by these developments we define strategies and payoff for infinite horizon discounted problems whose state is governed by a controlled semi-linear evolution equation in a Hilbert space. In this setup, we show the existence of value and then characterize it as the unique viscosity solution of the associated Hamilton-Jacobi-Isaacs (HJI for short) equation. To achieve this, we follow a dynamic programming method and hence we differ from Berkovitz's approach for finite horizon problems [4]. We also establish the existence of a saddle point for the game by constructing it in a feedback form.
The rest of this paper is organized as follows. The description of the game and some important preliminary results are given in Section 2. In Section 3, we deal with dynamic programming and characterization of the value function. Section 4 contains the construction of saddle point equilibrium. We conclude the paper with some remarks in Section 5.
2 Preliminaries
Let the compact metric spaces U and V be the control sets for players 1 and 2 respectively. For 0 < s < t , let
The sets  [s, t] and
[s, t] and  [s, t] are called the control spaces on the time interval [s, t] for players 1 and 2 respectively. The functions u(·) Î
[s, t] are called the control spaces on the time interval [s, t] for players 1 and 2 respectively. The functions u(·) Î  [s, t] and v(·) Î
[s, t] and v(·) Î  [s, t] are referred to as the precise or usual controls (or simply 'controls') on the time interval [s, t] for players 1 and 2 respectively. We denote
[s, t] are referred to as the precise or usual controls (or simply 'controls') on the time interval [s, t] for players 1 and 2 respectively. We denote  [0, ¥) and
[0, ¥) and  [0, ¥) by
[0, ¥) by  and
and  respectively.
respectively.
Let  , a real Hilbert space, be the state space. Let x(t) Î
, a real Hilbert space, be the state space. Let x(t) Î  denote the state at time t. The state x(·) with initial point x0Î
denote the state at time t. The state x(·) with initial point x0Î  is governed by the following controlled semi-linear evolution equation:
is governed by the following controlled semi-linear evolution equation:
where f:  × U × V ®
× U × V ®  , u(·) Î
, u(·) Î  , v(·) Î
, v(·) Î  and A :
and A :  É D(A) ®
É D(A) ®  is the generator of a contraction semigroup {S(t)} on
is the generator of a contraction semigroup {S(t)} on  . We assume that
. We assume that
(A1) The function f is continuous and, for all x, y Î  and (u, v) Î U × V,
and (u, v) Î U × V,
Under the assumption (A1), for each u(·) Î  , v(·) Î
, v(·) Î  and x0Î
and x0Î  , (2.1) has a unique global mild solution (see e.g., Proposition 5.3, p. 66 in [10]) which is denoted by f(·, x0, u(·), v(·)) and is referred to as the trajectory corresponding to the pair of controls (u(·), v(·)) with initial point x0.
, (2.1) has a unique global mild solution (see e.g., Proposition 5.3, p. 66 in [10]) which is denoted by f(·, x0, u(·), v(·)) and is referred to as the trajectory corresponding to the pair of controls (u(·), v(·)) with initial point x0.
Following Warga [13], we now describe relaxed controls and relaxed trajectories. Let
where  (U) and
(U) and  (V) are the spaces of probability measures on U and V respectively with the topology of weak convergence. The sets
(V) are the spaces of probability measures on U and V respectively with the topology of weak convergence. The sets 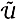 [s, t] and
[s, t] and 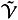 [s, t] are called the relaxed control spaces on the time interval [s, t] for players 1 and 2 respectively. These relaxed control spaces, equipped with weak* topology, are compact metric spaces. The relaxed control spaces
[s, t] are called the relaxed control spaces on the time interval [s, t] for players 1 and 2 respectively. These relaxed control spaces, equipped with weak* topology, are compact metric spaces. The relaxed control spaces 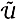 [0, ¥) and
[0, ¥) and 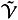 [0,¥) are denoted by
[0,¥) are denoted by 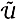 and
and 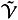 respectively. Note that by identifying u(·) and v(·) by du(·) and dv(·) respectively, precise controls can be treated as relaxed controls.
respectively. Note that by identifying u(·) and v(·) by du(·) and dv(·) respectively, precise controls can be treated as relaxed controls.
For m(·) Î 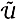 and n(·) Î
and n(·) Î 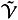 , the state equation in the relaxed control framework is given by
, the state equation in the relaxed control framework is given by
Since f satisfies (A1), it follows that  also satisfies (A1) with u Î U , v Î V replaced respectively by m Î
also satisfies (A1) with u Î U , v Î V replaced respectively by m Î  (U) , n Î
(U) , n Î  (V). Therefore for each x0Î
(V). Therefore for each x0Î  , m(·) Î
, m(·) Î 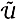 and n(·) Î
and n(·) Î 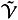 , the existence and uniqueness of a global mild solution to (2.2) follows analogously. This solution is called a relaxed trajectory and is denoted by y(·, x0, m(·), n(·)).
, the existence and uniqueness of a global mild solution to (2.2) follows analogously. This solution is called a relaxed trajectory and is denoted by y(·, x0, m(·), n(·)).
We now begin the description of the game by defining the strategies of players. A strategy for player 1 is a sequence P = {Pn} of partitions of [0, ¥), with ||Pn|| ® 0 , and a sequence G = {Gn} of instructions described as follows:
Let Pn = {0 = t0 < t1 < ¼}. The nth stage instruction Gn is given by a sequence  , where Gn,1Î
, where Gn,1Î  [t0, t1) and for j > 2,
[t0, t1) and for j > 2,
Similarly, a strategy for player 2 is a sequence  = {
= { n} of partitions of [0, ¥), with ||
n} of partitions of [0, ¥), with || n|| ® 0 , and a sequence D = {Dn} of instructions described as follows:
n|| ® 0 , and a sequence D = {Dn} of instructions described as follows:
Let
n = {0 = s0 < s1 < ¼}. The nth stage instruction Dn is given by a sequence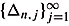 , where Dn,1Î
, where Dn,1Î 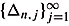 [s0, s1) and for j > 2,
[s0, s1) and for j > 2,
We suppress the dependence of the sequence of partitions on a strategy and, by an abuse of notation, denote a strategy by G or D. In what follows G stands for a strategy for player 1 and D stands for a strategy for player 2.
Note that a pair (Gn, Dn) of nth stage instructions uniquely determines a pair (un(·),vn(·)) Î  ×
×  as follows. Let
as follows. Let  n = {0 = r0 < r1 < ¼} be the common refinement of Pn and
n = {0 = r0 < r1 < ¼} be the common refinement of Pn and  n. The control functions un(·) and vn(·) are given by the sequences (un,1(·), un,2(·),¼) and (vn,1(·), vn,2(·),¼) respecively, where un,j(·) Î
n. The control functions un(·) and vn(·) are given by the sequences (un,1(·), un,2(·),¼) and (vn,1(·), vn,2(·),¼) respecively, where un,j(·) Î  [rj1, rj) and vn,j(·) Î
[rj1, rj) and vn,j(·) Î  [rj1, rj). Let u
[rj1, rj). Let u (·), v
(·), v (·) denote respectively the restrictions of un(·), vn(·) to the interval [r0, rj).
(·) denote respectively the restrictions of un(·), vn(·) to the interval [r0, rj).
On [r0, r1), set un,1(·) = Gn,1 and vn,1(·) = Dn,1.
Let j > 1. If rj = ti, then on [rj, rj+1) we take un,j+1(·) = Gn,i+1(u (·),v
(·),v (·)) and vn,j+1(·) = Dn,l+1(u
(·)) and vn,j+1(·) = Dn,l+1(u (·), v
(·), v (·)) , where l is the greatest integer such that sl < rj and sl = rj¢.
(·)) , where l is the greatest integer such that sl < rj and sl = rj¢.
If rj = sm, then on [rj, rj+1) take un,j+1(·) = Gn,k+1(u (·),v
(·),v (·)) and vn,j+1(·) = Dn,m+1(u
(·)) and vn,j+1(·) = Dn,m+1(u (·),v
(·),v (·)) , where k is the greatest integer such that tk < rj and tk = rm¢.
(·)) , where k is the greatest integer such that tk < rj and tk = rm¢.
The pair (un(·),vn(·)) determined this way is called the nth stage outcome of the pair (G, D) of strategies.
Let c:  × U × V ®
× U × V ®  be the running payoff function and let l > 0 be the discount factor. We assume that
be the running payoff function and let l > 0 be the discount factor. We assume that
(A2) The function c is bounded, continuous and, for all x, y Î  and (u, v) Î U × V
and (u, v) Î U × V
|c(x, u, v) c(y, u, v)|< K||x y||.
Without any loss of generality, we take c to be nonnegative. For x0Î  and (u(·), v(·)) Î
and (u(·), v(·)) Î  ×
×  , let f0(·, x0, u(·), v(·)) denote the solution of
, let f0(·, x0, u(·), v(·)) denote the solution of
Let  (·, x0, u(·), v(·)) denote
(·, x0, u(·), v(·)) denote  . The running cost
. The running cost  in the relaxed framework is defined by
in the relaxed framework is defined by
Note that  satisfies (A2) with (u, v) Î U × V replaced by (m, n) Î
satisfies (A2) with (u, v) Î U × V replaced by (m, n) Î  (U) ×
(U) ×  (V). Now the relaxed trajectory
(V). Now the relaxed trajectory 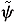 (·, x0, m(·), n(·)) is interpreted in an analogous way. Let
(·, x0, m(·), n(·)) is interpreted in an analogous way. Let
The next result is helpful in defining the concept of motion in the game. To achieve this, we make the following assumption.
(A3) The semigroup {S(t)} is compact.
Lemma 2.1. Assume (A1)-(A3). Let {(un(·), vn(·)} be the sequence of nth stage outcomes corresponding to a pair (G, D) of strategies and {x0n}, a sequence converging to x0. Then the sequence { (·, x0n, un(·), vn(·))} of nth stage trajectories is relatively compact in C([0, ¥);
(·, x0n, un(·), vn(·))} of nth stage trajectories is relatively compact in C([0, ¥);
Proof. Let  n(·) =
n(·) =  (·, x0n, un(·), vn(·)), hn(·) =
(·, x0n, un(·), vn(·)), hn(·) =  (·,
(·,  n(·), un(·), vn(·)),
n(·), un(·), vn(·)), 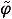 n(·) =
n(·) = 
It is enough to show that for each T > 0, the sequence of nth stage trajectories, when restricted to [0, T], is relatively compact in C([0, T]; 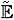 ). Fix T > 0. Let Q : L2([0, T];
). Fix T > 0. Let Q : L2([0, T]; 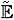 ) ® C([0, T];
) ® C([0, T]; 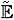 ) be the operator defined by
) be the operator defined by
Then
n (·) = n (·) + Q(hn(·))(·).
n (·) + Q(hn(·))(·).
Since the sequence
n(·) converges to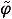 (·) uniformly, it is sufficient to prove the relative compactness of {Q(hn(·))(·) }. To achieve this we show that the operator Q is compact. This will imply the desired result since, by (A1) and (A2), {hn(·)} is bounded in L2([0, T];
(·) uniformly, it is sufficient to prove the relative compactness of {Q(hn(·))(·) }. To achieve this we show that the operator Q is compact. This will imply the desired result since, by (A1) and (A2), {hn(·)} is bounded in L2([0, T]; 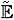 ). Let {hk(·)} be a sequence in the unit ball of L2([0, T];
). Let {hk(·)} be a sequence in the unit ball of L2([0, T]; 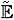 ). We need to show that {Qhk(·)(·)} is relatively compact. By Arzela-Ascoli theorem, the proof will be complete if we establish the pointwise relative compactness and equicontinuity of the sequence {Qhk(·)(·)}.
). We need to show that {Qhk(·)(·)} is relatively compact. By Arzela-Ascoli theorem, the proof will be complete if we establish the pointwise relative compactness and equicontinuity of the sequence {Qhk(·)(·)}.
Let t Î [0, T]. We first prove the relative compactness of {Qhk(·)(t)}. This is trivial if t = 0. So we assume that t > 0. Let 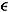 > 0 be given. Since {hk(·)} is in the unit ball, there exists d Î (0, t) such that for all k
> 0 be given. Since {hk(·)} is in the unit ball, there exists d Î (0, t) such that for all k
Note that
where
Since  (d) is compact and {yk} is bounded in
(d) is compact and {yk} is bounded in 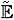 , there exist y1,¼, ym Î
, there exist y1,¼, ym Î 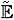 such that
such that  . Therefore {Q(hk(·))(t)} Ì
. Therefore {Q(hk(·))(t)} Ì  B(yi,
B(yi, 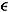 ). Thus we have established the relative compactness of {Q(hk(·))(t)}.
). Thus we have established the relative compactness of {Q(hk(·))(t)}.
Next we prove the equicontinuity of {Q(hk(·))(t)}. Let t, s Î [0, T] and s < t. The case when s = 0 is trivial. Assume that 0 < s. Now for d small enough,
Q(hk(·))(t) Q(hk(·))(s) = I1 + I2 + I3 ;
where
By Cauchy-Schwartz inequality, we get
where C is a constant independent of k. The map t 
 (t) is continuous in the uniform operator topology on (0, ¥) because {S(t)} is a compact semigroup. Thus from the above, we get the equicontinuity of {Q(hk(·))(·)}.
(t) is continuous in the uniform operator topology on (0, ¥) because {S(t)} is a compact semigroup. Thus from the above, we get the equicontinuity of {Q(hk(·))(·)}.
We now define the concept of motion. Let {x0n} be a sequence converging to x0 and let {(un(·), vn(·))} be the sequence of nth stage outcomes corresponding to the pair of strategies (G, D). By Lemma 2.1, the sequence of nth stage trajectories { (·, x0n, un(·), vn(·))} is relatively compact in C([0, ¥);
(·, x0n, un(·), vn(·))} is relatively compact in C([0, ¥); 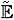 ). We define a motion to be the local uniform limit of a subsequence of a sequence of nth stage trajectories.
). We define a motion to be the local uniform limit of a subsequence of a sequence of nth stage trajectories.
A motion is denoted by  [·, x0, G, D]. Let
[·, x0, G, D]. Let  [·, x0, G, D] denote the set of all motions corresponding to (G, D) which start from x0. A motion
[·, x0, G, D] denote the set of all motions corresponding to (G, D) which start from x0. A motion  [·, x0, G, D] can be written as
[·, x0, G, D] can be written as
Let F0[·, x0, G, D], F[·,x0, G, D] respectively denote the set of all f0[·, x0, G, D] , f[·, x0, G, D]. The set of all  [t, x0, G, D] where
[t, x0, G, D] where  [·, x0, G, D] runs over
[·, x0, G, D] runs over  [·, x0, G, D] is denoted by
[·, x0, G, D] is denoted by  [t, x0, G, D]. Similarly, the sets F0[t, x0, G, D] and F[t, x0, G, D] are defined. Since c > 0, for any f0[·] = f0[·, x0, G, D], lim
[t, x0, G, D]. Similarly, the sets F0[t, x0, G, D] and F[t, x0, G, D] are defined. Since c > 0, for any f0[·] = f0[·, x0, G, D], lim f0[t] exists and is denoted by f0[¥, x0, G, D]. As above, F0[¥, x0, G, D] is the set of all f0[¥, x0, G, D]. If the initial point
f0[t] exists and is denoted by f0[¥, x0, G, D]. As above, F0[¥, x0, G, D] is the set of all f0[¥, x0, G, D]. If the initial point  of the augmented component f0(·) of the trajectory is not zero, then the corresponding extended trajectory is denoted by
of the augmented component f0(·) of the trajectory is not zero, then the corresponding extended trajectory is denoted by
By  (·, t0,
(·, t0,  0, u(·), v(·)), we mean the trajectory
0, u(·), v(·)), we mean the trajectory
Similarly, the relaxed trajectories 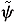 (·,
(·,  0, m(·), n(·)) and
0, m(·), n(·)) and 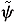 (·, t0,
(·, t0,  0, m(·), n(·)) are defined. To complete the description of the game, we need to define the payoff. The payoff associated with the pair of strategies (G, D) is set valued and is given by
0, m(·), n(·)) are defined. To complete the description of the game, we need to define the payoff. The payoff associated with the pair of strategies (G, D) is set valued and is given by
P(x0,G, D) = F0[¥, x0, G, D].
The player 1 tries to choose G so as to maximize all elements of P(x0, G, D) and player 2 tries to choose D so as to minimize all elements of P(x0, G, D). This gives rise to the upper and lower value functions which are respectively given by
(If {Da} is a collection of subsets of  , then supaDa : = supÈaDa and infaDa : = infÈaDa.) Therefore the upper and lower value functions are real valued functions. Clearly W+> W. If W+ = W = W, then we say that the game has a value and W is referred to as the value function.
, then supaDa : = supÈaDa and infaDa : = infÈaDa.) Therefore the upper and lower value functions are real valued functions. Clearly W+> W. If W+ = W = W, then we say that the game has a value and W is referred to as the value function.
A pair of strategies (G*, D*) is said to constitute a saddle point for the game starting from x0, if for all (G, D),
P(x0, G, D*) <P(x0, G*, D*) < P(x0,G*, D).
(By D1< D2 we mean r1< r2 for all (r1, r2) Î D1 × D2.) Note that if (G*, D*) is a saddle point, then P(x0, G*, D*) is singleton and
W+(x0) = W(x0) = P(x0, G*, D*).
By a constant component strategy Gc for player 1 corresponding to the sequence {un(·)} of controls, we mean a strategy where, for each n, the player 1 chooses the open loop control un(·) at the nth stage. If un(·) º u(·) for all n, then this strategy is referred to as a constant strategy corresponding to the open loop control u(·). Constant component strategies and constant strategies for player 2 are defind in a similar fashion.
In view of Lemma 2.1, the following result may be obtained by modifying the arguments in [1]. Hence we omit the proof.
Lemma 2.2. Assume (A1)-(A3).
(i) Let x0Î
be a constant strategy corresponding to (·) Î,
and let D be any strategy for player 2. Then for any motion
[·, x0, , D], there exists a relaxed control n(·) Î
such that
Conversely, given any relaxed trajectory
, D] such that (2.4) holds.(·, x0,
(·), n(·)), there exists a motion
[·, x0,
(ii) For any 0 < t < ¥ and constant strategy
, the set ÈD[t, x0, , D] is compact.
Analogous results hold with
, D replaced respectively by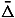 , G.
, G.
3 Dynamic programming and viscosity solution
Before proving the dynamic programming inequalities, we show the continuity properties of W+ and W. To this end, we first compare the trajectories with different initial points.
Lemma 3.1. Assume (A1) and (A2). For any a Î (0, 1] Ç(0, 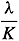 ), there exists Ca > 0 such that
), there exists Ca > 0 such that
|f0(t, x0, u(·), v(·)) f0(t, y0, u(·), v(·))|< Ca||x0 y0 ||a,
for all t > 0, x0, y0Î  and (u(·),v(·)) Î
and (u(·),v(·)) Î  ×
×
Proof. Let  1(·) =
1(·) =  (·, x0, u(·), v(·)) and
(·, x0, u(·), v(·)) and  2(·) =
2(·) =  (·, y0, u(·), v(·)). Obviously,
(·, y0, u(·), v(·)). Obviously,
From this, it follows by using Gronwall inequality that
||f1(t) f2(t)||<||x0 y0||eKt.
We have
Therefore for any a Î (0,1] Ç (0, 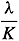 ), we obtain
), we obtain
Henceforth we take a Î (0,1] Ç (0, 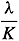 ) and Ca =
) and Ca =  .
.
Lemma 3.2. Assume (A1)-(A3). Let x0, y0Î  and (G, D) a pair of strategies. Then for any motion
and (G, D) a pair of strategies. Then for any motion  [·, x0, G, D], there is a motion
[·, x0, G, D], there is a motion  [·, y0, G, D] with the property that
[·, y0, G, D] with the property that
|f0[¥, x0, G, D] f0[¥, y0, G, D]| < Ca||x0 y0||a.
Proof. Consider a motion  [·, x0, G, D] and without any loss of generality let it be the local uniform limit of a sequence {
[·, x0, G, D] and without any loss of generality let it be the local uniform limit of a sequence { (·, x0n, un(·), vn(·))} of nth stage trajectories. Let
(·, x0n, un(·), vn(·))} of nth stage trajectories. Let  [·, y0, G, D] be the local uniform limit of a subsequence {
[·, y0, G, D] be the local uniform limit of a subsequence { (·, y0, unk(·), vnk(·))} of the sequence {
(·, y0, unk(·), vnk(·))} of the sequence { (·, y0, un(·), vn(·))} of nth stage trajectories. From Lemma 3.1, it follows that for t > 0,
(·, y0, un(·), vn(·))} of nth stage trajectories. From Lemma 3.1, it follows that for t > 0,
|f0(t, x0nk, unk(·), vnk(·)) f0(t, y0, unk(·), vnk(·))| < Ca|| x0nk y0||a.
Letting k ® ¥, we get
|f0[t, x0,G, D] f0[t, y0, G, D]| < Ca||x0 y0||a.
The required result now follows by lettiong t  ¥ in the above inequality.
¥ in the above inequality.
Lemma 3.3. Assume (A1)-(A3). The upper and lower value functions are bounded and Holder continuous on
with exponent a Î (0,1] Ç (0,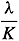 ) .
) .
Proof. The boundedness of c gives the boundedness of W+ and W. The Holder continuity of W+ and W follow immediately from Lemma 3.2.
Having established the continuity of W+ and W, we now prove dynamic programming inequalities.
Lemma 3.4. Assume (A1)-(A3). For x0Î  and 0 < t < ¥,
and 0 < t < ¥,
Proof. Take an arbitrary  (·) Î
(·) Î  and keep it fixed. It is enough to show that
and keep it fixed. It is enough to show that
Let E0 = { :
:  =
= 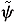 (t, x0,
(t, x0,  (·), n(·)) for some n(·) Î
(·), n(·)) for some n(·) Î 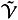 } and
} and 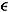 > 0. For any
> 0. For any
Therefore for each  Î E0, there exists a strategy G(
Î E0, there exists a strategy G( ) such that for all D,
) such that for all D,
Let d( ) > 0 be such that whenever ||
) > 0 be such that whenever ||
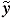 || < d(
|| < d( ) ,
) ,
Now E0 is compact (by Lemma 2.2 (ii)) and the collection {B( , d(
, d( )) :
)) :  Î E0} is an open cover for E0. Let
Î E0} is an open cover for E0. Let  1,
1,  2, ¼,
2, ¼,  k Î E0 be such that E0Ì
k Î E0 be such that E0Ì  B(
B( i, d(
i, d( i)) .
i)) .
In order to prove (3.3), it is sufficient to construct a strategy 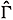 with the property that for all D and all motions
with the property that for all D and all motions  [·, x0,
[·, x0, 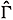 , D],
, D],
We first define 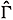 . Let P¢(i) = {
. Let P¢(i) = { } be the sequence of partitions associated with G(
} be the sequence of partitions associated with G( i); i = 1, 2,¼, k. Let
i); i = 1, 2,¼, k. Let  be the refinement of
be the refinement of  . Let Pn be the partition of [0, ¥) such that t is a partition point, [0, t] is partitioned into n equal intervals and the interval [t, ¥) is partitioned by the translation of
. Let Pn be the partition of [0, ¥) such that t is a partition point, [0, t] is partitioned into n equal intervals and the interval [t, ¥) is partitioned by the translation of  to the right by t. We take P = {Pn} to be the sequence of partitions associated with
to the right by t. We take P = {Pn} to be the sequence of partitions associated with 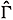 = {
= { n}. Let Pn = {0 = t0 < t1 < ¼}.
n}. Let Pn = {0 = t0 < t1 < ¼}.
We now define
n = ( n,1,
n,1,  n, 2, ¼).
n, 2, ¼).
For i = 1,¼, n, define  n,i to be the map which always selects
n,i to be the map which always selects  (·) on [ti1, ti).
(·) on [ti1, ti).
For i > n + 1 , we define 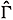 n,i as follows. Let u(·) Î
n,i as follows. Let u(·) Î  [t0, ti-1), v(·) Î
[t0, ti-1), v(·) Î  [t0, ti-1) and
[t0, ti-1) and  (·) =
(·) =  (·, x0, u(·), v(·)). If
(·, x0, u(·), v(·)). If  (t) Ï
(t) Ï  B(
B( i, d(
i, d( i)), then we define
i)), then we define 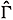 n,i(u(·), v(·)) to be a fixed element u0Î U.
n,i(u(·), v(·)) to be a fixed element u0Î U.
Let  (t) Î
(t) Î  B(
B( i, d(
i, d( i)) and j the least integer such that
i)) and j the least integer such that  (t) Î B(
(t) Î B( j, d(
j, d( j)). We then take
j)). We then take 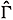 n,i to be Gn(
n,i to be Gn( j) in the following sense.
j) in the following sense.
Let  = {0 =
= {0 =  <
<  < ¼}. Let
< ¼}. Let  (·) be the control that Gn,1(
(·) be the control that Gn,1( j) selects on [
j) selects on [ ,
,  ). For any i such that n < i < n+i1, the map
). For any i such that n < i < n+i1, the map 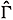 n,i selects
n,i selects  (·) on [ti1 , ti). If
(·) on [ti1 , ti). If  (·) denotes the control that Gn,2(
(·) denotes the control that Gn,2( j) selects on [
j) selects on [ ,
,  ), then for i with n + i1 < i < n + i2, the map
), then for i with n + i1 < i < n + i2, the map  n,i selects
n,i selects  (·) on [ti1 , ti). Now the definition of
(·) on [ti1 , ti). Now the definition of  is complete.
is complete.
It remains to prove (3.5). To this end, let D be any strategy for player 2,  [·, x0,
[·, x0,  , D] a motion and {(un(·), vn(·))} the sequence of nth stage outcomes corresponding to (
, D] a motion and {(un(·), vn(·))} the sequence of nth stage outcomes corresponding to ( , D). Without any loss of generality, we assume that this motion is the uniform limit of a sequence {
, D). Without any loss of generality, we assume that this motion is the uniform limit of a sequence { (·, x0n, un(·), vn(·))} of nth stage trajectories. Since un(·) =
(·, x0n, un(·), vn(·))} of nth stage trajectories. Since un(·) =  (·) on [t0, tn] = [0, t],
(·) on [t0, tn] = [0, t], 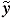 :=
:=  [t, x0,
[t, x0, 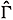 , D)] Î E0 . Let j be the smallest integer such that
, D)] Î E0 . Let j be the smallest integer such that 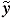 Î B(
Î B( j, d(
j, d( j)) and
j)) and 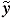 n :=
n :=  (t, x0n, un(·), vn(·)). Since
(t, x0n, un(·), vn(·)). Since 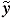 n ®
n ® 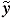 , for n large enough,
, for n large enough, 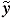 n Î B(
n Î B( j, d(
j, d( j)).
j)).
Let Dc = {D } be the constant component strategy corresponding to {vn(·)} with the associated sequence of partitions same as that of D restricted to [t, ¥) and translated back to [0, ¥). Therefore for large n, the pair (un(·), vn(·)) is the outcome of (Gn(
} be the constant component strategy corresponding to {vn(·)} with the associated sequence of partitions same as that of D restricted to [t, ¥) and translated back to [0, ¥). Therefore for large n, the pair (un(·), vn(·)) is the outcome of (Gn( j), D
j), D ).
).
Hence by (3.4), we obtain
By arguing analogously, we can prove the next result.
Lemma 3.5 Assume (A1)-(A3). For x0Î  and 0 < t < ¥,
and 0 < t < ¥,
The strict inequality can hold in (3.2) and (3.6). The following example illustrates this fact for (3.6).
Example:  =
=  , U = V = [1, 1], A = 0, f(x, u, v) = u + v, c(x, u, v) = c(x), a bounded, nonnegative and Lipschitz continuous function.
, U = V = [1, 1], A = 0, f(x, u, v) = u + v, c(x, u, v) = c(x), a bounded, nonnegative and Lipschitz continuous function.
Note that W(x) = c(x), since H+(x, p) = H(x, p) = c(x). Furthermore take c such that c(x) = |x| on [2,2]. Let x0 = 0. For 0 < t < 1, we get
Using dynamic programming inequalities, we next show that the upper (resp. lower) value function is a viscosity sub- (resp. super) solution of the HJI lower (resp. upper) equation. The HJI lower and upper equations are, respectively, the following:
where for x, p Î  ,
,
We take the definition of viscosity solution given by Crandall and Lions in [5] and [6]. We first recall their definition of viscosity solution. To this end, let
S0 : = {Y Î C1(
0 : = {g Î C1() | Y is weakly sequentially lower semi-continuous and A*DY Î C(
)}
) | g(x) = r(||x||) for some r Î C1(
) with r¢ > 0 }.
Definition 3.6. An upper (resp. lower) semi-continuous function W: ®
®  is called a viscosity sub-(reps. super) solution of (3.7) (resp. (3.8)) if whenever W Y g ( Y Î S0, g Î
is called a viscosity sub-(reps. super) solution of (3.7) (resp. (3.8)) if whenever W Y g ( Y Î S0, g Î  0) has a local maximum (resp. minimum) at x Î
0) has a local maximum (resp. minimum) at x Î  , we have
, we have
If W Î C(
) is both a viscosity subsolution and a viscosity supersolution of an equation, then we call it a viscosity solution.Lemma 3.7. Assume (A1)-(A3). The upper value function W+ is a viscosity subsolution of (3.7) and the lower value function W is a viscosity supersolution of (3.8).
Proof. We prove that W+ is a viscosity subsolution of (3.7). The other part can be proved in a similar fashion. Let Y Î S0, g Î  0 and let x0 be a local maximum of W+ Y g. Without any loss of generality we assume that W+(x0) = Y(x0) and g(x0) = 0.
0 and let x0 be a local maximum of W+ Y g. Without any loss of generality we assume that W+(x0) = Y(x0) and g(x0) = 0.
We need to show that
Fix an arbitrary  Î V. It is enough to show that
Î V. It is enough to show that
Let 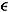 > 0. By Lemma 3.5, for each t > 0, there exists mt(·) Î
> 0. By Lemma 3.5, for each t > 0, there exists mt(·) Î 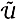 such that
such that
We denote 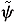 (·, x0, mt(·),
(·, x0, mt(·),  ) by
) by 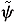 t(·) =
t(·) = 
Hence for small enough t,
This implies that for t small enough,
It can be shown that (see e.g., Lemmas 3.3, 3.4 in pp. 240-241, [10]) for t small enough,
Combining (3.10), (3.11), (3.12), (3.13) and letting t ® 0, we get
Since 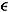 is arbitrary, we get the required inequality (3.9).
is arbitrary, we get the required inequality (3.9).
We next show the existence of value and characterize it as the unique viscosity solution of the associated HJI equation. To achieve this we make the following assumption.
(A0) There exists a positive symmetric linear operator B :  ®
®  and a constant c0 such that R(B) Ì D(A*) and (A*+c0I)B > I.
and a constant c0 such that R(B) Ì D(A*) and (A*+c0I)B > I.
Let  = áBx, xñ and
= áBx, xñ and  , the class of all bounded functions W:
, the class of all bounded functions W:  ®
®  with the property that for all x, y Î
with the property that for all x, y Î  , |W(x) W(y) | < w(|x y|B) for some modulus w. We shall prove the characterization in this class
, |W(x) W(y) | < w(|x y|B) for some modulus w. We shall prove the characterization in this class  . Note that the class F is contained in the class of bounded uniformly continuous functions.
. Note that the class F is contained in the class of bounded uniformly continuous functions.
We also require the so called Isaacs min-max condition. By 'local game' at ( ,
, 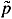 ) Î
) Î 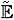 ×
× 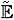 , we mean the zero-sum static game, in which player 1 is the minimizer and player 2 the maximizer, with payoff x0 + á p ,f(x, u, v)ñ p0c(x, u, v). The Isaacs condition is that for each (
, we mean the zero-sum static game, in which player 1 is the minimizer and player 2 the maximizer, with payoff x0 + á p ,f(x, u, v)ñ p0c(x, u, v). The Isaacs condition is that for each ( ,
, 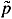 ) Î
) Î 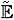 ×
× 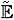 , the associated local game has a saddle point. In other words, we assume that
, the associated local game has a saddle point. In other words, we assume that
(A4) For all ( ,
, 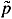 ) Î
) Î 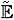 ×
× 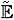 ,
,
Remark 3.8. In (A4) it is enough to take p0 = ±1. For proving the existence of value, we only need (A4) with p0 = +1. But in the next Section we want p0 = ±1.
Theorem 3.9. Assume (A0)-(A4). The differential game has a value and this value function is the unique viscosity solution of (3.7) (or (3.8)) in the class
.Proof. We first show that W+ and W belong to  . Boundedness of W+ and W has been proved in Lemma 3.3.
. Boundedness of W+ and W has been proved in Lemma 3.3.
Let x0, y0, u(·), v(·), f1(·), f2(·),  (·),
(·),  (·) be as in Lemma 3.1. Let
(·) be as in Lemma 3.1. Let 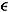 > 0. Since c is bounded, there exists T = T(
> 0. Since c is bounded, there exists T = T(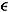 ) large enough such that
) large enough such that
It can be shown that (see e.g., Lemma 2.5, p. 233 in [10])
for some constant C. Therefore, we obtain
This implies that we can choose d = d(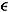 ) > 0 such that |
) > 0 such that | (¥)
(¥)  (¥)| <
(¥)| < 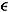 whenever |x0 y0|B < d. Hence there is a modulus w with the property that |
whenever |x0 y0|B < d. Hence there is a modulus w with the property that | (¥)
(¥)  (¥)|< w(|x0 y0|B). Now we can mimic the arguments in Lemmas 3.2 and 3.3 to get the fact that the upper and lower value functions are in the class
(¥)|< w(|x0 y0|B). Now we can mimic the arguments in Lemmas 3.2 and 3.3 to get the fact that the upper and lower value functions are in the class  .
.
Under (A4), both (3.7) and (3.8) coincide. Therefore W+ and W are respectively sub- and super solutions of this equation (HJI equation). Now, we have the comparison result for the HJI equation in the class  (see [6] and Chapter 6 in [10]). Therefore W+< W. But we always have W+> W. Hence W+ = W. The uniqueness follows from the same comparison result.
(see [6] and Chapter 6 in [10]). Therefore W+< W. But we always have W+> W. Hence W+ = W. The uniqueness follows from the same comparison result.
4 Saddle point
Under the Isaacs condition (A4), we prove the existence of a saddle point for the game. To achieve this we use only the dynamic programming inequalities in Section 3. We don't use the fact that the game has a value.
Fix an arbitrary x0Î  . Let r0 = W(x0) and r0 = W+(x0). Consider the sets
. Let r0 = W(x0) and r0 = W+(x0). Consider the sets
Clearly (0, ) Î C(r0) Ç C(r0) and, by the continuity of W+ and W, the sets C(r0) and C(r0) are closed.
) Î C(r0) Ç C(r0) and, by the continuity of W+ and W, the sets C(r0) and C(r0) are closed.
The next two results are very crucial in constructing the optimal strategies. These results follow respectively from Lemmas 3.4 and 3.5.
Lemma 4.1. Assume (A1)-(A3). Let (t,  ) Î C(r0) and d > 0. Then for any u(·) Î
) Î C(r0) and d > 0. Then for any u(·) Î 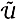 [t, t + d], there exists n(·) Î
[t, t + d], there exists n(·) Î 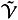 [t, t + d] such that (t + d,
[t, t + d] such that (t + d,
Proof. Suppose that the result is not true. Then there exist (t,  ) Î C(r0), d > 0 and u(·) Î
) Î C(r0), d > 0 and u(·) Î 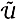 [t, t + d] such that for all n(·) Î
[t, t + d] such that for all n(·) Î 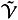 [t, t + d], (t + d,
[t, t + d], (t + d, 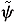 (t + d, t,
(t + d, t,  , u(·), n(·))) Ï C(r0).
, u(·), n(·))) Ï C(r0).
That is,
This together with Lemma 2.2 (ii) implies that
Applying Lemma 3.4, we obtain
x0 + eltW(x) > r0.
This contradicts the fact that (t,  ) Î C(r0).
) Î C(r0).
In an analogous manner, by using Lemmas 2.2 (ii) and 3.5, we can establish the next result.
Lemma 4.2. Assume (A1)-(A3). Let (t,  ) Î C(r0) and d > 0. Then for any v(·) Î
) Î C(r0) and d > 0. Then for any v(·) Î 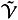 [t, t + d], there exists m(·) Î
[t, t + d], there exists m(·) Î 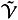 [t, t + d] such that (t + d,
[t, t + d] such that (t + d, 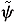 (t + d, t,
(t + d, t,
We now define extremal strategies and, using Lemmas 4.1 and 4.2, show that they constitute a saddle point. Any sequence F = {Fn}, Fn : [0, ¥) × [0, ¥) ×  ® U, defines a strategy G = G(F) for player 1 in the following way. We take the nth stage partition Pn = {0 = t0 < t1 < ¼} to be the one which divides [0, ¥) into subintervals of length
® U, defines a strategy G = G(F) for player 1 in the following way. We take the nth stage partition Pn = {0 = t0 < t1 < ¼} to be the one which divides [0, ¥) into subintervals of length  . Gn,1º Fn(0,
. Gn,1º Fn(0,  ). Let j > 2, (u(·), v(·)) Î
). Let j > 2, (u(·), v(·)) Î 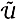 [t0, tj1) ×
[t0, tj1) × 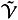 [t0, tj1), and
[t0, tj1), and  (·) =
(·) =  (·, x0, u(·), v(·)). We define Gn,j(u(·), v(·)) = Fn(tj1,
(·, x0, u(·), v(·)). We define Gn,j(u(·), v(·)) = Fn(tj1,  (tj1)).
(tj1)).
For any sequence G = {Gn}, where Gn : [0, ¥) × [0, ¥) ×  ® V, a strategy D = D(G) for player 2 is defined in an analogous manner. The strategies G(F) and D(G) are referred to as feedback strategies associated with F and G respectively. The optimal strategies Ge and De which we define now are of this feedback form. That is, Ge = G(Fe) and De = D(Ge). We define the sequence Ge = {Gen} and the definition of Fe = {Fen} is similar.
® V, a strategy D = D(G) for player 2 is defined in an analogous manner. The strategies G(F) and D(G) are referred to as feedback strategies associated with F and G respectively. The optimal strategies Ge and De which we define now are of this feedback form. That is, Ge = G(Fe) and De = D(Ge). We define the sequence Ge = {Gen} and the definition of Fe = {Fen} is similar.
Let (t,  ) Î [0, ¥) × [0, ¥) ×
) Î [0, ¥) × [0, ¥) ×  . If (t,
. If (t,  ) Î C(r0), then we define Gen(t,
) Î C(r0), then we define Gen(t,  ) to be a fixed element v0Î V. Let (t,
) to be a fixed element v0Î V. Let (t,  ) Ï C(r0) . Let Ct(r0) = {
) Ï C(r0) . Let Ct(r0) = { : (t,
: (t,  ) Î C(r0) } and
) Î C(r0) } and 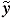 Î Ct(r0) be such that ||
Î Ct(r0) be such that ||
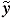 || <
|| <  (
(  , Ct(r0)) . We then define Gen(t,
, Ct(r0)) . We then define Gen(t,  ) to be v*, where (u*, v*) is a saddle point for the local game at (
) to be v*, where (u*, v*) is a saddle point for the local game at ( ,
, 
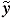 ).
).
The next result compares trajectories governed by two special pairs controls. The proof may be obtained by modifying the proof of the analogous finite dimensional result in [9].
Lemma 4.3. Assume (A1)-(A4). Let
, belong to a bounded subset M of [0, ¥) × , t Î [0,T), m(·) Î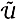 [t,T] and n(·) Î
[t,T] and n(·) Î 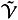 [t,T]. Let (u*,v*) be a saddle point for the local game at (
[t,T]. Let (u*,v*) be a saddle point for the local game at ( ,
, 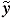 ). Let
). Let  (·) =
(·) = 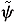 (·, t, , m(·), v*),
(·, t, , m(·), v*), 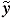 (·) =
(·) = 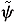 (·, t, , u*, n(·)),
(·, t, , u*, n(·)), 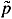 (·) =
(·) =  (·)
(·) 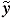 (·). Then there exists a modulus and b > 0, depending only on M and T, such that for 0 < d < T t,
(·). Then there exists a modulus and b > 0, depending only on M and T, such that for 0 < d < T t,
Using Lemmas 4.1, 4.2 and 4.3, we try to establish the optimality of (Ge, De).
Lemma 4.4. Assume (A1)-(A4). Let G be any strategy for player 1 and let  [·] =
[·] =  [·, x0, G, De] be a motion corresponding to (G, De). Then for all t > 0, (t,
[·, x0, G, De] be a motion corresponding to (G, De). Then for all t > 0, (t,  [t]) Î C(r0).
[t]) Î C(r0).
Proof. Let 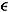 (t) = dist((t,
(t) = dist((t,  [t]),C(r0)) . Without any loss of generality, let
[t]),C(r0)) . Without any loss of generality, let  [·] be the local uniform limit of the sequence {
[·] be the local uniform limit of the sequence { (·, xon, un(·), vn(·))} of nth stage trajectories. Let
(·, xon, un(·), vn(·))} of nth stage trajectories. Let  n(·) =
n(·) =  (·, ·, xon, un(·), vn(·)) and
(·, ·, xon, un(·), vn(·)) and 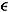 n(t) = dist((t,
n(t) = dist((t,  n(t)), C(r0)). Clearly for each t,
n(t)), C(r0)). Clearly for each t, 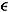 n(t) ®
n(t) ® 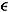 (t) as n ® ¥. Therefore it suffices to show that for all t > 0, limn ® ¥
(t) as n ® ¥. Therefore it suffices to show that for all t > 0, limn ® ¥
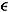 n(t).
n(t).
Let
n = {0 = tn,0 < tn,1 < ¼ < tn,Nn = N < ¼} be the nth stage partition associated with De. Let t Î (tn,j, tn,j+1], 0 < j < Nn1. Choose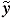 Î
Î 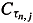 (r0) such that ||
(r0) such that || n(tn,j)
n(tn,j) 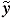 || <
|| < 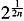 n(tn,j). Let (u*, v*) be a saddle point for the local game at (
n(tn,j). Let (u*, v*) be a saddle point for the local game at ( n(tn,j),
n(tn,j),  n(tn,j)
n(tn,j) 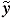 ). Now by Lemma 4.1, there exists n(·) Î
). Now by Lemma 4.1, there exists n(·) Î 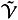 [tn,j, t] such that the relaxed trajectory
[tn,j, t] such that the relaxed trajectory 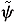 (·) =
(·) = 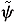 (·, tn,j,
(·, tn,j, 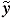 , u*, n(·)) has the property that (t,
, u*, n(·)) has the property that (t, 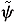 (t)) Î C(r0). Therefore
(t)) Î C(r0). Therefore
Applying Lemma 4.3, we get
Therefore
Letting n ® ¥, we get the desired result.
Similarly, we can prove the next result.
Lemma 4.5. Assume (A1)-(A4). Let D be any strategy for player 2 and let  [·] =
[·] =  [·, x0, Ge, D] be a motion corresponding to (Ge, D). Then for all t > 0, (t,
[·, x0, Ge, D] be a motion corresponding to (Ge, D). Then for all t > 0, (t,  [t]) Î C(r0).
[t]) Î C(r0).
Now we can show that the pair of strategies (Ge, De) constitute a saddle point equilibrium for the game.
Theorem 4.6. Assume (A1)-(A4). The pair (Ge, De) is a saddle point for the game with initial point x0.
Proof. From Lemmas 4.4 and 4.5, it follows that for any (G, D) and motions  [·, x0, G, D e],
[·, x0, G, D e],  [·, x0, Ge, D], we have
[·, x0, Ge, D], we have
This holds for all t > 0. Letting t  ¥, we get
¥, we get
Hence we obtain
The required result now follows.
5 Conclusions
We have extended the Berkovitz's framework to study infinite horizon discounted problems. In this setup, following a dynamic programming approach, we have shown that the two player zero-sum infinite dimensional differential game on the infinite horizon with discounted payoff has a value. This value function is then characterized as the unique viscosity solution of the associated HJI equation. This has been achieved by using the notion of viscosity solution proposed by Crandall-Lions in [5] and [6]. By using our dynamic programming inequalities and mimicking the arguments in [8], without using (A0), we can also characterize the value function in the class of bounded uniformly continuous functions by taking the definition of viscosity solution as in [7] which is a refinement of Tataru's notion (see [11] and [12]). In the Elliott-Kalton framework, this has been established by Kocan et. al. [8] under more general assumptions on A.
6 Acknowledgements
The author wishes to thank M.K. Ghosh for suggesting the problem and for useful discussions. The author is grateful to an anonymous referee for important comments.
Received: 04/II/03.
Accepted: 09/VI/03.
#563/03.
- [1] L.D. Berkovitz, The existence of value and saddle point in games of fixed duration, SIAM J. Control Optim., 23 (1985), 173-196. Errata and addendum, ibid, 26 (1988), 740-742.
- [2] L.D. Berkovitz, Differential games of generalized pursuit and evasion, SIAM J. Con. Optim., 24 (1986), 361-373.
- [3] L.D. Berkovitz, Differential games of survival, J. Math. Anal. Appl., 129 (1988), 493-504.
- [4] L.D. Berkovitz, Characterizations of the values of differential games, Appl. Math. Optim., 17 (1988), 177-183.
- [5] M.G. Crandall and P.L. Lions, Viscosity solutions of Hamilton-Jacobi equations in infinite dimensions, Part IV, J. Func. Anal., 90 (1990), 237-283.
- [6] M.G. Crandall and P.L. Lions, Viscosity solutions of Hamilton-Jacobi equations in infinite dimensions, Part V, J. Func. Anal., 97 (1991), 417-465.
- [7] M.G. Crandall and P.L. Lions, Viscosity solutions of Hamilton-Jacobi equations in infinite dimensions, Part VI, 'Evolution Equations, Control Theory and Biomathematics', Lecture Notes in Pure and Appl. Math., 155 (1994), Dekker, New York, 51-89.
- [8] M. Kocan, P. Soravia and A. Swiech, On differential games for infinite-dimensional systems with nonlinear unbounded operators, J. Math. Anal. Appl., 211 (1997), 395-423.
- [9] N.N. Krasovskii and A.I. Subbotin, Game-Theoretical Control Problems, Springer-Verlag, (1988).
- [10] X. Li and J. Yong, Optimal Control Theory for Infinite Dimensional Systems, Birkhauser, (1995).
- [11] D. Tataru, Viscosity solutions for Hamilton-Jacobi equations J. Math. Anal. Appl., 163 (1992), 345-392.
- [12] D. Tataru, Viscosity solutions for Hamilton-Jacobi equations with unbounded nonlinear terms: A simplified approach, J. Differential Equations, 111 (1994), 123-146.
- [13] J. Warga, Optimal Control of Differential and Functional Equations, Academic Press, (1972).
Publication Dates
-
Publication in this collection
20 July 2004 -
Date of issue
2003
History
-
Accepted
09 June 2003 -
Received
04 Feb 2003





























































