Abstract
In this paper we consider homogenization of the diffusion, adsorption and convection of chemical species in porous media, that are transported by unsaturated single phase flows. The unsaturated flow is described by the Richards' equation. We present in details a rigorous derivation of the corresponding dual porosity model. Then we give the derivation by homogenization of first-order kinetic models for the evolution of the chemical species. Finally, numerical simulations for the Freundlich and Langmuir isotherms are presented.
homogenization; Richards equation; dual porosity
Modeling solute transport through unsaturated porous media using homogenization I* * This research was supported by the GDR MOMAS (Modélisation Mathématique et Simulations numériques liées aux problèmes de gestion des déchets nucléaires: 2439 - ANDRA, BRGM, CEA, EDF, CNRS) as a part of the project '' Modélisation micro-macro des phénomènes couplés de transport-chimie-déformation en milieux argileux''.
Andro Mikelic; Carole Rosier
LaPCS, UFR Mathématiques, Université Claude Bernard Lyon 1 Bât. Doyen Jean Braconnier 21, avenue Claude Bernard 69622 Villeurbanne Cedex, France E-mails: Andro.Mikelic@univ-lyon1.fr/ Carole.Rosier@lmpa.univ-littoral.fr
ABSTRACT
In this paper we consider homogenization of the diffusion, adsorption and convection of chemical species in porous media, that are transported by unsaturated single phase flows. The unsaturated flow is described by the Richards' equation. We present in details a rigorous derivation of the corresponding dual porosity model. Then we give the derivation by homogenization of first-order kinetic models for the evolution of the chemical species. Finally, numerical simulations for the Freundlich and Langmuir isotherms are presented.
Mathematical subject classification: 35B27, 76M50, 35Q30.
Key words: homogenization, Richards equation, dual porosity.
1 Introduction
The underground solute transport involves a complex interplay among hydrological, physical, geochemical and biochemical processes. The geometry plays an important role in modeling. Usually the primary solid particles are assumed to be aggregated into porous pellets (aggregates). The inter-aggregate pore space is such that bulk flow of water only takes place between the aggregates. Consequently, solutes move inside the porous pellets only because of molecular diffusion. On the surface of the pellets the chemical species undergo adsorption or exchange processes.
In the article [23] there is a classification of the computationally significant types of reactions into homogeneous, heterogeneous sorption or ion exchange, and classical heterogeneous dissolution/precipitation reactions.
Our goal is to obtain the upscaled equations, valid at the macro level, starting from the mesoscopic geometry described above. We expect to justify the models from [23] and [15], at least for adsorption processes, and to obtain more precise modeling for dissolution/precipitation reactions involving free boundaries. Direct application of our results is to the hydrochemical computer codes which are of interest for ANDRA.
In this article we concentrate to the case when the chemical species undergo adsorption. A direct modeling approach to this problem is in [14], where the mathematical analysis of a model from the general paper of Rubin [23] is undertaken. Since the first difficulty is with the unsaturated flow, we concentrate our efforts mainly on the obtaining of the dual porosity Richards model and leave the more detailed considerations of the transport, diffusion and adsorption of chemical species to the subsequent papers. That's reason why ''I'' appears in the title.
For simplicity we suppose the porous media W be a unit cube.
Let Y = ]0,1[n, n = 2,3 be the unit cell and let ¶W =  È
È , G1Ç G2 = Æ, where each G1 and G2 is a n-1-dimensional manifold (with boundary).
, G1Ç G2 = Æ, where each G1 and G2 is a n-1-dimensional manifold (with boundary).
We assume then that the geometry of the cell Y defined as follows.
Ym, the pellet, is a connected open subset of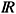 n,
n, 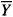 m Ì Y , with Lipschitz boundary; Yf = Y \
m Ì Y , with Lipschitz boundary; Yf = Y \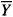 m , the unit inter-aggregate pore is connected.
m , the unit inter-aggregate pore is connected.
Now for a given bounded open set W Ì
n and e > 0 we define the union of the pore spaces
Then  is the union of all pellets and Ge is the boundary between
is the union of all pellets and Ge is the boundary between  and
and  .W =
.W =  È
È ÈGe.
ÈGe.
Under the above assumptions, the theory from [1] implies that there exists a linear and continuous extension operator Pe: W1,q ( ) ®
) ®  (W), and three constants k0, k1, k2 > 0, such that "u Î W1,q (
(W), and three constants k0, k1, k2 > 0, such that "u Î W1,q ( ) we have
) we have
Finally, W(ek0) = {x Î W : dist(x, ¶W) > ek0}.
2 Modeling of the filtration
In the modeling of the underground transport, first question is how to handle the fluid flow. In all models reviewed in [23] and [15], and further studied in [14], we remark that the concentration of the transported contaminants is such that the flow is not affected. This means that we should study the effective flow before looking at the mass balance equations for the transported species. All flows could be considered as incompressible.
For the saturated single phase flows we know that the filtration velocity is given by the Darcy's law. This situation is fairly well understood and using homogenization it is possible to obtain Darcy's law from the microscopic momentum equation. For more details in the case of periodic porous media we refer to the original contribution by Tartar [25] in the book [24] and to the review papers [4] and [20]. Let us note that that the derivation of the Darcy's law for random porous media is in [8]. Consequently, for the mesoscopic model we'll have the Darcy's law but with different permeabilities, corresponding to the pellets and to the inter-aggregate pores.
The homogenization of the mesoscopic model is straightforward if the permeabilities are of the same order, since it reduces to study of the convergence of the homogenization process for a scalar elliptic equation for the pressure, when the characteristic size of the inter-aggregate pores \ep tends to zero. If the permeability ratio between the pellets and the pore space is of order e2 then one obtains the dual-porosity model widely present in the oil literature. For its derivation in the case of a periodic porous medium we refer to [6]. Derivation for random porous media is in [13].
For the multiphase flows, we can't say much about the derivation of the mesoscopic models from the first principles. We refer to the review paper of Bourgeat [12] and to the calculations for the flow through a single pore in [19]. To the contrary, homogenization of the mesoscopic models was studied with success in many papers. We refer to [9] and [18] for the 2-phase flows in periodic geometries and with the permeabilities of same order, to the article [10] for the random case and to [11] for the 2-phase dual-porosity model.
Very frequently, solutes are transported by an unsaturated flow. Single phase unsaturated flows are described by the Richards' equation. Even if it seems that the equations describing the 2-phase flow of water and air are more realistic, the Richards's equation is widely used and in the hydrochemical computer codes one should solve it in a heterogeneous medium.
Hence in order to have an effective equation for the velocity and the pressure, we study the homogenization of the Richards equation. The Richards equation in the dual porosity case reads as follows (see e.g. [7])
where d is a small positive number, Pe, pe are the unknown (scaled) pressures, J is the water content and k is the hydraulic conductivity. Let us note that we have two functions J and k. Each J is a C1 strictly monotone increasing positive function on 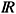 , equal to ds for s > 0. Each k is a C1 increasing function defined on [0,1]. They are positive and strictly monotone increasing for J > q0. They could be zero on [0, q0 ). Let V = { v Î H1 (W) | v = 0 on G1 } .
, equal to ds for s > 0. Each k is a C1 increasing function defined on [0,1]. They are positive and strictly monotone increasing for J > q0. They could be zero on [0, q0 ). Let V = { v Î H1 (W) | v = 0 on G1 } .
Proposition 1. Let PD Î H1 (0,T; L¥ (W)) Ç L2 (0,T; H1 (W)), PD > J-1 (q0 ) +d, d > 0. Let g Î L2 (G2 ×(0,T)). Then there exists at least one solution  e =
e =  Pe +
Pe +  PeÎ (PD+ L2 (0,T; V)) Ç L¥ (W×(0,T)) ,
PeÎ (PD+ L2 (0,T; V)) Ç L¥ (W×(0,T)) ,  e> J-1 (q0 ) + d and
e> J-1 (q0 ) + d and 
 +
+ 
 Î L2 (0,T; V') satisfying
Î L2 (0,T; V') satisfying
and satisfying the initial condition (10). Furthermore, it satisfies the a priori estimates
where constants are independent of e.
Proof. Proof of the proposition follows the lines of the article [5]. It should be noted that the conditions on the data guarantee the non-degeneracy of the coefficients.
Next we use the results from [1] presented in the introduction and extend Pe to W. The extension PePe satisfies
Lemma 2. We have
Using the a priori estimates derived in proposition 1 and lemma 2 and the concept of two scale convergence as in [3], we get the following compactness results
Proposition 3. There exists a subsequence such that
Proof. The proof is a direct consequence of the a priori estimates and of theorem 1.2 and proposition 1.4 in [3].
Again as in [3] we plug into (11) a test function of the form j(x,t) + ej1 (x, x/e, t) + Y(x, x/e, t), where j Î  (QT), j1Î
(QT), j1Î  (QT ;
(QT ;  (Y)) and Y Î
(Y)) and Y Î  (QT ;
(QT ;  (Y)) with Y = 0 for y Î Wf. Passing to the two-scale limit yields:
(Y)) with Y = 0 for y Î Wf. Passing to the two-scale limit yields:
where Qm is the two-scale limit of the (sub)sequence of Jm (pe)  . Let xj, òYfxj = 0, be the 1-periodic solution to
. Let xj, òYfxj = 0, be the 1-periodic solution to
and X the tensor whose (i, j) component is the average of ¶xj /¶yi . Then P1 = åjxj (y) ( ¶ P / ¶ xj-dj3 ) and the choice Y = 0 gives
We note that by Lemma 4.2 from [11], ¶tòYmQmdy Î L2 (W×(0,T)).
The real difficulty is in identifying Qm. Let us note that  pe doesn't converge strongly and oscillations are likely to persist. We proceed by using the the method of periodic modulation as in [11]. It was introduced in [6] and we repeat the definition:
pe doesn't converge strongly and oscillations are likely to persist. We proceed by using the the method of periodic modulation as in [11]. It was introduced in [6] and we repeat the definition:
Definition 4. For a given e > 0, we define a dilation operator De mapping measurable functions on  × (0,T) to mesurable functions on W × Ym × (0,T) by
× (0,T) to mesurable functions on W × Ym × (0,T) by
where ce (x) denote the lattice translation point of the e - cell domain containing x. We extend De u from Ym to Èk (Ym + k) periodically.
It is easy to see that
Lemma 5 (see [6] pp 828-831). For "u Î L2 (0,T ; W1,q ( )) we have
)) we have
Furthermore, let j, y Î L2 (0,T ; H1( ). Then
). Then
Proposition 6 ([11]). Let {ue} be a uniformly bounded sequence in L2( × (0,T)) which satisfy the conditions
× (0,T)) which satisfy the conditions
Deue
u0weakly in L2(QT;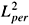 (Ym)) and
ue® u* Î L2(QT ;
(Ym)) and
ue® u* Î L2(QT ; 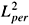 (Y )) in the two-scale sense.
(Y )) in the two-scale sense.
Then we have
Proposition 7. With the above notations we have
Let e > 0 and let De pe be defined by (25). Then De pe =  e satisfies in L2 (0,T;H-1 (Ym)) the equation
e satisfies in L2 (0,T;H-1 (Ym)) the equation
We consider the problem:
For fixed P Î L2 (0,T ; H1 (W)) Ç L¥ (QT) ,J-1 (q0 ) +d < P (a.e) on QT and P0Î L¥ (W) ,J-1 (q0 ) + d < PD (·, 0) (a.e) on W, the theory from [5] and [21] gives existence of a unique solution p* for (34)-(35).
Our final step is to compare the problems (34)-(35) and (32)-(33). We have the following result:
Proposition 8. Let De se be defined by (25) and let p* be a solution for (34)-(35). Then we have
where p is defined by (19).
Proof. We choose the test function by a change of pivot. Therefore, we introduce for (a.e.) (x, t) Î QT a function we Î  (Ym) by
(Ym) by
Obviously, we Î H1 (QT×Ym), ||Ñywe (x,y,0) || < Ce and
< Ce and
Now we introduce the function ze by ze = Jm ( Depe ) -Jm ( p* ) and Km (s) by Km (s) =  km(Jm (h)) dh. Obviously, ze satisfies the variational equation
km(Jm (h)) dh. Obviously, ze satisfies the variational equation
and the boundary condition
ze = Jm (De Pe) - Jm(P) in L2(0, T; H1/2(¶Ym)) for (a.e.) x Î W.
In order to estimate the L2 - norm of ze we choose Y = we as the test function. We have
Using the uniform bound for Ñywe in L2(QT × Ym) we find out that the right hand side is bounded by C e.
Furthermore
Therefore, we write (39) in the form
It remains to find an estimate from below for the diffusion term. We have
Therefore
and consequently,
{Km(Depe) - Km (p*)}{Jm(De pe) - Jm(p*)} ® 0 (a.e.) in QT ×Ym.
Hence, after passing to a subsequence, Depe - p*® 0 (a.e.) in QT × Wm and Depe - p*® 0 (a.e.) in Lq ( QT × Ym) for "q Î [ 1, +¥[ by Lebesgue's dominated convergence theorem.
Therefore the sequence { Pe, pe } converge to the unique1 1 It should be noted that the uniqueness follows from the energy equality. solution { P, p } of the problem
3 Modeling transport, diffusion and adsorption of chemical species
We are going to assume that certain chemical species are dissolved in the fluid. Their concentration is sufficiently small and the fluid flow is not affected. For simplicity of notation we write the equations for just one specie; the generalization to m substances is straightforward. The conservation of mass law is
where ve = kf(Jf (Pe)) (ÑPe - e3 ) is the filtration velocity, veue is the convection term, -DÑue is the dispersion and diffusion term and f(ue) represents the chemical reactions.
The simplest way to include adsorption effects is to introduce the concentration Ue of the substance absorbed on the pellet surface. It is reasonable to suppose that the actual adsorption rate be depends on ue and Ue. Thus we have
where b is a Hölder continuous function of u and U. In order to complete the model we add an equation describing the dynamics of the adsorbed concentration Ue which reads
Using the results from [17] we find out that { ue, Ue } converges in 2-scales to the solution { u, U } of the following problem
We suppose
g1 Î L2(G2× (0, T)) and Ug, ug Î H1 (0, T; L¥(W)) Ç L2(0, T; H1 (W)).
Well-known examples of nonlinear adsorption rates are the Freundlich isotherm b(u,U) = g( up -U), g > 0, 0 < p < 1 and the Langmuir isotherm b(u, U) = g(au / (1+bu) - U), a, b, g > 0.
The next step would be to add the surface diffusion as in [16] or to consider the nonlinear transmission to the pellet, as in [17]. Getting more complicated models from [23] would be subject of our subsequent publications.
4 Numerical simulations
We would like to point out the effects of chemical reactions. Consequently, without losing generality, we consider only a saturated flow in W = (0, 2p)2 and the periodic boundary conditions for the concentrations.
To obtain a precise approximation to the saturations, we approximate the spatial derivatives using the pseudo-spectral method. More precisely, we write u and U in terms of the corresponding spectral Fourier basis. The unknown functions in the nonlinear terms are evaluated in the collocation points, coming from Fourier's grid of the size 256 ×256. Then using the inverse FFT, the nonlinear terms are written in the spectral basis.
In the time discretization, we integrate exactly the linear terms: (a) thediffusion-convection term in (50) and (b) the linear term containing U in the adsorption rate b. For the nonlinear terms we use a third order explicit Adams-Bashforth scheme for f(u) in (50) and an implicit third order Adams-Bashforth scheme for b(·, u, ·) in (54). After scaling the equations with the characteristic time Tc = 2×104, we take the time step 10-3.
This numerical approach was developed in 2D turbulence simulation by Robert and Rosier (see [22]) and the method is very robust for the non-linear coupled transport and diffusion.
We present two numerical experiments. They are with same data, but with different isotherms. The data are given by the following table:
f(u) is taken to be linear. The results are at the figures which follow. They show important effects of the transport on the evolution of the concentration profiles. Also diffusive effects depend very much on the choice of the isotherms, as visible on the figures.
After these calculations, which correspond to the simplest homogenized model, we are planning to develop a numerical method for the unsaturated flow, to add the surface diffusion in the modeling of the adsorption and to include the effects of high Péclet number. The basic challenge is to develop fast solvers for dual-porosity models and for more details we refer to the recent article [2].
Received: 16/IV/03. Accepted: 11/XI/03.
#582/03.
- [1] E. Acerbi, V. Chiadň Piat, G. Dal Maso and D. Percivale, An extension theorem from connected sets and homogenization in general periodic domains, Nonlinear Anal., TMA, 18 (1992), pp. 481-496.
- [2] C. Alboin, J. Jaffré, P. Joly, J.E. Roberts and C. Serres, A comparison of methods for calculating the matrix block source term in a double porosity model for contaminant transport, Computational Geosciences, Vol. 6 (2002), p. 523-543.
- [3] G. Allaire, Homogenization and two-scale convergence, SIAM J. Math. Anal., 23 (1992), pp. 1482-1518.
- [4] G. Allaire, One-Phase Newtonian Flow, in Homogenization and Porous Media, U. Hornung, ed., Interdisciplinary Applied Mathematics Series, Vol. 6 (1997), pp. 45-68, Springer, New York.
- [5] H.W. Alt and S. Luckhaus, Quasilinear Elliptic-Parabolic Differential Equations, Math. Z., Vol. 183 (1983), pp. 311-341.
- [6] T. Arbogast, J. Douglas and U. Hornung, Derivation of the double porosity model of single phase flow via homogenization theory, SIAM J. Math. Anal., 21 (1990), pp. 823-836.
- [7] J. Bear, Dynamics of Fluids in Porous Media, Dover Publications, Inc., New York, (1988).
- [8] A.Y. Beliaev and S.M. Kozlov, Darcy equation for random porous media, Comm. Pure. Appl. Math., 49 (1995), pp. 1-34.
- [9] A. Bourgeat, Homogenized behavior of diphasic flow in naturally fissured reservoir withuniform fractures, Comp. Methods in Applied Mechanics and Engeneering, 47 (1984), pp. 205-217.
- [10] A. Bourgeat, S.M. Kozlov and A. Mikelic, Effective Equations of Two-Phase Flow in Random Media, Calculus of Variations and Partial Differential Equations, Vol. 3 (1995), p. 385-406.
- [11] A. Bourgeat, S. Luckhaus and A. Mikelic, A Rigorous Result for a Double Porosity Model of Immiscible Two-Phase Flows, SIAM J. Math. Anal., Vol. 27 (6) (1996), p. 1520-1543.
- [12] A. Bourgeat, Two-Phase Flow, in Homogenization and Porous Media, U. Hornung, ed., Interdisciplinary Applied Mathematics Series, Vol. 6 (1997), pp. 95-127, Springer, New York.
- [13] A. Bourgeat, A. Mikelic and A. Piatnitski, On the double porosity model of single phase flow in random media, Asymptotic Analysis, 34 (2003), 311-332.
- [14] A. Friedman and P. Knabner, A transport model with micro- and macro-structure, J. Differ. Equat., Vol. 98 (1992), p. 328-354.
- [15] J.C. Friedly and J. Rubin, Solute transport with multiple equilibrium-controlled or kinetically controlled chemical reactions, Water Resour. Res., Vol. 38 (1992), p. 1935-1953.
- [16] U. Hornung and W. Jäger, Diffusion, convection, adsorption and reaction of chemicals in porous media, J. Differ. Equat., Vol. 92 (1991), pp. 199-225.
- [17] U. Hornung, W. Jäger and A. Mikelic, Reactive Transport through an Array of Cells with Semi-Permeable Membranes, Modélisation Mathématique et Analyse Numérique (M2AN), Vol. 28 (1994), p. 59-94.
- [18] A. Mikelic, A Convergence Theorem for Homogenization of Two-phase Miscible Flow through Fractured Reservoirs with Uniform Fracture Distributions. Applicable Analysis, Vol. 33 (1989), 203-214.
- [19] A. Mikelic and L. Paoli, On the derivation of the Buckley-Leverett model from the two fluid Navier- Stokes equations in a thin domain, Computational Geosciences, Vol. 1 (1997), p. 59-83., Erratum, Vol. 4 (2000), p. 99-101.
- [20] A. Mikelic, Homogenization theory and applications to filtration through porous media, in ''Filtration in Porous Media and Industrial Applications'', Lecture Notes Centro Internazionale Matematico Estivo (C.I.M.E.) Series, Lecture Notes in Mathematics Vol. 1734, eds. M. Espedal, A. Fasano and A. Mikelic, Springer, 2000, p. 127-214.
- [21] F. Otto, L1-Contraction and Uniqueness for Quasilinear Elliptic-Parabolic Equations, J. Differ. Equat., Vol. 131 (1996), pp. 20-38.
- [22] R. Robert and C. Rosier, The modeling of small scales in two-dimensional turbulent flows: a statistical mechanics approach. J. Statist. Phys. 86 (3-4) (1997), 481-515.
- [23] J. Rubin, Transport of reacting solutes in porous media: Relation between mathematical nature of problem formulation and chemical nature of reactions, Water Resour. Res., Vol. 19 (1983), p. 1231-1252.
- [24] E. Sanchez-Palencia, Non-Homogeneous Media and Vibration Theory, Lecture Notes in Physics, 127 (1980), Springer Verlag.
- [25] L. Tartar, Convergence of the Homogenization Process, Appendix of [24].
Publication Dates
-
Publication in this collection
11 July 2005 -
Date of issue
Dec 2004
History
-
Received
16 Apr 2003 -
Accepted
11 Nov 2003







































