An augmented Lagrangian SQP method for solving some special class of nonlinear semi-definite programming problems

Abstract

In this paper, we consider a special class of nonlinear semi-definite programming problems that represents the fixed order H2/H<FONT FACE=Symbol>¥</FONT> synthesis problem. An augmented Lagrangian sequential quadratic programming method combined with a trust region globalization strategy is described, taking advantage of the problem structure and using inexact computations. Some numerical examples that illustrate the performance of the method are given.

semi-definite programming; linear quadratic control; nonlinear programming; trust region methods

An augmented Lagrangian SQP method for solving some special class of nonlinear semi-definite programming problems

El-Sayed M.E. Mostafa

Department of Mathematics, Faculty of Science, Alexandria Univ., Alexandria, Egypt. E-mail: [e-mail]

ABSTRACT

In this paper, we consider a special class of nonlinear semi-definite programming problems that represents the fixed order H₂/H_¥ synthesis problem. An augmented Lagrangian sequential quadratic programming method combined with a trust region globalization strategy is described, taking advantage of the problem structure and using inexact computations. Some numerical examples that illustrate the performance of the method are given.

Mathematical subject classification: 49N35, 49N10, 93D52, 93D22, 65K05.

Key words: semi-definite programming, linear quadratic control, nonlinear programming, trust region methods.

1 Introduction

In this paper, the following nonlinear semi-definite programming (NSDP) problem is considered:

where J: ^p×r × Sⁿ ® , H: ^p×r × Sⁿ ® Sⁿ, Y: ^p×r × Sⁿ × Sⁿ ® Sⁿ are assumed to be sufficiently smooth matrix functions and Sⁿ denotes the set of real symmetric n × n matrices. This problem is a nonlinear matrix programming problem and is generally nonconvex.

The augmented Lagrangian function associated with the equality constraint of (1) is defined as

where K Î ^n×n is the associated Lagrange multiplier and s is the penalty parameter.

Several problems in system and control theory can be reduced to some special class of NSDPs (see, e.g., [3], [1], [10], [6], [12]). NSDP formulations of control problems were made popular in the mid of 1990s. There were, however, no computational methods for solving general nonconvex NSDPs. Recently, nonlinear optimization techniques have been employed to solve NSDPs arising in optimal control (see, e.g., [1], [10], [6], [12]).

The main goal of this paper is to propose an augmented Lagrangian sequential quadratic programming (ALSQP) Algorithm that makes use of trust region for finding an approximate solution to (1). ALSQP methods have shown to be quite successful in solving nonlinear programming (NLP) problems. In particular, an ALSQP approach is effective in solving NLP problems, even when the problem is ill-conditioned or the constraints are highly nonlinear. We use trust region strategies to globalize the ALSQP iteration, because they facilitate the use of second derivative information when the problem is nonconvex. The reader is referred, for instance, to the book of Conn, Gould and Toint [4] for a survey of augmented Lagrangian methods and trust region methods.

The difficulties in solving (1) are due to the fact that this problem is a nonlinear and nonconvex matrix programming problem. NSDP formulations of optimal control applications own special structures that are desirably exploited. Having this in mind, we seek in the proposed ALSQP method to combine ideas of SDP-approaches, sequential quadratic programming, and trust region to construct an optimization solver for (1) that exploits the inherent structure of the considered NSDP problem.

This paper is organized as follows. In the next subsection we state the basic assumptions imposed on the problem NSDP. In addition, we discuss the framework of the ALSQP Algorithm. In §2 we present the formulation of the considered problem. In §3 we introduce the constrained trust region Algorithm for solving the quadratic programming trust region subproblem associated with the problem NSDP. In §4 we test numerically the performance of the ALSQP method through several test problems from the benchmark collection COMPleib [8].

Notations. For a matrix M Î n^×n the notations M 0, M 0, M 0, M 0 denote that M is positive definite, positive semi-definite, negative definite, negative semi-definite, respectively. Sometimes the arguments as in H(·) are omitted, which should be obvious from the context. Throughout the paper, ||·|| denotes the Frobenius norm given by ||M|| = , where á·, ·ñ is the inner product defined by áM₁,M₂ñ = Tr ( M₂), and Tr (·) is the trace operator.

1.1 Outline of the Algorithm ALSQP and assumptions

In this subsection, we state the basic assumptions imposed on the problem NSDP. In addition, we describe the framework of the ALSQP Algorithm.

Assumption 1.1. The following basic assumptions are used throughout the paper:

AS1. J and H are twice continuously differentiable in an open neighborhood of the local solution X_*, and their second derivatives are Lipschitz continuous at X_*.

AS2. There exist (X₀,V₀) Î _s, where

AS.3 The second-order sufficient optimality conditions hold at the solution, i.e., there exists a constant k > 0 satisfying

AS4. The mapping ÑH(X_*) is surjective.

AS5. There exists (X_*, V_*) solution of NSDP such that V_* 0,Y(X_*,V_*) 0.

Note that the surjectivity assumption is the classical regularity assumption of nonlinear programming.

ALSQP methods are iterative. The search directions in these methods are obtained by solving a sequence of quadratic programs (QP). Each QP minimizes at every iteration k a quadratic model of a certain augmented Lagrangian function subject to linearized constraints; in our case the QP takes the form:

where the trust region constraint ||DX||< d (d > 0 is the trust-region radius) is included to avoid possible unboundedness in the QP.

Given the current estimate (X_k,V_k) of the solution of the problem NSDP and the Lagrange multiplier K_k, the following Algorithm explains how to obtain the new iterate (X_k+DX,V_k+DV).

Algorithm 1.1. (Algorithm ALSQP for solving the problem NSDP)

a. Choose (X₀,V₀) Î _s, K₀Î n^×n, and s₀> 0. Set k: = 0 and go to the next step.

b. If the prescribed stopping criterion is reached, then stop; otherwise continue with the next step.

c. At every iteration k compute an approximate solution (DX, DV) to the problem QPTR such that (X_k+DX,V_k+DV) Î _s.

d. Set (X_k+1,V_k+1) = (X_k+DX,V_k+DV), update K_k+1, set k = k+1, and go to step b.

Some comments are now in order.

• Obviously, it is not trivial how to obtain an initial (X₀,V₀) Î _s (item a of the ALSQP Algorithm). In § 4, however, we describe a technique for determining (X₀,V₀) Î _s that relies on Lyapunov stability theory.

• The multiplier K can be updated without extra calculations while taking problem structure into consideration; see the end of §2 and the Algorithm 3.2.

The Algorithm ALSQP terminates if the following criterion is satisfied

where

_tol > 0 is the tolerance.

2 Problem formulation/application

In optimal control, an important nonlinear and nonconvex application is the problem of designing a static output feedback (SOF) control law that meets a desired performance criterion. A typical instance of an output feedback control system can be stated as follows. Consider a linear time-invariant state space model of order n_x,

where x Î , w Î , u Î , z Î , and y Î denote the state, the disturbance input, the control input, the regulated output, and the measured output, respectively. Furthermore, A, B, B₁, C, C₁, and D₁ are given constant matrices of appropriate size.

The static output feedback control law is given by

where F Î is unknown.

Substituting the control law (7) into our control system, then the closed loop counterpart yields:

where A(F) := A+BFC, B(F): = B₁, C(F): = C₁+D₁FC are the augmented closed loop operators, respectively.

The fixed order

₂/_¥ synthesis problem (see, e.g., [2], [5], [7]) is equivalent to the following NSDP problem:

where

and g > 0 is a given constant. Clearly, the problem NSDP is a generalization of the problem NSDP1, where X = (F,L) Î ^p×r × Sⁿ.

Observe that, if we assign a large constant value to , in (9), then we obtain the following special case that corresponds to the fixed order

₂ synthesis problem (see, e.g., [7], [9], [14]):

Note, however, that the ALSQP method reduces to solving (10) by simply assigning a large constant value to g in that method.

First and second-order derivatives of the augmented Lagrangian function (2) are obtained in the following Lemma, which will be needed later on to construct the trust region problem.

Lemma 2.1 [10, lemma 2.1]. Let (F,L,V) Î _s, K Î ^n×n be given. Then, the function J and the constraint function H are twice continuously differentiable on

_s. Furthermore, the first and the second order directional derivatives of

^s(F,L,K) are given by

where K is the solution of the adjoint equation,

and the directional derivatives of H(F,L) with respect to F and L are

where

Moreover, the Hessian of the augmented Lagrangian is Lipschitz continuous.

Proof. The differentiability of J and H is straightforward. First and second order directional derivatives of 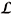s with respect to F and L yield the above equations (See, e.g., [11] for a similar result, but with using the Lagrangian function and not the augmented Lagrangian).

However, it is also possible to obtain those derivatives of

^s(X, K) from their corresponding counterparts of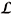 ⁰(X, K) according to the fact:

By using the result of Lemma 2.1 the first-order necessary optimality conditions for the problem NSDP1 are:

where Ã(·) = . For optimal control problems (14) represents the state equation, (13) corresponds to the adjoint equation, and the left-hand side of (12) corresponds to the gradient. It is worth noting that, for \s = 0 the adjoint equation (13) reduces to a Lyapunov equation that can be employed to determine a new Lagrange multiplier estimate in the proposed method.

Observe that, if the penalty parameter \s is set to zero in (12)-(14), then the Karush-Kuhn-Tucker (KKT) system for the problem NSDP1 is obtained. Onthe other hand, if g ® + ¥ in (12)-(14) and s = 0, the KKT system of the problem NSDP2 is achieved. In this case, Ã(F, L) ® A(F), H(F, L) ® (F, L), and Y(F, L, V) ® (F, V).

3 Constrained trust region method

Let the matrix variable X in the problem NSDP and consequently in the trust region problem QPTR be decomposed as X = (F, L) Î ^p×r × Sⁿ. Then, the problem QPTR can be rewritten in the form:

where

is the quadratic approximation of

^s, and d is the trust-region radius.

In order to avoid possible infeasibility when solving (15) we use the tangent space approach (see, e.g., [4]). In this approach, the solution DX of the trust region problem is a decomposition of a normal step DXⁿ and a tangential step DX^t; each one of them is obtained by solving an unconstrained trust region subproblem.

The tangent space approach relies on the null space operator of the Jacobian of the equality constraint. A drawback of the utilisation of directional derivatives is the lack of an explicit form of the Jacobian matrix. In the following Lemma we use a technique that is often used in optimal control to provide this null space operator, which does not require such a matrix explicitly.

Lemma 3.1. Let (F,L,V) Î _s, g > 0,DL Î n^×nbe given. The range space of the linear operator (F, L) defined by

coincides with the null space(Ñ H^T(F, L)) of the Jacobian of the equality constraint, where is the identity operator.

Proof. The operator H_L(F, L) is linear (see (11)) and is also bijective (see[9, Lemma 5]), then H_L(F, L) is invertible. Hence, the linearized equality constraint in (15) implies

This leads to the following decomposition of DX = (DL, DF):

where 0 is the zero operator. The null space of the Jacobian Ñ H^T is given by

where () is the range space of .

As seen above the step DX solution of (15) is decomposed as (see (16) ):

The following Lemma shows that the linearized equality constraint in the problem (15) is splitted into two Lyapunov equations.

Lemma 3.2. Let (F,L,V) Î _s, K Î ^n×nbe given, and let (DF, DL) Î × be the solution of (15), and let g > 0 be a given constant. The linearized equality constraint in (15) is decomposed into the following Lyapunov equations

where

Proof. (See also [10, Lemma 2.2] for a similar result but on the problem NSDP2) From the step decomposition (17) the linearized equality constraint of (15) can be rewritten as

H_L(F, L)DL^t+H_F(F, L)DF+H_L(F, L)DLⁿ+H(F, L) = 0.

Since DX^t = (F, L)DF lies in the null space of the Jacobian ÑH^T(F, L), then

H_L(F, L)DL^t+H_F(F, L)DF = 0,

which by using the derivatives (11) implies (19). Hence, the linearized equality constraint reduces to

H_L(F, L)DLⁿ+H(F, L) = 0,

and by using (11) gives (18).

An important feature of the tangent space approach is the decomposition of the trust region problem (15) into two unconstrained trust region subproblems. The first subproblem is:

It is particularly desirable to obtain an approximate solution DXⁿ = (DLⁿ, 0) to (20). An efficient solution can be obtained, however, by solving the linear matrix equation

in D

ⁿ followed by rescaling D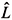ⁿ to lie within the trust region, i.e., DLⁿ ® udⁿ, where the scaling parameter u is given by

Observe that the linear matrix equation (21) is simply the Lyapunov equation (18). Roughly speaking, the computation of DXⁿ reduces to solving one Lyapunov equation per iteration.

Having computed DXⁿ, the tangential step DX^t(DF) = (DL^t(DF),DF) is obtained as a solution of the following unconstrained trust region subproblem:

where

and DL^t(DF) solves the Lyapunov equation (19).

Applying first-order necessary optimality conditions on the subproblem TTR give the following result.

Lemma 3.3 [10, lemma 2.5]. Let (F, L, V) Î s, s, g > 0 be given. Assume that DF Î is a solution of TTR, then DF satisfies the linear matrix equation

where N(F, L) = (B^TL+C(F)), and K, DL^t solve (13) (with s = 0), (19), respectively. Furthermore, Z₀, DKⁿ, DL^t, DK^t, DZ₁, and DZ₂ solve the Lyapunov equations (23)-(27), respectively, and l is the Lagrange multiplier associated with the trust-region constraint.

where

Proof. By using the results of Lemma 2.1, the direct differentiation of q^s(DF) with respect to DF yields Newton's equation (22) coupled with the aforementioned associated Lyapunov equations. The following two properties of trace derivatives have been particularly used to derive that equation

where M₁ and M₂ are matrices of appropriate dimensions.

Observe that, the coupled Lyapunov equations (23)-(27) arise as a result of differentiating all those terms of DL^t(DF) in the quadratic model q^s(DF) with respect to DF.

The approximate solutions of the unconstrained trust region subproblems NTR and TTR is described in the next Algorithm. The Algorithm starts by computing the normal step DXⁿ = (DLⁿ,0) followed by solving the linear matrix equation (22) coupled with the Lyapunov equations (19) and (23)-(27) to obtain DX^t(DF) = (DL^t(DF),DF). A conjugate gradient trust region method is considered to compute DX^t(DF) approximately.

Within the CG trust region method the iterates are forced to satisfy the inequality constraints (3). This means that the computed step by the CG method is enforced to fulfill the condition:

(F+DF,L+DLⁿ+DL^t(DF),V+DV) Î _s.

If the computed trial step does not lie strictly within

_s, then such a step is rejected and a decrease in d takes place.

Remark 3.1. The problem NSDP1 can be simplified by leaving the variable L to replace V in both inequality constraints. This idea reduces the computations in ALSQP to two Lyapunov equations for computing V and DV(DF), and clearly increases the efficiency of the method ALSQP. In this case the computed step DX = (DF,DLⁿ+DL^t(DF)) is forced to satisfy the coupled inequality constraints in the compact form:

(F+DF,L+DLⁿ+DL^t(DF)) Î _s.

The following Algorithm describes the computation of the steps DXⁿ and DX^t(DF), where DXⁿ is computed first followed by computing DX^t(DF).

Algorithm 3.1. (Computing DXⁿ and DX^t(DF) solutions of NTR and TTR)

I. Computing the normal step DXⁿ

Let (F,L) Î _s, K Î ^n×n, s > 0, and the constant matrices A, B, B₁, C, C₁, D₁ be given.

i. Solve the Lyapunov equation (18) for DLⁿ

ii. Scale DLⁿ so that ||DLⁿ||< d

II. Computing DX^t(DF)

Given DLⁿ, solve (23)-(24), and (13) (with s = 0) for Z₀, DKⁿ, K Î ^n×n, respectively. Let Î (0,1). Set T₀ = , and compute the residual (the R.H.S. of (22)):

U₀ = - N(F,L)((K+ s H(·))+Z₀+ s DKⁿ + H_LDLⁿ)) C^T - B^TDLⁿ(K+ s H(·))C^T.

Then, set D₀ = U₀.

Repeat at most n_u×n_y times

1. Solve for DL^t(D), DK^t(D), DZ₁(D), and DZ₂(D) the Lyapunov equations (19), (25)-(27), respectively.

2. Compute the ratio x = and then the parameter

where

3. If x > or x< 0, then set DF = T+D, and stop; otherwise, set T⁺ = T+xD.

4. Update the residual: U⁺ = U-x (D), and set _cg = min{,||U⁰||}.

5. If

< _cg, set DF = T⁺ and stop; otherwise go to the next step.

6. Compute z = , set D⁺ = U⁺+zD, and go to step 1.

End (repeat)

Having computed the trial step DX = (DF,DLⁿ+DL^t(DF)) and the new multiplier estimate K_k+1 it remains to accept or reject this step and to increase or decrease the trust region radius d_k according to the strategy of the trust region method (see [4]). The augmented Lagrangian function (2) is used as a merit function. The quantities Ared(DX;s) and Pred(DX;s) of the ''actual'' and ''predicted'' reductions of this merit function are used to measure progress made by the computed trial step towards optimality and feasibility, which are defined as

and

where X_k = (F_k,L_k). Note that from the problem structure the last term in Pred(DX;s) is exactly the linearized model of the equality constraint of (15). We know from Lemma 3.2 that the linearized equality constraint is decomposed into the two Lyapunov equations (18)-(19), which are solved in every iteration of the Algorithm ALSQP. As a result, Pred(DX;s) reduces to the simpler form

The ratio r_k = Ared(DX;s)/Pred(DX;s) is used to measure progress towards optimality and feasibility. According to the value of r_k the computed trial step DX is accepted or rejected, and consequently d_k is increased or decreased.

The constrained trust region Algorithm is stated in the following lines, which represents the major part of the Algorithm ALSQP, namely in item c. The update of the step and the multiplier mentioned in item d of the Algorithm ALSQP are stated more specifically below in the Algorithm.

Algorithm 3.2. (The constrained trust region Algorithm)

Given m_i, i = 1,2 with 0 < m₁ < m₂ <1, > 0,s₀> 1, choose (F₀,L₀) Î s, and K₀ solution of (13) (with s = 0). Set k = 0.

While (5) is not satisfied, do

1. Compute D and DF_k by the Algorithm 3.1. Given DF_k, solve (19) to obtain DL^t(DF_k), and then set DL_k = D+DL^t(DF_k).

2. Compute the new multiplier estimate K_k+1, e.g., by (13) (with s = 0).

3. Compute Ared_k and Pred_k by using (28) and (29), respectively. If

then set

otherwise, set s_k = s_k-1.

4. Compute the ratio r_k = Ared_k/Pred_k, update d_k, and accept or reject the step according to the following:

If r_k< m₁,

set d_k+1 = and reject the trial step.

Else if m₁< r_k < m₂,

set d_k+1 = d_k, F_k+1 = F_k+DF_k, L_k+1 = L_k+DL_k.

Else if r_k > m ₂,

set d_k+1 = 2d_k, F_k+1 = F_k+DF_k, L_k+1 = L_k+DL_k.

End (If)

End (do)

In the computations the following values have been assigned to the parameters in the Algorithm 3.2: m₁ = 0.1, m₂ = 0.7, and = 1. We use the following initial values: d₀ = 10², and s₀ = 1.

4 Numerical results

In this Section, an implementation for the Algorithm ALSQP is described. A Matlab code was written corresponding to this implementation. The constant g > 0 of the problem NSDP1 is initially estimated using the Matlab function hinflmi from the LMI Control System Toolbox. On the other hand, we need to solve several Lyapunov equations during the computation of the trial step. The Matlab function lyap(·,·) from the Control System Toolbox is used to solve approximately those equations.

All considered test problems were chosen from the benchmark collection COMPleib [8]. Obviously, for every test problem an initial point (F₀,L₀) Î _s is required. One successful approach is to choose an F₀ from the following set:

where Re(n_i(A(F))) are the real-parts of the eigenvalues of A(F). From Lyapunov stability theory, (see, e.g., [15, Theorem 11]) there is an equivalence between the following:

1. There exists F Î D_s.

2. There exists L 0 such that Y(F,L) 0.

3. For every C(F)^TC(F) there exists a unique solution L of the Lyapunov equation (14), and if C(F)^TC(F) 0 then L 0.

Hence, by choosing F₀Î D_s such that C(F₀)^TC(F₀) 0, then the L₀ solution of the Lyapunov equation (14) is strictly feasible with respect to the inequality constraints:

However, an initial F₀Î D_s can be determined, e.g., by using the code slpmm [7].

The performance of the ALSQP method is compared numerically with the CTR method developed in [9], the IPCTR method proposed in [10], and Newton's method combined with an Armijo stepsize rule as proposed in [16]. In the numerical examples, we denote the Newton Algorithm by Armijo. Note that the two methods CTR and IPCTR are based on the simpler problem NSDP2. On the other hand, the problem NSDP2 was formulated in [16] as an unconstrained minimization problem in the variable F and was solved by the above mentioned method.

In the following we consider two numerical examples from [8] that can be cast as nonlinear semi-definite programs of the form (1).

The ALSQP method terminates if the stopping criterion (5) reaches accuracy of 10^-7.

Example 4.1. The first test problem describes the longitudinal motion of a VTOL helicopter (see [8, HE1]). The data matrices of the continuous-time linearized state space model (see (6)) are the following:

The main goal is to compute an optimal SOF gain matrix F_* that meets a desired performance criterion, and at the same time the computed F_* must stabilize (in the Lyapunov sense) the closed loop control system (8). Equivalent to this task is to solve the optimization problem NSDP1 for finding a stationary point (F_*,L_*).

The zero matrix F₀ = is such that (F₀,L₀) Ï s. Therefore, the following point (F₀,L₀) is considered:

and L₀ is the corresponding solution of the Lyapunov equation (14).

In Table 1 the convergence rate for the method ALSQP is shown. The computed static output feedback gain matrix is

Table 2 gives a comparison between ALSQP and the other solvers on this problem for the same starting point (F₀,L₀). These results show that ALSQP is quite competitive with other solvers on this problem with respect to the number of iterations.

Figure 1 shows the effect of the computed SOF gain F_* on the closed-loop control system (8). In particular, F_* enforces all state variables to converge to zero.

Example 4.2. The second test problem is the Tenyain following model (see [8, TF1]). The given data matrices for this example are as follows:

The zero matrix F₀ = implies that (F₀,L₀) = (,L₀) Ï _s, where L₀ is the corresponding solution of the Lyapunov equation (14). Therefore, the following F₀ is chosen:

Table 3 shows the performance of the method ALSQP on this example. The computed SOF gain matrix is

Table 4 gives a comparison between ALSQP and other solvers on this problem starting from the same point (F₀,L₀).

Figure 2 shows the effect of the computed SOF feedback gain matrix F_* on the closed-loop control system (8).

The two examples show the fast local rate of convergence of the method ALSQP starting from remote points.

In Table 5 some preliminary tests are given. For each example, we report the problem name together with the problem dimensions (n_x,n_u, n_y,n_w,n_z), and the overall number of iterations. A dash indicates that the corresponding method fails to find an approximate solution of the considered nonconvex NSDP problems with accuracy _tol = 10^-7. In particular, ALSQP was tested by using the test problem [8, REA1] from two different starting points; the results corresponding to the second starting point are denoted by REA1*. In all these problems the four codes approached the same solution point.

The main conclusion that we can draw from the above results is that the method ALSQP outperforms other methods on most of the considered nonconvex and nonlinear semi-definite programming test problems.

Acknowledgements. The author wish to thank Dr. F. Leibfritz for constructive discussions on earlier version of this paper. He also would like to thank the Editor-in-Chief and an anonymous referee for their helpful comments which have improved the presentation of this paper.

Received: 17/III/05. Accepted: 01/VI/05.

#628/05.

• [1] P. Apkarian and H.D. Tuan, Concave programming in control theory, J. Global Optimization, 15 (1999), 343-370.
• [2] D.S. Bernstein and W.M. Haddad, LQG control with an H_Ľ performance bound: A Riccati equation approach, IEEE Transactions on Automatic Control, 34 (1989), 293-305.
• [3] S.P. Boyd, L. El-Ghaoui, E. Feron and V. Balakrishnan, Linear Matrix Inequalities in System and Control Theory, Vol. 15 of SIAM Studies in Applied Mathematics, SIAM, Philadelphia, 1994.
• [4] A.R. Conn, N.I.M. Gould and Ph.L. Toint, Trust region methods, SIAM Philadelphia, in the MPS/SIAM Series on Optimization, 2000.
• [5] P.P. Khargonekar and M.A. Rotea, Mixed H₂/H_Ľ control: A convex optimization approach, IEEE Transactions on Automatic Control, 36 (1991), 824-837.
• [6] M. Kocvara and M. Stingl, PENNON: a code for convex nonlinear and semi-definite programming, Optimization Methods and Software, 18 (2003), 317-333.
• [7] F. Leibfritz, A LMI-based algorithm for designing suboptimal static H₂/H_Ľ output feedback controllers, SIAM Journal on Control and Optimization, 39 (2001), 1711-1735.
• [8] F. Leibfritz, COMPleib: Constraint Matrix-optimization Problem library - a collection of test examples for nonlinear semi-definite programs, control system design and related problems Tech. Report-03, 2003. http://www.uni-trier.de/leibfr/COMPleib
• [9] F. Leibfritz and E.M.E. Mostafa, Trust region methods for solving the optimal output feedback design problem, Int. J. on Control, 76 (2003), 501-519.
• [10] F. Leibfritz and E.M.E. Mostafa, An interior-point trust region method for a special class of nonlinear SDP-problems, SIAM J. Optim., 12 (2002), 1048-1074.
• [11] E.M.E. Mostafa, Efficient trust region methods in numerical optimization, Ph.D. thesis, Dept. of Mathematics, Faculty of Science, Alexandria University, Egypt, 2000.
• [12] E.M.E. Mostafa, A trust region method for solving the decentralized static output feedback design problem, J. Appl. Math. & Computing., 18 (2005), 1-23.
• [13] T. Rautert and E.W. Sachs, Computational design of optimal output feedback controllers, SIAM J. Optim., 7 (1997), 837-852.
• [14] M.A. Rotea, The generalized H₂ control problem, Automatica, 29 (1993), 373-385.
• [15] E.D. Sonntag, Mathematical control theory, Springer Verlag, New York, Berlin, 1990.
• [16] H.T. Toivonen, A globally convergent algorithm for the optimal constant output feedback problem, Int. J. Control, 41 (1985), 1589-1599.

Publication Dates

• Publication in this collection
  20 Apr 2006
• Date of issue
  Dec 2005

History

• Accepted
  01 June 2005
• Received
  17 Mar 2005