Abstract
In this paper, we derive a sharp observability inequality for Kirchhoff plate equations with lower order terms. More precisely, for any T > 0 and suitable boundary observation domains (satisfying the geometric conditions that the multiplier method imposes), we prove an estimate with an explicit observability constant for Kirchhoff plate systems with an arbitrary finite number of components and in any space dimension with lower order bounded potentials.
Kirchhoff plate system; observability constant; Carleman inequalities; potential; Meshkov's construction
A sharp observability inequality for Kirchhoffplate systems with potentials* * The work is supported by the Grant MTM2005-00714 of the Spanish MEC, the DOMINO Project CIT-370200-2005-10 in the PROFIT program of the MEC (Spain), the SIMUMAT projet of the CAM (Spain), the EU TMR Project ''Smart Systems'', and the NSF of China under grants 10371084 and 10525105.
Xu ZhangI; Enrique Zuazua
Departamento de Matemáticas, Facultad de Ciencias Universidad Autónoma de Madrid, 28049 Madrid, Spain E-mail: enrique.zuazua@uam.es
IKey Laboratory of Systems and Control, Academy of Mathematics and Systems Sciences, Chinese Academy of Sciences, Beijing 100080, China E-mail: xuzhang@amss.ac.cn
ABSTRACT
In this paper, we derive a sharp observability inequality for Kirchhoff plate equations with lower order terms. More precisely, for any T > 0 and suitable boundary observation domains (satisfying the geometric conditions that the multiplier method imposes), we prove an estimate with an explicit observability constant for Kirchhoff plate systems with an arbitrary finite number of components and in any space dimension with lower order bounded potentials.
Mathematical subject classification: Primary: 93B07; Secondary: 93B05, 35B37.
Key words: Kirchhoff plate system, observability constant, Carleman inequalities, potential, Meshkov's construction.
1 Introduction
Let n > 1 and N > 1 be two integers. Let W be a bounded domain in 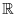 n with C4 boundary G, G0 be a nonempty open subset of G, and T > 0 be given and sufficiently large. Put Q
n with C4 boundary G, G0 be a nonempty open subset of G, and T > 0 be given and sufficiently large. Put Q 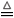 (0,T)× W, S
(0,T)× W, S 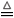 (0,T)×G and S0
(0,T)×G and S0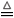 (0,T)×G0. For simplicity, we will use the notation yi =
(0,T)×G0. For simplicity, we will use the notation yi =  , where xi is the i-th coordinate of a generic point x = (x1,...,xn) in
, where xi is the i-th coordinate of a generic point x = (x1,...,xn) in 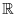 n. Throughout this paper, we will use C = C(T, W,G0) and C* = C*(W,G0) to denote generic positive constants depending on their arguments which may vary from line to line.
n. Throughout this paper, we will use C = C(T, W,G0) and C* = C*(W,G0) to denote generic positive constants depending on their arguments which may vary from line to line.
Set
We consider the following
N-valued plate system with a potential a Î L¥(0,T; Lp(W;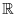 N×N)) for some p Î [n/3,¥]:
N×N)) for some p Î [n/3,¥]:
where y = (y1,...,yN)T, and the initial datum (y0,y1) is supposed to belong to 
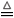 {j Î H3(W)| j|G = Dj|G = 0}N×(H2(W)Ç
{j Î H3(W)| j|G = Dj|G = 0}N×(H2(W)Ç (W))N, the state space of system (1). It is easy to show that system (1) admits one and only one weak solution y Î C([0,T];
(W))N, the state space of system (1). It is easy to show that system (1) admits one and only one weak solution y Î C([0,T]; ).
).
In what follows, we shall denote by |·|, ||·||p and |||·|||p the (canonical) norms on 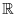 N, L¥(0,T;Lp(W;
N, L¥(0,T;Lp(W;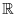 N×N)) and L¥(0,T;W1,p(W;
N×N)) and L¥(0,T;W1,p(W;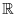 N×N)), respectively.
N×N)), respectively.
We shall study the observability constant K(a) of system (1), defined as the smallest (possibly infinite) constant such that the following observability estimate for system (1) holds:
This inequality, the so-called observability inequality, allows estimating thetotal energy of solutions in terms of the energy localized in the observation subdomain G0. It is relevant for control problems. In particular, in this linear setting, this (observability) inequality is equivalent to the so-called exact controllability property, i.e., that of driving solutions to rest by means of control forces localized in S0 (see [6, 11]). This type of inequality, with explicit estimates on the observability constant, is also relevant for the control of semilinear problems ([10]). Similar inequalities are also useful for solving a variety of Inverse Problems ([9]). We remark that, as for the wave equations, (2) holds for the Kirchhoff plate only if (W,G0,T) satisfies suitable conditions, i. e. G0 needs to satisfy certain geometric conditions and T needs to be large enough.
Obviously the observability constant K(a) in (2) not only depends on the potential a, but also on the domains W and G0 and on the time T. The main purpose of this paper is to analyze only its explicit and sharp dependence on the potential a.
The main tools to derive the explicit observability estimates are the so-called Carleman inequalities. Here we have chosen to work in the space  in which Carleman inequalities can be applied more naturally. But some other choices of the state space are possible. For example, one may consider similar problems in state spaces of the form (
in which Carleman inequalities can be applied more naturally. But some other choices of the state space are possible. For example, one may consider similar problems in state spaces of the form ( (W))N×(L2(W))N or (H2(W)Ç
(W))N×(L2(W))N or (H2(W)Ç (W))N×(
(W))N×( (W))N where the Kirchhoff plate system is also well posed. But the corresponding analysis on the observability constants, in turn, is technically more involved.
(W))N where the Kirchhoff plate system is also well posed. But the corresponding analysis on the observability constants, in turn, is technically more involved.
One of the key points to derive inequality (2) for system (1) is the possibility of decomposing the Kirchhoff plate operator  as follows:
as follows:
where I is the identity operator. Actually, we set
where y is the solution of (1). By the first equation of (1) and noting (3), it follows that
ay = ytt + D2y Dytt = (¶tt D)(y Dy) + Dy = ztt Dz + y z.
Therefore the Kirchhoff plate system (1) can be written equivalently as the following coupled elliptic-wave system
Consequently, in order to derive the desired observability inequality for system (1), it is natural to proceed in cascade by applying the global Carleman estimates to the second order operators in the two equations in system (5). We refer to [2, 3] for related works on Carleman inequalities for other cascade systems of partial differential equations.
Similar (boundary and/or internal) observability problems (in suitable spaces) have been considered for the heat and wave equations in [1], and for the Euler-Bernoulli plate equations in [5]. According to [1] and [5], the sharp observability constants for the heat, wave and Euler-Bernoulli plate equations with bounded potentials a (i.e., p = ¥) contain respectively the product of the following two terms (Recall that C* = C*(W,G0) and C = C(T, W,G0))
and
As explained in [1, 5], the role that each of these constants plays in the observability inequality is of different nature: H1(T, a), W1(T, a) and P1(T, a) are the constants which arise when applying Gronwall's inequality to establish the energy estimates for solutions of evolution equations; while H2(T, a), W2(T, a) and P2(T, a) appear when using global Carleman estimates to derive the observability inequality by absorbing the undesired lower order terms.
It is shown in [1, Theorems 1.1 and 1.2] and [5, Theorem 3] that the above observability constants are optimal for the heat, wave and Euler-Bernoulli plate systems (N > 2) with bounded potentials, in even dimensions n > 2. The proof of this optimality result uses the following two key ingredients:
1) For the heat and Euler-Bernoulli plate equations, because of the infinite speed of propagation, one can choose T as small as one likes and henceforth H 1(T, a) and P 1(T, a) can be bounded above by H 2(T, a) and P 2(T, a), respectively for T = O( ) and O(
) and O( ). On the other hand, for the wave equation, although one has to take T to be large enough (because of the finite velocity of propagation), for any finite T, W1(T, a) can bounded by W 2(T, a) because the power 1/2 for ||a||¥ in W 1(T, a), given by the modified energy estimate, is smaller than 2/3, the power for ||a||¥ in W 2(T, a), arising from the Carleman estimate. In this way, for any finite T large enough, one gets an upper bound on the observability constant (for the wave equation) of the order of exp(C
). On the other hand, for the wave equation, although one has to take T to be large enough (because of the finite velocity of propagation), for any finite T, W1(T, a) can bounded by W 2(T, a) because the power 1/2 for ||a||¥ in W 1(T, a), given by the modified energy estimate, is smaller than 2/3, the power for ||a||¥ in W 2(T, a), arising from the Carleman estimate. In this way, for any finite T large enough, one gets an upper bound on the observability constant (for the wave equation) of the order of exp(C ).
).
2) Based on the Meshkov's construction [8] which allows finding potentials and non-trivial solutions for elliptic systems decaying at infinity in a superexponential way, one can construct a family of solutions (for the heat, wave and Euler-Bernoulli plate equations) with suitable localization properties showing that most of the energy is concentrated away from the observation domain. According to this, the observed energies grow exponentially as exp(- ) for the wave and heat systems and as exp(-
) for the wave and heat systems and as exp(- ) for the Euler-Bernoulli plate ones.
) for the Euler-Bernoulli plate ones.
Things are more complicated for the Kirchhoff plate systems under consideration. Indeed, on one hand, due to the finite speed of propagation, one has to choose the observability time T to be large enough. On the other hand, a modified energy estimate for the Kirchhoff plate systems (see (10) in Lemma 1 in Section 2) yields a power 1/2 for ||a||¥ which can not be absorbed by the one, 1/3, arising from the Carleman estimate. To overcome this difficulty, the key observation in this paper is that, although T has to be taken to be large, one can manage to use the indispensable energy estimate only in a very short time interval when deriving the desired observability estimate. However, we do not know how to show the optimality of the observability constant at this moment. Indeed, when proving the optimality, the energy estimate has to be used in the whole time duration [0,T] and this breaks down the concentration effect that Meshkov's construction guarantees, which is valid only for very small time durations for the Kirchhoff plate systems. Therefore, proving the optimality of the observability estimates obtained in this paper is an interesting open problem.
The rest of this paper is organized as follows. In Section 2 we give some preliminary energy estimate for Kirchhoff plate systems, and show some fundamental weighted pointwise estimates for the wave and elliptic operators. In Section 3 we present the sharp observability estimate for the Kirchhoff plate system. In Section 4 we explain more carefully the main difficulty to show the optimality of the observability constant for Kirchhoff plate systems by means of the above mentioned Meshkov's construction.
2 Preliminaries
In this section, we show some preliminary energy estimates for Kirchhoff plate systems, and weighted pointwise estimates for the wave and elliptic operators. The estimates for the Kirchhoff plate system will then be obtained by noting the equivalence between system (1) and the coupled wave-elliptic system (5).
2.1 Energy estimates for Kirchhoff plate systems
Denote the energy of system (1) by
Note that this energy is equivalent to the square of the norm in  . For
. For
consider also the modified energy function:
It is clear that both energies are equivalent. Indeed,
The following estimate holds for the modified energy:
Lemma 1. Let a Î L¥(0,T;Lp(W;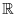 N×N)) for some p Î [n/3,¥]. Then there is a constant C0 = C0(W,p,n) > 0, independent of T, such that
N×N)) for some p Î [n/3,¥]. Then there is a constant C0 = C0(W,p,n) > 0, independent of T, such that
Proof. For simplicity, we assume N = 1. The same proof applies to a system with any finite number of components N. Using (8) and noting system (1), it is easy to see that
Put p1 =  and p2 =
and p2 =  . Noting that
. Noting that
by Hölder's inequality and Sobolev's embedding theorem, and recalling (7)-(8) and observing s0p1 = , we get
, we get
Similarly,
Now, combining (11)-(13), and applying Gronwall's inequality, we conclude the desired estimate (10).
2.2 Pointwise weighted estimates for the wave and elliptic operators
In this subsection, we present some pointwise weighted estimates for the wave and elliptic equations that will play a key role when deriving the sharp observability estimates for the Kirchhoff plate system.
First, we show a pointwise weighted estimate for the wave operator ''¶tt-D''. For this, for any (large) l > 0, any x0Î 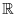 n and c Î
n and c Î 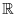 , set
, set
By taking (aij)n×n = I, the identity matrix, and q =  (with
(with  given by (14)) in [4, Corollary 4.1] (see also [7, Lemma 5.1]), one has the following pointwise weighted estimate for the wave operator.
given by (14)) in [4, Corollary 4.1] (see also [7, Lemma 5.1]), one has the following pointwise weighted estimate for the wave operator.
Lemma 2. For any u = u(t,x) Î C2(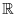 1+n), any k Î
1+n), any k Î 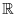 and v
and v 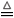 qu, it holds
qu, it holds
where
As a consequence of Lemma 2, we have the following pointwise weighted estimate for the elliptic operator.
Corollary 1. Let p = p(t,x) Î C2(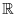 1+n), and set q = qp. Then
1+n), and set q = qp. Then
where
Proof. We fix an arbitrary t Î [0,T] and view the corresponding function which depends on x as a function of (x,s) with s being a fictitious time parameter. We then set
where X = eL and L = l|x-x0|2. Choosing c = 0 in (14), and applying Lemma 2 (with k = 0) in the variable (x,s) to the above U and V, we get
with  ,
,  and
and  given by (18). Now, for any c Î
given by (18). Now, for any c Î 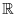 , multiplying both sides of (19) by
, multiplying both sides of (19) by  , noting
, noting
the desired inequality (17) follows.
Remark. The key point in Corollary 1 is that we choose the same weight q in (17) as that in (15). This will play a key role in the sequel when we deduce the sharp observability estimate for Kirchhoff plates.
In the sequel, for simplicity, we assume x0Î 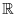 n \
n \  (For the general case where, possibly, x0Î
(For the general case where, possibly, x0Î  , we can modify an argument in [7, Case 2 in the proof of Theorem 5.1] to derive the same result). Hence
, we can modify an argument in [7, Case 2 in the proof of Theorem 5.1] to derive the same result). Hence
Also, for any b > 0, we set
It is easy to see that Q(t) decays rapidly to 0 as t ® 0 or t ® T. The desired pointwise Carleman-type estimate with singular weight Q for the wave operator reads as follows:
Theorem 1. Let u Î C2([0,T]× ) and v = qu. Then there exist four constants T0 > 0, l0 > 0, b0 > 0 and c0 > 0, independent of u, such that for all T > T0, b Î (0,b0) and l > l0 it holds
) and v = qu. Then there exist four constants T0 > 0, l0 > 0, b0 > 0 and c0 > 0, independent of u, such that for all T > T0, b Î (0,b0) and l > l0 it holds
with A and Y given by (16).
Remark. The main difference between the pointwise estimates (15) and (22) is that we introduce a singular ''pointwise'' weight in (22). As we will see later, this point plays a crucial role in the proof of Theorem 3 in the next section. Another difference between (15) and (22) is that T is arbitrary in the former estimate; while for the later one needs to take T0, and hence T, to be large enough.
Proof of Theorem 1. The proof is divided into several steps.
Step 1. We multiply both sides of inequality (15) by Q. Obviously, we have (recall (16) for A and Y)
Note that
Thus by (15), and using (23)-(24), we get
where B is given by (16).
Step 2. Recalling that  and Y are given respectively by (14) and (16), we get
and Y are given respectively by (14) and (16), we get
where
and
Thus, by (25) and (26), we have
Step 3. Let us show that F1, F2 and G are positive when l is large enough. For this purpose, we choose c Î (0,1) sufficiently small so that
and T( > 2R1) sufficiently large such that
Also, we choose
By (33) and recalling that c Î (0,4/5), it is easy to see that the nonsingular part 
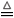 2(1-k) of F1 (resp.
2(1-k) of F1 (resp.
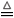 2(k+3-4c) of F1) is positive. Using (33) again, the nonsingular part of G reads
2(k+3-4c) of F1) is positive. Using (33) again, the nonsingular part of G reads
which, via the first inequality in (32), is positive provided that l is sufficiently large.
When t is near 0 and T, i.e., t Î I0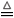 (0,d0)È(T-d0,T) for some sufficiently small d0Î (0,T/2), the dominant terms in Fi (i = 1,2) and G are the singular ones. For t Î I0, the singular part of F1 reads
(0,d0)È(T-d0,T) for some sufficiently small d0Î (0,T/2), the dominant terms in Fi (i = 1,2) and G are the singular ones. For t Î I0, the singular part of F1 reads
which, via the second inequality in (32), is positive provided that both d0 and l-1 are sufficiently small. Similarly, for t Î I0, the singular part of F2,
is positive provided that d0 is sufficiently small. Also, for t Î I0, the singular part of G reads
It is easy to see that, for t Î I0, it holds
which, via the second inequality in (32), is positive provided that both d0 and l-1 are sufficiently small.
By (27)-(29), we see that  and G = G0+G1. Since
and G = G0+G1. Since  ,
,  and G0 are positive, by the above argument, we see that F1, F2 and G are positive for t Î I0. For t Î (0,T)\I0, noting again the positivity of
and G0 are positive, by the above argument, we see that F1, F2 and G are positive for t Î I0. For t Î (0,T)\I0, noting again the positivity of  ,
,  and G0, one can choose b > 0 sufficiently small such that
and G0, one can choose b > 0 sufficiently small such that  ,
,  and G1 are very small, hence so that F1, F2 and G are positive. Hence (30) yields the desired (22). This completes the proof of Theorem 1.
and G1 are very small, hence so that F1, F2 and G are positive. Hence (30) yields the desired (22). This completes the proof of Theorem 1.
Similar to Theorem 1, by multiplying both sides of (17) by Q, we have
Theorem 2. Let p = p(t,x) Î C2([0,T]× ), and set q = qp. Then there exist two constants l0 > 0 and c0 > 0, independent of p, such that for all T > 0, b > 0 and l > l0it holds
), and set q = qp. Then there exist two constants l0 > 0 and c0 > 0, independent of p, such that for all T > 0, b > 0 and l > l0it holds
with and
and given by (18).
given by (18).
3 Sharp observability estimate
In this section we establish a sharp observability estimate for system (1).
For this purpose, for any fixed x0Î 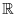 n\
n\ (As mentioned before, we do not really need to assume that x0 is out of
(As mentioned before, we do not really need to assume that x0 is out of  . Indeed, for the case where, possibly, x0Î
. Indeed, for the case where, possibly, x0Î  , we can modify an argument in [7, Case 2 in the proof of Theorem 5.1] to derive the same observability result in this section), we introduce the following set:
, we can modify an argument in [7, Case 2 in the proof of Theorem 5.1] to derive the same observability result in this section), we introduce the following set:
One of the main results in this paper is the following observability inequality with explicit dependence of the observability constant on the potential a for system (1):
Theorem 3. Let G0be given by (35) and p Î [5n/2,¥]. Then there is a constant C > 0 such that for any T > T0, with T0as in Theorem 1, and any a Î L¥(0,T;Lp(W;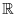 N×N)), the weak solution y of system (1) satisfies estimate (2) with the observability constant K(a) > 0 verifying
N×N)), the weak solution y of system (1) satisfies estimate (2) with the observability constant K(a) > 0 verifying
We now sketch the main points in the proof of Theorem 3. The first ingredient consists in decomposing the Kirchhoff plate equation into a coupled system of wave and elliptic equations as in (5) and to apply the pointwise estimates of the previous section in cascade. First, we apply Theorem 1 to z. Integrating (22) in Q, noting that Q(t) decays rapidly to 0 as t®0+ or t® T-, recalling that z|S = 0 (and hence Ñz =  n and zi =
n and zi =  ni on S), one may deduce that
ni on S), one may deduce that
with S0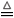 (0,T)×G0 and G0 being given in (35).
(0,T)×G0 and G0 being given in (35).
Similarly, applying Theorem 2 respectively to y and yt, we deduce that
and
It is easy to see that the term C òQq2Qz2dxdt (resp. CòQq2Qy2dxdt and CòQq2Q dxdt) in the right hand side of (37) (resp. (38) and (39)) can be absorbed by its left hand side. Hence, for any e0 > 0, (37) added first to e0l3×(38), then to e0l×(39), makes
dxdt) in the right hand side of (37) (resp. (38) and (39)) can be absorbed by its left hand side. Hence, for any e0 > 0, (37) added first to e0l3×(38), then to e0l×(39), makes
By taking e0 > 0 sufficiently small (which is independent of l), one can absorb the undesired terms Ce0òQq2Q(l3z2+lzt2)dxdt in the right hand side of (40) by its left hand side. Then, for this choice of e0 and taking taking l > 0 sufficiently large, one can absorb further the undesired terms CòQq2Qy2dxdt in the right hand side of (40). Consequently, we arrive at
Recalling z = y-Dy, one has
Combining (41) and (42), it follows
Now we have to get rid of the term  .
.
By the proof of [1, Theorem 2.2], for any e > 0, we have
By taking e small enough the first term  can be absorbed by the left hand side of (43). Then, for this choice of e and taking l sufficiently large, the term
can be absorbed by the left hand side of (43). Then, for this choice of e and taking l sufficiently large, the term
absorbed by l6òQq2Qy2dxdt. For this, we choose l such that
which yields l >  .
.
Therefore, recalling the definition of E(t) in (6), it follows from (43) that
Now, for ||a||p sufficiently large, put
Hence
Recall that p > 5n/2. Hence t0 is small when ||a||p is large. Therefore, by the definition of Q in (21), it is obvious that
By (9) and Lemma 1 (with s0 =  ), it follows that
), it follows that
Combining (45)-(48), and noting (46), it follows
Finally, the desired estimates (2) and (36) follow from (44) and (49).
4 An open problem on the optimality of the observability constant for Kirchhoff plate systems
In [5, Theorem 3], it is shown that when p = ¥ the observability constant P2(T, a) for the Euler-Bernoulli plate systems with at least two equations in even space dimensions n > 2 is optimal in what concerns the dependence on the potential a. The main idea to prove this optimality result is the same as that in [1], which is based on a suitable construction of u and q satisfying the following bi-Laplacian equation:
which decays at infinity sufficiently fast. More precisely, following Meshkov's construction [8, 5], we have the following result on u and q for (50):
Lemma 3. Let n> 2 be even. Then there exist two nontrivial complex-valued functions:
such that (50) is satisfied, and for some constant C:
One may expect that Lemma 3 can be applied to establish a similar optimality result for the observability constant K(a) for the Kirchhoff plate systems as well. However, this is an open problem. We now explain why the above Meshkov's construction does not seem to suffice for Kirchhoff plate systems. Based on the construction of u and q in Lemma 3, by suitable scaling and localization arguments, one can find a family of rescaled potentials aR(x) = R4q(Rx) with an L¥-norm of the order of R4 and a family of solutions uR(x) = u(Rx) of the corresponding bi-harmonic problem, with a decay of the order of
Without loss of generality we may assume that the boundary G (and therefore the observation subdomain G0) is included in the region |x| > 1. This yields a sequence of solutions of the bi-Laplacian system  in which the ratio between total energy and the energy concentrated in G0 and the norm of the boundary traces is of the order of exp(- R4/3). Taking into account that ||aR||¥ ~ R4, this ratio turns to be of the order of exp(-
in which the ratio between total energy and the energy concentrated in G0 and the norm of the boundary traces is of the order of exp(- R4/3). Taking into account that ||aR||¥ ~ R4, this ratio turns to be of the order of exp(- ). These solutions of the above mentioned bi-Laplacian system can be regarded also as solutions of the Kirchhoff plate system for suitable initial data. However, they do not fulfill homogeneous boundary conditions. Therefore, one needs to compensate them by subtracting the solution taking their boundary data and zero initial ones. In turn, one has to show that these solutions are as small as exp(-
). These solutions of the above mentioned bi-Laplacian system can be regarded also as solutions of the Kirchhoff plate system for suitable initial data. However, they do not fulfill homogeneous boundary conditions. Therefore, one needs to compensate them by subtracting the solution taking their boundary data and zero initial ones. In turn, one has to show that these solutions are as small as exp(- ) in the energy space
) in the energy space  . Due to the infinite speed of propagation, this can be easily done for the Euler-Bernoulli plate systems during a time interval of the order of T > µ
. Due to the infinite speed of propagation, this can be easily done for the Euler-Bernoulli plate systems during a time interval of the order of T > µ  (because it suffices to use the energy estimate, which yields an exponential growth exp(-T
(because it suffices to use the energy estimate, which yields an exponential growth exp(-T  ) for the energy evolution in a very short time). However, the same approach fails for Kirchhoff plate systems since, in order that the (boundary) observability estimate for these systems to hold, one needs to take the time T to be large enough. In fact, the key point is that, at this level the energy estimate yields an exponential growth exp (-T
) for the energy evolution in a very short time). However, the same approach fails for Kirchhoff plate systems since, in order that the (boundary) observability estimate for these systems to hold, one needs to take the time T to be large enough. In fact, the key point is that, at this level the energy estimate yields an exponential growth exp (-T  ) for the energy evolution, and it has to be used in the whole time duration [0, T ]. This breaks down the concentration effect that Meshkov's construction guarantees.
) for the energy evolution, and it has to be used in the whole time duration [0, T ]. This breaks down the concentration effect that Meshkov's construction guarantees.
Received: 01/IX/06. Accepted: 01/X/06.
#690/06.
- [1] D. Duyckaerts, X. Zhang and E. Zuazua, On the optimality of the observability inequality for parabolic and hyperbolic systems with potentials. Ann. Inst. H. Poincaré Anal. Non Linéaire, to appear.
- [2] E. Fernández-Cara and L. de Teresa, Null controllability of a cascade system of parabolic-hyperbolic equations. Discrete Contin. Dyn. Syst., 11 (2004), 699-714.
- [3] E. Fernández-Cara, S. Guerrero, O.Yu. Imanuvilov and J.-P. Puel, Local exact controllability of the Navier-Stokes system. J. Math. Pures Appl., 83 (2004), 1501-1542.
- [4] X. Fu, J. Yong and X. Zhang, Exact controllability for the multidimensional semilinear hyperbolic equations, in submission.
- [5] X. Fu, X. Zhang and E. Zuazua, On the optimality of the observability inequalities for plate systems with potentials, in Phase Space Analysis of Partial Differential Equations, A. Bove, F. Colombini and D. Del Santo (Eds.), Birkhäuser, (2006), 117-132.
- [6] J.L. Lions, Contrôlabilité exacte, stabilisation et perturbations de systčmes distribués, Tome 1, RMA 8, Paris, 1988.
- [7] A. López, X. Zhang and E. Zuazua, Null controllability of the heat equation as singular limit of the exact controllability of dissipative wave equations. J. Math. Pures Appl., 79 (2000), 741-808.
- [8] V.Z. Meshkov, On the possible rate of decrease at infinity of the solutions of second-order partial differential equations, (Russian). Mat. Sb., 182 (1991), 364-383; translation in Math. USSR-Sb., 72 (1992), 343-361.
- [9] M. Yamamoto and X. Zhang, Global uniqueness and stability for an inverse wave source problem with less regular data. J. Math. Anal. Appl., 263 (2001), 479-500.
- [10] E. Zuazua, Exact controllability for semilinear wave equations in one space dimension. Ann. Inst. H. Poincaré Anal. Non Linéaire, 10 (1993), 109-129.
- [11] E. Zuazua, Controllability and observability of partial differential equations: some results and open problems, in Handbook of Differential Equations: Evolutionary Differential Equations, vol. 3, C. Dafermos and E. Feireisl (Eds.), Elsevier Science, (2006), 527-621.
Publication Dates
-
Publication in this collection
19 Mar 2007 -
Date of issue
2006
History
-
Accepted
01 Oct 2006 -
Received
01 Sept 2006





































































