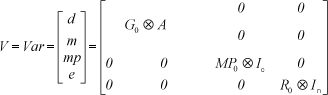Abstracts
Growth curves of Nellore cattle were analyzed using body weights measured at ages ranging from 1 day (birth weight) to 733 days. Traits considered were birth weight, 10 to 110 days weight, 102 to 202 days weight, 193 to 293 days weight, 283 to 383 days weight, 376 to 476 days weight, 551 to 651 days weight, and 633 to 733 days weight. Two data samples were created: one with 79,849 records from herds that had missing traits and another with 74,601 from herds with no missing traits. Records preadjusted to a fixed age were analyzed by a multiple trait model (MTM), which included the effects of contemporary group, age of dam class, additive direct, additive maternal, and maternal permanent environment. Analyses were carried out by a Bayesian method for all nine traits. The random regression model (RRM) included the effects of age of animal, contemporary group, age of dam class, additive direct, permanent environment, additive maternal, and maternal permanent environment. Legendre cubic polynomials were used to describe random effects. MTM estimated covariance components and genetic parameters for birth weight and sequential weights and RRM for all ages. Due to the fact that covariance components based on RRM were inflated for herds with missing traits, MTM should be used and converted to covariance functions.
beef cattle; multiple trait; random regression
Curvas de crescimento de gado Nelore foram analisadas com base nos pesos corporais coletados do nascer aos 733 dias de idade. As características consideradas foram peso ao nascer e pesos dos 10 aos 110, dos 102 aos 202, dos 193 aos 293, dos 283 aos 383, dos 376 aos 476, dos 467 aos 567, dos 551 aos 651 e dos 633 aos 733 dias de idade. Duas amostras foram geradas: a primeira, constituída de 79.849 medidas, continha dados de rebanhos com informações perdidas, e a segunda, de 74.601 medidas, originou-se de rebanhos com informações completas. Os pesos pré-ajustados para as idades fixas foram analisados por meio de um modelo de características múltiplas (MTM), com nove características, no qual se incluíram efeitos de grupo contemporâneo, classe de idade da vaca, aditivo direto, aditivo materno e ambiente materno permanente. Polinômios cúbicos de Legendre foram utilizados em um modelo de regressão aleatória (RRM), no qual foram incluídos efeitos de idade do animal, grupo contemporâneo, classe de idade da vaca, aditivo direto, ambiente permanente, aditivo materno e ambiente materno permanente. Tendo em vista que os componentes de covariância baseados em RRM são influenciados por informações perdidas, recomendam-se o MTM e a conversão desses componentes em funções de covariância.
bovinos de corte; características múltiplas; regressão aleatória
Analyses of growth curves of Nellore cattle by Bayesian method via Gibbs sampling
Análises de curvas de crescimento de gado Nelore pela metodologia Bayesiana via Gibbs sampling
P.R.C. NobreI; P.S. LopesII; R.A. TorresII; L.O.C. SilvaIII; A.J. RegazziII; R.A.A.Torres JúniorIII; I. MisztalIV
IFundapam - Geneplus BR 262, km 4 79002-970 - Campo Grande, MS
IIUniversidade Federal de Viçosa - Viçosa, MG
IIIEmbrapa Gado de Corte - Campo Grande, MS
IVUniversity of Georgia - USA
ABSTRACT
Growth curves of Nellore cattle were analyzed using body weights measured at ages ranging from 1 day (birth weight) to 733 days. Traits considered were birth weight, 10 to 110 days weight, 102 to 202 days weight, 193 to 293 days weight, 283 to 383 days weight, 376 to 476 days weight, 551 to 651 days weight, and 633 to 733 days weight. Two data samples were created: one with 79,849 records from herds that had missing traits and another with 74,601 from herds with no missing traits. Records preadjusted to a fixed age were analyzed by a multiple trait model (MTM), which included the effects of contemporary group, age of dam class, additive direct, additive maternal, and maternal permanent environment. Analyses were carried out by a Bayesian method for all nine traits. The random regression model (RRM) included the effects of age of animal, contemporary group, age of dam class, additive direct, permanent environment, additive maternal, and maternal permanent environment. Legendre cubic polynomials were used to describe random effects. MTM estimated covariance components and genetic parameters for birth weight and sequential weights and RRM for all ages. Due to the fact that covariance components based on RRM were inflated for herds with missing traits, MTM should be used and converted to covariance functions.
Keywords: beef cattle, multiple trait, random regression
RESUMO
Curvas de crescimento de gado Nelore foram analisadas com base nos pesos corporais coletados do nascer aos 733 dias de idade. As características consideradas foram peso ao nascer e pesos dos 10 aos 110, dos 102 aos 202, dos 193 aos 293, dos 283 aos 383, dos 376 aos 476, dos 467 aos 567, dos 551 aos 651 e dos 633 aos 733 dias de idade. Duas amostras foram geradas: a primeira, constituída de 79.849 medidas, continha dados de rebanhos com informações perdidas, e a segunda, de 74.601 medidas, originou-se de rebanhos com informações completas. Os pesos pré-ajustados para as idades fixas foram analisados por meio de um modelo de características múltiplas (MTM), com nove características, no qual se incluíram efeitos de grupo contemporâneo, classe de idade da vaca, aditivo direto, aditivo materno e ambiente materno permanente. Polinômios cúbicos de Legendre foram utilizados em um modelo de regressão aleatória (RRM), no qual foram incluídos efeitos de idade do animal, grupo contemporâneo, classe de idade da vaca, aditivo direto, ambiente permanente, aditivo materno e ambiente materno permanente. Tendo em vista que os componentes de covariância baseados em RRM são influenciados por informações perdidas, recomendam-se o MTM e a conversão desses componentes em funções de covariância.
Palavras-chave: bovinos de corte, características múltiplas, regressão aleatória
INTRODUCTION
One of the most popular topics in beef breeding currently is modeling continuous growth via longitudinal models (Meyer, 2000). In such models, weights at any age can be accommodated, and predictions can be obtained for any day of life. The application of such models requires knowledge of variance components. Additionally, decisions need to be made regarding the complexity of the model as growth can be approximated by many different functions.
Traditionally, variance components were estimated by restricted maximum likelihood - REML (Thompson, 1973; Sorensen, Kennedy, 1984). This method has good properties under selection and software packages are available. Unfortunately, computing with REML is very intensive, prohibiting use with more than a few traits at a time and with larger data sets. Also, REML formulas are very complicated to develop for less traditional models. Parameters estimated by REML are modes of joint restricted likelihood and asymptotic standard deviations.
The emergence of Gibbs sampling (GS) led to the growing popularity of Bayesian methodology. With Bayesian methodology (BM), one can obtain functions of marginal distributions for any parameter; such functions include means, modes, standard deviations, and high posterior density intervals. Formulas to implement GS are relatively simple even for complicated models. With optimization, BM via GS can be used to analyze much larger data sets and with more traits than REML.
With proper implementation, convergence of REML formulas is easily established. With BM via GS, iterations should continue beyond the burn-in period and until enough effective samples of required parameters are obtained. However, formulas to establish the burn-in and the number of effective samples do not seem perfect (Schaeffer, 1998). In practice, the convergence of GS depends on the data structure. While the convergence is very fast in simulated models, it might be drastically reduced with actual data sets, where traits are missing and pedigrees are incomplete.
Despite theoretically better properties of BM-GS, REML and BM-GS usually result in very similar parameter estimates. Differences are usually treated with suspicion and are generally believed to be due to incomplete convergence or incorrect implementation of BM-GS.
Nobre (2001) analyzed nine sequential weights of Nellore cattle by REML using random regression and multiple trait models. In the last model, computing costs limited estimation to the most five traits at a time.
Two data sets were used: one with all traits present and the other with traits successively missing; the ninth trait had only 3.8% of records present. These models and data sets are ideal to compare computing properties of implementations of REML and BM-GS. The purpose of this study was to obtain genetic parameters for sequential growth of beef cattle using RRM with data sets containing missing observations and to make comparisons with their estimates by REML.
MATERIALS AND METHODS
Data were collected by the Brazilian Zebu Breeders Association (ABCZ) and provided by the Brazilian Agricultural Research Corporation (EMBRAPA). The data consisted of records on 619,989 Nellore animals, progeny of 11,847 sires, and 273,263 dams raised under Brazilian pasture conditions. The records were collected from 1975 to 1999.
Traits considered were birth weight (BW), 10 to 110 d weight (W1 or weight at 60 d), 102 to 202 d weight (W2 or weight at 152 d), 193 to 293 d weight (W3 or weight at 243 d), 283 to 383 d weight (W4 or weight at 333 d), 376 to 476 d weight (W5 or weight at 426 d), 467 to 567 d weight (W6 or weight at 517 d), 551 to 651 d weight (W7 or weight at 601 d), and 633 to 733 d weight (W8 or weight at 683 d).
Edits included eliminating records of animals outside the range of three standard deviations from the overall mean for each weight, and eliminating records outside of the range in age classes provided above. Table 1 summarizes characteristics of the data set.
Dams in the data were 1.5 through 20 years of age at calving. Classes of age of dam were defined every year, but the first class was for dams whose age at calving was less than three years, and the last class was for dams whose age at calving was greater than 15 years. The season of measurement was defined every three months, i.e., October to December; January to March; April to June; and July to September, respectively.
Two sample data sets were formed by randomly sampling herds; one with missing traits from all herds and one with no missing traits from herds with no missing traits. The first data set was obtained from herds with more than 500 birth weight records and an average contemporary size group greater than 25 within each herd. The second data set was obtained from herds with more than 50 birth weight records and an average contemporary group size greater than 5 within each herd. Single record contemporary groups were eliminated, and then 7.5% and 5% of the herds that remained were sampled from both samples, respectively. The number of animals in the pedigree file was 20,186 and 16,161 for the samples, respectively. Both samples are described in Table 2.
Two models (MTM and RRM) were used for analyses. The multiple trait model (MTM) was:
where y was a vector of records preadjusted to fixed age; b was a vector of fixed effects (contemporary group and age of dam class); d was a vector of additive direct genetic random effects of the animal; m was a vector of additive maternal genetic random effects; mp was a vector of random effects of maternal permanent environment; X was the incidence matrix for fixed effects; Z1 , Z2 , and Z3 were incidence matrices for animal, maternal, and maternal permanent environmental effects, respectively; and e was the vector of residual random effects.
The variances and covariances were defined as follows:
where G0 was a covariance matrix of random genetic effects; MP0 was a covariance matrix of random maternal permanent environmental effects; R0 was a covariance matrix of random residual effects; A was the additive genetic relationship matrix; Ic was an identity matrix whose order was the number of dams; In was an identity matrix whose order was the number of animals; and  was the direct product operator.
was the direct product operator.
(Co)variance components were estimated for nine traits at a time by the GIBBS2F90 program (Misztal, 2001). The chain length was 100,000 and the burn-in period was 40,000 for both samples.
The random regression model (RRM) was defined as follows:
where yijklm was the observation in contemporary group i, age of dam class j, animal k, dam l, and record m; b d was the fixed regression coefficient d for age of animal; cgdi was the fixed regression coefficient d for contemporary group i; caddj was the fixed regression coefficient d for age of dam class j; ddk and pdk were random regression coefficients d for additive direct and permanent environmental effects of animal k; mdl and mpdl were random regression coefficients d for additive maternal and maternal permanent environmental effects of dam l; rdm was the random regression coefficient d for residual effect of record m; zd , zdi , zdj , zdk , zdl , and zdm were Legendre polynomials; and e ijklm was residual effect.
The random regression model could be written in matrix notation as:
where y was the vector of records; b was the vector of fixed regressions; d, p, m, mp, and r were vectors for additive direct genetic, permanent environment, additive maternal genetic, maternal permanent environment and residual effects, respectively; X was the incidence matrix for fixed effects; and Z1, Z2, Z3, Z4, and Z5 were incidence covariate matrices for additive direct genetic, permanent environment, additive maternal genetic, and maternal permanent environment effects, respectively; and e was a vector of constant residual effects.
The variances and covariances were defined as follows:
where G0 was an 8 x 8 covariance matrix of random regression for genetic effects; P0, MP0 and R0 were 4 x 4 covariance matrices of random regression for permanent environment, maternal permanent environment and residual effects, respectively;  was assumed constant residual variance; A was additive genetic relationship matrix; Ik was an identity matrix whose order is the number of animals; Il was an identity matrix whose order was the number of dams; Im was an identity matrix whose order was the number of records; In was the number of records; and
was assumed constant residual variance; A was additive genetic relationship matrix; Ik was an identity matrix whose order is the number of animals; Il was an identity matrix whose order was the number of dams; Im was an identity matrix whose order was the number of records; In was the number of records; and  was the direct product operator.
was the direct product operator.
(Co)variance components for the RRM were estimated by the GIBBS2F90 program (Misztal, 2001). The chain length was 50,000 and the burn-in period was 10,000 for both samples.
RESULTS AND DISCUSSION
Table 3 shows a summary of the mean covariance components estimated at different ages for missing traits and no missing traits with multiple trait model (MTM) analyses. The estimates of the additive direct variance for weight at different ages increased over all ages. However, when calculated for missing traits the values were greater than when estimated for no missing traits. Also, additive maternal variance components increased across all ages for missing traits. The estimates for both samples were consistent and presented a small increment after the age at 243 days. The estimates of direct and maternal additive covariance components decreased over time with MTM for missing traits and were variable for no missing traits.
The maternal permanent environment variance was higher for missing traits. The values increased over all ages, as did the additive maternal variance components for this sample. Residual variance components increased over ages for the two samples. The values for missing traits were higher than those for no missing traits. The residual variance components for no missing traits were more consistent than those for missing traits as well.
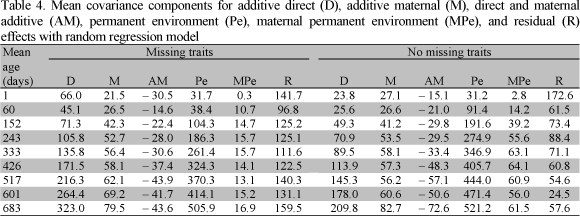
Estimates obtained with random regression model (RRM) are shown in Table 4 for missing and no missing traits. Estimates of the phenotypic variance for weights with RRM were greater than those calculated with the MTM for no missing traits for all ages, and only for the first ages (before 243 days) for missing traits. The additive direct variance at birth weight was higher when estimated by RRM than it was by MTM, not only for missing traits, but also for no missing traits. This might be an indication that birth weight is a different trait. After this age (one day) all estimates increased over all ages; however, additive maternal variance components were higher with MTM than with RRM when estimated for missing traits. In addition, the values obtained with MTM increased across all ages, while with RRM they were stable. The estimates of direct and maternal additive covariance with RRM for both samples decreased as age increased, and the values presented a slight variation among ages.
The maternal permanent environment variance showed a similar trend with both models and samples; small variation was observed after 243 days of age. On the other hand, the residual (permanent environment plus error) components with the RRM were not consistent over all ages for herds with missing traits. However, the residual (permanent environment plus error) components with RRM were higher than those with MTM for no missing traits. The estimates with RRM for the first weight (birth weight) and for the last weight (633 to 733 days) might be overestimated. The reason may be chain length insufficient, and also at 683 days the number of records reduced the degree of freedom.
Variance components calculated with MTM show that residual and additive direct variance components increased over ages. However, additive maternal and maternal permanent environment variances showed little change over the growth of the animals, not only for missing traits, but also for no missing traits.
The results with RRM are in partial agreement with those reported by Grignola et al. (1998) and Meyer (1999). Values of variance or covariance components implausible at the extremes of the ages in the data were also reported by Meyer (1999). According to the author, this could be in part explained by small numbers of observations and sampling variation in the partitioning of total variation. In the same study, Meyer (1999) suggested that this is likely to be caused by the large effect that values furthest from the mean have in a regression analysis, and then reported that a transformation of ages to logarithmic scale reduced the influence of the later ages in the data.
There was little difference in estimates of covariance components for additive direct and additive maternal between the models. Similarly, there was good agreement between maternal permanent environment and residual covariance components estimated at different ages with the two models.
The estimates for no missing traits were similar to those reported by Nobre (2001). The mean covariance components for additive maternal, direct and maternal additive, and maternal permanent environment were slightly lower than those by REML. This most likely was caused by insufficient chain length.
In this study the memory requirements of an optimized Bayesian analysis via Gibbs sampling was low enough for a nine or more traits in multiple trait analysis. However, running time was very long. A chain size of 100,000 seemed sufficient for a multiple trait analysis for missing traits but insufficient for no missing traits. A chain size of 50,000 seemed insufficient for a cubic random regression model. The analyses of convergence as done visually for the burn in and formulas for the number of effective samples may be misleading with the result that the end of burn-in may be pronounced too early and the number of effective samples may be larger for analysis of more complete than incomplete data. Analyses using BM via GS need to be designed and scrutinized carefully. For analyzes with standard models where inferences on shapes of parameters are not important, analyses by REML may be more robust.
Table 5 presents the additive direct and additive maternal genetic correlations obtained by MTM from both samples, respectively. The additive direct genetic correlations were positive for both samples. Additive direct correlations between birth weight and all other weights and between the weight at 60 days and all other weights were higher for missing traits than those for no missing traits. On the contrary, after the weight at 152 days, most of the additive direct genetic correlations for no missing traits were higher than those for missing traits.
Alenda and Martin (1987) and Garrick et al. (1989) reported estimates with similar magnitude to those reported in this study. On the other hand, Meyer (1995) reported correlations between additive direct genetic effects for growth close to 1.
The estimates of the additive maternal genetic correlations estimated with MTM are presented in Table 5. All the values were positive, but the magnitudes were moderate. Additive maternal genetic correlations between birth weight (one day) and all the other weights were smaller than those between all the other weights for both samples. In addition, values estimated for no missing traits were lower than those for missing traits. In general, the estimates decreased after the weight at 243 days. However, these values are in agreement with those obtained by Garrick et al. (1989), Waldron et al. (1993) and Eler et al. (1995). Additive maternal genetic effects that are not important for birth weight and small for weaning weight were reported by Meyer (1995).
The additive direct and additive maternal correlations with RRM for both samples are presented in Table 6. The additive direct genetic correlations with RRM were all positives. The estimates of the additive direct genetic correlations with RRM were not consistent for early ages. After the weight at 152 days these estimates were higher than those with MTM for missing traits. However, the estimates of the additive direct genetic correlations with RRM and no missing traits were higher than those with MTM for all ages. The estimates of the additive maternal genetic correlations with RRM were not consistent at birth weight with no missing traits. After this age (one day) all additive maternal genetic correlations were higher than those with MTM. On the other hand, additive maternal genetic correlations with RRM for missing traits were higher than those with MTM over the traits (Tables 5 and 6). In addition, for the same age the correlations were higher for early ages and lower for later ages. The highest estimates were obtained after the weight at 243 days with both models.
The estimates for additive direct genetic correlations for no missing traits were slightly higher than those for missing traits. In addition, lower correlations were estimated with RRM for both samples based on birth weight. This weight showed low correlation with other weights after the weight at 243 days. The correlations based on weight at 365 days were slightly higher when estimated for no missing traits.
The estimates for additive maternal genetic correlations for missing traits were slightly higher than those for no missing traits. The correlations between birth weight and other weights were lower than those based on the weight at 365 days and 733 days. Higher values were estimated with weight at 365 days, and those estimated with weight at 733 were moderate in magnitude.
The mean additive direct and additive maternal heritabilities at different ages based on MTM from both samples for the sequential weights are presented in Table 7. The highest additive direct heritability with MTM was at the last weights, not only for missing traits, but also for no missing traits. The average estimate with MTM for missing traits was 28.0 and for no missing traits was 19.3. The highest additive maternal heritability estimated from herds with missing traits was at early weights, and the average heritability for this sample 17.3; for no missing traits the highest additive maternal heritability was at the weight at 152 days. The average for the additive maternal heritability based on this sample was 17.6.
Heritability estimates additive direct and additive maternal, for birth weight from both samples with MTM may be biased because when this weight is not recorded producers can submit a breed average estimate for each sex. In addition, the estimates for additive maternal effect were slightly higher than previous results reported by Waldron et al. (1993) and Eler et al. (1995) when estimated with multiple trait models.
Table 8 shows the mean estimates of the heritabilities,additive direct and additive maternal, at different ages with RRM from both sample.
The additive direct heritabilities estimated with RRM (Table 8) were similar to those estimated with MTM (Table 7). On the other hand, additive maternal heritability obtained using RRM showed a small variation, ranging from 7 to 12 for both samples. The estimates of heritability for additive direct and additive maternal effects were slightly higher for both samples with MTM.
The additive direct heritabilities estimated with RRM (Table 8) were similar to those estimated with MTM (Table 7). On the other hand, additive maternal heritability obtained using RRM showed a small variation, ranging from 7 to 12 for both samples. The estimates of heritability for additive direct and additive maternal effects were slightly higher for both samples with MTM.'
Using RRM, the estimates of heritability for additive maternal effects decreased in importance after the weight at 243 days. This result is in agreement with the majority of reports in the literature (Garrick et al., 1989; Waldron et al., 1993; Robinson, 1996a).
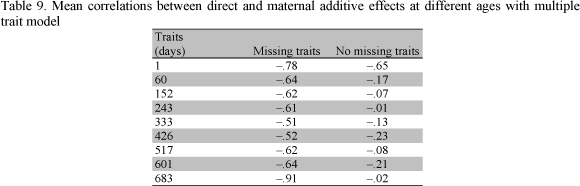
Table 9 reports the mean estimates of the correlations between direct and maternal additive effects from MTM for the two samples. The magnitude of the correlation between direct and maternal additive genetic effects was negative across models and ages with both samples. Similarly, with MTM, Vesely and Robinson (1971), Bertrand and Benyshek (1987), Trus and Wilton (1988), Garrick et al. (1989), Eler et al. (1995), Robinson (1996a) and Mattos et al. (2000) reported negative correlations between direct and maternal additive effects.
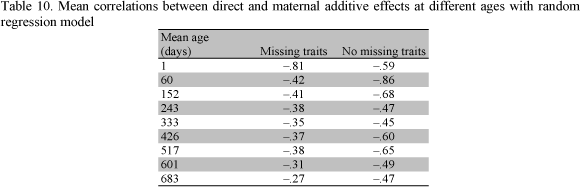
The mean estimates of the correlation between direct and maternal additive effects with RRM from both samples are presented in Table 10. The correlations estimated using MTM for missing traits were higher than those for no missing traits. These values presented a small variation when based on RRM with both samples.
The sign and magnitude of the genetic correlation between direct and maternal additive effects of growth traits is critical. According to Willham (1980) the estimation of additive maternal effects and their covariance components is inherently problematic since additive direct and additive maternal effects are generally confounded. Also, the expression of the additive maternal effects is sex limited, and occurs late in life of the female and lags by one generation. Robinson (1996b) reported that estimates of direct and maternal additive correlations may be negative not only because of genetic antagonisms, but also because of additional sire or sire x year variation or negative dam-offspring covariances. The author concluded that these causes will often be difficult to distinguish from true negative genetic correlations. The best method of detection is to fit the alternative models and assess their significance using likelihood ratio tests.
Moderate to large estimates of direct and maternal additive genetic correlations in this study indicate that these may have been inflated by such environmental covariance, i.e., the models of analyses considered may not have been comprehensive enough (Meyer, 1992).
The results of analyses using the two samples were quite different. While parameters obtained from no missing traits were generally less erratic than those from missing traits, they also resulted in values of direct and maternal additive genetic correlations that approached unrealistic values. The estimates from no missing traits showed artifacts for older ages and large differences between genetic correlations among earlier and later ages. An improvement could be obtained by using a data set with few missing traits and good connections between the direct and maternal effects. Results in this study should be viewed as trends rather than absolute values, and no definite "true" parameters should be expected. When many samples of the same population are analyzed, sampling variance may be quite large as reported by Mattos et al. (2000).
Growth curves in this study by RRM with missing traits showed larges increases of variance at later ages. It is likely that real data sets have many missing traits, and that data without missing traits are obtained by elimination of incomplete records. Use of selected data in analyses may result in selection bias. If an evaluation by RRM is desired, estimates of parameters by RRM may be not satisfactory.
One question in this study is whether cubic polynomials provided sufficient fit for RRM although the application of higher order polynomials is not possible because of excessive costs. The assumption of non-zero direct and maternal genetic correlation resulted in 8 x 8 (co)variance matrices for the genetic component, or as large required by seventh order polynomials if zero correlation was assumed. After examining tables for RRM, it seems that the cubic regressions allowed for sufficiently realistic modeling of curves of variances and correlations for the additive direct and additive maternal effects, and that artifacts were mainly due to special data structure. One possible exception is direct and maternal additive correlation, which seemed to be inflated with RRM as compared to MTM for both data sets.
Several strategies may be used for obtaining "better" estimates. One could be to use larger, more carefully selected data. Another strategy would be to use functions other than polynomials that are less susceptible to artifacts (i.e., frational polynomials as applied by Robert-Granié et al., 2002). In yet another strategy, multiple trait parameters could be "smothed" and converted to an RRM scale (Lidauer, Mäntysaari, 1999). Finally, the parameters by RRM could be constructed based on estimates from multiple trait and random regression models, and literature information (i.e., as in Misztal et al., 2000). With multiple trait methodology, parameters estimated for birth weight are optimal because that trait is obtained at the same age and subsequently no preadjustment is necessary. To ensure that evaluation of birth weight by RRM is optimal, it may be necessary to "adjust" RRM parameters so they would equal those of multiple trait for birth weight.
CONCLUSIONS
A complete multiple trait model with the number of traits equal to the number of ages would result in a highly overparameterised analysis. As a consequence, this would be likely to impose unnecessary computational demands. The results of analyses using the two data samples were quite different. When some records are missing, the variances associated with ages of most missing records become erratic, and all correlations fluctuate. When connections between the additive direct and additive maternal effects are weak, the correlations between the direct and maternal additive effects become more negative. Random regression models are more susceptible to artifacts due to data problems than multiple trait models. If a random regreesion model is to be used for genetic evaluation, genetic parameters estimated by random regression models may have to be adjusted based on estimates from multiple trait models and literature information.
Recebido para publicação em 29 de julho de 2002
Recebido para publicação, após modificações, em 12 de março de 2003
E-mail: geneplus@cnpgc.embrapa.br
- ALENDA, R.; MARTIN, T.G. Genetic parameters and consequences of selection for growth traits in a beef herd selected for yearling weight. J. Anim. Sci., v.70, p.734-741, 1987.
- BERTRAND, J.K.; BENYSHEK, L.L. Variance and covariance estimates for maternally influenced beef growth traits. J. Anim. Sci., v.64, p.728-734, 1987.
- ELER, J.P.; VAN VLECK, L.D.; FERRAZ, J.B.S. et al. Estimation of variances due to direct and maternal effects for growth traits of Nelore cattle. J. Anim. Sci., v.73, p.3253-3258, 1995.
- GARRICK, D.J.; POLLACK, E.J.; QUAAS, R.L. et al. Variance heterogeneity in direct and maternal weight traits by sex and percent purebred for Simmental-sired calves. J. Anim. Sci., v.67, p.2515-2518, 1989.
- GRIGNOLA, F.E.; JAMROZIK, J.; VARONA, L. et al. A random regression approach to estimate variance components for longitudinal records in beef cattle via Gibbs sampling. J. Anim. Sci., v.76, suppl. 1, p.57, 1998. (Abstr.).
- LIDAUER, M.; MÄNTYSAARI, E. Multiple trait reduced rank random regression test-day model for production traits. Proceedings…, INTERBULL MTG. INTERBULL CENTER, Uppsala, Sweden, 1999. V.22, p.74-80.
- MATTOS, D.; BERTRAND, J.K.; MISZTAL, I. Investigation of genotype by environment interactions for weaning weight for Herefords in three countries. J. Anim. Sci., v.78, p.2121-2126, 2000.
- MEYER, K. Estimates of genetic and phenotypic covariance functions for postweaning growth and mature weight of beef cows. J. Anim. Breed. Genet., v.116, p.181-205, 1999.
- MEYER, K. Estimates of genetic parameters and breeding values for New Zealand and Australian Angus cattle. Aust. J. Agric. Res., v.46, p.1219-1229, 1995.
- MEYER, K. Random regression to model phenotypic variation in monthly weights of Australian beef cows. Livest. Prod. Sci., v.65, p.19-38, 2000.
- MEYER, K. Variance components due to direct and maternal effects for growth traits of Australian beef cattle. Livest. Prod. Sci., v.31, p.179-204, 1992.
- MISZTAL, I. GIBBS2F90 manual. Available at: ftp://nce.ads.uga.edu/pub/ ignacy/blupf90/ 2001. Accessed Mar 22, 01.
- NOBRE, P.R.C. Analyses of sequential weights of Nellore cattle using multiple trait and random regressions models. 2001. Tese (Doutorado). Universidade Federal de Viçosa. Viçosa, MG.
- ROBERT-GRANIÉ, C.; MAZA, R.; FOULLEY, J.L. Use of fractional polynomial for modelling somatic cell scores in dairy cattle. In: WORLD CONGRESS GENETIC APPLIED LIVESTOCK PRODUCTION, 7, 2002. Proceedings… 2002. CDROM.
- ROBINSON, D.L. Estimation and interpretation of direct and maternal genetic parameters for weights of Australian Angus cattle. Livest. Prod. Sci., v.45, p.1-11, 1996a.
- ROBINSON, D.L. Models which might explain negative correlations between direct and maternal genetic effects. Livest. Prod. Sci., v.45, p.111-122, 1996b.
- SCHAEFFER, L.R. Variance component estimation course notes. Armidale: University of New England, Armidale, 1998.
- SORENSEN, D.A.; KENNEDY, B.W. Estimation of response to selection using least-squares and mixed model methodology. J. Anim. Sci., v.58, p.1097-1106, 1984.
- THOMPSON, R. The estimation of variance and covariance components with an application when records are subject to culling. Biometrics, v.29, p.527-550, 1973.
- TRUS, D.; WILTON, J.W. Genetic parameters for maternal traits in beef cattle. Can. J. Anim. Sci., v.68, p.119-128, 1988.
- VESELY, J.A.; ROBINSON, O.W. Genetic and maternal effect on preweaning growth and type score in beef calves. J. Anim.Sci., v.32, p.825-831, 1971.
- WALDRON, D.F.; MORRIS, C.A.; BAKER, R.L. et al. Maternal effects for growth traits in beef cattle. Livest. Prod. Sci., v.34, p.57-70, 1993.
- WILLHAM, R.L. Problems in estimating maternal effects. Livest. Prod. Sci., v.7, p.405-418, 1980.
Publication Dates
-
Publication in this collection
12 Nov 2003 -
Date of issue
Aug 2003
History
-
Received
29 July 2002 -
Accepted
12 Mar 2003