Resumos
Com o objetivo de testar modelos genéticos alternativos ao aditivo-dominante em populações multirraciais, foram utilizadas informações do peso ao sobreano (PS) de 35.931 novilhos, filhos de 752 touros e 30.535 vacas das raças Aberdeen Angus (A) e Nelore (N) e de diversos grupos genéticos possíveis por meio do cruzamento entre elas. Foram testados cinco diferentes modelos (M) genéticos: o M1 continha o efeito genético fixo aditivo direto (AD), heterozigótico direto (HD), epistático direto (ED) e aditivo-conjunto direto (ACD); o M2, igual ao M1, menos o efeito ACD; o M3, igual ao M1, menos o efeito ED; o M4, igual ao M1, menos os efeitos ED e ACD; e o M5, igual ao M1, menos os efeitos HD, ED e ACD. Os modelos foram submetidos a três métodos de análise diferentes: método dos quadrados mínimos (MQM), regressão de cumeeira (RC) e máxima verossimilhança restrita (REML). O método de RC produziu estimativas de coeficientes com magnitudes e sinais explicados biologicamente. As estimativas dos efeitos, das (co)variâncias, dos parâmetros e dos valores genéticos diferiram entre os modelos, indicando a importância da correta escolha do modelo de análise, devendo-se ter conhecimento prévio do fenômeno estudado e sua interpretação biológica e sempre preceder à escolha de um modelo de análise genética multirracial o estudo da relação existente entre as variáveis independentes. Importantes efeitos adicionais ao efeito AD foram acrescentados pelas inclusões dos efeitos HD e ED aos modelos de análise. A notação matemática dos efeitos ACD, aplicada atualmente na literatura e testada neste estudo, não foi capaz de explicar a complementaridade entre raças como esperado, havendo problemas com casos de multicolinearidade entre os efeitos estudados
complementaridade entre raças; efeito aditivo; epistasia; heterozigose; peso ao sobreano
In order to evaluate alternative genetic models to the additive dominant model, weights at yearling (PS) of 35,931 animals, sired by 752 bulls and 30,535 cows of Aberdeen Angus (A) and Nellore (N) breeds and the genetic groups from their crosses were used. Five different genetic models (M) were tested: M1, containing the direct additive fixed genetic effect (DA), heterozygote direct (HD), epystatic direct (ED), and direct joint additive direct (DJA); M2 was equal to M1, excluding DJA effect; M3 was equal to M1, excluding ED effect; M4 was equal M1, excluding ED and ACD effects, and M5 was equal to M1, excluding HD, ED, and DJA effects. The models were analyzed by different methods: Least Square Means Method (MQM), Ridge Regression Method (RC), and Restricted Maximum Likelihood Method (REML). Estimated coefficients by RC showed magnitude and sign which were biologically explained. The estimates of the covariances, parameters, and genetic values varied among the models, indicating the importance of the correct choice of the model for analysis, being necessary a previous knowledge of the studied phenomenon and its biological interpretation. Besides, it should always be considered the relationship between the independent variables before choosing a multibreed genetic analysis model. Important additional effects to the DA effect were considered by the inclusion of the HD and ED effects to the models for analysis. The DJA math notation, currently used in the literature and tested in the present study, was not able to explain the breed complementarity, due to the multi colinearity among the studied effects
additive effect; between breeds complementarily; epystatic effect; heterozygote effect; yearling weight
ZOOTECNIA E TECNOLOGIA E INSPEÇÃO DE PRODUTOS DE ORIGEM ANIMAL
Avaliação do desempenho na pós-desmama para uma população bovina multirracial Aberdeen Angus x Nelore utilizando-se diferentes modelos genéticos
Post weaning performance evaluation for a multibreed Aberdeen Angus x Nellore population using different genetic models
J.S. LopesI,IV; P.R.N. RoratoII; T. WeberI,IV; R.O. AraújoI,IV; M.A. DornellesI,V; J.G. CominIII,VI
IAluno de pós-graduação - UFSM - Santa Maria, RS
IIDepartamento de Zootecnia - UFSM - Santa Maria, RS
IIIAluna de graduação - UFSM - Santa Maria, RS
IVBolsista da CAPES
VBolsista do CNPq
VIBolsista PIBIC/CNPq
RESUMO
Com o objetivo de testar modelos genéticos alternativos ao aditivo-dominante em populações multirraciais, foram utilizadas informações do peso ao sobreano (PS) de 35.931 novilhos, filhos de 752 touros e 30.535 vacas das raças Aberdeen Angus (A) e Nelore (N) e de diversos grupos genéticos possíveis por meio do cruzamento entre elas. Foram testados cinco diferentes modelos (M) genéticos: o M1 continha o efeito genético fixo aditivo direto (AD), heterozigótico direto (HD), epistático direto (ED) e aditivo-conjunto direto (ACD); o M2, igual ao M1, menos o efeito ACD; o M3, igual ao M1, menos o efeito ED; o M4, igual ao M1, menos os efeitos ED e ACD; e o M5, igual ao M1, menos os efeitos HD, ED e ACD. Os modelos foram submetidos a três métodos de análise diferentes: método dos quadrados mínimos (MQM), regressão de cumeeira (RC) e máxima verossimilhança restrita (REML). O método de RC produziu estimativas de coeficientes com magnitudes e sinais explicados biologicamente. As estimativas dos efeitos, das (co)variâncias, dos parâmetros e dos valores genéticos diferiram entre os modelos, indicando a importância da correta escolha do modelo de análise, devendo-se ter conhecimento prévio do fenômeno estudado e sua interpretação biológica e sempre preceder à escolha de um modelo de análise genética multirracial o estudo da relação existente entre as variáveis independentes. Importantes efeitos adicionais ao efeito AD foram acrescentados pelas inclusões dos efeitos HD e ED aos modelos de análise. A notação matemática dos efeitos ACD, aplicada atualmente na literatura e testada neste estudo, não foi capaz de explicar a complementaridade entre raças como esperado, havendo problemas com casos de multicolinearidade entre os efeitos estudados.
Palavras-chave: complementaridade entre raças, efeito aditivo, epistasia, heterozigose, peso ao sobreano
ABSTRACT
In order to evaluate alternative genetic models to the additive dominant model, weights at yearling (PS) of 35,931 animals, sired by 752 bulls and 30,535 cows of Aberdeen Angus (A) and Nellore (N) breeds and the genetic groups from their crosses were used. Five different genetic models (M) were tested: M1, containing the direct additive fixed genetic effect (DA), heterozygote direct (HD), epystatic direct (ED), and direct joint additive direct (DJA); M2 was equal to M1, excluding DJA effect; M3 was equal to M1, excluding ED effect; M4 was equal M1, excluding ED and ACD effects, and M5 was equal to M1, excluding HD, ED, and DJA effects. The models were analyzed by different methods: Least Square Means Method (MQM), Ridge Regression Method (RC), and Restricted Maximum Likelihood Method (REML). Estimated coefficients by RC showed magnitude and sign which were biologically explained. The estimates of the covariances, parameters, and genetic values varied among the models, indicating the importance of the correct choice of the model for analysis, being necessary a previous knowledge of the studied phenomenon and its biological interpretation. Besides, it should always be considered the relationship between the independent variables before choosing a multibreed genetic analysis model. Important additional effects to the DA effect were considered by the inclusion of the HD and ED effects to the models for analysis. The DJA math notation, currently used in the literature and tested in the present study, was not able to explain the breed complementarity, due to the multi colinearity among the studied effects.
Keywords: additive effect, between breeds complementarily, epystatic effect, heterozygote effect, yearling weight
INTRODUÇÃO
Um país de proporções continentais como o Brasil, situado entre as latitudes 5ºN e 33ºS, apresenta grande diversidade de clima e, por conseguinte, de vegetação, além de inúmeros sistemas de criação diferentes e um grande número de raças de bovinos de corte de diferentes tipos biológicos. Neste cenário, é possível buscar a adequação do animal ao ambiente de produção, uma vez que é sabido que a magnitude da diferença em desempenho entre animais de raças puras e de produtos de cruzamentos depende, principalmente, do ambiente que é fornecido aos animais, das raças utilizadas e do valor genético dos indivíduos que são acasalados (Muniz e Queiroz, 1998). A distância genética existente entre as raças utilizadas influi diretamente na manifestação da heterose, sendo que a heterose ocasionada pelo acasalamento entre raças zebuínas e taurinas é cerca de duas vezes aquela proporcionada pelo acasalamento entre raças taurinas diferentes e/ou entre raças zebuínas diferentes (Fries, 1996).
Segundo Lopes et al. (2008), a utilização das raças europeias britânicas em cruzamentos é feita no intuito de aumentar a qualidade da carne dos produtos, além de aumentar a precocidade tanto de crescimento/acabamento quanto de reprodução. As raças zebuínas, em geral, são mais produtivas do que as taurinas em climas tropicais devido à sua maior resistência a parasitas e tolerância ao calor. Todavia, apresentam qualidade de carcaça inferior em relação às taurinas britânicas. Quando utilizadas em cruzamentos com raças taurinas, maximizam o efeito da heterose.
Assim, a predição do mérito genético dos animais se faz necessária, a fim de selecionar os melhores genótipos, fazendo-se uso de diferentes métodos estatísticos. Os modelos mais usados para avaliação de efeitos genéticos em características de crescimento de bovinos produtos de cruzamentos levam em consideração apenas os efeitos da ação aditiva e de dominância. Contudo, a partir da década de 80, têm sido relatadas evidências de que a contribuição dos efeitos epistáticos para a expressão de tais características nem sempre é negligenciável.
Em estudo para desenvolver equações de predição dos desempenhos de genótipos pertencentes a uma população multirracial Aberdeen Angus x Nelore, Kippert et al. (2008) salientaram a importância de efeitos adicionais ao efeito aditivo de raça, visto que observaram valores extremos de desempenho ocorrendo no mesmo grupo genético, diferindo o acasalamento que lhes dera origem, uma vez que, teoricamente, esses animais possuem o mesmo efeito aditivo de raça, mas apresentaram desempenhos distintos.
As estimativas de parâmetros de efeitos genéticos usando modelos que contemplam efeitos epistáticos e de complementaridade entre raças, obtidas por meio do método dos quadrados mínimos, têm se mostrado de difícil interpretação biológica. A presença de correlações entre as variáveis incluídas no modelo (multicolinearidade) resulta na obtenção de estimativas incoerentes, muitas vezes com sinal inverso, e pode ser o motivo para o uso corrente de modelos mais simples. Um procedimento alternativo para contornar os problemas causados pela multicolinearidade é o uso de métodos viesados de estimação dos coeficientes de regressão (Pimentel et al., 2006). A regressão de cumeeira é um desses métodos.
O objetivo deste trabalho foi avaliar a importância da inclusão dos efeitos genéticos não aditivos no modelo de análise dos registros de desempenho pós-desmama, para uma população bovina multirracial oriunda de cruzamentos entre as raças Aberdeen Angus e Nelore, utilizando-se diferentes metodologias e modelos genéticos.
MATERIAL E MÉTODOS
O estudo foi realizado com base em um arquivo que continha originalmente informações sobre o desempenho de 121.241 bezerros, filhos de 1.359 touros e 84.465 vacas das raças Aberdeen Angus (A) e Nelore (N) e de diversos grupos genéticos possíveis por meio do cruzamento entre eles, nascidos em 75 fazendas localizadas nos estados de Goiás, Minas Gerais, Mato Grosso do Sul, Paraná, Rio Grande do Sul, São Paulo e Tocantins, coletados entre os anos de 1986 e 2002.
Os dados foram estruturados empregando-se o aplicativo SAS/2001, de maneira a permitir que o arquivo fosse utilizado para a estimação dos efeitos genéticos e ambientais para a população.
Na editoração dos dados, foram criadas as variáveis: grupo de contemporâneos (GC), agrupando animais nascidos na mesma fazenda (1 a 75), ano (1986 a 2001) e estação de nascimento (1 a 4), pertencentes ao mesmo sexo (F e M) e grupo de manejo até o sobreano (1 a 129), totalizando 1.564 grupos; e idade ao sobreano em classes (ISC), correspondendo à idade ao sobreano expressa em meses (12 a 23).
Foram eliminados os dados relativos aos produtos de vacas cujo tipo de reprodução não fosse o de inseminação artificial ou monta dirigida, touros com menos de 10 filhos, GC com menos de cinco componentes, pesos ao sobreano (PS) fora da amplitude de 2,5 desvios-padrão para mais e para menos da média da população, grupos genéticos com menos de 100 animais ou observados em apenas uma fazenda, além de fazendas com apenas um único grupo genético. Após a editoração, o arquivo de trabalho ficou constituído por informações do PS de 35.931 novilhos, filhos de 752 touros e 30.535 vacas, totalizando 63.027 animais na matriz de parentesco.
Coeficientes para efeito aditivo direto (AD) foram definidos pela contribuição dos genes N na composição genética de cada indivíduo. Coeficientes para efeito aditivo-conjunto direto (ACD) entre A e N foram calculados como ACD=AD*(1-AD), teorizando um efeito aditivo quadrático. A heterozigose direta (HD) foi calculada como:  , em que
, em que  e
e  denotam a proporção do gene da raça 'i' no pai e na mãe do animal, respectivamente. Os efeitos de epistasia direta (ED) foram calculados como a heterozigose média presente nos gametas que geraram cada indivíduo ou como a heterozigose média nos pais de um indivíduo (Fries et al., 2000).
denotam a proporção do gene da raça 'i' no pai e na mãe do animal, respectivamente. Os efeitos de epistasia direta (ED) foram calculados como a heterozigose média presente nos gametas que geraram cada indivíduo ou como a heterozigose média nos pais de um indivíduo (Fries et al., 2000).
Foram testados cinco modelos, utilizando-se três metodologias de análise distintas: método dos quadrados mínimos (MQM) e o da regressão de cumeeira (RC) com λ=0,05, por meio do pacote estatístico SAS/2001, e o método da máxima verossimilhança restrita (REML), com o programa computacional Multi Traits Derivative Free Restricted Maximum Likelihood (MTDFREML) descrito por Boldman et al. (1995).
Para o MQM e a RC, o modelo estatístico um (Modelo 1) pode ser descrito como:
Yijk=µ+GCi+ISCj+β1AD+β2HD+β3ED+β4ACD+β5PD+ β6PD2+εijk , em que:
Yijk = é a observação do PS do k-ésimo animal, µ é a média geral da característica, GCi é o efeito do i-ésimo grupo de contemporâneos, ISCj é o feito da j-ésima classe de idade ao sobreano, β1, β2, β3, β4, β5 e β6 são os coeficientes de regressão dos efeitos genéticos AD, HD, ACD e ED, e para peso à desmama (PD), com efeitos linear e quadrático, respectivamente, ε e ijk é o erro aleatório associado a cada observação, NID (0, δ2).
O método da RC (Hoerl, 1962) consiste na adição de um escalar (λ) aos elementos da diagonal principal da matriz de coeficientes, visando quebrar as dependências lineares verificadas entre suas colunas. O estimador torna-se: = (X'X+ λI)-1X'y.
Originalmente, Hoerl e Kennard (1970) propuseram um método gráfico, denominado traço ridge, para escolha do valor de λ. Por esse método, as estimativas dos parâmetros são plotadas contra diversos valores de λ, partindo de zero. Escolhe-se, então, o valor de λ a partir do qual se pode verificar uma estabilização nos valores das estimativas. Entretanto, a elevação dos valores de λ leva ao decréscimo dos coeficientes de regressão e dos erros-padrão destas estimativas, o que pode prejudicar a estimação dos efeitos do modelo, principalmente aqueles que não estão envolvidos em casos de multicolinearidade.
O procedimento, implementado pelo SAS, conforme descrito por Freund e Littell (2000), é o seguinte:
SAS = [Rxx(I+Dλ)]-1RXy , em que: RXX é a matriz de correlações das variáveis explicativas, RXy é o vetor de correlações das variáveis explicativas com a variável resposta, e Dλ é uma matriz diagonal com valores de λ na diagonal.As estimativas dos parâmetros e valores genéticos foram obtidas por REML sob o modelo matricial: y = Xβ+Wg+Z1a+e, em que: y = vetor das observações dos PS; X=matriz de incidência associada aos efeitos ambientais (GC, ISC e PD); β=vetor de soluções para os efeitos fixos ambientais; W=matriz de incidência dos efeitos genéticos fixos (AD, HD, ED e ACD); g=vetor de soluções para os efeitos genéticos fixos; Z1=matriz de incidência associada ao efeito aleatório genético aditivo direto de cada animal; a=vetor de soluções para os efeitos aleatórios genéticos aditivos diretos; e e=vetor dos resíduos aleatórios.
Resumidamente, os modelos (M) foram os seguintes: M1 = conforme descrição supracitada; M2 = M1 menos os efeitos ACD; M3 = M1 menos os efeitos ED; M4 =M1 menos os efeitos ED e ACD e M5 = M1 menos os efeitos HD, ED e ACD.
A eficiência das metodologias, bem como a comparação entre os modelos, foi realizada pela análise dos coeficientes de determinação (R2), pelo teste F, pela estatística C(p) de Mallows, pelos fatores de inflação das variâncias (FIV) e pelas correlações de magnitude (correlação de Pearson) e de ranqueamento (correlação de Spearman), além do teste da razão da verossimilhança (TRV).
Para testar se a inclusão de parâmetros para os efeitos genéticos fixos efetivamente melhorou o modelo, em termos de ajuste, um teste F foi computado. O valor de F, conforme descrito por Weisberg (1980), foi calculado pela seguinte fórmula:
 , em que: SQRx e SQRx-1 são as somas de quadrados dos resíduos dos modelos x e x-1, respectivamente; e glx e glx-1 são os graus de liberdade dos resíduos dos modelos x e x-1, respectivamente, em que x representa os modelos 2, 3, 4 ou 5. O teste F fornece evidência contra o modelo mais simples (x-1) se o valor de F é maior que o valor tabelado para uma distribuição F(glx-1 - glx, glx, α).
, em que: SQRx e SQRx-1 são as somas de quadrados dos resíduos dos modelos x e x-1, respectivamente; e glx e glx-1 são os graus de liberdade dos resíduos dos modelos x e x-1, respectivamente, em que x representa os modelos 2, 3, 4 ou 5. O teste F fornece evidência contra o modelo mais simples (x-1) se o valor de F é maior que o valor tabelado para uma distribuição F(glx-1 - glx, glx, α).
Conforme descrito por Freund e Littell (2000), a estatística C(p) de Mallows (1973), uma medida da variância do erro mais o viés introduzido pela exclusão de uma variável do modelo, é calculada como se segue: C(p) = [SQR(p)/QME] - (N - 2p) + 1, em que: QME é o quadrado médio do erro do modelo completo; SQR(p), a soma de quadrados de um modelo contendo um subconjunto de p variáveis explicativas; e N, o número de observações. Quando se observa que C(p)>(p+1) para um modelo contendo p variáveis explicativas, existe evidência de viés em razão da exclusão de uma variável importante do modelo.
A identificação do problema de multicolinearidade em análises de regressão geralmente é feita pelo exame das correlações entre pares de variáveis explicativas. Porém, em alguns casos, associações entre três ou mais variáveis podem não ser detectadas pelo exame de correlações aos pares. Uma forma mais eficiente de diagnóstico de multicolinearidade é o exame dos fatores de inflação de variância (FIVs), definidos por:  , em que:
, em que:  é o quadrado do coeficiente de correlação múltipla que resulta da regressão da variável xi contra todas as outras variáveis explicativas incluídas no modelo.
é o quadrado do coeficiente de correlação múltipla que resulta da regressão da variável xi contra todas as outras variáveis explicativas incluídas no modelo.
O teste de razão de verossimilhança (TRV) foi utilizado para verificar se os modelos diferem estatisticamente entre si, pela diferença entre os valores de -2log L. Esse teste baseia-se na distribuição de qui-quadrado com g graus de liberdade e probabilidade de erro de 5%, em que g é a diferença em números de parâmetros estimados nos modelos comparados (Dobson, 1990).
RESULTADOS E DISCUSSÃO
Os animais pesavam, em média, 290,87kg à pesagem ao sobreano, com idade média de 517,48 dias, sendo que cerca de 70% dos animais foram pesados entre 16 e 20 meses de idade. Valores mais altos que estes foram encontrados por Lopes et al. (2008) (320,43kg), para a raça Nelore, nos três estados do sul do Brasil, e por Weber (2008) (302,65kg), para a raça Aberdeen Angus, ambos para peso ajustado para 550 dias de idade. Todavia, Pringle et al. (1997) observaram pesos superiores a 500kg aos 550 dias de idade, para animais Aberdeen Angus x Nelore, criados em confinamento nos Estados Unidos da América. Isso demonstra a lacuna existente e a possibilidade de incremento nos pesos ao sobreano da população estudada, seja como melhorias genéticas, ambientais ou ambas.
Os modelos testados sob o MQM explicaram aproximadamente 86% das variações observadas no peso ao sobreano (PS), com distinções na significância e magnitude dos efeitos genéticos fixos, principalmente para AD, e entre M1 e M3, que apresentam em particular o efeito ACD (Tab. 1), sugerindo a possibilidade de ocorrência de casos de colinearidade.
O estudo das correlações entre os efeitos genéticos fixos mostra a existência de forte correlação envolvendo, em especial, os efeitos HD e ACD (r=0,93), com média de correlação de Pearson de 0,43. Como muitas das relações lineares observadas na matriz de correlações podem não ser oriundas de correlações entre pares, mas de associações entre três ou mais variáveis independentes, foram calculados os fatores de inflação da variância (FIV) dos efeitos explicativos dos modelos, para confirmação da existência de multicolineariedade (Tab. 2). Segundo Freund e Wilson (1998), quando FIV é maior do que 10, tal fato indica a ocorrência de multicolinearidade. As maiores inflações nas variâncias ocorreram para HD e ACD, quando ambos são inseridos no modelo de análise, confirmando resultados de estudo de correlações. Com esta constatação, Roso et al. (2005) e Pimentel et al. (2006), entre outros, sugeriram a aplicação de métodos alternativos de estimação dos efeitos sobre o desempenho animal, tendo em vista o confundimento causado pela multicolinearidade. Foi empregado o método da RC, indicado por Hoerl e Kennard (1970) como um dos métodos alternativos de estimação que fornecem uma análise mais informativa dos dados na presença de multicolinearidade.
Com base na análise do gráfico traço ridge (Hoerl e Kennard, 1970), optou-se pelo valor de λ de 0,05, valor mínimo que proporcionou a quebra das multicolinearidades, reduzindo os fatores de inflação das variâncias, sem prejudicar e reduzir, de forma mais acentuada, os regressores e seus erros-padrão, visto que quanto mais alto o valor de λ, menor a correlação efetiva entre as variáveis independentes, mas, também, maior o viés da estimativa (Tab. 2).
Com a aplicação do método da RC (Tab. 3), estimaram-se regressores que pouco variaram entre os modelos aplicados, que podem ser explicados biologicamente, salvo para ACD, com relevância mais acentuada para os efeitos aditivos, heterozigóticos e epistáticos, nesta ordem de importância. Os efeitos negativos observados para o efeito AD denotam aumento do potencial produtivo com o aumento da contribuição de genes da raça Aberdeen Angus.
Avaliando-se os valores dos F comparativos, observou-se perda de ajuste ao se remover algum efeito. Apenas o valor da comparação entre M1 e M2 não foi significativo, indicando não haver prejuízo ao retirarem-se os efeitos genéticos aditivo-conjuntos. Semelhante à estatística C(p), o teste F demonstrou maior perda ao remover-se o efeito HD, em seguida o ED e, por fim, o efeito ACD.
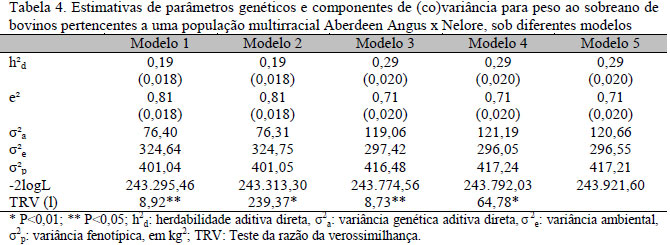
Para verificar os possíveis efeitos da multicolinearidade e das distinções impostas pelo uso de diferentes modelos nas avaliações genéticas multirraciais, foram estimadas as (co)variâncias genéticas e fenotípicas utilizadas posteriormente para predição dos valores genéticos dos animais da população em estudo (Tab. 4).
As estimativas de herdabilidade variaram de 0,19±0,018 a 0,29±0,020, indicando a possibilidade de ganho genético com o uso de seleção massal para PS, entretanto mais de 71% da variância fenotípica são causados por efeitos distintos ao genético aditivo aleatório. Valores de herdabilidade superiores foram encontrados por Kaps et al. (2000), para a raça Aberdeen Angus, nos EUA (0,49), por Ribeiro et al. (2001), para a raça Nelore, no estado da Paraíba (0,76), e por Lopes et al. (2008), para a raça Nelore, nos três estados da região sul do Brasil (0,35 a 0,51), demonstrando haver menor variabilidade ambiental nessas populações.
Os valores do TRV mostram a existência de diferença estatística entre os modelos testados (M4 e M5, M3 e M4, M2 e M3, e M1 e M2), embora com magnitudes distintas. Apesar disso, as reduzidas variâncias residuais estimadas pelos M4 e M5 demonstraram haver adequado ajuste das variâncias observadas nos PS pelos efeitos aditivos de raça e heterozigóticos.
As estimativas dos efeitos genéticos fixos por REML tiveram grande variação entre os diferentes modelos utilizados, inclusive com troca de sinal do efeito ACD, ratificando a existência de multicolinearidade (Tab. 5).
As correlações de magnitude (correlações de Pearson) e de ordem (correlações de Spearman) dos valores genéticos dos animais (VG's), preditos pelos diferentes modelos, variaram de 0,838 a 0,998, para as correlações de Pearson, e de 0,814 a 0,998, para as correlações de Spearman, indicando haver diferenças entre os valores genéticos dos animais com a mudança do modelo de análise, podendo levar a erros no momento da seleção dos reprodutores. Apesar disso, as acurácias médias estimadas pelos M1 e M4 foram semelhantes, - 0,79 e 0,76, respectivamente. As pequenas diferenças encontradas entre M1 e M2 e M3 e M4 reforçam os resultados obtidos pelas estimativas da estatística C(p), teste F e TRV.
Os resultados obtidos neste estudo permitiram afirmar que houve grande aumento na explicação da variação no PS ao se acrescentarem os efeitos heterozigóticos (M4) ao modelo aditivo (M5), além de ínfimas mudanças, ao se adicionarem os efeitos aditivo- conjuntos, reforçadas pelo fato negativo de esses últimos efeitos estarem fortemente envolvidos em casos de multicolinearidade.
Para Kinghorn (1993), um modelo que inclua o produto de genes para potencial de crescimento e genes para adaptação ao ambiente explicaria melhor o crescimento de gado de corte em ambiente tropical. Em termos biológicos, esta assertiva é completamente palpável, entretanto a notação matemática deste termo aplicado atualmente (ACD), como neste estudo, não produziu o efeito esperado, sendo que o efeito heterozigótico foi eficiente para explicar o melhor desempenho dos animais F1. Um problema adicional causado pela adição de um termo quadrático seria a alta correlação entre as colunas correspondentes a AD e AD*AD.
Houve também substancial ganho de ajuste ao se inserirem os efeitos epistáticos (M2), os quais afetam negativamente o desempenho dos animais da população estudada; segundo Wright (1978), efeito epistático, ou perda por epistasia, quebra aqueles sistemas interativos de genes, atuantes como blocos, formados ao longo do tempo pela seleção natural e que produzem combinações mais eficientes. Trematore et al. (1998), Fries et al. (2000) e Pimentel et al. (2006) observaram o mesmo resultado em seus estudos. Este modelo (M2) mostrou-se muito similar ao modelo mais completo (M1), com a vantagem de não conter multicolinearidades que possam adicionar viés às estimativas.
Fries et al. (2000) compararam o uso de três modelos na predição do desempenho de bezerros Hereford x Brahman: o primeiro continha os efeitos aditivos e heterozigóticos; o chamado modelo completo adicionou covariáveis para os efeitos epistáticos e aditivo-conjuntos, e o terceiro, chamado genotípico, incluiu efeitos para os 15 grupos genéticos existentes na população, representando 100% do ajuste. O primeiro modelo explicou 75,7% da variância e o segundo, 90,1%. Assim, mostraram que cerca de 60% da falta de ajuste do modelo mais simples poderiam ser reduzidos pela inclusão de efeitos para epistasia e complementaridade entre raças.
CONCLUSÕES
A inclusão dos efeitos heterozigóticos e epistáticos nos modelos de análise, adicionalmente ao aditivo, afeta, respectivamente, positiva e negativamente o peso ao sobreano dos animais. A notação matemática dos efeitos aditivo-conjuntos, retirada da literatura e testada neste estudo, não explica adequadamente a complementaridade entre raças como esperado, devido à multicolinearidade entre os efeitos genéticos estudados. Deve-se ter conhecimento prévio do fenômeno estudado, sua interpretação biológica e sempre preceder à escolha de um modelo de análise para uma população multirracial o estudo da relação existente entre as variáveis independentes. O método de regressão de cumeeira produz estimativas de coeficientes com magnitudes e sinais explicados biologicamente.
AGRADECIMENTOS
Às empresas GenSys Consultores Associados Ltda. e Natura Genética Sul-Americana S.A., pela cedência do banco de dados. À Coordenação de Aperfeiçoamento de Pessoal de Ensino Superior (CAPES), pelo aporte financeiro.
Recebido em 1 de julho de 2009
Aceito em 15 de outubro de 2010
Apoio: CAPES
E-mail: jadersilvalopes@gmail.com
- BOLDMAN, K.G.; KRIESE, L.A., VAN VLECK, L.D. et al. A manual for use of MTDFREML. A set of program to obtain estimates of variances and covariances [DRAFT]. Lincoln: Department of Agriculture/Agricultural Research Service, 1995. 120p.
- DOBSON, A.J. An introduction to generalized linear models Melbourne: Chapman and Hall, 1990, 174p.
- FREUND, R.J.; LITTELL, R.C. SAS System for Regression, 3.ed. Cary: SAS Institute, 2000. 235p.
- FREUND, R.J.; WILSON, W.J. Regression Analysis: Statistical Modeling of a response variable. San Diego: Academic, 1998. 444p.
- FRIES, L.A. Cruzamentos em gado de corte. In: SIMPÓSIO SOBRE PECUÁRIA DE CORTE: PRODUÇÃO DE NOVILHOS DE CORTE, 4., 1996, Piracicaba. Anais... Piracicaba, SP: FEALQ/ESALQ, 1996. (Palestra)
- FRIES, L.A.; JOHNSTON, D.J.; HEARNSHAW, H. et al. Evidence of epistatic effects on weaning weight in crossbred beef cattle. Asian-Austral. J. Anim. Sci., v.13, suppl.B, p.242, 2000.
- HOERL, A.E. Application of ridge analysis to regression problems. Chem. Engin. Prog., v.58, p.54-59, 1962.
- HOERL, A.E.; KENNARD, R.W. Ridge regression: biased estimation for onorthogonal problems. Technometrics, v.12, p.55-67, 1970.
- KAPS, M.; HERRING, W.O.; LAMBERSON, W.R. Genetic and environmental parameters for traits derived from the Brody Growth curve and their relationships with weaning weight in Angus cattle. J. Anim. Sci., v.78, p.1436-1442, 2000.
- KINGHORN, B.P. Theory of breed utilization. In: ______ Design of livestock breedingprograms: short course in animal breeding. Armidale: AGBU, 1993. p.187-204.
- KIPPERT, C.J.; RORATO, P.R.N.; LOPES, J.S. et al. Efeitos genéticos aditivos diretos e maternos e heterozigóticos sobre os desempenhos pré e pós-desmama em uma população multirracial Aberdeen Angus x Nelore. Rev. Bras. Zootec., v.37, p.1383-1391, 2008.
- LOPES, J.S.; RORATO, P.R.N.; WEBER, T. et al. Efeito da interação genótipo x ambiente sobre o peso ao nascimento, aos 205 e aos 550 dias de idade de bovinos da raça Nelore na região Sul do Brasil. Rev. Bras. Zootec., v.37, p.54-60, 2008.
- MALLOWS, C.P. Some comments on C(p). Technometrics, v.15, p.661-675, 1973.
- MUNIZ, C.A.S.; QUEIROZ, S.A. Avaliação do peso à desmama e do ganho médio de peso de bezerros cruzados, no estado do Mato Grosso do Sul. Rev. Bras. Zootec., v.27, p.504-512, 1998.
- PIMENTEL, E.C.G.; QUEIROZ, S.A.; CARVALHEIRO, R. et al. Estimativas de efeitos genéticos em bezerros cruzados por diferentes modelos e métodos de estimação. Rev. Bras. Zootec., v.35, supl., p.1020-1027, 2006.
- PRINGLE, T.D.; WILLIAMS, S.E.; LAMB, B.S. et al. Carcass characteristics, the capain proteinase system, and aged tenderness of Angus and Brahman crosbreed sterrs. J. Anim. Sci., v.75, p.2955-2961, 1997.
- RIBEIRO, M.N.; PIMENTA FILHO, E.C.; MARTINS, G.A. Herdabilidade para efeitos direto e materno das características de crescimento de bovinos Nelore no estado da Paraíba. Rev. Bras. Zootec., v.30, p.1224-1227, 2001.
- ROSO, V. M.; SCHENKEL, F. S.; MILLER, S. P. et al. Additive, dominance, and epistatic loss effects on preweaning weight gain of crossbred beef cattle from different Bos taurus breeds. J. Anim. Sci., v.83, p.1780-1787, 2005.
- TREMATORE, R.L.; ALENCAR, M.M.; BARBOSA, P.B. et al. Estimativas de efeitos aditivos e heteróticos para características de crescimento pré-desmama em bovinos Charolês-Nelore. Rev. Bras. Zootec., v.27, p.87-94, 1998.
- WEBER, T. Parâmetros genéticos e tendências genéticas e fenotípicas para características produtivas para uma população da raça Aberdeen Angus. 2008. 67f. Dissertação (Mestrado) - Universidade Federal de Santa Maria, Santa Maria, RS.
- WEISBERG, S. Applied Linear Regression 1.ed. New York: Wiley Series in probability and mathematical statistics, 1980. 283p.
- WRIGHT, S. The relation of livestock breeding to theories of evolution. J. Anim. Sci., v.46, p.1192-1200, 1978.
Datas de Publicação
-
Publicação nesta coleção
23 Fev 2011 -
Data do Fascículo
Dez 2010
Histórico
-
Recebido
01 Jul 2009 -
Aceito
15 Out 2010