Resumos
Obtiveram-se equações de predição dos valores de energia metabolizável aparente corrigida (EMAn) para alimentos energéticos mais utilizados nas dietas de frangos de corte por meio do princípio da meta-análise. Foi realizada uma revisão bibliográfica de estudos realizados no Brasil para catalogar informações sobre valores de EMAn e composição química dos alimentos (PB; EE; MM; FB, FDN e FDA). Também foram considerados os efeitos de sexo, macho, fêmea e mistos de idade (primeira e segunda semanas, terceira e quarta semanas, quinta e sexta semanas e acima de seis semanas ou indefinido), e da metodologia empregada no metabolismo (coleta total de excretas ou alimentação forçada + coleta total de excretas), formando um esquema fatorial (3x4x2). Adotou-se o procedimento de Stepwise para estudar a associação entre as variáveis, incluindo-as na equação em função de suas importâncias, e o Proc Reg do SAS para ajustar o modelo de regressão linear múltipla. As melhores equações para estimar a EMAn dos alimentos foram EMAn = 4371,18 - 26,48PB + 30,65EE - 126,93MM - 52,26FB - 25,14FDN + 24,40FDA (R²=0,81) e EMAn = 4205,23 + 30,58EE - 130,35MM - 58,29FB - 28,31FDN + 16,71FDA (R²=0,81). As variáveis FDN e FDA foram importantes nas equações ao influenciarem os valores energéticos dos alimentos.
frango de corte; energia metabolizável; FDA; FDN
Prediction equations were obtained for the apparent metabolizable energy (EMAn) values of energetic feedstuffs used in broiler chicken diets by meta-analysis. A bibliographical review of the studies carried out in Brazil was performed to collect information concerning energy values and chemical composition (CP, EE, MM, CF, NDF, and ADF) of feedstuffs. The effects of gender (male, female and mixed), age (1st and 2nd week, 3rd and 4th week, 5th and 6th week, and older 6th weeks or indefinite), and the metabolism assay methodology (excrete total collection or forced fed + excrete total collection) were also considered, constituting a factorial scheme (3x4x2). The stepwise procedure was used to study the association among equation variables by their importance, and Proc Reg (SAS) was used to fit the multiple linear regression model. The equations which best estimated the EAMn of the energetic feedstuffs were AME = 4,371.18 - 26.48CP + 30.65EE - 126.93MM - 52.26CF - 25.14NDF + 24.40FDA (R²=0.81) and AME = 4,205.23 + 30.58EE - 130.35MM - 58.29CF - 28.31NDF + 16.71NDA (R²=0.81). NDF and ADF variables were important in the equations, influencing the feedstuffs energetic values.
broiler; metabolizable energy; NDF; ADF
ZOOTECNIA E TECNOLOGIA E INSPEÇÃO DE PRODUTOS DE ORIGEM ANIMAL
Equações de predição para estimar valores da energia metabolizável de alimentos concentrados energéticos para aves utilizando meta-análise
Prediction equations to estimate metabolizable energy values of energetic concentrate feedstuffs for poultry by the meta-analysis process
G.A.J. NascimentoI; P.B. RodriguesII; R.T.F. FreitasII; R.V. Reis NetoIII,* * Autor para correspondência ; R.R. LimaIV; I.B. AllamanIII
IDepartamento de Zootecnia - UFCE - Fortaleza, CE
IIDepartamento de Zootecnia - UFLA - Lavras, MG
IIIAluno de pós-graduação - DZ-UFLA - Lavras, MG
IVDepartamento de Ciências Exatas - UFLA - Lavras, MG
RESUMO
Obtiveram-se equações de predição dos valores de energia metabolizável aparente corrigida (EMAn) para alimentos energéticos mais utilizados nas dietas de frangos de corte por meio do princípio da meta-análise. Foi realizada uma revisão bibliográfica de estudos realizados no Brasil para catalogar informações sobre valores de EMAn e composição química dos alimentos (PB; EE; MM; FB, FDN e FDA). Também foram considerados os efeitos de sexo, macho, fêmea e mistos de idade (primeira e segunda semanas, terceira e quarta semanas, quinta e sexta semanas e acima de seis semanas ou indefinido), e da metodologia empregada no metabolismo (coleta total de excretas ou alimentação forçada + coleta total de excretas), formando um esquema fatorial (3x4x2). Adotou-se o procedimento de Stepwise para estudar a associação entre as variáveis, incluindo-as na equação em função de suas importâncias, e o Proc Reg do SAS para ajustar o modelo de regressão linear múltipla. As melhores equações para estimar a EMAn dos alimentos foram EMAn = 4371,18 - 26,48PB + 30,65EE - 126,93MM - 52,26FB - 25,14FDN + 24,40FDA (R2=0,81) e EMAn = 4205,23 + 30,58EE - 130,35MM - 58,29FB - 28,31FDN + 16,71FDA (R2=0,81). As variáveis FDN e FDA foram importantes nas equações ao influenciarem os valores energéticos dos alimentos.
Palavras-chave: frango de corte, energia metabolizável, FDA, FDN
ABSTRACT
Prediction equations were obtained for the apparent metabolizable energy (EMAn) values of energetic feedstuffs used in broiler chicken diets by meta-analysis. A bibliographical review of the studies carried out in Brazil was performed to collect information concerning energy values and chemical composition (CP, EE, MM, CF, NDF, and ADF) of feedstuffs. The effects of gender (male, female and mixed), age (1st and 2nd week, 3rd and 4th week, 5th and 6th week, and older 6th weeks or indefinite), and the metabolism assay methodology (excrete total collection or forced fed + excrete total collection) were also considered, constituting a factorial scheme (3x4x2). The stepwise procedure was used to study the association among equation variables by their importance, and Proc Reg (SAS) was used to fit the multiple linear regression model. The equations which best estimated the EAMn of the energetic feedstuffs were AME = 4,371.18 - 26.48CP + 30.65EE - 126.93MM - 52.26CF - 25.14NDF + 24.40FDA (R2=0.81) and AME = 4,205.23 + 30.58EE - 130.35MM - 58.29CF - 28.31NDF + 16.71NDA (R2=0.81). NDF and ADF variables were important in the equations, influencing the feedstuffs energetic values.
Keywords: broiler, metabolizable energy, NDF, ADF
INTRODUÇÃO
Sabe-se que existem variações na composição dos alimentos normalmente utilizados na avicultura devido às regiões geográficas, às condições de plantio, à fertilidade de solo, à variabilidade genética dos cultivares, às formas de armazenamento e processamento dos grãos vegetais.
A formulação de rações envolve um criterioso uso de alimentos e subprodutos, combinados de forma que possam fornecer quantidade adequada dos nutrientes requeridos pelas aves. A realização de análises para determinar a composição química completa dos ingredientes utilizados na formulação é onerosa e impraticável por ser demorada e trabalhosa, levando ao constante uso de tabelas e matrizes de composição determinadas em laboratórios (Nutrient ..., 1994). Uma forma rápida de se determinar os valores energéticos e de digestibilidade de nutrientes dos alimentos é pelo uso de equações de predição, que são estabelecidas em função da composição química simplificada dos alimentos, normalmente de fácil e rápida obtenção. Alguns estudos realizados (Rodrigues et al., 2001; 2002; Borges et al., 2003; Nagata et al., 2004; Zonta et al., 2004) para estabelecer equações de predições de valores energéticos e nutritivos de uma série de alimentos foram elaborados com amostras que apresentavam pequena variabilidade. Esse problema pode, contudo, ser minimizado aumentando o número de informações de digestibilidade de nutrientes e composição química que utilizou dados oriundos de vários experimentos realizados no Brasil, procedimento semelhante ao adotado por Janssen (1989), na Europa.
O procedimento que usa métodos estatísticos para combinar ou comparar resultados de estudos distintos, mas relacionados, é definido como meta-análise (Kirby, 1993), e o seu propósito é aumentar o número de observações e o poder estatístico com a possibilidade de gerar conclusões para uma amplitude variada de estudos. Apesar das críticas e dos problemas enfrentados pela meta-análise, as evidências indicam que ela é um procedimento estatístico aceito, gradativamente, pela comunidade científica, e sua aplicação tem aumentado em todos os campos das ciências (Cooper, 1990).
O presente trabalho foi realizado com objetivo de obter equações de predição para estimar os valores de energia metabolizável, em função da composição química de alimentos energéticos, aplicando-se o princípio da meta-análise.
MATERIAL E MÉTODOS
As informações utilizadas neste trabalho referem-se a valores de energia metabolizável aparente corrigida pelo balanço de nitrogênio (EMAn) e composição química dos alimentos energéticos, ou seja, alimentos com teores de fibra inferiores a 18% e teores proteicos inferiores a 20% com base na matéria seca (MS), e usualmente utilizados na formulação das rações avícolas (Tab. 1), sendo o milho considerado como o principal, uma vez que é a principal fonte energética.
Os trabalhos coletados, provenientes de uma ampla revisão bibliográfica de modo a incluir o máximo possível de estudos realizados no Brasil nos últimos 40 anos, foram separados em completos - que apresentavam as variáveis de proteína bruta (PB), extrato etéreo (EE), matéria mineral (MM), fibra bruta (FB), fibra em detergente neutro (FDN) e fibra em detergente ácido (FDA) - e incompletos - que apresentavam somente PB, EE, MM e FB. Assim, para obtenção da equação de predição para estimar a EMAn dos alimentos energéticos mais utilizados nas rações de aves, foram catalogadas 375 informações, em que 197 foram consideradas completas e 178 incompletas.
Foram realizados os procedimentos estatísticos para determinar a equação de predição para estimar os valores da EMAn desses alimentos. Inicialmente, realizou-se o procedimento para obter informações completas e, subsequentemente, para todas as informações (completas e incompletas). Observaram-se os resultados estatísticos para cada análise separadamente, levando-se em consideração o coeficiente de determinação (R2) para as equações de predições ajustadas, em cada caso em particular.
Para conversão dos resultados de cada estudo para uma métrica comum, determinaram-se grupos em que foram considerados os efeitos que influenciam o valor energético dos alimentos diretamente, ou seja, que não modificam a composição química e que ocasionam variabilidade no valor energético dos alimentos, como, por exemplo, a metodologia empregada no ensaio de metabolismo (coleta total ou alimentação forçada + coleta total), sexo e idade dos animais experimentais. Após a identificação desses efeitos nos trabalhos revisados, foram determinados códigos para cada efeito em particular e, a partir daí, foram feitos agrupamentos desses códigos para determinar os grupos que seriam submetidos à análise dos mínimos quadrados ponderados, realizando o procedimento da meta-análise. Portanto, para o efeito sexo, obtiveram-se três códigos (machos = 1, fêmea = 2 e animais mistos = 3), para idade, quatro códigos (primeira e segunda semanas de vida = 1; terceira e quarta semanas = 2; quinta e sexta semanas = 3; acima dessas idades ou indefinido = 4) e para metodologia, apenas dois códigos (coleta total de excretas-CTE =1, alimentação forçada + CTE = 2). A formação dos grupos deu-se em função de um fatorial 3x4x2, sendo os três códigos de sexo x quatro de idade x dois de metodologias, podendo, então, totalizar até 24 grupos, mas não necessariamente que os 24 grupos fossem efetivados.
Como se trabalhou com o modelo estatístico de regressão linear múltipla incluindo os grupos já pré-determinados no estudo como fatores de ponderação, as estimativas dos parâmetros foram determinadas de acordo com o método dos mínimos quadrados ponderados, em que se considera o inverso da variância (1/s2i) para cada grupo (Hoffman e Vieira, 1977). Esse fator de ponderação determinou a variância existente para a variável dependente do modelo de regressão linear múltipla dentro de cada grupo, nesse caso a EMAn dos alimentos utilizados. Porém, existem outros fatores que também podem ser testados e que podem ser analisados e discutidos em trabalhos futuros.
Para elucidar a estrutura de relações entre as variáveis de composição química e de valores energéticos de cada alimento, foram estimadas as correlações de Pearson (Draper e Smith, 1981) entre todos os pares possíveis, utilizando-se o Proc Corr do SAS/1995. As medidas de dissimilaridades a serem utilizadas para compor a matriz de distâncias para todas as variáveis foram estimadas pelo método do vizinho mais próximo e de acordo com o resultado, se necessário, o dendrograma poderá ser obtido, para melhor visualização da relação existente entre as variáveis.
O ajuste do modelo de regressão linear múltipla foi feito pelo Proc Reg do SAS (1995), em que se considerou o seguinte modelo de regressão:
Yi = β0+ β1 + β1Xi1 + β2xi2 + β3xi3 + β4xi4 + β5xi5 + β6xi6 εi,
em que:
Yi = refere-se ao valor da EMAn do alimento, determinado em ensaio metabólico, no i-ésimo estudo; Xi1; ...; Xi6 = representam as variáveis de composição química do alimento, no i-ésimo estudo, sendo, respectivamente, PB, MM, EE, FB, FDN e FDA, εi = representa o erro associado à i-ésima observação, assumido, normal e independentemente distribuído, com média 0 e variância .
.
Para avaliar a importância das variáveis de composição química sobre o valor de EMAn do alimento, estimou-se o coeficiente de determinação parcial de cada variável (Tipo II) no modelo completo, e adotou-se o procedimento de seleção de equações ajustadas denominado stepwise (Draper e Smith, 1981). Para avaliar a importância das variáveis de composição química no valor energético dos alimentos, inicialmente estimou-se o coeficiente de determinação parcial de cada variável no modelo completo.
RESULTADOS E DISCUSSÃO
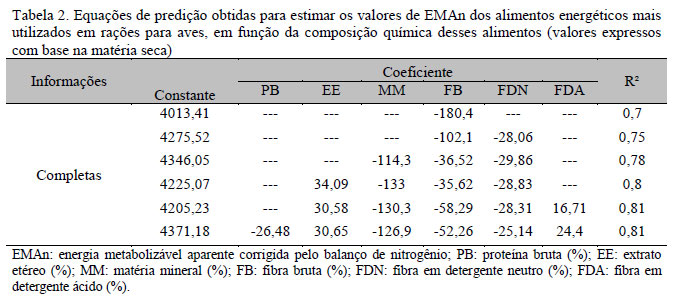
Ao se considerarem as 197 informações completas, as equações de predição obtidas que apresentaram os melhores ajustes para estimar o valor de EMAn para os alimentos energéticos, o R2 foi de 81% (Tab. 2).
Duas equações ajustaram-se com R2 semelhantes (81%) para determinar a EMAn dos alimentos energéticos, sendo uma com todas as variáveis analisadas, EMAn = 4371,18 - 26,48PB + 30,65EE - 126,93MM - 52,26FB - 25,14FDN + 24,40FDA, e outra, mais simples, com apenas cinco das variáveis estudadas: EMAn = 4205,23 + 30,58EE - 130,35MM - 58,29FB - 28,31FDN + 16,71FDA.
Penz Jr. e Kessler (1995) observaram estimativas de equações de predição com as respectivas medidas in vivo de alimentos concentrados energéticos e afirmaram que a equação é mais adequada para os ingredientes em apenas um ou dois componentes da equação. Assim, uma equação com menos variáveis, como por exemplo, composta de duas variáveis, e com R2 relativamente alto, irá minimizar o custo de análises laboratoriais e proporcionar maior rapidez para formulação de rações.
As duas equações ajustadas com R2 semelhantes nessa etapa do trabalho devem ser testadas futuramente por meio de ensaios metabólicos realizados com frangos de corte em fase de crescimento, conforme trabalho realizado por Nagata et al. (2004) e, caso a resposta seja idêntica e confiável estatisticamente nas duas situações, poderá ser adotada a equação com menos variáveis.
As correlações entre todas as variáveis da composição química e valores de EMAn dos alimentos energéticos com informações completas estão apresentadas na Tab. 3. Das seis variáveis de composição, cinco correlacionaram-se direta e negativamente (P<0,01) com a EMAn dos alimentos analisados, na seguinte ordem de importância: FDN (-0,860); FB (-0,856); PB (-0,817), MM (-0,801) e FDA (-0,576), o que acarretou prejuízos nos valores energéticos dos alimentos à medida que seu teores se elevam na composição alimentar.
Ao avaliarem vários alimentos energéticos e um proteico (quatro farelos de trigo, trigo grão, farinha morena, farinha de trigo, resíduo de biscoito, resíduo de macarrão, triguilho e gérmen de trigo), Nunes et al. (2001) observaram que, entre todos os parâmetros utilizados para determinar as equações de predição, o EE foi o único que teve correlação positiva com os valores de EMAn, porém com baixa correlação (0,32). Já para as demais variáveis independentes, as que apresentaram maior correlação com os valores de EMAn, porém correlação negativa, foram FDN (0,95), MM (0,94), FB (0,93), P (0,93), Ca (0,90), FDA (0,84).
Pelos resultados, a FDN apresenta-se como a variável mais importante no efeito da variabilidade energética dos alimentos, uma vez que ela se correlacionou positivamente com todas as outras variáveis, revelando alto grau de associação entre as variáveis. Primeiramente, a FDN sofre alteração em função do teor de FB do alimento, ou seja, à medida que a FB do alimento se eleva, a FDN também aumenta de forma considerável e, consequentemente, o valor energético do alimento diminui, já que a correlação existente entre FB e FDN é relativamente alta e positiva (0,872; P<0,01), enquanto a correlação entre FDN e EMAn do alimento também é alta, mas negativa (-0,860).
Rodrigues et al. (2001), ao estudarem o milho mais subprodutos e milhetos, notaram que as equações de predição com as variáveis PB, FB ou FDN, MM e amido apresentaram bons ajustes, com elevados valores de R2, o que mostra que mais de 96% da variabilidade nos valores da EMAn determinados com pintos em crescimento são explicadas por estas variáveis. Para Nunes et al. (2001), a equação que contém uma variável mostrou que a FDN foi a variável que proporcionou melhor valor de R2 (0,91), para EMAn.
No presente trabalho, a FB do alimento mostrou-se também muito importante, em se tratando de variação nos valores energéticos dos alimentos analisados, já que tem efeitos supostamente direto e indireto, uma vez que se correlacionou tanto com a EMAn como quanto todas as variáveis da composição química alimentar que terão efeito em uma possível variação na EMAn dos alimentos energéticos.
As correlações existentes entre a FB e as variáveis de composição química foram todas positivas e altamente significativas (P<0,01), na seguinte ordem de importância: FB e FDN (0,872); FB e MM (0,863); FB e PB (0,800) e em menor proporção entre a FB e a FDA (0,764). No entanto, se ocorrer elevação dos teores de qualquer uma dessas variáveis (FDN, MM, PB e FDA), o teor de FB do alimento também se eleva, fazendo com que ocorra prejuízo, ou seja, redução do valor de EMAn dos alimentos.
Observou-se que, além do efeito negativo e provavelmente direto das variáveis de composição química sobre os valores da EMAn dos alimentos, também ocorreram correlações positivas entre todas elas, portanto elevando-se qualquer uma delas na composição química do alimento, e isso será refletido na elevação de todas as outras, fazendo com que o efeito mais drástico seja a redução do valor de EMAn dos alimentos em dimensões diferentes, já as correlações apresentam-se diferentes de acordo com a importância das variáveis.
Considerando-se as 375 informações (completas+incompletas), catalogadas para os alimentos energéticos, a equação obtida, apesar de uma quantidade maior de dados, comparadas às 197 informações analisadas anteriormente para os mesmos alimentos, apresentou o melhor ajuste para o valor de EMAn, com R2 de 75%, valor menor do que o determinado para as equações ajustadas anteriormente (R2= 81%). As equações, nessa etapa, foram ajustadas e obtidas por intermédio da composição em PB, EE, MM e FB (Tab. 4).
Nessas 375 informações analisadas, foram desconsideradas as variáveis FDN e FDA para as análises de regressão múltipla, logo foi observado que, nas análises anteriores, a celulose, a lignina e principalmente a hemicelulose são parâmetros importantes na composição química e influenciam o valor da EMAn dos alimentos.
A equação que melhor se ajustou para estimar a EMAn dos alimentos energéticos, nessa etapa do trabalho, foi: EMAn = 4265,54 - 37,52PB + 22,21EE - 70,88MM - 97,07FB; com R2 de 75%. Quando se considera o conjunto das variáveis no modelo ajustado, a variável apontada como a mais importante no modelo foi a FB (R2 parcial = 0,6043), seguida da PB (R2 parcial = 0,1203), da MM (R2 parcial = 0,0165) e por fim do EE (R2 parcial = 0,0080).
As correlações entre todas as variáveis da composição química e valores de EMAn dos alimentos com informações incompletas são apresentadas na Tab. 5.
Atuando com efeito supostamente direto sobre os valores de EMAn dos alimentos, foram verificadas correlações negativas e significativas (P<0,01) para FB (-0,749), MM (-0,647) e PB (-0,549), em que FB tem influência maior na EMAn dos alimentos, e essas correlações revelam grau de associação entre essas variáveis (FB, MM e PB) e a energia. Por serem correlações negativas entre FB, MM, PB e o valor da EMAn dos alimentos, à medida que uma dessas três variáveis aumenta de teor, altera-se a EMAn dos alimentos, isto é, ela diminui, ou vice-versa.
Mais uma vez, a FB mostrou-se muito importante na variação da EMAn dos alimentos analisados, já que terá provavelmente efeitos direto e indireto, uma vez que se correlacionou tanto com a EMAn (-0,749) quanto como com todas as variáveis da composição química alimentar que terão efeito direto numa possível variação da EMAn. Isso implica dizer que, com o aumento do teor de FB do alimento, ocorrerá diminuição da EMAn dele como também aumento da MM e PB, resultando no efeito potencializado, pois como esses últimos estão correlacionados positivamente - 0,606 e 0,219 - com a FB, respectivamente, o efeito da FB sobre o valor energético do alimento será potencializado em razão da ação dessas duas variáveis, que atuam indiretamente, via FB, como também diretamente sobre a EMAn.
O aumento apenas de PB do alimento provoca aumento da MM e da FB e, em razão do aumento da MM proveniente da correlação existente entre PB e MM, ocorrerá um novo aumento da FB, em função da correlação positiva também entre MM e FB e, consequentemente, diminuição da EMAn do alimento.
A influência da PB na variação energética do alimento também foi constatada por Janssen (1989), em equações de predições para estimar valores energéticos de alimentos energéticos. Para o milheto: EMAn= 36,21PB + 69,60EE + 38,10ENN; para o sorgo: EMAn= 31,02PB + 77,03EE + 37,67ENN; para o gérmen de milho: EMAn= 21,12PB + 87,24EE + 32,29ENN; para a quirera de milho: EMAn= 36,21PB + 85,44EE + 37,26ENN e para o milho: EMAn= 36,21PB + 85,44EE + 37,26ENN). Deste modo, observa-se que em todas as equações a PB esteve sempre presente no ajuste. No entanto, ao testar a aplicabilidade dessas equações para diferentes alimentos energéticos, Nagata et al. (2004) verificaram que, de maneira geral, as equações superestimaram os valores energéticos dos alimentos testados.
No presente trabalho, constataram-se correlações positivas (P<0,01) entre as variáveis que atuam diretamente sobre os valores de EMAn dos alimentos, em que a mais alta foi entre FB e MM (0,616), seguida daquelas entre PB e MM (0,536), entre MM e EE (0,256), entre PB e FB (0,219) e, entre PB e EE (0,159). Portanto, pode-se concluir que FB tem mais influência (-0,749) sobre a variação da EMAn dos alimentos, porque a fibra sofrerá dupla influência tanto da PB como da MM dos alimentos.
O EE dos alimentos teve pouca influência na variação do teor da EMAn dos alimentos analisados, pois, pelas correlações apresentadas, essa variável não está correlacionada (P>0,05) diretamente com a EMAn, mas sim de forma bem discreta com a MM (0,256) e com a PB (0,159), o que será refletido no grau de importância do EE na composição final da equação ajustada na regressão múltipla.
Ao considerar o modelo da equação ajustada, EMAn = 4265,54 - 37,52PB + 22,21EE - 70,88MM - 97,07FB (R2= 0,75), levando em consideração a ação conjunta das variáveis no modelo, a variável apontada como a mais importante no modelo foi a FB (R2 parcial = 0,6043), seguida da PB (R2 parcial = 0,1203), da MM (R2 parcial = 0,0165) e do EE (R2 parcial = 0,0080). No presente caso, como no banco de dados não havia informações sobre FDN e FDA, a PB também se mostrou importante na variação da EMAn dos alimentos analisados, conjuntamente com as variáveis FB, MM e EE, em que a variabilidade nos valores energéticos explicada por estas variáveis foi de apenas 75%, sendo, no entanto, a FB considerada a variável mais importante.
A FB, além de atuar diretamente sobre a EMAn dos alimentos energéticos, também participa, provavelmente, de forma direta e considerável sobre todas as outras variáveis da composição química as quais, por sua vez, também atuam diretamente sobre esse mesmo valor energético (EMAn). No ajustamento do modelo de regressão múltipla, ao se considerar o efeito conjunto dessas variáveis na equação obtida, provavelmente o grau de importância da FB do alimento tenha se dado em função dessa observação, em que, consequentemente, tornou-se a variável mais importante na equação de predição ajustada.
A parede celular das fibras dos vegetais apresenta conteúdo de polissacarídios não amídicos (PNA's) de forma variável, acarretando efeito negativo na habilidade das aves em digerir alguns nutrientes, particularmente do amido, da proteína e da gordura (Smits e Annison, 1996), uma vez que o aumento da viscosidade do bolo alimentar gerada pela presença dos PNA's acarretará diminuição do contato do bolo alimentar com as células absortivas da membrana intestinal dos animais, fazendo com que ocorra redução na digestão e absorção dos nutrientes e, consequentemente, diminuição do valor energético dos alimentos (Philip et al., 1995).
Foi realizado o teste de multicolinearidade, de acordo com Montgomery e Peck (1981), para os alimentos energéticos, e não foi observada significância estatística em nenhum dos casos, portanto não houve necessidade de expor o diagrama dos resultados, conhecido como dendograma, uma vez que não se visualizariam inter-relações estatisticamente significativas entre as variáveis em estudo.
CONCLUSÕES
A precisão do ajuste das equações de predição para valores da EMAn, obtidas por meio da meta-análise, foi diretamente relacionada com a variabilidade na composição química dos alimentos. Assim, as equações que podem ser recomendadas para estimar os valores de EMAn dos alimentos energéticos são: EMAn = 4371,18 - 26,48PB + 30,65EE - 126,93MM - 52,26FB - 25,14FDN + 24,40FDA (R2= 81) e EMAn = 4205,23 + 30,58EE - 130,35MM - 58,29FB - 28,31FDN + 16,71FDA, ambas com R2 de 81%. As variáveis de composição química consideradas as mais importantes nas equações de predição ajustadas foram FB, FDN e FDA, pois explicam a maior parte da variabilidade nos valores de EMAn dos alimentos energéticos.
AGRADECIMENTOS
Os autores gostariam de agradecer ao Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), pelo financiamento do projeto.
Recebido em 12 de março de 2010
Aceito em 10 de fevereiro de 2011
Email: rafaneto2003@yahoo.com.br
- BORGES, F.M.O.; ROSTAGNO, H.S.; SAAD, C.E.P. et al. Equações de regressão para estimar valores energéticos de grão de trigo e seus subprodutos para frangos de corte, a partir de análises químicas. Arq. Bras. Med. Vet. Zootec., v.55, p.734-746, 2003.
- COOPER, H.M. Integrating research:a guide for literatura reviews. 2.ed. Newbury Park: Sage, 1990. 157p.
- DRAPER, N.R.; SMITH, H. Applied regression analysis. 2.ed. New York: John Wiley, 1981. 709p.
- HOFFMANN, R.; VIEIRA, S. Análise de regressão: uma introdução à econometria. São Paulo: HUCITEC - USP, 1977.
- JANSSEN, W.M.M.A. European table of energy values for poultry feedstuffs. 3.ed. Beekbergen: [s.n. ], 1989. 84p. (Spelderholt Center for Poultry Research and Information Services).
- KIRBY, K.N. Advanced data analysis with SYSTAT. New York: Van Nostrand Reinhold, 1993. 475p.
- MONTGOMERY, D.C.; PECK, E.A. Introduction to linear regression analysis.New York: J. Wiley, 1981. 504p.
- NAGATA, A.K.; RODRIGUES, P.B.; FREITAS, R.T.F. et al. Energia metabolizável de alguns alimentos energéticos para frangos de corte, determinada por ensaios metabólicos e por equações de predição. Cienc. Agrotecnol., v.28, p.668-677, 2004.
- NUTRIENT requeriments of poultry. 9.ed. Washington: National Academy of Science, 1994. 155p.
- NUNES, R.V.; ROSTAGNO, H.S.; ALBINO, L.F.T. et al. Composição bromatológica, energia metabolizável e equações de predição da energia do grão e de subprodutos do trigo para pintos de corte. Rev. Bras. Zootec, v.30, p.785-793, 2001.
- PENZ Jr., A.M.; KESSLER, A.M. O que a galinha come? Aves Ovos,v.15, p.66-76, 1995.
- PHILIP, J.S.; GILBERT, H.J.; SWITHARD, R.R. Growth, viscosity and beta-glucanase activity of intestinal fluid in broiler chickens feed on barley-based diets with or without exogenous beta-glucanase. Br. Poult. Sci., v.36, p.599-605, 1995.
- RODRIGUES, P.B.; ROSTAGNO, H.S.; ALBINO, L.F.T. et al. Valores energéticos da soja e subprodutos da soja, determinados com frangos de corte e galos adultos. Rev. Bras. Zootec., v.31, p.1771-1782, 2002.
- RODRIGUES, P.B.; ROSTAGNO, H.S.; ALBINO, L.F.T. et al. Valores energéticos do milheto, do milho e subprodutos do milho, determinados com frangos de corte e galos adultos. Rev. Bras. Zootec., v.30, p.1767-1778, 2001.
- SMITS, C.H.M.; ANNISON, G. Non-starch plant polysaccarides in broiler nutrition - towards a physiological valid approach to their determination. World Poult. Sci. J, v.52, p.203-221, 1996.
- ZONTA, M.C.M.; RODRIGUES, P.B.; ZONTA, A. et al. Energia metabolizável de ingredientes proteicos determinada pelo método de coleta total e por equações de predição. Cienc. Agrotecnol., v.28, p.1400-1407, 2004.
Datas de Publicação
-
Publicação nesta coleção
08 Abr 2011 -
Data do Fascículo
Fev 2011
Histórico
-
Recebido
12 Mar 2010 -
Aceito
10 Fev 2011