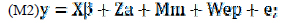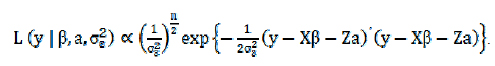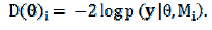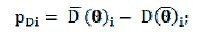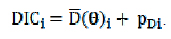RESUMO
Compararam-se dois modelos (com ou sem o efeito materno) na estimativa de parâmetros genéticos por meio do fator de Bayes (FB) e do critério de informação da deviance (DIC). Adicionalmente, avaliaram-se as tendências genéticas, maternas e fenotípicas em características de crescimento de bovinos da raça Tabapuã do estado da Bahia. O modelo que incluiu o efeito materno proporcionou menores valores de FB (167629,2; 117341,2 e 124804,8) e DIC (174550,0; 120242,7 e 128037,2) para pesos aos 205 (P205), 365 (P365) e 550 (P550) dias de idade, respectivamente. As estimativas médias, a posteriori, das herdabilidades diretas e maternas foram 0,33; 0,43 e 0,44 e 0,15; 0,14 e 0,16 para as três características, respectivamente. As tendências genéticas para o efeito direto foram de 0,4415 e 0,3613kg/ano para P205 e P365 e representam incrementos de apenas 0,25 e 0,15% nas médias das características ao ano. As tendências genéticas maternas para as três características demonstraram perdas e indicam ausência de seleção de matrizes para boa habilidade materna. Apesar de existir variabilidade genética suficiente para justificar ganhos genéticos via seleção, estes e os ganhos fenotípicos foram pequenos, sugerindo necessidade de melhorias genéticas e ambientais.
Palavras-chave:
bovino de corte; efeito materno; inferência bayesiana
ABSTRACT
We compared two models (with or without maternal effect) in the estimation of genetic parameters through Bayes Factor (BF) and the Deviance Information Criterion (DIC). Additionally, we evaluated the genetic, maternal and phenotypic trends in Tabapuã bovine growth characteristics in the state of Bahia. The model that included the maternal effect provided smaller BF values (167,629.2; 117,341.2 and 124,804.8) and DIC (174,550.0; 120,242.7 and 128,037.2) for weights at 205 (W205), 365 (W365) and 550 (W550) days of age, respectively. The average estimates, a posteriori, the direct and maternal heritability (0.33, 0.43 and 0.44) and (0.15, 0.14 and 0.16) for the three characteristics, respectively. Genetic trends for direct effect were 0.4415 and 0.3613kg/year for W205 and W365 and presented increases of 0.25 and 0.15% in the average characteristics of the year. The phenotypic trend for W205 was 0.7039kg/year. Maternal genetic trends for the three characteristics showed losses and indicate absence of selection matrices for good maternal ability. Despite the magnitude of the estimated direct and maternal heritability, they indicate genetic gain opportunities, genetic and phenotypic trends indicated few direct gains and no gains for maternal ability.
Keywords:
cattle; maternal effect; bayesianinference
INTRODUÇÃO
O conhecimento da influência materna em características de crescimento e a distinção adequada entre os efeitos genéticos diretos e maternos são fundamentais em programas de melhoramento genético. O efeito materno é caracterizado como uma contribuição sobre o fenótipo de um indivíduo atribuível diretamente ao fenótipo de sua mãe e, com a diminuição da idade de abate dos animais, sua importância tem sido cada vez mais considerada nas avaliações genéticas.
Tradicionalmente, os estudos abrangendo o uso de modelos com ou sem efeito materno são realizados por meio do método da máxima verossimilhança restrita (Cucco et al., 2009CUCCO, D.C.; FERRAZ, J.B.S.; PINTO, L.F.B. et al. Genetic parameters for pre-weaning traits in Brauvieh cattle. Genet. Mol. Res., v.8, p.291-298, 2009.; Baldi et al., 2010BALDI, F.; ALENCAR, M.M.; ALBUQUERQUE, L.G. Estimativas de parâmetros genéticos para características de crescimento em bovinos da raça Canchim utilizando modelos de dimensão finita. Rev. Bras. Zootec., v.11, p.2409-2417, 2010.; Cucco et al., 2010). A inferência bayesiana é uma alternativa que apresenta vantagens em relação à metodologia frequentista na obtenção de estimativas de parâmetros genéticos. Segundo Resende et al. (2001RESENDE, M.D.V.; DUDA, L.L.; GUIMARÃES, P.R.B. et al. Análise de modelos lineares mistos via inferência bayesiana. Rev. Mat. Estat., v.19, p.41-70, 2001.), a inferência bayesiana pode ser utilizada tanto em pequenos quanto em grandes conjuntos de dados e em modelos mais complexos, enquanto na metodologia frequentista o aumento da complexidade dos modelos prejudica a confiabilidade das avaliações genéticas.
Métodos como o critério de informação Akaike (AIC), critério de informação bayesiano (BIC) e teste de razão de verossimilhança (LRT) têm sido muito utilizados na comparação de modelos. Entretanto, esses métodos penalizam modelos mais parametrizados e tendem a um viés na avaliação genética (López e Carabaño, 2003LÓPEZ, R.P.; CARABAÑO, M.J. Comparing alternative random regression models to analysefirts-lactation daily yield data in hostein-friesian cattle. Livest. Prod. Sci., v.82, p.81-86, 2003. ). Em estudos bayesianos, metodologias apropriadas, como o fator de Bayes (FB) Newtone Raftery (1994NEWTON, M.A.; RAFTERY, A.E. Approximate bayesian inference with the weighted likelihood bootstrap. J. R. Stat. Soc. Ser. B., v.56, p.33-48, 1994. ) e o critério de informação da deviance (DIC) (Spiegelhalter et al., 2002), têm sido comumente empregadas na comparação de modelos (Cardoso et al., 2011CARDOSO, L.L.; BRACCINI NETO, J.; CARDOSO, F.F. et al. Hierarchical bayesian models for genotype x environment estimates in post-weaning gain of Hereford bovine via reaction norms. Rev. Bras. Zootec., v.40, p.294-300, 2011. ; Nascimento et al., 2011NASCIMENTO, M.; SILVA, F.F.; SÁFADI, T. et al. Abordagem bayesiana para avaliação da adaptabilidade e estabilidade de genótipos de alfafa. Pesqui. Agropecu. Bras., v.46, p.26-32, 2011. ). Estes métodos são mais informativos, pois permitem quantificar o grau de superioridade de um modelo em relação ao outro e podem ser utilizados na seleção de dois ou mais modelos, sejam eles discretos ou contínuos, simples ou complexos (Silva et al., 2008SILVA, F.F.; SÁFADI, T.; MUNIZ, J.A. et al. Comparação bayesiana de modelos de previsão de diferenças esperadas nas progênies no melhoramento genético de gado Nelore. Pesqui. Agropecu. Bras., v.43, p.37-45, 2008. ).
Dessa forma, objetivou-se comparar dois modelos (com ou sem o efeito materno) na estimativa de parâmetros genéticos e avaliar as tendências genéticas, maternas e fenotípicas para P205, P365 e P550 em bovinos da raça Tabapuã do estado da Bahia.
MATERIAL E MÉTODOS
Foram analisados registros de desempenho de 19.379; 13.887 e 12.015 animais para P205, P365 e P550, respectivamente. Os dados analisados foram provenientes do controle de desenvolvimento ponderal de animais da raça Tabapuã do estado da Bahia da Associação Brasileira de Criadores de Zebu (ABCZ). Os animais foram criados em regime de pasto e nascidos no período de 1975 a 2010.
Para edição do banco de dados, análise descritiva e remoção dos outliers, foi utilizado o programa Statistical Analysis Software (Sas..., 2003). A formação dos grupos de contemporâneos (GC) considerou as seguintes fontes de variação: sexo, ano, época de nascimento, regime alimentar, condição de criação e fazenda e número da fazenda. Os GC com menos de três animais foram excluídos das análises.
Os dois modelos animais unicaracterísticos matriciais utilizados foram:
em que: y = vetor de dados (P205, P365 e P550); β = vetor de efeitos fixos no modelo, associados à matriz de incidência X; a = vetor dos efeitos aleatórios de valor genético aditivo direto do animal, associado à matriz de incidência Z; m = vetor dos efeitos aleatórios de valor genético materno, associados à matriz de incidência M; ep = vetor dos efeitos aleatórios de ambiente permanente da vaca, associado à matriz de incidência W; e = vetor dos efeitos aleatórios residuais.
Para o modelo M1, assume-se inicialmente a distribuição condicional dos dados (y) como uma normal multivariada:
em que: I é a matriz identidade, e  a variância residual.
a variância residual.
Quando se assume um modelo quantitativo infinitesimal, tem-se que a distribuição de a é também normal multivariada:
em que: A é a matriz de parentesco genético aditivo, e  a variância genética aditiva na população em estudo.
a variância genética aditiva na população em estudo.
A função de verossimilhança para cada animal é dada por:
O segundo passo foi definir a distribuição a priori dos parâmetros do modelo.
Para o efeito fixo, foi definida uma priori do tipo constante, já que a noção do conhecimento a priori é vaga para β.
A distribuição a priori dos componentes de variância  (variância genética aditiva) e
(variância genética aditiva) e  (variância residual) foi especificada como uma distribuição qui-quadrado escalonada invertida, da forma:
(variância residual) foi especificada como uma distribuição qui-quadrado escalonada invertida, da forma:
Quando foi assumida uma distribuição a priori informativa, substituíram-se em v os graus de liberdade da distribuição qui-quadrado e em Morais et al., 2010MORAIS, T.S.S.; SILVA, F.F.; SILVA, C.H.O. et al. Análise bayesiana de sensibilidade do modelo AR(1) para dados em painel: uma aplicação em dados temporais de microarrays. Rev. Bras. Biom., v.28, p.171-192, 2010. ). , o valor inicial da variância. Tal estratégia é adotada visando fornecer mais informação ao modelo, de forma a aumentar a acurácia das estimativas (
, o valor inicial da variância. Tal estratégia é adotada visando fornecer mais informação ao modelo, de forma a aumentar a acurácia das estimativas (
Para assumir uma distribuição a priori não informativa, a qui-quadrada foi reduzida em uma uniforme imprópria, substituindo-se v = -2 e  = 0.
= 0.
Após definidas as distribuições acima, considerando-se independência entre as distribuições a priori, pôde-se escrever a distribuição conjunta a posteriori dos parâmetros do modelo.
em que se omitiu o condicionamento dos hiperparâmetros (parâmetros que auxiliam na especificação da priori e conhecida matriz de parentesco A).
Considerando-se a distribuição a priori dos componentes de variância como um qui-quadrado invertida, tem-se que a distribuição conjunta a posteriori pode ser reescrita:
Ao se assumir a distribuição uniforme para i = -2 e  = 0 (i = a, ε) . na expressão acima.
= 0 (i = a, ε) . na expressão acima. e
e  , basta fazer v
, basta fazer v
No contexto bayesiano, a inferência é obtida a partir da distribuição conjunta a posteriori, logo as distribuições a posteriori condicionais completas para cada parâmetro são:
em que o parâmetro de escala é 
em que o parâmetro de escala é
Por se tratar de distribuições que já estão implementadas em softwares, as aproximações para as distribuições marginais foram feitas pela implementação do amostrador de Gibbs, por meio de métodos de Monte Carlo via cadeias de Markov (MCMC).
Para o modelo M2, a função de verossimilhança e as distribuições a priori para os parâmetros seguem o mesmo desenvolvimento do modelo M1, porém contendo, além dos efeitos aditivo direto e residual, os efeitos maternos e de ambiente permanente como aleatórios.
O ajuste dos modelos M1 e M2 aos dados foi avaliado por meio de dois critérios bayesianos: critério de informação de deviance (DIC) e deviance baseada no fator de Bayes (FB).
O DIC é um meio de comparação de modelos, o qual sugere que comparações entre modelos sejam baseadas na distribuição a posteriori da deviance de cada modelo. É composto por uma medida de ajuste global, média a posteriori da deviance, e uma penalização por complexidade do modelo (número efetivo de parâmetros, pD), que é calculada pela diferença. A diferença entre a média a posteriori da deviance e a deviance é baseada na média a posteriori dos parâmetros do modelo.
A deviance do modelo i pode ser definida como:
Um estimador de Monte Carlo é obtido por:
A complexidade do modelo i como número efetivo de parâmetros é determinada por:
em que: a posteriori dos parâmetros. Finalmente, o DIC é calculado por: é a média
é a média
Obtém-se
m ciclos, avalia-se  , em que:
, em que: para se obter
para se obter  e, ao final de
e, ao final de
Menores valores de DIC indicam melhor ajuste do modelo, ou seja, um modelo mais próximo do modelo ideal.
O FB é uma medida global de ajuste dada pela razão entre as distribuições marginais dos dados p(y | M1) sob dois modelos diferentes (Mi, i = 1,2), de modo que:
Pode ser demonstrado que Newton e Raftery, 1994NEWTON, M.A.; RAFTERY, A.E. Approximate bayesian inference with the weighted likelihood bootstrap. J. R. Stat. Soc. Ser. B., v.56, p.33-48, 1994. ):  é um estimador de Monte Carlo (
é um estimador de Monte Carlo (
em que m é o número do ciclos de Gibbs e  , em que c é o maior valor de
, em que c é o maior valor de  , amostra da distribuição a posteriori dos parâmetros no ciclo j. Para se evitarem erros de precisão ao se calcular FB, calculou-se
, amostra da distribuição a posteriori dos parâmetros no ciclo j. Para se evitarem erros de precisão ao se calcular FB, calculou-se  , tomando-se o logaritmo:
, tomando-se o logaritmo:
e finalmente:
A cada ciclo de Gibbs, foi salvo o 1, enquanto valores menores suportam M2. e, no final dos m ciclos, o FB pôde ser obtido como descrito acima, de modo que valores maiores que 1 suportam M
e, no final dos m ciclos, o FB pôde ser obtido como descrito acima, de modo que valores maiores que 1 suportam M
A deviance baseada no estimador do FB para o modelo i é igual a deviance indicam melhor ajuste. e menores valores dessa
e menores valores dessa
Como o Gibbssampler é um algoritmo iterativo, fez-se necessária a verificação da convergência da cadeia. Primeiro rodou-se uma amostra piloto com uma cadeia total de 100000 iterações, um período de descarte burn-in de 10000 e 1 de intervalo de salvamento thinning para todas as características. Em seguida, aplicou-se o critério de Raftery e Lewis para se definir a quantidade ideal de iterações necessárias para que o amostrador de Gibbs apresentasse convergência à distribuição estacionária (Raftery e Lewis, 1992).
Após a definição do número de iterações da cadeia total (total), de burn-in e thinning, uma nova análise foi realizada, e sua convergência testada, aplicando-se o critério de Geweke, em que valores acima de 0,05 p-value corresponderam à convergência da cadeia (Geweke, 1992GEWEKE, J. Evaluating the accuracy of sampling‑based approaches to the calculation of posterior moments. In: BERNARDO, J.M.; DAVID, A.P.; SMITH, A.F.M. (Eds.). Bayesian statistics. New York: Oxford University, 1992. cap.4, p.625- 631.). Os testes dos critérios de Raftery e Lewis e Geweke foram realizados por meio do pacote estatístico BOA (Bayesian Output Analynis), implementado no programa R (R Development ..., 2010).
Na análise bayesiana, para cada parâmetro do modelo de regressão adotado, foram consideradas 300000 iterações (total), com um período de aquecimento burn-in de 30000 e 3 de thinning para P205, para P365, 500000, 50000 e 5, e para P550, 100000, 10000 e 1, respectivamente.
As estimativas das tendências genéticas diretas, maternas e fenotípicas para as características foram obtidas pela regressão linear ponderada da variável dependente (valores genéticos e pesos observados) sobre o ano de nascimento do animal, por meio do procedimento PROC REG (Sas..., 2003).
RESULTADOS E DISCUSSÃO
Todos os modelos obtiveram convergência a 5% (P>0,05) pelo critério de Geweke. O modelo M2 foi o mais indicado por apresentar menores valores para FB e DIC em todas as características (Tab. 1).
A superioridade do modelo M2 evidencia a importância dos efeitos maternos sobre o desempenho em bovinos de corte. De acordo com Silva et al. (2013SILVA, R.M.; SOUZA, J.C.; SILVA, L.O.C. et al. Parâmetros e tendências genéticas para pesos de várias idades em bovinos Nelore. Rev. Bras. Saúde Prod. Anim., v.14, p.21-28, 2013. ), o fenótipo do animal, além de ser caracterizado pela porção genética proveniente da mãe durante a formação do gameta (genótipo do bezerro), pode também ser caracterizado pelo ambiente materno (genótipo da vaca) oferecido ao filho até a desmama. Além disso, em animais criados a pasto, o efeito materno pode influenciar até mesmo em idades superiores pelo fato de estes permanecerem mais tempo com a mãe (Bolignon et al., 2006BOLIGNON, A.A.; RORATO, P.R.N.; WEBER, T. et al. Herdabilidades para ganho de peso da desmama ao sobreano e perímetro escrotal ao sobreano e tendências genéticas e fenotípicas para ganho de peso da desmama ao sobreano em bovinos Nelore: Angus. Rev. Bras. Zootec., v.35, p.1323-1328, 2006. ).
A contribuição do efeito materno na variação fenotípica foi crescente com o aumento da idade dos animais, apresentando valores de 111,07;167,89 e 377,89 para a variância materna e 99,5; 143,50 e 139,38 para a variância do efeito permanente (Tab. 2). Esses resultados indicam a possibilidade de exploração da variabilidade desses efeitos para a seleção de matrizes com boa habilidade materna. Silva et al. (2013SILVA, R.M.; SOUZA, J.C.; SILVA, L.O.C. et al. Parâmetros e tendências genéticas para pesos de várias idades em bovinos Nelore. Rev. Bras. Saúde Prod. Anim., v.14, p.21-28, 2013. ) também observaram a contribuição do efeito materno na variação fenotípica total em animais criados em regime de pasto para P205, P365 e P550. Para esses autores, a contribuição do efeito materno na variação fenotípica indica que há uma tendência de esses animais sofrerem maior influência dos efeitos maternos e que a inclusão destes no modelo de avaliação deve ser ponderada de acordo com a estratégia metodológica empregada para se obterem estimativas dos parâmetros genéticos mais acurados.
As médias a posteriori das herdabilidades diretas para o modelo M2 foram de média a alta magnitude (Tab. 2), indicando possibilidade de ganhos por seleção. Nesse caso, o uso do fenótipo do animal torna-se interessante como critério de seleção, visto que muito da variação dos pesos é decorrente do efeito genético direto.
Em geral, as estimativas de herdabilidades maternas para características de peso são de baixas magnitudes. Entretanto, as herdabilidades maternas pelo modelo M2 apresentaram valores que justificam a seleção para esse efeito na raça Tabapuã do estado da Bahia. As médias a posteriori das herdabilidades foram de 0,15 (P205); 0,14 (P365) e 0,16 (P550) (Tab. 2), sendo esses valores superiores aos encontrados por Souza Júnior et al. (2011); Lacerda et al.,(2014LACERDA, J.J.D.; CANEIRO, P.L.S.; MARTINS FILHO, R. et al. Parâmetros e tendências genéticas para características de crescimento em bovinos da raça Nelore no estado da Bahia utilizando inferência bayesiana. Rev. Bras. Saúde Prod. Anim., v.15, p.10-19, 2014.), em zebuínos do Nordeste do Brasil.
O progresso genético no rebanho foi avaliado pelas tendências genéticas e permitiu avaliar a mudança ocasionada pelo processo de seleção para determinadas características ao longo dos anos. As tendências genéticas, maternas e fenotípicas, foram calculadas com base no modelo M2 para todos os pesos (Fig. 1 a 6).
. Tendências genéticas para as características peso aos 205 e 365 dias de idade, respectivamente, em bovinos da raça Tabapuã, no estado da Bahia, por meio da inferência bayesiana.
. Tendências maternas para as características peso aos 205, 365 e 550 dias de idade, respectivamente, em bovinos da raça Tabapuã, no estado da Bahia, por meio da inferência bayesiana.
Tendência fenotípica para a característica peso aos 205 dias de idade (P205) em bovinos da raça Tabapuã no estado da Bahia, por meio da inferência bayesiana.
As tendências genéticas dos efeitos diretos para P205 e P365 foram significativas (P<0,0001) e iguais a 0,4415 e 0,3613kg/ano (Fig. 1 e 2). Os ganhos acumulados, em 35 anos, foram de 15,45 e 12,64kg para P205 e P365 e representaram incrementos de 0,25 e 0,15% na média do peso, respectivamente. É possível obter uma taxa de mudança genética anual de 1 a 3% da média da população sob estudo. Incrementos superiores têm sido registrados em rebanhos bovinos de diferentes raças (Lima et al.,2005LIMA, A.E.S.; FERRAZ FILHO, P.B.; SILVA, L.O.C. et al. Efeitos genéticos diretos e maternos e suas tendências em pesos à desmama de bovinos da raça Nelore mocha, na região pecuária de Goiás. Arch. Vet. Sci., v.10, p.69-74, 2005., na raça Nelore Mocha, e Souza Júnior et al.,2011, na raça Nelore. Resultados inferiores foram observados por Ferraz Filho et al. (2002), que encontraram ganhos de 0,1134; 0,2068 e 0,2757kg/ano, para P205, P365 e P550, e por Caires et al. (2012CAIRES, D.N.; MALHADO, C.H.M.; SOUZA, L.A.S. et al. Tabapuã breed in northeasterm Brazil: genetic progress and population struture. Rev. Bras. Zootec., v.41, p.1858-1865, 2012. ), de 0,0509kg/ano (P205) e 0,1249kg/ano (P365), ambos em animais da raça Tabapuã. A tendência genética para P550 não foi significativa em decorrência do menor número de registros.
As tendências genéticas maternas foram significativas (P<0,001) com valores de -0,2583; -0,2141 e -0,3344kg/ano, para P205, P365 e P550, respectivamente (Fig. 3, 4 e 5). Perdas acumuladas em 35 anos de estudos apresentaram valores de 9,0; 7,4 e 11,7kg/ano, o que é corroborado pelas correlações negativas e altas entre os efeitos aditivos diretos e maternos (-0,84, -0,93 e -0,97, para P205, 365 e 550, respectivamente). Esses valores pressupõem ausência de seleção de matrizes com boa habilidade materna, embora haja variabilidade suficiente no rebanho (Tab. 2). O comportamento decrescente para as tendências maternas deve-se, segundo Gonçalves et al. (2011GONÇALVES, F.M.; PIRES, A.V.; PEREIRA, I.G. et al. Avaliação genética para peso corporal em um rebanho Nelore. Arq. Bras. Med. Vet. Zootec., v.63, p.158-164, 2011. ), à ênfase (seleção) para as características de produção (desempenho ponderal) em animais destinados para corte.
A tendência fenotípica para P205 mostrou-se significativa (P<0,0001) e igual a 0,7039kg/ano e representou um ganho de apenas 24,63kg durante o período estudado (Fig. 6). Esse ganho relatado é considerado modesto e reflete pequenos ganhos genéticos e ambientais. Outros estudos com zebuínos do Nordeste (Amaral et al., 2014AMARAL, R.S.; CARNEIRO, P.L.S.; MARTINS FILHO, R. et al. Tendências, parâmetros fenotípicos e genéticos de características de crescimento em bovinos Nelore mocho do nordeste brasileiro. Rev. Bras. Saúde Prod. Anim., v.15, p.261-271, 2014. ; Lacerda et al., 2014LACERDA, J.J.D.; CANEIRO, P.L.S.; MARTINS FILHO, R. et al. Parâmetros e tendências genéticas para características de crescimento em bovinos da raça Nelore no estado da Bahia utilizando inferência bayesiana. Rev. Bras. Saúde Prod. Anim., v.15, p.10-19, 2014.) evidenciaram ganhos superiores. As tendências fenotípicas para os pesos aos 365 e 550 dias de idade não foram significativas.
De um modo geral, os resultados evidenciam variabilidade genética aditiva e materna, o que poderia favorecer a seleção com possibilidade de ganhos genéticos diretos e maternos. O efeito genético direto foi pequeno, entretanto compôs maior parte do efeito fenotípico. Apesar disso, as magnitudes das tendências para o efeito genético aditivo direto indicam que a seleção para os pesos analisados não levaram a ganhos satisfatórios. Ao analisar o efeito maternal sobre as mesmas características, sugere-se inexistência de seleção de fêmeas com boa habilidade materna. Em estudos com zebuínos, Bolignon et al. (2006BOLIGNON, A.A.; RORATO, P.R.N.; WEBER, T. et al. Herdabilidades para ganho de peso da desmama ao sobreano e perímetro escrotal ao sobreano e tendências genéticas e fenotípicas para ganho de peso da desmama ao sobreano em bovinos Nelore: Angus. Rev. Bras. Zootec., v.35, p.1323-1328, 2006. ) e Lacerda et al. (2014LACERDA, J.J.D.; CANEIRO, P.L.S.; MARTINS FILHO, R. et al. Parâmetros e tendências genéticas para características de crescimento em bovinos da raça Nelore no estado da Bahia utilizando inferência bayesiana. Rev. Bras. Saúde Prod. Anim., v.15, p.10-19, 2014.) mostraram que o efeito genético tem sido menor que o efeito fenotípico, e, nesses casos, as melhorias no ambiente tornam-se um fator determinante para o ganho fenotípico.
CONCLUSÕES
O modelo M2, que considerou a inclusão dos efeitos materno e ambiente permanente, mostrou melhor ajuste para as três características por meio dos critérios de avaliação bayesianos (FB e DIC) e deve ser incluído nas avaliações genéticas, de forma a aumentar a acurácia das estimativas. As estimativas médias a posteriori dos coeficientes de herdabilidades indicam existência de variabilidade genética aditiva direta no Tabapuã no estado da Bahia, evidenciando oportunidade de ganho genético com a seleção; as estimativas médias a posteriori das herdabilidades maternas foram de baixa magnitude, mas superiores aos valores observados em outros estudos, indicando possibilidades de ganhos por seleção. Embora exista variabilidade que permita a seleção para habilidade materna, observou-se inexistência de seleção ao longo dos anos. Também há variabilidade genética suficiente para justificar ganhos genéticos diretos via seleção, estes e os ganhos fenotípicos foram pequenos, sugerindo necessidade de melhorias genéticas e ambientais.
REFERÊNCIAS
- AMARAL, R.S.; CARNEIRO, P.L.S.; MARTINS FILHO, R. et al. Tendências, parâmetros fenotípicos e genéticos de características de crescimento em bovinos Nelore mocho do nordeste brasileiro. Rev. Bras. Saúde Prod. Anim., v.15, p.261-271, 2014.
- BALDI, F.; ALENCAR, M.M.; ALBUQUERQUE, L.G. Estimativas de parâmetros genéticos para características de crescimento em bovinos da raça Canchim utilizando modelos de dimensão finita. Rev. Bras. Zootec., v.11, p.2409-2417, 2010.
- BOLIGNON, A.A.; RORATO, P.R.N.; WEBER, T. et al. Herdabilidades para ganho de peso da desmama ao sobreano e perímetro escrotal ao sobreano e tendências genéticas e fenotípicas para ganho de peso da desmama ao sobreano em bovinos Nelore: Angus. Rev. Bras. Zootec., v.35, p.1323-1328, 2006.
- CAIRES, D.N.; MALHADO, C.H.M.; SOUZA, L.A.S. et al. Tabapuã breed in northeasterm Brazil: genetic progress and population struture. Rev. Bras. Zootec., v.41, p.1858-1865, 2012.
- CARDOSO, L.L.; BRACCINI NETO, J.; CARDOSO, F.F. et al. Hierarchical bayesian models for genotype x environment estimates in post-weaning gain of Hereford bovine via reaction norms. Rev. Bras. Zootec., v.40, p.294-300, 2011.
- CUCCO, D.C.; FERRAZ, J.B.S.; ELER, J.P. et al. Genetic parameters for postweaning traits in Brauvieh cattle. Genet. Mol. Res., v.9, p.545-553, 2010.
- CUCCO, D.C.; FERRAZ, J.B.S.; PINTO, L.F.B. et al. Genetic parameters for pre-weaning traits in Brauvieh cattle. Genet. Mol. Res., v.8, p.291-298, 2009.
- FERRAZ FILHO, P.B.; RAMOS, A.A.; SILVA, L.O.C. et al. Tendência genética de efeitos direto e materno sobre os pesos à desmama e pós-desmama de bovinos da raça Tabapuã no Brasil. Rev. Bras. Zootec., v.31, p.635-640, 2002.
- GEWEKE, J. Evaluating the accuracy of sampling‑based approaches to the calculation of posterior moments. In: BERNARDO, J.M.; DAVID, A.P.; SMITH, A.F.M. (Eds.). Bayesian statistics. New York: Oxford University, 1992. cap.4, p.625- 631.
- GONÇALVES, F.M.; PIRES, A.V.; PEREIRA, I.G. et al. Avaliação genética para peso corporal em um rebanho Nelore. Arq. Bras. Med. Vet. Zootec., v.63, p.158-164, 2011.
- LACERDA, J.J.D.; CANEIRO, P.L.S.; MARTINS FILHO, R. et al. Parâmetros e tendências genéticas para características de crescimento em bovinos da raça Nelore no estado da Bahia utilizando inferência bayesiana. Rev. Bras. Saúde Prod. Anim., v.15, p.10-19, 2014.
- LIMA, A.E.S.; FERRAZ FILHO, P.B.; SILVA, L.O.C. et al. Efeitos genéticos diretos e maternos e suas tendências em pesos à desmama de bovinos da raça Nelore mocha, na região pecuária de Goiás. Arch. Vet. Sci., v.10, p.69-74, 2005.
- LÓPEZ, R.P.; CARABAÑO, M.J. Comparing alternative random regression models to analysefirts-lactation daily yield data in hostein-friesian cattle. Livest. Prod. Sci., v.82, p.81-86, 2003.
- MORAIS, T.S.S.; SILVA, F.F.; SILVA, C.H.O. et al. Análise bayesiana de sensibilidade do modelo AR(1) para dados em painel: uma aplicação em dados temporais de microarrays. Rev. Bras. Biom., v.28, p.171-192, 2010.
- NASCIMENTO, M.; SILVA, F.F.; SÁFADI, T. et al. Abordagem bayesiana para avaliação da adaptabilidade e estabilidade de genótipos de alfafa. Pesqui. Agropecu. Bras., v.46, p.26-32, 2011.
- NEWTON, M.A.; RAFTERY, A.E. Approximate bayesian inference with the weighted likelihood bootstrap. J. R. Stat. Soc. Ser. B., v.56, p.33-48, 1994.
- R DEVELOPMENT core team: a language and environment for statistical computing. Versão 3.1.0. Vienna: R Foundation for Statistical Computing, 2010. Disponível em: <http://www.R‑project.org>. Acessado em: 10 jan. 2010.
» http://www.R‑project.org - RAFTERY, A.E.; LEWIS, S.M. Comment: one long run with diagnostics: implementation strategies for Markov chain Monte Carlo. Stat. Sci., v.7, p.493-497, 1992.
- RESENDE, M.D.V.; DUDA, L.L.; GUIMARÃES, P.R.B. et al. Análise de modelos lineares mistos via inferência bayesiana. Rev. Mat. Estat., v.19, p.41-70, 2001.
- SAS user's guide, versão 8.2.1. Cary: SAS, 2003.
- SILVA, F.F.; SÁFADI, T.; MUNIZ, J.A. et al. Comparação bayesiana de modelos de previsão de diferenças esperadas nas progênies no melhoramento genético de gado Nelore. Pesqui. Agropecu. Bras., v.43, p.37-45, 2008.
- SILVA, R.M.; SOUZA, J.C.; SILVA, L.O.C. et al. Parâmetros e tendências genéticas para pesos de várias idades em bovinos Nelore. Rev. Bras. Saúde Prod. Anim., v.14, p.21-28, 2013.
- SOUZA JÚNIOR. C.; SILVA, L.O.C.; GONDO, A. et al. Parâmetros e tendências genética de peso de bovinos criados à pasto no Brasil. Arch. Zootec., v.60, p.457-456, 2011.
- SPIEGELHALTER, D.J.; BEST, N.G.; CARLIN, B.P. et al. Bayesian measures of model complexity and fit. J. R. Stat. Soc. Ser. B. Stat. Meth., v.64, p.583-616, 2002.
Datas de Publicação
-
Publicação nesta coleção
Jul-Aug 2016
Histórico
-
Recebido
18 Mar 2015 -
Aceito
11 Fev 2016