Spatial and temporal characteristics of Outgoing Longwave Radiation (OLR): an update

Spatial and temporal characteristics of Outgoing Longwave Radiation (OLR): an update

Rajaram Purushottam Kane

Instituto Nacional de Pesquisas Espaciais, P.O. Box 515, 12245-970 São José dos Campos, SP, Brazil. Phone: [phone]; Fax: [phone]- E-mail: [e-mail]

ABSTRACT

A study of the Outgoing longwave radiation (OLR) values (Unit, W/m) observed by various satellites during 1979-2002 revealed that the OLR values varied considerably from one geographical region to another ( ~ 100-300 units). The climatology was latitude dependent. At middle and high latitudes, the range (minimum to maximum) was ~ 40-60 units, with maximum in local summer and minimum in local winter, but at lower latitudes, the range reduced considerably and was uncertain near equator. Near equator, the long-term changes (as seen in 12-month moving averages) were: OLR decreases during ENSO events in the eastern Pacific up to the dateline, and OLR increases during ENSO events in the Australasian region. Outside the equatorial region, the OLR changes were small during ENSO events and negligible in other years. In some longitudes at middle and high latitudes, the OLR changes occurred several months after the El Niño events, coinciding with La Niña (cold water events, opposite of warm water El Niño events).

Keywords: spectra, OLR (Outgoing Longwave Radiation).

RESUMO

Um estudo dos valores (em unidades de W/m) da emissão de radiação de ondas longas (OLR) observados por sensores em vários satélites entre 1979 e 2002 revelou que os valores de OLR variavam consideravelmente de uma região geográfica para outra ( ~ 100-300 unidades). A climatologia era dependente da latitude. Em latitudes medias e altas, a faixa de variação (mínima e máxima) era de ~ 40-60 unidades, com valores máximos no verão local e mínimos no inverno, porém, em baixas latitudes, a faixa se tornava consideravelmente reduzida e oscilante próximo do equador. Neste caso, as mudanças de longo termo (como observado em médias móveis de 12 meses) eram: os valores de OLR decresciam até o dateline durante os eventos ENSO do Pacífico oriental e aumentavam durante os eventos ENSO na região da Austrália. Fora da região equatorial, as mudanças do OLR eram pequenas durante os eventos ENSO e insignificante nos outros anos. Em algumas longitudes, em latitudes médias e altas, as mudanças OLR ocorreram em diversos meses após os eventos El Niño, coincidindo com La Niña (eventos de águas frias, opostos aos de águas quentes dos eventos El Niño).

Palavras-chave: spectra, OLR (Outgoing Longwave Radiation ).

INTRODUCTION

Terrestrial energy budget is mainly governed by the incoming Total Solar Irradiance (TSI) and the Outgoing Longwave Radiation (OLR). Among these, TSI is almost constant (often called 'Solar Constant'). Hence the variations of terrestrial weather and climate should have a considerable contribution from the space and time variations of OLR. The studies of OLR prior to theadvent of satellites are reviewed by Hunt et al. (1986). A history of satellite missions and measurements of the Earth's radiation budget during 1957-1984 has been traced by House et al. (1986). Winston et al. (1979) used the scanning radiometer (SR) aboard operational meteorological satellites to compute OLR andpublished a data set for June 1974-March 1978. Heddinghaus & Krueger (1981) subjected this data set to an Empirical Orthogonal Function (EOF) analysis and determined the annual and semiannual cycles and interannual variations for that period. Bess et al. (1992) used EOF approach on a 10-year data set, found that the first EOF accounted for 66% of the variance, the first two EOFs described mainly the annual cycle, the third EOF described mainly the semiannual cycle, and the fourth EOF described much of the 1976-1977 and 1982-1983 El Niño/Southern Oscillation (ENSO) phenomena (besides other details). Chelliah & Arkin (1992) used OLR data derived from NOAA's polar-orbiting satellites for more than 15 years, performed a Rotated Principal Component Analysis (RPCA) on monthly OLR anomalies over the global tropics (30ºN-30ºS) on a 10º longitude by 5º latitude grid for June 1974-March 1989, excluding calendar year 1978.The spatial-loading pattern and the time series for the first principal component (first RPC), the 'canonical ENSO mode', represented the major large-scale features in the tropics during the typical phase of the major warm (El Niño) and cold (La Niña) events in the tropical Pacific during the analysis period. However, the characteristics of the dramatic 1982-1983 warm event (El Niño) were different from the canonical ENSO mode and completely dominated the second RPC. (The third and fourth leading RPCs described the changes in the satellite-observing system).Barnett & Preisendorfer (1978) have attempted multifield analog predictions of short-term climate fluctuations using a climate state vector. For the tropical regions, several workers have used OLR as indicators of annual, interannual and interseasonal variability of convective activity. Liebmann & Hartmann (1982) studied the interannual variations of OLR associated with tropical circulation changes during 1974-1978. Kousky (1988) studied OLR climatology for the South American sector. Ferreira & Gurgel (2002) studied the annual and interannual variability of OLR above South America and its vicinity. Kayano et al. (1995) studied the OLR biases and their impacts on EOF modes of interannual variability in the tropics.

In the present communication, OLR data are used for 1974-2002 (omitting 1978) to illustrate the geographical distribution, climatology, and long-term variations of OLR during this interval, and in particular, to obtain their spectra .

DATA

OLR data were available on several websites, for example, http://ingrid.ldeo.columbia.edu/maproom/.Global/.Precipitation/ Monthly_OLR.html, http://ingrid.ldeo.columbia.edu/SOURCES/ .NOAA/.NCEP/.CPC/.GLOBAL/.monthly/.olr/, http://tao.atmos. washington.edu/data_sets/olr/index.html, in a 2.5º × 2.5º grid in different formats and were accessed as needed for different purposes.

PLOTS

Geographical distribution

Figure 1 shows a plot of the absolute OLR values (W/m) in a 10º × 10º grid, latitudes top to bottom (North to South), longitudes left to right (0-360 E, or 360W-0), for (a) July 1974 (northern summer) in the upper half and (b) January 1975 (northern winter) in the lower half. The OLR values in different ranges are indicated by symbols (100-125, xx; 125-150, x; 150-175, B; 175-200, small open circle; 200-225, small full circle; 225-250, big full circle; 250-275, full square; > 275 full square with an open circle in the center). The average value is ~ 220 and small full circles (200-225) would represent average values. (There was noEl Niño event during 1974-1975, only later in 1976-1977). The following may be noted:

(1) The summer and winter values are very different at very high latitudes (near the poles). The winter values (xx) are almost half of the summer values (small full circles). This is because the OLR is associated with surface temperature and clouds and the levels of surface temperature and cloud cover are very different in summer and winter. In thetropics, the seasonal variability also depends on the presence or absence of convective activity.

(2) The values in low latitudes are far above average, but there are considerable longitude differences. In the website http://tao.atmos.washington.edu/data_sets/olr/index.html, Todd Mitchell mentions, "Low annual mean OLR values ( < 200 Wm) associated with deep atmospheric convection are found over the equatorial land masses, Amazon basin, and in the western equatorial Pacific. OLR < 200 Wm are also associated with the cold temperatures of the Himalayas. High annual mean OLR values ( > 280 Wm) are observed over the central and eastern Sahara and the Arabian Peninsula". Figure 1 shows somewhat different patterns. In the 40ºN-40ºS belt, all values are above average in the northern summer and average or above average in northern winter. The high values extend over large longitude ranges. Very high values are seen over western equatorial Pacific also (5ºN-5ºS, 120º-150ºW). (This pattern for 1974-1975 may not be exactly so in other years, but will probably be roughly valid).

If values are averaged over wider ranges, the pattern looks as shown in Figure 2, for a 20º latitude by 40º longitude grid, for July 1974 in the upper part (overall mean OLR value 226), June 1975 in the middle (overall mean OLR value 213), and their average in the lower part (overall mean OLR value 219). In the average, the south pole region has values below average. Values above average are in the 50ºN-50ºS belt, more so in the 30ºN-30ºS belt, with values varying in a large range (200-275) at different longitudes.

Climatology

The climatology (values for January, February, etc., averaged over several years) is shown in Figure 3, for 60º longitude ranges in successive columns. The following may be noted:

(1) The month-to-month pattern is basically annual, with maximum in summer (July-August in northern hemisphere, December-January in southern hemisphere) and minimum in winter, particularly conspicuous at middle and highlatitudes.

(2) The ranges (minimum to maximum) are about the same at very high latitudes (50-60 OLR units), but reduce at lower latitudes, faster in the southern hemisphere.

(3) In low latitudes, the climatology is obscure. The maxima are diffuse and not necessarily in mid-summer. This might have resulted in the semiannual component mentioned by Bess et al. (1992).

However, it may be noted that the latitude range of 22.5ºchosen here may be too large and may be obliterating changes in finer latitude ranges. It is well known that in parts of the tropics, OLR values are smaller in the summer hemisphere (May-August in the northern hemisphere, November-February in the southern hemisphere) due to convective clouds (cloud tops with low temperatures). In these regions, OLR values are higher in the winter hemisphere due to the absence of convection. In contrast, in middle and high latitudes, winter values of OLR are low dueto lower surface temperature, not due to cloud cover.

Long-term variation

Even though deseasoned monthly anomaly values were available, these were sometimes erratic. Hence, further 12-month moving averages calculated. There was a gap in data for several months in 1978. Hence, only data for 1979 onwards are considered. Figure 4 shows the plot of 12-month moving averages (runningmeans) centered 3 months apart (4 values per year) for the equatorial region (5ºN-5ºS). The top plots are for the well-knownphenomenon ENSO, which is briefly as follows.

Along the coast of Peru-Ecuador in South America, there is occasionally a warming of the ocean current, called El Niño (The Child, in Spanish), because it generally develops near Christmas, the birth of Jesus Christ. In some years, the current may extend southward along the coast of Peru to latitude 12ºS, killing plankton and fish in the coastal waters. Quinn et al. (1978,1987) determined the occurrence of El Niño events on the basis of the disruption of fishery, hydrological data, sea-surface temperature and rainfall along and near the Peru-Ecuador coast,defining intensities based on the positive sea-surface temperature anomalies along the coast as: Strong, in excess of 3ºC; Moderate, 2.0º-3.0ºC; Weak, 1.0º-2.0ºC. The warming at the coast extends to farther regions of the Pacific to the west of Peru-Ecuador. Monthly SST (sea surface temperature) anomalies are available on the Climate Prediction Center website http://www.cpc.ncep.noaa.gov/data/indices/, for regions Niño 1+2 (0-10ºS, 90º-80ºW), Niño 3 (5ºN-5ºS, 150º-90ºW), Niño 3.4 (5ºN-5ºS, 170º-120ºW), Niño 4 (5ºN-5ºS, 160ºE-150ºW).

A phenomenon intimately related to the El Niño occurrence is the Southern Oscillation (SO). It is a global pattern of short-term climatic fluctuations with a characteristic period of 2-7 years (e.g., Trenberth, 1997). A SO index can be simply represented by the Tahiti T (18ºS, 150ºW) minus Darwin D (12ºS, 131ºE) mean sea level pressure difference (T-D). Normally, the pressure at Tahiti is higher than that at Darwin by a few millibars. However, this pressure difference fluctuates (like a seesaw), sometimes reduces to zero (or becomes even negative) and this reduction is often associated with the occurrence of El Niños. In Figure 4, the top plot is for SST anomalies in the Niño 1+2 region. The positive anomalies are painted black and show the prominent El Niños of 1982-1983 (strong), 1986-1987 (moderate), 1991-1994 (weak and diffuse), and 1997-1998 (very strong). The next plot is for (T-D), (data from Parker, 1983, and the Climate Prediction Center website http://www.cpc.ncep.noaa.gov/data/indices/). The positive anomalies are painted black, negative anomalies are shown hatched, and these match very well with the negative anomalies and positive anomalies of SST (anticorrelation). Interestingly,during 1991-1994, SST anomalies are not large and are not uniform over the whole period, but (T-D) is consistently negative over the whole period, indicating that SST and (T-D) could havedifferent evolutions.

The succeeding nine plots in Figure 4 are for OLR anomalies at longitudes 0-40ºE, 40º-80ºE, and 320º-360ºE. The tenth plot is for their average. The standard deviations of the OLR series are indicated. The following may be noted:

(1) The series for 160º-200ºE (160ºE-160ºW, through dateline 180º, western Pacific, almost the same as Niño 4), has the largest standard deviation (12.9 units) and shows prominent decreases of OLR during the El Niño events.

(2)The effect is also seen (slightly reduced standard deviation, 10.4) in the next longitude range 200º-240ºE (160º-120ºW, almost Niño 3.4), and still more reduced in 240º-280ºE (5.6 units) (120º-80ºW, almost Niño 3). Thus, the OLR of the whole Pacific responds (shows decreases)during El Niño events.

(3) On the other side, the longitude range 120º-160ºE (Australasia) has a considerable standard deviation (6.0), but the effects are opposite, namely, increases of OLR instead of decreases. This positive effect is also seen in 80º-120ºE (Indonesia).

(4) At other longitudes, the effects are negligibly small.

Thus, El Niño effects are mostly confined to the Pacific. In the website http://tao.atmos.washington.edu/data_sets/olr/index.html, Todd Mitchell mentions, "The regions of large OLR variance ( > 10 Wm) are over a broad region of the Indian and Pacific Oceans with largest values ( > 20 Wm) on and slightly to the south of the equator in the western Pacific", which is roughly correct. Todd Mitchell also mentions, "Warm equatorial Pacific SST anomalies are associated with below normal OLR (enhanced deep atmospheric convection) between 165ºE and the Ecuador coast in the equatorial Pacific, and enhanced OLR (diminished convective rainfall) over Papua New Guinea and eastern equatorial Brazil".

Figure 5 shows similar plots for the low latitude ranges 5ºN-25ºN, followed by 5ºS-25ºS, each for nine longitude ranges. Only 80º-120ºE (5.0 units), 120º-160ºE (6.0 units), 160º-200ºE (5.1 units) in the northern hemisphere and 120º-160ºE (4.1 units) in the southern hemisphere show substantial standard deviations, and the effects seem to be positive (OLR increases), in some cases with a lag of one year. Effects at other longitudes are small. Note that the vertical scale in Figure 5 is expanded double as compared to Figure 4.

Figure 6 shows similar plots for the middle latitude ranges 25ºN-45ºN, followed by 25ºS-45ºS, each for nine longitude ranges. The vertical scale is expanded double as compared to Figure 5. All the standard deviations are small (less than 4.0, often less than 2.0). Some positive anomalies match with SST anomalies but most of them do not match. Interestingly, during 1991-1994, OLR anomalies are consistently negative (like T-D) at almost all longitudes. Also, some anomalies are large about an year after an El Niño. Since this interval is often a La Niña event (cold water events, negative SST anomalies opposite to El Niño, positive T-D anomalies), it is likely that OLR anomalies outside the equatorial regions are related to La Niñas.

Figure 7 shows similar plots for the high latitude ranges 45ºN-65ºN, followed by 45ºS-65ºS, each for nine longitude ranges. The vertical scale is the same as in Figure 6. All the standard deviations are small (less than 2.3). Most of the large positive (painted black) or negative (shown hatched) OLR anomalies seem to be in years following an El Niño (La Niña years).

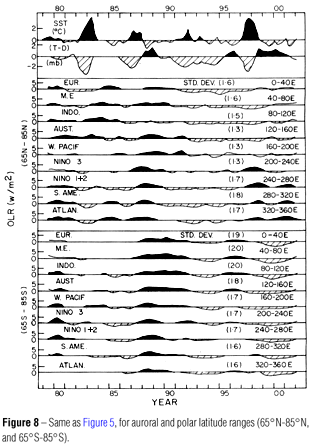
Figure 8 shows similar plots for the auroral and polar latitude ranges 65ºN-85ºN, followed by 65ºS-85ºS, each for nine longitude ranges. The vertical scale is the same as in Figure 6. All the standard deviations are small (less than 2.1). Most of the large positive (painted black) or negative (shown hatched) OLR anomalies seem to be in years following an El Niño (La Niña years).

It would thus seem that El Niño relationship is seen clearly only in the equatorial latitudes, while outside, the magnitudes are small and the relationship is delayed and coincides with the succeeding La Niña year. As will be illustrated in the next section, the OLR variations have spectra similar to those of surface temperature, and since OLR is intimately related to surface temperature, the OLR variations are directly related to surface temperaturevariations.

SPECTRA

If there is a strong relationship between OLR and ENSO, their spectra should tally completely. To obtain quantitative estimates of the characteristics of the interannual variability, the serieswere subjected to spectral analysis. The method used was MEM (Maximum Entropy Method, Burg, 1967; Ulrych & Bishop, 1975), which locates peaks much more accurately than the conventional BT (Blackman & Tukey, 1958) method. However, the amplitude (Power) estimates in MEM are not very reliable (Kane, 1977, 1979; Kane & Trivedi, 1982). Hence, MEM was used only for detecting all the possible peaks T_k (k = 1 to n), using LPEF (Length of the Prediction Error Filter) as 50% of the data length. These T_k were then used in the expression:

where f(t) is the observed series and E the error factor. A Multiple Regression Analysis (MRA, Bevington, 1969) was then carried out to estimate A_o, a_k, b_k, and their standard errors (by a least-square fit). From these, amplitudes r_k and their standard error s_k (common for all r_k in this methodology, which assumes white noise) were calculated. Any r_k exceeding 2s is significant at a 95% (a priori) confidence level.

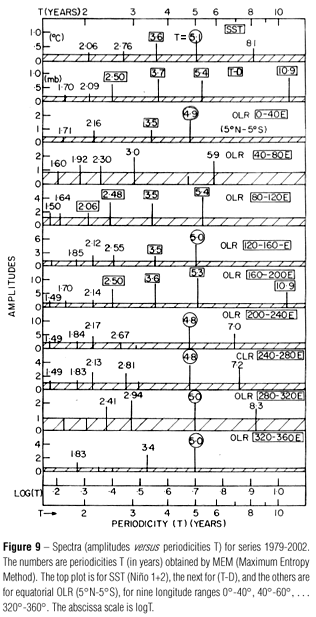
Figure 9 shows the spectra (amplitudes versus periodicities). The abscissa scale is log(T). The hatched portions indicate the 2σ limit and lines protrouding above this area are significant at a better than 95% (a priori ) confidence level. The top plot is for SST of Niño 1+2 region. The most prominent periodicity is T = 5.1 years. The next prominent ones are T = 3.6 and 8.1 years. There are some QBOs (Quasi-biennial oscillations) of 2.06 and 2.76 year periodicity, barely significant. The next plot is for the Southern Oscillation index (T-D). The periodicities are almost the same as for SST, but not quite. MEM is very, very accurate in periodicity determination. As shown in Kane (1977, 1979), spectra of artificial samples show that the accuracy near 2.00 years is better than ±0.03 years, and at 5.00 years, better than ±0.05years. Hence T = 2.06 and 3.6 years of SST may be considered as the same as T = 2.09 and 3.7 years of (T-D), but T = 2.76, 5.1, 8.1 years of SST are definitely different from T = 2.50, 5.4, 10.9 years of (T-D), showing that Pacific SST and the seesaw of (T-D) may have slightly different evolutions. This was seen glaringly in the top plots of Figure 4 where for 1991-1994, SST in Niño 1+2 region had a small, erratic (intermittent) evolution while (T-D) had a consistent negative anomaly.

The other plots in Figure 9 are for equatorial (5ºN-5ºS) OLR in 0-40ºE, 40º-80ºE, 320º-360ºE longitude belts (series plotted in Fig. 4). The following may be noted:

(1) The periodicities marked with rectangles (T = 2.06-2.09, 2.50, 3.5-3.7, 5.3-5.4 years) are common to (T-D) and some OLR series, notably OLR (160º-200ºE).

(2) The periodicities marked with a circle (T = 4.8-5.1 years) are common to SST and some OLR series.

(3) If broader periodicity ranges are considered acceptable,T = 2.06-2.17, 2.48-2.55, 3.4-3.7, 4.8-5.4 years may be considered as a complete ENSO signal, seen in longitudes 0-40º, 80º-120º, 120º-160º, 160º-200º, 320º-360ºE. In longitudes 200º-320ºE (40º-160ºW, eastern and middle Pacific), T = ~ 3.6 years is conspicuous by its absence and only T = 4.8-5.0 years is prominent.

(4) The T = 8.1 year periodicity of SST is roughly seen in longitudes 200º-320ºE, while T = 10.9 years (sunspot cycle?) of (T-D) is seen only in 160º-200ºE.

(5) The T = 1.70 year (20 months) signal of (T-D) (barely significant) is seen in some OLR series (barely significant). On the other hand, signals at ~ 1.50 and ~ 1.84 years (18 and 22 months) are seen in some OLR series but not in SST or (T-D).

Almost all these series in the 5ºN-5ºS latitude belt had large standard deviations (exceeding 3.0 OLR units). For other latitudes, the standard deviations were smaller and the spectra would not be reliable. Nevertheless, some series like 25º-45ºS, 280º-320ºE (standard deviation 2.6, Figure 6, second plot from bottom) were subjected to spectral analysis and showed prominent periodicities at T = 3.5 and ~ 6.0 years, while some others like 65º-85ºS, 40º-80ºE (standard deviation 2.0, Figure 8, eighth plot from bottom) showed only a prominent periodicity at T = ~ 7.0 years. Thus, there was partial or full matching with the ENSOsignal.

In this connection, the spectra of temperature series would be of great relevance. Kane & Buriti (1997) subjected temperature value series at different altitudes (including surface) and latitudes. For higher altitudes, the spectra matched with the stratospheric low latitude zonal winds particularly for the tropics. For low altitudes, including surface, periodicities observed were very similar to those obtained here. Hence, the relationship between OLR and surface temperatures is valid even for spectra.

CONCLUSIONS

A study of the Outgoing Longwave Radiation (OLR) values (Unit W/m) observed by various satellites during 1979-2002 revealed the following characteristics:

(1) The OLR values varied considerably from one geographical region to another ( ~ 100-300 units), probably due to a variety of Earth surfaces (landmasses with different or no vegetations, snow covers, sea surface, etc.) also, but mainly due to differences in the surface temperatures and local cloud covers.

(2) The climatology was latitude dependent. At middle and high latitudes, the range (minimum to maximum) was ~ 40-60 units, with maximum in local summer and minimum in local winter, but at lower latitudes, the range reduced considerably and was uncertain near equator.

(3) Near equator, the long-term changes (as seen in 12-month moving averages) were: OLR decreases during ENSO events in the eastern Pacific up to the dateline, and OLR increases during ENSO events in the Australasian region. Outside the equatorial region, the OLR changes were small during ENSO events and negligible in other years. In some longitudes at middle and high latitudes, the OLR changes occurred several months after the El Niño events, coinciding with La Niña (cold water events, opposite of warm water El Niño events), which generally follow El Niños. All these should be related to convection in the Pacific, local circulations and to the generation mechanisms of El Niños and La Niñas.

(4) A spectral analysis of OLR series indicated periodicities of 3.6, 5.1, 8.1 years etc. These are similar to the periodicities in low altitude (including surface) of atmospheric temperatures as described in Kane & Buriti (1997). Thus, all OLR characteristics including spectra are related to surface temperatures as expected, because physically, OLR intensity depends upon surface temperatures, besides cloud cover.

In some cases, small long-term trends were noticed, but were not studied further as Tashima & Hartmann (1999) have reported that such trends in ORL (for example, observed by the Nimbus-7 satellite during 1979-1987) were mostly instrumental in nature.

ACKNOWLEDGMENTS

Thanks are due to various workers who were involved in obtaining the OLR data and to those who presented the data in several websites, notably NOAA-NCEP (Washington, DC) and NOAA-CIRES (Boulder, Colorado). Thanks are due to Todd Mitchell for very valuable suggestions and to Vaman Kulkarni and ArcilanAssireu for computational assistance. Thanks are due to the referees for valuable suggestions. This work was partially supported by FNDCT, Brazil under contract FINEP-537/CT.

Recebido em 2 março, 2007 / Aceito em 2 junho, 2008

Received on March 2, 2007 / Accepted on June 2, 2008

NOTE ABOUT THE AUTHOR

Rajaram Purushottam Kane. Born on 12 November 1926 at Damoh, MP, India. M.Sc. Physics in 1946 from Banaras Hindu University, India. Ph.D. in 1953 from Bombay University, India. Visited the Institute of Nuclear Studies at the University of Chicago, USA as a Fulbright Smith-Mundt post-doc fellow during 1953-1954. From 1955 to 1978, worked as a research fellow and Professor at PRL (Physical Research Laboratory), Ahmedabad, India. Participated actively (Coordinator of Cosmic Ray data in India) in the activities of IGY (International Geophysical Years, 1957-1958). Since 1978, working as a Researcher at INPE (Instituto Nacional de Pesquisas Espaciais), São José dos Campos, SP, Brazil.

• BARNETT AG & PREISENDORFER R. 1978. Multifield analog predictions of short-term climate fluctuations using a climate state vector. J. Atmos. Sci., 35: 1771-1789.
• BESS TD, SMITH GL, CHARLOCK TP & ROSE FG. 1992. Annual and interannual variations of Earth-Radiation based on a 10-year data set. J. Geophys. Res., 97: 12825-12835.
• BEVINGTON PR. 1969. Data Reduction and Error Analysis for the Physical Sciences. McGraw-Hill, New York, pp. 164-176.
• BLACKMAN RB & TUKEY JW. 1958. The Measurement of Power Spectra. Dover, New York, 190 pp.
• BURG JP. 1967. Maximum Entropy Spectral Analysis, paper presented at the 37th Meeting. Society of Exploration Geophysics, Oklahoma City, October.
• CHELLIAH M & ARKIN P. 1992. Large-scale interannual variability of monthly outgoing longwave radiation anomalies over the global tropics. J. Climate, 5: 371-389.
• FERREIRA NJ & GURGEL H de C. 2002. Variabilidade dos ciclos anual e interanual da radiaçăo de ondas longas emergentes sobre a América do Sul e vizinhanças. Rev. Brasileira de Engenharia Agrícola e Ambiental, 6: 440-444.
• HEDDINGHAUS TR & KRUEGER AF. 1981. Annual and interannual variations in outgoing longwave radiation over the tropics. Mon. Wea. Rev., 109: 1208-1218.
• HOUSE FB, GRUBER A, HUNT GE & MECHERIKUNNEL AT. 1986. History of satellite missions and measurements of the Earth's radiation budget (1957-1984). Rev. Geophys., 24: 357-377.
• HUNT GE, KANDEL R & MECHERIKUNNEL AT. 1986. A history of presatellite investigations of the Earth's radiation budget. Rev. Geophys., 24: 351-356.
• KANE RP. 1977. Power spectrum analysis of solar and geophysicalparameters. J. Geomag. Geoelect., 29: 471-495.
• KANE RP. 1979. Maximum Entropy Spectral Analysis of some artificial samples. J. Geophys. Res., 84: 965-966.
• KANE RP & BURITI RA. 1997. Latitude and altitude dependence of the interannual variability and trends of atmospheric temperatures. Pure and Applied Geophysics, 149: 775-792.
• KANE RP & TRIVEDI NB. 1982. Comparison of maximum entropy spectral analysis (MESA) and least-square linear prediction (LSLP) methods for some artificial samples. Geophysics, 47: 1731-1736.
• KAYANO MT, KOUSKY VE & JANOWIAK JE. 1995. Outgoing longwave radiation biases and their impacts on Empirical Orthogonal functionmodes of interannual variability in the tropics. J. Geophys. Res. (Atmospheres), 100(D2): 3173-3180.
• KOUSKY VE. 1988. Pentad outgoing longwave radiation climatology for the South American sector. Rev. Brasileira de Meteorologia, 3: 217-231.
• LIEBMANN B & HARTMANN DL. 1982. Interannual variations of outgoing IR associated with tropical circulation changes during 1974-78. J. Atmos. Sci., 39: 1153-1162.
• PARKER DE. 1983. Documentation of a southern oscillation index. Meteorol. Mag., 112: 184-188.
• QUINN WH, ZOPF DG, SHORT KS & KUO YANG RTW. 1978. Historical trends and statistics of the Southern Oscillation, El Nińo, and Indonesian droughts. Fish. Bull. (USA), 76: 663-678.
• QUINN WH, NEAL VT & ANTUNEZ DE MAYOLO SE. 1987. El Nińo occurrences over the past four and a half centuries. J. Geophys. Res., 92: 14449-14461.
• TASHIMA DH & HARTMANN DL. 1999. Regional trends in Nimbus-7 OLR: Effects of a spectrally nonuniform albedo. J. Climate, 12: 1458-1466.
• TRENBERTH KE. 1997. The definition of El Nińo. Bull. Amer. Meteor. Soc., 78: 2771-2777.
• ULRYCH TJ & BISHOP TN. 1975. Maximum Entropy Spectral Analysis and autoregressive decomposition. Rev. Geophys., 13: 183-200.
• WINSTON JS, GRUBER A, GRAY JR TI, VARNADORE MS, EARNEST CL & MANELLO NP. 1979. Earth-atmosphere radiation budget analysis derived from NOAA satellite data, June 1974-February 1978, vols. 1 and 2, NOAA S/T 79-187. Natl. Oceanic and Atmos. Admin. Washington, D.C.

Publication Dates

• Publication in this collection
  22 Sept 2008
• Date of issue
  June 2008

History

• Received
  02 Mar 2007
• Accepted
  02 June 2008