Abstracts
Geomagnetic jerks are abrupt changes in the secular variation generated in the Earth's core. Even the most basic characteristics of jerks as its origin and duration, are still a matter of debate in the scientific community. Data obtained by magnetic observatories and satellites are used in these studies. The main characteristic of jerks is that they are not simultaneous at the Earth's surface, with a general pattern of a first arrival in the Northern hemisphere, with a later appearance in the South by about two years. The non-simultaneous behavior of jerks is important to constrain the electrical conductivity of the lower mantle and for a better understanding on how jerks are generated in the core. The main objective of this paper is to discuss methods of detection of jerks at Vassouras (VSS) observatory (Brazil). In addition, we want to highlight the relevance of detection of jerks in observatories in the Southern hemisphere by encouraging the improvement of the data Quality and the discussion of the main geomagnetic jerks characteristics.
geomagnetic jerks; Vassouras magnetic observatory; wavelet analysis
Os jerks são mudanças abruptas na variação secular geradas no núcleo terrestre. Até as características mais básicas dos jerks, como sua origem e duração, são ainda controversas. Dados obtidos em observatórios magnéticos e satélites são usados neste tipo de estudo. A principal característica dos jerks é Que eles não são simultâneos na superfície da Terra, com um padrão geral de chegada mais cedo no hemisfério Norte e mais tarde no hemisfério Sul, com um intervalo da ordem de 2 anos. O padrão não simultâneo dos jerks é importante para estudos sobre a condutividade elétrica do manto inferior e para um melhor entendimento de como os jerks são gerados no núcleo. O principal objetivo deste artigo é discutir métodos de detecção dos jerks no observatório de Vassouras (VSS, Brasil). Ressaltamos a relevância da identificação dos jerks em observatórios no hemisfério Sul, estimulando a melhora da qualidade dos dados e a discussão das principais características dos jerks.
impulsos da variação secular geomagnética (jerks); observatório magnético de Vassouras; análise de wavelet
Observatório Nacional, MCT, Rua General José Cristino, 77, São Cristóvão, 20921-400 Rio de Janeiro, RJ, Brazil. Phone: (21) 3504-9146/9286; Fax: (21) 2580-7081 -E-mails: kpinheiro@on.br; jandyr@on.br
ABSTRACT
Geomagnetic jerks are abrupt changes in the secular variation generated in the Earth's core. Even the most basic characteristics of jerks as its origin and duration, are still a matter of debate in the scientific community. Data obtained by magnetic observatories and satellites are used in these studies. The main characteristic of jerks is that they are not simultaneous at the Earth's surface, with a general pattern of a first arrival in the Northern hemisphere, with a later appearance in the South by about two years. The non-simultaneous behavior of jerks is important to constrain the electrical conductivity of the lower mantle and for a better understanding on how jerks are generated in the core. The main objective of this paper is to discuss methods of detection of jerks at Vassouras (VSS) observatory (Brazil). In addition, we want to highlight the relevance of detection of jerks in observatories in the Southern hemisphere by encouraging the improvement of the data Quality and the discussion of the main geomagnetic jerks characteristics.
Keywords: geomagnetic jerks, Vassouras magnetic observatory, wavelet analysis.
RESUMO
Os jerks são mudanças abruptas na variação secular geradas no núcleo terrestre. Até as características mais básicas dos jerks, como sua origem e duração, são ainda controversas. Dados obtidos em observatórios magnéticos e satélites são usados neste tipo de estudo. A principal característica dos jerks é Que eles não são simultâneos na superfície da Terra, com um padrão geral de chegada mais cedo no hemisfério Norte e mais tarde no hemisfério Sul, com um intervalo da ordem de 2 anos. O padrão não simultâneo dos jerks é importante para estudos sobre a condutividade elétrica do manto inferior e para um melhor entendimento de como os jerks são gerados no núcleo. O principal objetivo deste artigo é discutir métodos de detecção dos jerks no observatório de Vassouras (VSS, Brasil). Ressaltamos a relevância da identificação dos jerks em observatórios no hemisfério Sul, estimulando a melhora da qualidade dos dados e a discussão das principais características dos jerks.
Palavras-chave: impulsos da variação secular geomagnética (jerks), observatório magnético de Vassouras, análise de wavelet.
INTRODUCTION
The geomagnetic field observed at the Earth's surface results from contributions of the external, core, induced and crustal fields. In this paper we focus on the temporal variations of the internal magnetic field generated in the core.
The secular variation corresponds to the first time derivative of the magnetic field. Jerks manifest as changes of the secular variation trend (Courtillot & Le Mouël, 1984; Le Huy et al., 1998) identified as a V-shape and as a step-like function in the secular acceleration (Fig. 1). However, in real geomagnetic data these V-patterns can not be easily detected, therefore various techniQues have been used to decrease the external magnetic field influence from the data and to identify jerks.
The occurrence date of jerks is a subject of intense debate which depends strongly on the method and dataset used. Some authors used annual means that contain less influence of the external field, while others analyzed monthly means in order to have a better temporal resolution.
The most common method applied to detect jerks is the fitting of two straight lines to the secular variation, by least-squares. The wavelet analysis is another method that has been applied to identify jerks. Alexandrescu et al. (1996) used the continuous wavelet transform and found five events characterized as worldwide jerks, occurred during the last century: 1901, 1913, 1925,1969 and 1978 (Fig. 2). Some works point to more recent global jerks at 1991 (De Michelis et al., 1998,2000) and at 1999 (Mandea et al., 2000).
The global or local extension of geomagnetic jerks is another widely discussed topic. For example, the 1932 jerk is local since it was mostly observed in the southern hemisphere and not seen in any European observatory. Another local jerk was detected in 1949, observed mainly in the Pacific area and in the American region (Alexandrescu et al., 1996). A more recent and local jerk occurring at 2003 was found by Olsen & Mandea (2007) by using satellite data.
However the best-studied jerks of global extension occurred in 1969,1978 and 1991. These three events show a non-simultaneous behavior. This means that the same event occurs in slightly different times at distinct observatories; usually these jerks appear ata later time in the southern hemisphere, with a time delay of about two years (Alexandrescu et al., 1996; De Michelis et al., 2000; Chambodut & Mandea, 2005).
Jerk occurrence times are an important issue in geomagnetism since its non-simultaneous behavior has been used in studies of constraints of the electrical conductivity of the lower mantle that is poorly known (Alexandrescu, 1999; Nagao et al., 2003; Pinheiro & Jackson, 2008).
The aim of this paper is to detect jerks in Vassouras observatory using different techniques and discuss the advantages and disadvantages of each method.
METHODOLOGIES TO DETECT JERKS
The usual disadvantage of the general piecewise method to analyze jerks is that it forces a jerk at an imposed epoch, whether or not the data contain such a discontinuity. For instance, Le Mouël et al. (1982) fitted straight-line segments to the secular variation of some observatories, before and after 1969-1970. They found that the gradients are seen to vary at different observatories and in some cases the slopes are indistinguishable (e.g. Honolulu observatory). These results showed that the jerk amplitude, defined as the difference of slope of the two straight line segments, also varies at the Earth's surface.
In addition, even in data where jerks are clear, there is an uncertainty in determining the date when they happen as it is believed that they are not instantaneous, resulting in a SV curve changing sign over an approximate 2 year period.
An alternative approach that does not consider a priori information is presented in Whaler (1987). A linear-segment-finding algorithm is applied and the hypothesis that the points all lie on the same line is tested for all possible segments over the whole interval.
More recently, Alexandrescu et al. (1996) and De Michelis & Tozzi (2005) applied a wavelet analysis assuming sudden events of an unknown nature at undefined dates may have occurred in the geomagnetic field.
In this paper we applied the classical and the wavelet analysis in order to detect jerks and exemplify how the exact time depends on the method and dataset used.
WAVELET ANALYSIS
A wavelet is a waveform of limited duration that has an average value of zero and tends to be irregular and asymmetric. Its main property is the dilation, which is the variation of the wavelet scale: the larger the scale, the lower the frequency analyzed.
The advantage of using wavelets is that it is possible to investigate both the global (low frequency) and the detail (high frequency) of the signal by stretching and squeezing the wavelet while sliding it along the signal. In contrast to Fourier analysis, it is possible to detect localized time features of the signal.
The sensitivity of wavelets to local characteristics in a signal is an advantage in the study of jerks since they are assumed to be singularities introduced at the core-mantle boundary (CMB).
A singularity is a discontinuity in an a derivative of the signal, where a is the regularity of the singularity.
A problem with wavelet analysis is that the boundary effects are important and prevent detection of events close to the beginning and end of the time series. In this case it is necessary to apply a more classical method such as simply analyzing the trend of secular variation.
A synthetic example, to illustrate the ability of wavelets to detect jerks, is shown in Figure 3. We simulated two changes of slope which cause a convergence of the wavelet transform coefficients to the exact point of the discontinuity. The regularity of the discontinuity is an important characteristic of the jerk and it is calculated by a log-log plot of the scales versus modulus of the coefficients along the line of maxima.
VASSOURAS OBSERVATORY (VSS)
In this paper we analyze geomagnetic jerks at Vassouras observatory, in Rio de Janeiro (Brazil), as it is shown in Figure 4. Monthly and annual means of the X and Y components were analyzed.
In this work we recovered data from Vassouras observatory, but a gap from 1946 to 1947 still remained. That is the reason why the time series was divided in two parts: one from 1915 to 1946 and the second one from 1947 to 2001. Gaps in the dataset shorter than 6 months were accepted and in these cases a linear interpolation was applied.
RESULTS AND DISCUSSION
The monthly means of the X and Y components at Vassouras observatory (Fig. 5) show variations of their slope that might be candidates to jerks. For example in Y component we can see some changes occurring for example at 1925 and around 1980. By following the usual procedure to detect jerks we calculated the first time derivative expecting to enhance these changes. However, as shown in Figure 6, it was not possible to detect changes of trend probably due to a low signal-to-noise ratio at Vassouras and because the first derivative enhances signal and noise alike.
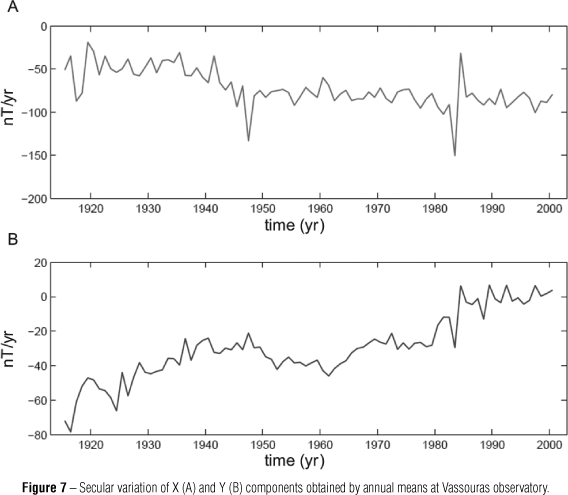
By applying a 12-month running average to the time series or to calculate the secular variation considering the annual means, the external field influence decrease. Figure 7 shows a filtered data in which is possible to see some variations in the slope that may be candidate jerks. The problem is that there is still a clear lack of accuracy on estimating the occurrence dates for the jerks.
Note that depending on how one fits the lines the dates will vary substantially.
One way to try to solve this limitation is using wavelet analysis. The wavelet transform was applied to the monthly means of the X and Y component at Vassouras observatory to detect the geomagnetic jerks.
Figures 8 and 9 show the wavel et transform of Y component. It is clear the presence of noise in the space-time scale in both lower and higher scales. The lines of maxima of the wavelet transform do not converge and are not straight, as in the synthetic example (Fig. 3).
We built the log-log plot of the coefficients along the maxima lines of the wavelet coefficients (Fig. 10) from 16 to 32. This range of scale was chosen because we expected jerks to be present in higher scales that correspond to changes in the low frequency content of the signal, below that scale range the data is noisy. We selected the ridge functions that have positive slopes that characterize the presence of jerks (Alexandrescu et al., 1995). Table 1 shows the occurrence dates for the jerks in Y component are 1922.5 (a = 1.67), 1941 (a = 1.47) and 1969 (a = 1.37) and in X component it is 1932.9 (a = 2.03).
Because of the high content of noise in the plane time-scale we tried another solution to detect jerks (Fig. 11). We applied the wavelet filter to recover the lower frequency contents in the annual means by the approximation given by the wavelet in the higher scales. The application of wavelet filtering reveals that the noise in the smaller scales may be the main cause for the problems in the wavelet transform.
We achieved a reasonable separation of signal and noise. It allows the determination of the dates of occurrence in the filtered signal using linear regression (Fig. 11). There are other approximations that could be done, but the idea was to delineate variations in a V-shape that would occur in this filtered data.
CONCLUSION
The signal to noise ratio at Vassouras observatory is low, this causes the time derivatives to be noisy and more difficult to detect the jerk occurrence times.
We compared the occurrence dates present in Table 1 with occurrences of solar cycle and only the dates 1949 and 1969 were on period of maxima activity. This may indicates that most of the dates are not related to the solar cycle, which agrees with an internal origin for the phenomena.
Not all events at Vassouras appeared in both X and Y components at the same time. Some of them are only detectable in one of the components, as is showed in Table 1. In most of the cases the impulses are more conspicuous in the Y component.
Table 2 shows the dates and methods used to find evidence of impulses. Marked dates are the most probable dates for geomagnetic jerks at Vassouras observatory. This is common in other observatories too.
We concluded that the wavelet transform is not an effective method to detect jerk in all observatories. When the signal-to-noise ratio is low, as in Vassouras observatory, the wavelet transform coefficients panel is cluttered with discontinuity-like noise features. Moreover the resultant ridge functions are too noisy to allow the estimation of regularity.
The best results were obtained using the wavel et transform to filter the geomagnetic data in which we decreased the influence of spikes and other high-frequency noise. The signal-to-noise ratio was substantially improved by recovering the long-period contents of the signal and the lines are better fitted to the filtered data. We believe that there is not a unique way to detect the geomagnetic jerks in any observatory around the world. Each observatory should have unique characteristics and limitations to the best methodology to be employed.
Recebido em 21 maio, 2009 / Aceito em 19 fevereiro, 2010
Received on May 21,2009 / Accepted on February 19, 2010
NOTES ABOUT THE AUTHORS
Katia Jasbinschek dos Reis Pinheiro. Graduação em Oceanografia pela Universidade do Estado do Rio de Janeiro (2001), mestrado em Geofísica pelo Observatório Nacional (2003) e doutorado no ETH Zurique (Suíça) em geomagnetismo. Trabalhou como contratada na Petrobrás na área de geofísica ambiental (2002-2004). Tem experiência na area de Geociências, com ênfase em geomagnetismo, atuando principalmente nos seguintes temas: variação secular geomagnética e condutividade elétrica do manto. Trabalha como pesquisadora de geomagnetismo no Observatório Nacional (MCT).
Jandyr de Menezes Travassos. Possui graduação em Física (1976) e mestrado em Geologia (1981) pela Universidade Federal do Rio de Janeiro. PhD em Geofísica pela University of Edinburgh (1987). Atualmente é pesquisador titular U-III do Observatório Nacional. Tem experiência na área de Geofísica, com ênfase em Geofísica Aplicada, atuando principalmente com métodos eletromagnéticos.
- ALEXANDRESCU M, GIBERT D, HULOT G, LE MOUEL J-L & SARACCO G. 1995. Detection of geomagnetic jerks using wavelet analysis. J. Geophys. Res., 100:1255712572.
- ALEXANDRESCU M, GIBERT D, HULOT G, LE MOUEL J-L & SARACCO G. 1996. Worldwide wavelet analysis of geomagnetic jerks. J. Geophys. Res., 101(B10): 21975-21994.
- ALEXANDRESCU M, GIBERT D, LE MOUEL J-L, HULOT G & SARACCO G. 1999. An estimate of average lower mantle conductivity by wavelet analysis of geomagnetic jerks. J. Geophys. Res., 104(B8): 17,73517,745.
- CHAMBODUT A & MANDEA M. 2005. Evidence for geomagnetic jerks in comprehensive models. Earth Planets Space, 57:139-149.
- COURTILLOT V & LE MOUEL J-L. 1984. Geomagnetic secular variation impulses. Nature, Review article, 311: 709-716.
- DE MICHELIS P & TOZZI R. 2005. A Local Intermittency Measure (LIM) approach to the detection of geomagnetic jerks. Earth Planet. Sci. Lett., 235: 261-272.
- DE MICHELIS P, CAFARELLA L & MELONI A. 1998. Worldwide character of the 1991 geomagnetic jerk. Earth Planet. Sci. Lett., 25(3): 377-380.
- DE MICHELIS P, CAFARELLA L & MELONI A. 2000. A global analysis of the 1991 geomagnetic jerk. Geophys. J. Int., 143: 545-556.
- LE HUY M, ALEXANDRESCU M, HULOT G & LE MOUEL J-L. 1998. On the characteristics of successive geomagnetic jerks. Earth Planets Space, 50: 723732.
- LE MOUEL J-L, DUCRUIX J & DUYEN CH. 1982. The worldwide character of the 1969-1970 impulse of the secular acceleration rate. Phys. Earth Planet. Int., 28: 337350.
- MANDEA M, BELLANGER E & LE MOUEL J-L. 2000. A geomagnetic jerk for the end of the 20th century? Earth Planet. Sci. Lett., 183: 369373.
- NAGAO H, IYEMORI T, HIGUCHI T & ARAKI T. 2003. Lower mantle conductivity anomalies estimated from geomagnetic jerks. J. Geophys. Res., 108(B5): 2254.
- OLSEN N & MANDEA M. 2007. Investigation of a secular variation impulse using satellite data: The 2003 geomagnetic jerk. Earth Planet. Sci. Lett., 255: 94105.
- PINHEIRO K & JACKSON A. 2008. Can a 1D mantle electrical conductivity model generate magnetic jerk differential time delays? Geophys. J. Int., 173(3): 781792.
- WHALER KA. 1987. A new method for analysing geomagnetic impulses. Phys. Earth Planet. Int., 48: 221240.
Impulses of the geomagnetic secular variation (jerks) at vassouras magnetic observatory detected by wavelet analysis
Publication Dates
-
Publication in this collection
01 Dec 2010 -
Date of issue
Mar 2010
History
-
Received
21 May 2009 -
Accepted
19 Feb 2010