Resumos
Os movimentos turbulentos são caracterizados por flutuações instantâneas de velocidade, temperatura e outros escalares. Como conseqüência destas flutuações, o estado turbulento em um fluido contribui significativamente no transporte de momentum, calor e massa. Define-se turbulência como um estado de escoamento do fluido no qual as variáveis instantâneas exibem flutuações irregulares e aparentemente aleatórias tal que, na prática, apenas propriedades estatísticas podem ser reconhecidas e submetidas a uma análise. O estudo dos fenômenos de transporte fica dificultado, sobremaneira, pela presença destas flutuações. Qualquer simplificação na análise dos efeitos da turbulência é extremamente vantajosa do ponto de vista físico, matemático e numérico. A busca constante por tais simplificações é um dos principais objetivos no desenvolvimento de novos modelos de turbulência. Este artigo tem como objetivo fazer uma revisão sobre o fenômeno da turbulência e sua modelagem, onde são apresentados os seus fundamentos teóricos e as principais técnicas de abordagem utilizadas na modelagem do fenômeno.
turbulência; modelagem da turbulência; camada limite; escalas da turbulência
The movements are characterized by turbulent fluctuations in instantaneous speed, temperature and other scalars. As a consequence of these fluctuations, the turbulent state in fluid contributes significantly to transport momentum, heat and mass. Turbulence is defined as a state of the flow in which the time dependent variables exhibit irregular fluctuations which are seemingly random such that, in practice, only statistical properties can be recognized and subjected to analysis. The study of transport phenomena is greatly hampered by the presence of these fluctuations. Any simplification in the analysis of the effects of turbulence is extremely advantageous in physical, mathematical and numerical terms. The constant search for such simplifications is one of the main goals in the developing of new models of turbulence. This article aims to review the phenomenon of turbulence and its modeling, focusing on its theoretical foundations and on the main technical approaches used in the modeling of the phenomenon.
turbulence; turbulence modeling; boundary layer; scales of turbulence
Uma revisão sobre a turbulência e sua modelagem
José Francisco Almeida de SouzaI; Leopoldo Rota de OliveiraII; José Luiz Lima de AzevedoII; Ivan Dias SoaresIII; Maurício Magalhães MataIV
IUniversidade Federal do Rio Grande - FURG, Rua Eng. Alfredo Huch, 475, Centro, 96211-900 Rio Grande, RS, Brasil. Tel.: (53) 3233-6876; Fax: (53) 3233-6652 - E-mail: joseazevedo@furg.br
IIUniversidade Federal do Rio Grande - FURG, Rua Eng. Alfredo Huch, 475, Centro, 96211-900 Rio Grande, RS, Brasil. Tel.: (53) 3233-6880; Fax: (53) 3233-6652 - E-mails: pgoflro@furg.br; ctijlla@yahoo.com.br
IIIUniversidade Federal do Rio Grande - FURG, Rua Eng. Alfredo Huch, 475, Centro, 96211-900 Rio Grande, RS, Brasil. Tel.: (53) 3233-6874; Fax: (53) 3233-6652 - E-mail: dfsivan@furg.br
IVUniversidade Federal do Rio Grande - FURG, Rua Eng. Alfredo Huch, 475, Centro, 96211-900 Rio Grande, RS, Brasil. Tel.: (53) 3233-6879; Fax: (53) 3233-6652 - E-mail: mauricio.mata@furg.br
RESUMO
Os movimentos turbulentos são caracterizados por flutuações instantâneas de velocidade, temperatura e outros escalares. Como conseqüência destas flutuações, o estado turbulento em um fluido contribui significativamente no transporte de momentum, calor e massa. Define-se turbulência como um estado de escoamento do fluido no qual as variáveis instantâneas exibem flutuações irregulares e aparentemente aleatórias tal que, na prática, apenas propriedades estatísticas podem ser reconhecidas e submetidas a uma análise. O estudo dos fenômenos de transporte fica dificultado, sobremaneira, pela presença destas flutuações. Qualquer simplificação na análise dos efeitos da turbulência é extremamente vantajosa do ponto de vista físico, matemático e numérico. A busca constante por tais simplificações é um dos principais objetivos no desenvolvimento de novos modelos de turbulência. Este artigo tem como objetivo fazer uma revisão sobre o fenômeno da turbulência e sua modelagem, onde são apresentados os seus fundamentos teóricos e as principais técnicas de abordagem utilizadas na modelagem do fenômeno.
Palavras-chave: turbulência, modelagem da turbulência, camada limite, escalas da turbulência.
ABSTRACT
The movements are characterized by turbulent fluctuations in instantaneous speed, temperature and other scalars. As a consequence of these fluctuations, the turbulent state in fluid contributes significantly to transport momentum, heat and mass. Turbulence is defined as a state of the flow in which the time dependent variables exhibit irregular fluctuations which are seemingly random such that, in practice, only statistical properties can be recognized and subjected to analysis. The study of transport phenomena is greatly hampered by the presence of these fluctuations. Any simplification in the analysis of the effects of turbulence is extremely advantageous in physical, mathematical and numerical terms. The constant search for such simplifications is one of the main goals in the developing of new models of turbulence. This article aims to review the phenomenon of turbulence and its modeling, focusing on its theoretical foundations and on the main technical approaches used in the modeling of the phenomenon.
Keywords: turbulence, turbulence modeling, boundary layer, scales of turbulence.
INTRODUÇÃO
Os movimentos turbulentos são caracterizados por flutuações instantâneas de velocidade, temperatura e outros escalares. Como consequência destas flutuações, o estado turbulento em um fluido contribui significativamente no transporte de momentum, calor e massa na maioria dos escoamentos de interesse prático e, por isso, têm uma influência determinante nas distribuições destas propriedades no campo de escoamento. Os escoamentos em rios e canais, em tubulações, na esteira de um navio ou avião, na camada limite atmosférica e a maioria das correntes oceânicas pertencem a esta categoria de movimento. 0 "Glossary of Oceanographic Terms" (Baker et al, 1966 apud Schwind, 1980) apresenta a seguinte definição para escoamento turbulento: "É um estado de escoamento do fluido no qual as velocidades instantâneas exibem flutuações irregulares e aparentemente aleatórias tal que, na prática, apenas propriedades estatísticas podem ser reconhecidas e submetidas a uma análise". Estas flutuações constituem as principais deformações do escoamento e são capazes de transportar momentum, energia e outras propriedades a taxas muito maiores que aquelas da difusão molecular nos escoamentos laminares (e.g., Schwind, 1980).
Muitas teorias e conceitos têm sido formulados na tentativa de obter uma descrição universalista para o fenômeno da turbulência que seja adequada a qualquer problema de interesse prático. Enquanto tal descrição não é alcançada, e há dúvidas se algum dia o será, modelos simplificados têm sido propostos como forma de analisar problemas específicos em cada área de interesse (Eiger, 1989). O certo é que a turbulência é um fator complicador na análise dos fenômenos de transporte de massa, momentum e energia. Em termos práticos, se for possível que em um determinado problema a influência da turbulência seja considerada de forma simplificada, isto será extremamente vantajoso do ponto de vista físico, matemático e numérico. Por exemplo, escoamentos em canais e tubulações são usualmente estudados com o auxílio da conhecida fórmula universal de perda de carga, a qual descreve satisfatoriamente o escoamento para as finalidades a que se propõe. Entretanto, se estivermos interessados em conhecer a distribuição de um poluente no canal ou tubulação, esta abordagem não será mais adequada, pois não fornece detalhes da distribuição das propriedades do escoamento.
A complexidade dos escoamentos turbulentos não permite uma abordagem estritamente analítica do problema (e.g., Kundu & Cohen, 2002), o que já foi destacado por diversos autores. Tennekes & Lumley (1972) destacam que: (i) uma característica muito importante dos escoamentos turbulentos é a sua habilidade para misturar ou transportar propriedades a taxas muito mais elevadas (várias ordens de magnitude) do que aquelas alcançadas pela difusão molecular; (ii) escoamentos turbulentos são sempre dissipativos e o mecanismo da turbulência necessita de uma alimentação contínua de energia para suprir as perdas viscosas de modo que, se nenhuma energia for fornecida ao escoamento, a turbulência decai rapidamente e (iii) a turbulência é um fenômeno continuum, ou seja, mesmo os menores vórtices encontrados nestes escoamentos são tipicamente muito maiores que a escala de comprimento molecular, fazendo com que a Hipótese do Continuum seja válida e o escoamento turbulento seja governado pelas equações de Navier-Stokes. Eiger (1989) cita que a vorticidade desempenha um papel fundamental na análise da turbulência, pois escoamentos turbulentos são sempre rotacionais. Isto significa que teorias bem estabelecidas de escoamento potencial (estritamente bidimensionais) não se aplicam ao estudo da turbulência. Além disso, é possível provar que, para que a turbulência seja mantida, mecanismos tridimensionais devem estar presentes no escoamento (vortex stretching). Kundu & Cohen (2002) enfatizam ainda que escoamentos turbulentos são altamente não lineares.
Além das citações acima, Tennekes & Lumley (1972), Schwind (1980) e Kundu & Cohen (2002) salientam que escoamentos turbulentos são aleatórios e não preditíveis, portanto, tornando-se impossível uma abordagem determinística do fenômeno (característica conhecida como "irregularidade").
Estes aspectos do movimento turbulento sugerem que muitos escoamentos que parecem "aleatórios", tais como as ondas de gravidade no oceano ou na atmosfera e ruídos acústicos, por terem perdas viscosas insignificantes, não são de fato turbulentos (Tennekes & Lumley, 1972; Kundu & Cohen, 2002).
Este artigo tem como objetivo fazer uma revisão sobre o fenômeno da turbulência. Inicialmente é feita uma breve introdução sobre a turbulência e a sua complexidade. A seguir, são apresentados os fundamentos teóricos, conceitos e definições associados com a turbulência. Posteriormente, são abordados os aspectos relacionados à sua modelagem. Finalmente, apresenta-se a discussão e as considerações finais deste trabalho.
FUNDAMENTOS TEÓRICOS
Esta seção é destinada à apresentação da fundamentação teórica necessária para a formulação e compreensão dos modelos matemáticos associados com a turbulência. São descritos aspectos relacionados com camada limite, tipos de escoamento, escalas da turbulência, algumas propriedades dos escoamentos turbulentos e descrições de regiões específicas do escoamento, dentre outros.
Vórtices e isotropia
Alguns conceitos essenciais para o estudo da turbulência serão apresentados nesta subseção. Apesar do estado caótico que caracteriza os escoamentos turbulentos, certos padrões básicos têm sido identificados quer pela via teórica, quer pela via experimental (e.g., Eiger, 1989). O conceito de vórtice está associado a estes padrões básicos, também denominados de estruturas coerentes ou grandes vórtices, observáveis nas maiores escalas do escoamento turbulento. Cabe salientar que a turbulência se manifesta em diferentes escalas de comprimento, as quais estão relacionadas com as dimensões características destes vórtices. Entretanto, nas pequenas escalas não conseguimos identificar vórtices individualmente, e a equação "pequenos vórtices" não significa mais do que aquela parte do movimento turbulento que apresenta coerência apenas em curtas distâncias (isotropia local). É usual definirmos o movimento turbulento como uma superposição de vórtices de diferentes tamanhos que interagem entre si, trocando energia, momentum e outras propriedades.
A analogia entre estes vórtices e as moléculas de um gás, as quais são as entidades fundamentais da bem estabelecida Teoria Cinética dos Gases, serviu como base para o estudo dos fenômenos turbulentos. Entretanto, a analogia não é perfeita, porque enquanto moléculas são entidades bem definidas e facilmente identificáveis, vórtices não o são. Ao contrário das moléculas, vórtices exibem dimensões variáveis no tempo e espaço, trocam massa entre si e são caracterizados por uma orientação. Uma "colisão" entre dois vórtices, por exemplo, é um fenômeno muito mais complexo que uma colisão entre duas moléculas (Eiger, 1989), o que evidencia a imperfeição da analogia.
Uma das características dos escoamentos turbulentos é a presença simultânea de uma grande quantidade de vórtices numa vasta gama de escalas temporais e espaciais. O espectro de energia da turbulência é análogo ao espectro de cores que aparece quando uma luz branca atravessa um prisma. Neste processo, observamos que a luz branca é composta por diversas cores (i.e., vários comprimentos de onda ou freqüências) superpostas. Com relação à turbulência podemos desenvolver uma análise similar e identificar, dentro do campo turbulento, vórtices de diferentes tamanhos contribuindo para a energia turbulenta total (Stull, 1988). Dentro deste espectro, os maiores vórtices drenam energia do escoamento médio e a transferem para outros menores, e estes para outros menores ainda, e assim sucessivamente. Cria-se então um processo contínuo de transferência de energia, que vai em direção a uma escala de tamanhos onde a energia passa a ser dissipada pelas tensões viscosas, atingindo-se um estado de equilíbrio (Rosman, 1989). Esse processo é conhecido por "cascata de energia" e foi descrito por Kolmogorov em 1941 (e.g., Schwind, 1980). A Figura 1 mostra um espectro de potência típico de escoamentos turbulentos, o qual representa a energia cinética turbulenta ao longo das escalas espaciais do escoamento em função da frequência de flutuação.
Os grandes vórtices dependem fortemente da geometria do escoamento e da maneira como são gerados, por isso possuem características anisotrópicas e comportamento um tanto determinístico. Ao considerarmos vórtices cada vez menores, a influência da geometria do escoamento vai desaparecendo e o padrão do campo turbulento torna-se cada vez mais aleatório e, consequentemente, mais isotrópico. Em corpos d'água rasos o comprimento típico dos maiores vórtices é geralmente muito maior que a profundidade, logo, para haver prevalência da isotropia é preciso que as escalas envolvidas sejam inferiores a da profundidade (Rosman, 1989).
De acordo com Eiger (1989), um escoamento turbulento exibe um espectro contínuo de dimensões de vórtices, de modo que a quantidade de diferentes tamanhos presentes no espectro é diretamente proporcional ao número de Reynolds do escoamento médio. Este espectro é limitado superiormente pelos contornos físicos do escoamento (banda esquerda da Fig. 1). Por exemplo, no escoamento em um canal é impossível a existência de um vórtice cuja dimensão vertical seja maior que a profundidade do canal. Destaca-se que os vórtices maiores apresentam freqüências de flutuação mais baixas e, conforme pode ser observado na Figura 1, possuem as maiores escalas de comprimento, ocorrendo o oposto na situação dos vórtices menores.
Os vórtices mais energéticos do escoamento turbulento são aqueles que, do ponto de vista estatístico, mais contribuem para o transporte turbulento de massa, energia e momentum. Na impossibilidade de simular numericamente todos os componentes do espectro, devido às limitações computacionais, os menores vórtices (escalas) são incorporados ao modelo numérico após serem parametrizados pelos chamados modelos de turbulência.
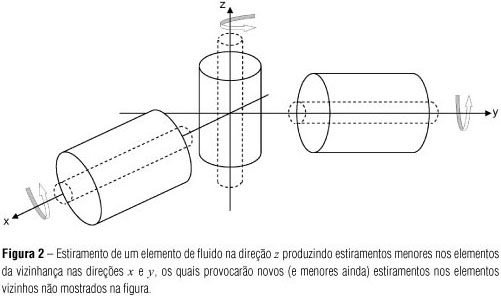
Consideremos agora um elemento de fluido em rotação ao redor do seu eixo z, como ilustra a Figura 2. Se este elemento estiver sujeito à influência de uma deformação linear ao longo da direção z, ou seja, ∂w/∂z > 0(∂w/∂z < 0), onde w é a componente da velocidade do escoamento na direção z, o elemento será estirado (contraído) nesta direção, a área da sua seção transversal no plano xy diminuirá (aumentará) e sua velocidade de rotação aumentará (diminuirá) em virtude da conservação do seu momento angular. Desta forma, este(a) estiramento (contração) diminuirá (aumentará) a escala de comprimento do próprio elemento nas direções perpendiculares (x e y) estirando (contraindo) os elementos de fluido da vizinhança nestas direções, os quais também sofrerão variação no seu momento angular, conforme sugere a Figura 2, e assim por diante (Zhurbas, 2001).
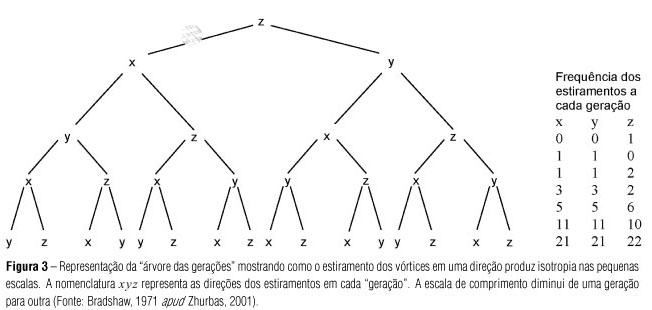
Percebe-se, por exemplo, que um estiramento na direção z (1ª geração) propaga-se para os elementos vizinhos nas direções x e y, produzindo-se então estiramentos de menor escala nestas direções (2ª geração) que, por sua vez, propagam-se e produzem estiramentos nas direções y e z e nas direções x e z, respectivamente (3ª geração), e assim por diante. Uma "árvore de gerações" (Bradshaw, 1971 apud Zhurbas, 2001), que mostra a direção destes estiramentos a cada geração, é apresentada na Figura 3. Podemos ver, qualitativamente, que um estiramento inicial numa dada direção produz quantidades aproximadamente iguais de pequenos estiramentos em cada uma das direções x, y e z após poucas "gerações" do processo, conforme mostra a tabela da Figura 3. Destaca-se que os vórtices que caracterizam o movimento turbulento estão associados com os estiramentos indicados nesta figura. Com isso, a escala de comprimento característica destes movimentos vai diminuindo a cada geração, de modo que os vórtices de pequena escala "esquecem" a orientação preferencial do movimento de larga escala (Zhurbas, 2001), isto é, tendem à isotropia conforme sugere a tabela da Figura 3. Dentro deste contexto, a energia vai sendo transferida dos maiores para os menores vórtices e, finalmente, nos menores vórtices ela é dissipada em calor.
Camada Limite e escalas associadas
Escoamentos com altos números de Reynolds são caracterizados pela existência de várias escalas de comprimento, as quais possuem um limite superior, que é imposto pelas dimensões físicas do escoamento (corpo d'água), e um limite inferior, o qual é determinado pela ação difusiva da viscosidade molecular. Esta subseção é dedicada à revisão do conceito de Camada Limite, introduzido por Prandtl em 1904, e à análise das escalas envolvidas nas camadas limite laminar e turbulenta, assim como as Escalas de Kolmogorov.
Prandtl mostrou que a maioria dos escoamentos viscosos pode ser analisada pela divisão do escoamento em duas regiões: uma próxima da superfície sólida confinante e a outra cobrindo o restante do escoamento. Apenas em uma pequena região adjacente ao contorno, denominada camada limite, se faz importante o efeito da viscosidade. Observa-se que, em qualquer escoamento viscoso, o fluido em contato direto com a superfície possui a mesma velocidade desta superfície (condição de "nãodeslizamento"). Na região além desta camada o efeito da viscosidade é desprezível e o fluido pode ser tratado como não viscoso.
Uma melhor visualização da formação da camada limite pode ser obtida analisando-se um escoamento com velocidade uniforme sobre uma placa plana. Este fluido, na vizinhança imediata da superfície, fica sujeito à ação de forças de cisalhamento devidas à desaceleração imposta pela placa (ver Fig. 4). Estas forças tendem a ajustar a velocidade do fluido àquela da superfície em virtude da condição de "não-deslizamento".
Nesta figura, U∞ representa a velocidade do escoamento livre, ou seja, longe da influência da superfície. No caso específico da Figura 4 (escoamento unidirecional na direção x) a tensão de cisalhamento τyx será dada por
Na Equação (1), conhecida como Lei de Newton da Viscosidade, µ é o coeficiente de viscosidade dinâmica molecular do fluido e u(y) é a função que define o perfil de velocidade do escoamento. Se a placa estiver em repouso o momentum junto à superfície será nulo, enquanto no escoamento livre será expresso por ρU∞. Isto significa que a presença da placa provoca, na camada adjacente, um déficit de momentum em relação àquele do escoamento livre. Por exemplo, o movimento ao redor da asa de um avião, do casco de um navio ou sobre o fundo do oceano, podem ser representados, de maneira aproximada, pelo escoamento do fluido sobre uma placa plana.
A tensão de cisalhamento, que atua sobre o perfil de velocidade nas adjacências da superfície, trazendo a velocidade do fluido para o mesmo valor daquele do contorno, mostra que tanto as forças de inércia quanto as viscosas são importantes na camada limite. Não é de surpreender então que o número de Reynolds seja importante na caracterização dos escoamentos em camada limite. O comprimento ou dimensão característica utilizado na determinação deste parâmetro é aquele que caracteriza o escoamento na região de interesse, podendo ser tanto o comprimento na direção do escoamento, sobre o qual a camada limite se desenvolve, como alguma medida (transversal) da espessura da mesma (e.g., Tritton, 1977).
O escoamento na camada limite pode ser tanto laminar como turbulento. Esta camada se desenvolve inicialmente laminar e as instabilidades fazem com que ela se torne turbulenta. A Figura 4 (lado esquerdo) mostra que uma região laminar se forma na borda esquerda da placa ("bordo de ataque"), a qual cresce em espessura, atingindo uma região de transição onde o escoamento muda de laminar para turbulento. Devido às perturbações de velocidade na direção y, o perfil de velocidade do escoamento dentro da camada limite turbulenta é mais "achatado" que o correspondente perfil para a camada limite laminar. Na região turbulenta da camada limite a turbulência diminui em direção à parede em tal extensão que começam a predominar os efeitos laminares (viscosos). Isto sugere que mesmo na camada limite turbulenta se desenvolve uma fina subcamada laminar, onde os efeitos viscosos (moleculares) predominam sobre os efeitos de inércia, conforme mostra a Figura 5 (e.g., Shames, 1973).
Camada Limite Laminar (CLL) e escalas associadas
Um escoamento laminar viscoso, suposto incompressível, estacionário e com viscosidade constante, pode ser descrito pelas equações de Navier-Stokes na forma1 1 A notação indicial será utilizada em grande parte deste trabalho
Na Equação (2) ui(j) é a velocidade do escoamento na direção xi(j), p é a pressão, v é o coeficiente de viscosidade cinemática e ρ é a massa específica do fluido.
Uma análise de escala aplicada na Equação (2) permite estimar o termo de inércia como tendo ordem O(U2/L), onde U e L são as escalas características de velocidade e comprimento do escoamento (na direção paralela à superfície), respectivamente, enquanto o termo de fricção viscosa possui ordem O(vU/L2). A relação entre estes dois termos, que compara as forças de inércia com as forças viscosas que atuam sobre o fluido, é o número de Reynolds, dado por Re = UL/v. Um elevado valor de Re indica que o termo viscoso é negligenciável quando comparado com o termo de inércia. Entretanto, determinadas condições de contorno podem tornar impossível negligenciar este termo em alguma parte do escoamento. Por exemplo, no escoamento sobre uma superfície sólida é necessária a existência de uma "camada limite". Conforme citado anteriormente os efeitos viscosos são importantes nesta região, o que sugere a associação destes efeitos com uma nova escala de comprimento que seja compatível com a camada limite. Pode-se então investigar uma escala de comprimento l onde os termos viscosos subsistam e sejam tão importantes quanto os termos advectivos (inércia), o que implica em um número de Reynolds na camada limite, ReCL, de ordem (1). Tendo em vista que a ordem do termo viscoso foi agora modificada para ordem O(vU/l2), pode-se escrever
Na Equação (3), Re é o número de Reynolds no escoamento livre. A partir desta equação, a escala da espessura da camada limite laminar l pode ser relacionada com a escala de comprimento do escoamento livre L pela seguinte equação:
Uma escala de tempo t, característica dos processos difusivos viscosos, possui ordem O(L/U), o que permite, a partir de (3), escrever
A escala de comprimento l, associada à espessura da CLL, é transversal à superfície (ver lado esquerdo da Fig. 4), tendo em vista que ela está associada à difusão de momentum na direção normal ao escoamento. Destaca-se que esta difusão, na direção paralela ao escoamento, é negligenciável quando comparada ao transporte advectivo de momentum nesta mesma direção (e.g., Tennekes & Lumley, 1972). A Equação (4) mostra que a escala da espessura da CLL é consideravelmente menor que a escala L do campo de escoamento no qual ela se desenvolve, sendo tão menor quanto maior o número de Reynolds do escoamento.
Camada Limite Turbulenta (CLT) e escalas associadas
As escalas de comprimento e velocidade na CLT são ilustradas no lado direito da Figura 4. A turbulência transfere o déficit de momentum, a partir da superfície, na direção normal ao escoamento, a uma taxa lt/t~ut, onde lt é a escala de comprimento associada à espessura da CLT, t é a escala de tempo e ut é a escala das flutuações da velocidade do escoamento dentro da CLT.
Como os processos advectivo e difusivo ocorrem simultaneamente, podemos escrever t~L/U~lt/ut, ou,
O mesmo procedimento seguido aqui para encontrar uma relação entre as escalas difusiva e advectiva na CLT poderia ter sido aplicado para encontrar a relação entre as escalas difusiva e advectiva na CLL (seção anterior). Todavia, lá preferimos fazer uma análise de escala entre os termos advectivo e difusivo na Equação (2), do momentum.
A Equação (6) mostra que a escala da espessura da CLT, assim como a da CLL, conforme a Equação (4), é consideravelmente menor que a escala L do campo de escoamento no qual ela se desenvolve.
Escalas de Kolmogorov
Podemos observar que a escolha de lt (ver Fig. 4) como escala de comprimento característica da CLT faz com que, implicitamente, estejamos considerando apenas os vórtices de maior escala desta camada. À medida, porém, que nos aproximamos da superfície, o tamanho dos vórtices vai diminuindo e outras escalas menores têm que ser consideradas (e.g., Móller e Silvestrini, 2004). Entretanto, não devemos perder de vista que a viscosidade molecular impõe um limite inferior para a escala dos menores vórtices. Em escalas muito pequenas a viscosidade molecular se torna muito efetiva e os termos viscosos previnem a geração de escalas menores ainda, quando então a energia cinética dos pequenos vórtices é dissipada antes que atinjam a escala molecular. Este mecanismo garante que os menores vórtices sejam ainda maiores que as dimensões moleculares, o que dá sustentação à hipótese do continuum, sobre a qual se baseia a teoria dos escoamentos turbulentos e a mecânica dos fluidos (Deschamps, 2002). Como os movimentos nas menores escalas tendem a ter escalas de tempo também menores (pois as flutuações ficam mais rápidas), podemos assumir que estes movimentos são estatisticamente independentes da turbulência de larga escala e do escoamento médio, comparavelmente mais lentos. Se esta hipótese é válida, este movimento de pequena escala depende somente da taxa de energia que ele recebe das grandes escalas e da viscosidade molecular. No equilíbrio, a taxa de suprimento de energia (oriunda das grandes escalas) tem que ser igual à taxa de dissipação de energia (envolvida com as pequenas escalas) e esta concepção é a base da chamada teoria do equilíbrio universal de Kolmogorov (e.g., Tennekes & Lumley, 1972 e Mõller & Silvestrini, 2004).
Esta discussão sugere que os parâmetros que governam o movimento nas pequenas escalas devem incluir, no mínimo, a taxa de dissipação de energia por unidade de massa ε(m2s-3) e a viscosidade cinemática v(m2s-1). Com estes novos parâmetros, seguidos de uma análise dimensional, pode-se formar escalas de comprimento, tempo e velocidade características do movimento associado com as pequenas escalas, que são expressas por:
Escala de comprimento:
Escala de tempo:
Escala de velocidade:
Estas escalas são referidas como microescalas de Kolmogorov. O número de Reynolds formado com estas escalas é expresso por Rek(V·λ/v). Com a utilização das expressões (7) e (9) observa-se que o número de Reynolds é unitário nas pequenas escalas de Kolmogorov, o que ilustra que o movimento nas pequenas escalas é viscoso e que a dissipação viscosa se adapta ao suprimento de energia pelo ajuste destas escalas (e.g., Möller & Silvestrini, 2004).
Com base nestes conceitos, se a taxa de dissipação viscosa E puder ser relacionada com as escalas de comprimento e velocidade da turbulência de larga escala, uma melhor compreensão das diferenças entre os aspectos macro e micro da turbulência pode ser formada. Para escoamentos completamente desenvolvidos, a taxa de dissipação viscosa (nas pequenas escalas) é igual à taxa na qual a energia, por unidade de massa, é suprida aos grandes vórtices pelo escoamento médio (grandes escalas), a qual é expressa por (U2/t), onde t = L/U. Assim pode-se escrever
Observa-se então que a dissipação viscosa pode ser expressa em função de grandezas características do escoamento médio.
Relações entre as pequenas e as grandes escalas
A substituição da Equação (10) nas expressões (7) a (9) permite a obtenção das seguintes relações entre as pequenas e as grandes escalas da turbulência:
Observa-se que as escalas de comprimento, tempo e velocidade dos menores vórtices da turbulência são muito menores que aquelas dos grandes vórtices e, principalmente, esta diferença é tão maior quanto maior for o número de Reynolds do escoamento médio. Escoamentos geofísicos, por exemplo, em virtude das suas largas dimensões horizontais, comumente apresentam números de Reynolds da ordem de 108. Neste caso, as relações entre as escalas de comprimento, tempo e velocidade das pequenas e largas escalas serão, respectivamente, λ = 106L, τ = 10-4t e V = 10-2U.
Viscosidade e difusividade turbulentas
A mais antiga proposta de modelagem da turbulência, a qual utiliza o conceito de viscosidade turbulenta, ainda constitui parte importante da maioria dos modelos de turbulência. Este conceito foi introduzido por Boussinesq em 1877 que, em analogia com a Lei da Viscosidade de Newton [ver Equação (1)], estabeleceu uma relação entre as tensões turbulentas  e os gradientes de velocidade média do escoamento, de acordo com a equação
e os gradientes de velocidade média do escoamento, de acordo com a equação
Nesta equação, vt é a viscosidade turbulenta, δij é o delta de Kronecker (cujo valor é 1, se i = j e 0, se i ≠ j) e k representa a energia cinética turbulenta (por unidade de massa), que é expressa por
A presença do termo que contém o delta de Kronecker na Equação (14) é necessária para a correta consideração das tensões normais que compõem a diagonal principal do tensor das tensões turbulentas, quando então i = j. Caso este termo não estivesse incluído na Equação (14), a soma das tensões normais seria nula para atender o princípio de conservação da massa no escoamento médio, ou seja,
Entre a Equação (14) e a equação análoga para as tensões viscosas [ver Equação (1)] existem dois aspectos que as diferenciam fundamentalmente. O primeiro é que, em contraste com a viscosidade molecular v, a viscosidade turbulenta não é uma propriedade do fluido e sim do escoamento, pois depende fortemente do estado da turbulência, ou seja, vt pode variar significativamente de um ponto a outro no interior do escoamento. De acordo com a Teoria Cinética dos Gases, o coeficiente de viscosidade molecular é proporcional ao livre caminho médio das moléculas do fluido e a uma velocidade característica destas moléculas. Isto significa que sob determinadas condições de temperatura e pressão, o coeficiente υ mantém um valor constante e característico para cada fluido. No movimento turbulento, o correspondente coeficiente de proporcionalidade recebe a denominação de coeficiente de viscosidade turbulenta vt e, por analogia, é considerado proporcional a uma velocidade e um comprimento característicos das flutuações turbulentas, o qual Prandtl denominou "comprimento de mistura".
Como já salientado, a analogia entre os escoamentos laminar e turbulento não é perfeita, pelo fato que os vórtices não podem ser considerados corpos rígidos, nem entidades capazes de manter sua identidade no tempo e espaço (como são supostas as moléculas na Teoria Cinética). Além disso, o "livre caminho" dos grandes vórtices não é pequeno quando comparado com o domínio do escoamento, como é requerido pela Teoria Cinética (Rodi, 1993). Deve-se observar ainda que, além do coeficiente de viscosidade turbulenta vt variar de ponto para ponto no campo de escoamento, isto é feito de forma não previsível teoricamente, forçando então o uso de informações experimentais para que se possa estabelecer esta variação (Eiger, 1989).
Embora frágil do ponto de vista físico, o conceito de viscosidade turbulenta tem demonstrado ser extremamente útil para muitos escoamentos de interesse prático (e.g., Tennekes & Lumley, 1972; Stull, 1988; Rodi, 1993). Vamos agora enfatizar o fato que a viscosidade turbulenta vt é proporcional à escala de velocidade Û e de comprimento  , ambas caracterizando o movimento turbulento de larga escala, de forma que se pode escrever
, ambas caracterizando o movimento turbulento de larga escala, de forma que se pode escrever
Destaca-se que, na realidade, é a distribuição destas duas escalas ao longo do campo de escoamento que pode ser razoavelmente bem aproximada (e.g., Eiger, 1989; Rodi, 1993).
Quanto ao segundo aspecto a ser considerado, observase que a Equação (14) introduz um coeficiente de viscosidade turbulento igual para todas as componentes das tensões de Reynolds τij Esta concepção de viscosidade turbulenta isotrópica é uma simplificação, cujo realismo é limitado em escoamentos mais complexos. Por isso, em algumas situações, introduzimos coeficientes de viscosidade turbulentos diferentes para diferentes direções do campo de escoamento. Por exemplo, em grandes corpos d'água como oceanos, rios, estuários, é comum prescrever coeficientes de viscosidade diferentes para as direções horizontal e vertical, para que a anisotropia seja considerada. Cumpre salientar que, a despeito da fragilidade física do conceito de viscosidade turbulenta, ele tem sido muito bem sucedido e ainda é a base da maioria dos modelos em uso (e.g., Rodi, 1993).
Com relação à difusividade turbulenta, em analogia com a difusão molecular, será suposto que a difusão turbulenta de uma propriedade qualquer seja proporcional ao gradiente do valor médio da propriedade. Sendo assim, para uma propriedade φ, podemos escrever
onde D é a difusividade turbulenta da propriedade considerada. A difusividade turbulenta possui a mesma fragilidade conceituai da viscosidade turbulenta, ou seja, ela não é uma propriedade do fluido. A analogia de Reynolds entre o transporte de massa/calor e o transporte de momentum sugere que haja uma relação muito aproximada entre a difusividade e a viscosidade turbulentas (e.g., Rodi, 1993). De fato, esta relação pode ser escrita na forma
onde σt corresponde ao número de Prandtl turbulento, para o transporte de calor, ou o número de Schmidt, para o transporte de massa. Note que D e vt têm as mesmas dimensões e suas unidades são m2s-1. Sabe-se que, ao contrário da difusividade turbulenta de momentum e calor ou massa, σt varia muito pouco de um ponto a outro do escoamento e até mesmo de um escoamento para outro.
Interpretação estatística da turbulência
As variáveis de um escoamento turbulento não são determinísticas e, como tal, devem ser tratadas como variáveis aleatórias. As propriedades estatísticas média, desvio padrão e variância são coletivamente chamadas momentos estatísticos da variável. Quando os momentos estatísticos de uma variável aleatória são independentes do tempo dizemos que o processo é estacionário. Se eles forem independentes do espaço, o processo é dito homogêneo e se forem independentes da orientação dos eixos coordenados em relação aos quais a variável foi medida, o processo é considerado isotrópico (e.g., Kundu & Cohen, 2002). Em outras palavras, a turbulência será dita homogênea se as estatísticas forem invariantes por translação dos eixos coordenados, e dita isotrópica se invariantes por rotação dos eixos (e.g., Silveira Neto, 2002a).
Apesar da turbulência homogênea e isotrópica ser uma idealização, o escoamento observado na frente de uma "grade de turbulência" constitui uma boa aproximação experimental para este tipo de escoamento, permitindo que predições teóricas sejam comprovadas experimentalmente. Uma "grade de turbulência" consiste de uma grade posicionada transversalmente ao escoamento, no interior de um túnel de vento, conforme mostra a Figura 6. Esta grade permite o estudo da turbulência homogênea e isotrópica, possibilitando então a determinação de vários parâmetros que governam as taxas de transporte de quantidade de movimento, calor e escalares no interior dos escoamentos turbulentos (e.g., Silveira Neto, 2002a).
Destaca-se que nos escoamentos turbulentos os valores instantâneos das variáveis (u, v, w, θ, ρ, p, S...) flutuam, com certa frequência, em torno de um valor médio. Para a maioria dos propósitos, conhecer o comportamento médio do escoamento, e, portanto, o valor médio assumido por suas variáveis descritivas, é suficiente. Para outros, entretanto, é justamente no caráter flutuante destas variáveis que estamos interessados. Reynolds, em 1895, foi o primeiro a sugerir que o escoamento instantâneo fosse desdobrado em uma componente média (de grande escala) e outra flutuante (de pequena escala) pela separação das variáveis, conforme mostra a Equação (20):
Na Equação (20),  corresponde ao valor instantâneo de uma variável qualquer,
corresponde ao valor instantâneo de uma variável qualquer,  à componente média desta variável e x' a sua parte flutuante. Na aplicação da técnica de separação de Reynolds a média efetuada sobre as realizações obedece a certas regras que são mostradas a seguir. Para maiores detalhes, sugere-se a leitura de Stull (1988) e Kundu & Cohen (2002). A aplicação da Equação (20) a duas propriedades a e b deve obedecer às seguintes regras de promediação:
à componente média desta variável e x' a sua parte flutuante. Na aplicação da técnica de separação de Reynolds a média efetuada sobre as realizações obedece a certas regras que são mostradas a seguir. Para maiores detalhes, sugere-se a leitura de Stull (1988) e Kundu & Cohen (2002). A aplicação da Equação (20) a duas propriedades a e b deve obedecer às seguintes regras de promediação:
No conjunto de Equações (21) os valores médios  representam o primeiro momento estatístico, enquanto as variâncias e covariâncias
representam o primeiro momento estatístico, enquanto as variâncias e covariâncias  são interpretadas como o segundo momento (e.g., Stull, 1988).
são interpretadas como o segundo momento (e.g., Stull, 1988).
O comprimento de mistura de Prandtl
Considere a situação simples de um escoamento turbulento unidirecional na direção x, com velocidade u(y), conforme apresentado na Figura 7a. Apesar da velocidade v na direção y ser nula, sua flutuação v' move a parcela de fluido situada na posição 1 para cima, assim como a parcela situada na posição 2 é deslocada para baixo. Assim, a parcela 1 é substituída pela 2 e vice-versa. Este tipo de troca ocorre em todo o campo de escoamento turbulento, produzindo uma interação entre as camadas do fluido em escala macroscópica. Partindo dessa observação, Prandtl, em 1925, desenvolveu sua hipótese do comprimento de mistura e propôs um modelo algébrico de turbulência (e.g., Deschamps, 2002).
Se du/dy é positiva, como indicado na Figura 7b, então as velocidades das partículas obedecem a desigualdade u(y + lm) > u(y) > u(y - lm). Será suposto agora que a partícula na camada (y + lm), devido à turbulência, sofra uma perturbação v' < 0 (vertical), e se desloque para baixo até a camada y. Este deslocamento lm mede a distância necessária para que a troca de momentum produza flutuações de velocidade u' da mesma ordem de grandeza daquelas que ocorrem num escoamento turbulento real. A parcela fluida, ao chegar à posição y, tende a acelerar e aumentar a velocidade u das partículas desta região de uma quantidade u'. Em outras palavras, ela transfere uma determinada quantidade de movimento às partículas da região y. Note que a flutuação v' < 0 provocou o surgimento de outra flutuação, no caso, u' > 0. O produto destas flutuações ( ) é negativo e representa uma das componentes do tensor de Reynolds
) é negativo e representa uma das componentes do tensor de Reynolds  , por unidade de massa.
, por unidade de massa.
A distância lm, que Prandtl chamou "comprimento de mistura", é aquela que produz flutuações de velocidade da mesma ordem de magnitude que as ocorridas num escoamento turbulento real. A flutuação de velocidade provocada pelo deslocamento da parcela de fluido, quando se desloca para baixo desde (y + lm) até y, é expressa por
a qual representa o valor de |u'| no campo de escoamento real. As barras indicam o módulo de u' uma vez que esta flutuação pode ser positiva ou negativa, conforme a partícula se desloque para baixo ou para cima, respectivamente. Dividindo-se a Equação (22) por lm = Δy, resulta
Esta Equação (23), no limite, fornece
O mesmo resultado seria obtido caso uma partícula de fluido se deslocasse para cima desde (y - lm) até y. Então, o valor médio das flutuações produzidas no entorno da posição y será expresso por
Prandtl também supôs que o valor médio do módulo das flutuações v', da outra componente da velocidade, fosse da mesma ordem de magnitude do módulo das flutuações u', expressa por (25), ou seja,
onde c1 é uma constante de ajuste.
O produto  que representa as tensões de Reynolds, se deve à presença das componentes flutuantes do escoamento, ou seja, não corresponde a uma tensão real do ponto de vista físico. Devido a este fato, são também chamadas de tensões turbulentas, aparentes ou fictícias. Assim, pode-se escrever
que representa as tensões de Reynolds, se deve à presença das componentes flutuantes do escoamento, ou seja, não corresponde a uma tensão real do ponto de vista físico. Devido a este fato, são também chamadas de tensões turbulentas, aparentes ou fictícias. Assim, pode-se escrever
Conforme mostrado acima, quando u' é positiva, v' é negativa e vice-versa, de modo que o produto médio  será diferente de zero e sempre negativo. Em vista disso, Prandtl supôs que
será diferente de zero e sempre negativo. Em vista disso, Prandtl supôs que  , onde c2 é um fator de correlação, cujo valor está compreendido entre 0 e 1. A partir das Equações (24) e (26) podemos escrever
, onde c2 é um fator de correlação, cujo valor está compreendido entre 0 e 1. A partir das Equações (24) e (26) podemos escrever
Na Equação (28) c3 = c1c2. Uma vez que o valor de lm ainda precisa ser determinado a partir de algum experimento ou fórmula empírica, podemos incluir nele o valor da constante c3, fazendo-se  e expressar a tensão aparente na forma
e expressar a tensão aparente na forma
Se na Equação (29) for definido que
pode-se, com a utilização de (30), reescrever a Equação (29) na forma
Na Equação (31) vt é o coeficiente de viscosidade cinemática turbulenta. A Equação (31) é uma versão simplificada da Equação (14) para um escoamento unidirecional que ocorre na direção x com um gradiente de velocidade u na direção y. A Equação (31) é a hipótese do comprimento de mistura de Prandtl. Ela relaciona a viscosidade turbulenta ao gradiente da velocidade média local e envolve o parâmetro comprimento de mistura lm como incógnita (Rodi, 1993). Substituindo-se  de (27) em (31) chega-se à Equação (32), que representa o análogo, para um escoamento turbulento, da Lei da Viscosidade de Newton, que é representada pela Equação (1), ou seja,
de (27) em (31) chega-se à Equação (32), que representa o análogo, para um escoamento turbulento, da Lei da Viscosidade de Newton, que é representada pela Equação (1), ou seja,
Na Equação (32), o parâmetro µt, é o coeficiente de viscosidade dinâmico turbulento, onde vt = µt/ρ. Eliminando-se o "sublinhado" na Equação (29), assim como as barras, visto que a derivada é elevada ao quadrado, obtém-se
A seguir, as características do escoamento próximo a contornos sólidos serão examinadas, uma vez que a presença destes altera o comportamento do escoamento e a estrutura da turbulência em relação à corrente livre (Versteeg & Malalasekera, 1995).
A Lei da Parede
Na região próxima de um contorno sólido ocorre um decréscimo na transferência de quantidade de movimento entre as camadas do fluido, pois a turbulência é inibida, ou até suprimida, devido à diminuição da escala de comprimento dos vórtices. Isto significa que o comprimento de mistura diminui à medida que o contorno sólido está mais próximo. Observando isso, Prandtl fez a hipótese de que o comprimento de mistura nesta região é proporcional à distância normal à parede, conforme mostra a equação
onde y é a distância perpendicular à parede e κ é a constante de von Karman, igual a 0,4. A Equação (34) mostra que o tamanho característico dos vórtices cresce quando nos afastamos da parede e tende para uma dimensão característica do escoamento ou para um valor limite, quando então a parede deixa de exercer qualquer influência sobre a turbulência local.
A Figura 8 mostra uma camada limite turbulenta sobre uma placa plana, onde U∞ é a velocidade da corrente livre e δ uma dimensão característica do escoamento nesta região, que pode ser a espessura desta camada, a qual é composta por duas regiões. A primeira, aderida à parede, é chamada subcamada laminar, onde predomina os efeitos viscosos e a segunda, denominada subcamada turbulenta, que se estende até a fronteira da camada limite, onde predomina os efeitos turbulentos. Como o perfil de velocidade é diferente em cada uma destas regiões, alguns autores reconhecem a existência de uma camada intermediária, que seria necessária para o ajuste dos diferentes perfis (Shames, 1973). A Figura 8 mostra as diferentes regiões da camada limite, as quais serão analisadas abaixo.
Subcamada viscosa da camada limite turbulenta
Como consequência da condição de nenhum deslizamento, o fluido é estacionário junto à parede sólida. De acordo com a Lei da Viscosidade de Newton, a tensão de cisalhamento na superfície τo é expressa pela equação:
Uma vez que esta camada é muito fina supõe-se que a tensão de cisalhamento permanece constante ao longo de toda a sua espessura. Assim, integrando-se (35) ao longo desta espessura resulta numa equação que governa o perfil da velocidade u na subcamadaviscosa, dada por
Na obtenção desta equação linear foi considerado que a velocidade u é nula em y = 0 (condição de nenhum deslizamento). Por isso, algumas vezes, esta região é também chamada subcamada linear.
Uma importante relação no estudo da camada limite é a chamada velocidade de atrito, que é expressa por  . Dividindo-se (36) por u* obtém-se uma relação adimensional para a velocidade e para a distância normal à parede, da seguinte forma
. Dividindo-se (36) por u* obtém-se uma relação adimensional para a velocidade e para a distância normal à parede, da seguinte forma
onde  definem, respectivamente, a velocidade e a distância em termos adimensionais. A subcamada viscosa é muito fina e se estende da superfície até y+ = 5 (e.g., Kundu & Cohen, 2002). Da Equação (37) conclui-se que u+ = y+, mostrando a relação linear que existe entre os adimensionais.
definem, respectivamente, a velocidade e a distância em termos adimensionais. A subcamada viscosa é muito fina e se estende da superfície até y+ = 5 (e.g., Kundu & Cohen, 2002). Da Equação (37) conclui-se que u+ = y+, mostrando a relação linear que existe entre os adimensionais.
Subcamada turbulenta da camada limite turbulenta
Para y+ > 30 (e.g., Kundu & Cohen, 2002) existe uma região onde os efeitos de inércia dominam e o escoamento é turbulento. Nesta região, a tensão de cisalhamento τ varia suavemente com a distância à parede, fazendo com que a forma do perfil de velocidade mude em relação àquele da subcamada viscosa. Após alguma manipulação algébrica com as Equações (30), (31), (34) e (36) obtém-se o perfil de velocidade para a subcamada turbulenta, o qual tem como equação
onde κ = 0,4 e C = 5 é uma constante de integração cujo valor é obtido experimentalmente (e.g., Kundu & Cohen, 2002). Com esses valores, a Equação (38) se transforma em
As Equações (37) e (39), as quais descrevem os dois perfis de velocidade nas regiões viscosa e turbulenta, respectivamente, são representadas na Figura 9.
Destaca-se que entre a subcamada viscosa e a subcamada turbulenta (5 < y+ < 30) existe uma região onde tanto o efeito viscoso como o turbulento são importantes (região de ajuste dos dois perfis).
MODELAGEM DA TURBULÊNCIA
Esta seção é destinada aos aspectos relacionados com a modelagem da turbulência. Inicialmente serão apresentadas as principais técnicas de abordagem para o estudo da turbulência, seguindo-se uma descrição dos métodos numéricos.
Técnicas de abordagem da turbulência
Para o estudo da turbulência estão disponíveis três metodologias de abordagem, i.e., as metodologias analítica, numérica e experimental.
A metodologia experimental é conduzida em laboratórios de turbulência e apresenta vantagens e desvantagens. Os experimentos, em geral, ficam limitados pela infraestrutura do laboratório, disponibilidade de equipamentos e pela escala máxima do modelo físico, a qual, frequentemente, é inadequada aos objetivos práticos do estudo (Yu & Righetto, 1999). A maior vantagem desta metodologia é poder tratar com a configuração do problema real, especialmente quando não se dispõe de um modelo matemático bem estabelecido que represente adequadamente o problema que se deseja modelar.
As metodologias analítica e numérica formam uma classe de métodos teóricos que procuram resolver as equações diferenciais que compõem o modelo matemático que descreve o fenômeno físico de interesse. A diferença entre elas está na complexidade das equações matemáticas que cada uma pode resolver. A abordagem analítica, em geral, exige geometrias e condições de contorno muito simples e hipóteses simplificadoras, visando reduzir a complexidade matemática do problema. A simulação numérica, por sua vez, permite a solução de problemas mais complexos. Grandes esforços têm sido empreendidos para o desenvolvimento de ferramentas que possam ser empregadas na modelagem numérica e que permitam a obtenção de respostas mais rápidas e precisas.
Modelagem numérica da turbulência
Como citado acima, a modelagem numérica é uma das ferramentas disponíveis para o estudo da turbulência. Entretanto, mesmo dentro deste enfoque, existem diferentes técnicas de abordagem, as quais serão brevemente descritas a seguir. Destacam-se os métodos: (i) baseados na clássica decomposição de Reynolds, (ii) de simulação numérica direta e (iii) de simulação das grandes escalas da turbulência.
Modelos baseados na decomposição de Reynolds (RANS)
Os modelos de turbulência baseados na decomposição de Reynolds são também conhecidos como modelos RANS (Reynolds Averaged Navier-Stokes), modelos de fechamento em um ponto (single-point closures) ou modelos de fechamento local (local closure). A denominação RANS se deve ao fato das variáveis das equações de Navier-Stokes serem decompostas numa parte média e outra flutuante, conforme já apresentado. A segunda e terceira denominações se devem ao fato da variável turbulenta, em qualquer ponto do escoamento, ser parametrizada a partir do gradiente do valor médio da variável no mesmo ponto ou local.
Dentro desta classe de modelos, a parametrização das incógnitas turbulentas (por exemplo,  ) é feita através de equações algébricas ou diferenciais, relacionando-as com propriedades do escoamento médio (normalmente com
) é feita através de equações algébricas ou diferenciais, relacionando-as com propriedades do escoamento médio (normalmente com  ). Estas parametrizações empregam o conceito de viscosidade/difusividade turbulenta e o conceito de Comprimento de Mistura. As expressões abaixo são exemplos deste tipo de parametrização:
). Estas parametrizações empregam o conceito de viscosidade/difusividade turbulenta e o conceito de Comprimento de Mistura. As expressões abaixo são exemplos deste tipo de parametrização:
A variável θ representa a temperatura, s é a salinidade e D a difusividade turbulenta.
Modelos empíricos
Uma classe de modelos que vem recebendo a atenção dos modelistas compreende os chamados modelos empíricos, também baseados nas equações RANS simplificadas pela aproximação da camada limite. Ao contrário dos modelos RANS apresentados na subseção anterior, cujos fluxos turbulentos são modelados com base nas Equações (40), aqui a modelagem dos fluxos é conduzida de forma diversa, fundamentada no conhecimento empírico dos fluxos na camada limite (e.g. Burchard et al, 2008). A parametrização do perfil-K, ou simplesmente KPP, constitui o mais recente modelo que representa esta classe. Introduzido por Large et al. (1994) ele se distingue dos demais modelos empíricos, e também de todos os modelos apresentados neste artigo, pela introdução da correlação não-local (non-local closure) entre os fluxos, ou seja, correlação de fluxos turbulentos em diferentes pontos do escoamento.
Large et al. (1994) desenvolveram a parametrização do perfil-K para aplicações no oceano profundo. O primeiro passo é a determinação da profundidade (-h) da camada limite superficial. O método considera separadamente a região da camada limite superficial (z > -h) e a região interior, abaixo dela (z < -h) sendo os coeficientes de viscosidade/difusividade parametrizados de forma diferente em cada uma destas regiões. O esquema KPP consiste em ajustar a taxa de mistura apropriada para a camada limite superficial (z > -h) àquela do oceano interior (z < -h) através de uma função polinomial chamada função de forma que faz o ajuste entre as duas na base da camada limite. O procedimento conduz a um perfil contínuo para a viscosidade/difusividade que vai da superfície ao fundo do oceano.
O esquema KPP de Large et al. (1994) foi concebido para aplicações em modelos globais, no oceano profundo, e por isso não considera a presença da camada limite de fundo. A aplicação deste modelo à região da plataforma, onde a camada limite de fundo pode exercer influência sobre os processos de mistura na camada interior e superficial, pode resultar em intensidades de mistura irreais. Durski et al. (2004) ampliaram o campo de aplicação do esquema KPP para a região da plataforma continental estendendo o ajuste entre as taxas de mistura para levar em consideração, também, a presença da camada limite de fundo.
Durski et al. (2004) fizeram estudos comparativos entre o esquema KPP e o modelo nível 2.5 MY82. Um destes estudos foi o aprofundamento da camada de mistura superficial em um fluido estratificado e inicialmente em repouso sujeito a uma tensão de vento atuando na superfície. O outro se relaciona com o fenômeno da ressurgência costeira induzida pela ação do vento. Em ambos os estudos o resultado em favor de um ou outro esquema de fechamento turbulento ficou na dependência das intensidades da tensão do vento e da estratificação da coluna d'água. Maiores detalhes a respeito do modelo KPP podem ser encontrados nas referências citadas.
Simulação Numérica Direta (DNS)
Esta técnica de modelagem é conhecida na literatura inglesa por direct numeric simulation (DNS), e consiste em resolver as equações completas de Navier-Stokes para todos os pontos da grade e para todas as escalas temporais e espaciais do movimento. O problema é que o escoamento turbulento é sempre tridimensional e transiente, caracterizado pela presença de uma miríade de vórtices que ocupam uma larga faixa de escalas de comprimento e de tempo e, portanto, para a resolução de todas estas escalas é requerida uma discretização espacial e temporal extremamente refinada, o que demanda um grande esforço computacional. Uma característica dos escoamentos turbulentos é o seu alto grau de liberdade, o qual corresponde ao número de equações lineares discretizadas a resolver em todos os pontos da grade, para que se possa bem caracterizar o escoamento (Silveira Neto, 2002b).
O elevado número de graus de liberdade, para números de Reynolds de interesse prático, limita assim a utilização desta metodologia à escoamentos com baixos números de Reynolds (Silveira Neto, 2002b; Silvestrini, 2003). Apesar das limitações, como a DNS resolve diretamente as equações de Navier-Stokes sem a necessidade de parametrizações, ela se constitui em uma importante ferramenta de análise, tanto qualitativa como quantitativa, da transição do escoamento à turbulência, uma vez que simula todas as escalas espaciais e temporais (Martinez, 2006). De acordo com Silvestrini (2003) a DNS deve ser interpretada como uma ferramenta de pesquisa, análoga a um experimento de laboratório, a partir da qual pode-se obter informações importantes para a simulação do movimento turbulento.
Simulação das Grandes Escalas da turbulência
A Simulação das Grandes Escalas (SGE) ou Large Eddy Simulation (LES) é outra alternativa disponível para a simulação numérica de escoamentos turbulentos, a qual vem ao encontro das dificuldades enfrentadas com a técnica da simulação direta, descrita na seção anterior. Nesta técnica, utiliza-se um filtro que separa as grandes estruturas da turbulência, ou seja, os grandes vórtices que transportam energia e quantidade de movimento, das pequenas estruturas, representadas pelos pequenos vórtices, onde prevalece a isotropia (Silveira Neto, 2002b). O procedimento tem o objetivo de reduzir o número de graus de liberdade e, com isso, permitir a simulação de escoamentos com maior número de Reynolds em comparação com a DNS.
A simulação das grandes escalas é conduzida tal como a técnica DNS, com discretizações espaciais e temporais bastante refinadas, onde são resolvidas as equações instantâneas de Navier-Stokes apenas para as escalas energéticas do escoamento. As pequenas escalas de comprimento e tempo, as quais têm um comportamento mais isotrópico e menos dependente dos contornos físicos, são conhecidas como escalas submalha e são modeladas por um modelo algébrico simples, o qual é denominado modelo submalha.
De acordo com Silvestrini (2003), em LES as pequenas escalas são pobremente resolvidas de forma que a principal finalidade da parametrização submalha é extrair energia das grandes escalas fazendo o "papel" da cascata de energia. Do ponto de vista das flutuações das variáveis, a técnica LES pode ser situada entre a técnica DNS, onde todas as flutuações são, em princípio, resolvidas, e a modelagem RANS, onde somente os valores médios são resolvidos, enquanto as flutuações são parametrizadas (e.g. Silvestrini, 2003).
A seguir, um maior detalhamento dos modelos RANS será apresentado, visto que estes modelos são largamente utilizados na modelagem de escoamentos geofísicos. Para os leitores interessados em mais detalhes sobre os modelos DNS e LES recomenda-se a leitura de Silveira Neto (2002b), Silvestrini (2003) e Martinez (2006).
Modelos RANS
A existência de uma grande quantidade de modelos de turbulência baseados na técnica de decomposição de Reynolds torna difícil definir um critério único que permita uma distinção adequada entre eles. Alguns destes modelos, por exemplo, não utilizam o conceito de viscosidade/difusividade, mas empregam equações diferenciais para o transporte de "entidades" que caracterizam a turbulência, tais como o momentum,  e o fluxo de propriedades escalares associadas ao escoamento,
e o fluxo de propriedades escalares associadas ao escoamento,  onde φ representa um escalar qualquer. Tais modelos estão fora do objetivo deste trabalho, cuja finalidade é descrever modelos que utilizam o conceito de viscosidade turbulenta. Dentre estes, alguns fazem uso de uma viscosidade/difusividade constante que, apesar da simplicidade, torna a modelagem da turbulência muito limitada, pois não considera sequer as variações locais da estrutura da turbulência e, por isso, não podem ser utilizados, em geral, para descrever corretamente os detalhes do campo de escoamento médio.
onde φ representa um escalar qualquer. Tais modelos estão fora do objetivo deste trabalho, cuja finalidade é descrever modelos que utilizam o conceito de viscosidade turbulenta. Dentre estes, alguns fazem uso de uma viscosidade/difusividade constante que, apesar da simplicidade, torna a modelagem da turbulência muito limitada, pois não considera sequer as variações locais da estrutura da turbulência e, por isso, não podem ser utilizados, em geral, para descrever corretamente os detalhes do campo de escoamento médio.
Os modelos mais simples que adotam uma distribuição para vt no campo de escoamento, o fazem relacionando este parâmetro diretamente à distribuição da velocidade média, por exemplo, com o gradiente local desta. Estes modelos, implicitamente, assumem que a turbulência é dissipada no mesmo local onde foi gerada, o que significa que não existe transporte da turbulência (ou da entidade que a caracteriza) no campo de escoamento. Para os casos onde o estado da turbulência num ponto seja influenciado pela turbulência em outro local do escoamento (ou pela turbulência gerada em tempos pretéritos), os modelos mais simples, que negligenciam o transporte da turbulência, são inadequados.
Modelos que empregam equações de transporte para "quantidades" que caracterizem o estado de turbulência do escoamento foram desenvolvidos para levar em consideração o transporte da turbulência. Estas "quantidades", que caracterizam a turbulência, podem ser chamadas "entidades turbulentas". Uma equação de transporte é aquela que contém termos que: (i) representem o transporte advectivo da entidade através do escoamento médio, (ii) representem o transporte difusivo pelo movimento turbulento, (iii) possam reproduzir a geração de turbulência devido aos gradientes de velocidade média (cisalhamento) ou de densidade (buoyancy) e (iv) representem a dissipação (destruição) da entidade turbulenta nas pequenas escalas (e.g., Rodi, 1993).
Alguns destes modelos empregam uma equação de transporte para a escala de velocidade  , supondo que esta entidade bem represente a intensidade da turbulência (flutuações do campo de velocidade média). Existem modelos, mais complexos ainda, que resolvem duas equações de transporte para duas entidades representativas do estado da turbulência do escoamento como, por exemplo, a escala de velocidade
, supondo que esta entidade bem represente a intensidade da turbulência (flutuações do campo de velocidade média). Existem modelos, mais complexos ainda, que resolvem duas equações de transporte para duas entidades representativas do estado da turbulência do escoamento como, por exemplo, a escala de velocidade  e a escala de comprimento característica da turbulência,
e a escala de comprimento característica da turbulência,  (Mellor & Yamada, 1982; Hassid & Galperin, 1983; Blumberg & Mellor, 1987; Galperin et al, 1988; Kantha & Clayson, 1994; Burchard & Petersen, 1999; Umlauf & Burchard, 2003; llicak et al, 2008).
(Mellor & Yamada, 1982; Hassid & Galperin, 1983; Blumberg & Mellor, 1987; Galperin et al, 1988; Kantha & Clayson, 1994; Burchard & Petersen, 1999; Umlauf & Burchard, 2003; llicak et al, 2008).
Independentemente do critério de classificação, é importante que a turbulência seja vista como uma entidade que pode ser produzida, dissipada e transportada através do escoamento. Entretanto, muitos modelos, até que bem sucedidos em alguns casos, não consideram equações para o transporte destas entidades e, portanto, não devem ser empregados para situações muito distintas daquela para a qual foram validados (Eiger, 1989).
A subseção abaixo apresenta as principais classificações dos modelos RANS, com destaque para aquela com relação à ordem do fechamento.
Classificação quanto à ordem do fechamento
Em geral, quando um escoamento é modelado, descreve-se o seu comportamento médio através de um conjunto de equações diferenciais parciais escritas para as variáveis médias. Entretanto, a obtenção deste conjunto de equações incorpora novas incógnitas, características dos processos de pequena escala e representadas por correlações das flutuações das variáveis médias, tais como: (i)  , interpretadas como "tensões de Reynolds"; (ii)
, interpretadas como "tensões de Reynolds"; (ii)  , como fluxo turbulento de calor;
, como fluxo turbulento de calor;  , como fluxo turbulento de sal e outras. Equações evolutivas (prognósticas) podem ser escritas para que o valor destas incógnitas possa ser encontrado. Este procedimento, além de aumentar o número de equações diferenciais a resolver, faz surgir correlações tríplices (momentos de terceira ordem) como novas incógnitas
, como fluxo turbulento de sal e outras. Equações evolutivas (prognósticas) podem ser escritas para que o valor destas incógnitas possa ser encontrado. Este procedimento, além de aumentar o número de equações diferenciais a resolver, faz surgir correlações tríplices (momentos de terceira ordem) como novas incógnitas  , entre outras), mantendo sempre o número de incógnitas maior que o de equações, permanecendo o sistema em aberto. Na teoria da turbulência isto é conhecido como problema de fechamento.
, entre outras), mantendo sempre o número de incógnitas maior que o de equações, permanecendo o sistema em aberto. Na teoria da turbulência isto é conhecido como problema de fechamento.
Do ponto de vista estatístico, estas novas correlações são reconhecidas como momentos de segunda ordem ou de terceira ordem (segundos momentos ou terceiros momentos, respectivamente), criando-se então a nomenclatura encontrada para certas formas de classificação dos modelos de fechamento. Baseada nesta explicação, uma classificação muito freqüentemente encontrada na literatura especializada faz referência à "ordem do fechamento" adotada. De acordo com essa classificação são encontrados:
a) Modelos de Primeira Ordem - Nestes modelos o sistema de equações escrito para as variáveis médias  é resolvido e as tensões de Reynolds e os fluxos
é resolvido e as tensões de Reynolds e os fluxos  são parametrizados através de uma equação algébrica, por exemplo, em função da velocidade média.
são parametrizados através de uma equação algébrica, por exemplo, em função da velocidade média.
b) Modelos de Segunda Ordem - Para estes modelos são escritas equações diferenciais evolutivas para os momentos de segunda ordem e os terceiros momentos são parametrizados, ou seja, as equações diferenciais para  são resolvidas e as correlações tríplices
são resolvidas e as correlações tríplices  são parametrizadas utilizando-se relações do tipo difusão-gradiente dos segundos momentos. Destaca-se que o Modelo das Tensões de Reynolds se enquadra nesta ordem de fechamento.
são parametrizadas utilizando-se relações do tipo difusão-gradiente dos segundos momentos. Destaca-se que o Modelo das Tensões de Reynolds se enquadra nesta ordem de fechamento.
É claro que quanto mais alta é a ordem do fechamento, maior é o número de equações diferenciais parciais a resolver e maior será o custo computacional. Existem concepções de fechamento que utilizam apenas uma parte das equações disponíveis dentro de cada categoria. Por exemplo, suponha que as equações do escoamento médio sejam resolvidas juntamente com as equações evolutivas para a energia cinética turbulenta e para as variâncias de temperatura e salinidade. Neste caso, parametrizando-se os segundos momentos restantes, tem-se um fechamento de ordem mais alta que a primeira, porém mais baixa que a segunda, porque nem todos os momentos de segunda ordem possuiriam equação evolutiva (por exemplo, os fluxos de calor e sal). Um modelo deste tipo seria classificado como de uma e meia ordem de fechamento (Stull, 1988).
Um modelo de ordem zero, dentro desta classificação, não resolveria qualquer equação prognostica, nem mesmo para as variáveis médias. Neste caso, a velocidade, temperatura e salinidade médias são parametrizadas diretamente em função do espaço e tempo. Obviamente, um modelo deste tipo não corresponde nem a um fechamento "local", e nem "não local", pelo simples fato que ignora completamente a turbulência. Um modelo de meia ordem resolveria as equações do escoamento médio e parametrizaria apenas alguns momentos de segunda ordem, deixando de fora, por exemplo, os fluxos de calor e sal. Obviamente não seria um modelo de primeira ordem completo.
Apesar de não haver hoje em dia nenhum interesse em modelos de ordem zero, de meia ordem e até mesmo de primeira ordem, eles podem ser definidos e já tiveram bastante utilidade.
Classificação quanto ao número de equações diferenciais utilizadas para o fechamento
Para os modelos de turbulência centrados na hipótese de Boussinesq [ver Equação (14)] existe uma classificação baseada no número suplementar de equações diferenciais ordinárias e parciais necessárias para resolver o problema de fechamento da turbulência. Exemplos desta classificação (e.g., Stull, 1988; Fontoura Rodrigues, 2003) são os modelos à zero equação, a uma equação e a duas equações, os quais utilizam, respectivamente, nenhuma, uma e duas equações diferenciais parciais (EDP) auxiliares na determinação da viscosidade turbulenta. Modelos a meia equação fazem uso de uma equação diferencial ordinária (EDO), enquanto modelos a uma e meia equação utilizam uma EDP e uma EDO.
Classificação por categoria
Uma classificação menos frequente divide os modelos em categorias, o que é feito da seguinte forma (Fontoura Rodrigues, 2003): (a) Categoria I - que reúne todos os modelos que se fundamentam no conceito de viscosidade turbulenta, (b) Categoria II - dos modelos que partem das equações evolutivas para o tensor das tensões de Reynolds e (c) Categoria III - que reúne modelos de simulação das grandes escalas da turbulência (LES - Large Eddy Simulation), concebidos por Deardorff (1970 apud Fontoura Rodrigues, 2003). Estes modelos fogem dos objetivos deste trabalho.
A hierarquia de Mellor & Yamada
Mellor & Yamada (1974), alegando haver certa confusão na nomenclatura adotada para a classificação dos modelos, julgaram conveniente a adoção de uma "nova" nomenclatura para esta classificação que fosse semanticamente neutra. Para tanto, propuseram que os modelos fossem classificados por níveis de complexidade, sendo o mais complexo classificado como nível 4, correspondendo ao modelo das tensões de Reynolds, enquanto o mais simples, nível 1, corresponderia a um modelo algébrico. Entre os níveis 3 e 2 desta classificação enquadra-se o conhecido modelo nível 21/2 de Mellor & Yamada (1982), o qual se constituiu numa referência para a modelagem da circulação oceânica, e que corresponde a uma simplificação do nível 3 (e.g. Hassid & Galperin, 1983; Blumberg & Mellor, 1987; Galperin et al, 1988; Kantha & Clayson, 1994; Burchard, 2001; Burchard & Bolding, 2001; Umlauf et al., 2003; llicak et al., 2008).
Esta classificação se fundamenta no chamado parâmetro de anisotropia aij. De forma absolutamente simplista, se pode dizer que os autores partem da equação para as tensões de Reynolds e avaliam o quanto cada termo da equação se afasta da condição de isotropia. Com isso, negligenciando de forma racional os termos de ordem mais alta, os autores vão obtendo modelos com diferentes níveis de complexidade. Este procedimento não é trivial e sua análise será feita em um trabalho futuro.
DISCUSSÃO E CONSIDERAÇÕES FINAIS
Este trabalho procurou apresentar uma visão geral do fenômeno da turbulência e os vários tipos de modelos de turbulência existentes.
Conforme apresentado na seção introdutória, a turbulência é um fenômeno bastante complexo. A analogia com a Teoria Cinética dos Gases, apesar de não ser perfeita, permitiu uma melhor compreensão do fenômeno e serviu como base para o estudo e modelagem da turbulência (e.g., Eiger, 1989). Por exemplo, a isotropia que fundamenta o estudo da Teoria Cinética só é observável nas pequenas escalas da turbulência enquanto, nas grandes escalas, os vórtices dependem fortemente da geometria do escoamento e exibem um comportamento anisotrópico.
Algumas contribuições se mostraram fundamentais para o avanço da modelagem da turbulência. Boussinesq em 1887, por exemplo, deu um passo importante ao introduzir o conceito de viscosidade turbulenta. Igualmente importante, foi a iniciativa de Reynolds, em 1895, de separar o escoamento em uma parte média e outra flutuante, cujo efeito desta última sobre o escoamento médio é introduzido por meio de modelagem. Outra contribuição significativa no estudo da turbulência foi dada por Prandtl, cujos estudos entre 1904 e 1925, conduziram ao conceito de Camada Limite e a chamada Teoria da Camada Limite, evidenciando que o efeito da viscosidade em um escoamento só é relevante em uma pequena região adjacente aos contornos, podendo ser tratado como invíscido longe deles. Também se deve à Prandtl a introdução do conceito de Comprimento de Mistura, no qual os modelos de turbulência mais simples se baseiam.
Um recurso valioso, porém pouco explorado na literatura especializada, é aquele apresentado por Bradshaw (1971 apud Zhurbas, 2001), que foi denominado "árvore de gerações". Esta representação permite uma visualização da cascata de energia e a compreensão da forma como a turbulência tende à isotropia nas escalas menores da cascata.
Com o avanço dos recursos computacionais, modelos mais sofisticados foram sendo desenvolvidos, tais como os modelos a uma equação e a duas equações, todos do tipo RANS. Modelos empíricos, tal como a parametrização do perfil-K (KPP), desenvolvido por Large et al. (1994) para modelos globais, e a versão KPP de Durski et al. (2004), modificada para a região da plataforma, também são disponíveis e constituem boas alternativas ao modelista. Ainda com aplicações limitadas, e em ordem crescente de esforço computacional, se pode citar o Modelo das Tensões de Reynolds, a Simulação das Grandes Escalas da Turbulência (LES) e a Simulação Numérica Direta (DNS).
Uma grande variedade de modelos hidrodinâmicos utilizados na modelagem de escoamentos geofísicos nas mais diversas regiões do globo, empregam um ou outro dos modelos de turbulência comentados neste artigo. O Princeton Ocean Model (POM), por exemplo, utiliza o conhecido esquema de fechamento turbulento de nível 2.5 (e.g., Mellor & Yamada, 1982), o qual pode também ser classificado como um modelo de turbulência a duas equações, sendo uma para a energia cinética turbulenta e outra para a macro-escala de comprimento (e.g., Blumberg & Mellor, 1987; Kantha & Clayson, 2000a,b). Mais detalhes podem ser encontrados em: http://www.aos.princeton.edu/WWWPUBLIC/htclocs.pom/.
No Regional Ocean Modeling System (ROMS) a parametriza-ção dos processos de mistura vertical pode utilizar um esquema de fechamento local (em um ponto) ou não local (em dois pontos). O modelador pode escolher entre as várias opções disponíveis de fechamento turbulento. Maiores detalhes deste modelo podem ser encontrados em: http://www.myroms.org/index.php.
No HYbrid Coordinate Ocean Model (HY'COM) o modelador dispõe de uma variedade de submodelos de turbulência para escolha, entre elas o modelo a duas equações de Mellor & Yamada (1982) e o modelo KPP. Maiores detalhes podem ser encontrados em: http://hycom.rsmas.miami.edu/hycom-model/documentation.html. Já o MOdel Hydrodynamic(MOHID), um sistema de modelagem de corpos d'água tridimensionais emprega, entre outros, um esquema de fechamento turbulento a duas equações para a parametrização da mistura vertical. Maiores detalhes em http://www.mohid.com/what_is_mohid.htm.
Finalmente, pode-se constatar que, hoje em dia, os modelos de turbulência a duas equações se constituem na ferramenta mais utilizada na simulação numérica de escoamentos turbulentos geofísicos. Segundo Fontoura Rodrigues (2003), é a relação custo-benefício destes modelos a principal razão de seu sucesso em aplicações técnicas e científicas.
AGRADECIMENTOS
Este trabalho é uma contribuição ao Projeto MOVAR (CNPq / Edital Universal-2008:474057/2008-9).
Recebido em 25 março, 2010 / Aceito em 25 fevereiro, 2011
Received on March 25, 2010 /Accepted on February 25, 2011
NOTAS SOBRE OS AUTORES
José Francisco Almeida de Souza possui Graduação em Engenharia Civil pela FURG (1979) e Mestrado em Engenharia Civil, área de concentração de Recursos Hídricos e Saneamento, pela UFRGS (1990). É professor da FURG e atualmente cursa o Doutorado em Oceanografia Física, Química e Geológica nesta instituição. Sua pesquisa atual está direcionada para a modelagem da turbulência com aplicação na formação de plumas flutuantes com a utilização do Princeton Ocean Model (POM). Tem como área de interesse os aspectos turbulentos da circulação costeira e estuarina.
Leopoldo Rota de Oliveira é graduado em Física pela UFPEL (1998) e possui Mestrado (2003) e Doutorado em Oceanografia Física, Química e Geológica pela FURG (2008). Trabalhou como docente na área de Física (4 anos UFPEL/FURG). Seus trabalhos científicos têm ênfase em Oceanografia Física, sobre a circulação oceânica de meso e larga-escala, atuando principalmente nos seguintes temas: Variabilidade da Corrente do Brasil e Confluência Brasil-Malvinas, Conversões de energia e processos de instabilidade, fluxo de calor superficial para o Oceano Atlântico sudoeste.
José Luiz Lima de Azevedo possui Graduação em Engenharia Química pela FURG (1982) e Mestrado em Engenharia Elétrica pela UFSC (1996) e Doutorado em Oceanografia Física, Química e Geológica da FURG (2009). É professor da FURG desde 1984. Sua pesquisa atual está direcionada para a modelagem analítica e numérica do encontro de vórtices anticiclônicos com a borda continental e a respectiva corrente de contorno. Tem ainda como áreas de interesse a modelagem numérica, com a utilização do Princeton Ocean Model (POM) e do modelo Bleck & Boudra, e o estudo de dados climatológicos oriundos dos flutuadores perfiladores do projeto ARGO.
Ivan Dias Soares possui Graduação em Oceanologia pela FURG (1986), Mestrado em Oceanografia Física pela USP (1995) e Doutorado em Meteorologia e Oceanografia Física pela Rosenstiel School of Marine and Atmospheric Science - University of Miami, Florida, USA (2003). Atualmente é professor adjunto IV da FURG. Área de atuação: modelagem numérica de processos costeiros e oceânicos.
Maurício Magalhães Mata é graduado em Oceanografia pela FURG (1991) e Mestre em Sensoriamento Remoto pela UFRGS (1996). Em 2001 tornou-se Doutor em Oceanografia Física pela Flinders University of South Australia, Adelaide, Austrália. Desde 1992 é professor permanente do Instituto de Oceanografia da FURG. Atualmente é Coordenador do Curso de Pós-Graduação em Oceanografia Física, Química e Geológica da FURG. Sua linha de pesquisa concentra-se na circulação oceânica de meso e larga-escala, com ênfase em correntes de contorno oeste e Oceanografia Antártica. Tem especial interesse nos processos interanuais que controlam a formação e exportação de águas de fundo no entorno do continente Antártico.
- BLUMBERG AF & MELLOR GL. 1987. A Description of a Three-Dimensional Coastal Ocean Circulation Model. In: HEAPS NS. (Ed.). Three dimensional ocean models. American Geophysical Union, Washington D.C. p.1-16.
- BURCHARD H. 2001. On the q2L Equation by Mellor & Yamada (1982). Notes and Correspondence. Journal of Physical Oceanography 31: 1377-1387.
- BURCHARD H& BOLDING K. 2001. Comparative Analysis of Four Second-Moment Turbulence Closure Models for the Oceanic Mixed Layer. Journal of Physical Oceanography 31:1943-1968.
- BURCHARD H& PETERSEN 0. 1999. Models of turbulence in the marine environment - A comparative study of two-equation turbulence models. Journal of Marine Systems, 21: 29-53.
- BURCHARD H, CRAIG PD, GEMMRICH JR, VAN HAREN H, MATHIEU P-P MEIER HEM, SMITH WAMN, PRANDKE H, RIPPETH TP, SKYL-LINGSTAD ED, SMYTH WD, WELSH DJS & WIJESEKERA HW. 2008. Observational and numerical modeling methods for quantifying coastal ocean turbulence and mixing. Progress in Oceanography 76(4): 399- 442.
- DESCHAMPSCJ.2002. Modelos Algébricos e Diferenciais. In: Coleção Cadernos de Turbulência. Associação Brasileira de Ciências Mecânicas - ABCM. Rio de Janeiro. Vol. 1, Cap. 3, p. 101-155.
- DURSKI SM, GLENN SM & HAIDVOGEL DB. 2004. Vertical mixing schemes in the coastal ocean: Comparison of the level 2.5 Mellor-Yamada scheme with an enhanced version of the K profile parameterization. Journal of Geophysical Research, 109: C01015, doi: 10.1029/2002JC001702.
- EIGER S. 1989. Modelos de Escoamentos Turbulentos. In: SILVA RCV (Ed.). Métodos Numéricos em Recursos Hídricos. Coleção da ABRH-Associação Brasileira de Recursos Hídricos, Vol. 1, Cap. 2, p. 84-155.
- FONTOURA RODRIGUES JLA. 2003. Escoamentos Turbulentos Parietais. In: Coleção Cadernos de Turbulência. Associação Brasileira de Ciências Mecânicas - ABCM. Rio de Janeiro. Vol. 2, Cap. 3, p. 153- 204.
- GALPERIN B, KANTHA LH, HASSID S & ROSATI A. 1988. A Quasi-equilibrium Turbulent Energy Model for Geophysical Flows. Journal of the Atmospheric Sciences, 45: 55-62.
- HASSID S & GALPERIN B. 1983. A Turbulent Energy Model for Geophysical Flows. Boundary-Layer Meteorology 26: 397-412.
- ILICAK M, ÖZGÖKMEN TM, PETERS H, BAUMERT H& ISKANDARANI M. 2008. Performance of two-equation turbulence closures in three-dimensional simulations of Red Sea overflow. Ocean Modeling, 24: 122-139.
- KANTHA LH & CLAYSON CA. 1994. An improved Mixed Layer Model for Geophysical Applications. Journal of Geophysical Research, 99(012):25,235-25,266.
- KANTHA LH & CLAYSON CA. 2000a. Numerical Models of Oceans and Oceanic Process. In: International Geophysics Series, Volume 66, Academic Press Inc., 940 p.
- KANTHA LH & CLAYSON CA. 2000b. Small Scale Process in Geophysical Fluid Flows. In: International Geophysics Series, Volume 67, Academic Press Inc., 885 p.
- KUNDU PK & COHEN IM. 2002. Fluid Mechanics. Academic Press Inc., 2ed.,730p.
- LARGE WG, McWILLIAMS JC & DONEY SC. 1994. Oceanic vertical mixing: A review and a model with a nonlocal boundary layer parameterization. Rev. Geophys., 32: 363-403.
- LESIEUR M. 1997. Turbulence in Fluids. Kluwer Academic Publishers, 3ed.,412p.
- MARTINEZ DMV. 2006. Transição à Turbulência na Camada de Mistura Estavelmente Estratificada utilizando Simulação Numérica Direta e Simulação de Grandes Escalas. Tese de Doutorado. Instituto de Pesquisas Hidráulicas, Universidade Federal do Rio Grande do Sul. 152 p. Disponível em: <http://www.lume.ufrgs.br/handle/10183/7230>. Acesso em: 18 dez. 2009.
- MELLOR GL & YAMADA T. 1974. A Hierarchy of Turbulence Closure Models for Planetary Boundary Layers. Journal of the Atmospheric Sciences, 31:1791-1806.
- MELLOR GL & YAMADA T. 1982. Development of a Turbulence Closure Model for Geophysical Fluid Problems. Reviews of Geophysics and Space Physics, 20:851-875.
- MÖLLER SV & SILVESTRINIJH. 2004. Turbulência: Fundamentos. In: Coleção Cadernos de Turbulência. Associação Brasileira de Ciências Mecânicas - ABCM. Rio de Janeiro. Vol. 4, Cap. 1, p. 1-32.
- RODI W. 1993. Turbulence Models and Their Application in Hydraulics - A state-of-the-art review. International Association for Hydraulic Research-IAHR, 3 ed., 104 p.
- ROSMAN PCC. 1989. Modelos de Circulação em Corpos d'Água Rasos. In: SILVA RCV (Ed.). Métodos Numéricos em Recursos Hídricos. Coleção da ABRH - Associação Brasileira de Recursos Hídricos, Vol. 1, Cap. 3, p. 156-221.
- SCHWIND JJ. 1980. Geophysical Fluid Dynamics for Oceanographers. Prentice-Hall Inc., 307 p.
- SHAMES IH. 1973. Mecânica dos Fluidos - Análise de Escoamentos. Ed. Edgard Blücher Ltda., 533 p.
- SILVEIRA NETO A. 2002a. Fundamentos da Turbulência nos Fluidos. In: Coleção Cadernos de Turbulência. Associação Brasileira de Ciências Mecânicas-ABCM. Rio de Janeiro. Vol. 1, Cap. 1, p. 1-48.
- SILVEIRA NETO A. 2002b. Simulação de Grandes Escalas de Escoamentos Turbulentos. In: Coleção Cadernos de Turbulência. Associação Brasileira de Ciências Mecânicas-ABCM. Rio de Janeiro. Vol. 1, Cap. 4, p. 159-190.
- SILVESTRINI JH. 2003. Simulação Numérica Direta e de Grandes Escalas de Escoamentos Transicionais e Turbulentos. In: Coleção Cadernos de Turbulência. Associação Brasileira de Ciências Mecânicas-ABCM. Rio de Janeiro. Vol. 2, Cap. 1, p. 1-81.
- STULL RB. 1988. An Introduction to Boundary Layer Meteorology. Kluwer Academic Publishers. Reprinted with errata-1997. 667 p.
- TENNEKES H& LUMLEY JL. 1972. A First Course in Turbulence. The MIT Press, 300 p.
- TRITTON DJ. 1977. Physical Fluid Dynamics. Printed in Great Britain at the University Press, Cambridge, 346 p.
- UMLAUF L & BURCHARD H. 2003. A generic length-scale equation for geophysical turbulence models. Journal of Marine Research, 61: 235- 265.
- UMLAUF L, BURCHARD H& HUTTER K. 2003. Extending the k-w turbulence model towards oceanic applications. Ocean Modelling, 5:195-218.
- VERSTEEG HK & MALALASEKERA W. 1995. An Introduction to Computational Fluid Dynamics-The Finite Volume Method. Co-published in the United States with John Wiley & Sons Inc., 257 p.
- YU L & RIGHETTO AM. 1999. Modelos de Turbulência e Aplicações a Corpos de Água Naturais. In: SILVA RCV (Ed.). Métodos Numéricos em Recursos Hídricos. Coleção da ABRH-Associação Brasileira de Recursos Hídricos, Vol. 4, Cap. 1, p. 1-122.
- ZHURBAS V 2001. Introduction to Turbulence. Lectures on Oceanography. P.P. Shirshov Institute of Oceanology of the Russian Academy of Sciences. Disponível em: <http://www.msi.ttu.ee/~elken/PhysOceanLimList.htm>. Acesso em: 14 jan. 2010.
Datas de Publicação
-
Publicação nesta coleção
12 Ago 2011 -
Data do Fascículo
Mar 2011
Histórico
-
Recebido
25 Mar 2010 -
Aceito
25 Fev 2011