Abstracts
In real epidemic processes, the basic reproduction number R0 is the combined outcome of multiple probabilistic events. Nevertheless, it is frequently modeled as a deterministic function of epidemiological variables. This paper discusses the importance of adequate treatment of uncertainties in such models. This is done by comparing two methods of uncertainty analysis: Monte Carlo uncertainty analysis (MCUA) and the Bayesian melding (BM) method. These methods are applied to a model for the determination of R0 of dengue fever based on entomological parameters. The BM was shown to provide a complete treatment of the uncertainties associated with model parameters. In contrast to MCUA, the incorporation of uncertainties led to realistic posterior distributions for parameter and variables. The incorporation, by the BM, of all the available information, from observational data to expert opinions, allows for the constructive use of uncertainties generating informative posterior distributions for all of the model's components that are coherent as a set.
Bayes Theorem; Dengue; Epidemiologic Models; Uncertainty
Em processos epidêmicos reais, o número básico de reprodução R0, é o resultado conjunto de múltiplos eventos probabilísticos. Entretanto, é modelado freqüentemente como função determinística de variáveis epidemiológicas. O artigo discute a importância do tratamento adequado das incertezas nesse tipo de modelo, por meio da comparação de dois métodos de análise de incerteza: análise de incerteza Monte Carlo (MCUA) e o método de Bayesian melding (BM). Os dois métodos são aplicados a um modelo para determinar o R0 do dengue com base em parâmetros entomológicos. O BM produziu um tratamento completo das incertezas associadas com parâmetros do modelo. Ao contrário da MCUA, a incorporação de incertezas levou a distribuições posteriores realistas para os parâmetros e variáveis. A incorporação pelo BM de toda a informação disponível, desde dados observacionais até opiniões de especialistas, permite o uso construtivo de incertezas, gerando distribuições posteriores informativas para todos os componentes do modelo que são coerentes enquanto conjunto.
Teorema de Bayes; Dengue; Modelos Epidemiológicos; Incerteza
ARTIGO ARTICLE
Complete treatment of uncertainties in a model for dengue R0 estimation
Tratamento completo de incertezas num modelo para estimativa do R0 do dengue
Flávio Codeço Coelho; Cláudia Torres Codeço; Claudio José Struchiner
Programa de Computação Científica, Fundação Oswaldo Cruz, Rio de Janeiro, Brasil
Correspondence Correspondence: F. C. Coelho Programa de Computação Científica Fundação Oswaldo Cruz Av. Brasil 4365, Rio de Janeiro, RJ 21040-900, Brasil fccoelho@fiocruz.br
ABSTRACT
In real epidemic processes, the basic reproduction number R0 is the combined outcome of multiple probabilistic events. Nevertheless, it is frequently modeled as a deterministic function of epidemiological variables. This paper discusses the importance of adequate treatment of uncertainties in such models. This is done by comparing two methods of uncertainty analysis: Monte Carlo uncertainty analysis (MCUA) and the Bayesian melding (BM) method. These methods are applied to a model for the determination of R0 of dengue fever based on entomological parameters. The BM was shown to provide a complete treatment of the uncertainties associated with model parameters. In contrast to MCUA, the incorporation of uncertainties led to realistic posterior distributions for parameter and variables. The incorporation, by the BM, of all the available information, from observational data to expert opinions, allows for the constructive use of uncertainties generating informative posterior distributions for all of the model's components that are coherent as a set.
Bayes Theorem; Dengue; Epidemiologic Models; Uncertainty
RESUMO
Em processos epidêmicos reais, o número básico de reprodução R0, é o resultado conjunto de múltiplos eventos probabilísticos. Entretanto, é modelado freqüentemente como função determinística de variáveis epidemiológicas. O artigo discute a importância do tratamento adequado das incertezas nesse tipo de modelo, por meio da comparação de dois métodos de análise de incerteza: análise de incerteza Monte Carlo (MCUA) e o método de Bayesian melding (BM). Os dois métodos são aplicados a um modelo para determinar o R0 do dengue com base em parâmetros entomológicos. O BM produziu um tratamento completo das incertezas associadas com parâmetros do modelo. Ao contrário da MCUA, a incorporação de incertezas levou a distribuições posteriores realistas para os parâmetros e variáveis. A incorporação pelo BM de toda a informação disponível, desde dados observacionais até opiniões de especialistas, permite o uso construtivo de incertezas, gerando distribuições posteriores informativas para todos os componentes do modelo que são coerentes enquanto conjunto.
Teorema de Bayes; Dengue; Modelos Epidemiológicos; Incerteza
Introduction
Dengue fever is a vector-borne disease currently demonstrating patterns of increasing spread and virulence. In the early 20th century, with the invention of DDT, the eradication of dengue and yellow fever via eradication of their vector became a goal that worked for some time in various regions of the world. Reinvasion of these areas and increasing resistance to insecticides have prompted the development of new strategies, including human behavioral changes, local chemical applications, biological control, etc. As strategies become more complex, the evaluation of cost-effectiveness and scenario analysis become important 1.
One approach for the comparison of control strategies is the development of mathematical models that explicitly describe the mechanisms involved in the transmission of the pathogen between host and vectors. Such models can be used to predict the expected number of cases under different control scenarios. An important summary measure in this context is the disease's reproduction number, R0. For vector-borne diseases, R0 is defined as the expected number of secondary human infections generated by one typical infected human introduced in a totally susceptible population through the vector population 2. The greater the R0, the faster the disease spreads in the population. The ultimate goal of any control effort is to reduce R0 below 1, a threshold below which disease tends towards extinction.
There are various approaches for estimating R0. First, one can estimate R0 from epidemic data as the growth rate of the epidemic curve increases (number of infected individuals x t), since faster epidemics imply a higher R0. Using this approach, Massad et al. 3 estimated the dengue R0 for 64 counties (municipalities) in the State of São Paulo, Brazil, with values ranging from 2.74 to 11.57. Uncertainty regarding these values is presented as confidence intervals, obtained by standard regression procedures.
A second approach is to estimate R0 from a mathematical model that expresses the number as a function of biological parameters. This model is built to represent the biological mechanism believed to be at work in real epidemics of the disease. In this case, the estimation procedure involves the definition of a range of "biologically reasonable" values for the parameters, and using the mathematical expression to calculate a range of "plausible values for R0". This procedure is termed uncertainty analysis 4 based on the idea of attributing probability distributions to the input parameters and generating a probability distribution for from repeated runs of the model driven by a Monte Carlo procedure 1,4,5. Here, we will call this approach Monte Carlo uncertainty analysis (MCUA). A Bayesian version of this approach includes likelihood functions for the input variables 6. More recently, a new methodology called Bayesian melding (BM) was proposed by Poole & Raftery 7 to extend both the MCUA and its Bayesian version by taking full account of all information available and uncertainty about both inputs and the output (R0) of the model.
The goal of this paper is to discuss the importance of incorporating uncertainties into the analysis of mechanistic models. To help illustrate this point we compare two uncertainty analysis methods applied to a model for a dengue epidemic's R0 and discuss how their different performance is related to their completeness and the underlying conception of the origin of uncertainties. This has implications for scenario analyses in dengue control, because it affects how we interpret the results epidemiologically.
The paper is organized as follows: (1) the estimation procedures are introduced in terms of their main assumptions; (2) application of these methods to estimation of dengue using the R0 expression for dengue fever 3:
where Mp is the relative density of (female) mosquitoes per person, a is the average daily bite rate , is the average duration of the infectious period in humans, µ is the mortality rate for female mosquitoes, t is the average duration of the extrinsic incubation period (in days), b is the transmission coefficient from mosquitoes to humans, and c is the transmission coefficient from humans to mosquitoes; (3) discussion of each method of uncertainty analysis and its influence on the results of simulation studies.
, is the average duration of the infectious period in humans, µ is the mortality rate for female mosquitoes, t is the average duration of the extrinsic incubation period (in days), b is the transmission coefficient from mosquitoes to humans, and c is the transmission coefficient from humans to mosquitoes; (3) discussion of each method of uncertainty analysis and its influence on the results of simulation studies.
Methodology
Estimation approaches and their definition of uncertainty
Uncertainty about parameter estimates in any modeling exercise can be interpreted in more than one way. The interpretation of uncertainty that is adopted will have an effect on both the methodology and results of an uncertainty analysis. Here, we will present two common interpretations of uncertainty. In the first view, uncertainties represent our ignorance about the parameters (which are fixed unknown values) that compose the model. Therefore their possible sources would be: (1) lack of (quality) data from which to estimate a given parameter, (2) measurement error in data collection procedures, and (3) sample variation. These are important sources of uncertainty that must be reckoned with. Meanwhile, according to a second view, we recognize that parameter uncertainty stems from the fact that many parameters are the output of a stochastic process that cannot be adequately represented by a single number. Therefore, uncertainty must be viewed as a combination of the intrinsic variability of the parameter and the external sources mentioned above. This means that even if we could eliminate all measurement error and have a random and representative sampling process, we would still have uncertainties about the parameters. Thus, parameter uncertainty is no longer a result of our estimation process but a feature of our estimate.
Monte Carlo uncertainty analysis
MCUA starts from the paradigm of the first view of uncertainty as presented above, in which the input parameters of the model (q) are constants whose true values are unknown. Thus, uncertainty is viewed as the result of our lack of knowledge of the true nature of the model parameters. In order to deal with the uncertainties about the most likely value of the parameters, intervals are defined for each parameter of interest corresponding to what we consider acceptable ranges of variation. For example, a review of the literature shows that Aedes aegypti daily feeding frequency varies from 0.5 to 1.2 (see Table 1). The analysis then consists of a Monte Carlo procedure. In this procedure, a random sample of size n is taken from within the intervals attributed to each of the parameters being analyzed. The model is then calculated n times (each time with a different set of parameters values), generating a "sample" of output values F(R0).
In this type of analysis, not all parameters need to have intervals attributed to them. Some may be kept constant throughout the analysis. Usually, only the parameters to which the model's output is more sensitive are included in the uncertainty analysis. This pre-selection of parameters, however, does not reduce the computational cost of the analysis, since this cost is associated mainly with the number of times the simulation has to be repeated. The reduction of the number of parameters included in the analysis may reduce the variability of the sample obtained for the output variables, but at the cost of ignoring possibly relevant uncertainty sources.
A full run of the model is done for each set of samples obtained. From the model's output on all runs, a joint probability density function (PDF) for the model's outputs(F) is approximated and their properties can be estimated by marginalizing this sample distribution for each parameter. The sample sizes for this procedure vary but are seldom less than 50,000, which is the number of times the model has to be run.
Bayesian uncertainty analysis
The Bayesian approach to uncertainty analysis starts with a different perspective on the nature of model parameters. The parameters are now treated as random variables of which we usually have little or no information. Therefore, PDFs are attributed to them from our prior knowledge (or lack thereof). The MCUA method also used prior distributions for the parameters, but they represented our lack of knowledge about the true values of the parameters. Now, the prior distribution represents our beliefs about the real probability distributions of the parameters. The choice of adequate priors is a complex topic in Bayesian inference. The best way to convert beliefs into probability distributions is a highly debated topic 8. In the absence of detailed prior information about a parameter, we resort to the "principle of insufficient reason" proposed and used by Laplace 9 and use a uniform prior distribution covering a certain range of values. Such a distribution is also known as a non-informative or vague prior distribution. Prior distributions [p(q)], as their name indicates, are defined before we look at the data (D). Any data available will be used to update our prior distributions, hopefully turning them into better approximations of the actual distributions of our parameters (posterior distributions).
In short, the goal of the Bayesian analysis is to update these prior distributions simultaneously, with the help of available data in order to yield a joint posterior distribution for the input parameters [p(F)] 6. The prior distributions are updated using the Bayes formula:
where L(F) = p(D|F) is the likelihood of the parameters 10.
The method described so far will serve as a basis for the BM method, which will expand upon these concepts.
Bayesian melding
One important way in which the BM procedure differs from classical Bayesian inference is by calling for the definition of prior distributions for both the model's inputs and outputs. These priors are (as usual) based on available expert knowledge about their values. We denote the joint prior distribution of inputs by p(q).
The joint prior distribution for the model's output is denoted by p(F). Another feature of BM is that it recognizes that there is another (implicit) prior distribution for F that is induced by p(q) when applied to the model (M), which is then denoted by p[M(q)]. These two priors on the output need to be pooled together by means of logarithmic pooling in order to avoid the Borel paradox 7. The pooling is necessary since each prior frequently derives from different sources of information and may be incoherent. Thus, producing coherence between the two priors amounts to reaching consensus between the two sources of information. It must be noted, however, that pooling can only deal with minor forms of incoherence, which amounts to saying that if both priors do not substantially overlap, the model or data adequacy must be questioned 7. The pooling is weighted by a constant that is set according to the relative weight we wish to assign to each prior during the pooling. For example, a 0.5 gives equal weights to both priors. From this point on, standard Bayesian inference may follow.
If data are available on any of the inputs or outputs, they can be used to form likelihoods for q and F, which are denoted by Linp(q) and Lout(F). This way, any data available can be included in the inference process. However, the BM procedure can update p(q) even in the absence of data, since the presence of a pooled prior distribution for F will provide a constraint from which we can filter out unacceptable combinations of parameters. Thus, BM does not require the existence of likelihoods to be useful as a calibration tool, even though in this case it would not be doing Bayesian inference. Nevertheless, the procedure would narrow the range of the parameter distributions, which is expected of a calibration procedure.
The inference procedure works like standard Bayesian inference. The marginal posterior distribution of the inputs, p[q](q) is given by the Bayesian theorem:
The posterior distribution of q, p[q](F), cannot be obtained analytically and extracting a sample from it can be difficult or impossible. To circumvent this problem we obtain an approximate sample from p[q](q) using the sampling importance re-sampling (SIR) algorithm as proposed in Rubin 11.
Inference about F, or any function of it, can be made from its marginal posterior distribution, the distribution of F= M(q) when q~p[q](q).
The SIR algorithm
Implementation of the BM method centers on the SIR algorithm, which is used to determine the posterior distributions for all the model's components. A succinct description of the steps involved in the algorithm follows: (1) draw a k-sized sample from each of the parameter's prior distribution. This sampling will generate a set of k vectors (q1,..., qk) with each vector containing as many elements as there are1 input parameters in the model; (2) for each qi, we run the model obtaining the corresponding Fi = M(qi); the resulting distribution is p[M(qi)]; (3) obtain a kernel density estimate of F; (4) form the importance sampling weights:
And (5) re-sample l values with replacement from each of the parameter's priors with values qi and probabilities proportional to wi.
The result of step 5 is an approximate sample from the posterior distributions of the input parameters.
The a on step 4 is a weight factor for the pooling of the two output prior distributions; a was set to 0.5.
Discussion
To discuss the pros and cons of the uncertainty analysis methods presented, we simulated an epidemic scenario for dengue based on the model of equation. Although the model on which this discussion is based is quite simple, the choice was made for didactic reasons. The methodology applies equally to more complicated models being extensible without modification to stochastic models 7.
The model was analyzed by both the MCUA and BM analysis. For both analyses the priors used for the parameters were the same (Table 1).
Priors and likelihoods
The components of equation were assigned prior distributions (see Table 1) based on data from the literature 1,12,13,14. We assigned uniform priors to all input and output parameters. These types of priors can also be referred to as vague priors since they assign the same probability for every value within the range chosen for the parameter. The ranges chosen for the prior distributions were chosen so as to include the "real" parameter values (derived from the literature 1). The same priors were used for the MCUA and BM analysis. If less vague priors were to be used, such as a normal distribution, for instance, the performance of both methods would be enhanced. However, the information necessary to better define those distributions is frequently not available. Thus, it is important that the method be able to perform well even when all priors are wide and vague.
Even though it would be possible (in the BM) to construct likelihoods for every parameter for which there are data, we chose to include a likelihood only for R0. By using a minimal amount of data, we emphasize the method's power.
Calibration testing
In order to evaluate the ability of BM to use available data to calibrate (reduce the uncertainty) in the model components, a value for R0 was calculated from a set of arbitrarily chosen values for the model parameters (Table 2). The BM was run with vague priors (Table 1) for the model input parameters, which included the values from Table 2 in their support. A small set of R0 values was sampled from a normal distribution with mean equal to the value for R0 calculated from the values of Table 2 and standard deviation equal to 0.2 (chosen to be similar to the values reported by Massad et al. 3). This set of R0 values was used as data.
The prior distributions for q¸ were not centered on the parameter values (Table 2). We made this choice in order to demonstrate the method's ability to explore the whole surface of the joint prior distribution, i.e., its robustness to bias in the priors.
Monte Carlo uncertainty analysis
The MCUA method returns ranges for F only. Actually, it returns a sample from a supposed distribution of F (Figure 1). From this sample, confidence intervals for an expected value can be calculated.
The statistical analysis of the generated distribution of R0 tells us only that we should not underestimate the role of uncertainty about input parameters. The distribution is quite wide, indicating that the extra information represented by the prior distributions of the model's parameters lead to an arguably more realistic although not very precise estimate of R0. These undesirable aspects of the technique's output derive from the fact that no constraints are applied to which combinations of parameter values are acceptable, and that we purposefully in this case used very wide prior distributions for q, meaning that we do not know a great deal about them.
Bayesian melding
The simulations were run with simulated data as described above. The dataset (n = 12) was sampled from a normal distribution with a mean given by the calculation of R0 from the parameter values chosen (Table 2) and standard deviation equal to 0.2.
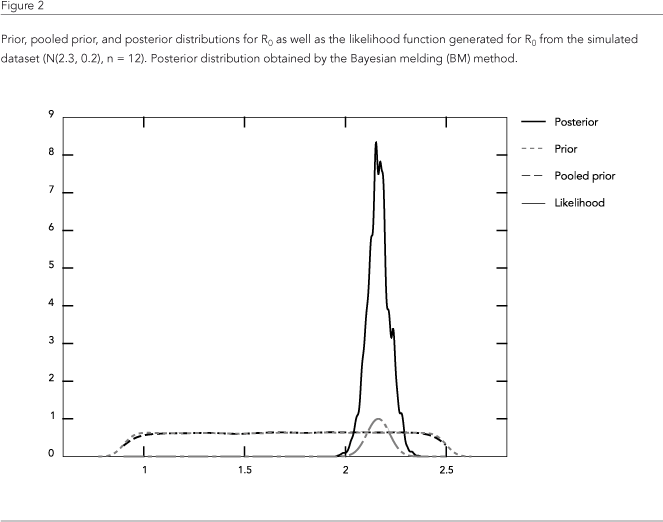
Table 2 shows the median and standard deviations of the posterior distributions of all the parameters. Figure 2 shows the priors (both specified and pooled) and posterior distributions of R0 as calculated by BM, as well as the likelihood function for R0.
It should be noted that even with a small dataset, the posterior distribution of R0 is strongly influenced by the likelihood function derived from the data. If we do not include data on the model's output, the BM yields a posterior distribution that is virtually identical to its prior (Figure 3). The lack of data does not affect the posteriors of the model's input parameters so drastically, as shown on Table 2.
Conclusion
The incorporation of intrinsic uncertainties associated with model parameters can lead to considerable difficulty in the model's interpretation, especially if little information is available to restrict the boundaries of the prior distributions attributed to parameters. The results from MCUA show that with vague priors for Ä the range for the model's output can become quite large. Moreover, MCUA does not provide us with any means to validate/update our priors based on available data.
The BM procedure on the other hand offers a more complete treatment of the problem, allowing us to incorporate all sources of uncertainty and available information. BM even goes beyond Bayesian uncertainty analysis by assigning not one but two prior distributions to the model's output: one from prior knowledge and another induced by the model (representing the information contained in the model structure). The pooling of these two priors allows us to weigh prior knowledge against expert opinion (model structure). BM also showed a remarkable ability to zero in on the "real" parameter values even when given biased uniform priors and little data. The availability of larger datasets (to construct the likelihoods) would cause the posterior distribution to more closely approximate the shape of the likelihood function instead of that of the prior distribution. It is important to notice however that BM may not converge on the "real" parameter values if there is a lack of identifiability in the model, that is, if there is more than one set of parameter values that can yield the same output. Another possible culprit for convergence failure is the SIR algorithm, which may not converge if the joint posterior surface is very complex. BM failed to converge on two parameters in our example model (Mp and t), although it came very close to the correct region of the parameter space (see Table 2). Another important requirement for the BM method to work is that the support for priors and likelihoods overlaps. The reason for this is very intuitive, since we cannot update beliefs if the data do not refer to them.
Even when BM is used without data, its results are better than those of MCUA, because the existence of a prior distribution in the model output allows us to filter out results that are outside the acceptable range for the phenomenon being modeled (Table 2).
We conclude that the BM method is the one that takes best advantage of the explanatory potential of mechanistic models, while maintaining model realism by taking into account the stochastic nature of all the model's elements. Moreover, the BM method updates our knowledge about both the inputs and the output of the model, serving simultaneously as a calibration and uncertainty analysis tool.
The BM method can be extended beyond what was presented here to test hypotheses about the model structure. Alternative models can be compared using Bayesian factors 7 which can be easily derived from the SIR algorithm.
Contributors
All the authors contributed equally to the conception, execution, and writing of this paper.
Acknowledgments
The authors wish to thank the Programa de Desenvolvimento Tecnológico em Saúde Pública Dengue, Fundação Oswaldo Cruz [PDTSP-Dengue; Program for Technological Development and Innovation/Dengue, Oswaldo Cruz Foundation], Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro [FAPERJ; Carlos Chagas Research Foundation, Rio de Janeiro State], and the Conselho Nacional de Desenvolvimento Científico e Tecnológico [CNPq; Brazilian National Research Council] for the financial support to conduct this work.
Submitted on 08/Mar/2006
Final version resubmitted on 24/Apr/2007
Approved on 24/Apr/2007
- 1. Luz PM, Codeço CT, Massad E, Struchiner CJ. Uncertainties regarding dengue modeling in Rio de Janeiro, Brazil. Mem Inst Oswaldo Cruz 2003; 98:871-8.
- 2. MacDonald G. The analysis of equilibrium in malaria. Trop Dis Bull 1952; 49:813-29.
- 3. Massad E, Burattini MN, Coutinho FA, Lopez LF. Dengue and the risk of urban yellow fever reintroduction in São Paulo State, Brazil. Rev Saúde Pública 2003; 37:477-84.
- 4. Sanchez MA, Blower SM. Uncertainty and sensitivity analysis of the basic reproductive rate. Tuberculosis as an example. Am J Epidemiol 1997; 145:1127-37.
- 5. Chowell G, Castillo-Chavez C, Fenimore PW, Kribs-Zaleta CM, Arriola L, Hyman JM. Model parameters and outbreak control for SARS. Emerg Infect Dis 2004; 10:1258-63.
- 6. Cancré N, Tall A, Rogier C, Faye J, Sarr O, Trape J-F, et al. Bayesian analysis of an epidemiologic model of Plasmodium falciparum malaria infection in Ndiop, Senegal. Am J Epidemiol 2000; 152:760-70.
- 7. Poole D, Raftery A. Inference for deterministic simulations models: the Bayesian melding approach. J Am Stat Assoc 2000; 95:1244-55.
- 8. Kass RE, Wasserman L. The selection of prior distributions by formal rules. J Am Stat Assoc 1996; 91:1343-70.
- 9. Laplace PS. Essai philosophique sur les probabilités. 5th Ed. Paris: Gauthier-Villars; 1825.
- 10. Gibson GJ, Kleczkowski A, Gilligan CA. Bayesian analysis of botanical epidemics using stochastic compartmental models. Proc Natl Acad Sci U S A 2004; 101:12120-4.
- 11. Rubin D. Using the SIR algorithm to simulate posterior distributions. Bayesian Statistics 1988; 3:395-402.
- 12. Massad E, Coutinho FA, Burattini MN, Lopez LF. The risk of yellow fever in a dengue-infested area. Trans R Soc Trop Med Hyg 2001; 95:370-4.
- 13. Dietz K. The estimation of the basic reproduction number for infectious diseases. Stat Methods Med Res 1993; 2:23-41.
- 14. Marques CA, Forattini OP, Massad E. The basic reproduction number for dengue fever in São Paulo State, Brazil: 1990-1991 epidemic. Trans R Soc Trop Med Hyg 1994; 88:58-9.
Publication Dates
-
Publication in this collection
27 Mar 2008 -
Date of issue
Apr 2008
History
-
Reviewed
24 Apr 2007 -
Received
08 Mar 2006 -
Accepted
24 Apr 2007