Abstract:
Diarrhea by rotavirus is one of the main causes of mortality in children in developing countries, although the hospitalization rates (HR) for acute diarrhea have been found to have fallen since the introduction of the rotavirus vaccine. However, the patterns of the rotavirus are still not well understood and seasonal peaks occur throughout the year, with variations between countries and over time. The main objective of this study was to analyze the temporal behavior of HR caused by acute diarrhea in children under the age of one in the south of Brazil, between 2000 and 2011, and to explore changes in seasonality patters after the introduction of the vaccine against the rotavirus in 2006. Harmonic and multiscale wavelet analyses were used to detect seasonality and the points of change in the temporal scale. The statistical significance of each seasonality that was identified was tested using Fisher's test. The harmonic and wavelet analyses show annual seasonal and six-monthly patterns for HR, as well as a clear change after the introduction of the vaccine in 2006.
Keywords:
Rotavirus; Dysentery; Time Series Studies
Resumo:
A diarreia por rotavírus é uma das principais causas de mortalidade em crianças nos países em desenvolvimento, embora tenha sido observada a redução nas taxas de hospitalização (HR) por diarreias aguda desde que a vacina do rotavírus foi introduzida. A dinâmica do rotavírus, no entanto, ainda é mal compreendida e picos sazonais ocorrem durante todo o ano, com variações entre países e ao longo do tempo. O principal objetivo foi analisar o comportamento temporal das HR devido a diarreia aguda em crianças menores de um ano de idade no sul do Brasil, de 2000 a 2011, e investigar mudanças no padrão de sazonalidade após a introdução da vacina contra o rotavírus em 2006. Análises harmônica e multiescala wavelet foram utilizadas para detectar a sazonalidade e pontos de mudança na série temporal. A significância estatística de cada sazonalidade identificada foi testada pelo teste de Fisher. As análises harmônica e wavelet mostraram padrões sazonais anual e semestral das HR, bem como a nítida mudança após a introdução da vacina em 2006.
Palavras-chave:
Rotavirus; Disenteria; Estudos de Séries Temporais
Resumen:
La diarrea por rotavirus es una de las principales causas de mortalidad en niños en los países en desarrollo, aunque se haya observado una reducción en las tasas de hospitalización (HR) por diarreas agudas, desde que se introdujo la vacuna del rotavirus. La dinámica del rotavirus, no obstante, aunque está mal comprendida -y se producen picos estacionales- tiene lugar durante todo el año, con variaciones entre países y a lo largo del tiempo. El principal objetivo fue analizar el comportamiento temporal de las HR, debido a la diarrea aguda en niños menores de un año de edad en el sur de Brasil, de 2000 a 2011, e investigar cambios en el patrón de estacionalidad tras la introducción de la vacuna contra el rotavirus en 2006. Los análisis harmónico y multiescala wavelet se utilizaron para detectar la estacionalidad y puntos de cambio en la serie temporal. La significancia estadística de cada estacionalidad identificada fue testada por el test de Fisher. Los análisis harmónico y wavelet mostraron patrones estacionales anual y semestral de los HR, así como un nítido cambio tras la introducción de la vacuna en 2006.
Palabras-clave:
Rotavirus; Disentería; Estudios de Series Temporales
Introduction
In Brazil, in 2002, acute diarrhea caused 120,000 hospitalizations in the Brazilian Unified National Health System (SUS) and the death of 2,745 children under the age of five, 80% of whom were under one 11. Secretaria de Atenção à Saúde/Secretaria de Vigilância em Saúde, Ministério da Saúde. Manual de vigilância do óbito infantil e fetal e do Comitê de Prevenção do Óbito Infantil e Fetal. Brasília: Ministério da Saúde; 2009. (Série A. Normas e Manuais Técnicos).. Since 2006, when the oral vaccine of the human rotavirus was included in the National Program of Immunization (PNI), a reduction in hospitalization rates (HR) for acute diarrhea has been observed in several studies. Some results for Brazil were obtained using descriptive analyses and regression methods 22. Lanzieri TM, Costa I, Shafi FA, Cunha MH, Ortega-Barria E, Linhares AC. Trends in hospitalizations from all-cause gastroenteritis in children younger than 5 years of age in Brazil before and after human rotavirus vaccine introduction, 1998-2007. Pediatr Infect Dis J 2010; 673-5.), (33. Carmo GMI, Yeen C, Cortes J, Siqueira AA, Oliveira WK, Cortes-Escalante JJ, et al. Decline in diarrhea mortality and admissions after routine childhood rotavirus immunization in Brasil: a time-series analysis. PLoS Med 2011; 8:e1001024.) where only behaviors related to changes over the years were taken into account and up to 2009. On the other hand, the effect of the rotavirus vaccine on HRs due to acute diarrhea was investigated using specific models for time series with an analysis of the intervention using the Box-Jenkins methodology 44. Matsukawa MLT, Moriwaki AM, Uchimura NS, Souza EM, Uchimura TT. Intervention analysis of introduction of rotavirus vaccine on hospital admission rates due to acute diarrhea. Cad Saúde Pública 2014; 30:2101-11.. The average percentage reduction in comparison to the mean level in the pre-vaccine period was about 50% for younger and 1-year-old children in Southern Brazil at the end of 2011. For some localities, a more than 90% drop was found. Reductions have also been observed worldwide 55. Blasio BF, Kasymbekova K, Flem E. Dynamic model of rotavirus transmission and the impact of rotavirus vaccination in Kyrgyzstan. Vaccine 2010; 28:7923-32.), (66. Curns AT, Steiner CA, Barret M, Hunter K, Wilson E, Parashar UD. Reduction in acute gastroenteritis hospitalizations among US children after introduction of rotavirus vaccine: analysis of hospital. Discharge Datafrom 18 US States. J Infect Dis 2010; 201:1617-24.), (77. Desai R, Curns AT , Steiner CA , Tate JE, Patel MM, Parashar UD. All-cause gastroenteritis and rotavirus-coded hospitalizations among US children, 2000-2009. Clin Infect Dis 2012; 55:e28-34.. That drastic decrease in disease incidence thus reduces the workload of professionals who provide health-care services related to gastroenteritis.
However, in less-developed regions and in developing countries, diarrhea due to rotavirus is still a major cause of young-child mortality 88. World Health Organization. Diarrhea: why children are still dying and what can be done. New York: United Nations Children's Fund; 2009. and the rotavirus dynamics are sometimes not fully understood.
According to some authors, there are several reasons why the dynamics of rotavirus infection may differ in developing countries compared with developed countries 99. Cook SM, Glass RI, Le Baron CH, Ho MS. Global seasonality of rotavirus infections. Bull World Health Organ 1990; 68:171-7.), (1010. Shim E, Galvani AP. Impact of transmission dynamics on the cost-effectiveness of rotavirus vaccination. Vaccine 2009; 27:4025-30.), (1111. Pitzer VE, Viboud C, Lopman BA, Patel MM , Parashar UD , Grenfell BT. Influence of birth rates and transmission rates on the global seasonality of rotavirus incidence. J R Soc Interface 2011; 8:1584-93.. One relevant fact is that many developing countries are located in the tropics where traditionally rotavirus activity has been thought to lack seasonality. However, recent country-level evaluations of rotavirus epidemiology have suggested that this pattern may not be as global as previously thought, because rotavirus tends to be more common in colder and drier months 1111. Pitzer VE, Viboud C, Lopman BA, Patel MM , Parashar UD , Grenfell BT. Influence of birth rates and transmission rates on the global seasonality of rotavirus incidence. J R Soc Interface 2011; 8:1584-93.), (1212. Kane EM, Turcios RM, Arvay ML, Garcia S, Bresee JS, Glass RI. The epidemiology of rotavirus diarrhea in Latin America. Anticipating rotavirus vaccines. Rev Panam Salud Pública 2004; 16:371-7.. This result was also found in the meta-analysis of the seasonal epidemiology of rotavirus in the tropics 1313. Levy K, Hubbard AE, Eisenberg JN. Seasonality of rotavirus disease in the tropics: a systematic review and meta-analysis. Int J Epidemiol 2009; 38:1487-96., where 26 studies reporting continuous monthly rotavirus incidence were evaluated.
Although seasonality started to be recognized even in the tropics, seasonal peaks are found to occur year-round in different countries 1111. Pitzer VE, Viboud C, Lopman BA, Patel MM , Parashar UD , Grenfell BT. Influence of birth rates and transmission rates on the global seasonality of rotavirus incidence. J R Soc Interface 2011; 8:1584-93.), (1212. Kane EM, Turcios RM, Arvay ML, Garcia S, Bresee JS, Glass RI. The epidemiology of rotavirus diarrhea in Latin America. Anticipating rotavirus vaccines. Rev Panam Salud Pública 2004; 16:371-7.), (1313. Levy K, Hubbard AE, Eisenberg JN. Seasonality of rotavirus disease in the tropics: a systematic review and meta-analysis. Int J Epidemiol 2009; 38:1487-96.), (1414. Bresee J, Fang ZY, Wang B, Nelson EA, Tam J, Soenarto Y, et al. First report from the Asian Rotavirus Surveillance Network. Emerg Infect Dis 2004; 10:988-95. and to vary over time in the same country 1515. Cilla G, Pérez-Trallero E, López-Lopategui M, Gilsetas A, Gomáriz M. Incidence, seasonality and serotypes of rotavirus in Gipuzkoa (Basque Country), Spain. A 14-year study. Epidemiol Infect 2000; 125:677-83..
Due to the inter- and intra-country variability of the rotavirus infection dynamics, detailed investigations in specific regions are needed, particularly in the tropics. Hence, we aim to analyze the temporal behavior of the HR due to acute diarrhea in children younger than one year old in Southern Brazil, from 2000 to 2011. The main interest is to detect changes in seasonality of time series after the introduction of the rotavirus vaccine in 2006. In doing so, harmonic and multiscale wavelet analyses were investigated, which allow for seasonalities, changing points and other hidden information to be detected.
Methodology
A descriptive-analytical observational study of monthly hospitalization rates (HR) due to acute diarrhea in children younger than one year old was performed between 2000 and 2011 in Paraná State, located in Southern Brazil, with an area of nearly 200 million km2. The state has a humid subtropical climate in the Northwest, and coastal plains and a subtropical climate in the South. The choice of the age group was due to the fact that most of the diarrhea hospitalizations occur in children younger than one year old. The State is administratively divided into 399 municipalities that are grouped into 22 regional health divisions, which are represented in the six macro-regions (State Health Department of Paraná. http://www.saude.pr.gov.br/modules/conteudo/conteudo.php?conteudo=2752): East, Campos Gerais, South Center, West, Northwest and North.
The study population was composed of all children younger than one year old living in the six macro-regions of Paraná State who were hospitalized under the SUS due to acute diarrheal diseases between January 2000 and December 2011. Since 2006, children have been receiving the rotavirus vaccine.
The data were taken from the SUS's Hospital Information System (SIH/SUS) using the 10th revision of the International Classification of Diseases (CID-10), with the codes A00 and A09. Although all occurrences of acute diarrhea have been grouped, the time series reflects the rotavirus presence in each region.
The calculation of the HR due to acute diarrhea was performed by dividing the number of hospitalizations due to acute diarrhea by the live births, multiplying the coefficient by 10,000.
Due to the serial dependency/correlation of the data over time, an adequate time series analysis is required. On the other hand, when the stationarity cannot be induced, the majority of the classical time series methods are not sufficient or cannot be applied. Indeed, many effects cannot be identified directly in the data by a time point of view. In this sense, harmonic analysis makes it possible to identify the frequency of occurrence of periodic effects when the time series is stationary, but we cannot know when the identified periodic behaviors occurred. As an extension of this harmonic analysis, the wavelet multiscale analysis can be applied to non-stationary data, identifying periodic effects and also when each one occurred over time.
While the harmonic analysis decomposes the time series in periodic components (sines and cosines), the wavelet analysis performs the decomposition from wavelet functions 1616. Chatfield C. The analysis of times series: an introduction. London: Chapman and Hall; 2003.), (1717. Cryer JD, Chan KS. Time series analysis: with applications in R. New York: Springer-Verlag; 2008. (Serie Springer Texts in Statistics).), (1818. Nason GP. Wavelet methods in statistics with R. New York: Springer-Verlag; 2008.. Contrarily to sines and cosines, the wavelets are function (waves) of duration in a short time interval 1818. Nason GP. Wavelet methods in statistics with R. New York: Springer-Verlag; 2008.. This is what makes them localized in time and able to identify when an event or change has occurred.
The effect of the harmonic analysis corresponds to a partition of the time series variability in different frequencies, allowing us to verify the percentage of the total variability that is explained by each frequency component. Supposing the series has deterministic seasonalities, the first component, which is also called the harmonic component, corresponds to the annual periodicity (12 months). The second represents the semi-annual periodicity (6 months) and so on. A model with explanatory variables represented by these harmonics is known as a harmonic model. Furthermore, it is possible to plot a graph, called the Fourier periodogram, which allows for the identification of the important frequencies in the time series. Although it is called a periodogram, the horizontal axis shows the frequencies, and the seasonal periods are obtained by the inverse of these frequencies 1616. Chatfield C. The analysis of times series: an introduction. London: Chapman and Hall; 2003.. However, not all identified frequencies in the periodogram are significant: it is necessary to apply the Fisher's test 1919. Fisher R. Tests of significance in harmonic analysis. Proceedings of the Royal Society A, Matehematical, Physical and Engineering Sciences 1929; 125:54-9. to verify if the periodicities are statistically significant. In the same sense, a wavelet periodogram can be constructed, which allows for the decomposition of the time series variance in different scales, i.e. in frequency bands representing different power-of-two periodicities 1818. Nason GP. Wavelet methods in statistics with R. New York: Springer-Verlag; 2008.. Specifically, a modified version of the wavelet analysis was applied, built from the non-decimated wavelet transform, which is time invariant and more adequate to investigate time series 1818. Nason GP. Wavelet methods in statistics with R. New York: Springer-Verlag; 2008.. Thus, both harmonic and wavelet multiscale analyses are important methodologies to detect periodic effects, seasonality, changing points and other important hidden information. All the analyses were implemented in R software (The R Foundation for Statistical Computing, Vienna, Austria; http://www.r-project.org), using packages such as TSA and wavethresh.
The development of the study occurred as recommended by Resolution 196/1996 of the National Health Council but it is also in agreement with Resolution 466/2012. The project was approved by the Ethics Research Committee at the State University of Maringá (Legal Report 140/2009) and the Term of Free and Informed Consent was not used because the data were secondary.
Results
The time series of the hospitalization rates by acute diarrhea were considered in three sets: the whole time series (2000-2011), before (2000-2005) and after (2007-2011) rotavirus vaccine introduction, which occurred during the year 2006. The stationarity of the time series was checked using the Phillips-Perron test and it could only be verified separately for the periods before (2000-2005) and after (2007-2011) rotavirus vaccine introduction. As in each set the HR time series did not present any trend (solid gray line in Figure 1), the HR mean level in 10,000 children younger the one year old was 18.7 before and 9.8 after the introduction of the vaccine in Paraná State.
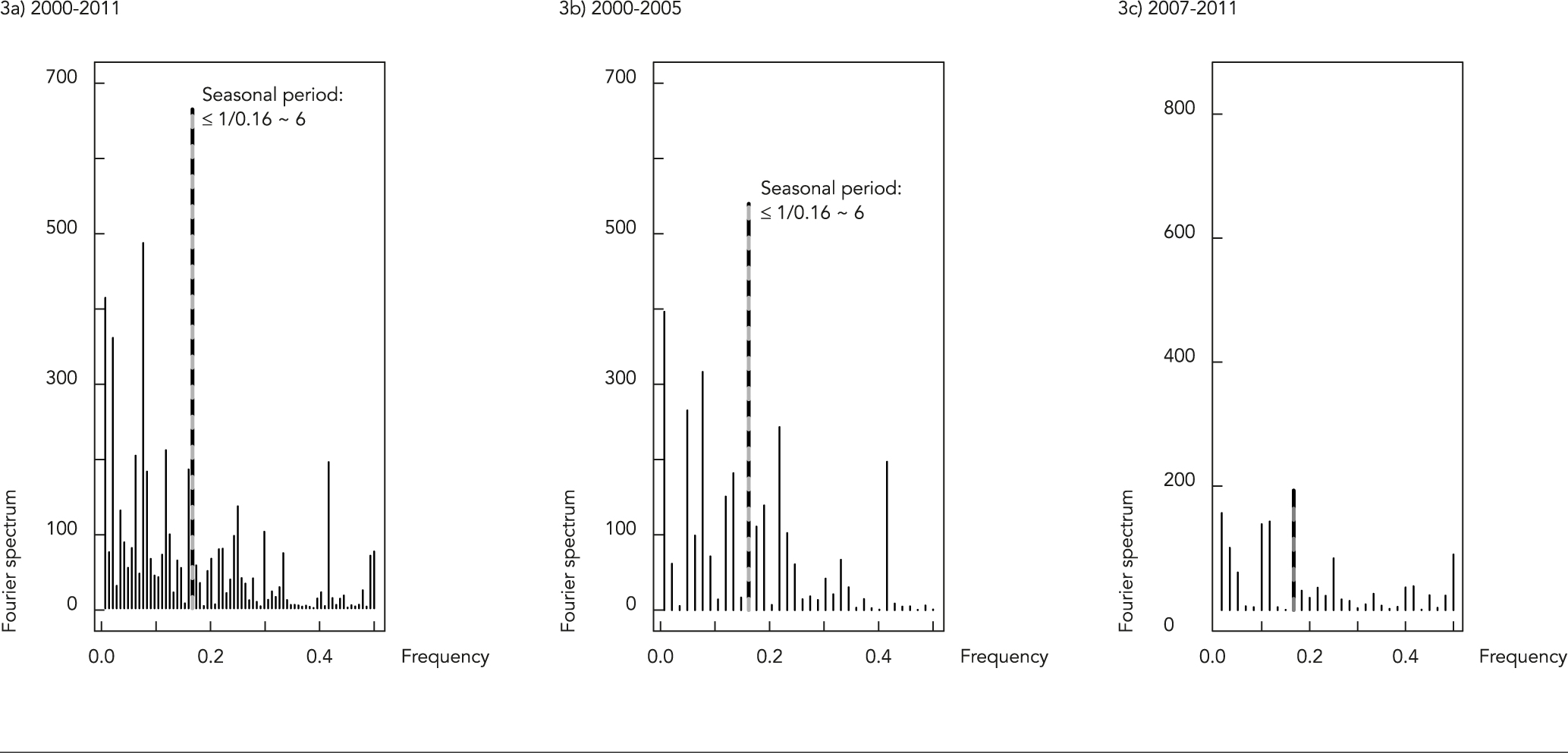
Before the harmonic modeling, the Fourier periodograms were analyzed in the three sets: the whole time series (2000-2011), before (2000-2005) and after (2007-2011) rotavirus vaccine. Although the whole time series is not stationary, we are also applying the Fourier periodogram to this set to reinforce the need for taking care of this assumption by comparing these results with the correct ones from the separated stationary periods (before and after). In Figure 2, the Fourier periodograms are presented for the East region first, because the seasonal behavior identified for this region was different from all the others.
In Figure 2a, the spikes occurred in frequencies of 0.078125 and 0.0859373. As the period is the inverse of the frequency, the periodicities indicated by these frequencies are 1/0.078125 = 12.8 and 1/0.0859373 = 11.64 months, representing the annual seasonality.
The importance of evaluating the periodograms before and after the vaccine introduction separately could be verified. In Figure 2a the presence of the annual seasonality is attributed from 2000 to 2011, while the annual seasonality is evident just before the vaccine introduction as shown in Figures 2b and 2c. That reinforces the fact that the Fourier periodogram must be applied only to stationary time series and indicates only the seasonality presence but not where it occurs.
For the macro-regions East, Campos Gerais, South Center, West, Northwest and North, the Fourier periodograms showed a semi-annual seasonality (6.09 months), because the frequency indicated was 0.1640625. As the Fourier periodograms are quite similar to these five macro-regions, one was arbitrarily chosen to illustrate the results and the other graphics were omitted. In Figure 3, the Fourier periodograms for the whole time series (2000-2011), before (2000-2005) and after (2007-2011) rotavirus vaccine are presented for the Campos Gerais region.
Fourier periodograms of hospitalization rates for acute diarrhea for East region, Paraná State, Brazil.
As occurred in the East macro-region, the seasonal behavior for the other macro-regions was also less evident or almost disappeared after the introduction of the vaccine in 2006 (Figure 3c).
Fourier periodograms of hospitalization rates for acute diarrhea for Campos Gerais region, Paraná State, Brazil.
Once the Fourier periodogram confirmed the presence of annual or semi-annual seasonality for all macro-regional health centers, a model with these first 2 harmonics was estimated for each time series (before and after vaccine introduction). In Figure 1, the adjusted harmonic models are plotted in black for each macro-region time series (gray).
From the harmonic analysis, the difference between the seasonal behavior before and after the vaccine introduction, as well as among the macro-regions could be evidenced. Before the vaccine introduction in 2006, the East region (Figure 1) had a different seasonal behavior in relationship to the others of the state, showing an annual seasonality, with spikes in the months of June. For the other health regions, the seasonal spikes that occurred in August before 2006 were drastically reduced after the vaccine introduction. This month represents the end of the winter and a dry month.
After 2006, the seasonality was much less evident, as shown in the Fourier periodograms (Figures 2 and 3). Thus, as the harmonic models are adjusting mainly deterministic seasonalities, it is expected that the estimated models do not fit the time series well after 2006.
Furthermore, in Figure 1, we can see that the second spike that occurred in February before 2006 (dashed vertical line) remained after the vaccine introduction. For the West, Northwest and North regions, the largest incidences of acute diarrhea continued to occur in February. This highlights the efficacy of the rotavirus vaccine because the seasonal spikes are not occurring in cold months anymore, but in a hot month, probably due to other diarrheic diseases. That semi-annual seasonality was less evident for the East region, which has well defined changes in climate during the year.
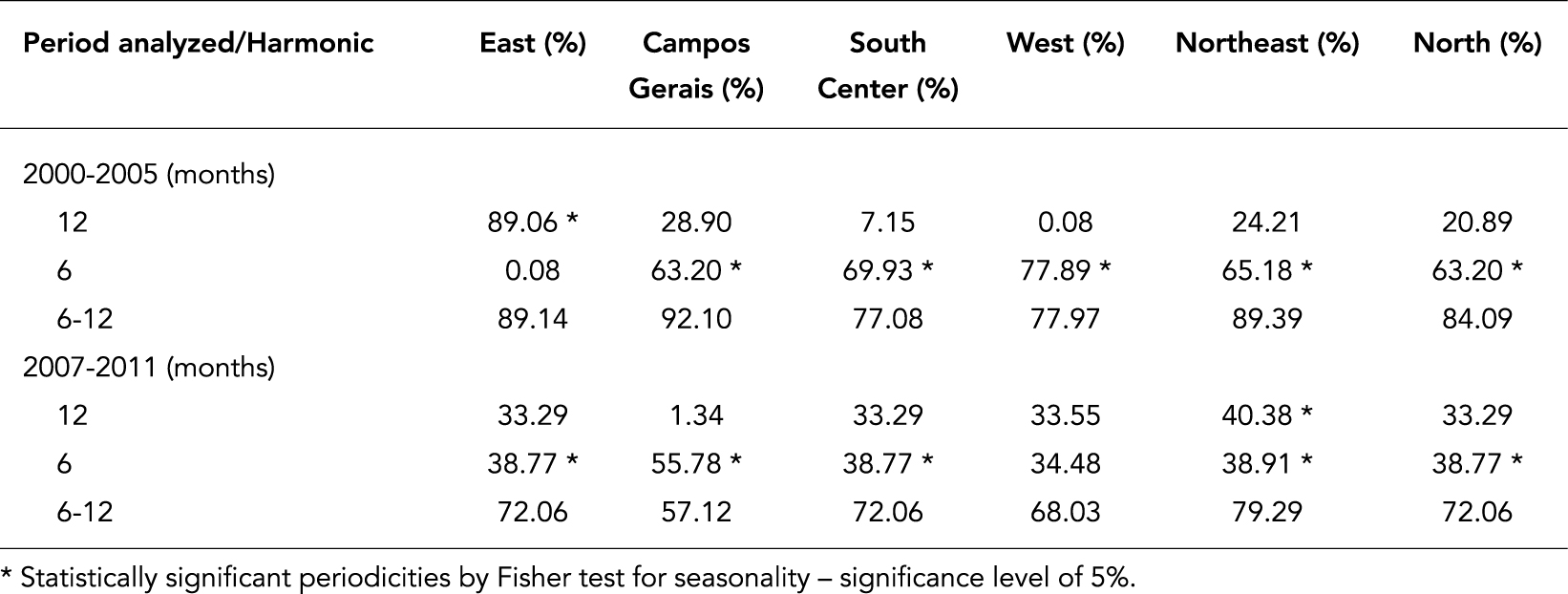
Besides the visual interpretation of the harmonic models presented in Figure 1, it is important to evaluate how much each seasonal component contributes to the total time series variability. Hence, the percentages of explained variance by the first two harmonics (annual and semi-annual) are presented in Table 1.
Explained variability of time series considering the harmonic analysis for the 6 health centers of Paraná State, Brazil.
In Table 1, we note for the East macro-region that the first harmonic, relative to the annual periodicity was responsible for about 89% of the whole variability of the time series before the vaccine introduction. For the other regions, the more pronounced harmonic was the second, which corresponds to the semi-annual seasonality. For the Campos Gerais and South Center macro-regions, this harmonic accounted about 63% and 69% of the time series variability, respectively. The percentages of explained variability for the West, Northweast and North regions were similar: 77.08%, 65.18% and 63.20%, respectively. Together, the first two harmonics accounted for up to 92.10% of the time series, representing a relevant result. Furthermore, we confirmed that the seasonal components that most contributed to the modeling are in agreement with the seasonalities identified in the Fourier periodogram, which were found to be statistically significant using the Fisher's test. After vaccine introduction, we can see that all semi- and annual harmonics, with the exception of Campos Gerais, represented about 40% of the explained variability. Together, these harmonics accounted for less than for the period before the vaccine, reaching 79.29% for the Northeast region. Inferior representativeness of the two first harmonics and explained variance after the vaccine introduction are in agreement with the aforementioned results (Figures 2 and 3).
For a more detailed analysis that can be applied to the whole time series to show the changes along the time and frequency simultaneously, the wavelet analysis was performed. The wavelet periodogram was estimated for different resolution levels. In Figure 4 the wavelet periodogram and the global spectrum is presented. The global spectrum represents the whole variance in each resolution level.
Wavelet periodogram and global spectrum of the hospitalization rate for acute diarrhea for East region, Paraná State, Brazil.
As the decomposition is performed in a power-of-two scale, resolution level 6 represents the effects from 64 (26) to 128 (27) months (5 years and 4 months - 10 years and 8 months) while level 5 represents the effects from 32 (25) to 64 (26) months (2 years and 8 months - 5 years and 4 months). Although, in the global spectrum, the resolution levels 5 and 6 are more evident (Figure 4), such levels represent the smooth and long-term variations, which for the application in question, are not of interest. On the other hand, we can observe in Figure 4 that a spike occurs in resolution level 3 of the global wavelet spectrum. That resolution level represents the effects from 8 (23) to 12 (24) months, i.e., includes the periodicity of 12 months, indicating the annual seasonality. We also can verify a change in the seasonality in resolution level 3 of the wavelet periodogram after the vaccine introduction in 2006 (month 84 in Figure 4). Actually, this resolution level almost disappears after the vaccine introduction, indicating the drastic reduction of the seasonal pattern. Hence, from a temporal-localized investigation, it is possible to detect or confirm change points in the time series.
Similar graphics and the same behaviors presented in Figure 4 were obtained for the other macro-regions. Thus, those graphics were omitted.
Discussion and final considerations
We found in this study the presence of an annual seasonality with spikes in the months of June or August depending on the region, but, both confirmed the results found in the literature with the largest rotavirus disease incidence in the cold and dry months 1111. Pitzer VE, Viboud C, Lopman BA, Patel MM , Parashar UD , Grenfell BT. Influence of birth rates and transmission rates on the global seasonality of rotavirus incidence. J R Soc Interface 2011; 8:1584-93.), (1212. Kane EM, Turcios RM, Arvay ML, Garcia S, Bresee JS, Glass RI. The epidemiology of rotavirus diarrhea in Latin America. Anticipating rotavirus vaccines. Rev Panam Salud Pública 2004; 16:371-7.), (1313. Levy K, Hubbard AE, Eisenberg JN. Seasonality of rotavirus disease in the tropics: a systematic review and meta-analysis. Int J Epidemiol 2009; 38:1487-96.), (2020. Pazdiora P, Beneš Č. Rotavirus gastroenteritis in the Czech Republic before the start of vaccination. Epidemiol Mikrobiol Imunol 2013; 62:131-7.), (2121. García-Basteiro AL, Bosch A, Sicuri E, Bayas JM, Trilla A, Hayes EB. Hospitalizations due to rotavirus gastroenteritis in Catalonia, Spain, 2003-2008. BMC Res Notes 2011; 4:429..
Regarding the changes in seasonal spikes, after the vaccine introduction in 2006, from the harmonic and multiscale wavelet analyses, we verified that the seasonal behavior (mainly those occurred in August) became much less explicit and almost disappeared for some macro-regions in Paraná State. That suggests vaccine efficacy, even without the rotavirus being evaluated directly. This drastic reduction detected after the vaccine introduction was also observed in the literature. Actually, vaccination is expected to reduce the observed seasonal peak in rotavirus disease incidence and reduce the overall burden of disease. This fact was clearly shown by a deterministic age-structured model of rotavirus transmission that explicitly captured the natural history of infection and reproduced the strong seasonal pattern of rotavirus disease to investigate the population-level effects of vaccination in England and Wales 2222. Atchison C, Lopman B, Edmunds WJ. Modelling the seasonality of rotavirus disease and the impact of vaccination in England and Wales. Vaccine 2010; 28:3118-26..
However, while vaccination is expected to decrease the overall burden of disease, it may increase the degree of seasonal variation in the incidence of rotavirus in some settings 1111. Pitzer VE, Viboud C, Lopman BA, Patel MM , Parashar UD , Grenfell BT. Influence of birth rates and transmission rates on the global seasonality of rotavirus incidence. J R Soc Interface 2011; 8:1584-93.. The results obtained from both harmonic and wavelet analysis clearly confirmed that.
From the harmonic modeling, it was possible to identify that the East region had a different seasonal behavior from the others of the state, presenting an annual seasonality, responsible for 89.06% of the variability of the time series. The different behavior of the East region, which includes Curitiba and Paranaguá cities, really has specific climatic conditions that contribute to spikes in June. For the other macro-regions, the semi-annual seasonal component was responsible for at least 63.20% of the variability, reaching almost 78%. From the modeling, two seasonal spikes were identified: the most incidents were in August, followed by February. The wavelet analysis made it possible to complement the results showing the clear behavior change after the vaccine introduction and when it occurred.
From the Fisher's test, it was possible to confirm that the annual seasonality observed in the Fourier periodogram was statistically significant (p < 0.001) for the East region. The same occurred with the semi-annual seasonality for the other five macro health regions.
As some authors have observed 1111. Pitzer VE, Viboud C, Lopman BA, Patel MM , Parashar UD , Grenfell BT. Influence of birth rates and transmission rates on the global seasonality of rotavirus incidence. J R Soc Interface 2011; 8:1584-93.), (1212. Kane EM, Turcios RM, Arvay ML, Garcia S, Bresee JS, Glass RI. The epidemiology of rotavirus diarrhea in Latin America. Anticipating rotavirus vaccines. Rev Panam Salud Pública 2004; 16:371-7.), (1313. Levy K, Hubbard AE, Eisenberg JN. Seasonality of rotavirus disease in the tropics: a systematic review and meta-analysis. Int J Epidemiol 2009; 38:1487-96.), (1414. Bresee J, Fang ZY, Wang B, Nelson EA, Tam J, Soenarto Y, et al. First report from the Asian Rotavirus Surveillance Network. Emerg Infect Dis 2004; 10:988-95., although seasonality started to be recognized even in the tropics, seasonal peaks have been occurring year-round in different countries. Our study corroborates the presence of seasonality in tropics, its spatial change even in different regions inside the state (Paraná State) as well as temporal changes in the same locality 1515. Cilla G, Pérez-Trallero E, López-Lopategui M, Gilsetas A, Gomáriz M. Incidence, seasonality and serotypes of rotavirus in Gipuzkoa (Basque Country), Spain. A 14-year study. Epidemiol Infect 2000; 125:677-83.. We could see that before the introduction of the vaccine in 2006, the East region (Figure 1) presented the most different seasonal behavior in relationship to the others of the state. Although we did not investigate environmental factors, this region really has a well-defined and regular climate when compared to the other regions.
Another important result to be discussed is the second seasonal peak in February, which can be observed even after the rotavirus vaccine introduction. Although not statistically significant (p > 0.05) from the Fisher`s test, it was significant in the harmonic model. Considering this is a hot month, probably the hospitalizations that occur in February are also due to other diarrheic diseases. On the other hand, the relationship between climate and diarrheic diseases is complex due to the large number of confounding variables 1111. Pitzer VE, Viboud C, Lopman BA, Patel MM , Parashar UD , Grenfell BT. Influence of birth rates and transmission rates on the global seasonality of rotavirus incidence. J R Soc Interface 2011; 8:1584-93.), (2323. Mellor JE, Smith JA, Learmonth GP, Netshandama VO, Dillingham RA. Modeling the complexities of water, hygiene, and health in Limpopo Province, South Africa. Environ Sci Technol 2012; 46:13512-20.), (2424. Mellor JE , Smith JA , Samie A, Dillingham RA . Coliform sources and mechanisms for regrowth in household drinking water in Limpopo, South Africa. J Environ Eng (New York) 2013; 139:1152-61., the means of transmission 2525. Mellor J, Abebe L, Ehdaie B, Dillingham R, Smith J. Modeling the sustainability of a ceramic water filter intervention. Water Res 2014; 49:286-99. that can affect the disease rates, and the fact that diarrhea can be caused by multiple pathogens 2626. Walker CLF, Sack D, Black RE. Etiology of diarrhea in older children, adolescents and adults: a systematic review. PLoS Negl Trop Dis 2010; 4:e768.), (2727. Guerrant RL, Hughes JM, Lima NL, Crane J. Diarrhea in developed and developing countries: magnitude, special settings, and etiologies. Rev Infect Dis 1990; 12 Suppl 1:S41-50.. The limitations related to the data discussed in Masukawa et al. 44. Matsukawa MLT, Moriwaki AM, Uchimura NS, Souza EM, Uchimura TT. Intervention analysis of introduction of rotavirus vaccine on hospital admission rates due to acute diarrhea. Cad Saúde Pública 2014; 30:2101-11. are also inherent to this research.
Due to the fact that the rotavirus is spatially dependent, in future studies, this evaluation should be extended to other states and the whole of Brazil.
Acknowledgments
The authors wish to acknowledge two peer reviewers who made contributions that added to the quality of the paper.
References
-
1Secretaria de Atenção à Saúde/Secretaria de Vigilância em Saúde, Ministério da Saúde. Manual de vigilância do óbito infantil e fetal e do Comitê de Prevenção do Óbito Infantil e Fetal. Brasília: Ministério da Saúde; 2009. (Série A. Normas e Manuais Técnicos).
-
2Lanzieri TM, Costa I, Shafi FA, Cunha MH, Ortega-Barria E, Linhares AC. Trends in hospitalizations from all-cause gastroenteritis in children younger than 5 years of age in Brazil before and after human rotavirus vaccine introduction, 1998-2007. Pediatr Infect Dis J 2010; 673-5.
-
3Carmo GMI, Yeen C, Cortes J, Siqueira AA, Oliveira WK, Cortes-Escalante JJ, et al. Decline in diarrhea mortality and admissions after routine childhood rotavirus immunization in Brasil: a time-series analysis. PLoS Med 2011; 8:e1001024.
-
4Matsukawa MLT, Moriwaki AM, Uchimura NS, Souza EM, Uchimura TT. Intervention analysis of introduction of rotavirus vaccine on hospital admission rates due to acute diarrhea. Cad Saúde Pública 2014; 30:2101-11.
-
5Blasio BF, Kasymbekova K, Flem E. Dynamic model of rotavirus transmission and the impact of rotavirus vaccination in Kyrgyzstan. Vaccine 2010; 28:7923-32.
-
6Curns AT, Steiner CA, Barret M, Hunter K, Wilson E, Parashar UD. Reduction in acute gastroenteritis hospitalizations among US children after introduction of rotavirus vaccine: analysis of hospital. Discharge Datafrom 18 US States. J Infect Dis 2010; 201:1617-24.
-
7Desai R, Curns AT , Steiner CA , Tate JE, Patel MM, Parashar UD. All-cause gastroenteritis and rotavirus-coded hospitalizations among US children, 2000-2009. Clin Infect Dis 2012; 55:e28-34.
-
8World Health Organization. Diarrhea: why children are still dying and what can be done. New York: United Nations Children's Fund; 2009.
-
9Cook SM, Glass RI, Le Baron CH, Ho MS. Global seasonality of rotavirus infections. Bull World Health Organ 1990; 68:171-7.
-
10Shim E, Galvani AP. Impact of transmission dynamics on the cost-effectiveness of rotavirus vaccination. Vaccine 2009; 27:4025-30.
-
11Pitzer VE, Viboud C, Lopman BA, Patel MM , Parashar UD , Grenfell BT. Influence of birth rates and transmission rates on the global seasonality of rotavirus incidence. J R Soc Interface 2011; 8:1584-93.
- 12. Kane EM, Turcios RM, Arvay ML, Garcia S, Bresee JS, Glass RI. The epidemiology of rotavirus diarrhea in Latin America. Anticipating rotavirus vaccines. Rev Panam Salud Pública 2004; 16:371-7.
-
13Levy K, Hubbard AE, Eisenberg JN. Seasonality of rotavirus disease in the tropics: a systematic review and meta-analysis. Int J Epidemiol 2009; 38:1487-96.
-
14Bresee J, Fang ZY, Wang B, Nelson EA, Tam J, Soenarto Y, et al. First report from the Asian Rotavirus Surveillance Network. Emerg Infect Dis 2004; 10:988-95.
-
15Cilla G, Pérez-Trallero E, López-Lopategui M, Gilsetas A, Gomáriz M. Incidence, seasonality and serotypes of rotavirus in Gipuzkoa (Basque Country), Spain. A 14-year study. Epidemiol Infect 2000; 125:677-83.
-
16Chatfield C. The analysis of times series: an introduction. London: Chapman and Hall; 2003.
-
17Cryer JD, Chan KS. Time series analysis: with applications in R. New York: Springer-Verlag; 2008. (Serie Springer Texts in Statistics).
-
18Nason GP. Wavelet methods in statistics with R. New York: Springer-Verlag; 2008.
-
19Fisher R. Tests of significance in harmonic analysis. Proceedings of the Royal Society A, Matehematical, Physical and Engineering Sciences 1929; 125:54-9.
-
20Pazdiora P, Beneš Č. Rotavirus gastroenteritis in the Czech Republic before the start of vaccination. Epidemiol Mikrobiol Imunol 2013; 62:131-7.
-
21García-Basteiro AL, Bosch A, Sicuri E, Bayas JM, Trilla A, Hayes EB. Hospitalizations due to rotavirus gastroenteritis in Catalonia, Spain, 2003-2008. BMC Res Notes 2011; 4:429.
-
22Atchison C, Lopman B, Edmunds WJ. Modelling the seasonality of rotavirus disease and the impact of vaccination in England and Wales. Vaccine 2010; 28:3118-26.
-
23Mellor JE, Smith JA, Learmonth GP, Netshandama VO, Dillingham RA. Modeling the complexities of water, hygiene, and health in Limpopo Province, South Africa. Environ Sci Technol 2012; 46:13512-20.
-
24Mellor JE , Smith JA , Samie A, Dillingham RA . Coliform sources and mechanisms for regrowth in household drinking water in Limpopo, South Africa. J Environ Eng (New York) 2013; 139:1152-61.
-
25Mellor J, Abebe L, Ehdaie B, Dillingham R, Smith J. Modeling the sustainability of a ceramic water filter intervention. Water Res 2014; 49:286-99.
-
26Walker CLF, Sack D, Black RE. Etiology of diarrhea in older children, adolescents and adults: a systematic review. PLoS Negl Trop Dis 2010; 4:e768.
-
27Guerrant RL, Hughes JM, Lima NL, Crane J. Diarrhea in developed and developing countries: magnitude, special settings, and etiologies. Rev Infect Dis 1990; 12 Suppl 1:S41-50.
Publication Dates
-
Publication in this collection
Oct 2016
History
-
Received
19 May 2015 -
Reviewed
20 Nov 2015 -
Accepted
07 Dec 2015