Abstracts
The stem allometry (stem diameter vs. tree height) of a Neotropical palm (Euterpe edulis) found in rain and seasonal forest of Southeastern Brazil was examined. Observed height-diameter relationships along the stem (diameter at ground level, (dgl), and diameter at breast height (dbh) were compared to three theoretical stability mechanical models: elastic similarity, stress similarity and geometric similarity. Slopes of log-transformed height-diameter relationships did not lie near those predicted by any stability mechanical models. Significant differences in stem allometry were found when comparing dgl to dbh, suggesting greater increase in dbh with height. The relationship between stability safety factor (SSF) and palm height showed that both dgl and dbh were found to be above McMahon's theoretical buckling limit for dicotyledonous trees, but some individuals approached this limit in relation to dbh. Despite displaying a similar decreasing pattern of SSF with height, differences found in SSF along the stem - greater SSF for dgl when compared to dbh - indicate that the risk of mechanism failure in palms depends upon the size and varies along the stem. Distinct allometric relationships along the stem obtained for Euterpe edulis may be reflecting possible differences in stem design and growth strategies.
stability safety factor; risk of buckling; mechanical instability; tropical semideciduous forest; Brazil
Neste trabalho foram analisadas as relações entre o diâmetro e a altura de uma palmeira Neotropical (Euterpe edulis) comum na Floresta Atlântica do SE do Brasil. As relações observadas entre a altura e o diâmetro ao longo do estipe (diâmetro ao nível do solo (DAS), e diâmetro ao nível do peito (DAP) foram comparadas a três modelos teóricos de estabilidade mecânica: similaridade elástica, similaridade de estresse e similaridade geométrica. As inclinações das regressões altura-diâmetro não se ajustaram a nenhum dos modelos de estabilidade mecânica. Diferenças significativas na alometria do estipe foram encontradas comparando-se as relações altura-DAS com altura-DAP, sugerindo maior incremento em DAP com a altura. A relação entre o fator de segurança do diâmetro contra quebra e a altura mostrou que tanto o DAS como o DAP encontram-se acima do limite teórico de quebra de McMahon para árvores, mas alguns indivíduos aproximam-se deste limite em relação ao DAP. Apesar de apresentarem padrão similar de decréscimo do fator de segurança com a altura, as diferenças encontradas para o fator de segurança ao longo do estipe - maior fator de segurança para o DAS quando comparado com o DAP - indicam que o risco de quebra em palmeiras depende do tamanho e varia ao longo do estipe. As relações alométricas distintas ao longo do estipe obtidas para Euterpe edulis podem estar refletindo possíveis diferenças na forma do estipe e nas estratégias de crescimento.
fator de segurança; risco de quebra; instabilidade mecânica; floresta tropical semidecídua; Brasil
Untitled1
Allometry of a neotropical palm, Euterpe edulis Mart.
Alometria de uma palmeira Neotropical, Euterpe edulis Mart.
Luciana F. AlvesI,1 1 Corresponding Author: lu-alves@hotmail.com ; Fernando R. MartinsII; Flavio A.M. SantosII
IDepartamento de Ecologia, Universidade de São Paulo, Rua do Matão, 321, Trav. 14, CEP 05508-900, São Paulo, SP, Brasil
IIDepartamento de Botânica, Universidade Estadual de Campinas, UNICAMP, C. Postal 6109, CEP 13083-970, Campinas, SP, Brasil
ABSTRACT
The stem allometry (stem diameter vs. tree height) of a Neotropical palm (Euterpe edulis) found in rain and seasonal forest of Southeastern Brazil was examined. Observed height-diameter relationships along the stem (diameter at ground level, (dgl), and diameter at breast height (dbh) were compared to three theoretical stability mechanical models: elastic similarity, stress similarity and geometric similarity. Slopes of log-transformed height-diameter relationships did not lie near those predicted by any stability mechanical models. Significant differences in stem allometry were found when comparing dgl to dbh, suggesting greater increase in dbh with height. The relationship between stability safety factor (SSF) and palm height showed that both dgl and dbh were found to be above McMahon's theoretical buckling limit for dicotyledonous trees, but some individuals approached this limit in relation to dbh. Despite displaying a similar decreasing pattern of SSF with height, differences found in SSF along the stem greater SSF for dgl when compared to dbh indicate that the risk of mechanism failure in palms depends upon the size and varies along the stem. Distinct allometric relationships along the stem obtained for Euterpe edulis may be reflecting possible differences in stem design and growth strategies.
Key words: stability safety factor, risk of buckling, mechanical instability, tropical semideciduous forest, Brazil
RESUMO
Neste trabalho foram analisadas as relações entre o diâmetro e a altura de uma palmeira Neotropical (Euterpe edulis) comum na Floresta Atlântica do SE do Brasil. As relações observadas entre a altura e o diâmetro ao longo do estipe (diâmetro ao nível do solo (DAS), e diâmetro ao nível do peito (DAP) foram comparadas a três modelos teóricos de estabilidade mecânica: similaridade elástica, similaridade de estresse e similaridade geométrica. As inclinações das regressões altura-diâmetro não se ajustaram a nenhum dos modelos de estabilidade mecânica. Diferenças significativas na alometria do estipe foram encontradas comparando-se as relações altura-DAS com altura-DAP, sugerindo maior incremento em DAP com a altura. A relação entre o fator de segurança do diâmetro contra quebra e a altura mostrou que tanto o DAS como o DAP encontram-se acima do limite teórico de quebra de McMahon para árvores, mas alguns indivíduos aproximam-se deste limite em relação ao DAP. Apesar de apresentarem padrão similar de decréscimo do fator de segurança com a altura, as diferenças encontradas para o fator de segurança ao longo do estipe maior fator de segurança para o DAS quando comparado com o DAP indicam que o risco de quebra em palmeiras depende do tamanho e varia ao longo do estipe. As relações alométricas distintas ao longo do estipe obtidas para Euterpe edulis podem estar refletindo possíveis diferenças na forma do estipe e nas estratégias de crescimento.
Palavras-chave: fator de segurança, risco de quebra, instabilidade mecânica, floresta tropical semidecídua, Brasil
Introduction
Trees are dynamic structures, and must meet a balance between stability and efficiency in their mechanical properties through growth process (Wilson & Archer 1979). The stem tissue of arborescent plants must be sufficiently durable, rigid, and abundant to resist to mechanical failure (Rich et al. 1986) due to static loads of self-weight and dynamic loads generated primarily by winds (Wilson & Archer 1979). Each species (or group of species) shares a basic biomechanical "design," which theoretically reduces the probability of elastic buckling and therefore maintains the stability of vertical stems (Niklas 1995).
Three mechanical stability models have been proposed to describe the allometric relationships between tree height and trunk diameter. The elastic similarity model states that different-sized trees maintain the same average safety factor against buckling under their own weight, regardless of size (McMahon 1973; McMahon & Kronauer 1976; McMahon & Bonner 1983). This model has originated from the observation that the height (H) of many trees tend to be limited to 1/4 of the height that would cause an uniform cylinder of the same diameter (D) to buckle under its own weight (McMahon 1973). For an uniform cylinder, the logarithm of the critical buckling height is linearly related to the logarithm of diameter with a slope of 0.67 or 2/3, therefore H µ D2/3, or D µ H3/2 (Dean & Long 1986). According to the constant-stress (or stress similarity)model, the size of the stem at any point varies so that the bending stress remains constant along the stem. In this model, H µ D1/2, or D µ H2.0 (Dean & Long 1986). The geometric similarity model means that, if plants retain isometry throughout growth in such a way that main structures remain geometrically similar, then height scales in direct proportion to diameter, that is H µ D1.0 (Norberg 1988). All these models predict that wood properties do not change with tree size (Niklas 1994).
Dicotyledonous trees and gymnosperms generally follow the elastic similarity or the stress similarity model, whereas non-woody species seem to agree with the geometric similarity model (McMahon 1973; McMahon & Kronauer 1976; Dean & Long 1986; Rich et al. 1986; Norberg 1988; Niklas 1993a; b; Claussen & Maycock 1995; King 1996). The elastic similarity implies that the relative margin of safety against mechanical failure is maintained during height growth by increasing diameter via lateral cambium activity (Rich 1986). Therefore, constraints on further increases in height in non-woody species would result from limitations on the maximum stiffness and strength that plant tissue can achieve (Niklas 1993b). Although palms lack a vascular cambium (Tomlinson 1961), many palm species achieve heights equal to those attained by many of the largest dicots and gymnosperms (Niklas 1994; Schatz et al. 1985; Kahn 1986; Kahn & Castro 1985). Arborescent palms compensate for increased structural demands during height growth by: 1) achieving earlier a sufficient diameter for future support requirements, 2) undergoing a continuous but usually slight-secondary thickening (i.e. diffuse secondary growth, (Tomlinson 1961), and/or 3) changing tissue properties along the stem (Schoute 1912; Tomlinson 1961; Waterhouse & Quinn 1978; Rich 1986; 1987). As palms show much less increase in diameter with increasing total height when compared to dicotyledonous trees (Rich et al. 1986; King 1996), one could expect that the allometry of stem diameter and height would vary with level up the trunk, in order to minimize the risks of mechanical failure, and so optimize height growth rate. Allometric relationships observed for tropical palms have demonstrated that diameter does not always scale in direct proportion to height (Schatz et al. 1985; Rich 1986; Rich et al. 1986), meaning that shape may change during growth.
In order to investigate whether palms may display differences in mechanical stability along the stem to attain a tree stature, we analyzed the stem allometry of Euterpe edulis Mart. (Arecaceae), a common arborescent palm species of the SE Brazilian Atlantic rain forest. The questions addressed are: 1) Does this palm species conform to any theoretical stability mechanical models proposed to describe the allometric relationships between diameter and height? 2) How vary the allometry of diameter and height along the stem for Euterpe edulis? The results are discussed in terms of stem design and growth strategies of this palm species.
Material and methods
Study site - This study was carried out at Santa Genebra Reserve, a 250ha tropical semideciduous forest fragment situated in Campinas (22º49'S, 47º06'W; 585m a.s.l.), SE Brazil. The climate is seasonal, with mean annual rainfall of 1,366mm. The year can be divided into wet (November-February), dry (May-August) and transitional (April-May and September-October) seasons. Mean annual temperature is 20.6ºC, ranging from about 15.5ºC to 27.3ºC (Galetti 1993).
Study species - Euterpe edulis Mart. is a common arborescent palm in rain and seasonal forests of SE Brazil (Uhl & Dransfield 1987; Henderson et al. 1995). This species, usually known as "palmito" or heart of palm (Bovi & Godoy Jr. 1991), is the main commercial source of palm heart in Brazil. Despite its food and commercial value, natural populations of Euterpe edulis have been intensively exploited in Brazil in a non-sustainable basis (Orlande et al. 1996). As the palm tree is always sacrificed to remove the palm heart, natural populations have been drastically reduced.
Euterpe edulis presents a monopodial growth, which solitary stem does not exceed the canopy layer at the study site (ca. 15m height). It occurs largely in a ~10ha swampy forest area at Santa Genebra Reserve, together with two other palm species, Geonoma brevispatha and Syagrus romanzoffiana (Silva Matos et al. 1999). Other canopy species typical of swampy forests are frequently observed, like Talauma ovata, Erythrina falcata and Tabebuiaumbellata (Alves 1994). Several aspects of the population ecology of Euterpe edulis have been studied at this study site, like demography (Silva Matos et al. 1999), seed and seedling ecology (Silva Matos & Watkinson 1998), leaf ecology (Carvalho et al. 1999) and herbivory (Silva Matos 2000), intraspecific competition and spatial pattern (Alves 1994).
Field sampling and data analysis - In 1993, we established a one-hectare plot (100×100m) located in a swampy area in the forest, which presents a hydromorphic soil with gley features. Typically, there is water in weak, little streams all the year round, but during long rainless periods, some sections tend to dry out. We mapped and tagged with numbered aluminum tags all stems of Euterpe edulis with diameter at ground level (hereafter dgl) > 10cm, classified as immature and adults, according to Silva (1991). As some palms may show a visible cone of roots emerging at the lower internodes of the stem base (Henderson et al. 1995), we measured dgl just above this cone of roots. We measured for dgl, diameter at breast height (dbh), and height to the highest expanded leaf (H).
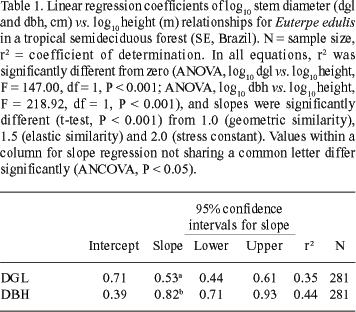
Changes in stem shape with height were tested by plotting the dbh/dgl ratio against height. This relationship is expected to be constant, if stem shape does not change with size. Tree height and stem diameter (dbh and dgl) data of each palm were log10transformed and linear least squares (LS) regressions were calculated. Allometric relationships were then expressed by the power function equation: y = a xb, or log y = log a + b log x, where y is stem diameter (cm), x is palm height (m), a is the y intercept, and b is the slope. Significant differences between regression coefficients concerning dgl and dbh were tested by ANCOVA (Snedecor & Cochran 1967; Huitema 1980). To test for any significant differences (P < 0.05), each slope (b) was then compared with proposed coefficients for elastic similarity (b = 1.5, McMahon 1973), geometric similarity (b = 1.0, Norberg 1988), and stress similarity (b = 2.0, Dean & Long 1986), by a t-test (Zar 1999).
Through the ratio of the actual stem diameter (Ddgl or Ddbh) to the minimum stem diameter (Dmin) required to prevent buckling, we calculated the stability safety factor, SSF (King 1981), which is a measure of the degree of safety against buckling based on stem dimensions and McMahon's buckling equation, Dmin = 0.109 H3/2 (McMahon 1973). This factor is an approach estimate, since dry density of wood, one of the predictors of stem mechanical properties, is not available for Euterpe edulis. The minimum stem diameter (Dmin) was calculated for dgl and dbh. The SSF for dgl and dbh was plotted against height and fitted by DWLS (Distance Weighted Least Squares) option of SYSTAT (1998). DWLS fits a line through a set of points by least squares, where every point on the smoothed line requires a weighted quadratic multiple regression on all the points. Such smoothed line shows a tendency in SSF variation with height. Unlike linear or polynomial smoothing, DWLS is calculated to allow a local flexibility, that fits the data better (SYSTAT 1998). Statistical analyses were carried out on the software package SYSTAT (SYSTAT 1998) and ANCOVA3.2 (F.A.M. Santos, unpublished).
Results
Palms ranged in size from 4.1 to 17.2cm diam. at breast height (dbh), 10.2 to 27.4cm diam. at ground level (dgl), and heights varied from 3.15 to 12.5m. There was a smooth, but significant increase in dbh/dgl ratio with height (y = 0.415 + 0.019 (height); r2 = 0.118, P < 0.001, n = 281; b > 0, t test, P < 0.01). This increase of dbh/dgl ratio from smaller to larger-sized palms suggests changes in shape, with a shift to greater dbh increment in relation to dgl as palms grow in height.
All linear regressions were significant (P < 0.001; Tab. 1), but dbh variation was better explained by height (r2 = 0.44) than dgl variation (r2 = 0.35). The comparison of regression coefficients (b) showed that the scaling exponents for Euterpe edulis did not lie near those predicted by any stability mechanical model (Tab. 1). Significant differences were observed for the slope estimates of stem diameter vs. height relationships (F = 4.7807; P < 0.05; ANCOVA). This indicates greater increase in dbh with height when compared to dgl (Fig. 1, Tab. 1). Both allometric relationships were above McMahon's (1973) theoretical buckling limit for dicotyledonous trees (Fig. 1a), but some individuals approached this critical limit, in relation to dbh (Fig. 1b).
The stability safety factor of stem diameter against buckling (SSF) performed a decreasing pattern with increasing height, for both dgl and dbh (Fig. 2). Smaller to medium-sized palms up to 9m showed greater variability for SSF than larger ones (Fig. 2). Over 9m height, palms showed lower but less variable SSF values (Fig. 2). The mean (se) values of the stability safety factor (SSF) were 6.54 (0.13) and 3.79 (0.07) for dgl and dbh, respectively, in sampled palms ranging from 3.15 to 12.5m height. Despite displaying a similar decreasing pattern of SSF with height, a ttest revealed that mean SSFdgl was significantly greater than mean SSFdbh (t test = 18.72, P < 0.001, n = 281). Differences in margins of safety within stem apparently enables taller palms to bend through larger angles without breaking.
Discussion
The stem allometry of Euterpe edulis did not conform to any theoretical stability mechanical models. As expected for non-woody species, elastic similarity is not maintained by increases in stem diameter with 1.5 power of height. The stem diameter did not even scale isometrically with height, meaning that the shape of palms changed during growth.
Distinct allometric relationships along the stem obtained for Euterpe edulis may be reflecting possible differences in stem design and growth strategies. Diameter at ground level in younger palms must be initially overbuilt to provide a sufficient margin of safety, thus preventing buckling, and allowing future support requirements during height growth. The formation of a wide stem-base in palms takes place during the establishment growth (i.e., the immediate post-seedling phase) when diameter progressively increases (Tomlinson 1961). In Euterpeedulis, this initial increase in stem diameter is apparently achieved before substantial upward growth begins. Silva (1991) found a conspicuous shift in diameter-height distribution of Euterpeedulis saplings until reach about 6cm in dgl and 1.25m height, suggesting that saplings below this size would grow faster in diameter at ground level than in height.
Similar to dicots and gymnosperms, the relative costs of maintaining a palm stem in upward position with a constant degree of safety against mechanical failure increase greatly with height growth (Rich et al. 1986). As palms first invest in expanding the stem near the ground, smaller palms are always more structurally stable than taller palms, i.e., they have greater strength per unit cost (Rich 1986; 1987). The observed pattern of decreasing SSF with height suggests that there is a limited increase in tissue strength and stiffness within palm stems with height growth. However, differences in SSF along the stem - greater SSF for dgl when compared to dbh - indicate that the risk of mechanical failure in palms depends upon the size and varies within the stem. Achieving earlier a relatively large diameter at ground level might not be sufficient to minimize the risks of mechanical failure, and attain a tree stature. A limited increase of dbh/dgl ratio, with a shift to greater dbh increment in relation to dgl as palms grow in height, is probably adequate to prevent a steep increase of mechanical failure risks. Anatomical studies of rain forest palms have demonstrated that mechanical properties of palm stems can vary as a function of radial position and height (Waterhouse & Quinn 1978; Rich 1986; 1987). Structurally meaningful mechanical properties, including dry density of wood, elastic modulus and modulus of rupture (measures of stiffness and strength, respectively), are highest toward the base and periphery of palm stems, and decrease markedly with height above ground (Rich 1986; 1987). It is possible that Euterpe edulis displays these same mechanical features along the stem as indicated by the differences found in the stability safety factor considering stem diameter at different heights.
As well as dicotyledonous trees, access to light is believed to be an important constraint for forest palms. A higher investment in vertical relative to radial growth permits attaining a vertical position in the forest profile that confers large benefits of increased illumination. However, this investment may also represent a real risk of buckling and death. Differences found in the stem allometry considering diameter at different heights pointed out that Euterpe edulis are able to grow to tree stature by being initially overbuilt in relation to stem diameter at ground level, and by changing shape along the stem with height to avoid mechanical instability. Our findings indicate that a trade-off between height and diameter growth also holds for Euterpe edulis. Only palms with larger stems at ground level and flexible stems at breast height can achieve taller forms. The acquisition of a substantial conical base upon which the stem can firmly stand would facilitate rapid vertical growth when adequate light conditions are available, as small gaps created by treefalls and/or falling debris. As palms grow taller, there is an increase chance that it will fall over (lower SSF), but this limit is not attained. To prevent a failure, palm stems probably undergo shifts in structural properties, increasing stem stiffness and strength with height growth. Differences in margins of safety along the stem apparently enable taller palms to bend through larger angles without breaking as they reach the forest canopy level. Although low, observed safety factors allow taller palms to support their crown at a greater height for a given stem size, increasing the intercepted light from above. Thus, changes in stem shape may contribute to the ability of this species to attain a canopy position in a highly competitive light environment within the constraints of monocot anatomy.
Acknowledgements
We are grateful to T.C.S. Sposito for helpful comments on this manuscript and for valuable advice on statistical analysis. We are also grateful to R.M. Carvalho, D.M. Silva Matos, E.M. Vieira and E.A. Fischer for providing field assistance. We thank the Fundação José Pedro de Oliveira for permission to carry out this work in the Santa Genebra Reserve. This research was supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) graduate fellowship to the first author.
Received: September 25, 2002. Accepted: October 15, 2003
- Alves, L.F. 1994. Competição intraespecífica e padrão espacial em uma população de Euterpeedulis Mart. (Arecaceae) Master Thesis. Universidade Estadual de Campinas, Campinas.
- Bovi, M.L.A. & Godoy Jr., G. 1991. Juvenile-mature corrrelations in heart of palm plants. Revista Brasileira de Genética 14: 739-751.
- Carvalho, R.M.; Martins, F.R. & Santos, F.A.M. 1999. Leaf ecology of pre-reproductive ontogenetic stages of the palm Euterpe edulis Mart. (Arecaceae). Annals of Botany 83: 225-233.
- Claussen, J.W. & Maycock, C.R. 1995. Stem allometry in a North Queensland tropical rainforest. Biotropica 27: 421-426.
- Dean, T.J. & Long, J.N. 1986. Validity of constant-stress and elastic-instability principles of stem formation in Pinus contorta and Trifolium pratense Annals of Botany 58:833-840.
- Galetti, M. 1993. Diet of scaly-headed parrot (Pionus maximiliani) in a semideciduous forest in southeastern Brazil. Biotropica 25: 419-425.
- Henderson A.; Galeano, G. & Bernal, R. 1995. Field guide to the tropical palms of the Americas Princeton University Press, Princeton.
- Huitema, B.E. 1980. The analysis of covariance and alternatives John Wiley, New York.
- Kahn, F. 1986. Life forms of amazonian palms in relation to forest structure and dynamics. Biotropica 18: 214-218.
- Kahn, F. & Castro, A. 1985. The palm community in a forest of Central Amazonia, Brazil. Biotropica 17: 210-216.
- King, D. 1981. Tree dimensions: maximizing the rate of height growth in dense stands. Oecologia 51: 351-356.
- King, D. 1996. Allometry and life history of tropical trees. Journal of Tropical Ecology 12: 25-44.
- McMahon, T. 1973. Size and shape in biology. Science 179: 1201-1204.
- McMahon, T. & Bonner, J.T. 1983. On size and life Scientific American Library, New York.
- McMahon, T. & Kronauer, R.E. 1976. Tree structures: deducing the principle of mechanical design. Journal of Theoretical Biology 59: 443-466.
- Niklas, K.J. 1993a. The scaling of plant height: a comparison among major plant clades and anatomical grades. Annals of Botany 72: 165-172.
- Niklas, K.J. 1993b. Influence of tissue density-specific mechanical properties on the scaling of plant height. Annals of Botany 72: 173-179.
- Niklas, K.J. 1994. Plant allometry - the scaling of form and process The University of Chicago Press, Chicago.
- Niklas, K.J. 1995. Plant height and the properties of some herbaceous stems. Annals of Botany 75: 133-142.
- Norberg, R.Å. 1988. Theory of growth geometry of plants and self-thinning of plant populations: geometric similarity, elastic similarity, and different growth modes of plant parts. American Naturalist 131: 220-256.
- Orlande, T.; Laarman, J. & Mortimer, J. 1996. Palmito sustainability and economics in Brazil's Atlantic coastal forest. Forest Ecology and Management 80: 257-265.
- Rich, P.M. 1986. Mechanical architecture of arborescent rain forest palms. Principes 30: 117-131.
- Rich, P.M. 1987. Mechanical structure of the stem of arborescent palms. Botanical Gazette 148: 42-50.
- Rich, P.M.; Helenurm, K.; Kearns, D.; Morse, S.R.; Palmer, M.W. & Short, L. 1986. Height and stem diameter relationships for dicotyledonous trees and arborescent palms of Costa Rican tropical wet forest. Bulletin of the Torrey Botanical Club 113: 241-246.
- Schatz, G.E.; Williamson, G.B.; Cogswell, C.M. & Stam, A.C. 1985. Stilt roots and growth of arboreal palms. Biotropica 17:206-209.
- Schoute J.C. 1912. Über das Dickenwachstum der Palmen.Ann. Jardin Bot. Buitenzorg, Deuxieme Serie 11: 1-209.
- Silva, D.M. 1991. Estrutura de tamanho e padrão espacial de uma população de Euterpe edulis Mart. (Arecaceae) em mata mesófila semidecídua no município de Campinas,SP Master Thesis. Universidade Estadual de Campinas, Campinas.
- Silva-Matos D.M. 2000. Herbivore and plant demography: a case study in a fragment of semideciduous forest in Brazil. Journal of Tropical Ecology 16: 159-165.
- Silva-Matos, D.M. & Watkinson, A.R. 1998. The fecundity, seed, and seedling ecology of the edible palm Euterpe edulis in southeastern Brazil. Biotropica 30: 595-603.
- Silva-Matos, D.M.; Freckleton, R. & Watkinson, A.R. 1999. The role of density dependence in the population dynamics of a tropical palm. Ecology 80: 2635-2650.
- Snedecor, G.W. & Cochran, W.G. 1967. Statistical Methods 6th ed. Iowa State University Press, Ames, Iowa.
- SYSTAT. 1998. SYSTAT version 8.0 SPSS Inc., USA. Tomlinson, P.B. 1961. Anatomy of Monocotyledons. v. 2. Palmae Clarendon, Oxford.
- Uhl, N.W. & Dransfield, J. 1987. Genera Palmarum Allen Press, Lawrence.
- Waterhouse, J.T. & Quinn, C.J. 1978. Growth patterns in the stem of the palm Archontophoenix cunninghamiana Botanical Journal of the Linnean Society 77: 73-93.
- Wilson, B.F. & Archer, R.R. 1979. Tree designs: some biological solutions to mechanical problems. BioScience 29:293-298.
- Zar, J.H. 1999. Biostatistical Analysis 4th ed. Prentice-Hall International, Inc., New Jersey.
Publication Dates
-
Publication in this collection
23 Sept 2004 -
Date of issue
June 2004
History
-
Accepted
15 Oct 2003 -
Received
25 Sept 2003