Abstracts
The wound rotor induction machine (WRIM) presents characteristics that make it attractive as an energy storage system where the energy is stored as kinetic energy in the rotor moving parts. When operating in the doubly fed mode (DFIM), with the rotor fed by a variable frequency power converter, the WRIM behaves as a synchronous machine, differing from the latter in the variable speed operation and larger dumping effect when subjected to disturbances. As the converter only needs to be designed to handle a fraction of the total power, the system can be used at a high level of power. This paper presents the analysis of a Doubly Fed Induction Machine (DFIM) used as a controlled active and reactive power compensator. The simulation and experimental results obtained show that this system can be used for voltage control in a power system as well as load-leveling device.
Power quality; voltage sags; doubly-fed machines
A máquina de indução de rotor bobinado (MIRB) apresenta características que a tornam atrativa para aplicação em sistemas de armazenamento cinético de energia. Quando operando no modo de dupla alimentação, com o rotor sendo alimentado por um conversor eletrônico de potência, a MIRB se comoprta como uma máquina síncrona, com a diferença de poder operar com velocidade variável e apresentar um maior amortecimento quando submetida a distúrbios. O fato do conversor precisar processar apenas parte da potência total do sistema favorece sua aplicação em níveis de potência mais elevados. Este artigo analisa a aplicação da Máquina de Indução Duplamente Alimentada como um compensador controlável de potências ativa e reativa. Os resultados, experimentais e de simulação, apresentados, indicam que este sistema pode ser usado no controle de tensão e no balanço de potência em um sistema elétrico.
Qualidade de energia; afundamentos de tensão; máquina de dupla alimentação
ELETRÔNICA DE POTÊNCIA
Variable speed synchronous condenser using doubly-fed induction machine
Antonio Carlos Ferreira; Luciano Moraes de Souza; Edson H. Watanabe
Universidade Federal do Rio de Janeiro, COPPE - Programa de Engenharia Elétrica, P.O. Box 68.504 21.945-970 - Rio de Janeiro - RJ - ferreira@coep.ufrj.br - souza@coe.ufrj.br - watanabe@coe.ufrj.br
ABSTRACT
The wound rotor induction machine (WRIM) presents characteristics that make it attractive as an energy storage system where the energy is stored as kinetic energy in the rotor moving parts. When operating in the doubly fed mode (DFIM), with the rotor fed by a variable frequency power converter, the WRIM behaves as a synchronous machine, differing from the latter in the variable speed operation and larger dumping effect when subjected to disturbances. As the converter only needs to be designed to handle a fraction of the total power, the system can be used at a high level of power. This paper presents the analysis of a Doubly Fed Induction Machine (DFIM) used as a controlled active and reactive power compensator. The simulation and experimental results obtained show that this system can be used for voltage control in a power system as well as load-leveling device.
Keywords: Power quality, voltage sags, doubly-fed machines
RESUMO
A máquina de indução de rotor bobinado (MIRB) apresenta características que a tornam atrativa para aplicação em sistemas de armazenamento cinético de energia. Quando operando no modo de dupla alimentação, com o rotor sendo alimentado por um conversor eletrônico de potência, a MIRB se comoprta como uma máquina síncrona, com a diferença de poder operar com velocidade variável e apresentar um maior amortecimento quando submetida a distúrbios. O fato do conversor precisar processar apenas parte da potência total do sistema favorece sua aplicação em níveis de potência mais elevados. Este artigo analisa a aplicação da Máquina de Indução Duplamente Alimentada como um compensador controlável de potências ativa e reativa. Os resultados, experimentais e de simulação, apresentados, indicam que este sistema pode ser usado no controle de tensão e no balanço de potência em um sistema elétrico.
Palavras-chave: Qualidade de energia, afundamentos de tensão, máquina de dupla alimentação.
1 INTRODUCTION
Voltage sags and voltage swells are responsible for almost 80% of the complaints related to power quality. Generally, the systems presently suggested to mitigate the effect of voltage sags rely on energy storage systems and one of them is that using the kinetic energy stored in the rotating parts of electrical machines, which has been generally referred to as "flywheel generator" (Bolen, 1992; Ter-Gazarian, 1994). These systems have been receiving attention and are being proposed for voltage and frequency control (Weissbach et alli 1999; Akagi, 2000).
When using a wound rotor induction machine (WRIM), with the stator connected to the grid and the rotor fed by a power converter, this converter only needs to be rated for a fraction of the total system power. Therefore, this system may be useful in the application at high levels of power (above hundreds of MVA). Also, the possibility of operating at variable speed in conjunction with the power converter control make the machine present higher dumping factor of the oscillations due to faults in the grid when compared to a conventional synchronous machine system, where the speed is fixed by the grid frequency (Shafer and Simond, 1998). As the WRIM can withstand higher speed variations it can exchange higher amount of energy with the grid and help to restore the energy balance. Also, with an appropriate converter control , which can control the frequency of the imposed rotor currents, the machine can be brought back to its initial operating point faster than the conventional synchronous machine.
Recently, the use of a Doubly Fed Induction Machine (DFIM) as a variable speed synchronous condenser (VSSC) was presented by Ferreira et alli (2000). It has been shown that the VSSC can be used to control its terminal voltage by controlling the capacitive or inductive reactive power. This control is achieved by the adjustment of the converter output voltage. It has also been shown how the system can work as a low speed flywheel generator, being able to supply or absorb active power and the de-coupling of these two controls has been suggested.
The aim of this paper is twofold. Firstly an analytical model of the DFIM will be developed. This model will be used to demonstrate how the power factor of the stator winding can be controlled by the converter. This analysis will be confirmed with simulations and laboratory measurements on a 3 HP machine. Secondly, a vector control scheme which de-couples the reactive and active power control will be presented This control will be validated by simulations based on SABER? simulator.
2 POWER FACTOR CONTROL
Figure 1 shows a steady-state equivalent circuit for the DFIM. This equivalent circuit can be used to analyze the effect of the converter output voltage on stator winding power. The following assumptions ca be made: fixed stator winding voltage and constant rotor voltage frequency, as imposed by the converter.
where:
 : Stator voltage;
: Stator voltage;
 : Rotor voltage referred to the stator;
: Rotor voltage referred to the stator;
rs: Stator resistance;
rr: Rotor resistance referred to the stator;
Xs: Stator leakage reactance;
Xr: Rotor leakage reactance referred to the stator;
Xm: Magnetizing inductance;
s: rotor slip.
With the previous assumptions, the equivalent circuit can be further simplified if we use Thevenin's Theorem. Therefore defining
and
where 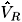 is the equivalent Thevenin voltage and rR + jXR is the equivalent Thevenin impedance. We can also write
is the equivalent Thevenin voltage and rR + jXR is the equivalent Thevenin impedance. We can also write
where:
Defining:
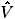 = VsÐ0
= VsÐ0 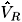 = VRÐ d
= VRÐ d 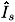 = IsÐ f
= IsÐ f where f is the power factor angle, the power in the stator winding can be calculated as
Writing the current Is as a function of Vs, VR and Z, and substituting in (5) results in the expression for the power absorbed from the system
and
where:
a = 90 q.
Equations (6) and (7) can now be used to investigate the effect of the rotor voltage on the stator winding power factor, assuming that the active power is constant. If the rotor voltage is increased, from (6), the term sin (d a) will have to be decreased. Therefore cos (d a) will be increased and so will the second term on the right hand side of (7). In (7) we see that the reactive power is composed of two components. One depends only on the stator voltage and the machine parameters and is constant for a fixed voltage. The other depends on stator and rotor voltages and the cosine of the Thevenin voltage phase minus the impedance angle. Keeping the active power constant, we can generally find a value for the rotor voltage, which will cancel the reactive power in (7). From this value, an increase in the rotor voltage will result in a negative value for Q, which means that the machine is generating capacitive reactive power to the grid (the sink convention was assumed in the development of the model). Decreasing the rotor voltage will result in a positive value for Q, therefore the motor will be generating an inductive reactive power.
This analysis can be better illustrated in Figure 2 which shows simulated results relating the reactive power in the stator of a DFIM to the voltage applied to the rotor. The machine is connected to an infinite bus and for a fixed value of rotor voltage frequency (namely 1.0 Hz) the converter voltage was varied. For the simulated motor the turns ratio between stator and rotor windings is equall to one, therefore Vr in Figure 2 is the actual rms voltage applied to the rotor.
The same behavior can be seen in Figures 3, 4 and 5 which show measurements of stator voltage and current of a 3 HP DFIM at the Power Electronics Laboratory at COPPE/UFRJ. Those figures show that by varying the rotor voltage we can obtain lagging (Figure 4), unity (Figure 3) or leading (Figure 5) power factors in the stator. In those figures, the fundamental rms components of the rotor voltages are 6 V, 6.9 V and 8.6 V, respectively, which are those displayed by the commercial converter used in the test-rig. It should be noted that different motors were used for simulation and laboratory measurements and therefore no attempt was made to correlate the values of voltage and power.
3 VOLTAGE CONTROL
Ferreira et alli (2000) presented some simulation results for the application of the DFIM as a synchronous condenser, controlling the voltage in a power system. The rotor voltage was directly controlled and the rotor frequency was kept constant. Figure 6 shows the laboratory test rig, which was used to validate those simulations. The system consists of a DFIM, which is fed from the mains via a three-phase autotransformer. The inductors between the machine and the transformer are used to ensure that there is a voltage difference between these two terminals. The rotor is fed from a commercial inverter, which works with constant V/f ratio. As the control scheme relies on a fixed frequency/variable voltage characteristics, the second autotransformer is used to control the converter input voltage, therefore the DC link voltage. It should be pointed out that this was a simple laboratory set-up used just to validate the study.
The test consists in reducing the first transformer voltage in order to reduce the voltage at the machine terminals, simulating a fault on the supply system. After that the converter output voltage is varied in order to bring the stator voltage back to its initial level. This can be seen in Figure 7, which shows the voltage at the compensator terminals measured by an oscilloscope. Figure 7 shows that until t=1.2 seconds the DFIM stator voltage is around 98.3 Vrms when it is decreased approximately 10 %. At t=2.7 seconds the rotor voltage is increased from 5.5 Vrms to 9.0 Vrms which brings the stator voltage to its pre-fault level. The effect of the reactive power in the stator winding of the DFIM on its terminal voltage can be seen in 4, which shows the instantaneous three phase reactive power calculated from the measured values of voltage and current. Due to converter limitations, which limited the voltage range applied to the rotor, it was not possible to adjust the system to operate with a unity power factor before the voltage was reduced, as it would normally be the case. Therefore, in this test the voltage was restored with a reduction in the reactive power absorbed by the DFIM
4 VECTOR CONTROL
Both simulated and experimental results presented in the previous sections used a scalar control strategy where only the magnitude and/or frequency of the rotor voltage were varied. Those results were useful to validate the application of the DFIM in mitigating voltage fluctuations at sensitive load terminals in power systems. As presented by Ferreira et alli (2000) the same system can be used as a flywheel generator and operate as a load leveling system. However it is believed that the equipment response can be greatly improved if a field orientated control is implemented.
In this analysis, a mathematical model of the symmetrical DFIM is used, where instantaneous values of voltage and current at the stator and rotor windings phases, va, vb, vc, vA, vB, vC and ia, ib, ic, iA, iB iC, are transformed to an arbitrary reference frame using Park's transformation as in Figure 9, where
a,b,c, refer to the magnetic axis of the stator phases;
A,B,C, refer to the magnetic axis of the rotor phases;
d,q, arbitrary rotating reference frame.
As shown by Krause (1986), the machine can be modeled by a set of equations, which relates applied voltages to voltage drops and flux linkages as
and
where, vds and vqs are the stator voltage components. lds and lqs are stator flux linkages components and are given by
and
where ids and iqs are the stator current components. A similar set of equations may be written for the rotor where the suffix "r" refers to rotor quantities. Therefore
and
The above system of equations is general and can be used for any reference frame. For example, taking the magnetic axis of stator phase "a" as reference, and substituting it for the flux linkages, it can be written
where
and
Defining the leakage factor ss, where Ls = ( 1 + ss)Msr, we may write:
As presented by Leonhard (1997), with a proper choice of a reference frame, the control of active and reactive power in the stator can be decoupled and be implemented by controlling the two components of the rotor current. In this paper the reference frame proposed by Leonhard (1997) is used, where the "d" axis is aligned with an extended magnetizing current vector responsible for the stator flux including stator leakage, defined as
Substituting from (19) into (18) gives
Working with the "d" and "q" components, we may write
and
where Ts is the time constant of the stator circuit, which are used in the calculation of m as in Figure 10. Therefore, with this choice of a reference frame, the stator reactive power is related to the "d" component of the rotor current and the active power is related to the "q" component as indicated in 4.1.
4.1 Reactive Power Control
The control implemented relies on the knowledge of the reactive component of the stator current. In this work this component is calculated using the instantaneous power theory (Akagi et alii, 1983). This can be easily accomplished if we transform the instantaneous values of voltage and current at the stator windings phases, va, vb, vcand ia, ib, ic, to a stationary reference frame using Clarke's transformation
and
The reactive power can be calculated from
Defining D =  it can be written
it can be written
from where the reactive power component of the stator current can be calculated as
Figures 12, 13 and 14 show simulated results where a variation of the "d" component of the rotor voltage is applied. The rotor is supplied with a Current Regulated Pulse Width Modulation Converter (CR-PWM). Figure 12 shows that at t=2.0 seconds there is a step change in the reactive current reference from -1 pu to +1 pu and Figure 13 shows that this is followed by a similar change in the stator reactive power. 4.2 shows a negligible variation on the rotor speed as expected from the decoupled control.
4.2 Operation as a load leveling device
One of the great advantages of the system using a DFIM is that the kinetic energy stored in the rotating parts can be used to supply or absorb active power from the grid. This, however, can be done for a limited period of time, despite the absence of any mechanical device connected to its shaft and using a power converter rated for a fraction of the total power. Considering the kinetic energy stored at two different speeds
and
where W is the kinetic energy stored in the rotor, w is its angular speed in rad/s and J its total inertia in kg.m2. If the rotor speed can be varied over a time interval, the stored energy will vary as
and will cause an active power flow given by
Equation (31) indicates that if the rotor speed is reduced the energy difference will be transformed in active power and will be supplied to the grid. On the other hand, in order to increase the rotor speed, energy will have to be extracted from the grid in the form of active power. Equation (31) also suggests a relationship between the active power in the stator and the speed variation, which can be used in the decoupled control presented in 4.1. This can be seen in Figures 15, 16 and 17, which show the effect of a step change in the rotor speed reference (wref in Figure 11). Figure 15 shows that step changes were imposed at t = 1.4 seconds and 1.46 seconds. Figures 16 and 17 show the effect of those changes on the rotor current "q" component and therefore on the active power flow in the stator windings. 6 shows the variation of the current in the stator windings. It should be noted that the step changes were imposed just as a proof of concept. The development of a control algorithm which will relate speed variations with the required stator active power is currently under study.
5 CONCLUSIONS
This paper presented a detailed analysis of a doubly fed induction machine (DFIM) to be used as a variable speed synchronous condenser (VSSC). It was shown that the VSCC can replace the conventional synchronous condenser in reactive power compensation with the advantage of being able to provide short time active power compensation. It is the authors opinion that this system will be very useful to guarantee electric energy quality in some points of the grid where high fluctuation of the load is present.
6 ACKNOWLEDGEMENTS
This work is supported by a FINEP/PRONEX grant.
Artigo submetido em 31/01/02
1a. Revisão em 15/08/02, 2a. Revisão em 01/04/03
Aceito sob recomendação do Ed. Assoc. Prof. Denizar C. Martins
- Bolen, M.H.J. Bolen (1992). Understanding Power Quality Problems, IEEE Press, New York
- Ter-Gazarian, A. (1994). Energy Storage for Power System IEE Series 6, Great Britain.
- Weissbach, R.S., G.G. Karady and R.G. Farmer (1999). "Dynamic voltage compensation on distribution feeders using flywheel energy storage", IEEE Transactions on Power Delivery, vol. 14, No. 2, April
- Akagi H. (2000). "Active Filters and Energy Storage Systems Operated under Non-Periodic Conditions", IEEE Summer Meeting.
- Shafer D., J.J.Simond (1998). "Adjustable Speed Asynchronous machine in Hydro Power plants and its advantages for the electric grid stability", Cigré Paris Session, Paris.
- Ferreira, A.C., L.M. de Souza and E. H. Watanabe (2000,). "Voltage Control Using Variable Speed Synchronous Condenser", in IV Industry Applications Conference, vol 2, pp. 703-708, Porto Alegre, Brazil
- Leonhard, W. (1997). Control of Electrical Drives, Berlin Springer, Germany
- Akagi, H. Y Kanazawa and A. Nabae (1983). "Generalized Theory of the Instantaneous Reactive Power in Three Phase Circuits", in Proceedings of the IPEC'83 - Int. Power Electronics Conf, Tokyo, pp. 1375-1386
- Krause, P.C. (1986). Analysis of Electric Machinery, McGrraw Hill, USA
Publication Dates
-
Publication in this collection
13 Aug 2004 -
Date of issue
June 2004
History
-
Accepted
01 Apr 2003 -
Received
31 Jan 2002 -
Reviewed
15 Aug 2002

















































