Análise comparativa entre geradores síncronos e geradores de indução com rotor tipo gaiola de esquilo para aplicação em geração distribuída

SISTEMAS DE POTÊNCIA

Análise comparativa entre geradores síncronos e geradores de indução com rotor tipo gaiola de esquilo para aplicação em geração distribuída

Walmir Freitas^I; José Carlos M. Vieira Jr.^I; André Morelato França^I; Luiz Carlos P. da Silva^II; Vivaldo F. da Costa^II

^IDepartamento de Sistemas de Energia Elétrica, Universidade Estadual de Campinas Caixa Postal 6101, 13083-852, Campinas, São Paulo, Brasil, [e-mail], [e-mail], [e-mail]

^IIDepartamento de Controle e Sistemas de Energia, Universidade Estadual de Campinas Caixa Postal 6101, 13083-852, Campinas, São Paulo, Brasil, [e-mail], [e-mail]

RESUMO

Neste trabalho apresenta-se uma detalhada análise comparativa entre máquinas síncronas e de indução para uso em sistemas de geração distribuída. Os impactos desses geradores no desempenho de redes de distribuição são determinados e confrontados utilizando diferentes ferramentas e modelos de simulação computacional. As questões técnicas analisadas são perfil de tensão de regime permanente, perdas elétricas, estabilidade de tensão, estabilidade transitória, afundamento de tensão devido a faltas desequilibradas e correntes de curto-circuito. Os resultados de simulação mostram que a melhor decisão do ponto de vista técnico deve ser tomada baseada nas características da rede, i.e. dependerá da maior restrição operativa da rede referente ao aumento da capacidade de geração distribuída.

Palavras-chave: geração distribuída, gerador de indução, gerador síncrono, perfil de tensão de regime permanente, estabilidade transitória, estabilidade de tensão, correntes de curto-circuito.

ABSTRACT

This paper presents a detailed comparative analysis between synchronous and induction machines for distributed generation applications. The impacts of these generators on the performance of distribution networks are determined and compared by using different computational simulation tools and models.The technical factors analyzed are steady state voltage profile, electrical losses, voltage stability, transient stability, voltage sags due to unbalanced faults and short-circuit currents. The results show that the most suitable choice depends on the network technical characteristics, i.e. what are the main operating restrictions related to distributed generation.

Keywords: distributed generation, induction generators, short-circuit currents steady state voltage profile, synchronous generator, transient stability, voltage stability.

1 INTRODUÇÃO

Recentemente, o interesse por geração distribuída tem aumentado consideravelmente em razão da reestruturação do setor de energia elétrica, necessidade de aproveitamento de diferentes fontes primárias de energia, avanços tecnológicos e maior conscientização sobre conservação ambiental (CIGRÉ Working Group 37.23, 1999; CIRED Working Group 4, 1999; Jenkins et al., 2000). Fatos como a recente crise de energia elétrica no Brasil, em 2001, e o grande blecaute nos Estados Unidos e Canadá, em 2003, devem contribuir para o crescimento do número de geradores de médio porte conectados diretamente em redes de distribuição de energia elétrica. Embora novas formas de geração de energia elétrica têm despertado bastante interesse, e.g. células a combustível e células fotovoltaicas, atualmente, a maioria dos sistemas de geração distribuída emprega máquinas de corrente alternada tanto síncronas quanto assíncronas (CIGRÉ Working Group 37.23, 1999; CIRED Working Group 4, 1999; Jenkins et al., 2000).

Tendo esses fatos como base, é imprescindível entender as influências dessa tendência na operação e projeto de redes de distribuição de energia elétrica. Portanto, o objetivo deste trabalho é determinar os principais impactos decorrentes da instalação de geradores de corrente alternada de médio porte na operação de redes de distribuição e, principalmente, comparar as diferenças entre geradores síncronos e de indução do ponto de vista técnico. Os principais aspectos técnicos analisados são perfil de tensão de regime permanente, perdas elétricas, estabilidade de tensão, estabilidade transitória, afundamentos de tensão devido a faltas desequilibradas e correntes de curto-circuito. Os resultados podem ser utilizados por concessionárias e produtores independentes de energia elétrica para determinar qual tipo de máquina é mais adequada para seus sistemas, considerando as principais características restritivas da rede no que diz respeito ao aumento da quantidade de geração distribuída.

Este trabalho está organizado como segue. Os modelos dos diversos componentes de rede e os métodos de simulação adotados neste trabalho são discutidos na Seção 2. Na Seção 3, analisam-se os impactos da instalação de geradores de corrente alternada no perfil de tensão de regime permanente. As perdas elétricas são determinadas na Seção 4. A estabilidade de tensão de redes de distribuição na presença de geradores de corrente alternada é investigada na Seção 5. Na Seção 6, a estabilidade da rede frente a grandes perturbações é analisada. Na Seção 7, estudam-se afundamentos de tensão provocados por faltas desequilibradas. As correntes de curto-circuito fornecidas por geradores de corrente alternada são determinadas e analisadas na Seção 8.

2 MODELO DO SISTEMA

Neste trabalho, os diversos componentes de rede foram representados por modelos trifásicos. Nos estudos sobre perfil de tensão de regime permanente, perdas elétricas e estabilidade, as variáveis da rede foram representadas por fasores. Ao passo que nos estudos sobre afundamentos de tensão e correntes de curto-circuito, simulação eletromagnética foi adotada, ou seja, as variáveis da rede foram representadas por valores instantâneos.

Adicionalmente, alimentadores de distribuição foram modelados como uma impedância série RL, visto serem linhas curtas. Transformadores foram representados utilizando o circuito T, ou seja, as perdas do núcleo foram consideradas. Nos estudos sobre perfil de tensão de regime permanente, cargas foram representadas como tendo características de potência constante, como é usual em estudos estáticos. Ao passo que nos estudos dinâmicos, componentes de potência ativa das cargas foram modeladas como corrente constante e componentes de potência reativa foram consideradas como impedância constante, como recomendado em IEEE Task Force (1993) para análise dinâmica.

2.1 Geradores de Indução

Embora a maioria das máquinas de indução em operação como gerador seja empregada em parques eólicos (Jenkins et al., 2000; Akhmatov et al., 2003), tais máquinas também têm sido utilizadas em usinas termoelétricas e hidroelétricas de pequeno e médio porte (Jenkins et al., 2000; Belhomme et al., 1995; McQuin et al., 1989; Parsons, 1984). Assim, com o intuito de obter resultados genéricos, o torque mecânico dos geradores de indução foi considerado constante, i.e. a dinâmica do regulador de velocidade e da fonte primária de energia foi desprezada. Adicionalmente, é importante destacar que recentemente tem crescido o interesse pelo uso do gerador de indução com dupla alimentação (Ekanayake et al., 2003; Ledesma e Usaola, 2005). Contudo, neste trabalho, optou-se por investigar apenas o uso de geradores de indução com rotor tipo gaiola de esquilo sem controles eletrônicos adicionais, visto que este ainda é o tipo de máquina mais utilizada em sistemas de geração distribuída. Assim, o gerador com rotor tipo gaiola de esquilo foi representado por um modelo de sexta ordem nos estudos de transitórios eletromagnéticos, o qual foi reduzido para um modelo de quarta ordem nos estudos de simulação fasorial, ou seja, os transitórios do estator foram desprezados (Kundur, 1994). O modelo matemático completo é mostrada a seguir. Em todos os casos analisados, parte da potência reativa consumida pelo gerador de indução é fornecida por um banco trifásico de capacitores instalado junto ao terminal do gerador, cuja capacidade de compensação adotada é igual a 1/3 da potência nominal do gerador, como é comum nesses casos (Jenkins et al., 2000).

Sistema elétrico:

sendo:

Sistema mecânico:

sendo:

R_s = resistência do estator (pu). = resistência do rotor referida para o estator (pu). L_s = L_ls + L_m = indutância do estator (pu). = + L_m = indutância do rotor referida para o estator (pu). L_ls = indutância de dispersão do estator (pu). = indutância de dispersão do rotor referida para o estator (pu). L_m = indutância magnetização (pu). H = constante de inércia (segundo). P = número de pares de pólos. V_ds, i_ds = tensão e corrente do estator de eixo direto d (pu). V_qs, i_qs = tensão e corrente do estator de eixo em quadratura q (pu). = tensão e corrente do rotor de eixo direto d (pu). = tensão e corrente do rotor de eixo em quadratura q (pu). y_qs, y_ds = fluxos magnéticos do estator de eixo em quadratura q e eixo direto d (pu). = fluxos magnéticos do rotor de eixo em quadratura q e eixo direto d (pu). w_m = velocidade mecânica angular do rotor (pu). w_r = velocidade elétrica angular do rotor (pu). w = velocidade angular do estrutura de referência girante (pu). q_r = posição elétrica angular do rotor (rad. elétricos). T_e = torque eletromagnético (pu). T_m = torque mecânico (pu).

2.2 Geradores Síncronos

A forma de geração distribuída mais empregada no Brasil é composta por turbo-geradores. Por conseguinte, neste trabalho, nos casos de simulação eletromagnética, um modelo de oitava ordem (modelo subtransitório) foi adotado para representar a dinâmica do gerador síncrono, o qual foi reduzido para um modelo de sexta ordem nos estudos de simulação fasorial, ou seja os transitórios do estator foram desprezados (Kundur, 1994). O modelo matemático empregado é apresentado a seguir.

Sistema elétrico:

sendo:

Sistema mecânico:

sendo:

R_s = resistência do estator (pu). = resistência do enrolamento de campo (pu). = resistência do enrolamento amortecedor de eixo direto (pu). = resistência do primeiro enrolamento amortecedor de eixo em quadratura (pu). = resistência do segundo enrolamento amortecedor de eixo em quadratura (pu). L_d = L_l + L_md = indutância de eixo direto (pu). L_q = L_l + L_mq = indutância de eixo em quadratura (pu). L_l = indutância de dispersão do estator (pu). L_md = indutância mútua de eixo direto (pu). L_mq = indutância mútua de eixo em quadratura (pu). = indutância do enrolamento de campo (pu). = indutância do enrolamento amortecedor de eixo direto (pu). = indutância do primeiro enrolamento amortecedor de eixo em quadratura (pu). = indutância do segundo enrolamento amortecedor de eixo em quadratura (pu). H = constante de inércia (segundo). V_d, i_d = tensão e corrente do estator de eixo direto d (pu). V_q, i_q = tensão e corrente do estator de eixo em quadratura q (pu). = tensão e corrente de campo (pu). = tensão e corrente do enrolamento amortecedor de eixo direto (pu). = tensão e corrente do primeiro enrolamento amortecedor de eixo em quadratura (pu). = tensão e corrente do segundo enrolamento amortecedor de eixo em quadratura (pu). y_q, y_d = fluxos magnéticos do estator de eixo em quadratura e eixo direto (pu). = fluxos magnéticos do rotor de eixo em quadratura q e eixo direto d (pu). w_r = velocidade angular do rotor (pu). q_r = posição elétrica angular do rotor (rad. elétricos). T_e = torque eletromagnético (pu). T_m = torque mecânico (pu).

Muitas vezes, a filosofia de controle de geradores síncronos de médio porte conectados em redes de distribuição é diferente daquela adotada no caso de geradores síncronos de grande porte conectados em sistemas transmissão, sobretudo no que diz respeito ao sistema de controle de tensão e freqüência.

No caso de sistemas de transmissão, por exemplo, o regulador de velocidade dos geradores de grande porte é ajustado de forma a manter operação com freqüência constante. Ao passo que no caso de redes de distribuição, usualmente, os geradores são operados de forma a manter potência ativa constante independentemente da freqüência da rede (Jenkins et al., 2000). Assim, neste trabalho, optou-se por considerar o torque mecânico constante.

O sistema de excitação de geradores conectados em redes de transmissão é normalmente controlado de forma a manter a tensão terminal constante. Porém, no caso de geradores síncronos conectados em redes de distribuição, atualmente, não há consenso entre diferentes guias e práticas adotadas por concessionárias distintas sobre qual é a melhor filosofia de controle a ser adotada para o sistema de excitação. Tipicamente, há duas formas de controle que podem ser empregadas: tensão constante ou fator de potência (potência reativa) constante (CIGRÉ Working Group 37.23, 1999; CIRED Working Group 4, 1999; Jenkins et al., 2000; Hurley et al., 1999). Portanto neste trabalho, ambas as formas de controle são analisadas. Uma descrição detalhada sobre o sistema de excitação de geradores síncronos atuando como um regulador de tensão ou de fator de potência é apresentada em Hurley et al. (1999). Assim, somente os conceitos básicos são revistos aqui.

A estrutura geral do sistema de excitação de um gerador síncrono é mostrada na Figura 1, a qual consiste de circuitos de medição e processamento de sinais, um regulador e uma excitatriz. Um determinado sinal de erro é enviado para o regulador e a tensão de campo E_fd da excitatriz é ajustada baseada na saída do regulador. Além disso, o conjunto regulador/excitatriz usualmente é equipado com limitadores de sobre/sub excitação, os quais, de fato, limitam a quantidade de potência reativa injetada ou consumida pelo gerador (Kundur, 1994). A excitatriz pode ser controlada para atuar como um regulador de tensão ou de fator de potência, como discutido a seguir.

Regulador de tensão: neste caso, o sinal medido X é dado por (1) - sendo: _T o fasor da tensão terminal, _T o fasor da corrente terminal, j é o operador complexo e X_C é a reatância de compensação de corrente reativa. Normalmente, um valor positivo de X_C (reactive droop compensation) é empregado para compartilhar a corrente reativa entre diferentes geradores conectados a uma mesma barra. Por outro lado, um valor negativo de X_C (line drop compensation) é adotado com o objetivo de controlar a tensão em uma barra remota, usualmente a tensão terminal do lado de alta do transformador. Neste trabalho, para manter a generalidade dos estudos, compensação de corrente reativa foi negligenciada (X_C = 0). Nesse caso, a tensão terminal do gerador é diretamente comparada com a tensão de referência. O uso de compensação de corrente reativa não deve ser confundido com o uso de reguladores de fator de potência (Hurley et al., 1999).

Regulador de fator de potência: neste caso, o sinal medido X é o fator de potência. A tensão de campo é automaticamente ajustada para manter o fator de potência constante. Esse tipo de regulador é freqüentemente utilizado no controle de excitação de grandes motores síncronos (Hurley et al., 1999). No caso de geradores distribuídos, tal estratégia de controle é adotada por produtores independentes para evitar o pagamento de penalidades devido ao consumo de potência reativa ou para maximizar a geração de potência ativa. Neste caso, usualmente, operação com fator de potência unitário é adotada.

Nos estudos apresentados nas próximas seções, no caso do regulador de tensão, a tensão de referência foi escolhida igual a 1 pu. Enquanto que, no caso do regulador de fator de potência, adotou-se o valor de referência do fator de potência igual a 1.

3 PERFIL DE TENSÃO DE REGIME PERMANENTE

Um dos principais fatores técnicos que pode limitar a quantidade de geração distribuída conectada em redes de distribuição é o aumento das tensões nodais durante carga leve na presença de geradores distribuídos (Jenkins et al., 2000; Masters, 2002). De forma simplificada, tal problema ocorre em redes de distribuição devido ao baixo valor da relação X/R e a configuração radial adotada nestes sistemas (Masters, 2002). Antes de instalar um gerador em uma determinada rede de distribuição, é necessário garantir que o perfil de tensão da rede não será adversamente afetado. Assim, os seguintes casos mais críticos precisam ser analisados (Masters, 2002):

• Máximo carregamento e sem geração.

• Mínimo carregamento e máxima geração.

• Máximo carregamento e máxima geração.

Embora algumas concessionárias considerem mínimo carregamento igual à carga nula, neste trabalho, mínimo carregamento foi considerado igual a 10% do máximo carregamento. Além disso, a máxima variação de tensão permissível adota foi ±5% (1,05/0,95 pu).

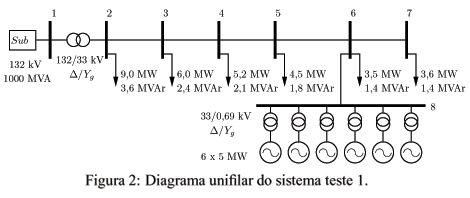
O diagrama unifilar da rede utilizada nesta seção é mostrado na Figura 2. Tal rede é composta por um sistema de subtransmissão de 132 kV, 60 Hz com nível de curto-circuito de 1000 MVA, representado por um equivalente de Thevenin, alimentando uma rede de distribuição de 33 kV através de um transformador conectado em D/Yg. A relação X/R do alimentador de distribuição é 4,5. O tap do transformador da subestação foi ajustado de forma a garantir que não haja violação do perfil de tensão durante máximo e mínimo carregamento considerando o caso sem geradores (tap = 1,05%). Suponha que um produtor independente deseje instalar 6 geradores de corrente alternada com capacidade de 5 MW cada junto à barra 8 através de transformadores dedicados, como representado na Figura 2. Para esta situação diversas simulações foram realizadas para verificar qual forma de geração permite tal instalação do ponto de vista de perfil de tensão.

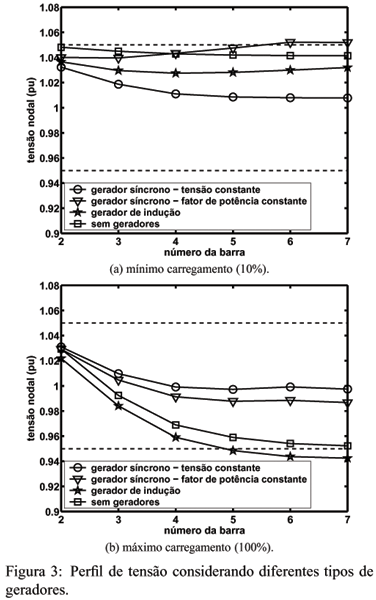
O perfil de tensão da rede considerando máximo e mínimo carregamento é mostrado na Figura 3 para os casos sem gerador, com gerador de indução, com gerador síncrono controlado por tensão e com gerador síncrono controlado por fator de potência. Nesta figura, as duas linhas horizontais tracejadas indicam o valor máximo e mínimo de tensão permissível (0,95/1,05 pu). Além disso, neste caso, todos os geradores estão injetando potência nominal na rede (5 MW cada). Verifica-se que, durante mínimo carregamento, o uso dos geradores síncronos operando com fator de potência constante faz com que a tensão em algumas barras viole o limite máximo de tensão. Por outro lado, no caso de máximo carregamento, o uso de geradores de indução acarreta a violação do valor mínimo de tensão em algumas barras. Enquanto que no caso do uso de geradores síncronos operando com tensão constante, os limites de tensão não são violados independentemente do carregamento da rede. Neste caso, os geradores síncronos operam com fator de potência igual a 0,9861 indutivo durante mínimo carregamento e 0,9992 capacitivo durante máximo carregamento, fazendo com que não haja violações dos limites de tensão.

Com o objetivo de determinar quantos geradores podem operar simultaneamente com capacidade nominal para cada tipo de máquina considerando máximo e mínimo carregamento o seguinte estudo foi realizado. Para cada tipo de gerador e carregamento do sistema, instalou-se apenas um gerador na rede e o perfil de tensão foi calculado. O estudo foi repetido acrescentando-se mais um gerador. Tal procedimento foi executado até que o limite de tensão foi violado ou os seis geradores foram considerados em operação simultaneamente. Assim, pode-se determinar qual a quantidade máxima de geradores é possível instalar na barra 8. Os resultados são apresentados na Tabela 1, sendo que na terceira coluna descreve-se o fator que limita a instalação de mais um gerador. Pode-se verificar que somente o caso com geradores síncronos controlados por tensão permite que todos os geradores sejam operados simultaneamente. No caso em que os geradores síncronos são controlados por fator de potência, somente 2 geradores podem ser instalados de forma a evitar violação do limite máximo de tensão durante mínimo carregamento. Por outro lado, usando-se máquinas de indução, somente 5 geradores podem ser instalados de forma a evitar violação do limite mínimo de tensão durante máximo carregamento.

3.1 Variação de Tensão de Regime Permanente Durante Desconexão do Gerador

Um importante aspecto relacionado com perfil de tensão de regime permanente é determinar quanto a tensão da rede varia quando os geradores são inesperadamente desconectados, visto que os controladores de tensão de redes de distribuição, e.g. controle de tap de transformadores sob carga, serem relativamente lentos. Assim, deseja-se que tal variação seja tão pequena quanto possível. Para analisar essa questão, o seguinte índice global pode ser utilizado para quantificar o impacto provocado pela desconexão dos geradores:

sendo: nb o número de barras do sistema, V_i^g a tensão nodal da barra i na presença de geradores e V_i^s a tensão nodal da barra i no caso sem geradores. Os resultados obtidos considerando que os seis geradores são desconectados simultaneamente para os casos com máximo e mínimo carregamento são apresentados na Tabela 2. Observa-se que o caso com geradores síncronos operando com fator de potência unitário ou com gerador de indução implica na menor variação de tensão. Nesse caso, o gerador síncrono não injeta ou consome potência reativa, diminuindo a diferença da distribuição de correntes reativas quando comparado com o caso sem geradores. No caso do gerador de indução, parte da potência reativa consumida pelo gerador é fornecida pelo banco de capacitores instalado localmente (Jenkins et al., 2000), também influenciando pouco a distribuição de correntes reativas quando comparado com o caso sem geradores. Por outro lado, o caso com gerador síncrono controlado por tensão, a variação de tensão é maior, visto tal forma de geração modificar bastante o perfil de tensão da rede quando comparado com o caso sem geradores, conforme ilustra a Figura 3.

3.2 Regulação de Tensão de Regime Permanente

Outra questão importante relacionada com perfil de tensão de regime permanente é a regulação de tensão do sistema, i.e. qual a diferença das tensões nodais durante máximo e mínimo carregamento. É desejável que essa variação seja tão pequena quanto possível. Para analisar essa questão o seguinte índice global pode ser utilizado:

sendo: V_i^max a tensão nodal da barra i durante máximo carregamento e V_i^min a tensão nodal da barra i durante mínimo carregamento. Os resultados obtidos são apresentados na Tabela 3. Observa-se que, excetuando-se o caso sem geradores, o uso do gerador síncrono controlado por tensão leva a uma melhor regulação de tensão do sistema. O uso de geradores síncronos operando com fator de potência constante e geradores de indução também melhora a regulação de tensão do sistema, porém não tanto quanto o caso anterior. Isso ocorre porque parte da potência ativa requerida pelas cargas é fornecida localmente pelos geradores, diminuindo a queda de tensão ao longo do alimentador e, por conseguinte, melhorando a regulação de tensão do sistema.

4 PERDAS ELÉTRICAS

Embora o item perdas elétricas não seja um fator técnico que possa limitar a quantidade de geração conectada em redes de distribuição, ele é um importante fator econômico (Borges e Falcão, 2003; Salman, 1996). Assim, nesta seção, as perdas de potência ativa do sistema apresentado na Figura 2 são determinadas considerando diferentes cenários de geração e carga. Os resultados são apresentados na Tabela 4. O valor das perdas para o caso sem geradores também é mostrado. Os seguintes fatos podem ser observados:

Máximo carregamento: verifica-se que durante máximo carregamento a instalação de um gerador de corrente alternada ajuda a diminuir as perdas elétricas do sistema. A cada novo gerador instalado as perdas diminuem ainda mais até o caso em que três geradores são instalados. Então a inclusão de um novo gerador leva a um aumento das perdas elétricas, indicando saturação na capacidade de diminuir as perdas do sistema. O uso de geradores síncronos controlados por tensão leva a um melhor desempenho em relação ao quesito perdas, visto que tal gerador fornece potência ativa e reativa localmente. Por outro lado, o uso do gerador de indução não acarreta uma grande redução das perdas, e no caso com seis geradores, de fato, as perdas são maiores do que as obtidas para a situação sem geradores. Neste caso, o gerador consome potência reativa da rede, afetando adversamente as perdas elétricas.

Mínimo carregamento: neste caso, a presença de geradores leva a um aumento das perdas elétricas, independentemente do tipo de gerador empregado. Nesta situação, grande parte da potência ativa gerada pelos geradores é exportada para o sistema de subtransmissão, afetando adversamente as perdas. O uso de geradores síncronos leva ao pior desempenho da rede no quesito perdas elétricas pois, para manter a tensão constante em 1 pu, o gerador consome potência reativa. Contudo, destaca-se que, como o carregamento local é mínimo, o aumento das perdas em certos casos pode ser financeiramente compensado com a comercialização do excedente de geração.

5 ESTABILIDADE DE TENSÃO

De forma geral, a instalação de geradores próximos às cargas pode permitir um aumento da margem de estabilidade de tensão de redes de distribuição. Porém, o quanto que a instalação do gerador pode contribuir para o aumento da margem de estabilidade depende da troca de potência reativa entre o gerador e o sistema. Portanto, nesta seção, as curvas PVs do sistema apresentado na Figura 4 são obtidas. Tal sistema é composto por um sistema de subtransmissão de 132 kV, 60 Hz com nível de curto-circuito de 1500 MVA, o qual alimenta uma rede de distribuição de 33 kV através de dois transformadores conectados em D/Yg. Na extremidade desse sistema há um gerador de corrente alternada com capacidade de 30 MW. Usualmente, geradores distribuídos não são redespacháveis. Assim, as curvas PVs do sistema foram obtidas variando-se as cargas ativas e reativas mas mantendo o gerador operando em sua capacidade nominal. Além disso, as curvas PVs foram obtidas através de sucessivas simulações dinâmicas no domínio do tempo (simulação de estabilidade transitória) com duração de 50 segundos. Em t = 0 segundo, um aumento de carga de 1% foi aplicado, então uma simulação dinâmica com duração de 50 segundos foi executada. Os valores de tensão nodal, potência ativa e reativa das cargas, e tensão terminal e velocidade do rotor do gerador em t = 50 segundos foram armazenados. Este procedimento foi realizado sucessivamente até a curva PV ter sido obtida. O intervalo de simulação de 50 segundos mostrou ser suficiente para o sistema convergir para um novo ponto de regime permanente após o aumento das cargas. Esse procedimento foi adotado para garantir que todas as informações relacionadas com a dinâmica do sistema fossem incluídas nos resultados. A curva PV da barra 4 é mostrada na Figura 5. Verifica-se que o uso de um gerador síncrono aumenta a margem de estabilidade de tensão do sistema. Além disso, o uso da excitatriz do gerador como um regulador de tensão permite que o ganho seja maior. Por outro lado, no caso de um gerador de indução, embora inicialmente o perfil de tensão seja melhorado, a margem de estabilidade de tensão do sistema é reduzida. Neste caso, o deslocamento do ponto A para o ponto B ocorre com apenas um incremento de carga. É possível verificar, através de simulação dinâmica, que isso acontece porque ao aumentar a carga do sistema além do ponto A, o gerador de indução torna-se instável. Isso ocorre pois a cada redução da tensão terminal, o escorregamento do gerador aumenta. No limite, o gerador de indução torna-se instável. Neste instante, de fato, o sistema de proteção de sobre-velocidade do gerador atuaria, desconectando-o, e o sistema, teoricamente, retornaria para a curva PV para a situação sem geradores caso não haja cargas dinâmicas no sistema.

6 ESTABILIDADE TRANSITÓRIA

O tempo de atuação do sistema de proteção em redes de distribuição é relativamente elevado. Adicionalmente, o valor da constante de inércia de geradores distribuídos é baixo, usualmente menor que 2 segundos. Por conseguinte, estabilidade transitória pode limitar consideravelmente a quantidade de potência ativa injetada por geradores distribuídos. Assim, nesta seção, a resposta de geradores de corrente alternada durante uma contingência é analisada.

Durante uma falta trifásica, geradores síncronos aceleram, podendo tornar-se instáveis devido à perda de sincronismo com o resto do sistema. Isso pode ser verificado analisando-se a resposta do ângulo do rotor no tempo. Por outro lado, no caso de geradores de indução, durante uma falta o gerador acelera e, conseqüentemente, o consumo de potência reativa aumenta, podendo levar o sistema a um colapso de tensão. Assim, o fenômeno de instabilidade de geradores de indução pode ser verificado analisando-se a resposta da tensão terminal ou do desvio de velocidade do rotor no tempo (Akhmatov et al., 2003; Samuelsson e Lindahl, 2005; Freitas et al., 2004).

Na Figura 6, usando o sistema teste 2, apresentam-se as respostas dinâmicas de diferentes geradores de corrente alternada perante um curto-circuito trifásico aplicado na barra 4 em t = 0,500 segundo, eliminado em 15 ciclos através da desconexão do ramo 2-4, quando os geradores estavam injetando 25 MW na rede. Verifica-se que somente o caso com um gerador síncrono controlado por tensão é estável.

O comportamento diferente de cada gerador de corrente alternada pode ser explicado analisando-se a troca de potência reativa entre o gerador e a rede elétrica no tempo, a qual é mostrada na Figura 7. No caso de gerador de indução, a troca de potência reativa mostrada na Figura 7(c) leva em consideração a potência reativa fornecida pelo banco de capacitores conectado nos terminais da máquina. Observa-se que no caso do gerador síncrono com controle de tensão, durante e após a falta, a quantidade de potência reativa injetada pelo gerador na rede aumenta, beneficiando a performance dinâmica do gerador. No caso do gerador síncrono operando com fator de potência constante, após o início da falta, observa-se que ele injeta potência reativa na rede por um breve período devido ao atraso da resposta do sistema de excitação. Entretanto o aumento da potência reativa é logo anulado, pois o regulador de tensão tenta manter nula a injeção de potência reativa na rede. Tal comportamento afeta de forma adversa a dinâmica do gerador, tornando-o instável. Por outro lado, no caso do gerador de indução, durante um breve período após o início do curto, o gerador passa a injetar reativos na rede devido ao fenômeno de auto-excitação. Porém, logo na seqüência, o gerador passa a consumir uma grande quantidade de potência reativa, levando o sistema ao colapso de tensão caso o gerador não seja desconectado.

Um importante aspecto relacionado com a questão da estabilidade transitória é determinar qual a máxima potência que o gerador pode injetar na rede mantendo uma resposta estável para um determinado tempo de atuação do sistema de proteção, ou seja, a potência crítica para um determinado tempo de eliminação da falta. Para investigar essa questão, numerosas simulações repetidas foram realizadas considerando diferentes tempos de eliminação da falta. A mesma contingência descrita anteriormente foi simulada, i.e. um curto-circuito trifásico aplicado na barra 4 eliminado através da desconexão do ramo 2-4. Os resultados são resumidos na Tabela 5. Verifica-se que o uso do gerador síncrono operando com tensão constante permite obter os maiores valores de potência crítica. Por outro lado, o uso do gerador de indução ou do gerador síncrono controlado por fator de potência leva a menores valores de potência crítica.

7 AFUNDAMENTO DE TENSÃO

A ocorrência de curtos-circuitos desequilibrados em redes de distribuição é bastante freqüente. Durante esses curtos, ocorrem afundamentos de tensão nas barras do sistema. A presença de geradores de corrente alternada pode influenciar a duração e a magnitude desses afundamentos de tensão em razão da alteração dos níveis de curto-circuito da rede e do comportamento dinâmico da troca de potência reativa entre o gerador e a rede. Assim, nesta seção, apresenta-se uma análise sobre afundamentos de tensão durante uma falta desequilibrada usando simulações eletromagnéticas. A rede elétrica utilizada foi a mesma apresentada na Figura 4.

Nas Figuras 8(a) e 8(b), apresentam-se as respostas de tensão das barras 4 e 5, respectivamente, para um curto-circuito fase-A-terra com duração de 400 ms aplicado na barra 4 em t = 200 ms considerando os casos com e sem geradores. No caso da barra 4, verifica-se que a severidade do afundamento de tensão é maior na presença dos geradores. Isso ocorre por causa do aumento do nível de curto-circuito na rede com a instalação do gerador de corrente alternada. Por outro lado, no caso da barra 5, verifica-se que, na presença de um gerador síncrono operando com tensão constante, a severidade do afundamento de tensão é menor. Enquanto que no caso do gerador de indução o afundamento da tensão na barra 5 aumenta. Ao passo que no caso do gerador síncrono operando com fator de potência constante praticamente não há diferença com relação ao caso sem gerador. O gerador de corrente alternada está conectado na barra 5, assim, o fator que influencia a resposta de tensão nesta barra é predominantemente o comportamento da potência reativa trocada entre o gerador e a rede elétrica. Como visto anteriormente, somente o gerador síncrono operando com tensão constante aumenta de forma sustentada a injeção de potência reativa durante faltas.

Para melhor entender o impacto de cada tipo de geração nesse quesito; diversas simulações eletromagnéticas foram realizadas considerando diferentes tempos de eliminação da falta descrita anteriormente. De maneira geral, afundamentos de tensão devido a faltas podem ser caracterizados pela magnitude e duração, i.e. mínimo valor rms (root mean square) de tensão e tempo que a tensão permanece abaixo de um determinado valor, respectivamente (Bollen, 2000; IEEE Standards Coordinating Committee 22, 1995). Para calcular a duração do afundamento de tensão, neste trabalho, o valor de 0,85 pu foi adotado. Os resultados são resumidos na Tabela 6, considerando a resposta de tensão da barra 4 (barra onde a falta é aplicada) e da barra 5 (barra onde o gerador de corrente alternada é instalado). No caso da resposta de tensão da barra 5, pode-se confirmar que o uso do gerador síncrono controlado por tensão melhora o desempenho da tensão da barra em relação ao quesito magnitude de afundamento de tensão. No caso do gerador síncrono com controle de fator de potência, em alguns casos há melhora no item magnitude de afundamento de tensão na barra 5, porém quando o tempo de eliminação da falta cresce, a presença do gerador contribui de forma negativa para a resposta de tensão desta barra. Por outro lado, no caso do gerador de indução, independentemente do tempo de duração da falta, tanto a magnitude quanto a duração do afundamento de tensão são maiores se comparada com o caso sem geradores. Tais diferenças podem ser explicadas pelo comportamento dinâmico da potência reativa trocada entre o gerador e o sistema, como discutido anteriormente. Por outro lado, independentemente do tipo de gerador de corrente alternada utilizado, em todos os casos, há uma piora no desempenho dinâmico da resposta de tensão da barra 4 devido à alteração do nível de curto-circuito da rede. Assim, verifica-se que o uso de um gerador síncrono em uma instalação industrial (autoprodutor) pode melhorar a performance desta barra quanto ao quesito afundamento de tensão durante faltas desequilibradas. Porém, os demais consumidores podem ser prejudicados pela instalação desse gerador.

8 CORRENTE DE CURTO-CIRCUITO

A instalação de geradores rotativos em redes de distribuição pode aumentar os valores das correntes de curto-circuito, obrigando que as capacidades dos elementos do sistema de proteção e/ou, em casos extremos, dos componentes de redes, sejam atualizados. Assim, nesta seção, as correntes fornecidas por geradores síncronos e de indução durante faltas equilibradas e desequilibradas são determinadas usando simulação eletromagnética.

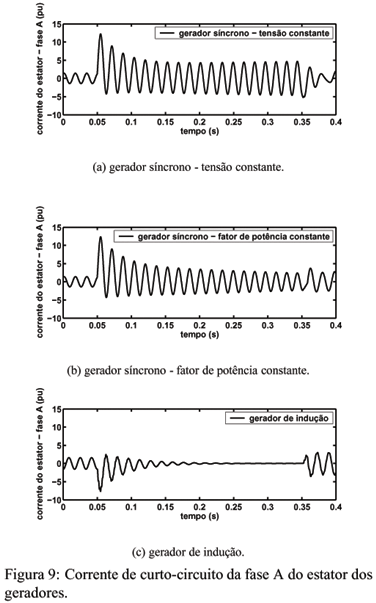
Na Figura 9, apresenta-se o comportamento dinâmico da fase A da corrente do estator dos geradores de corrente alternada para um curto-circuito trifásico aplicado na barra 5 em t = 50 ms e eliminado em t = 350 ms sem desconexão de ramos. O sistema utilizado é o mesmo apresentado na Figura 4. Verifica-se que a resposta de corrente é diferente para cada tipo de gerador. No caso do gerador de indução, embora inicialmente a magnitude de corrente seja bastante elevada (cerca de 7 pu), a corrente decai rapidamente, visto tal máquina não ter a capacidade de fornecer corrente de curto-circuito de forma sustentada. Essa característica pode ser importante caso deseje-se instalar geradores distribuídos em redes de distribuição com restrições de capacidade de corrente de curto-circuito. Teoricamente, a falta de capacidade de fornecimento de corrente de falta de forma sustentada pode ser um problema para o sistema de proteção do gerador detectar a falta. Porém, no caso de geradores de indução, relés de sub/sobre tensão temporizados podem ser empregados com este objetivo. No caso de geradores síncronos, verifica-se que o uso do sistema de excitação como um regulador de tensão, permite que o gerador forneça corrente de falta de forma sustentada. Porém, no caso do gerador síncrono operando com fator de potência constante, tal capacidade é diminuída.

Para melhor compreender o comportamento da corrente de curto-circuito fornecida pelos diferentes geradores de corrente alternada, diversas simulações eletromagnéticas foram realizadas considerando diferentes faltas. Os resultados estão resumidos na Tabela 7. Nessa tabela, na segunda coluna é apresentado o valor máximo da corrente do estator da fase A durante o curto. As demais colunas fornecem o valor rms da corrente em diferentes instantes após a aplicação da falta. Os resultados discutidos anteriormente podem ser corroborados. Verifica-se que em todos os casos o gerador síncrono com fator de potência constante leva a um maior valor da corrente máxima de curto-circuito e, por outro lado, o uso do gerador de indução acarreta valores menores. Isso pode ser parcialmente explicado pelo valor da tensão terminal pré-falta para cada caso, como mostrado na Tabela 8. Quanto maior o valor da tensão terminal pré-falta, maior a magnitude inicial da corrente de curto-circuito fornecida pelo gerador de corrente alternada. Também, verifica-se que somente o gerador síncrono operando com tensão constante é capaz de fornecer corrente de falta de forma sustentada.

9 CONCLUSÕES

Neste trabalho, apresentou-se um estudo detalhado sobre os impactos provocados pela conexão de geradores síncronos e de indução em redes de distribuição com o objetivo de determinar as principais diferenças entre estes geradores. No caso de geradores síncronos, analisou-se operação com tensão ou fator de potência constante. De forma geral, do ponto de vista de perfil de tensão de regime permanente, estabilidade de tensão e estabilidade transitória, o uso de geradores síncronos controlados por tensão leva a um melhor desempenho da rede e permite que a capacidade máxima permissível de geração distribuída seja mais elevada. Porém, caso seja de interesse do governo e/ou concessionárias, as penalidades impostas a este tipo de geradores durante operação indutiva devem ser eliminadas. O uso de gerador de indução mostrou-se interessante no caso de redes com restrições da capacidade de curto-circuito, visto tais máquinas não fornecerem correntes de falta de forma sustentada, porém, permitindo a detecção de falta usando relés de sub/sobre tensão. No caso de afundamentos de tensão, verificou-se que o uso de geradores síncronos com tensão constante pode melhorar o desempenho da resposta de tensão da barra em que o gerador é instalado, contudo, os demais consumidores podem ficar expostos a afundamentos de tensão mais intensos. De maneira geral, o uso de geradores síncronos com fator de potência constante não é a pior opção do ponto de vista do desempenho global do sistema.

10 AGRADECIMENTO

Os autores gostariam de agradecer à Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) pelo suporte financeiro fornecido para o desenvolvimento deste trabalho.

Artigo submetido em 01/05/2004

1a. Revisão em 11/04/2005;

2a. Revisão em 28/09/2005;

Aceito sob recomendação do Ed. Assoc. Prof. Glauco Taranto

• Akhmatov, V., Knudsen, H., Nielsen, A. H., Pedersen, J. K. Poulsen, N. K. 2003 . Modelling and transient stability of large wind farms, International Journal on Electrical Power and Energy Systems 25(1): 123-144.
• Belhomme, R., Plamondon, M., Nakra, H. e C. Gagnon, D. D. 1995 . Case study on the integration of a non-utility induction generator to the hydro-quebec distribution network, IEEE Transactions on Power Delivery 10(3).
• Bollen, M. H. J. 2000 . Understanding Power Quality Problems: Voltage Sags and Interruptions, 1 edn, Institute of Electrical and Electronic Engineers.
• Borges, C. L. T. Falcăo, D. M. 2003 . Impact of distributed generation allocation and sizing on reliability, losses and voltage profile, IEEE/PES Power Tech Conference Proceedings
• CIGRÉ Working Group 37.23 1999 . Impact of increasing contribution of dispersed generation on the power system, Technical report, CIGRÉ.
• CIRED Working Group 4 1999 . Dispersed generation, Technical report, CIRED.
• Ekanayake, J., Holdsworth, L. Jenkins, N. 2003 . Control of dfig wind turbines, Power Engineering Journal 17(1): 28-32.
• Freitas, W., Morelato, A. Xu, W. 2004 . Improvement of induction generator stability using braking resistors, IEEE Transactions on Power Systems 19(2): 1274-1249.
• Hurley, J. D., Bize, L. N. Mummert, C. R. 1999 . The adverse effects of excitation system var and power factor controller, IEEE Transaction on Energy Conversion 14(4): 1636-1641.
• IEEE Standards Coordinating Committee 22 1995 . Recommended practice for monitoring electric power quality, IEEE Std 1159-1995 .
• IEEE Task Force 1993 . Load representation for dynamic performance analysis, IEEE Transactions on Power Delivery 8(1): 472-482.
• Jenkins, N., Allan, R., Crossley, P., Kirschen, D. Strbac, G. 2000 . Embedded Generation, 1 edn, Institute of Electrical Engineers.
• Kundur, P. 1994 . Power System Stability and Control, 1 edn, McGraw-Hill Inc.
• Ledesma, P. Usaola, J. 2005 . Doubly fed induction generator model for transient stability analysis, IEEE Transactions on Energy Conversion 20(2): 388-397.
• Masters, C. L. 2002 . Voltage rise: the big issue when connecting embedded generation to long 11 kV overhead lines, Power Engineering Journal 16(1): 5-12.
• McQuin, N. P., Willians, P. N. Williamson, S. 1989 . Transient electrical and mechanical behavior of large induction generator installations, 4th International Conference on Electrical Machines and Drives, pp. 251-255.
• Parsons, J. R. 1984 . Cogeneration application of induction generators, IEEE Transactions on Industry Applications 20
• Salman, S. K. 1996 . The impact of embedded generation on voltage regulation and losses of distribution networks, IEE Colloquium on the Impact of Embedded Generation on Distribution Networks, pp. 2/1-2/5.
• Samuelsson, O. Lindahl, S. 2005 . On speed stability, IEEE Transactions on Power Systems 20(2): 1179-1180.

Datas de Publicação

• Publicação nesta coleção
  17 Abr 2006
• Data do Fascículo
  Set 2005

Histórico

• Aceito
  28 Set 2005
• Revisado
  11 Abr 2005
• Recebido
  01 Maio 2004