Abstracts
This paper proposes improved H-2 and H-infinity conditions for continuous-time linear systems with polytopic uncertainties based on a recent result for the discrete-time case. Basically, the performance conditions are built on an augmented-space with additional multipliers resulting in a decoupling between the Lyapunov and system matrices. This nice property is used to develop new conditions for the robust stability, performance analysis, and control synthesis of linear systems using parameter dependent Lyapunov functions in a numerical tractable way.
Robustness; H2/H<FONT FACE=Symbol>¥</FONT> norms; convex optimization
Este artigo propõe novas condições para as normas H-2 e H-infinito para sistemas lineares incertos utilizando as idéias originalmente propostas para sistemas discretos. Basicamente, as condições de desempenho são obtidas em espaço de estados aumentado onde novas variáveis livres são adicionadas ao problema resultando em uma separação entre as matrizes do sistema e de Lyapunov. Este propriedade é utilizada no desenvolvimento de novos critérios para análise de estabilidade robusta e desempenho, e síntese de controle para sistemas lineares utilizando funções de Lyapunov dependente de parâmetros que podem ser resolvidas através de problemas de otimização convexa.
Robustez; normas H2 e H<FONT FACE=Symbol>¥</FONT>; otimização convexa
SISTEMAS LINEARES
Improved H2 and H¥ conditions for robust analysis and control synthesis of linear systems
Alexandre TrofinoI; Daniel F. CoutinhoII; Karina A. BarbosaIII
IDept. Automation and Systems, UFSC, PO Box 476, 88040-900, Florianópolis, SC, Brazil. trofino@das.ufsc.br
IIDept. Electrical Engineering, PUCRS, Av. Ipiranga 6681, 90619-900, Porto Alegre, RS, Brazil. daniel@ee.pucrs.br
IIIDept. of Systems and Control, LNCC/MCT, Av. Getúlio Vargas 333, 25651-070, Petrópolis, RJ, Brazil. karinab@lncc.br
ABSTRACT
This paper proposes improved H-2 and H-infinity conditions for continuous-time linear systems with polytopic uncertainties based on a recent result for the discrete-time case. Basically, the performance conditions are built on an augmented-space with additional multipliers resulting in a decoupling between the Lyapunov and system matrices. This nice property is used to develop new conditions for the robust stability, performance analysis, and control synthesis of linear systems using parameter dependent Lyapunov functions in a numerical tractable way.
Keywords: Robustness, H2/H¥ norms, convex optimization.
RESUMO
Este artigo propõe novas condições para as normas H-2 e H-infinito para sistemas lineares incertos utilizando as idéias originalmente propostas para sistemas discretos. Basicamente, as condições de desempenho são obtidas em espaço de estados aumentado onde novas variáveis livres são adicionadas ao problema resultando em uma separação entre as matrizes do sistema e de Lyapunov. Este propriedade é utilizada no desenvolvimento de novos critérios para análise de estabilidade robusta e desempenho, e síntese de controle para sistemas lineares utilizando funções de Lyapunov dependente de parâmetros que podem ser resolvidas através de problemas de otimização convexa.
Palavras-chave: Robustez, normas H2 e H¥, otimização convexa.
1 INTRODUCTION
Recently, de Oliveira et al. (1999) have proposed an enhanced stability test for discrete-time systems for which the controller parametrization does not explicitly depends on the Lyapunov function. This allows for instance the use of parameter dependent Lyapunov function to design a fixed robust
2 or ¥ controller or even to solve mixed control problems in a less conservative way. Moreover, it was shown that their method recover the usual LMI test for quadratic stability as a particular case. Thus the new condition will never give a more conservative result if compared with the usual quadratic stability test. These nice properties are basically due to the LMI characterization in an augmented-space which introduces a new slack variable bypassing the product term that appears in the Lyapunov stability condition for discrete-time systems. In other words, the following usual condition
¥ controller or even to solve mixed control problems in a less conservative way. Moreover, it was shown that their method recover the usual LMI test for quadratic stability as a particular case. Thus the new condition will never give a more conservative result if compared with the usual quadratic stability test. These nice properties are basically due to the LMI characterization in an augmented-space which introduces a new slack variable bypassing the product term that appears in the Lyapunov stability condition for discrete-time systems. In other words, the following usual condition
is replaced by the following improved condition
Notice that the term A¢PA in (1) is the main source of conservativeness when dealing with uncertain system and robust design with mixed performance specifications. The reason is that robust performance tests are less conservative when P is parameterized in terms of the uncertainties and the performance indexes, but the robust controller parametrization requires a single P to be used. The improved condition in (2) eliminates the constraint of a single Lyapunov function because the controller parametrization does not depend on P.
Since the publication of the aforementioned paper, several researchers have tried to get a similar result for linear continuous time systems. However, the proposed results are not convex, as for instance the techniques in (Shaked, 2001), (Trofino and de Souza, 2002), and even the convex approach proposed by Apkarian et al. (2001) has shown to be more conservative than the usual quadratic stability test in many cases. At the same time, Ebihara and Hagiwara (2002) have proposed a dilated LMI version of the standard LMI tests for robust control synthesis under mixed performance specifications by means of parameter-dependent Lyapunov functions. As in the previous references, the method is not convex when solving robust control problems because a scalar must be tuned using a line search procedure. Some nice properties of this line search problem are presented in the paper.
From the above scenario, this paper aims to present new LMI conditions for
2 and ¥ analysis of linear uncertain continuous time systems. Similarly to Similarly to Apkarian et al. (2001) and (Ebihara and Hagiwara, 2002), the proposed approach is convex but in some cases may be more conservative than the usual LMI conditions based on quadratic stability, this behavior relies on the fact that the dilated conditions only recover the standard LMI quadratic stability tests for the nominal case. A strong argument to use the improved conditions instead of the usual LMI tests is its application for designing robust controllers with parameter-dependent Lyapunov functions considering
¥ analysis of linear uncertain continuous time systems. Similarly to Similarly to Apkarian et al. (2001) and (Ebihara and Hagiwara, 2002), the proposed approach is convex but in some cases may be more conservative than the usual LMI conditions based on quadratic stability, this behavior relies on the fact that the dilated conditions only recover the standard LMI quadratic stability tests for the nominal case. A strong argument to use the improved conditions instead of the usual LMI tests is its application for designing robust controllers with parameter-dependent Lyapunov functions considering  2 or
2 or  ¥ specifications and even mixed performance criteria. Aiming to stress that the proposed results can lead to less conservative upper bounds of the performance criteria for uncertain systems, this paper focus on the performance analysis and the results illustrated through exhaustive numerical tests. Basically, the numerical experiments reported in Section 6 reveals that over 16000 randomly generated systems the proposed methodology has achieved a better result in about 83 % of cases in the robust
¥ specifications and even mixed performance criteria. Aiming to stress that the proposed results can lead to less conservative upper bounds of the performance criteria for uncertain systems, this paper focus on the performance analysis and the results illustrated through exhaustive numerical tests. Basically, the numerical experiments reported in Section 6 reveals that over 16000 randomly generated systems the proposed methodology has achieved a better result in about 83 % of cases in the robust  2 norm against the usual quadratic stability tests and the approach of Apkarian et al. (2001) that surprisingly has got a better result for only one system. The results for the
2 norm against the usual quadratic stability tests and the approach of Apkarian et al. (2001) that surprisingly has got a better result for only one system. The results for the  ¥ norm of uncertain systems are yet conservative and require further improvements. Section 7 presents the control results for both
¥ norm of uncertain systems are yet conservative and require further improvements. Section 7 presents the control results for both  2 and
2 and  ¥ performance specifications.
¥ performance specifications.
Notation. The notation used throughout this paper is standard. 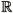 n denotes the set of n-dimensional real vectors,
n denotes the set of n-dimensional real vectors, 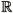 n×m is the set of n × m real matrices, In is the n × n identity matrix, 0n is the n × n matrix of zeros. For a real matrix S, S¢ denotes its transpose, and S > 0 means that S is symmetric and positive-definite. The symbol
n×m is the set of n × m real matrices, In is the n × n identity matrix, 0n is the n × n matrix of zeros. For a real matrix S, S¢ denotes its transpose, and S > 0 means that S is symmetric and positive-definite. The symbol  for a block matrix represents its symmetrical block outside the main diagonal. Matrix and vector dimensions are omitted whenever they can be inferred from the context.
for a block matrix represents its symmetrical block outside the main diagonal. Matrix and vector dimensions are omitted whenever they can be inferred from the context.
2 PROBLEM STATEMENT
Consider the following time-invariant system
where x Î 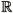 n denotes the state, w Î
n denotes the state, w Î 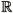 m the disturbance input vector, z Î
m the disturbance input vector, z Î 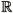 q the performance vector, A, B, C, D are real matrices of compatible dimensions. To represent some system dynamics and parameters that are not precisely known or are difficult to be exactly modelled, suppose the matrices of the system
q the performance vector, A, B, C, D are real matrices of compatible dimensions. To represent some system dynamics and parameters that are not precisely known or are difficult to be exactly modelled, suppose the matrices of the system  can take any value in a given polytope P as indicated below (Boyd et al., 1994):
can take any value in a given polytope P as indicated below (Boyd et al., 1994):
where Co{·} refers to the convex hull of {·}. For convenience, we may alternatively represent the uncertain system  by the notation
by the notation  Î
Î  where the set
where the set  is as follows:
is as follows:
One can characterize the system performance in terms of input-to-output experiments by means of the
2 and ¥ norms. When the disturbance signal is impulsive, the
¥ norms. When the disturbance signal is impulsive, the  2-norm is the most indicated (assuming that D = 0), on the contrary for square integrable signals the
2-norm is the most indicated (assuming that D = 0), on the contrary for square integrable signals the 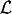 2-gain of the input-to-output operator (or simply
2-gain of the input-to-output operator (or simply  ¥-norm) can be used. For completeness, we provide the following definitions of system norms.
¥-norm) can be used. For completeness, we provide the following definitions of system norms.
Definition 1 The  2-norm of system
2-norm of system  is given by
is given by
where
i(t) is the system response to a unitary impulse in the i - th input channel with x(0) = 0 and D = 0. If the disturbance signal w(t) is a white noise with zero mean value and unitary power density spectra, the  2-norm may be interpreted as follows
2-norm may be interpreted as follows
where e(z(t)¢ z(t)) denotes the mathematical expectation of the random variable z(t)¢z(t).
Alternatively, supposing x(0) = 0, the greatest energy gain that can be obtained from the disturbance signal w(t) Î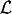 2 to the output z(t) corresponds to the
2 to the output z(t) corresponds to the  ¥-norm of the uncertain system
¥-norm of the uncertain system  leading to the following definition.
leading to the following definition.
Definition 2 The  ¥-norm of system
¥-norm of system  is given by
is given by
where
2 denotes the space of square integrable vector functions on [0, ¥).From the above scenario, the problem to be addressed in this paper is to obtain a new set of less conservative LMI conditions to compute the
2 and ¥ system norms in a numerical tractable way.
¥ system norms in a numerical tractable way.
3
2 Analysis Assuming that D = 0, a bound on the  2-norm of system
2-norm of system  can be computed by the following standard result from the LMI theory and the observability Gramian (Boyd et al., 1994).
can be computed by the following standard result from the LMI theory and the observability Gramian (Boyd et al., 1994).
Lemma 1Consider system with D = 0. Suppose there exist symmetric matrices P and N with appropriate dimensions satisfying the follow optimization problem for all
with D = 0. Suppose there exist symmetric matrices P and N with appropriate dimensions satisfying the follow optimization problem for all  Î
Î  .
.
Then,
 is quadratically stable and the following holds:
is quadratically stable and the following holds:
From above, notice that the decision variable P multiplies the system matrix, and when A is an affine function of another decision variable, as for instance the control-gain K in design control problems, Lemma 1 can be easily applied for control design if the system matrices are perfectly known. However, for the class of systems considered in this paper a robust controller can be obtained only by considering a single Lyapunov matrix P (Shaked, 2001) which may be very conservative. To overcome this problem, an augmented-LMI version of Lemma 1 is proposed in the following.
Theorem 2Consider system with D = 0. Suppose there exist positive definite matrices W,N and a free matrix G, with appropriate dimensions, satisfying the following optimization problem for all
with D = 0. Suppose there exist positive definite matrices W,N and a free matrix G, with appropriate dimensions, satisfying the following optimization problem for all  Î
Î  .
.
where = A + In and
= A + In and 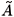 = A - In.
= A - In.
Then,
 is quadratically stable and the following holds:
is quadratically stable and the following holds:
Prrof: Suppose there exist W, G, N such that optimization problem (10) is satisfied.
Applying the Schur complement to the first LMI of (10) leads to
N - B¢G¢W-1GB > 0
Now, defining the Lyapunov matrix as
we get N - B¢ PB > 0.
Consider the second LMI of (10) and applying the Schur complement yields
From the fact that1 1 See, e.g., (de Oliveira et al., 1999) and (Shaked, 2001).
W + 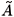 ¢ G¢ + G
¢ G¢ + G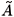 +
+ 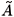 ¢G¢W-1G
¢G¢W-1G
condition (13) implies
 ¢P
¢P -
- 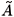 ¢P
¢P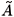 + 2C¢C = 2(A¢P + PA + C¢C) < 0
+ 2C¢C = 2(A¢P + PA + C¢C) < 0
taking into account the definition of P in (12).
Finally, the rest of the proof follows from Lemma 1.
Remark 1 The advantage of considering Theorem 2 instead of Lemma 1 is obvious for polytopic systems, since we can employ parameter-dependent Lyapunov matrices in Theorem 2 by only considering that W = Wi (for i = 1, ¼, p) in (10).
4
¥ AnalysisFrom the following LMI version of the Bounded Real Lemma (Boyd et al., 1994), an upper bound on the
¥-norm of system can be determined.
can be determined.
Lemma 3Consider system . Suppose there exist a symmetric matrix P with appropriate dimension and a scalar g satisfying the follow optimization problem for all
. Suppose there exist a symmetric matrix P with appropriate dimension and a scalar g satisfying the follow optimization problem for all  Î
Î  .
.
Then,
 is quadratically stable and the following holds:
is quadratically stable and the following holds:
From the same arguments of Section 3, the above Lemma may be conservative for control design of polytopic systems and also for multi-objective performance criteria (Apkarian et al., 2001). To overcome this problem, we give the following improved
¥ condition.Theorem 4 Consider system and suppose there exist a positive definite matrix W, a free matrix G and a positive scalar g satisfying the following optimization problem for all
and suppose there exist a positive definite matrix W, a free matrix G and a positive scalar g satisfying the following optimization problem for all  Î
Î  .
.
where WG = W + G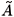 +
+ 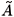 ¢G¢,
¢G¢,  = A + In and
= A + In and 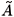 = A - In.
= A - In.
Then,
 is quadratically stable and the following holds:
is quadratically stable and the following holds:
Proof: Suppose that Theorem 4 is satisfied. Also, for convenience, define the following notation:
From above, notice that we can recast (16) as follows
From Theorem 2, the above implies the following
Finally, the above LMI is equivalent to (14) and the rest of this proof follows from Lemma 3.
Observe that the 4-th row and column of (16) can be removed, without loss of generality, reducing the size of the LMI.
Remark 2 From the same arguments of Remark 1, the improvement of Theorem 4 over the standard Bounded Real Lemma (BRL) is clear when we consider parameter-dependent Lyapunov matrices by taking W = Wi (for i = 1, ¼, p) in (16).
5 CONSERVATIVENESS
To show the source of conservativeness of the proposed method, consider the following identity:
Without loss of generality let us decompose P as P = G¢W-1G for some free matrix G and some W > 0 to get
Using the last inequality as an upper bound for 2(A¢P + PA) we get the following LMI with the Schur complement
Clearly (22) implies F< 0. However, the converse is not true in general. An exception occurs when the choice G = -W
-1 is possible. In this case we get
which in turn yields
The choices G = -W
-1 and P = (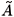 ¢)-1W-1 are possible whenever the matrix A is not uncertain, because otherwise P,G will depend on the same uncertain parameters leading (22) to be non-convex in these parameters. This shows that (22) is equivalent to the usual LMI quadratic stability test F< 0 in the nominal case but it may be conservative in the uncertain case. The same conclusion follows from the results in Section 3, i.e. they may be conservative in the uncertain case but not in the nominal case. However, due to the particular structure of the matrices in (18) the relation
¢)-1W-1 are possible whenever the matrix A is not uncertain, because otherwise P,G will depend on the same uncertain parameters leading (22) to be non-convex in these parameters. This shows that (22) is equivalent to the usual LMI quadratic stability test F< 0 in the nominal case but it may be conservative in the uncertain case. The same conclusion follows from the results in Section 3, i.e. they may be conservative in the uncertain case but not in the nominal case. However, due to the particular structure of the matrices in (18) the relation 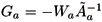 is no longer possible which suggests the results in section 4 may have an additional degree of conservatism. This point needs further investigation.
is no longer possible which suggests the results in section 4 may have an additional degree of conservatism. This point needs further investigation.
6 NUMERICAL EXAMPLES
This section reports a conservativeness analysis of the proposed improved conditions by means of exhaustive tests over 16000 linear uncertain systems which are randomly generated using Gaussian distribution with zero mean and unitary variance. Let us start with the results from Theorem 2. For each system  , the robust
, the robust  2 norm is compute by:
2 norm is compute by:
(i) Theorem 2 with parameter-dependent Lyapunov functions (see Remark 1), refereed to as (N);
(ii) The approach of Apkarian et al. (2001), refereed to as (T);
(iii) The standard
2-norm computation of Lemma 1 (quadratic stability approach) which is referred to as (Q).
The robust methods to compute the
2-norm can be applied whenever the underlying system is robustly stable. In this sense, it is required the Hurwitz stability of each matrix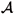 generated from the convex combination of A1, ¼, Ap to numerically verify ||
generated from the convex combination of A1, ¼, Ap to numerically verify || ||2 by means of a fine grid procedure. In addition, whenever necessary, we have to modify
||2 by means of a fine grid procedure. In addition, whenever necessary, we have to modify 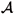 so that the Hurwitz stability is guaranteed for all
so that the Hurwitz stability is guaranteed for all 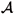 Î PA Co {A1, ¼, Ap}. To minimize the computational burden, such procedure has been applied only to the extreme values of
Î PA Co {A1, ¼, Ap}. To minimize the computational burden, such procedure has been applied only to the extreme values of 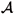 . Specifically, whenever the randomly generated matrix Ai is not Hurwitz stable, (s + 1)In has been subtracted from Ai, where s is the maximum real part of the eigenvalues of Ai. Although the later procedure cannot ensure the Hurwitz stability of
. Specifically, whenever the randomly generated matrix Ai is not Hurwitz stable, (s + 1)In has been subtracted from Ai, where s is the maximum real part of the eigenvalues of Ai. Although the later procedure cannot ensure the Hurwitz stability of 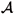 over PA, it can significantly reduce the number of generated systems that are not asymptotically stable over PA.
over PA, it can significantly reduce the number of generated systems that are not asymptotically stable over PA.
To carry out the statistical tests, we assume four different values for n and p which are respectively the state vector dimension and the vertex number. Precisely, we have taken 1000 systems for each situation n = 3, ¼, 6 and p = 2, ¼, 5, and our attention is focused on comparing:
(a) The number of times that each method provides a feasible solution; and
(b) The number of times that each method achieve the best performance.
Table 1 shows the number of systems that lead to feasible solutions to the methods (N), (T) and (Q). Observe that, the new method (N) and the approach (Q) present similar number of feasible solutions. Moreover, one can note that the approach (T) has worse performance.
Table 2 shows the number of systems in which the approaches (N), (T) and (Q) achieved the lowest upper-bound on || ||2. It turns out that the proposed
||2. It turns out that the proposed  2 condition has achieved the best performance in a large majority of cases, and the improvement is even better with the increasing of the number of vertices, even though the standard quadratic stability test demonstrates a better performance in some situations. In addition, the methodology proposed by Apkarian et al. (2001) has outperformed our approach and the quadratic method for only one system.
2 condition has achieved the best performance in a large majority of cases, and the improvement is even better with the increasing of the number of vertices, even though the standard quadratic stability test demonstrates a better performance in some situations. In addition, the methodology proposed by Apkarian et al. (2001) has outperformed our approach and the quadratic method for only one system.
A similar study is now carried out to analyze the conservativeness of the proposed
¥ condition. To this end we solve the robust ¥ problem by using the following approaches:
¥ problem by using the following approaches:
(i) Theorem 4 with parameter-dependent Lyapunov functions, refereed to as (N¥);
(ii) The standard
¥-norm computation of Lemma 3 (quadratic stability approach) which is referred to as (Q¥),
To the authors' knowledge, there is no other convex approach to robust
¥-norm computation in the continuous-time context. Assuming n = 5, p = 3 the number of feasible solution over 1000 systems are 985 with the proposed method (N¥) and 986 with the usual method (Q¥). The quadratic approach (Q¥) has achieved the best performance in 542 cases, and the new approach (N¥) in 303 cases. The same  ¥ upper bound was obtained with both methods in 141 cases. The situation is similar for other values of p and n. These numerical experiments confirm the claim in the previous section that the results for
¥ upper bound was obtained with both methods in 141 cases. The situation is similar for other values of p and n. These numerical experiments confirm the claim in the previous section that the results for  ¥ are yet conservative and need to be improved.
¥ are yet conservative and need to be improved.
7 STATE-FEEDBACK CONTROL
One of the most advantages of the proposed
2 and ¥ conditions is the possibility of designing a robust state-feedback control law considering parameter-dependent Lyapunov functions. Notice that convex conditions for control design can be easily obtained from the Dual version of Theorems 2 and 4. To extend these theorems for control design, consider
¥ conditions is the possibility of designing a robust state-feedback control law considering parameter-dependent Lyapunov functions. Notice that convex conditions for control design can be easily obtained from the Dual version of Theorems 2 and 4. To extend these theorems for control design, consider  as defined in (3) with an additional control input u(t) Î
as defined in (3) with an additional control input u(t) Î 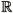 r, i.e.:
r, i.e.:
where K Î 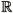 r×n is the control-gain to be determined, E Î
r×n is the control-gain to be determined, E Î 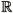 n×r, and F Î
n×r, and F Î 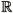 q×r are uncertain matrices. Similarly to Section 2, the uncertain system
q×r are uncertain matrices. Similarly to Section 2, the uncertain system  is represented by the notation
is represented by the notation  Î
Î  , where the set
, where the set  is redefined accordingly to (25).
is redefined accordingly to (25).
7.1
2 Design Setting D = 0, a state-feedback control law that stabilizes system  (while minimizing an upper-bound on its
(while minimizing an upper-bound on its  2-norm for all
2-norm for all  Î
Î  ) can be obtained by means of the dual version of Theorem 2.
) can be obtained by means of the dual version of Theorem 2.
The dual version of the improved
2 condition is devised from the controllability Gramian (Green and Limebeer, 1995) leading to the following result.Theorem 5Consider system with D = 0. Suppose there exist symmetric matrices Wi, N (i = 1, ¼, p), and non-symmetric ones G, Y with appropriate dimensions satisfying the following optimization problem for all
with D = 0. Suppose there exist symmetric matrices Wi, N (i = 1, ¼, p), and non-symmetric ones G, Y with appropriate dimensions satisfying the following optimization problem for all  Î
Î  .
.
where i = 1, ¼, p.
Then,
 is asymptotically stable with
is asymptotically stable with
u(t) = YG-1x(t),
and || ||2satisfies (11) for all
||2satisfies (11) for all  Î
Î  .
.
Proof: The proof of above Theorem is straightforward from the controllability Gramian and the control parametrization Y = KG.
Example 1 Consider a mass/spring/damper system given by the following representation (Zhou, 1998):
where x = [ x1x2 x3x4 ]¢, k1Î [ 0.8,1.2 ], k2Î [ 3.2,4.8 ], and
Applying Theorem 5, we get an upper-bound on the system 2-norm (in closed-loop) of l = 0.3478 with a control matrix
K = - [ 0.4839 0.2348 0.6042 0.2929 ].
It turns out that our approach has lead to a better result than the one proposed in (Apkarian et al., 2001) which get an upper-bound of l = 0.3959.
7.2
¥ DesignSimilarly to the
2 case, one can obtain a (robust) stabilizing state-feedback controller such that an upper-bound on the ¥-norm of
¥-norm of  is minimized by means of a dual version of Theorem 4.
is minimized by means of a dual version of Theorem 4.
Basically, we redefine the BRL in terms of the Lyapunov matrix inverse and then apply standard results from the matrix theory. These manipulations yields the following result.
Theorem 6Consider system and suppose there exist symmetric matrices W1, ¼, Wp, non-symmetric ones, G and Y, and a positive scalar g satisfying the following optimization problem for all
and suppose there exist symmetric matrices W1, ¼, Wp, non-symmetric ones, G and Y, and a positive scalar g satisfying the following optimization problem for all  Î
Î  .
.
where i Î { 1, ¼, p}, and
Then,
 is asymptotically stable with
is asymptotically stable with
u(t) = YG-1x(t),
and (17) is satisfied for all Î
Î  .
.
Proof: The proof of above Theorem is straightforward from the dual version of Theorem 4, i.e., by setting P = P-1, G = G-1, A = A¢, B = C¢ and C = B¢, and then applying the control parametrization Y = KG.
Example 2 Consider the following linear time-invariant system borrowed from (Gahinet et al., 1994):
where x = [ x1x2 x3x4 ]¢, k Î [ 0.09 , 0.4 ], and f Î [ 0.0038 , 0.04 ].
The problem to be addressed is to design a state-feedback law u = Kx such that the closed-loop system is robustly stable while minimizing an upper-bound on the worst-case  ¥-norm of the above system.
¥-norm of the above system.
Applying Theorem 6, we get an upper-bound g = 1.498 with a control-gain given by
K = - [ 51.523 399.593 22.331 664.714 ]
Table 3 shows a comparative study among the standard Bounded Real Lemma (BRL) in (Boyd et al., 1994), the improved LMI test of (Shaked, 2001, Lemma 3.1), and our approach. In spite of the fact that our approach seems to be more conservative than the Shaked's one, we stress the fact that our approach is convex while in (Shaked, 2001) a parameter e has to be optimized.
8 CONCLUDING REMARKS
This paper have proposed improved
2 and ¥ conditions for continuous-time linear systems with polytopic uncertainties. Basically, the performance conditions are built on an augmented-space with additional multipliers resulting in a decoupling between the Lyapunov and system matrices. This nice property can be used to design robust state-feedback controllers with parameter dependent Lyapunov functions taking into account both
¥ conditions for continuous-time linear systems with polytopic uncertainties. Basically, the performance conditions are built on an augmented-space with additional multipliers resulting in a decoupling between the Lyapunov and system matrices. This nice property can be used to design robust state-feedback controllers with parameter dependent Lyapunov functions taking into account both  2 and
2 and  ¥ norms. Statistical numerical tests have proven the advantage of the proposed
¥ norms. Statistical numerical tests have proven the advantage of the proposed  2 approach over previous results from the robust control literature. In addition, we have presented the
2 approach over previous results from the robust control literature. In addition, we have presented the  2 and
2 and  ¥ conditions for state-feedback design also considering parameter-dependent Lyapunov functions and a robust control law. Future research will concentrate on improving the
¥ conditions for state-feedback design also considering parameter-dependent Lyapunov functions and a robust control law. Future research will concentrate on improving the  ¥ results that are yet conservative and extend the results for filtering and control problems.
¥ results that are yet conservative and extend the results for filtering and control problems.
ACKNOWLEDGMENTS
This work was supported in part by "Conselho Nacional de Desenvolvimento Científico e Tecnológico - CNPq", Brazil, under PRONEX grant No. 0331.00/00. ,The work of the first author has been supported in part by CNPq, Brazil, under grant 305665/03-0/PQ and the third author by "Coordenação de Aperfeiçoamento de Pessoal de Ensino Superior - CAPES", Brazil.
Artigo submetido em 15/12/04
1a. Revisão em 21/06/05
ARTIGO CONVIDADO:
Versão completa e revisada de artigo apresentado no CBA-2004
Aceito sob recomendação do Ed. Assoc. Prof. Liu Hsu
- Apkarian, P., Tuan, H. D. Bernussou, J. (2001). Continuous-Time Analysis, Eigenstructure Assignment, and H2 Synthesis With Enhanced Linear Matrix Inequality (LMI) Characterizations, IEEE Transactions on Automatic Control 46(12): 1941-1946.
- Boyd, S., Ghaoui, L. E., Feron, E. Balakrishnan, V. (1994). Linear matrix inequalities in systems and control theory, SIAM books.
- de Oliveira, M. C., Bernussou, J. Geromel, J. C. (1999). A New Discrete-Time Robust Stability Condition, System & Control Letters 37: 261-265.
- Ebihara, Y. Hagiwara, T. (2002). Robust Controller Synthesis with Parameter-Dependent Lyapunov Variables: A Dilated LMI Approach, Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, pp. 4179-4184.
- Gahinet, P., Nemirovskii, A., Laub, A. J. Chilali, M. (1994). LMI Control Toolbox, The Mathworks Inc.
- Green, M. Limebeer, D. J. N. (1995). Linear Robust Control, Prentice Hall.
- Shaked, U. (2001). Improved LMI Representations for the Analysis and the Design of Continuous-Time Systems with Polytopic Type Uncertainty, IEEE Transactions on Automatic Control 46(4): 652-656.
- Trofino, A. de Souza, C. E. (2002). H2 Control of Rational Parameter-Dependent Continuous-Time Systems: A Parametric Lyapunov Function Approach, Proceedings of the 15th IFAC World Congress, Barcelona, Spain, pp. 2344-2349.
- Zhou, K. (1998). Essentials of Robust Control, Prentice Hall.
Publication Dates
-
Publication in this collection
08 May 2006 -
Date of issue
Dec 2005
History
-
Received
15 Dec 2004 -
Reviewed
21 June 2005 -
Accepted
21 June 2005








































