Resumos
Em instalações industriais, é comum a existência de processos multivariáveis que possuem variáveis com fortes interações entre si, além de não linearidades e de objetivos de controle conflitantes Assim, a sintonia de diversos controladores em plantas industriais complexas constitui um desafio aos engenheiros de processo e operadores. Este artigo aborda o problema de sintonizar n controladores PI/PID (Proporcional, Integral e Derivativo) em processos multivariáveis como um problema de otimização multiobjetivo. Um algoritmo genético multiobjetivo, modificado por uma técnica de nicho e formação de castas, é proposto para resolver o problema. A otimização é realizada em dois níveis. No primeiro, uma função local que agrupa os critérios ITSE (Integral Time Squared Error) e variância mínima é calculada para avaliar separadamente o desempenho de cada malha. Em seguida, uma função de custo global, considerando todas as malhas é usada para calcular um conjunto de soluções (conjunto de parâmetros do controlador PI/PID) para o problema de otimização. A metodologia foi aplicada no controle PI de uma unidade de craqueamento catalítico e o seu desempenho foi comparado ao de um controlador preditivo por matriz dinâmica. Os resultados mostram a aplicabilidade e eficiência da metodologia proposta.
Controle multivariável; Controle PI/PID; Algoritmo genético multiobjetivo; nichos; castas
Nonlinear multiple-input multiple-output (MIMO) processes which are common in industrial plants are characterized by significant interactions and nonlinearities among their variables. Thus, the tuning of several controllers in complex industrial plants is a challenge for process engineers and operators. This paper addresses the problem of simultaneously tuning n proportional-integral-derivative (PI/PID) controllers in a coupled multivariable process as a multi-criteria optimization problem. A multi objective genetic algorithm modified by a niching technique with castes formation is proposed to solve this problem. The optimization is carried out in two levels. In the first level a local function that considers both the integral time squared error (ITSE) and the minimum variance criteria is computed to separately evaluate the performance of each closed loop. Thereafter, a global cost function that considers all the loops is used to compute a set of solutions (a set of PI/PID parameters) to the optimization problem. The proposed system was applied to the control of a fluid catalytic cracking (FCC) unit, and its performance was compared to dynamic matrix control (DMC). The results show the applicability and effectiveness of the proposed method.
MIMO control; PI/PID control; Multi objective genetic algorithm; niching; castes
SISTEMAS INTELIGENTES
Um método evolucionário para sintonia de controladores PI/PID em processos multivariáveis
Lúcia Valéria R. de Arruda; Maria Cristina Szpak Swiech; Flávio Neves-Jr; Myriam Regattieri Delgado
Programa de Pós-Graduação em Engenharia Elétrica e Informática Industrial, Universidade Tecnológica Federal do Paraná, Av. 7 de Setembro, 3165, CEP 802301-901 - Curitiba - PR; lvrarruda@utfpr.edu.br; mmcrist@yahoo.com.br; neves@utfpr.edu.br; myriamdelg@utfpr.edu.br
RESUMO
Em instalações industriais, é comum a existência de processos multivariáveis que possuem variáveis com fortes interações entre si, além de não linearidades e de objetivos de controle conflitantes Assim, a sintonia de diversos controladores em plantas industriais complexas constitui um desafio aos engenheiros de processo e operadores. Este artigo aborda o problema de sintonizar n controladores PI/PID (Proporcional, Integral e Derivativo) em processos multivariáveis como um problema de otimização multiobjetivo. Um algoritmo genético multiobjetivo, modificado por uma técnica de nicho e formação de castas, é proposto para resolver o problema. A otimização é realizada em dois níveis. No primeiro, uma função local que agrupa os critérios ITSE (Integral Time Squared Error) e variância mínima é calculada para avaliar separadamente o desempenho de cada malha. Em seguida, uma função de custo global, considerando todas as malhas é usada para calcular um conjunto de soluções (conjunto de parâmetros do controlador PI/PID) para o problema de otimização. A metodologia foi aplicada no controle PI de uma unidade de craqueamento catalítico e o seu desempenho foi comparado ao de um controlador preditivo por matriz dinâmica. Os resultados mostram a aplicabilidade e eficiência da metodologia proposta.
Palavras-Chave: Controle multivariável, Controle PI/PID, Algoritmo genético multiobjetivo, nichos, castas.
ABSTRACT
Nonlinear multiple-input multiple-output (MIMO) processes which are common in industrial plants are characterized by significant interactions and nonlinearities among their variables. Thus, the tuning of several controllers in complex industrial plants is a challenge for process engineers and operators. This paper addresses the problem of simultaneously tuning n proportional-integral-derivative (PI/PID) controllers in a coupled multivariable process as a multi-criteria optimization problem. A multi objective genetic algorithm modified by a niching technique with castes formation is proposed to solve this problem. The optimization is carried out in two levels. In the first level a local function that considers both the integral time squared error (ITSE) and the minimum variance criteria is computed to separately evaluate the performance of each closed loop. Thereafter, a global cost function that considers all the loops is used to compute a set of solutions (a set of PI/PID parameters) to the optimization problem. The proposed system was applied to the control of a fluid catalytic cracking (FCC) unit, and its performance was compared to dynamic matrix control (DMC). The results show the applicability and effectiveness of the proposed method.
Keywords: MIMO control, PI/PID control, Multi objective genetic algorithm, niching, castes.
1 INTRODUÇÃO
O controle Proporcional-Integral-Derivativo (PID) é ainda hoje predominante no meio industrial. Mais que 90% de todas as malhas existentes são do tipo PI / PID atingindo uma larga faixa de aplicações: controle de processos, drivers para motores, indústria automobilística, controladores de vôo, pilotos automáticos, instrumentação, entre outros (Åstrom e Hagglund, 2001). Além disso, com a migração da tecnologia pneumática e elétrica para digital, o controlador PID se apresenta no mercado sob diversas formas e produtos como, por exemplo, os controladores single-loop standard, os componentes de software em controladores lógicos programáveis (CLP) e em sistemas digitais de controle distribuído (SDCD), os controladores embarcados em robôs e veículos autônomos, cd-players, etc.
Apesar desta importância, os controladores PID apresentam desempenho insuficiente em algumas aplicações. Tem sido relatado na literatura que uma porcentagem significante dos controladores instalados operam em modo manual e que mais de 50% dos PIDs instalados que operam em modo automático apresentam grandes variâncias (Oviedo et al. 2006). Este problema de desempenho é em muitos casos resultante de uma sintonia pobre devido, principalmente, à:
-
Ausência de conhecimentos dos operadores e engenheiros de comissionamento.
-
Adoção de métodos de sintonia genéricos que são baseados em critérios ad hoc os quais não são compatíveis com as características dos processos em análise;
-
Grande variedade de estruturas de controladores PIDs existentes, as quais levam a erros na aplicação das regras de sintonia.
A situação se agrava na indústria de processos químicos, que nos últimos anos tem adotado largamente o controle preditivo como estratégia de controle avançado, a qual requer malhas PID bem sintonizadas na camada regulatória da planta. Além disso, os processos químicos são naturalmente multivariáveis e com interações significantes entre as suas variáveis de entrada e saída, levando o engenheiro de processos, responsável por centenas de malhas, a necessitar de uma estratégia de sintonia de fácil implantação, mas necessariamente robusta (Åstrom e Hagglund, 2004).
Nesse contexto, este artigo propõe uma técnica baseada em algoritmos genéticos para sintonia de múltiplas malhas de controladores PI/PID em processos multivariáveis. Cada malha de controle é avaliada independentemente através de uma função de desempenho que considera aspectos de robustez, rejeição de perturbação, capacidade de seguir a referência, e variações no sinal de controle. Em seguida, o problema da sintonia conjunta dos n controladores é formulado como um problema de otimização multiobjetivo através da minimização de uma função custo que considera todas as malhas conjuntamente. Esta função custo é construída a partir da soma ponderada de todos os objetivos individuais (desempenho de cada malha). Um algoritmo genético (AG) baseado em nichos e formação de castas é proposto para solução do problema multiobjetivo: encontrar um conjunto de valores (múltiplas soluções) para cada um dos três parâmetros de todos os controladores PI/PIDs que otimizem esta função custo.
O projeto e a sintonia de controladores PI/PID multivariáveis têm sido estudados ao longo dos anos. Muitos métodos foram desenvolvidos e várias melhorias têm sido apresentadas. Entre estes destacam-se: Davison (1978) propôs uma metodologia para sintonia on-line de reguladores em um problema de controle robusto descentralizado. Luyben (1986) apresentou um método de sintonia simples para controle descentralizado de PID baseado na aplicação do método do relé em cada malha monovariável. Hsu et al. (1992) desenvolveram um algoritmo para síntese automática de reguladores auto-ajustáveis para processos MIMO lineares e invariantes no tempo. Yusof e Omatu (1993) apresentaram um PID descentralizado com auto-sintonia baseada em estratégias de estimação. Wang et al (1997) propuseram um método de sintonia para controladores PID em processos MIMO acoplados a partir do teste do relé descentralizado. E mais recentemente citam-se os trabalhos de Toh e Rangaiah (2002), Ayadi e Benhadj (2005) e Halaing et al (2007) que propuseram métodos de sintonia de controladores PIDs multivariáveis baseados em modelos.
Por outro lado, a utilização de métodos evolucionários em geral e de AG em particular nas áreas de controle e modelagem tem sido objeto de várias publicações desde o início dos anos 90. Fleming e Purshouse (2002) relataram várias aplicações de AG para projeto e sintonia de controladores PI/PID, LQG, MPC, H2/H¥ e controladores nebulosos e neuro-nebulosos. Segundo esses autores, apesar dos muitos trabalhos publicados, as pesquisas ainda se encontram "em sua infância'' e vários problemas permanecem em aberto. No caso especial de projeto e sintonia automática de controladores PI/PID em processos multivariáveis, algumas aplicações recentes têm sido relatadas (Herreros et al., 2002)-(Vlachos et al., 2002)-(Lewin e Parag, 2003)-(Farag e Werner, 2006)-(Chang, 2007). Com exceção do trabalho de Herreros e colaboradores (2002), todos estes autores formulam o problema do controle descentralizado multivariável como um problema de otimização simples. E para resolvê-lo, propõem modificações no algoritmo genético de Goldberg (1989). Com isto obtém-se apenas uma solução de sintonia a qual não pode ser considerada ótima uma vez que o problema de projeto/sintonia de controladores PI/PID é uma problema de otimização não-convexo (Åstrom et al, 1998).
O algoritmo genético MRCD (Multiple-objective Robust Control Design) proposto em (Herreros et al., 2002) é formulado numa abordagem multiobjetivo com seleção de Pareto, a qual será detalhada na próxima seção. Esse algoritmo utiliza múltiplas populações e técnicas especiais de elitismo, mutação e cruzamento a fim de assegurar a diversidade e a convergência para um conjunto de soluções. As especificações de desempenho são dadas em termos de normas H2/H¥ para cada malha individual. Essa metodologia pode ser aplicada indistintamente para síntese de controladores PI / PID em processos monovariável e multivariável, no entanto, necessita de um modelo matemático do processo a ser controlado. Além disso, a sua aplicação na sintonia automática é restrita, pois como faz uso de múltiplas populações, o tempo computacional associado ao cálculo das soluções, o qual já é normalmente elevado para abordagens evolutivas, torna-se proibitivo em aplicações on-line (Coello, 2000) - (Fonseca e Fleming, 2002).
A abordagem proposta neste artigo é uma alternativa à abordagem em (Herreros et al., 2002). As funções de avaliação de malha são baseadas em três critérios: Integral do Erro Quadrático Ponderado pelo Tempo (ITSE) e variância mínima aplicada aos sinais de controle u(t) e de saída y(t). Estes critérios são bem aceitos na indústria e mais fáceis de aplicar e calcular que critérios baseados em normas. A metodologia proposta não depende de um modelo matemático para o processo e pode ser utilizada com outros controladores, como por exemplo, um controlador nebuloso (Swiech et al, 2005). O algoritmo genético proposto procura múltiplas soluções para o problema de otimização multiobjetivo através da formação de nichos (Coello, 2000) e castas. Em cada nicho, os indivíduos da população são ordenados e posteriormente divididos e/ou agregados em grupos (castas) para o processo de reprodução. Segundo Goldberg (1989) e Mahfoud (1995), enquanto os AGs tradicionais realizam otimizações simples, os AGs que incorporam métodos de nichos são mais adequados para tratar problemas de otimização de funções multimodais, simulação de sistemas complexos e adaptativos, otimização de funções multiobjetivos, entre outros. Apesar dos nichos serem uma técnica conhecida na área de Computação Evolutiva, a formação de castas, na forma como é aqui apresentada, se constitui uma inovação do algoritmo proposto.
Além disto, como o algoritmo proposto utiliza uma abordagem de soma ponderada para avaliação de cada solução, é mais eficiente computacionalmente, podendo ser utilizado em aplicações que demandam menores tempos de processamento para se alcançar uma solução (Coello, 2000) - (Fonseca e Fleming, 2002). Entretanto, ao se optar por uma função ponderada na solução do problema multi-objetivo, a formação de um super-indivíduo (solução não-dominada única) pode ocorrer e deve ser minimizada pela introdução das castas, as quais funcionam como uma memória do algoritmo, permitindo a manutenção de um conjunto de soluções obtidas ao longo da evolução, ao invés de uma única solução para o problema.
2 FORMULAÇÃO DO PROBLEMA DE OTIMIZAÇÃO MULTIOBJETIVO
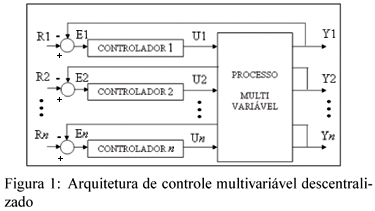
Os sistemas industriais de controle envolvem, em sua maioria, o controle de múltiplas variáveis de entrada e saída de processos. O uso de múltiplos controladores, um para cada variável a ser controlada numa estrutura descentralizada, é uma das estratégias utilizadas neste tipo de plantas, em substituição à utilização de um único controlador multivariável. Isto porque a implantação e supervisão de várias malhas de controladores independentes são tarefas mais fáceis de realizar na prática (Luyben, 1990). Nesta estratégia, considera-se que o processo multivariável é composto por n saídas independentes que podem ser controladas por n controladores monovariáveis, conforme ilustrado na figura 1.
No entanto, a maior parte dos processos reais apresenta acoplamento entre suas variáveis, o que significa que uma variável controlada (saída do processo) sofre influência de diversas variáveis manipuladas (entradas do processo). Neste caso, a sintonia dos n controladores, como descrito anteriormente, não é uma tarefa trivial. Existe a dificuldade de mensurar a contribuição de cada variável manipulada em cada uma das variáveis de saída. A modificação no parâmetro de um controlador pode melhorar o desempenho de uma variável específica, mas por outro lado, piorar sensivelmente o desempenho de outras variáveis. Portanto, a sistematização de metodologias para sintonia de todos os controladores em conjunto é importante para sistemas com estas características.
Com este objetivo, o problema de sintonia de n controladores do tipo PI/PID é modelado neste artigo como um problema de otimização multiobjetivo. Este problema é resolvido por um algoritmo genético modificado que calcula de maneira simultânea, os diferentes parâmetros de configuração de cada controlador empregado.
Um problema de otimização multiobjetivo envolve a minimização (ou maximização) de vários critérios conflitantes que não podem ser satisfeitos simultaneamente. Nestes casos, procura-se um conjunto de soluções ótimas em que nenhuma solução do conjunto pode ser considerada superior às outras quando todos os critérios são analisados separadamente. Este conjunto é denominado conjunto ótimo de Pareto e as soluções que o compõem são conhecidas como soluções não- dominadas (Coello, 2000).
Na literatura, os métodos de resolução de problemas de otimização multiobjetivo baseados em algoritmos genéticos podem ser classificados em três grupos (Coello, 2000)-(Zitzter et al, 2004):
-
Abordagem por agregação de objetivos: Os vários objetivos são combinados em uma única função objetivo, e uma solução única é obtida como um problema simples de otimização. O método do critério global (Coello e Christiansen, 2000) e a programação orientada a objetivos (Coello, 2000) são exemplos de métodos deste grupo.
-
Abordagens que calculam um conjunto de soluções não-Pareto: um conjunto de soluções diferentes é obtido através de tratamento específico de objetivos e/ou do uso de técnicas populacionais, especiação e elitismo. A solução final é escolhida a posteriori. O algoritmo VEGA (Vector Evaluted Genetic Algorithm) proposto por Schaffer (1984) é um exemplo deste tipo de método.
-
Abordagens baseadas em conjunto de Pareto: Um conjunto de soluções de Pareto é obtido através da utilização de uma função objetivo de Pareto. O Método MOGA (Multiobjective Genetic Algorithm) proposto por Fonseca e Fleming (1993) e mais recentemente o método NSGA (Non-Dominated Sorting Genetic Algorithm) proposto por Kasat e Gupta (2003) são exemplos de métodos deste grupo. O algoritmo MRCD (Herreros et al., 2002) citado anteriormente também se enquadra nesta abordagem.
Como os métodos no primeiro grupo, o método desenvolvido neste artigo usa uma função objetivo única, obtida através da soma ponderada dos vários critérios envolvidos. Entretanto técnicas específicas de nicho e formação de casta (elitismo) são utilizadas pelo AG para construir o conjunto de soluções, como nos métodos do segundo grupo. Em seguida, ao final da evolução, uma análise de Pareto é realizada para selecionar as soluções não-dominadas deste conjunto. Estas soluções podem ser avaliadas pelos operadores do processo, antes de sua utilização na planta
2.1 Estrutura dos controladores
Uma das estruturas de controle PID mais utilizadas na literatura é a proposta por Åstrom e Hagglund (1995).
onde e = y - r, u, y e r são respectivamente, o erro, o sinal de controle, a saída e a referência da malha de controle. Os parâmetros Kp, TI e TD são respectivamente o ganho proporcional, a constante de tempo integral e a constante de tempo derivativa do PID. O parâmetro N é usado para limitar o ganho de alta freqüência do termo derivativo, melhorando assim a imunidade ao ruído do controlador (Åstrom e Hagglund, 1995).
Para gerar controladores discretos no tempo, discretiza-se a equação (1) com um período de amostragem T, utilizando a aproximação de Tutsim para o termo integral e a aproximação para trás (backward) para o termo derivativo, gerando a seguinte função de transferência:
Os controladores utilizados na seção 5 deste artigo são do tipo PI, compostos pelos dois primeiros termos da equação (2) e organizados em uma estrutura descentralizada. Nessa seção utiliza-se a metodologia proposta para calcular os parâmetros Kp e TI das diferentes malhas de um processo multivariável. No entanto, a extensão para o caso PID é simples, bastando para isto considerar todos os termos da equação (2).
2.2 Construção da função de avaliação de malha
Para construir a função objetivo do problema de otimização, o desempenho de cada malha de controle é avaliado individualmente. Para isto, primeiro devem ser escolhidos os pares entrada -saída que formam cada malha. O método RGA (Relative Gain Array) ou o índice de Nierdelinsky (Luyben, 1990) - (Campi e Morari, 1998) podem ser usados para tal objetivo. Em seguida, devem-se escolher para cada malha, os critérios de desempenho a serem atingidos em termos de sobressinal, tempo de acomodação, tempo de subida, entre outros. Neste artigo, os critérios da Integral do Erro Quadrático Ponderado pelo Tempo (ITSE) e de variância mínima aplicados ao sinal de controle u(t) e à saída y(t) do processo são combinados em uma função de avaliação para cada malha:
onde  (y(t)) e
(y(t)) e  (u(t)) são respectivamente a variância da saída e a variância do sinal de controle para a i-ésima malha,
(u(t)) são respectivamente a variância da saída e a variância do sinal de controle para a i-ésima malha,  e
e  são fatores de escala permitindo que os três termos da função tenham a mesma ordem de grandeza e
são fatores de escala permitindo que os três termos da função tenham a mesma ordem de grandeza e  ,
,  e
e  são fatores de ponderação, escolhidos no intervalo [0, 1], que refletem a importância dada a cada critério na análise de desempenho.
são fatores de ponderação, escolhidos no intervalo [0, 1], que refletem a importância dada a cada critério na análise de desempenho.
A escolha destes fatores ( ,
,  e
e  ) permite ao engenheiro de processo estabelecer prioridades entre os critérios, de acordo com os requisitos específicos de cada malha. Por exemplo, se o objetivo de controle é manter a variável de saída dentro de um determinado intervalo, então um erro de regime é admissível, e o fator w1 pode ser pequeno se comparado a w2 e w3. Desta forma, a escolha destes valores reflete os compromissos de desempenho para cada malha individualmente.
) permite ao engenheiro de processo estabelecer prioridades entre os critérios, de acordo com os requisitos específicos de cada malha. Por exemplo, se o objetivo de controle é manter a variável de saída dentro de um determinado intervalo, então um erro de regime é admissível, e o fator w1 pode ser pequeno se comparado a w2 e w3. Desta forma, a escolha destes valores reflete os compromissos de desempenho para cada malha individualmente.
A utilização do critério ITSE é baseada nos resultados apresentados em Killinsworth e Krstic (2006) que demonstraram que o critério ITSE possibilita desempenho em malha fechada superior em comparação com critérios mais conhecidos como o IAE (Integral of Absolute value Error) e ITAE (Integral Time of Absolute value Error). O segundo membro da função custo procura diminuir oscilações na saída do sistema, a partir da minimização da variância observada no sinal de saída y (t) do processo. Este critério é importante para a robustez do sistema em malha fechada na presença de perturbações. O terceiro membro, relativo à variância do sinal de controle u(t), tem por objetivo a procura por uma sintonia que gere sinais de controle mais suaves (Aström e Wittenmark, 1995).
2.3 Construção da função objetivo
Para um processo com n malhas, a função de avaliação de malha deve ser considerada de forma independente para cada uma das malhas. O equilíbrio das respostas obtidas determina o conjunto de sintonia que apresenta o melhor desempenho, considerando todas as saídas simultaneamente. Este equilíbrio pode ser determinado a partir do somatório do valor obtido para cada saída, ou a partir de qualquer outro tipo de soma ponderada. Neste trabalho, o conjunto de parâmetros de sintonia escolhido para os controladores é aquele que minimiza a seguinte função objetivo:
Sendo fi dado pela equação (3) e qi o coeficiente de ponderação para a i-ésima malha. A otimização desta função objetivo tem assegurado bons resultados mesmo para sistemas fortemente acoplados, e pode ser utilizada em diferentes processos (Swiech, 2005). A escolha do coeficiente de ponderação qi > qj para todo j ¹ i, garante que a saída i terá maior influência no resultado, e a sintonia a ser implantada será aquela que minimiza a malha i, permitindo assim uma priorização das malhas. Este coeficiente de ponderação também pode ser utilizado para escalonar as saídas que tenham valores de referência de diferentes magnitudes.
O processo de sintonia dos controladores PIDs em um processo multivariável, através da metodologia proposta neste trabalho, é feito diretamente pela busca dos melhores valores para cada um dos parâmetros de cada controlador PID (ganho proporcional (KPi), constante de tempo integral (TIi) e constante de tempo derivativa (TDi)). Esta busca é realizada por um algoritmo genético modificado cuja função de avaliação (fitness) é dada pela equação (4). Este algoritmo genético, detalhado na seção a seguir, apresenta uma representação cromossômica simples, com poucos genes, permitindo encontrar um conjunto de soluções de forma rápida e eficiente.
O uso de uma abordagem por agregação de objetivos para a otimização multicritério permite variar a importância de cada objetivo de um modo fácil para o operador. Este procedimento não é trivial em abordagens por conjuntos de Pareto. O método da soma ponderada é também bastante eficiente computacionalmente (Coello, 2000) - (Fonseca e Fleming, 2002). No entanto, a solução calculada é na maioria dos casos, fortemente não-dominada (super-indivíduo) e dependente das ponderações utilizadas para combinar os objetivos. Para atenuar estes problemas, a metodologia proposta neste artigo, além de incluir a casta elitista que guarda soluções obtidas em diferentes momentos da busca, realiza após a evolução, uma análise das soluções obtidas separando-as em dominadas e não-dominadas.
Para isto, considerando duas soluções quaisquer x(1) e x(2) de um problema que tem mais de um objetivo, f = (f1, f2,... , fi), i = 1,..., n e n > 2, têm-se duas possibilidades - ou uma solução domina a outra ou ninguém domina ninguém. Diz-se que a solução x(1) domina x(2.1) se ambas as condições são verdadeiras (Coello, 2000):
Onde  significa melhor,
significa melhor,  pior e "!'' para negação. Se alguma condição for violada, então x(1) não domina x(2).
pior e "!'' para negação. Se alguma condição for violada, então x(1) não domina x(2).
3 ALGORITMO GENÉTICO BASEADO EM NICHOS E CASTAS
Em abordagens evolucionárias para otimização multiobjetivo, métodos de nicho e especiação são úteis para estabilizar as múltiplas sub-populações que surgem na fronteira ótima de Pareto e assim evitar uma competição excessiva entre membros muito diferentes da população (Goldberg, 1989). Assim, este trabalho propõe um AG que utiliza quatro diferentes nichos obtidos pelo ordenamento da população como forma de restringir a competição aos indivíduos potencialmente similares.
O uso de elitismo em AG garante a sobrevivência do melhor indivíduo para a próxima geração assegurando a convergência assintótica dos algoritmos (Villalobos-Arias et all, 2006). No entanto, existe a possibilidade de convergência prematura do algoritmo devido à reprodução preponderante de super-indivíduos. Esta possibilidade é reforçada quando se utilizam abordagens baseadas em agregação de objetivos as quais favorecem a reprodução de soluções fortemente não-dominadas (Coello, 2000).
Para atenuar este problema, a abordagem desenvolvida neste artigo propõe o uso de nichos uma vez que os métodos de nicho também são capazes de manter várias soluções diferentes por um período de tempo infinito em relação ao tamanho da população (Mahfoud, 1995). Além disso, o método propõe a criação de um grupo específico isolado do restante da população. Neste grupo, denominado casta elitista, são mantidas cópias de todos os melhores indivíduos, obtidos desde os primeiros estágios da evolução. Estas cópias são protegidas da ação dos operadores genéticos que ocorrem em outra casta denominada casta de reprodução. Deste modo, a casta elitista é responsável por assegurar a sobrevivência dos melhores indivíduos para as próximas gerações e manter uma memória do processo evolutivo através da preservação de indivíduos obtidos anteriormente. Finalmente, na última geração, um conjunto de soluções potenciais para o problema de otimização multiobjetivo está disponível nesta casta, em adição ao melhor indivíduo encontrado, que representa uma solução final única. Este conjunto é posteriormente analisado com base no critério de Pareto e as soluções não-dominadas são disponibilizadas.
Desta forma, as técnicas de nichos e formação de casta são combinadas nesta abordagem com um método de seleção de Pareto (aplicado ao final da evolução) para assegurar o desempenho do algoritmo genético e também garantir soluções com diferentes compromissos em relação aos múltiplos critérios de otimização. O algoritmo genético baseado em castas é detalhado a seguir:
Início
Passo 1: Inicialize a população com vetores aleatórios.
Enquanto a condição de parada não for alcançada (número máximo de gerações)
Passo 2: Para cada indivíduo na população corrente, avalie a sua função objetivo (eq. 4)
Passo 3: Ordene a população baseado no valor desta função objetivo.
Passo 4: Divida a população ordenada em três nichos contendo respectivamente 20% (nicho 1), 50% (nicho 2) e 30% (nicho 3) dos indivíduos.
Passo 5: Construa um "grupo elitista'' copiando 10% dos melhores indivíduos (sem repetição) a partir do nicho 1 e talvez do nicho 2.
Passo 6: Construa o "grupo bom'' selecionando indivíduos do nicho 1 (repetições são permitidas).
Passo 7: Construa o "grupo médio'' copiando todos os indivíduos do grupo 2.
Passo 8: Construa o "grupo de eliminação'' selecionando indivíduos do grupo 3.
Passo 9: Copie todos os indivíduos do grupo elitista na casta elitista.
Passo 10: Reúna os grupos "bom'', 'médio'' e "eliminação'' formando a casta de reprodução.
Passo 11: Aplique os operadores genéticos de mutação e recombinação na casta de reprodução.
Passo 12: Forme uma nova população reunindo as castas elitista e de reprodução.
Passo 13: Atualize a população corrente com a nova população e incremente o contador de gerações.
fim enquanto .
Passo 14: Aplique uma análise de Pareto (eq. 5 e 6) às soluções presentes na casta elitista para que possam ser extraídas as soluções não-dominadas.
Fim
De acordo com o algoritmo mostrado anteriormente, para formar a população do algoritmo genético, os indivíduos são avaliados e ordenados de acordo como seu grau de aptidão. Posteriormente estes são divididos em três nichos correspondendo respectivamente a 20%, 50% e 30% do total de indivíduos na população. Estes três nichos são organizados em 4 grupos, conforme mostrado na figura 2, que formam as duas castas a serem utilizadas para a geração da próxima população. O grupo 1, que forma a casta elitista é composto por 10% do tamanho da população, e abriga os melhores elementos da geração anterior, sem que haja repetição de uma mesma solução. O grupo 2 é formado por indivíduos do nicho 1 que representam os melhores elementos da população corrente, podendo haver repetições e são selecionados pelo método da roleta (Goldberg, 1989). O grupo 3 é formado pela transmissão direta dos indivíduos no nicho 2. Os indivíduos deste grupo têm nível de aptidão intermediário. O último grupo é composto pelas soluções menos adequadas da população corrente, que sofrem um processo de seleção/eliminação pelo método da roleta e são transmitidas apenas em parte para a nova geração. Convém ressaltar que a formação de grupos é um mecanismo de competição restrita (Goldberg, 1989) que assegura que a competição, exceto para o grupo elitista, ocorre apenas entre indivíduos de valores de aptidão similares. A Figura 2 apresenta o procedimento utilizado pelo algoritmo genético baseado em castas (passos 4 a 10) para a construção das castas descritas.
A casta elitista foi projetada para guardar um número significativo de bons elementos (10% da população) durante toda a evolução do algoritmo. Desde a primeira geração, os melhores indivíduos são guardados e só podem ser substituídos por outros de melhor desempenho comprovado. Dentro da casta elitista, não ocorrem operações de mutação e recombinação, exatamente para não existir o risco de uma alteração mal sucedida em uma solução boa.
Na casta de reprodução são utilizados os operadores genéticos de mutação e recombinação para a construção da nova geração. A mutação sorteia genes dentro de uma população substituindo totalmente seus valores por outros gerados de maneira aleatória. Para que exista uma segurança quanto à possibilidade dos espaços de busca não terem sido bem dimensionados, o operador de mutação é projetado para sortear números aleatórios dentro e fora da faixa de variação pré-determinada. Para tanto, a faixa de variação é aumentada arbitrariamente em três vezes, e os sorteios ocorrem na proporção de 5 (faixa de variação original) para 1 (faixa de variação três vezes maior). Desta maneira, o algoritmo fica aberto a soluções diferentes das esperadas, mas, se algumas dessas soluções apresentarem baixo nível de aptidão serão eliminadas em poucas gerações através do método de seleção utilizado pelo AG. A operação de recombinação, além de sortear dois cromossomos aleatoriamente dentro da população, sorteia também o ponto de quebra e troca entre as duas soluções, sendo este ponto, portanto, diferente em cada atuação deste operador. Em seguida, os filhos substituem os pais. Esta mistura de indivíduos permite manter a diversidade da população, impedindo que nichos isolados de bons indivíduos levem a uma convergência rápida para soluções sub-ótimas.
A utilização de duas castas produz um bom compromisso entre a pressão seletiva e a diversidade de população, uma vez que a casta elitista mantém sempre o grupo dos melhores indivíduos mesmo quando a casta de reprodução converge para um superindivíduo. Além disto, como os melhores indivíduos estão salvos na casta elitista, não há problemas em misturar e substituir os elementos de nichos diferentes na casta reprodução para garantir a diversidade.
Depois de formada, a nova geração tem todos os seus indivíduos avaliados, ordenados e posteriormente subdivididos nos três nichos para continuação do ciclo de busca. No final da evolução, são disponíveis na casta elitista, não apenas um, mas vários indivíduos que formam o conjunto das melhores soluções encontradas pelo algoritmo genético.
Para a escolha do tamanho das castas e nichos da figura 2 foram realizados vários experimentos com processos de ordem e naturezas diferentes e com diferentes controladores. A metodologia se revelou robusta em relação a estes valores. Por exemplo, para o tamanho do nicho 1 variando entre 15% a 25% da população, os resultados apresentados em todos os processos são muito similares (Swiech, 2005).
Para a sintonia de controladores PI/PID, foi definida a utilização de cromossomos com número de genes igual ao número de parâmetros de configuração Kp, Ti, Td (Td, é mantido igual a zero no caso PI) multiplicado pelo número de controladores existentes na planta, isto é, o número de malhas simples a serem sintonizadas. A representação dos genes é feita por ponto flutuante, e a faixa de variação é determinada isoladamente para cada gene que compõe o cromossomo. Esta determinação é realizada a partir de ensaios preliminares que visam encontrar os valores de ganho último das malhas, através do método do período crítico (Åstrom e Hagglund, 1995). Os valores de amplitude de ganho encontrados são utilizados como limitador da faixa de variação de cada parâmetro para a geração da população inicial no início do processo evolutivo.
4 CONTROLE DE UNIDADES DE CRAQUEAMENTO CATALÍTICO.
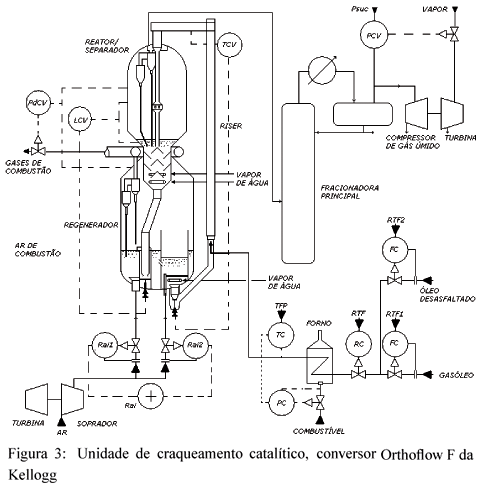
A unidade de craqueamento catalítico utilizada neste trabalho é mostrada na figura 3, onde identificam-se o conversor FCC propriamente dito, a fracionadora principal e dois compressores de gases operando em paralelo, além do forno de aquecimento da carga. O conversor é do tipo Orthoflow F da Kellogg. Um simulador foi desenvolvido em C++ por Prosdóssimo (2003), baseado nas principais equações de balanço de massa, energia e pressão para este tipo de conversor. Estas equações são resolvidas utilizando o método de Range-Kutta com passo de integração igual a 10-3. Este modelo dinâmico não-linear foi originalmente proposto em (Moro e Odlak, 1995).
O rendimento de uma unidade FCC é determinado pela quantidade de cada subproduto obtido, isto é, pelo percentual volumétrico da carga (gasóleo e óleo desasfaltado) que é convertido em cada um dos subprodutos do craqueamento (gasolina, GLP, gás combustível, coque, entre outros). Os principais fatores que influenciam esta conversão são (Sadeghbeig, 2000):
-
A qualidade da carga que determina diretamente as frações de produtos obtidos,
-
A temperatura de reação, quanto mais alta a temperatura maior é a quantidade de GLP produzida em detrimento da produção de gasolina e vice-versa,
-
A atividade do catalisador que determina o tempo de reação (acelera ou retarda o craqueamento)
-
Razão catalisador / carga que aumenta ou reduz as reações de craqueamento.
No modelo utilizado neste artigo, os fatores acima são controlados através de 5 malhas de controle regulatório do tipo PI (Prosdóssimo, 2003), as quais estão indicadas na figura 3:
-
Malha de controle de temperatura de saída do riser (Trx) feita via abertura da válvula TCV que controla a circulação de catalisador regenerado para o riser.
-
Malha de controle de temperatura da fase densa do regenerador (Trg2) através da válvula Raí que controla a vazão de ar para os dois estágios do regenerador
-
Malha para controle do inventário de catalisador no vaso separador (Hra), feito através da válvula LCV.
-
Malha de controle do diferencial de pressão entre o vaso separador e o regenerador (DPr), via abertura da válvula PdCV.
-
Malha de controle da pressão de sucção do compressor de gás úmido (Psuc), feito via controle da válvula PCV.
Para validação da metodologia proposta neste trabalho, foi simulada uma campanha de 5 horas (300 minutos) de duração, com variações previstas dos pontos de operação de acordo com a tabela 1. Além disto, diversas variáveis operacionais do processo possuem limites operacionais inferiores e superiores que devem ser respeitados durante a campanha. Para as variáveis controladas, estes limites também foram incluídos na tabela 1, para as demais variáveis do modelo, os limites podem ser obtidos em (Prosdóssimo, 2003).
5 SIMULAÇÕES E RESULTADOS.
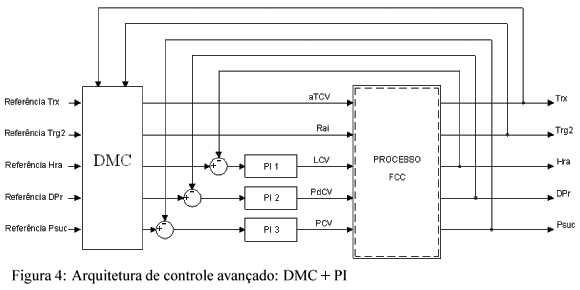
Para validação da metodologia proposta foram realizados dois casos de estudo para a campanha descrita acima. No primeiro caso, um controlador DMC multivariável foi utilizado para manipular diretamente a abertura das válvulas aTCV e Rai, controlando as temperaturas do riser (Trx) e do regenerador (Trg2) e para gerar as referências para os PIs nas malhas restantes (LCV-Hra, PdCV-DPr, PCV-Psuc). Nestas malhas os parâmetros de sintonia dos PIs foram obtidos utilizando as técnicas tradicionais de Ziegler-Nichols e Cohen-Coon e estão mostrados na tabela 2. A arquitetura de controle é mostrada na figura 4.
Os parâmetros utilizados na sintonia do controlador DMC estão na tabela 3 e foram obtidos por tentativa e erro a partir de vários experimentos, utilizando o simulador de FCC. Estes parâmetros apresentaram os melhores resultados a partir de uma análise visual das respostas. Os resultados obtidos neste estudo de caso servirão como referência em uma comparação com a metodologia proposta neste artigo.
No segundo estudo de caso, considerou-se apenas o nível regulatório (PI) em que todas as malhas foram sintonizadas conjuntamente através da metodologia proposta neste artigo, conforme mostra a arquitetura de controle da figura 5. Para a sintonia dos controladores PI, foi definida a utilização de cromossomos com 10 genes, que representam diretamente os parâmetros (Kp1, Ti1, Kp2, Ti2, Kp3, Ti3, Kp4, Ti4, Kp5, Ti5) relativos ao ganho proporcional (Kpi) e a constante de tempo integral (Tii) das cinco malhas de controle (TCV-Trx, Raí-Trg2, LCV-Hra, PdCV-DPr, PCV-Psuc). Os genes tiveram espaços de busca diferenciados entre si, a faixa de variação para o ganho proporcional das malhas 1, 3 e 4 (Kp1, Kp3, Kp4) foi determinada como sendo entre [-1 e 1], a faixa variação para o ganho proporcional da malha 2 (Kp2) está entre [-20 e 20] e o ganho da malha 5 (Kp5) entre [-10 e 10] e, finalmente a faixa de variação da constante de tempo integral em todas as malhas foi determinada entre [0 e 1]. Não foi estabelecida nenhuma prioridade entre as malhas (qi = 1, para i = 1,..., 5 na equação 4) e os critérios de desempenho foram ponderados por  = 0,7,
= 0,7,  = 0,2 e
= 0,2 e  = 0,1, para i = 1,..., 5 na equação 3, para todas as malhas. Isto significa que foi dada prioridade a minimização do critério ITSE em detrimento aos critérios de variância mínima de saída e entrada.
= 0,1, para i = 1,..., 5 na equação 3, para todas as malhas. Isto significa que foi dada prioridade a minimização do critério ITSE em detrimento aos critérios de variância mínima de saída e entrada.
As configurações adotadas para o algoritmo genético são: população inicial de 100 indivíduos, taxa de mutação de 0,05 e taxa de recombinação de 0,10, de acordo com as recomendações dadas em (Grefenstette, 1986). Foram executados 10 experimentos de 150 gerações cada, com população iniciada aleatoriamente nos espaços de busca descritos acima. Os resultados estatísticos em termos de média, mediana, desvio padrão, máximo e mínimo da função de avaliação de malha (equação 3) e da função objetivo (equação 4) estão mostrados na tabela 4.
Outros resultados são apresentados no histograma da figura 6, em que os valores de função de avaliação de malha são mostrados para cada um dos 10 experimentos.
A partir dos resultados da tabela 4, vê-se que as malhas 2 e 4 são de difícil sintonia, apresentando valores de desvio padrão dez vezes maiores se comparado às malhas restantes. Analisando o histograma da figura 6, vê-se que estes desvios são causados pela ocorrência de valores altos para a função de avaliação destas malhas nos experimentos 8 e 10. Estes valores são causados por soluções que apesar de ótimas para alguns critérios são muito ruins em um ou dois critérios.
A melhor solução (valor mínimo de J na tabela 4) foi obtida no experimento 2, e como pode ser observado na figura 6, esta solução apresenta o menor valor de função de avaliação para a malha 5 (Psuc) e valores muito próximos do ótimo para todas as outras malhas. Os parâmetros de sintonia obtidos com este experimento são dados na Tabela 5. As curvas obtidas com estes valores de sintonia serão comparadas àquelas obtidas com o estudo de caso 1.
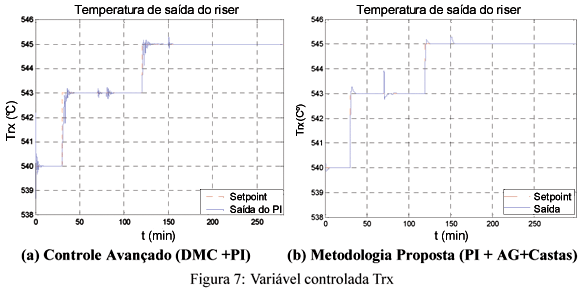
Para ambos os casos, as respostas das variáveis controladas estão ilustradas nas figuras 7 a 11. As variáveis manipuladas estão ilustradas nas figuras 11 a 16. Analisando as figuras 7 a 11 percebe-se que a sintonia obtida via PI+AG+Castas privilegia a velocidade de resposta e apresenta menos oscilações na variável controlada que as respostas do controle avançado (DMC+PI). Esta sintonia apresenta valores de sobressinal comparáveis ao do controle avançado, exceto para a malha 4 (figura 10) e apresenta também melhor rejeição de perturbação (variação da referência em outras malhas), exceto mais uma vez para a malha 4. Outra sintonia poderia ter sido escolhida que favorecesse um melhor desempenho para a malha 4, no entanto, esta foi escolhida por apresentar de modo geral, um resultado comparável ou melhor do que aquele apresentado pelo controle avançado, lembrando ainda que este último é formado por uma camada regulatória (PI) associado a um controle DMC que também é resultante da solução de um problema de otimização de desempenho.
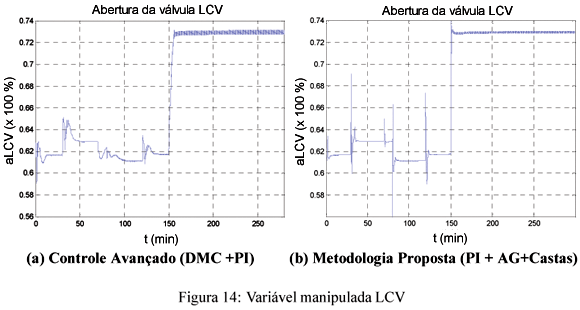
A análise das figuras 12 a 16 mostra que a sintonia por PI+AG+Castas apresenta maiores amplitudes de controle quando da variação das referências. No entanto, os sinais calculados pela metodologia proposta (PI+AG+Castas) são menos oscilatórios (efeito ringing) que os calculados com o controle avançado (DMC+PI). Este fato é notado nas figuras 14 e 15, nos instantes 80 a 120 minutos e a partir do instante 150 minutos, quando não há mais variação das referências.
O tempo de execução de um experimento (100 indivíduos + 100 gerações) é de aproximadamente 1 hora em um computador Athlon TMXP 2600+, 2GHz, 512 Mb RAM. No entanto, ressalva-se que o simulador de FCC foi implementado em Borland C++ e que o algoritmo genético foi implementado em MATLAB. Este tempo é inferior a outros exemplos relatados na literatura para o controle de unidades FCC. Por exemplo, o algoritmo NSGA proposto por Kasat e Gupta (2003) e citado anteriormente leva 48h para achar um conjunto de pareto para o controle de uma unidade de FCC com apenas dois objetivos. O algoritmo genético com simulated anealing proposto em (Sankararao e Gupta, 2007) leva 6 horas para resolver o mesmo problema do NSGA. Em termos de controle preditivo, o controlador DMC apresentado em (Ansari e Tade, 2000) requer, para cada variável manipulada do processo FCC, 2 a 6h a fim de se gerar um modelo que possa ser utilizado pelo controlador DMC.
6 CONCLUSÕES.
A sintonia de diversos controladores em um processo multivariável constitui um desafio aos engenheiros de processo e operadores uma vez que ela depende de um completo conhecimento das plantas que são muitas vezes complexas, e que podem possuir variáveis com fortes interações entre si, além de não linearidades e de objetivos de controle conflitantes.
Este artigo apresentou uma proposta de sintonia de controladores PI/PIDs para sistemas multivariáveis através do uso de algoritmos genéticos com nichos e formação de castas. Uma vantagem desta metodologia é que um sistema de controle multivariável com várias malhas independentes, pode ter todos seus controladores ajustados de forma unificada e racional. Para isto o problema de sintonia de controladores foi modelado como um problema de otimização multiobjetivo, no qual o desempenho de cada malha é considerado um critério independente a ser minimizado. A função de avaliação de desempenho para cada malha individual agrupa os critérios ITSE e variância mínima em uma mesma função. Estes critérios são ponderados facilmente de acordo com a preferência operacional do usuário. Em seguida, a função de avaliação de cada malha é agrupada numa abordagem de soma ponderada e o usuário pode atribuir prioridades entre as malhas.
Esta modelagem não está restrita apenas a controladores do tipo PI/PID, uma vez que a função objetivo do problema de otimização é independente do tipo de controlador utilizado. Uma desvantagem do método é que para sintonia on-line torna-se necessário o uso de um simulador, executando em paralelo com o processo.
Outra contribuição do trabalho é o uso de um método evolucionário para a solução do problema de otimização multiobjetivo o qual é baseado em um algoritmo genético modificado pela introdução de uma técnica de nicho e formação de casta. O método de nicho adotado permitiu restringir a competição aos indivíduos com aptidão (fitness) semelhantes, além de possibilitar a formação de duas castas na população: casta elitista e casta de reprodução. Ao final da evolução, a casta elitista que agrega 10% dos melhores indivíduos da população, forneceu não apenas a melhor sintonia para o problema de controle, mas um conjunto de sintonias. Este conjunto pode produzir um sub-conjunto de soluções não-dominadas que serão avaliadas pelo engenheiro de processo, permitindo que ele escolha uma sintonia de acordo com suas preferências operacionais.
Por fim, este artigo aplicou a técnica proposta ao controle de uma unidade de craqueamento catalítico apresentando resultados que demonstram a eficiência da técnica, bem como sua flexibilidade e facilidade de aplicação na sintonia de vários controladores.
Como trabalho futuro, pretende-se incluir a análise de Pareto como critério para aceitação de indivíduos na casta elitista, de forma a garantir que todos os indivíduos desta casta representem soluções não-dominadas.
AGRADECIMENTOS
Os autores agradecem o apoio financeiro da Agência Nacional do Petróleo (ANP) através do CTPETRO/FINEP Financiadora de Estudos e Projetos: Programa de Recursos Humanos para o Setor de Petróleo e Gás Natural (PRH-ANP/MCT 10 UTFPR).
Artigo submetido em 18/04/2006
1a. Revisão em 07/02/2007
2a. Revisão em 06/11/2007
Aceito sob recomendação do Editor Associado Prof. Ivan Nunes da Silva
- Ansari, R. M. and M.O. Tadé (2000). Constrained nonlinear multivariable control of a fluid catalytic cracking process, Journal of Process Control, Vol. 10, nş 6, pp 539 - 555.
- Ĺström, K.J. and T. Hägglund (2001). The future of PID control. Control Engineering Practice, Vol. 9, nş 11, pp. 1163-1175.
- Ĺström, K.J. and T. Hägglund (2004). Revisiting the Ziegler-Nichols step response method for PID control. Journal of Process Control, Vol. 14, nş 6, pp. 635-650.
- Ĺström, K.J., H. Panagopoulos and T. Hägglund (1998). Design of PI controllers based on non-convex optimization. Automatica, Vol 34, nş 5, pp. 585 - 601.
- Ĺström, K.J. and B. Wittenmark (1995). Adaptive Control, 2nd ed., Addison- Wesley, Reading, MA.
- Ayadi, B. and B.J. Benhadj (2005). MIMO PID controllers synthesis using orthogonal functions. Preprints of the 16th IFAC World Congress, Prague, Czech Republic.
- Campi, P.J. and M. Morari (1994). Achievable closed-loop properties of systems under decentralized control: conditions involving the steady-state gain. IEEE Transactions on Automatic Control, Vol 39, nş 5, pp. 932-943.
- Chang, W-D. (2007). A Multi-crossover genetic approach to PID controllers tuning. Expert Systems with Applications, Vol. 33, nş 3, pp. 620-626.
- Coello, C.A.C. (2000) An updated survey of GA-based multiobjective optimization techniques. ACM Computing Surveys, Vol 32, nş 2, pp.109-143.
- Coello, C.A. and A.D. Christiansen (2000). Multiobjective optimization of trusses using genetic algorithms. Computers & Structures, Vol. 75, n 6, pp. 647-660.
- Davison, E.J. (1978). Decentralized robust control of unknown systems using tuning regulators, IEEE Transactions Automatic Control, Vol. 23, nş 2, pp. 276-289.
- Farag, A. and H. Werner (2006). Robust decentralized control of a High Voltage DC system using evolutionary approach. Intelligent Automation and Soft Computing, Vol 12, nş 1, pp. 31-39.
- Fleming, P.J. and R.C. Purshouse (2002). Evolutionary algorithms in control systems engineering: a survey. Control Engineering Practice, Vol. 10, nş 11, pp. 1223-1241.
- Fonseca, C.M. and P.J. Fleming (1993) Genetic Algorithms for Multiobjective Optimization: Formulation, Discussion and Generalization. Proceedings of the Fifth International Conference on Genetic Algorithms, pp. 416-423
- Goldberg, D.E. (1989). Genetic algorithms in search, optimization, and machine learning. Adison-Wesley. Ann Arbor.
- Grefenstette, J.J. (1986). Optimization of control parameters for genetic algorithms. IEEE Transactions on Systems, Man and Cybernetics, Vol. 16, nş 1, pp. 122-128.
- Herreros, A., E. Baeyens and J.R. Peran (2002). Design of PID-type controllers using multiobjective genetic algorithms, ISA Transactions, Vol. 41, pp. 457-472.
- Hlaing, Y.M., M.S. Chiu, and S. Lakshminarayanan (2007). Modelling and control of multivariable process using generalized Hammerstein model, Chemical Engineering Research & Design, Vol. 85 (A4), pp. 445 - 454.
- Hsu, L., M. Chan and A. Bhaya (1992). Automated synthesis of decentralized tuning regulators for systems with measurable DC gain. Automatica, Vol. 28, nş 1, pp. 185 - 191.
- Kasat R.B. and S.K. Gupta (2003). Multi-objective optimization of an industrial fluidized-bed catalytic cracking unit (FCCU) using genetic algorithm (GA) with the jumping genes operator. Computers and Chemical Engineering, Vol. 27, nş 12, pp. 1785-1800.
- Killingsworth N.J. and M. Krstic (2006). PID tuning using extremum seeking, IEEE Control Systems Magazine, Vol. 26, nş 1, pp. 70-79.
- Lewin, D.R. and A. Parag (2003). A constrained genetic algorithm for decentralized control system structure selection and optimization, Automatica, Vol. 39, nş 10, pp. 1801 - 1807.
- Luyben, W.L. (1986). A simple method for tuning SISO controllers in a multivariable system. Industrial & Engineering Chemistry Product Research and Development, Vol. 25, pp. 654-660.
- Luyben, W.L (1990). Process Modeling, Simulation and Control for Chemical Engineers. 2nd edition, McGraw Hill, New York, USA.
- Mahfoud, S.W. (1995). Niching Methods for Genetic Algorithms. Ph.D. Dissertation, University of Illinois, USA.
- Moro, L.F.L. and D. Odloak (1995). Constrained multivariable control of fluid catalytic craking converters. Journal of Process Control, Vol. 5, nş 1, pp. 29-39.
- Oviedo, J.J., T. Boelen and P. Van Overschee (2006). Robust Advanced PID control (RaPID): PID tuning based on engineering specifications. IEEE Control Systems Magazine, Vol. 26, nş 1, pp. 15-19.
- Prosdóssimo, C. (2003). Uma contribuiçăo ao controle preditivo multivariável de unidades de craqueamento catalítico. Dissertaçăo de mestrado. Programa de pós graduaçăo em engenharia elétrica e informática industrial. Universidade Tecnológica Federal do Paraná, Curitiba-PR.
- Sadeghberg, R. (2000). Fluid Catalytic Cracking Handbook, 2nd Edition, GPP, Houston.
- Sankararao, B. and S. K. Gupta (2007). Multi-objective optimization of an industrial fluidized-bed catalytic cracking unit (FCCU) using two jumping gene adaptations of simulated annealing, Computers and Chemical Engineering, Vol. 31, nş 11, pp 1496-1515.
- Schaffer, J.D. (1984). Some experiments in machine learning using vector evaluated genetic algorithms. Doctoral dissertation, Vanderbilt University, Nashville.
- Swiech, M.C.S. (2005) Algoritmos genéticos para sintonia simultânea de múltiplos controladores em processos de refino. Dissertaçăo de mestrado. Programa de pós graduaçăo em engenharia elétrica e informática industrial. Universidade Tecnológica Federal do Paraná, Curitiba-PR.
- Swiech, M.C.S., E. Oroski and L.V.R. Arruda (2005). Algoritmos genéticos para sintonia conjunta de controladores híbridos independentes em processos multivariáveis. Anais do VII Simpósio Brasileiro de Automaçăo Inteligente, Săo Luis - MA, pp. 1-7.
- Toh, W.K. and G.P. Rangaiah (2002). A methodology for autotuning of multivariable systems, Industrial & Engineering Chemistry Research, Vol. 41, nş 18, pp. 4605 - 4615.
- Villalobos-Arias, M., C.A.C. Coello and O. Hernadez-Lerma (2006). Asymptotic convergence of metaheuristics for multiobjective optimization problems. Soft Computing, Vol. 10, nş 11, pp. 1001-1005.
- Vlachos, C., D. Williams and J.B. Gomm (2002). Solution to the Shell standard control problem using genetically tuned PID controllers. Control Engineering Practice, Vol.10, nş 2, pp. 151- 163.
- Wang, Q.G., B. Zou, T. H. Lee and Q. Bi (1997). Auto-tuning of multivariable PID controllers from decentralized relay feedback, Automatica, Vol 3, nş 3, pp. 319 -330.
- Zitzler, E., M. Laumanns and S. Bleuler (2004). A Tutorial on Evolutionary Multiobjective Optimization, in X. Gandibleux, M. Sevaux, K. Sörensen and V. T'kindt (Ed.), Metaheuristics for Multiobjective Optimisation, Lecture Notes in Economics and Mathematical Systems Vol. 535, pp. 3-37, Springer, Berlin.
- Yusof, R. and S. Omatu (1993). A multivariable self-tuning PID controller. International Journal of Control, Vol 57, nş 6, pp. 1387-14036.
Datas de Publicação
-
Publicação nesta coleção
18 Abr 2008 -
Data do Fascículo
Mar 2008
Histórico
-
Recebido
18 Abr 2006