Resumos
Retificadores multipulsos, obtidos a partir de conexões especiais de autotransformadores, ou conexões diferenciais, estão em crescente desenvolvimento para equipar o estágio de entrada de conversores estáticos. Essas topologias retificadoras são cada vez mais atrativas não só pela robustez, como pela característica em mitigar harmônicos importantes na corrente da linha, reduzindo a distorção harmônica total de corrente (DHTi) e elevando o fator de potência. Diferentemente das conexões defasadoras isoladas(delta-estrela, ziguezague, etc.), quando se trata de autotransformador, a maior parte da energia requerida pela carga é diretamente conduzida através dos enrolamentos e apenas uma pequena fração é processada pelo núcleo, aumentando assim a densidade de potência do conversor. Este trabalho apresenta um método matemático simples baseado em diagramas fasoriais, que resulta em expressões capazes de definir todas as conexões diferenciais para as topologias Estrela e Delta, tanto elevadoras como abaixadoras de tensão, em retificadores de 12 ou 18 pulsos. As expressões obtidas, também apresentadas sob a forma de ábacos possibilitam que, para qualquer tensão da rede, seja escolhida uma determinada tensão de saída, ou vice-versa. Este fato mostra que, diferentemente das conexões defasadoras de tensão usuais, a família de conversores proposta pode ser projetada para qualquer relação entre as tensões da rede de entrada e da carga. Uma aplicação imediata seria o "retrofit", ou seja, substituir um sistema retificador trifásico convencional, com baixa qualidade da energia processada, pelo retificador de 12 ou 18 pulsos, com conexões Estrela ou Deltas-diferenciais, mantendo os níveis originais de tensão da rede e da carga. O procedimento de projeto, simples e rápido, é desenvolvido e aplicado a um protótipo de 6 kW, 18 pulsos, do tipo Delta-diferencial, com tensão média retificada de 400 V na carga.
conexão diferencial; autotransformador; multipulsos; retificador trifásico; fator de potência
Multipulse rectifier topologies based on auto-connections or differential connections, are more and more applied as interface stages between the mains and power converters. These topologies are becoming increasingly attractive not only for robustness, butto mitigate many low order current harmonics in the utility, reducing the total harmonic distortion of the line currents (THDi) and increasing the power factor requirements. Unlike isolated connections (delta-wye, zigzag, etc.), when the differential transformer is employed, most of the energy required by the load is directly conducted through the windings. Thus, only a small fraction of the kVA is processed by the magnetic core. This feature increases the power density of the converter. This paper presents a mathematical model based on phasor diagrams, which results in a single expression able to merge all differential connections (wye and delta), for both step-up and step-down rectifiers for 12 or 18 pulses. The proposed family of converters can be designed for any relationship between the line input voltage and the DC voltage, unlike the conventional phase-shift voltage connections. An immediate application would be the "retrofit", i.e. to replace a conventional rectifier with poor quality of the processed energy by the 12 or 18-pulse rectifiers with Wye or Delta-differential connections, keeping the original values for the input and load voltages. The simple and fast design procedure is developed and tested for a prototype rating 6 kW and 400 V on DC load.
Differential connection; autotransformer; multipulse; three-phase rectifier; power factor correction
ELETRÔNICA DE POTÊNCIA
Priscila da Silva Oliveira; Rodolfo Castanho Fernandes; Falcondes José Mendes de Seixas
UNESP - Univ. Estadual Paulista - Departamento de Engenharia Elétrica Campus de Ilha Solteira - SP, Brasil falcon@dee.feis.unesp.br
RESUMO
Retificadores multipulsos, obtidos a partir de conexões especiais de autotransformadores, ou conexões diferenciais, estão em crescente desenvolvimento para equipar o estágio de entrada de conversores estáticos. Essas topologias retificadoras são cada vez mais atrativas não só pela robustez, como pela característica em mitigar harmônicos importantes na corrente da linha, reduzindo a distorção harmônica total de corrente (DHTi) e elevando o fator de potência. Diferentemente das conexões defasadoras isoladas(delta-estrela, ziguezague, etc.), quando se trata de autotransformador, a maior parte da energia requerida pela carga é diretamente conduzida através dos enrolamentos e apenas uma pequena fração é processada pelo núcleo, aumentando assim a densidade de potência do conversor. Este trabalho apresenta um método matemático simples baseado em diagramas fasoriais, que resulta em expressões capazes de definir todas as conexões diferenciais para as topologias Estrela e Delta, tanto elevadoras como abaixadoras de tensão, em retificadores de 12 ou 18 pulsos. As expressões obtidas, também apresentadas sob a forma de ábacos possibilitam que, para qualquer tensão da rede, seja escolhida uma determinada tensão de saída, ou vice-versa. Este fato mostra que, diferentemente das conexões defasadoras de tensão usuais, a família de conversores proposta pode ser projetada para qualquer relação entre as tensões da rede de entrada e da carga. Uma aplicação imediata seria o "retrofit", ou seja, substituir um sistema retificador trifásico convencional, com baixa qualidade da energia processada, pelo retificador de 12 ou 18 pulsos, com conexões Estrela ou Deltas-diferenciais, mantendo os níveis originais de tensão da rede e da carga. O procedimento de projeto, simples e rápido, é desenvolvido e aplicado a um protótipo de 6 kW, 18 pulsos, do tipo Delta-diferencial, com tensão média retificada de 400 V na carga.
Palavras-chave: conexão diferencial, autotransformador, multipulsos, retificador trifásico, fator de potência.
ABSTRACT
Multipulse rectifier topologies based on auto-connections or differential connections, are more and more applied as interface stages between the mains and power converters. These topologies are becoming increasingly attractive not only for robustness, butto mitigate many low order current harmonics in the utility, reducing the total harmonic distortion of the line currents (THDi) and increasing the power factor requirements. Unlike isolated connections (delta-wye, zigzag, etc.), when the differential transformer is employed, most of the energy required by the load is directly conducted through the windings. Thus, only a small fraction of the kVA is processed by the magnetic core. This feature increases the power density of the converter. This paper presents a mathematical model based on phasor diagrams, which results in a single expression able to merge all differential connections (wye and delta), for both step-up and step-down rectifiers for 12 or 18 pulses. The proposed family of converters can be designed for any relationship between the line input voltage and the DC voltage, unlike the conventional phase-shift voltage connections. An immediate application would be the "retrofit", i.e. to replace a conventional rectifier with poor quality of the processed energy by the 12 or 18-pulse rectifiers with Wye or Delta-differential connections, keeping the original values for the input and load voltages. The simple and fast design procedure is developed and tested for a prototype rating 6 kW and 400 V on DC load.
Keywords: Differential connection, autotransformer, multipulse, three-phase rectifier, power factor correction.
1. INTRODUÇÃO
O fator qualidade de energia, em conversores aplicados na eletrônica de potência, vem sendo amplamente discutido. Existem trabalhos recentes na literatura, que buscam uma melhora na qualidade da corrente de entrada em retificadores trifásicos a diodos, com a associação de um estágio CC-CC regulador (por exemplo, os estágios Boost ou SEPIC) ao estágio retificador, resultando em conversores híbridos como é apresentado por Freitas et alli (2006), além de outros conversores trifásicos que utilizam modulação por largura de pulsos (PWM), como mostrado por Pomílio et alii (1997). Técnicas como comutação suave e estratégias de controle digital também são relatadas por Freitas et alii (2006) e Kazmierkowski et alii(2009), a fim de se obter baixas perdas eelevado Fator de Potência (FP) no estágio CA-CC. Os conversores CA-CC podem ser utilizados nas mais diversas aplicações, incluindo aproveitamentos de energia renovável, como o condicionamento de energia em turbinas eólicas, apresentado por Chen et alli (2009). Os retificadores com controle do ângulo de disparo, utilizando tiristores em sua topologia retificadora, pertencem à outra classe de conversores CA-CC e são mais adequados a elevadas potências, onde as correntes estão na faixa de quiloamperes.
A aplicação de conversores multipulsos trifásicos para correção do fator de potência é uma técnica bem aceita como discute Paice (1996), pois promove baixa ondulação na tensão de saída e uma redução na distorção harmônica total de corrente de entrada. Nosúltimos anos, muitos trabalhos vêm propondo novas topologias multipulsos e classificando as inúmeras já conhecidas. Estas topologias podem ser classificadas como isoladas ou não-isoladas e também com relação ao número de pulsos na tensão retificada ou nacorrente de entrada (6, 12, 18, 24 pulsos....), como é mostrado por Singh et alli (2008).
Para transformadores isolados, o defasamento angular requerido pode ser obtido combinando as conexões Estrela, Ziguezague, Delta, Polígono, Scott ou T, conforme Paice (1996) e Schaefer (1965). Para um conversor de 12 pulsos uma forma de se obter sistemas defasados de 30 entre si é usando as conexões Delta/ Delta-Estrela. O conversor apresenta um primário conectado em Delta e dois secundários, sendo um em Delta em fase com o primário e o outro em Estrela com a defasagem natural de 30 com relação ao primário. Outra forma de provocar o ângulo de defasagem correto para um conversor de 12 pulsos é obter um sistema trifásico atrasado de 15, no secundário do transformador, e outro adiantado de 15, considerando a rede como referência. Isto pode ser feito utilizando as conexões Delta/Ziguezague-Ziguezague ou Delta/Polígono-Polígono.
Para se obter um conversor de 18 pulsos são necessárias três pontes retificadoras. Neste caso o espectro harmônico das correntes de linha é formado somente pelas ordens harmônicas k18 ± 1 (k=1, 2, 3...). O defasamento angular requerido para o conversor de 18 pulsos é de 20 entre as pontes retificadoras e pode ser obtido através de inúmeras combinações entre as conexões de transformador, como apresentam Singh et alli (2008) e Paice (1996). Uma forma de se obter um conversor de 18 pulsos isolado é através da conexão Delta/Ziguezague-Estrela-Ziguezague. Nesta configuração, a conexão Estrela presente no secundário apresenta um sistema trifásico defasado de 30 com relação ao primário que está conectado em Delta, um segundo sistema trifásico secundário é conectado em Ziguezague, este sistema possui um avanço de 20 com relação ao secundário em Estrela (avanço de 50 com relação ao primário) e o terceiro sistema trifásico do secundário, também conectado em Ziguezague, possui um atraso de 20 com relação ao secundário em Estrela (resultando em um atraso de 10 com relação ao primário).
Outra maneira de se obter um conversor isolado é promover o isolamento em alta freqüência, introduzindo um estágio CC-CC após o estágio retificador, como é apresentado Seixas e Gonçalves (2007), Seixas e Barbi (2004 e 2001a), garantindo assim, a isolação galvânica. Esta técnica permite que a tensão de saída seja regulada usando uma estratégia de controle apropriada para o estágio intermediário CC-CC.
Este trabalho prioriza os conversores com conexões não-isoladas de transformadores, que empregam conexões especiais de autotransformador (as topologias de autotransformador referidas são as conexões Estrela-diferencial e Delta-diferencial). Um grande número de conexões de autotransformadores pode ser encontrado na literatura, como apresentam Singh et alli (2008), Gonçalves (2001) e Burgos et alli (2005).. Uma grande vantagem dessas conexões está no fato de que, somente uma fração da potência total requerida pela carga é processada pelo núcleo magnético do autotransformador (baixa taxa kVA, ou seja, baixa relação entre a potência processada pelo núcleo magnético e potência entregue à carga), resultando em reduzidos pesos e volumes. Por exemplo, o núcleo magnético de um conversor de 12 ou 18 pulsos com conexão Delta-diferencial de autotransformador pode chegar a processar 20% ou menos da potência requerida pela carga. No entanto, elementos magnéticos adicionais como transformadores de interfase, (IPTs - Interphase Transformers), também chamados de reatores ou indutores de interfase são necessários quando as pontes retificadoras de seis pulsos são conectadas em paralelo, isto se deve às diferenças instantâneas entre as tensões das pontes retificadoras. Estas diferenças são responsáveis pelo desbalanceamento das correntes dos secundários do transformador. Além disso, nestas condições não ocorre o cancelamento natural das componentes harmônicas esperadas em conversores multipulsos. Para conversores de 12 pulsos não-isolados, com conexões Estrela ou Delta-diferencial, são necessários quatro IPTs conectados do lado CC. Nas topologias de 18 pulsos são necessários seis IPTs. A fim de melhorar a utilização desses elementos e minimizar o volume adicional introduzido por eles, alguns aprimoramentos têm sido propostos nos últimos anos. Como, por exemplo, o emprego de IPTs ativos que combinam algumas funções dos bloqueadores de seqüência zero (ZSBT - Zero Sequence Blocking Transfromers) e IPTs convencionais. Além disso, esforços para simplificar as estruturas dos autotransformadores e reduzir o número adicional de enrolamentos vêm sendo relatados.
A proposta deste trabalho é apresentar um estudo matemático com relação aos conversores multipulsos CA-CC trifásicos, baseados nas conexões Delta-diferencial ou Estrela-diferencial de autotransformadores, e obter expressões generalizadas que permitam um cálculo rápido e fácil de parâmetros importantes para o projeto de conversores de 12 e 18 pulsos. Através de diagramas fasoriais, expressões trigonométricas são obtidas e generalizadas para qualquer valor de tensões de entrada e saída. Estas expressões apresentam o cálculo para as tensões sobre todos os enrolamentos do autotransformador. Essa análise matemática reúne todas as topologias Delta-diferencial e Estrela-diferencial, elevadoras e abaixadoras de tensão, tanto para conversores de 12 como de 18 pulsos.
Através das expressões gerais obtidas podem-se traçar curvas, que possibilitam a determinação da relação de espiras para todos os enrolamentos secundários do autotransformador, além de suas respectivas polaridades. No entanto, a maior contribuição deste trabalho é a possibilidade de escolher qualquer tensão de saída para o conversor em função de qualquer tensão de entrada e vice-versa.
2. CONEXÕES ESTRELA-DIFERENCIAIS
2.1. Análises das tensões sobre os enrolamentos
A Figura 1 (a) apresenta o diagrama fasorial para o sistema primário de tensões (Va, Vb e Vc) e os sistemas de tensões secundários adequadamente defasados, chamados de (VR1, VS1 e VT1) para o sistema em avanço e de (VR2, VS2 e VT2 ) para o sistema em atraso. O ângulo θ determina a operação do conversor em 12 pulsos (θ = 15°) ou 18 pulsos (θ = 20°). O conversor de 18 pulsos requer também um sistema trifásico de tensões em fase com as tensões primárias. Este sistema é denotado por (VRn, VSn e VTn), como é apresentado por Gonçalves e Seixas (2006a e 2006b), Gonçalves (2001) e por Seixas (2001b).
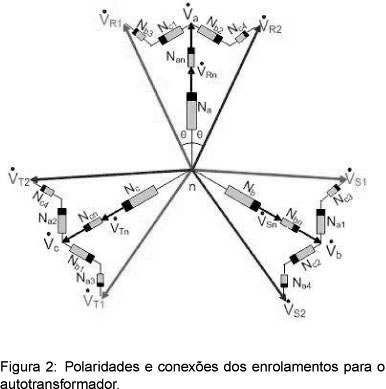
A Figura 1 (b) representa o núcleo magnético trifásico, com o primário conectado em Estrela, os enrolamentos denominados Na, Nb e Nc são montados nas pernas (A), (B) e (C) respectivamente. Os secundários são compostos por 15 enrolamentos para o conversor de 18 pulsos e 12 enrolamentos para o conversor de 12 pulsos. Os enrolamentos Na1, Na2, Na3, Na4 e Nan são montados sobre a perna (A), já os enrolamentos Nb1, Nb2, Nb3, Nb4,Nbn e Nc1, Nc2, Nc3, Nc4, Ncn, são posicionados sobre as pernas (B) e (C) respectivamente. A forma como são feitas as conexões destes enrolamentos esta representadas na figura 2. Esta conexão é chamada de genérica, pois, a partir dela podem-se gerar conexões elevadoras ou abaixadoras de tensão para conversores de 12 e 18 pulsos, para a topologia Estrela-diferencial. No caso do conversor de 12 pulsos, os enrolamentos Nan, Nbn, e Ncn apresentados na figura 2 não são necessários. As tensões sobre os enrolamentos são representadas pelos mesmos índices, por exemplo, Va1 corresponde à tensão sobre o enrolamento Na1. É importante mencionar que o índice n (por exemplo, Nan) refere-se ao ponto neutro e não denota o enésimo enrolamento.
Os sistemas de tensão apropriadamente defasados são obtidos a partir de enrolamentos secundários auxiliares. Logo, as tensões resultantes de saída são formadas pela composição das tensões de entrada e das tensões nos enrolamentos secundários auxiliares.
As tensões são consideradas positivas quando estão de acordo com a direção (polaridade) das tensões de referência (sistema de tensão primário).
2.1.1. Equações para Vc1 > 0 e Vb3 > 0:
A Figura 3 (a) apresenta o diagrama fasorial simplificado quando as tensões são positivas nos enrolamentos Nc1 e Nb3. A tensão auxiliar Vx é definida entre o ponto neutro e o ponto comum dos enrolamentos Nc1 e Nb3. O ângulo chamado de é definido como o ângulo entre as tensões Vx e Va(tensão de referência). As tensões Vc1 e Vb3 têm a mesma direção de Vc e Vb, respectivamente.
Considerando os triângulos formados pelo módulo das tensões (Vx, VR1 e Vb3) e (Vx, Vc1 e Va ), apresentados na figura 3 (a), as seguintes expressões podem ser escritas:
Para esta condição (tensões Vc1 e Vb3 são valores positivos), α varia entre θ e 60° em relação a referência (tensão primária). Logo,
Para α= 60° e θ = 0°→ Vc1= Vx= Vb3= Va→VR1= 0;
Para α= θ→Vβ3= 0.
A tensão resultante no secundário (VR1) é sempre menor que a tensão de entrada (Va). Essa é uma situação particular na qual se tem uma conexão abaixadora (step-down).
2.1.2. Equações para Vcl > 0 e Vb3 < 0:
Quando Nb3 tem polaridade invertida, resulta em uma tensão Vb3 negativa α, está entre θ e 0°. A tensão de saída (VR1) pode ser menor, igual ou maior que a tensão de entrada. A Figura 3 (b) apresenta o diagrama fasorial simplificado para esta condição.
A partir dos triângulos em destaque na figura 3 (b), obtêm-se as seguintes expressões:
2.1.3. Equações para Vcl < 0 e Vb3 < 0:
Neste caso, Vc1 e Vb3 assumem valores negativos e varia entre 0° e -60°. A tensão VR1 é maior que a tensão de entrada, ou seja, tem-se a conexão elevadora de tensão (step-up). A Figura 3 (c) mostra o diagrama fasorial para esta condição e as equações associadas a este diagrama são:
2.2. Expressão genérica
Considerando as expressões de (1) a (6) e usando identidades trigonométricas é possível obter uma única expressão que descreve as tensões através dos enrolamentos secundários em função da tensão de referência (Va) e dos ângulos α e θ. Esta expressão é apresentada em (7). As tensões VR1, Vc1 e Vb3 são facilmente determinadas em (8), (9) e (10) respectivamente.
Através da equação (8) para uma tensão de fase (Va) conhecida, escolhe-se um valor para a tensão de fase resultante nos secundários VR1 e calcula-se o valor do ângulo auxiliar α. Com os valores de α e Va, se obtém os valores para Vc1 e Vb3 através das expressões (9) e (10).
2.3. Enrolamentos adicionais para conversores de 18 pulsos
Os conversores de 18 pulsos necessitam de um terceiro sistema de tensões secundárias, o qual está em fase com as tensões primárias e as tensões da rede. As tensões do sistema adicional VRn, VSn e VTn devem ter o mesmo valor em módulo das tensões dos sistemas defasados de +20° (VR1, VS1, VT1) e -20° (VR2, VS2, VT2), como mostra a figura 1 (a). Assim, o enrolamento Nan é montado na mesma perna do enrolamento Na, e gera a tensão Van que está em fase com a tensão Va, o mesmo é válido para os enrolamentos Nbn e Ncn. A amplitude da tensão através de Nan é apresentada na equação (11).
É importante relembrar que o conversor de 12 pulsos não requer esses enrolamentos adicionais, pois possui apenas dois sistemas defasados, um adiantado de +15° e outro atrasado de -15°.
2.4. Relações de espiras
As relações de espiras entre os enrolamentos do autotransformador são obtidas através das relações entre as tensões aplicadas sobre os enrolamentos secundários e primários. O valor de Ka é definido como o quociente entre Van e Va como se pode ver na equação (12).
A relação entre Vc1 e Va define o valor de Kb, como é mostrado em (13).
Finalmente a equação (14) apresenta a relação entre Vb3 e Va e define o valor de Kc.
As polaridades dos enrolamentos são adotadas positivas quando eles estão na mesma direção de seus respectivos enrolamentos primários. Assim, se uma tensão secundária resultar em um valor negativo, seu enrolamento tem polaridade oposta ao enrolamento primário montado na mesma perna do núcleo. Como conseqüência o valor da relação de espiras é negativo.
A partir da expressão (8) chega-se a expressão (15), que apresenta o valor do ângulo auxiliar α.
2.5. Curvas para os conversores de 12 e 18 pulsos com conexão Estrela-diferencial
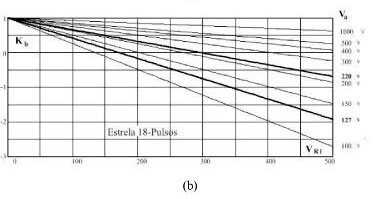
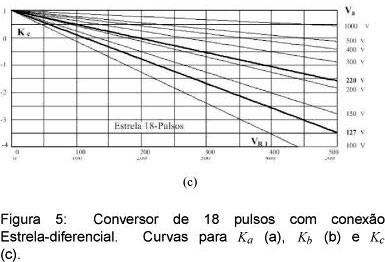
As Figuras 4 e 5 apresentam ábacos que permitem obter os valores das relações de espiras, sem a necessidade dos cálculos apresentados anteriormente. Observa-se pelas curvas que os valores das relações de espiras para uma mesma tensão de saída, não são os mesmos, se a tensão de entrada for diferente, ou seja, para cada tensão de entrada tem-se uma curva distinta. Escolhendo-se a tensão de saída desejada (VR1) e sabendo-se qual é a tensão de entrada, é simples e rápido obter as relações entre as tensões sobre os enrolamentos e obter os valores de Ka, Kb e Kc, a partir das curvas apresentadas para os conversores de 12 e 18 pulsos.
A Figura 4 apresenta curvas para os conversores de 12 pulsos (θ = 15°), este conversor necessita apenas de dois enrolamentos secundários por fase. Logo, tem-se apenas as relações Kb na figura 4(a) e Kc na figura 4(b).
A Figura 5 apresenta curvas para os conversores de 18 pulsos (θ = 20°), este conversor necessita de um enrolamento a mais por fase, logo se tem as relações Ka na figura 5 (a), Kb na figura 5 (b) e Kc na figura 5 (c).
Quando uma relação de espiras é nula, significa que o enrolamento não existe e recai em um caso especial de conexão. Por exemplo, quando Kc é nulo, Vb3=0 e se tem α = θ
3. CONEXÕES DELTA-DIFERENCIAIS
3.1. Análises das tensões sobre os enrolamentos
A análise das tensões para a conexão Delta-diferencial é similar à apresentada para a conexão Estrela-diferencial como apresenta Gonçalves e Seixas (2006b). No entanto, as tensões aplicadas sobre os enrolamentos primários são tensões de linha (Vab, Vbc e Vca). A Figura 6 (a) apresenta o diagrama fasorial para a topologia Delta. O diagrama fasorial apresenta o sistema trifásico de tensões primárias (Vab, Vbc e Vca), as tensões de fase e de linha do sistema adiantado de θ (VR1, VS1 e VT1) e (VRS1, VST1 e VTR1), as tensões de fase e de linha do sistema atrasado de θ (VR2, VS2 e VT2) e (VRS2, VST2 e VTR2), e o sistema em fase com as tensões primárias (VRn, VSn e VTn).
Para o conversor de 18 pulsos o terceiro sistema trifásico em fase com a rede é necessário, as tensões devem ter o mesmo valor em módulo das demais tensões secundárias resultantes. No caso do conversor Delta-diferencial de 18 pulsos são necessários dois enrolamentos auxiliares a mais por fase em comparação com a topologia Estrela, que utiliza apenas um enrolamento auxiliar por fase para gerar o terceiro sistema trifásico. A Figura 6 (b) apresenta o núcleo magnético para a conexão Delta-diferencial. Assim,a conexão Delta de 12 pulsos (θ = 15°) é composta pelos enrolamentos primários e 12 enrolamentos secundários auxiliares, já a conexão de 18 pulsos (θ = 20°) necessita de 18 enrolamentos secundários.
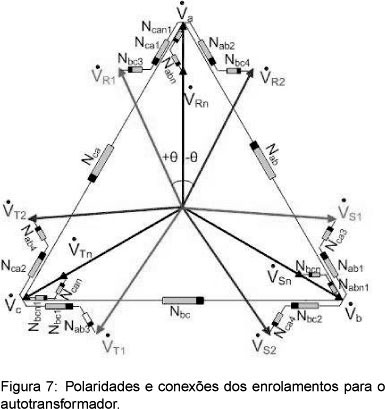
Os enrolamentos primários são definidos como Nab, Nbc e Nca. Os enrolamentos secundários Nab1, Nab2, Nab3, Nab4, Nabn e Nabn são montados sobre uma mesma perna (A) do núcleo, junto ao enrolamento Nab. Os enrolamentos Nbc1, Nbc2, Nbc3, Nbc4, Nbcn e Nbcn1 são montados em uma mesma perna do núcleo (B), juntamente com o enrolamento primário Nbc. Finalmente, os enrolamentos Nca1, Nca2, Nca3, Nca4, Ncan e Ncan1 são montados na perna (C) do núcleo, juntamente com o enrolamento primário Nca. Estes enrolamentos são conectados de acordo com a Figura 7, que apresenta todos os enrolamentos presentes na conexão Delta-diferencial generalizada. Para o conversor de 12 pulsos os enrolamentos Nabn, Nabn1, Nbcn, Nbcn1, Ncan, e Ncan1 não são necessários.
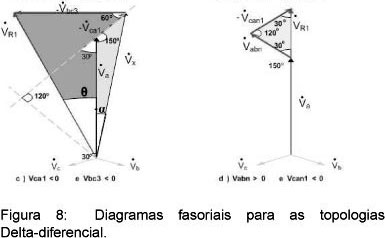
3.1.1. Equações para Vca1 > 0 e Vbc3 > 0:
A Figura 8 apresenta diagramas fasoriais para as tensões através dos enrolamentos Nca1 e Nbc3. Como foi apresentado para a topologia Estrela, a tensão auxiliar Vx é definida como a tensão entre o neutro e o ponto comum entre as tensões secundárias sobre os enrolamentos Nca1 e Nbc3. Considerando os triângulos (Vx, Vca1 e Va) e (Vx, VR1 e Vbc3), apresentado na figura 8 (a), são válidas as expressões (16) e (17).
A partir da figura 8 (a) observa-se que α varia de θ a 90°. Assim, os limites encontrados são:
Para α = 90° → Vca1= 2, Vbc3 = Va . cos(30°) e VR1 = 0;
Para α = θ →Vc3 = 0.
A tensão de saída no secundário do autotransformador (VR1) é sempre menor que a tensão de fase de entrada (Va). Por este motivo, esta conexão é chamada abaixadora de tensão.
3.1.2. Equações para Vca1 > 0 e Vbc3 < 0:
Para este caso o diagrama fasorial é apresentado na Figura 8 (b), a partir dele, obtêm-se as expressões (18) e (19).
O ângulo α varia entre θ e 0°, e VR1 pode ser menor, igual ou maior que a tensão de entrada.
3.1.3. Equações para Vca1 < 0 e Vbc3 < 0:
Neste caso, α varia entre 0° e -30°, enquanto VR1 é maior que Va, como mostra o diagrama fasorial da figura 8(c). As expressões (20) e (21) são obtidas a partir deste diagrama.
3.2. Expressão genérica
Usando o mesmo procedimento adotado para a conexão Estrela de autotransformador, uma expressão única é obtida e apresentada em (22). Essa expressão está definida em função dos ângulos α, θ e da tensão de entrada e descreve as tensões atravésde todos os enrolamentos secundários.
Os valores para VR1, Vca1 e Vbc3 podem se calculados através das expressões (23) a (25), respectivamente.
3.3. Enrolamentos adicionais para conversores de 18 pulsos
Neste caso, são necessários dois enrolamentos a mais por fase para gerar um terceiro sistema trifásico, em fase com as tensões de fase do primário do autotransformador e com as tensões da rede. Os enrolamentos adicionais Nabn e Nabn1 são montados sobre a mesma perna do núcleo junto ao enrolamento primários Nab as tensões sobre estes enrolamentos secundários são Vabn e Vabn1 em fase com Va. A soma de Vab, Vabn e Vcan1 resulta em VRn, que deve possuir mesma amplitude de VR1 e VR2 e estar em fase com a referência (Va), como mostrado na figure 8 (d). A tensão através dos enrolamentos secundários Nabn e Nabn1 é apresentada na equação (26).
3.4. Relações de espiras
A relação de espiras Ka é apresentada na equação (27). O valor de Ka é obtido pela relação entre as tensões Vabn ou Vabn1 e a tensão primária de linha Vab.
A relação entre as tensões Vca1 e Va define Kb, representado por (28).
Finalmente, Kc está apresentado na equação (29).
Rearranjando a equação (23), é possível obter a equação (30) que apresenta o cálculo do ângulo α.
3.5. Curvas para os conversores de 12 e 18 pulsos com conexão Delta-Diferencial
Da mesma maneira como foram obtidas as curvas para a conexão Estrela-diferencial, foram obtidas curvas para a conexão Delta-diferencial. Estas curvas estão apresentadas nas Figuras 9 e 10. Elas facilitam encontrar as relações de espiras Ka, Kb e Kc de forma rápida e fácil, basta escolher a curva que corresponde à tensão de entrada e depois entrar com o valor de tensão secundária desejada.
A Figura 9 apresenta curvas para os conversores de 12 pulsos (θ = 15°). Este conversor necessita apenas de dois enrolamentos secundários por fase, logo se têm apenas as relações Kb (Vca1/Va) figura 9 (a) e Kc (Vbc3/Va) figura 9 (b).
A Figura 10 apresenta curvas para os conversores de 18 pulsos (θ = 20°), Ka na figura 10 (a), Kb na figura 10 (b) e Kc na figura 10 (c).
4. GENERALIZAÇÃO DAS CONEXÕES ESTRELA E DELTA-DIFERENCIAIS
Existe uma grande semelhança entre as expressões (7) e (22). Este fato é entendido como uma oportunidade para que estas expressões sejam reescritas, a fim de se obter uma única expressão que represente ambas as topologias Delta e Estrela de autotransformador para conversores de 12 e 18.
A principal diferença entre as conexões Estrela-diferencial e Delta-diferencial é que, no caso da conexão Estrela, as tensões secundárias relacionam tensões de fase e, na conexão Delta, relacionam tensões de linha. É importante esclarecer que a conexão que será apresentada não é uma nova conexão. Será apresentado um novo equacionamento que generaliza as conexões Estrela e Delta apresentadas anteriormente. Com este equacionamento não serão necessárias mais equações distintas para as topologias Estrela e Delta de transformador, elas serão representadas por uma única expressão que representará as duas famílias de autotransformadores para conversores de 12 ou 18 pulsos.
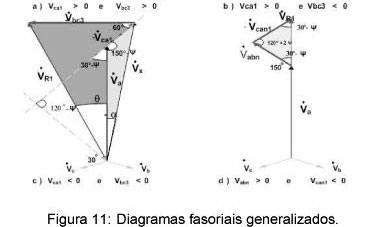
4.1. Diagrama fasorial generalizado
O ângulo entre as tensões de fase da conexão Estrela e a tensão de linha da conexão Delta é de 30°. Assim para a conexão Delta o ângulo entre Va e Vca1 é 30°, enquanto que, para a conexão Estrela o ângulo entre Va e Vc1 é de 60°. Considerando um ângulo adicional Ψ, o diagrama fasorial apresentado na figura 8 pode ser reescrito considerando agora o ângulo Ψ como mostra a figura 11. Este diagrama representa ambas as conexões Estrela-diferencial (quando Ψ = 30°) e Delta-diferencial (quando Ψ = 0°).
O diagrama fasorial da figura 11 é utilizado para obter as expressões de (31) a (40), estas expressões são válidas para ambas as conexões. A expressão é deduzida para uma fase somente, porém, o mesmo resultado é estendido às demais fases.
4.1.1. Expressões generalizadas para Vca1 > 0 e Vbc3 > 0:
Aplicando a lei dos senos aos triângulos formados pelas amplitudes das tensões secundárias e primárias, a partir do diagrama da figura 11 (a), as expressões (31) e (32) são obtidas.
4.1.2. Expressões generalizadas paraVca1> 0 eVbc3< 0:
A partir da figura 11 (b) se obtém as expressões (33) e (34):
4.1.3. Expressões generalizadas para Vca1 < 0 e Vbc3 < 0:
Finalmente, a partir da figura 11 (c), as expressões (35) e (36) podem ser escritas.
4.2. Expressão final que representa as topologias Estrela e Delta
Observa-se das expressões de (31) a (36) que todas elas apresentam os mesmos parâmetros, tensões secundárias Vca1 e Vbc3, tensão auxiliar Vx, tensão de fase primária Va, tensão resultante no secundário do autotransformador VR1, o ângulo θ (que determina se o conversor é de 12 ou 18 pulsos), Ψ (que indica o tipo de conexão, Estrela ou Delta) e α (ângulo auxiliar). Rearranjando as equações (31) a (36) se obtém a expressão (37), esta é a expressão final generalizada,foco principal deste trabalho.
Os valores eficazes de VR1, Vca1 e Vbc3 podem ser facilmente calculados através das expressões (38), (39) e (40), respectivamente. Essas expressões podem ser solucionadas facilmente.
4.3. Enrolamentos adicionais para o conversor de 18 pulsos
As equações (41) e (42) definem as tensões através dos enrolamentos secundários adicionais. Nota-se que, para a conexão Estrela (onde Ψ = 30°), a tensão Vabn1 é nula. Este fato ocorre porque este enrolamento adicional é necessário apenas para as conexões Delta-diferenciais generalizadas.
4.4. Relações de espiras
As equações de (27) à (29) podem ser reescritas com base nos diagramas fasoriais generalizados, obtendo-se as equações de (43) à (45), válidas para as ligações Delta e Estrela. A relação de espiras Ka, é calculada através da equação (43).
A relação de espiras Kb é definida na equação (44).
A relação de espiras Kc é definida pela equação (45).
Todas as curvas apresentadas nas figuras 6 e 7 para a conexão Estrela de autotransformador e as figuras 11 e 12 para a conexão Delta são válidas. O ângulo α pode ser calculado através da equação (46), conhecendo-se Va, VR1, θ e Ψ. Aplicando o valor de nas equações (39) e (40), as tensões secundárias Vca1 e Vbc3 são determinadas.
5. EXEMPLO DE PROJETO E RESULTADOS EXPERIMENTAIS
5.1. Exemplo de projeto
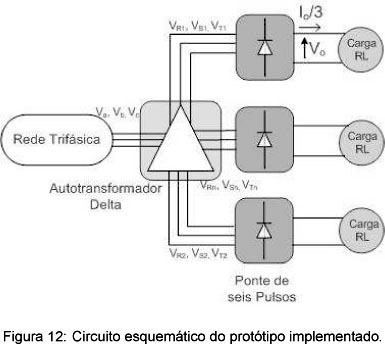
A tabela 1 resume os parâmetros para o protótipo de um conversor de 18 pulsos com conexão Delta-diferencial com potência de 6,2 kW. A tensão Va é a tensão eficaz de fase na rede, a tensão VR1 é a tensão de fase resultante no secundário do autotransformador, esta tensão é escolhida de forma a se obter uma tensão média na carga (VL) de 400 V (relembrando que para um retificador de seis pulsos em ponte VL corresponde a 2,34 vezes o valor de VR1). A Figura 12 apresenta o circuito do protótipo implementado.
Como o objetivo do trabalho é propor um método de projeto para conversores com conexões diferenciais de autotransformador e não especificar uma única aplicação para o conversor, o protótipo apresentado na figura 12 tem suas saídas com cargas independentes. Porém estes conversores podem ser utilizados para alimentar inversores, sistemas ininterruptos de energia (UPS), fontes para telecomunicações, entre outras, basta conectar as pontes em paralelo através de indutores de interfase (IPT), indispensáveis a este tipo de conexão. Para os testes experimentais, o valor da carga resistivo-indutiva é de 80Ω e 500 mH, para carga plena. A Figura 13 apresenta um algoritmo fácil e rápido que descreve o procedimento de projeto para conversores de 12 ou 18 pulsos com conexões Estrela ou Delta diferenciais. Aplicando os valores de Va e VR1 em (46) tem-se o ângulo α= -6,892° que aplicado às expressões (39) a (42), permite determinar Vca1, Vbc3, Vabn e Vabn1. A tensão sobre os enrolamentos primários, Nab, Nbc e Nca é de 220 V. Resolvendo a expressão (39) e estendendo o resultado para todos os enrolamentos similares, a tensão sobre os enrolamentos Nab1,Nab2, Nbc1, Nbc2, Nca1 e Nca2 é de -38,9 V. A expressão (40) apresenta o cálculo para a tensão sobre os enrolamentos secundários Nab3,Nab4, Nbc3, Nbc4, Nca3 e Nca4, cujo valor é de -77,94 V. Finalmente, das expressões (41) e (42) obtém-seas tensões sobre os enrolamentos Nabn, Nabn1, Nbcn, Nbcn1, Ncan e Ncan1, que são iguais a 25,4 V. Com os valores de Vab, Vabn, Vca1 e Vbc3 obtém-se os valores das relações de espira através das equações (43) a (45): Ka = 8,672, Kb = -5,665 e Kc = -2,825 (o valor negativo indica que os enrolamentos tem polaridades opostas aos enrolamentos primários, que formam a referência). A partir deste ponto, conhecendo as relações de espiras entre os enrolamentos, o procedimento de projeto é exatamente o mesmo aplicado a transformadores convencionais.
5.2. Resultados experimentais
A Tabela 2 apresenta detalhes do projeto físico do autotransformador, como número de espiras, lâminas utilizadas, peso, etc.
A Figura 14 (a) apresenta o protótipo desenvolvido, com pontes retificadoras e dissipador térmico. A figura 14 (b) apresenta as tensões para uma fase dos três sistemas secundários gerados. A tensão VRSn está em fase com a tensão nos enrolamentos primários (tensão de linha na rede), VRS1 está adiantada com relação a referência e a tensão VRS2 está em atraso com relação a referência. A defasagem de ±20°, necessária para o conversor de 18 pulsos, é confirmada através do ensaio do protótipo. O autotransformador apresenta regulação de tensão, relação entre as tensões de saída com máxima carga e a vazio, de 2,8%.
A Figura 15 (a) apresenta as correntes na rede e a tensão em uma das fases da rede. Observa-se que as correntes estão em fase com as respectivas tensões da rede e são equilibradas. Detalhes da Figura 15 (a) são apresentados na Figura 15 (b). Observa-se que as correntes na rede possuem mesma amplitude e estão defasadas de 120° entre si. Há, portanto, bom equilíbrio entre as correntes. Nas figuras 15 (a) e 15 (b) a corrente está na escala de 10 mV/A. O fator de deslocamento para este conversor é próximo da unidade (0,995), pois o ângulo de deslocamento é pequeno (6°), assim, as correntes da rede estão praticamente em fase com as tensões.
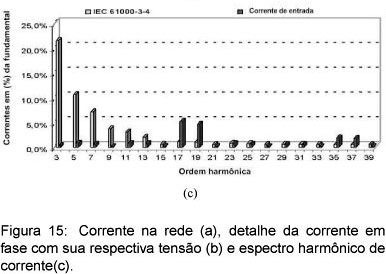
A Figura 15 (c) apresenta o espectro harmônico para a corrente na rede, em comparação com a norma IEC 61000-3-4. Como se espera para este conversor, as amplitudes harmônicas mais significativas ocorrem para a 17ª, 19ª, 35ª e 37ª ordens harmônicas. A DHTi é 7,84% e o FP de 0,992. Comparando o espectro harmônico com a norma IEC 61000-3-4 (para correntes maiores que 16A por fase), é visível que o conversor atende até a 15ª harmônica. Assim, se for de interesse, filtros podem ser introduzidos a fim de eliminar componentes de mais alta freqüência. Exatamente por serem projetados para freqüências acima de 1kHz é esperado que o volume e peso destes filtros sejam baixos. A taxa kVA, relação entre a potência processada pelo núcleo magnético (kVA) e a potência que é requerida pela carga (kW), é de 43,6%. Assim, o núcleo magnético processa apenas uma parte da potência entregue a carga, possibilitanto redução no peso e volume do autotransformador.
A Figura 16 apresenta a curva de rendimento para o conversor implementado. Mesmo para baixa carga o rendimento é elevado. A curva mostra também que as perdas são quase constantes ao longo de toda a faixa de potência. Em plena carga o rendimento é de 97% e as perdas totais medidas são de 180 W, incluindo perdas no núcleo magnético, enrolamentos, perdas ôhmicas e perdas nas pontes retificadoras. As pontes utilizadas (SKD 25/16) são responsáveis por 61,1% das perdas totais.
6. CONCLUSÕES
Este trabalho apresenta o desenvolvimento matemático e fasorial para obtenção de um conjunto de expressões genéricas que descreve todas as conexões diferenciais de autotransformador, para as topologias Estrela e Delta, utilizados em conversores de 12 e 18pulsos. A análise apresentada neste trabalho é de grande importância, pois torna simples o projeto de conversores multipulsos com conexões diferenciais de transformador, inclusive para aqueles pouco familiarizados nesta área de pesquisa.
O procedimento de projeto é descrito através de um fluxograma que apresenta um método rápido e fácil para o cálculo das relações de espiras e determinação das polaridades para todos os enrolamentos secundários. Considerando as expressões obtidas, curvas foram traçadas para facilitar ainda mais a obtenção das relações de espiras. Essas curvas ou ábacos fornecem diretamente as relações de espiras entre enrolamentos e indica a polaridade para se ter uma determinada tensão resultante (VR1, por exemplo), em função da tensão da rede de entrada. Percebe-se um comportamento linear dessas curvas e uma possibilidade de se projetar conversores tanto abaixadores quanto elevadores de tensão.
O trabalho foi validado através da construção e ensaio do protótipo de um conversor de 18 pulsos com topologia Delta-diferencial, com potência de 6,2 kW e tensão média na carga de 400 V. Neste projeto, a potência processada pelo núcleo do autotransformador foi de 43,6 % da potência nominal da carga, ou seja, 2,7 kW. Através dos ensaios observou-se que o conversor (autotransformador e pontes retificadoras) atendeu às expectativas apresentando baixa DHTi, em torno de 7,84% e, conseqüentemente, elevado FP (0,992). Além disso, apresentou um rendimento superior a 97% e peso total de 17 kg.
7. AGRADECIMENTOS
Os autores agradecem a CAPES e a FAPESP pelo apoio financeiro ao projeto. Este trabalho é dedicado à memória do nosso amigo e pesquisador Vinicius Assad Gonçalves.
Artigo submetido em 03/05/2010 (Id.: 01140)
Revisado em 18/09/2010
Aceito sob recomendação do Editor Associado Prof. Takashi Yoneyama
- Burgos, R. P., A. Uan-Zo-li, F. Lacaux, A. Roshan, F. Wang, D. Boroyevich (2005). New Step-Up and Step-Down 18-Pulse Direct Asymmetric Autotransformer Rectifier Units. in Proc. IEEE Power Electronics Specialists Conf., pp. 1149-1155.
- Chen, Z., J. M. Guerrero, F. Blaabjerg (2009). A Review of the State of the Art of Power Electronics for Wind Turbines. IEEE Trans. on Power Electronics, Vol. 24, pp. 1859-1875.
- Freitas, L. C. G. M., G. Simões, C.A. Canesin, L.C. Freitas (2006). Programmable PFC Based Hybrid Multipulse Rectifer for Ultra Clean Power Application. IEEE Trans. on Power Electronics, Vol. 21, pp. 959-966.
- Gonçalves V. A., F. J. Seixas (2006a). Generalization of the Y - Differential Autotransformer. Elsevier: Eletric Power System Research, pp. 271- 394.
- Gonçalves V. A., F. J. Seixas. (2006b). Conexões Y e Delta Diferencias - Generalização para Retificadores de 12 e 18 pulsos. CBA (Congresso Brasilero de Automática), pp. 2626 - 2631.
- Gonçalves., V. A. (2001). Redução de Harmônicos de Corrente em Retificadores de Multiplos Pulsos - Generalização das Conexões Diferenciai. Dissertação de Mestrado. UNESP - Faculdade de Engenharia de Ilha Solterira, pp. 177.
- Kazmierkowski, M., P. R. Krishnan, F. Blaabjerg (2009). Control in Power Electronics. San Diego, CA: Elsevier, Chap. 11, 12 and 13.
- Pomilio, J. A., L. Rossetto, P. Tomasin, (1997). Performance Improvement of Soft-Switched PWM Rectifiers with Inductive Load. IEEE Trans. on Power Electronics, Vol. 12, pp. 153-160.
- Paice D. A. (1996). Power Electronic Converter Harmonic Multipulse Methods for Clean Power. New York: IEEE Press.
- Schaefer, Rectifier Circuits (1965). Theory and Design. Norwalk: John Wiley and Sons.
- Seixas F. J. M., V. A. Gonçalves (2007). Generalização das Conexões Delta - Diferenciais para Retificadores de 12 e 18 pulsos. Eletrônica de Potência, Vol. 12, nº. 1; pp. 35 - 42
- Seixas F. J. M., I. Barbi (2004). A 12 kW Three-Phase Low THD Rectifier with High-Frequency Isolation and Regulated DC Output. IEEE Trans. on Power Electronics, Vol. 19, pp. 371-377.
- Seixas, F. J. M., I. Barbi (2001a). A New Three-Phase Low THD Power Supply with High-Frequency Isolation and 60V/200A Regulated DC Output. in Proc. IEEE Power Electronics Specialists Conf., pp.1629-1634.
- Seixas F. J. M. (2001b). Conversores CA - CC de 12 kW com elevado Fator de Potência utilizando Autotransformador com Conexão Diferencial de Multipulsos, Tese (Doutorado). Universidade Federal de Santa Catarina, pp. 205.
- Singh, B., S. Gairola, B. N. Singh, A. Chandra, K. Al-Haddad, K. (2008). Multipulse AC-DC Converters for Improving Power Quality: A Review. IEEE Trans. on Power Electronics, Vol. 23, pp. 260-268.
Família de retificadores multipulsos com topologias diferenciais de transformadores
Datas de Publicação
-
Publicação nesta coleção
25 Mar 2011 -
Data do Fascículo
Fev 2011
Histórico
-
Aceito
18 Set 2010 -
Recebido
03 Maio 2010