Resumos
O objetivo do artigo é apresentar o modelo MEECA, que representa uma metodologia econométrica inovadora para geração de cenários economicamente consistentes de longo prazo de projeções de culturas agropecuárias. Essa metodologia é baseada na econometria espacial, levando em conta os efeitos espaciais, a saber, a dependência e a heterogeneidade espaciais. Nas regressões incorporamos uma série de termos espaciais, tais como efeitos de transbordamento, expansão espacial dos coeficientes, defasagem espacial do erro etc. Essa metodologia é aplicada para a estimação dos modelos econométrico-espaciais de algumas culturas agropecuárias na Amazônia, a saber, a rizicultura, a sojicultura, a cultura do milho, a cultura dos outros produtos extrativos, bovinocultura e outros produtos pecuários. O modelo MEECA está diretamente integrado a um modelo de equilíbrio geral aplicado, garantindo a consistência sistêmica das projeções.
projeções econômicas; econometria espacial; integração de modelos; culturas agropecuárias
The objective of this article is to present the MEECA model, an innovative econometric methodology for generating economically consistent long term scenarios of projections for agriculture and living stock. This methodology is based upon the spatial econometrics, taking into account the spatial effects, namely, the spatial dependence and the spatial heterogeneity. In the regressions, we incorporate various spatial terms, such as spillover effects, spatial expansion of coefficients, spatial error lag, etc. This methodology is applied for the estimation of the spatial econometric models of some agricultural and living stock products in the Amazon region, namely, rice, soy bean, corn, other extractive products (excluding wood), cattle and other living stock products. The MEECA model is directly linked to an applied general equilibrium model, guaranteeing the systemic consistency of the projections.
economic projections; spatial econometrics; models integration; agricultural and living stock products
MEECA: um modelo econométrico espacial para projeção consistente de culturas agropecuárias
Eduardo Simões de AlmeidaI; Eduardo Amaral HaddadII
IDoutor em Economia - Professor do Departamento de Economia, Administração e Sociologia da ESALQ/USP - E-mail: ealmeida@esalq.usp.br - Av. Pádua Dias, 11, Cx. Postal 9, CEP 13418-900, Piracicaba, SP
IIPh.D. em Economia - Professor do Departamento de Economia, FEA/USP, Pesquisador da Fipe e Adjunct Research Assistant Professor, REAL/UIUC, E-mail: ehaddad@usp.br, IPE/USP Av. Prof. Luciano Gualberto, 908 Ala C Sala 113 Cidade Universitária CEP 05508-900 - São Paulo, SP
RESUMO
O objetivo do artigo é apresentar o modelo MEECA, que representa uma metodologia econométrica inovadora para geração de cenários economicamente consistentes de longo prazo de projeções de culturas agropecuárias. Essa metodologia é baseada na econometria espacial, levando em conta os efeitos espaciais, a saber, a dependência e a heterogeneidade espaciais. Nas regressões incorporamos uma série de termos espaciais, tais como efeitos de transbordamento, expansão espacial dos coeficientes, defasagem espacial do erro etc. Essa metodologia é aplicada para a estimação dos modelos econométrico-espaciais de algumas culturas agropecuárias na Amazônia, a saber, a rizicultura, a sojicultura, a cultura do milho, a cultura dos outros produtos extrativos, bovinocultura e outros produtos pecuários. O modelo MEECA está diretamente integrado a um modelo de equilíbrio geral aplicado, garantindo a consistência sistêmica das projeções.
Palavras-chave: projeções econômicas, econometria espacial, integração de modelos, culturas agropecuárias.
Classificação JEL: C53 e C68
ABSTRACT
The objective of this article is to present the MEECA model, an innovative econometric methodology for generating economically consistent long term scenarios of projections for agriculture and living stock. This methodology is based upon the spatial econometrics, taking into account the spatial effects, namely, the spatial dependence and the spatial heterogeneity. In the regressions, we incorporate various spatial terms, such as spillover effects, spatial expansion of coefficients, spatial error lag, etc. This methodology is applied for the estimation of the spatial econometric models of some agricultural and living stock products in the Amazon region, namely, rice, soy bean, corn, other extractive products (excluding wood), cattle and other living stock products. The MEECA model is directly linked to an applied general equilibrium model, guaranteeing the systemic consistency of the projections.
Key words: economic projections, spatial econometrics, models integration, agricultural and living stock products.
JEL Classification: C53 e C68
1 Introdução
Este artigo apresenta uma metodologia para geração de cenários consistentes de longo prazo de projeções de culturas agrícolas. Considerando um cenário de referência para o período 2001-2020, os resultados são gerados a partir de projeções com o modelo EFES, integrado a suas extensões estadual, mesorregional e municipal, que alimentam um módulo de desagregações específicas, apresentado neste trabalho. Partindo de um cenário tendencial em que são geradas projeções setoriais e regionais para a economia brasileira, baseadas em hipóteses sobre o comportamento de agregados macroeconômicos, mudanças tecnológicas e de preferências, projeções demográficas, alterações no cenário internacional e informações sobre a tendência dos investimentos setoriais/regionais , pode-se avaliar a trajetória de variáveis econômicas em um horizonte temporal pré-definido. Assim, são reportadas estimativas da trajetória tendencial da economia, contemplando os efeitos sobre o nível de atividade setorial dos estados e municípios, e de agregações especiais dos resultados municipais para áreas de interesse.
O cenário tendencial apresentado caracteriza uma situação provável para a economia brasileira no futuro, dadas as restrições sob as quais opera e as suposições feitas sobre alguns de seus aspectos estruturais fundamentais, tais como, taxa de investimento, padrão de consumo das famílias, evolução da produtividade em alguns setores, etc. Essa situação é resultante das suposições feitas, das restrições presentes, e da experiência de evolução da economia em passado relativamente recente. Basicamente, o cenário tendencial deve ser entendido como uma situação para a qual caminhará a economia nacional, na hipótese de que os fatores e políticas presentes nesse passado recente continuem a exercer alguma influência no período de projeção.
O modelo EFES1 1 Economic Forecasting Equilibrium System. Efes, ou Éfeso, é uma das doze cidades da Jônia, antigo distrito grego na costa ocidental da Ásia Menor, conhecida na antigüidade por seus santuários sagrados, sendo o mais famoso aquele dedicado à deusa Ártemis, onde, segundo consta, o apóstolo Paulo desafiou os artífices que lucravam com o comércio de miniaturas de divindades pagãs (Atos, 19: 23-41). foi desenvolvido no âmbito do Projeto SIPAPE (Sistema Integrado de Planejamento e Análise de Políticas Econômicas), desenvolvido na Fipe-USP, cujo objetivo geral é a especificação e implementação de um sistema de informações integrado para projeção macroeconômica, setorial e regional, e análise de políticas econômicas. Como parte deste projeto, este modelo de equilíbrio geral computável (EGC) está integrado a um modelo de consistência macroeconômica, permitindo a geração de resultados desagregados para 42 setores e 80 produtos, consistentes com cenários macroeconômicos pré-estabelecidos.2 2 Para maiores detalhes, ver Haddad e Domingues (2001).
Ao contrário de outros modelos EGC desenvolvidos para a economia brasileira, utilizados para a análise de políticas em exercícios de estática comparativa (e.g. Guilhoto, 1995; Campos-Filho, 1998; Haddad 1999)3 3 Ver Guilhoto (1995) para uma revisão de modelos EGC construídos para o Brasil até 1995, e Domingues (2002) para o período mais recente. , EFES é um modelo especificado com componentes de dinâmica suficientes para gerar projeções temporais para a economia brasileira. Dessa forma, podem-se observar trajetórias de investimento e acumulação de capital por setor, uma característica até agora pouco explorada em modelos EGC.
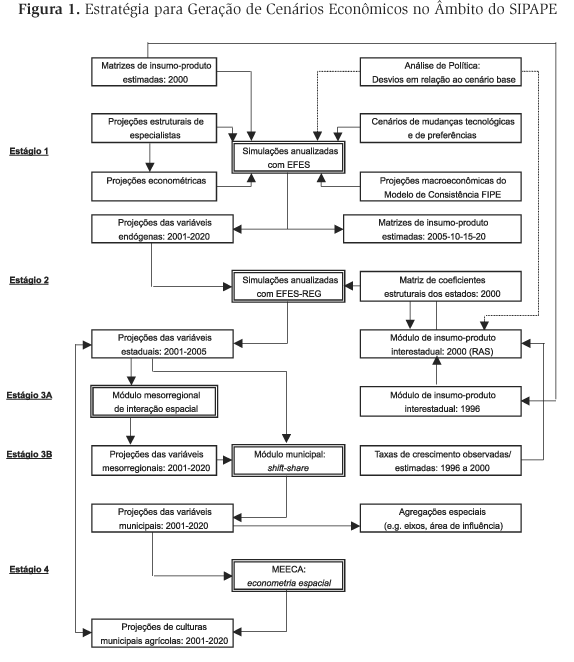
A Figura 1 apresenta, esquematicamente, a estratégia de simulação para a obtenção das projeções do cenário tendencial (estágios 1, 2, 3A, 3B) e de projeções consistentes para culturas agrícolas (estágio 4), considerando a integração dos vários módulos.
A utilização do modelo EFES em simulações de projeção possibilita a produção de resultados estruturais e macroeconômicos sobre a evolução da economia brasileira no período de estudo. No ambiente de projeção (estágio 1), o modelo é alimentado por projeções macroeconômicas de um modelo de consistência. Entre as informações utilizadas, está a evolução da inflação, da taxa de câmbio, dos gastos do governo, do investimento agregado e das exportações. Como insumo ao modelo EFES fazem parte também projeções de especialistas sobre alterações nas preferências e tecnologia. Políticas setoriais específicas também podem ser introduzidas nas simulações de projeção.
Alimentado com as informações acima, o modelo EFES produz projeções estruturais e macroeconômicas para a economia brasileira. A evolução da oferta doméstica e externa (importações) dos bens pode ser observada, assim como as variações do nível de emprego, investimento e estoque de capital em cada um dos setores de atividade do modelo. Indicadores macroeconômicos como volume de importações, saldo comercial, emprego e PIB também podem ser acompanhados. Deve ser destacado que esse amplo conjunto de resultados é totalmente consistente com as informações de entrada do modelo, com a estrutura da economia brasileira e com a teoria econômica estabelecida.
Deve-se ressaltar que as projeções do modelo não representam previsões, stricto sensu, para a economia brasileira. Os resultados derivados do modelo refletem trajetórias das variáveis endógenas para cenários exógenos específicos. A grande vantagem deste instrumental refere-se à sua flexibilidade na geração de cenários para a economia brasileira dentro de um arcabouço teórico de equilíbrio geral totalmente baseado em fundamentos econômicos. Apesar de limitações associadas a hipóteses restritivas sobre o comportamento dos agentes econômicos, a utilização do modelo EFES mostra-se bastante promissora e flexível, podendo salientar algumas aplicações genéricas, tais como: a) geração de projeções setoriais baseadas em cenários macroeconômicos alternativos; b) análise dos impactos de políticas econômicas (e.g. avaliação de portfólios de investimento) sobre trajetórias de crescimento da economia; c) integração com modelos regionais objetivando a geração de cenários para regiões e estados brasileiros.
Neste trabalho, utiliza-se ainda a extensão regional do modelo EFES (EFES-REG), desenvolvida para geração das decomposições estaduais dos resultados das simulações (estágio 2). Os coeficientes estruturais dos estados são utilizados (e atualizados a cada sub-período) nos processos de calibragem e re-calibragem do modelo. A obtenção destes coeficientes dá-se a partir de informações provenientes de uma matriz interestadual de insumo-produto.
Para se determinar o efeito de propagação espacial de projetos específicos, para os quais a localização é conhecida, uma variação do modelo gravitacional é utilizada, considerando-se as interações entre mesorregiões brasileiras. Com informações específicas sobre a localização municipal de vários projetos de investimento, pode-se determinar uma matriz de distribuição dos efeitos espaciais entre as mesorregiões que é utilizada na decomposição espacial dos impactos econômicos destes investimentos (estágio 3A).
Finalmente, o método proposto para geração de projeções municipais a partir das projeções estaduais/messorregionais baseia-se em uma desagregação top-down dos resultados (estágio 3B).4 4 Para captarmos a dinâmica regional (e.g. variação do nível de atividade entre dois pontos no tempo), isolando os efeitos específicos do processo de crescimento de cada região, em condições de informações limitadas, o módulo municipal utiliza os princípios do modelo tradicional de análise diferencial-estrutural. A análise diferencial-estrutural ( shift-share analysis) é um método essencialmente descritivo. É um método prático para avaliação de impactos de mudanças estruturais sobre economias subnacionais, partindo da constatação de que é possível separar estatisticamente, em qualquer intervalo de tempo, os componentes de crescimento de uma região que refletem o crescimento nacional, o mix de atividades da região e sua posição competitiva. A abordagem desenvolvida é bastante parcimoniosa em termos de seus requisitos de dados: apenas são necessárias informações sobre a estrutura setorial dos municípios brasileiros. Estas informações são utilizadas em pós-simulações com o modelo de equilíbrio geral integrado para desagregar as projeções básicas de um nível de 27 unidades da Federação e 137 mesorregiões para 4.974 municípios.5 5 Para fins de consistência, é utilizada a base municipal existente em 1996. Um resultado típico refere-se a um cenário do PIB setorial por município para o período de projeção. Deve-se enfatizar, mais uma vez, que as estimativas referentes a tal cenário são derivadas de um modelo determinista e, sendo assim, não devem representar previsões da economia brasileira. Tem-se, outrossim, um cenário consistente da evolução da mesma, dadas as premissas utilizadas.
Os resultados setoriais municipais podem ser desagregados através de módulos satélites que utilizam estas informações para geração de dinâmica subsetorial (estágio 4). Neste artigo, apresenta-se o Modelo Econométrico Espacial de Culturas Agropecuárias (MEECA), desenvolvido para gerar projeções espacializadas de produtos agropecuários, consistentes com as projeções do cenário tendencial, em todos seus níveis de agregação.
Este artigo está assim estruturado, além desta introdução. Na próxima seção, são apresentados os procedimentos metodológicos do modelo MEECA. Na terceira seção, os dados são discutidos. Na quarta seção, os resultados das regressões dos modelos econométricos espaciais são analisados. A última seção reserva as conclusões de relevo.
2 Metodologia
A diferença entre a econometria espacial e a econometria tradicional refere-se ao padrão da interação sócio-econômica entre os agentes num sistema, assim como as características da estrutura desse sistema no espaço. Essas interações e as características estruturais que podem ser instáveis no espaço geram efeitos espaciais em vários processos econômicos (Anselin, 1988; Anselin e Bera, 1997, Figueiredo, 2002, Anselin, 2003).
No espaço econômico, o padrão da interação tem uma natureza multidirecional que produz efeitos espaciais que violam o pressuposto vital do modelo clássico de regressão linear, a saber, os erros são homocedásticos e não autocorrelacionados. Um modelo econométrico de regressão linear tradicional tem a limitação de não ter a capacidade de controlar esses efeitos espaciais.
Levando em conta essas diferenças, desenvolvemos uma metodologia para a construção de modelos econométricos para a estimação dos coeficientes de equações das culturas agropecuárias, controlando para efeitos espaciais, a saber, a heterogeneidade espacial e a dependência espacial.
Em termos intuitivos, a heterogeneidade espacial manifesta-se quando ocorre instabilidade estrutural no espaço. Tal instabilidade pode ser observada na forma de coeficientes variáveis, de variância não constante ou da existência de formas funcionais diferentes para determinados subconjuntos de dados. Nesse caso, a conseqüência prática é a inadequação de se ajustar um mesmo modelo teórico para todo o conjunto de dados.
Formal e genericamente, podemos representar todas as possibilidades de manifestação da heterogeneidade espacial como:
em que yi é o logaritmo da variável de interesse (por exemplo, produção de arroz); X é a matriz de variáveis explicativas e b é vetor de coeficientes associados a ela; ui são os termos aleatórios, enquanto W é a matriz de variância-covariância diagonal.
Essa equação destaca os três aspectos da questão da heterogeneidade espacial. O primeiro aspecto, denominado de mudança estrutural, diz respeito à instabilidade estrutural expressa na forma de coeficientes (ou parâmetros) variáveis no espaço (bi). Fenômenos sócio-econômicos podem levar à mudança estrutural. O segundo aspecto refere-se à heterocedasticidade (ui e W), que provoca a perda de eficiência nas estimativas. O terceiro aspecto da heterogeneidade espacial trata da forma funcional distinta (fi). Como o tratamento da heterogeneidade na forma funcional pela literatura é rara, não será alvo de investigação neste artigo.
A heterogeneidade nos coeficientes bi pode ser tratada de diversas maneiras. Talvez a mais simples delas seja pela inclusão de dummies regionais que mostram que certos subconjuntos dos dados têm uma resposta distinta conforme a região onde o fenômeno se manifesta. Outra forma, mais sofisticada, é aplicar o método de expansão de Casseti (1972) no contexto espacial, ou seja, fazer com que as variáveis de expansão sejam as coordenadas (latitude e longitude).
Genericamente, a dependência espacial (ou a autocorrelação espacial, como também é conhecida) significa que o valor de uma variável de interesse numa certa localidade depende do valor dessa variável nas localidades vizinhas.
Talvez a forma mais simples para definir uma matriz de pesos espaciais seja uma matriz binária de vizinhança: se duas regiões são vizinhas, ou seja, partilham de uma fronteira, atribue-se o valor unitário; caso contrário, atribue-se o valor nulo. Formalmente:
Por convenção, wii=0, ou seja, nenhuma região i pode ser vizinha dela mesma. Apesar da aparente simplicidade desse conceito, escondem-se várias possibilidades para definir vizinhança, conforme distintas convenções de contiguidade. O problema reside em como se define o conceito de fronteira geográfica por intermédio da observação de um mapa. O mapa é uma mera representação abstrata da real configuração geográfica. Por isso, contém erros de medida. Levando em conta esses erros de medida, e em alusão ao movimento de peças num tabuleiro de xadrez, a convenção de contiguidade é dita ser rainha (queen), caso, além das fronteiras com extensão diferente de zero, puderem ser considerados os vértices (nós), na visualização de um mapa, como contíguos. Caso apenas as fronteiras físicas com extensão diferente de zero entre as regiões sejam levadas em conta, a convenção de contiguidade é considerada como torre (rook).6 6 Na situação em que apenas os vértices são considerados como vizinhos, a convenção é chamada de bispo ( bishop). Essas duas convenções são as mais utilizadas na literatura, pois atendem às condições de regularidade impostas pela necessidade de invocar as propriedades assintóticas dos estimadores e dos testes. Essas condições significam que os pesos precisam ser não-negativos e finitos e que correspondam a uma determinada métrica.7 7 Por exemplo, os trabalhos pioneiros de Moran e Geary na elaboração de estatísticas de dependência espacial baseavam-se em matrizes binárias de vizinhança que, além de exibirem as propriedades acima, são simétricas. Adicionalmente, esse tipo de matriz ostenta a propriedade da simetria. Por causa disso, adotamos a convenção rainha para a matriz binária de vizinhança W para ser incorporada nos modelos e serem efetuadas as regressões.
A desvantagem da matriz binária de pesos espaciais reside no fato de que não é garantida uma conectividade balanceada, uma vez que haja regiões com grande área com muitos vizinhos, ao passo que existirão regiões com pouca área e com poucos vizinhos.
É possível destacar duas fontes de dependência espacial. Em primeiro lugar, erros de medida para observações em lugares contíguos podem causar dependência no espaço. Em segundo lugar, a existência de uma variedade de modelos de interação social introduz dependência entre os agentes econômicos num sistema, tais como processos de difusão de tecnologia ou de imitação (Anselin, 1988). Cabe notar que esse tipo de fenômeno é muito facilmente verificável na agricultura, uma vez que os produtores agropecuários têm facilidade de observar como os seus vizinhos estão produzindo. Ademais, as culturas agropecuárias dependem de recursos naturais que são, por definição, concentrados no espaço geográfico, reforçando esse efeito de agrupamento produtivo.
Assim sendo, um modelo econométrico espacial, que pode incorporar vários componentes que procuram captar efeitos de vizinhança, tais como defasagens espaciais ou efeitos de transbordamento espacial, mostra-se mais adequado para investigar o comportamento das produções agropecuárias.
O modelo econométrico espacial que deve ser estimado depende dos aspectos que envolvem o processo espacial subjacente ao fenômeno em estudo. A autocorrelação espacial pode manifestar-se na variável dependente, nas variáveis explicativas ou no termo de erro. Os componentes que serão incorporados no modelo a fim de capturar o efeito da autocorrelação espacial consubstanciam em termos de defasagem espacial na variável dependente, nas variáveis explicativas e no termo de erro, como Wy, WX, We e Wu, respectivamente. Isoladamente ou em combinação num mesmo modelo, são esses componentes que darão conta de representar o processo espacial subjacente.8 8 Figueiredo (2002, pp. 51-54) apresenta diversos significados da autocorrelação espacial com ênfase na questão da produtividade agrícola.
A autocorrelação espacial na forma de Wy pode significar uma difusão espacial quando um atributo é adotado por uma população fixa ou um espraimento espacial no caso em que a própria população (como sementes ou fertilizantes podem ser levados pela chuva ou pelo sistema de irrigação para regiões vizinhas) espalha-se pelo espaço.
O modelo espacial incorporando o termo de defasagem Wy pode ser representado pela seguinte equação:
na qual Wy é a defasagem espacial (ou seja, a média da produção agropecuária em estudo nos vizinhos), r é o parâmetro da defasagem auto-regressiva espacial e é o termo de erro bem comportado, ou seja, segue uma distribuição normal de média zero e variância constante.
A defasagem espacial no erro pode significar um instrumento para detectar erros de especificação no modelo, tais como ausência de variáveis explicativas, heterocedasticidade ou variáveis não-observáveis ou uma correção para variáveis não-observáveis ou, ainda, um distúrbio (nuisance) nas estimações. Um modelo econométrico espacial incorporando o termo de defasagem no erro pode ser expresso por:
ou
em que l é o parâmetro do erro auto-regressivo espacial de primeira ordem, enquanto que g é o parâmetro do erro de média móvel de primeira ordem.
Assim sendo, o processo estocástico espacial no erro pode assumir duas formas: um processo auto-regressivo de primeira ordem ou um processo de médias móveis de primeira ordem. A diferença reside no alcance localizado ou globalizado da autocorrelação no erro. A equação (5) exprime uma autocorrelação do erro mais amplo, afetando todo o sistema (e.g. uma praga afetando uma cultura que se espalha através de todas as regiões). Já a equação (6) dá a idéia de um alcance localizado (e.g. a poluição de um rio que afeta somente a região e os seus vizinhos diretos). Cabe notar que os componentes da autocorrelação no erro são, nesses casos, Wu e We.9 9 Para se ler mais a respeito disso, consulte Anselin (2003).
Por fim, a autocorrelação pode ocorrer nas variáveis explicativas, havendo a necessidade de incorporar um componente para capturar esse efeito de transbordamento ou de externalidades. Para isso, adota-se, algumas vezes, o modelo cruzado regressivo:
em que t é um vetor de parâmetros a serem estimados. Em nossa aplicação para exemplificar o modelo MEECA, a matriz X é composta pelo logaritmo do produto interno bruto do setor agropecuário (PIBAGR), o logaritmo do produto interno bruto do setor industrial (PIBIND) e/ou o logaritmo do produto interno do setor de serviços (PIBSER). PIBAGR, PIBIND e PIBSER são as componentes de ligação (integração) entre o módulo municipal e o modelo MEECA, que as utiliza como variáveis explicativas relevantes. Por sua vez, a matriz de defasagens das variáveis explicativas, WX, é composta pelo termo WPIBAGR , que é a variável que captura a influência da produção agropecuária do município vizinho (efeito transbordamento ou spillover effect); significado semelhante é válido para as variáveis WPIBIND e WPIBSER.
Considerando-se as informações geradas pelas projeções das variáveis municipais (estágio 3B na Figura 1), a especificação de um modelo econométrico espacial para uma certa produção agropecuária em nível municipal seria feito em duas etapas. Na primeira etapa procurar-se-ia modelar a autocorrelação espacial, enquanto numa segunda etapa, tentar-se-ia tratar a heterogeneidade espacial.
A especificação final do modelo econométrico-espacial de uma determinada cultura agropecuária depende de uma bateria de testes estatísticos que avaliam várias propriedades de excelência do modelo, tais como a significância estatística dos coeficientes, a qualidade do ajuste do modelo aos dados, a ausência de má-especificação do modelo. O modelo MEECA para uma certa cultura agropecuária normalmente conterá apenas alguns dos componentes espaciais especificados ao longo desta seção.
Uma vez que os fenômenos da heterogeneidade espacial e da autocorrelação espacial, muitas vezes, não são distinguidos facilmente na prática, durante a estimação do modelo MEECA, costuma-se adotar uma dessas duas abordagens: a) modela-se inicialmente a heterogeneidade espacial e testa-se para a autocorrelação espacial nos resíduos; b) modela-se inicialmente a autocorrelação espacial e testa-se para a heterogeneidade espacial. Sempre se procura corrigir estes dois efeitos espaciais no modelo final a fim de que se possam obter estimativas não-viesadas e precisas.
3 Dados
Para a implementação do modelo MEECA são necessárias, além das informações sobre o nível de produção setorial municipal, informações georeferenciadas sobre as culturas agropecuárias de interesse, que representam um subconjunto exaustivo do setor agropecuário.
Os dados sobre o valor da produção de cada cultura agropecuária nos municípios da área de estudo, no caso, a Amazônia brasileira, vêm do Censo Agropecuário de 1996 do IBGE. As culturas agropecuárias selecionadas para a aplicação do modelo MEECA são a rizicultura, a sojicultura, a cultura do milho, outros produtos extrativos, bovinocultura e outros produtos pecuários.
Os dados básicos sobre o PIB setorial, utilizados para gerar as projeções tendenciais do PIB módulo municipal têm como fonte pesquisas do IBGE, IPEA e Fipe. As variáveis estão em valores de 1996 e foram projetadas, em simulações históricas, para o ano de 2000, e em simulações de projeção para o período 2000-2020.
4 Resultados10 10 Os resultados foram obtidos por meio do pacote econométrico SpaceStat versão 1.91, desenvolvido por Anselin (1992).
Inicialmente, todos os modelos para culturas agropecuárias foram estimados por Mínimos Quadrados Ordinários. A tabela 1 apresenta os testes de diagnóstico para as regressões estimadas. Os resíduos não são normais pelo teste Jarque-Bera em todas as regressões. O teste global I de Moran aponta para a presença de autocorrelação espacial nos resíduos. O problema desse teste é a sua sensibilidade para a ausência de normalidade. Por isso, computou-se o teste Kelejian-Robinson, que não pressupõe a normalidade dos resíduos.11 11 Anselin e Florax (1995) mostraram que o teste Kelejian-Robinson é mais apropriado para grandes amostras. Como se trabalha com uma amostra de tamanho médio, é preciso não tirar conclusões levando em conta apenas a informação desse teste. Por meio desse teste global, é possível perceber evidências da existência de autocorrelação nos resíduos. A desvantagem dos testes globais é que, caso a hipótese nula seja rejeitada, eles não fornecem indicações a respeito da forma que a autocorrelação espacial pode assumir. Por isso, computam-se os testes específicos do tipo multiplicador de Lagrange (ML) para o erro auto-regressivo e para a defasagem, acompanhados de suas versões robustas.12 12 Ver mais a respeito desses testes em Anselin e Bera (1998). Os testes residuais para autocorrelação do tipo multiplicador de Lagrange indicam o modelo de erro auto-regressivo espacial como o mais apropriado para todas as regressões.13 13 A identificação dos modelos é baseada no procedimento descrito em Florax et al. (2003).
Uma vez que os resíduos não são normais, usamos o método para estimar modelos auto-regressivos de erro espacial, desenvolvido por Kelejian e Prucha (1999). Esse método estima o parâmetro l de um modelo de erro auto-regressivo espacial da equação (2), usando a abordagem dos Momentos Generalizados (MG). Tal método não assume que o termo de erro seja distribuído normalmente, apenas que ele atenda à propriedade de que seja independente e identicamente distribuído (i.i.d.) e tenha variância constante. O parâmetro l obtido por meio do método (MG) de Kelejian-Prucha é consistente, mas não eficiente. Não existe inferência sobre o parâmetro l, uma vez que se comporta como um parâmetro de perturbação (nuisance parameter).
Os resultados das estimações dos modelos econométricos-espaciais para culturas agropecuárias (MEECA) estão exibidos na Tabela 2.
No que diz respeito ao modelo para o arroz, o coeficiente para o PIB agropecuário assume o valor de 1,493 e é altamente significante. Como as variáveis estão em logaritmo, pode ser interpretada como sendo elasticidades. Assim, um aumento de 1% no PIB agropecuário está associado a uma elevação de quase 1,5% na produção de arroz. Esse coeficiente foi expandido segundo uma função linear das coordenadas do centróide do município. Há evidências da existência de uma tendência positiva Norte-Sul e uma negativa Oeste-Leste nos coeficientes. Ou seja, o coeficiente do PIB agropecuário tende a aumentar linearmente quando se desloca de Norte para o Sul, e tende a decrescer linearmente quando se desloca de Oeste para Leste.
No que se refere ao modelo para a soja, tanto o coeficiente do PIB agropecuário (0,594) quanto o coeficiente do PIB industrial (0,120) são significativamente diferentes de zero em termos estatísticos. Cabe notar que ambos coeficientes são menores que a unidade mas maiores do que zero , sugerindo uma maior integração na cadeia produtiva regional.
No que concerne ao modelo para o milho, o parâmetro estimado para o PIB agropecuário mostrou-se menor que a unidade (0,581) e significativamente diferente de zero. O coeficiente da variável de expansão com a longitude foi significativo, indicando que existe uma tendência espacial Norte-Sul nesse coeficiente.
Quanto ao modelo para outros produtos extrativos, o coeficiente para o PIB agropecuário é positivo, porém menor que um, e significativo do ponto de vista estatístico. O efeito de transbordamento representado pelo PIB agropecuário tem coeficiente negativo (-0,360) e significativamente diferente de zero em 5%. A interpretação é que um aumento de 1% no PIB agropecuário dos municípios vizinhos provoca um decréscimo de 0,36% na produção de outros produtos extrativos no município. O coeficiente negativo sinaliza que existe uma relação de competição entre a produção de produtos extrativos no município e seus vizinhos.
Com relação ao modelo para os bovinos, o coeficiente para o PIB agropecuário é positivo e significativamente diferente de zero. A elasticidade do PIB agropecuário é de 1,205 e revela-se altamente significativo. Esse coeficiente foi expandido segundo uma função linear das coordenadas do centróide do município. Há evidências da existência de uma tendência positiva Norte-Sul e uma negativa Oeste-Leste no coeficiente do PIB agropecuário.
Resultados semelhantes ao modelo anterior são obtidos para o restante da pecuária. O coeficiente do PIB agropecuário é de 1,100. Existem também evidências de uma tendência positiva no coeficiente do PIB agropecuário de Norte para Sul e uma tendência negativa nesse mesmo coeficiente de Oeste para Leste.
A partir das estimativas dos coeficientes desses modelos, é possível fazer as projeções para as culturas agropecuárias, utilizando como variáveis independentes as projeções tendenciais do PIB setorial municipal obtidas como resultado das simulações do modelo de equilíbrio geral aplicado EFES.
Para exemplificar os resultados do modelo MEECA, podemos considerar uma determinada cultura. O Mapa 1, abaixo, apresenta a distribuição da produção de arroz na Amazônia, no ano de 1996. O Mapa 2 exibe as projeções para a cultura do arroz na forma de taxa média anual no período 2000 a 2020, no qual se percebe uma faixa mais dinâmica na fronteira Sudeste da região.
5 Considerações Finais
Este trabalho fornece estimativas dos modelos econométrico-espaciais para as culturas do arroz, soja, milho, outros produtos extrativos (exclusive madeira), bovinos e outros produtos pecuários. Os testes estatísticos apontaram para a adequação de se estimar todas as regressões das culturas como modelos de erro auto-regressivo espacial.
Em todos os modelos, o coeficiente do PIB agropecuário mostrou-se significativo estatisticamente no nível de 1%. O coeficiente do PIB industrial revelou-se significativo estatisticamente em 1% apenas para o modelo da sojicultura. Na maioria dos modelos, com exceção dos parâmetros estimados da soja e de outros produtos extrativos, encontramos evidências de que o coeficiente do PIB agropecuário apresenta uma expansão linear no espaço econômico de acordo com as coordenadas. Para o modelo de outros produtos extrativos, estimamos o efeito transbordamento do PIB agropecuário, isto é, o PIB agropecuário dos vizinhos também é fator explicativo da produção desta cultura, apesar de ser um efeito negativo denotando que existe, neste caso, uma relação de competição entre os municípios que exploram os outros produtos extrativos (exclusive madeira).
Após a estimação, à guisa de exemplo, fizemos com a cultura do arroz as projeções de crescimento desta cultura entre 2000 e 2020. Os valores dos PIB para os anos futuros, que entraram nas regressões como variáveis independentes, foram computados pelo modelo de equilíbrio geral computável EFES e suas extensões regionais, que está integrado à metodologia do MEECA com o intuito de gerar projeções consistentes do ponto de vista econômico.
As perspectivas dessa metodologia inovadora são promissoras, podendo se constituir em uma ferramenta relevante para produzir projeções sistemicamente consistentes para as culturas agropecuárias.
6 Referências Bibliográficas
Recebido em maio de 2003 e revisto em agosto de 2004
- ANSELIN, L. Spatial externalities, spatial multipliers, and spatial econometrics. International Regional Science Review, v. 26, n. 2, p. 153-166, 2003.
- ANSELIN, L. SpaceStat Tutorial Urbana-Champaign: University of Illinois, 1992. (mimeo.)
- ANSELIN, L. (1988). Spatial Eeconometrics: methods and models Boston: Kluwer Academic, 1988.
- ANSELIN, L. and BERA, A. (19987). Spatial dependence in linear regression models with an introduction to spatial econometrics. In: Ullah A. and Giles D. E. (eds.) Handbook of Applied Economic Statistics, Marcel Dekker, New York, 237-28.
- ANSELIN, L. and FLORAX, J. G. M. (1995). Small Ssample of Ttests for Sspatial Ddependence in Rregression Mmodels: Ssome Ffurther Rresults. In: Anselin, L. and Florax, R. J. G. M. (eds) New Direction in Spatial Econometrics, Springer, New York.
- CAMPOS-FILHO, L. (1998). Unilateral Liberalisation and Mercosul: Implications for Resource Allocation. University of London, Unpublished Ph.D. Dissertation
- DOMINGUES, E. P. Dimensão Regional e Setorial da Integração Brasileira na Área de Livre Comércio das Américas Tese de Doutorado, FEA/USP, 2002. (mimeo)
- FIGUEIREDO, A. M. R. Resposta da produção agrícola aos preços no Centro-Oeste brasileiro: uma análise de econometria espacial para o período 1975-1995/1996 Tese de Doutorado, Universidade Federal de Viçosa, 2002. (mimeo)
- FLORAX, R., FOLMER, H. e REY, S. (2002). Specification searches in spatial econometrics: the relevance of Hendry's methodology Working Paper, Department of Spatial Economics, Free University Amsterdam.
- GUILHOTO, J. J. M. Um Modelo Computável de Equilíbrio Geral para Planejamento e Análise de Políticas Agrícolas (PAPA) na Economia Brasileira. Tese de Livre Docência, ESALQ/USP, Piracicaba, 1995. (mimeo)
- HADDAD, E. (1999). Regional Inequality and Structural Changes: Lessons from the Brazilian Economy Ashgate, Aldershot.
- HADDAD, E. A. e E. P. DOMINGUES (2001). EFES - Um Modelo Aplicado de Equilíbrio Geral para a Economia Brasileira: Projeções Setoriais para 1999-2004. Estudos Econômicos, vol. 31, n. 1.
- HAINING, R. (1990) Spatial data analysis in the social and environmental sciences New York: Cambridge University.
- KELEJIAN, H. H. e PRUCHA, I. R. (1999). A Generalized Moments Estimator for the Autoregressive Parameter in a Spatial model. International Economic Review, vol. 40, n. 2.
- MOREIRA, A. e MIGON, H. (2000) Heterogeneidade espacial da produtividade na agropecuária: Brasil 1970/1996. Rio de Janeiro: IPEA/NEMESIS/PRONEX. Disponível em: http://www.nemesis.org.br/docs/ajax1.pdf
Datas de Publicação
-
Publicação nesta coleção
23 Jun 2005 -
Data do Fascículo
Set 2004
Histórico
-
Aceito
Ago 2004 -
Recebido
Maio 2003