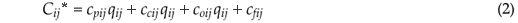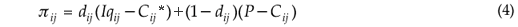Resumos
A hipótese básica do trabalho é que, mesmo quando cientes dos riscos econômicos envolvidos, alguns produtores não reconhecem, individualmente, a importância em adotar medidas preventivas, uma vez que a ocorrência de algumas doenças não é frequente. Ademais, a existência de externalidades faz com que a ação de um produtor em relação às medidas sanitárias afete os demais produtores da mesma região, o que também pode não ser percebido por eles. O presente trabalho busca desenvolver um procedimento teórico que permita inferir sobre as decisões estratégicas de produtores quanto à prevenção contra doenças em animais, face ao risco de contaminação de seu rebanho. O desenvolvimento do modelo é baseado na Teoria dos Jogos e na análise de Benefício-Custo como base para a tomada de decisão. Depois de modelado o problema, infere-se sobre as possíveis atuações do governo, no uso de incentivos econômicos (como indenizações e multas) para que o equilíbrio seja o da prevenção. Em seguida, o modelo teórico é aplicado a um caso de surto de febre aftosa no Brasil. O resultado mostrou que, na ausência de um mercado diferenciado para animal não vacinado, o equilíbrio do jogo tende para a situação em que produtores decidem vacinar seu rebanho, sugerindo que não existe a necessidade de intervenção do governo. Na prática, no entanto, o governo brasileiro estabelece políticas de incentivo, visto que alguns produtores não vacinam seu rebanho mesmo conhecendo os riscos, o que sugere falta de racionalidade.
Teoria dos Jogos; febre aftosa; produção e comercialização; pecuária; análise benefício; teoria da decisão
The basic hypothesis of this study is that producers do not realize, individually, the importance of adopting preventive measures, even aware of the economic risks for them and for the local economy, because outbreaks of some diseases are not frequent. Moreover, the presence of externalities makes the action of one producer regarding sanitary measures of the herd affect other producers in the same region, which cannot be perceived by them, either. This study aims to develop a theoretical procedure to infer about strategic decisions taken by producers to prevent animal disease in their herds, in face of the risk of contamination. The development of the model is based on the Game Theory, and the cost-benefit analysis as support for decision-making process. After modeling the problem and determining the equilibriums, they are used to elaborate inferences about possible actions of the government through economic incentives (such as indemnities and fines) to encourage the prevention. Then, the theoretical model is applied to a specific case of a foot-and-mouth disease (FMD) outbreak in Brazil. Results indicate that with the absence of a differentiated market for non-vaccinated animals, the game equilibrium tends to the situation in which decisions of producer are to vaccinate their herd, suggesting that government intervention is not necessary. In practice, however, the Brazilian government uses incentive policies for cattle vaccination since some producers do not vaccinate their animals, despite their awareness of the risks, which suggests lack of rationality.
Game Theory; Foot-and-mouth disease; Meat sector; Benefit; Decision making theory
Procedimento para análise de decisão quanto à prevenção de doenças em animais: uma aplicação da Teoria dos Jogos
Luciana Torrezan SilveiraI; Heloisa Lee BurnquistII
IDoutora em Economia Aplicada pela Esalq (Escola Superior de Agricultura Luiz de Queiroz), USP. Especialista em Inteligência de Mercado Copersucar. Email: ltsilveira@copersucar.com.br
IIProfessora Ph.D. do Departamento de Economia, Administração e Sociologia da Esalq (Escola Superior de Agricultura Luiz de Queiroz), USP. E-mail: hlburnqu@esalq.usp.br
RESUMO
A hipótese básica do trabalho é que, mesmo quando cientes dos riscos econômicos envolvidos, alguns produtores não reconhecem, individualmente, a importância em adotar medidas preventivas, uma vez que a ocorrência de algumas doenças não é frequente. Ademais, a existência de externalidades faz com que a ação de um produtor em relação às medidas sanitárias afete os demais produtores da mesma região, o que também pode não ser percebido por eles. O presente trabalho busca desenvolver um procedimento teórico que permita inferir sobre as decisões estratégicas de produtores quanto à prevenção contra doenças em animais, face ao risco de contaminação de seu rebanho. O desenvolvimento do modelo é baseado na Teoria dos Jogos e na análise de Benefício-Custo como base para a tomada de decisão. Depois de modelado o problema, infere-se sobre as possíveis atuações do governo, no uso de incentivos econômicos (como indenizações e multas) para que o equilíbrio seja o da prevenção. Em seguida, o modelo teórico é aplicado a um caso de surto de febre aftosa no Brasil. O resultado mostrou que, na ausência de um mercado diferenciado para animal não vacinado, o equilíbrio do jogo tende para a situação em que produtores decidem vacinar seu rebanho, sugerindo que não existe a necessidade de intervenção do governo. Na prática, no entanto, o governo brasileiro estabelece políticas de incentivo, visto que alguns produtores não vacinam seu rebanho mesmo conhecendo os riscos, o que sugere falta de racionalidade.
Palavras-chaves: Teoria dos Jogos; febre aftosa; produção e comercialização; pecuária; análise benefício/custo; teoria da decisão.
Classificação JEL: C72, D81, Q18.
ABSTRACT
The basic hypothesis of this study is that producers do not realize, individually, the importance of adopting preventive measures, even aware of the economic risks for them and for the local economy, because outbreaks of some diseases are not frequent. Moreover, the presence of externalities makes the action of one producer regarding sanitary measures of the herd affect other producers in the same region, which cannot be perceived by them, either. This study aims to develop a theoretical procedure to infer about strategic decisions taken by producers to prevent animal disease in their herds, in face of the risk of contamination. The development of the model is based on the Game Theory, and the cost-benefit analysis as support for decision-making process. After modeling the problem and determining the equilibriums, they are used to elaborate inferences about possible actions of the government through economic incentives (such as indemnities and fines) to encourage the prevention. Then, the theoretical model is applied to a specific case of a foot-and-mouth disease (FMD) outbreak in Brazil. Results indicate that with the absence of a differentiated market for non-vaccinated animals, the game equilibrium tends to the situation in which decisions of producer are to vaccinate their herd, suggesting that government intervention is not necessary. In practice, however, the Brazilian government uses incentive policies for cattle vaccination since some producers do not vaccinate their animals, despite their awareness of the risks, which suggests lack of rationality.
Key-words: Game Theory; Foot-and-mouth disease; Meat sector; Benefit/cost analysis; Decision making theory.
1. Introdução
A importância do setor de carnes para a economia brasileira pode ser verificada pelos seus números, uma vez que foi responsável por cerca de 17,4% das exportações do agronegócio e 6,2% dos embarques totais do País em 2006, com uma receita de US$ 8,6 bilhões, segundo dados do Ministério do Desenvolvimento, Indústria e Comércio Exterior (BRASIL, 2007). Desde o início da década de 2000, o Brasil vem assumindo posição de destaque tanto no mercado internacional de carne bovina como de frango.
Apesar das boas perspectivas atribuídas ao setor, a identificação de focos de doenças nos rebanhos comerciais tem se tornado um obstáculo importante ao crescimento do comércio internacional de carnes.
No caso do Brasil, o surto de febre aftosa ocorrido nos estados de Mato Grosso do Sul e Paraná, em outubro e dezembro de 2005, respectivamente, fez com que um número expressivo de países vetasse a entrada do produto brasileiro, o que influenciou imediatamente o comércio de carnes dessa região. Os efeitos do surto de 2005 se estenderam até o primeiro semestre de 2006, quando se verificou queda de 79,6% no volume de carne bovina congelada comercializada em Mato Grosso do Sul e de 76,5% no de carne fresca ou refrigerada (BRASIL, 2007).
Além da febre aftosa, outros tipos de doenças com implicações para o comércio internacional de carnes vêm sendo verificados ao longo dos últimos anos, como a gripe aviária, febre suína clássica, febre suína africana, doença de Newcastle, BSE (Encefalopatia Espogiforme Bovina, também conhecida como "vaca louca"), peste bovina, entre outras.
Reações dessa natureza à contaminação de produtos agro-alimentares vêm se tornando cada vez mais freqüentes nas relações de comércio internacional, ao longo dos últimos anos. Diante da eclosão de surtos de doenças em animais, importadores imediatamente proíbem a comercialização não apenas de carnes, como de subprodutos originados dos países afetados.
Além da queda nas exportações devido aos embargos impostos pelos países importadores, a eclosão de surtos de doenças em animais implica em custos significativos de controle e recuperação da condição sanitária para os países diretamente afetados. Ademais, esses países perdem a confiança de importadores importantes em relação à sanidade e segurança de seus produtos.
Aparentemente, a prevenção de doenças é uma estratégia adequada para evitar efeitos adversos gerados pelos surtos (KEELING et al., 2003; BARRET, 2003). No entanto, a prevenção implica em custos ao produtor, que nem sempre se dispõe a assumi-los, por considerar o risco de infecção relativamente pequeno e por desconsiderar o custo decorrente de um surto para a economia do País.
Nesse contexto, torna-se importante o desenvolvimento de um procedimento que permita inferir sobre as decisões estratégicas dos produtores quanto à prevenção contra doenças em animais, tomando como base os preceitos da Teoria dos Jogos, face ao risco de incidência de doenças que tenham implicações econômicas.
Diversos trabalhos identificados na literatura (BAUCH; EARN, 2004; BARRET, 2003) tratam de analisar, por meio da Teoria dos Jogos, o equilíbrio esperado para o caso da prevenção contra doenças através da vacinação. Esses autores determinam que, quando a vacinação não é mandatória, o equilíbrio esperado é que os indivíduos não se vacinem ou que a vacinação da população alcance uma proporção aquém do considerado ótimo. Isso ocorre porque, se um número relativamente grande de indivíduos é vacinado, aqueles que não o foram também passam a contar com uma proteção indireta à doença. Isso pode ser interpretado como uma externalidade positiva da vacinação e, que por vezes, desestimula a vacinação de todos os indivíduos. Se a maioria dos indivíduos seguirem essa lógica, o equilíbrio do jogo passa a ser a situação em que os indivíduos não se vacinam.
Cabe analisar, então, as decisões estratégicas dos produtores de animais, interagindo com relação às estratégias tomadas para evitar o risco da doença, e do setor público, em termos de política, para garantir que o equilíbrio do jogo seja o da ação preventiva.
2. Hipóteses e objetivos
A hipótese básica da presente pesquisa é que, embora a ocorrência de uma determinada doença possa apresentar impactos econômicos expressivos tanto para o produtor como para outros agentes da economia, alguns produtores não reconhecem, individualmente, a importância em adotar medidas preventivas, uma vez que a ocorrência da doença não é frequente. Considera-se importante, portanto, modelar as ações e interações entre os indivíduos, associando-as a possíveis estratégias e parâmetros, de forma a facilitar a identificação dos possíveis resultados econômicos dessas ações e, consequentemente, inferir se estas estão de acordo com o esperado pelos agentes reguladores.
Uma segunda hipótese, decorrente da primeira, é que existe a necessidade de ação por parte de terceiros agentes possivelmente o governo organizando incentivos para promover decisões privadas de prevenção pelos produtores, quando esses não reconhecem as consequências externas de suas ações. Quando a tomada de ação pelo produtor para reduzir o risco de ocorrência da doença afeta os demais, o mercado, por si só, não é capaz de sinalizar a necessidade de ação para o produtor.
O objetivo geral deste trabalho é aplicar a Teoria dos Jogos à análise de economia agrícola, considerando o caso da adoção de medidas preventivas em animais contra a ocorrência de surtos endêmicos, dado que os impactos da contaminação estendem-se a todos os produtores de uma região afetada e possivelmente à economia do País.
O emprego dessa teoria para tal modelagem parece adequado, uma vez que envolve uma situação interativa, em que uma ação estratégica tomada por um produtor pode ser afetada pela ação de outro produtor, ou mesmo do governo, por meio de medida regulamentadora.
Mais especificamente procura-se:
1. Modelar o problema, considerando a decisão quanto à adoção de medidas preventivas contra doenças em animais por parte dos produtores, com base na análise de benefício/custo referente a cada situação proposta;
2. Inferir sobre os possíveis comportamentos dos produtores, face ao risco de contaminação de seu rebanho, bem como sobre possíveis atuações de um agente regulador, se necessário;
3. Validação e teste do modelo, utilizando-se de dados empíricos para um caso de febre aftosa ocorrido no Brasil.
3. Procedimento Metodológico
3.1. Jogo sem a intervenção do governo
A modelagem do jogo estratégico teve como base outros modelos aplicados para análises com objetivos semelhantes. Um desses é apresentado por Mattoo (1996), aplicado à questão da exigência de padrões para produtos/serviços entre países, e outro por Rich et al. (2005), que desenvolveram um modelo espacial de jogo em que dois produtores vizinhos de gado bovino decidem adotar níveis de esforços elevados ou baixos para o controle da febre aftosa.
Na definição de um modelo básico, supõe-se, para efeito de simplificação, a existência de apenas 2 produtores (Produtores 1 e 2) localizados geograficamente próximos, representando dois jogadores.
O jogo segue dois estágios:
(i) No primeiro, os produtores decidem se adotam as ações voluntárias de prevenção contra uma determinada doença (representada pela estratégia A) ou não adotam (estratégia B);
(ii) No segundo estágio do jogo, a "natureza joga", de maneira que o surto da doença ocorre (representada pela situação S) ou não ocorre (representada por N). Atribuem-se probabilidades a essas ocorrências.
O resultado do jogo, ou seja, o payoff recebido por cada jogador, depende da sua escolha e da estratégia do seu oponente, seguindo o princípio da interdependência estratégica da Teoria dos Jogos. No caso aqui descrito, de prevenção contra doenças, a facilidade de disseminação dos agentes causadores da enfermidade (vírus, bactérias, etc.) faz com que as ações de prevenção tomadas por um produtor influenciem os payoffs e conseqüentemente as ações tomadas por seus vizinhos.
Assim, a decisão tomada por cada produtor entre (A) ou (B) deverá ser baseada na expectativa de ganho e/ou perda econômicos que esse agente incorrerá diante de cada possível escolha, dada a provável decisão de seu concorrente e as condições da natureza quanto à probabilidade de ocorrência de um surto de febre aftosa (S) ou desse não ocorrer (N).
Como um primeiro cenário, considera-se que o governo não intervém (instituindo multa ou indenização) para estimular as medidas de prevenção. O objetivo é determinar o equilíbrio do jogo, sem a intervenção do setor público, para inferir se sua atuação é necessária para que os produtores adotem tais medidas.
Modelando a situação do Cenário 1 na forma de um jogo estratégico, tem-se:
Jogadores (i): produtores 1 e 2.
Ações: adotar (A) ou não adotar (B) as ações de prevenção.
Preferências: representadas pelas funções de payoff dos produtores i em cada situação j possível, ou seja, Yij (p, cij, dij), para i = 1, 2; j = 1, 2, 3, 4 (j = 1 se ambos adotam a prevenção, j = 2 se apenas o produtor 1 previne; j = 3 se apenas o produtor 2 previne; e j = 4 se ambos não previnem).
No qual:
p = preço recebido pelo gado assumindo-se inicialmente que este é o mesmo para os produtores 1 e 2, independente desses adotarem ou não ações de prevenção, e que é exógeno;
cij= custos de produção do rebanho, custo de prevenção, e despesas com controle da doença, uma vez adquirida, que também são exógenos;
dij= probabilidade do animal adquirir a doença.
O payoff de um produtor individual é dado pela diferença entre a Esperança de suas receitas e seus custos, incluindo aqui as despesas com a prevenção da doença e os custos de controle e/ou descontaminação em relação à mesma, se adquirida (custo de sacrifício ou recuperação dos animais doentes e de controle sanitário na região afetada, dentre outras1 1 As medidas de descontaminação dependem da doença em questão. Para algumas delas, como a febre aftosa, a medida geralmente adotada é o sacrifício de todos os animais do rebanho afetado, tanto os doentes quanto os suspeitos e os que entraram em contato com os infectados. ).
Os possíveis resultados do jogo são:
1. (A,A)2 2 Um resultado representado na forma (X,Y) indica que o primeiro jogador decide pela ação X e, o segundo, pela ação Y. Ambos os produtores adotam as práticas de prevenção
Existe uma probabilidade d11 para o produtor 1 de que seus animais venham a contrair a doença, e d21 para o produtor 2, mesmo que a prevenção tenha sido realizada por ambos3 3 As pressuposições sobre as probabilidades dij serão esclarecidas adiante. .
Nesse possível resultado, pressupõe-se que ambos incorrem em custos de prevenção, independente do surto da doença ocorrer ou não. Se esse não ocorrer para nenhum deles, suas vendas para o exterior não são prejudicadas (a não ser que algum país decida não importar animal e/ou carne de países que adotam medidas preventivas). Se ocorrer o surto, para pelo menos 1 produtor, ambos podem incorrer em prejuízos econômicos pelo fechamento dos mercados importadores de carne. Espera-se que o prejuízo seja maior ao produtor cujo rebanho é afetado, pois este terá que sacrificar os animais e tomar outras medidas para descontaminação da sua propriedade em relação à doença. O produtor que não teve problema com a doença pode vender seu animal, porém, o preço pode ser diferente ao negociado no mercado antes do surto da doença4 4 Dependendo da natureza da doença, da expressividade do surto, do tipo de mercado em questão, e da inserção do país no mercado internacional de carnes, os preços recebidos pelos produtores cujo rebanho está sadio podem sofrer queda ou aumento. A redução pode ocorrer porque diversos países deixam de comprar a carne do país afetado, porém os preços podem aumentar porque houve quebra de oferta de carne em decorrência da doença. .
A possibilidade do produtor que não teve problemas com a doença vender seu produto no mercado doméstico é uma pressuposição do modelo, mas, na prática, pode nem sempre ocorrer, visto que, em alguns casos, se o produtor estiver localizado dentro de um determinado raio do surto, seus animais também devem ser sacrificados.
A Esperança do payoff πijde cada produtor i pode ser calculada com base nas diferentes situações possíveis de j, considerando que a doença pode ocorrer com uma probabilidade dij, resultando num payoff Yij*, ou não ocorrer com uma probabilidade (1- dij), resultando num payoff de Yij.
Assim, as Esperanças dos payoffs para os produtores 1 e 2 quando ambos adotam medidas de prevenção são: π11 = d11(Y11*) + (1 d11)(Y11) e π21 = d21(Y21*) + (1 d21)(Y21), respectivamente.
2. (A,B) Apenas o produtor 1 adota as práticas de prevenção:
Neste caso, pressupõe-se que o produtor 1 tem uma probabilidade d12 de ter problemas com a doença e o produtor 2 tem uma probabilidade d22 de ter problemas. A probabilidade de ocorrer a doença depende da decisão dos produtores em adotar ou não medidas preventivas. Essa dependência é expressa no payoff, considerando que d12 < d22. Apenas o produtor 1 incorre em custos de prevenção. As mesmas pressuposições do resultado anterior são válidas no caso de pelo menos um dos rebanhos adquirir a doença no tocante ao fechamento do mercado internacional e do sacrifício dos animais. A Esperança dos payoffs de 1 e de 2 será, respectivamente: π12 = d12(Y12*) + (1 d12)(Y12) e π22 = d22(Y22*) + (1 d22)(Y22).
3. (B,A) - Apenas o produtor 2 adota as práticas de prevenção:
Neste caso, a situação anterior se inverte; ou seja, pressupõe-se que o produtor 1 tem uma probabilidade d13 de contaminação de seu gado, e o produtor 2 tem uma probabilidade d23 de infecção. Assim, somente o produtor 2 tem o custo com prevenção. A Esperança dos payoffs para os produtores 1 e 2 será dada, respectivamente, por: π13 = d13(Y13*) + (1 d13)(Y13) e π23 = d23(Y23*) + (1 d23)(Y23).
4. (B,B) - Ambos produtores não adotam as práticas de prevenção:
O produtor 1 possui uma probabilidade d14 de ter seu rebanho afetado pela doença, e o produtor 2, uma probabilidade d24. Nenhum deles incorre em custos com prevenção. A Esperança dos payoffs de 1 e de 2 será calculada, respectivamente como: π14 = d14(Y14*) + (1 d14)(Y14) e π24 = d24(Y24*) + (1 d24)(Y24).
A representação do jogo na forma estratégica, em uma matriz de payoffs, pode ser visualizada na Figura 1.
Como modelado a princípio, trata-se de um jogo simultâneo não-cooperativo, com informação completa (os jogadores conhecem a função de payoff esperada em cada situação j= 1 a 4, e inclusive a do seu concorrente), porém, com informação imperfeita (o produtor não tem certeza quanto à ação do seu concorrente).
O que se espera identificar por meio desse modelo aplicado a um determinado caso de doença em animais é se o seu resultado, ou equilíbrio, é equivalente ao de um jogo do tipo "dilema dos prisioneiros", que é o esperado a princípio (o dilema surge entre a questão da prevenção e conseqüente redução da probabilidade de contaminação dos animais vs. custos de prevenção). Nesse tipo de jogo, os jogadores obtêm ganhos maiores ao cooperarem ao decidirem tomar medidas preventivas , mas têm incentivo para não adotá-las, seguindo um comportamento "free rider". Adotando a postura do free rider, os agentes buscam a maximização do benefício individual, e não do benefício coletivo, o que leva a um resultado menos favorável.
Para um produtor, uma situação individualmente ideal é aquela em que somente o seu vizinho adota as ações de prevenção, arcando sozinho com os custos do procedimento, enquanto ele recebe o benefício indireto do procedimento sem incorrer em gastos, na medida em que a probabilidade de seus animais serem infectados pela doença diminui.
Deve-se ressaltar que o modelo desenvolvido possibilita a análise de risco por meio dos custos e benefícios econômicos do ponto de vista do produtor. A partir desses resultados, são delineadas decisões quanto à prevenção contra doenças em animais, não considerando os custos sociais ou sobre outros setores decorrentes dos surtos de doenças, tais como o nível de emprego, arrecadação de impostos, turismo, setor de insumos, dentre outros vinculados à cadeia produtiva.
3.2. Jogo com a intervenção do governo
A hipótese assumida no presente trabalho é que o governo espera, a princípio, que todos os produtores adotem as ações de prevenção contra doenças, evitando os prejuízos causados por um surto da doença à Balança Comercial, bem como ao reconhecimento do país no exterior no que se refere à segurança/sanidade de seus produtos5 5 Considerando as áreas que não são reconhecidas pela OIE como livres de determinada doença sem a aplicação de medidas preventivas, visto que nas áreas reconhecidas como livres, onde a doença já foi erradicada, o governo não deve estimular a adoção da prevenção. .
Dessa forma, o governo insere-se como um player, tomador de decisão no "jogo" proposto, quando se considera que, como forma de estímulo às ações de prevenção, ele concede uma indenização I por animal ao produtor que teve que sacrificar seus animais doentes e suspeitos, somente se esse tiver como comprovar a prática da prevenção. Caso contrário, o produtor teria que arcar integralmente com os prejuízos para o seu rebanho, decorrentes de um surto da doença.
Uma outra forma de intervenção governamental pode ser simulada pela instituição de uma multa (M) por animal ao produtor que não adota medidas de prevenção, e assumindo-se que o governo tem uma probabilidade (s) de descobrir de fato se o produtor não adotou as medidas preventivas quando a doença não ocorre, sendo 0 < s < 1. Parece plausível considerar que o controle do governo quanto à realização da prevenção pode não ser tão eficiente, dado que em alguns casos é baseado em testes realizados aleatoriamente nos animais.
Pressupõe-se que, quando o produtor tem seu rebanho afetado pela doença, o governo tem a capacidade de realizar testes com o animal para saber se as ações de prevenção foram realizadas. Portanto, se o produtor não praticou a prevenção e seu rebanho contraiu a doença, o governo não concede a indenização e aplica a multa ao produtor.
Assim, na extensão do jogo com a introdução do governo, as preferências do produtor são representadas pela seguinte função de payoff: πij(p, Cij, dij, I, s, M), com a instituição da multa Me da indenização Ipor parte do governo. As variáveis sem subscrito indicam que o seu valor não se altera, independente do produtor adotar ou não medidas preventivas.
Vale mencionar que a aplicação da multa M e o esforço de fiscalização da adoção das medidas preventivas (a qual influencia a probabilidade s) implicam em custos para o governo, os quais são considerados nulos no modelo, para efeito de simplificação.
3.3. Definição dos payoffs
A estimativa do payoff recebido por cada produtor, em cada situação, é dada pelo lucro líquido, ou seja, pela diferença entre as receitas e custos. Considera-se que tal estimativa é a base da tomada de decisão quanto a adotar ou não ações preventivas.
Pressupõe-se que os produtores são semelhantes quanto à estrutura de produção e, portanto, têm funções de lucro semelhantes. Além disso, por estarem localizados numa mesma região e terem estrutura semelhante, pressupõe-se que as probabilidades de contaminação serão as mesmas para ambos se estes se encontram numa mesma situação em relação à prevenção.
De forma generalizada, a Esperança do lucro de ambos os produtores, a ser maximizada, será:
No qual:
i = 1, 2 (indicando os produtores que participam do jogo modelado);
j = 1, 2, 3, 4 (j = 1 se ambos adotam a prevenção, j = 2 se apenas o produtor 1 previne; j = 3 se apenas o produtor 2 previne; e j = 4 se ambos não previnem); dij= probabilidade do animal contrair a doença, dependendo de i e j; pressupõe-se que: d11= d21 < d12 = d23 < d13 = d22 < d14 = d24;
P = receita total da venda dos animais do rebanho, ou seja:
P = p . qij
no qual:
qij = quantidade total de animais no rebanho do produtor i, para cada possível situação j(i = 1,2; j = 1,2,3,4).
p = preço unitário exógeno recebido pela venda do animal.
Cij* = custos de produção incorridos, em caso de incidência da doença, que incluem os custos de controle/descontaminação e de prevenção, dependendo de cada situação hipotética para i e j. Esses podem ser representados de forma desagregada, como:
no qual:
cpij= custo unitário de prevenção, para evitar a incidência da doença, incorrido para i= 1 e j= 1, 2; e para i = 2 e j = 1, 3;
ccij = custo unitário de controle/descontaminação em relação à doença, uma vez adquirida; incorrido em todas as situações para i e j, na parcela da Esperança do lucro que considera a probabilidade da doença ocorrer;
coij= outros custos de produção, representando custos variáveis, que não referentes à prevenção ou controle/descontaminação da doença, incorridos em todas as situações simuladas (i = 1,2; j = 1,2,3,4);
cfij= outros custos fixos de produção, incorridos em todas as situações simuladas (i = 1,2; j = 1,2,3,4).
Cij= custos de produção incorridos se a doença não ocorrer e, portanto, não inclui os custos de controle/descontaminação da doença. As outras parcelas do custo são iguais ao Cij*, sendo assim definido:
Ademais, para o cenário em que o governo pode intervir no mercado, pressupõe-se que o produtor recebe uma indenização I por animal se a doença ocorrer e ele tiver adotado as práticas preventivas. Porém, terá que pagar uma multa no valor de M por animal se não adotar as práticas, o que pode ser comprovado pelo governo com uma probabilidade s se a doença não ocorre, e com toda a certeza se a doença ocorrer, ou seja:
para i = 1, j = 1, 2 e i = 2, j = 1, 3, situações em que o produtor i adota as práticas preventivas;
para i = 1, j = 3, 4 e i = 2, j = 2, 4, situações em que o produtor i não adota as práticas preventivas.
Supõe-se que o número de animais qia ser produzido pelos produtores é o considerado ótimo, que maximiza o lucro dos mesmos. Além disso, pressupõe-se que, em razão de suas características, o mercado é competitivo, visto que o setor produtor de animais para consumo humano geralmente é pulverizado, com muitos produtores e muitos compradores, de forma que um produtor sozinho não consegue influenciar preços, que é, portanto, exógeno.
A matriz de payoffs para os dois produtores, não considerando a possível intervenção do governo, pode ser representada conforme indicada na Figura 2.
No cenário 2, considerando a possível intervenção do governo, a matriz de payoffs é representada conforme se visualiza na Figura 3.
Considera-se, para fins de simplificação da análise, e por não se constituir em pressuposição pouco razoável, que os custos de prevenção, controle da doença e outros custos de produção para um determinado produtor são os mesmos em todos os cenários considerados na presente análise, com j = 1,2,3,4. Sob tal pressuposição, tem-se as seguintes igualdades: cp11 = cp12, cp21= cp23; cci1 = cci2 = cci3 = cci4; coi1= coi2= coi3= coi4; e cfi1 = cfi2 = cfi3= cfi4, para i= 1, 2. Porém, esses custos não são necessariamente iguais entre os produtores.
4. Resultados
4.1. Simulação para o caso de febre aftosa em bovinos, em um cenário base
Com base nos dados de custo de produção levantados em dezembro/2005 pelo Cepea (Centro de Estudos Avançados em Economia Aplicada), da Esalq (Escola Superior de Agricultura Luiz de Queiroz), da USP (Universidae de São Paulo), para uma fazenda representativa da região de Naviraí (MS), cujo rebanho é composto por 2.376 animais, supõe-se que a expressão de lucro dos produtores é a seguinte (relativa ao período de recria e engorda do gado de dois anos):
No qual:
cpi= R$ 6,00/cabeça
cci= R$ 122,00/cabeça6 6 Os custos de sacrifício dos animais doentes e que pertencem ao rebanho contaminado foram calculados a partir do surto ocorrido em 2005 no estado do Paraná, por meio do montante total gasto com o controle da doença e o número de animais sacrificados, segundo dados da Agência Estadual de Notícias (AEN, 2006).
coi = R$ 320,00/cabeça
cfi= R$ 179.000,00
p = R$ 820,00/cabeça7 7 Preço levantado pelo Cepea em Mato Grosso do Sul em setembro/05 (mês imediatamente anterior à ocorrência de febre aftosa no estado.
Pressupõe-se, a princípio, que os dois produtores têm os mesmos custos de produção, para um rebanho de tamanho semelhante, e que o número qide animais de cada rebanho é o considerado ótimo, que maximiza o lucro.
Dessa forma, a esperança do lucro dos produtores será:
πij= dij(- 6 qi- 122 qi- 320 qi 179.000) + (1-dij) (820 qi- 6 qi- 122 qi- 320 qi- 179.000)
Como não foi possível encontrar na literatura de referência uma indicação precisa do risco de infecção da doença, alguns cenários serão simulados considerando-se diferentes probabilidades, de forma hipotética.
Além disso, visto que no caso da febre aftosa os custos de controle da doença e sacrifício dos animais (cci) são cobertos pelo governo, estes não serão considerados na função de custo do produtor, sendo introduzidos somente em cenário posterior para efeito de simulação.
Compõe-se, então, um cenário base, a partir do qual as simulações seguintes serão realizadas, no qual assume-se as seguintes probabilidades hipotéticas: d11 = d21 = 0,10; d12 = d23 = 0,2; d13 = d22 = 0,3; d14 = d24 = 0,4; para as outras variáveis, considera-se os valores já explicitados anteriormente. A matriz de payoffs do cenário base é apresentada na Figura 4.
A partir da matriz de payoffs, verifica-se que a estratégia dominante para ambos os jogadores é vacinar o rebanho e, assim, o jogo proposto possui apenas um equilíbrio em estratégia dominante, que é (A,A). No equilíbrio, nenhum dos jogadores tem estímulo para mudar sua estratégia unilateralmente, dado que obtém um payoff menor se o fizer e, portanto, não há necessidade de intervenção do governo para estimular a vacinação dos animais.
É importante salientar que o fato de (A,A) ser o equilíbrio do jogo não significa que num caso real as outras situações (equilíbrios (A,B), (B,A), e (B,B)) não deverão ocorrer. Como enunciado pela Teoria dos Jogos, se houver diferenças entre o resultado encontrado e o equilíbrio de Nash predito, provavelmente houve um engano por parte de um ou de ambos os tomadores de decisão, ou algum deles não entendeu de maneira correta as preferências de seu oponente, ou por simplesmente algum deles não ter entendido o jogo ou não ser racional.
Se ambos os jogadores utilizam uma estratégia Maximin8 8 Estratégia Maximin é aquela que maximiza o mínimo ganho que possa ser obtido, ou seja, dentre todos os piores resultados que um agente pode obter, a estratégia Maximin busca a melhor. , o resultado também tende para a melhor situação para ambos, ou seja, o equilíbrio (A,A).
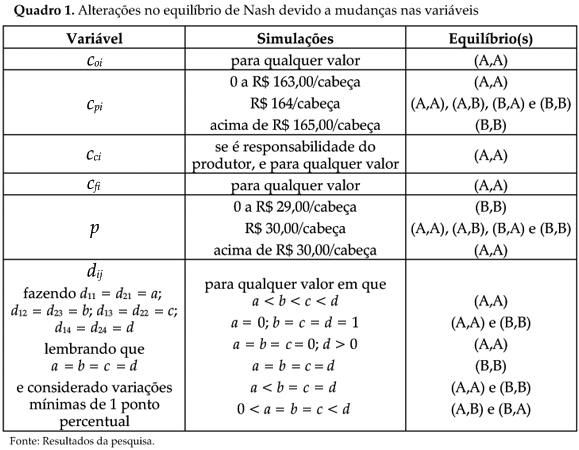
A partir desse cenário serão realizadas diferentes simulações para o jogo, nas quais serão determinadas as alterações no equilíbrio do jogo a partir de mudanças no valor nas variáveis consideradas. Estas simulações estão apresentadas esquematicamente no Quadro 1.
Verifica-se no Quadro 1 que, para quaisquer valores referentes aos outros custos de produção (coi) e aos custos fixos (cfi), mantendo as outras variáveis nos valores assumidos no cenário base, o equilíbrio de Nash em estratégias dominantes é a situação em que ambos decidem vacinar seu rebanho, ou seja, (A,A).
Considerando um cenário em que o custo de controle (cci) deve ser coberto pelo produtor, o equilíbrio do jogo também é (A,A), para qualquer valor assumido por cci.
Em relação ao custo de prevenção (cpi), verifica-se que se este assume um valor até R$ 163,00/cabeça, mantendo as outras variáveis nos valores do cenário base, o jogo possui um único equilíbrio de Nash, que é (A,A). Já para um custo de prevenção de R$ 164,00/cabeça, o jogo passa a ter quatro equilíbrios de Nash equiprováveis, que são as quatro possíveis situações do jogo, ou seja, (A,A), (A,B), (B,A), e (B,B). Se o custo de prevenção é superior ou igual a R$ 165,00/cabeça, o equilíbrio do jogo passa a ser (B,B).
Quanto à variável preço (p), verifica-se que, se este é menor que R$ 29,00/cabeça (mantendo o cenário base para as outras variáveis), o equilíbrio do jogo é a situação em que nenhum dos produtores decide vacinar seu rebanho, ou seja (B,B). Para um preço de R$ 30,00/cabeça, o jogo passa a ter quatro equilíbrios, que são todas as possíveis situações para o jogo, ou seja, (A,A), (A,B), (B,A), e (B,B). Já para um preço superior a R$ 30,00/cabeça, o jogo tem um equilíbrio único, que é (A,A).
Considerando o valor das probabilidades envolvidas, verifica-se que, se estas forem diferentes e seguindo a ordem de grandeza pressuposta na modelagem do jogo, o equilíbrio é sempre (A,A), para qualquer valor assumido por estas variáveis (mantendo as outras variáveis no valor do cenário base, e considerando variação mínima de 1 ponto percentual nas probabilidades). Para alguns casos extremos, como se a probabilidade de um animal vacinado contrair a doença for nula quando todos vacinam (d11 = d21 = 0) e quando existe certeza que se pelo menos um deles não vacinar seu rebanho todos contraem a doença (d12 = d23 = d13 = d22 = d14 = d24 = 1), ambos (A,A) e (B,B), são equilíbrios do jogo. Estes também serão equilíbrios equiprováveis do jogo se a probabilidade dos animais de ambos os jogadores adquirirem a doença quando pelo menos um deles não vacinar forem iguais (d12 = d23 = d13 = d22 = d14 = d24), e a probabilidade do animal vacinado adoecer for menor.
Já se as probabilidades forem todas iguais, ou seja, não dependerem da vacinação do rebanho, o equilíbrio do jogo será (B,B).
Se as probabilidades dos animais adquirirem a doença quando pelo menos um deles decide vacinar forem iguais (d11 = d21 = d13 = d22 = d12 = d23), e iguais a zero, e a probabilidade do animal adoecer dado que nenhum deles vacinou for maior que zero, o equilíbiro do jogo será (A,A).
Uma outra situação seria se as probabilidades dos animais adquirirem a doença quando pelo menos um deles vacina forem iguais (d11 = d21 = d13 = d22 = d12 = d23), e superiores a zero. Nesse caso, os equilíbrios do jogo passam a ser (A,B) e (B,A), ou seja, apenas um deles decide vacinar.
O que se percebe, portanto, é que o custo de prevenção contra febre aftosa é relativamente baixo, não compensando para o produtor correr os riscos de não vacinar seu rebanho. É mais vantajoso para o produtor não adotar as medidas preventivas apenas se a diferença de probabilidade de um animal vacinado e não vacinado adquirir a doença for muito pequena, e praticamente nula, como verificado na simulação.
4.4.1. Considerando a existência de um prêmio para animais não vacinados
Também pode-se pressupor que existem consumidores que estão dispostos a pagar um prêmio para o animal não vacinado, entre 10% e 50% segundo Ekboir et al. (2002 apud RICH, 2004). Isso pode gerar um estímulo para que nenhum produtor adote as medidas preventivas, com o objetivo de obter o status de livre de aftosa sem vacinação pela OIE9 9 Sabe-se que para que um país obtenha o status de livre de aftosa sem vacinação um longo processo é necessário, de acordo com as normas estabelecidas pela OIE (Organização Mundial de Saúde Animal). Na simulação realizada neste trabalho, considera-se por simplificação apenas a questão do preço do animal não vacinado, e não os custos para obter o status desejado. .
Pressupõe-se, portanto, que, se nenhum produtor vacinar seus animais, eles obtêm um preço superior ao praticado se ao menos um deles vacinasse. Considerando os mesmos valores adotados no cenário base para as outras variáveis, e um prêmio de 10%, a matriz de payoffs dos produtores é apresentada na Figura 5. O equilíbrio de Nash em estratégias dominantes é ainda a situação (A,A).
Com um prêmio de 33% para o animal não vacinado, no entanto, o cenário se altera, e o jogo passa a ter dois equilíbrios de Nash, que são (A,A) e (B,B), determinados a partir da matriz de payoffs apresentada na Figura 6. Para um prêmio superior a 33%, portanto, o jogo tem dois equilíbrios equiprováveis.
Para esse caso, em ambos os equilíbrios de Nash (A,A) e (B,B) , nenhum dos jogadores tem estímulo para mudar sua estratégia unilateralmente, dado que obtém um payoff menor se o fizerem.
Dentre os dois equilíbrios desse jogo, conhecido na literatura como jogo de coordenação, (A,A) é preferível à (B,B) por ambos os jogadores. Porém, essa preferência não indica que o equilíbrio (A,A) possui uma chance maior de ocorrer. Isso depende das expectativas de um jogador sobre as estratégias de seu oponente. Se os jogadores decidirem cooperar entre si, poderiam garantir a ocorrência do equilíbrio (A,A), prevenindo seus rebanhos da doença, e obtendo payoffs superiores. Porém, se um deles espera que o outro não irá adotar (por considerar que este pode falhar ou que sua racionalidade é limitada), ele também não adota, dado que o resultado será melhor do que somente ele adotar. Mas o outro produtor pode ter entendido perfeitamente o jogo e decidir adotar as medidas. Nesse caso, o resultado é ruim para ambos, e pior para aquele que não adotou (e inferiu de maneira incorreta sobre a decisão de seu oponente).
Se ambos os jogadores utilizam uma estratégia Maximin, o resultado tende para a melhor situação para ambos, ou seja, o equilíbrio (A,A).
Entretanto, um jogo em que um dos equilíbrios de Nash é a situação (B,B) deve preocupar o governo e os agentes sanitários do país. Estes devem buscar incentivos para que, de maneira voluntária, o único equilíbrio do jogo seja (A,A). Esses incentivos podem ser o pagamento de indenização e/ou a aplicação de multas.
Para este caso, no qual um prêmio de 33% é oferecido se os produtores não vacinarem seu rebanho, se o governo oferecer uma indenização por cabeça de pelo menos 3% do preço do animal para o produtor que vacinou seu rebanho mas mesmo assim teve problemas com a doença, o equilíbrio passa a ser apenas a situação (A,A). Se o governo optar por aplicar uma multa sobre os produtores que não vacinaram seu rebanho, e considerando que existe uma probabilidade de 50% do governo detectar que o produtor de fato não adotou a vacinação se os animais não apresentarem sintomas da doença, e detecta a não-vacinação com absoluta certeza caso os animais adoeçam, é necessário uma multa de pelo menos R$ 7,00/cabeça para que o equilíbrio do jogo passe a ser apenas a situação (A,A).
4.1.2. Pressupondo uma situação em que a barreira sanitária imposta em decorrência do surto de febre aftosa gera impacto sobre os preços dos animais
Considerou-se, até então, que se o rebanho de um dos produtores contrai o vírus da febre aftosa, o produtor que não teve problemas com a doença consegue vender seus animais pelo mesmo preço praticado no mercado antes do surto ocorrer. Essa pressuposição pode ser verdadeira considerando um mercado perfeitamente competitivo, para uma região onde, uma vez que o surto da doença ocorre e existe a necessidade de se sacrificar os animais contaminados, existe um mercado consumidor suficiente para absorver a oferta do(s) produtor(es) cujos rebanhos mantiveram-se sadios. Sabe-se que, quando uma região sofre um surto da doença (como no caso ocorrido em Mato Grosso do Sul, em outubro de 2005), os produtores que não tiveram problemas podem vender seus animais somente para os frigoríficos localizados dentro do estado, mas estes não podem exportar a carne porque os países importadores impõem barreiras sanitárias à região, de modo geral.
Porém, em regiões como os estados de Mato Grosso e de Mato Grosso do Sul, onde existe um grande número de produtores, no qual o mercado consumidor é relativamente pequeno, as exportações de carne são muito importantes para a economia regional e, portanto, os preços do gado devem sofrer alterações na circunstância de um surto ocorrer.
Duas pressuposições podem ser feitas: muitos animais têm de ser sacrificados em decorrência da doença e a oferta de animais sadios dentro do estado se torna pequena, fazendo com que os preços recebidos pelos animais aumente; ou a oferta restante ainda é relativamente grande e, como diversos países deixam de importar a carne brasileira ou da região afetada, o preço dos animais se reduz.
Os payoffs, nesse caso, devem considerar as probabilidades de apenas um dos rebanhos adquirir a doença, de ambos, e de nenhum, nos quatro cenários possíveis quanto à vacinação ambos vacinam, apenas um deles vacina (produtor 1 ou 2), ou nenhum vacina. Os preços dos animais também são diferenciados para o caso de nenhum rebanho contrair a doença (p) ou de pelo menos um dos rebanhos ser infectado (p*). Como pressuposto, p* pode ser maior ou menor que p, dependendo se o mercado local absorve ou não a oferta restante de carnes no caso de um surto da doença.
Assim, têm-se os possíveis equilíbrios e payoffs para os produtores:
1. (A,A) Ambos vacinam
Possibilidades:
rebanhos de 1 e 2 contraem a doença: probabilidade = d11 . d21
rebanho de 1 contrai a doença: probabilidade = d11.(1 d21)
rebanho de 2 contrai a doença: probabilidade = d21.(1 d11)
rebanhos de 1 e 2 não contraem a doença: probabilidade = (1 d11).(1 d21)
Payoffs:
π11 = q1 . [d11 . d21 . ( co1 cp1 cc1)] + [d11 . (1 d21) . ( co1 cp1 cc1)] + [d21 . (1 d11) . (p* co1 cp11)] + [(1 d11) . (1 d21).(p co1 cp1)] cf1
π21 = q2 . [d 11 . d21 . ( co2 cp2 cc2)] + [d11 . (1 d21) . ( p* co2 cp2)] + [d21 . (1 d11) . ( co2 cp2 cc2)] + [(1 d11) . (1 d21).(p co2 cp2)] cf2
2. (A,B) Apenas o produtor 1 vacina
Possibilidades:
rebanhos de 1 e 2 contraem a doença: probabilidade = d12 . d22
rebanho de 1 contrai a doença: probabilidade = d12 (1 d22)
rebanho de 2 contrai a doença: probabilidade = d22 (1 d12)
rebanhos de 1 e 2 não contraem a doença: probabilidade = (1 d12).(1 d22)
Payoffs:
π12 = q1 . [d12 . d22 . ( co1 cp1 cc1)] + [d12 . (1 d22) . ( co1 cp1 cc1)] + [d22 . (1 d12) . (p* co1 cp11)] + [(1 d12) . (1 d22).(p co1 cp1)] cf1
π22 = q2 . [d12 . d22 . ( co2 cp2 cc2 )] + [d12 . (1 d22) . ( p* co2)] + [d22 . (1 d12) . ( co2 c c2)] + [(1 d12) . (1 d22).(p co2)] cf2
3. (B,A) Apenas o produtor 2 vacina
Possibilidades:
rebanhos de 1 e 2 contraem a doença: probabilidade = d13 . d23
rebanho de 1 contrai a doença: probabilidade = d13 . (1 d23)
rebanho de 2 contrai a doença: probabilidade = d23 . (1 d13)
rebanhos de 1 e 2 não contraem a doença: probabilidade = (1 d13).(1 d23)
Payoffs:
π13 = q1 . [d13 . d23 . ( co1 cc1 )] + [d13 . (1 d23) . ( co1 cc1)] + [d23 . (1 d13) . (p* co1 )] + [(1 d13) . (1 d23).(p co1)] cf1
π23 = q2 . [d13 . d23 . ( co2 cp2 cc2)] + [d13 . (1 d23) . ( p* co2 cp2)] + [d23 . (1 d13) . ( co2 cp2 cc2)] + [(1 d13) . (1 d23).(p co2 cp2)] cf2
4. (B,B) Nenhum produtor vacina
Possibilidades:
rebanhos de 1 e 2 contraem a doença: probabilidade = d14 . d24
rebanho de 1 contrai a doença: probabilidade = d14 . (1 d24)
rebanho de 2 contrai a doença: probabilidade = d24 . (1 d14)
rebanhos de 1 e 2 não contraem a doença: probabilidade = (1 d14).(1 d24)
Payoffs:
π14 = q1 . [d14 . d24 . ( co1 cc1)] + [d14 . (1 d24) . ( co1 cc1)] + [d24 . (1 d14) . (p* c o1 )] + [(1 d14) . (1 d24).(p co1)] cf1
π224 = q2 . [d14 . d24 . ( co2 cc2)] + [d14 . (1 d24) . ( p* co2)] + [d24 . (1 d14) . ( co2 cc2)] + [(1 d14) . (1 d24).(p co2)] cf2
Substituindo as variáveis pelos valores adotados no cenário base, e considerando que se o rebanho de um dos produtores adquirir a doença, o outro produtor consegue vender seu gado por um preço cerca de 20% inferior ao praticado no mercado antes do surto ocorrer, tem-se a matriz de payoffs da Figura 7.
Na Figura 7, verifica-se que o equilíbrio do jogo em estratégia dominante é a situação (A,A). Assim, mesmo que um produtor saiba que seu vizinho não vacina seu rebanho e que se o rebanho deste contrair a doença irá prejudicar suas vendas, é melhor para ele vacinar.
Simulando-se que o preço dos animais reduz-se em até 100% no caso de um surto ocorrer na região do produtor, o que seria o mesmo que considerar que o produtor deve sacrificar seu rebanho mesmo que este esteja sadio se sua propriedade estiver dentro de um determinado raio do surto da doença, a melhor estratégia para ele ainda seria adotar as ações de prevenção.
Mais uma vez, não há necessidade do governo intervir para estimular a vacinação dos animais.
Considerando-se, ao contrário, que o preço dos animais aumente cerca de 20% no caso de um surto ocorrer na região, a matriz de payoffs passa a ser a apresentada na Figura 8.
O equilíbrio de Nash em estratégias dominantes ainda é a situação em que ambos decidem vacinar o rebanho, ou seja, (A,A). Mesmo que o preço aumente mais no caso de um surto ocorrer, por exemplo em 100%, o equilíbrio de Nash em estratégias dominantes continua sendo (A,A).
4.2. Extensões do modelo variações na estrutura do jogo
4.2.1. Jogo sequencial com informação completa
Considerando-se que o jogo é seqüencial, ao invés de simultâneo, ou seja, os produtores não tomam a decisão ao mesmo tempo, mas, sim, um depois do outro, e pressupondo que a informação é perfeita, o segundo jogador tem a possibilidade de observar a decisão do primeiro e reagir à ela.
A estrutura simplificada do jogo é apresentada na Figura 9 (e considerando o valor das variáveis do cenário base).
O equilíbrio desse jogo (também conhecido como Equilíbrio de Nash Perfeito de Subjogos ENPS10 10 Equilíbrio perfeito de subjogo é definido como um conjunto de estratégias que induz ao equilíbrio de Nash em todos os subjogos (OSBORNE, 2004), ou seja, requer uma escolha racional em todos os subjogos e no jogo completo. Um subjogo de h é definido como a parte do jogo que resta depois que h ocorre, com h sendo qualquer nó do jogo (OSBORNE, 2004). Uma outra interpretação dada por Osborne (2004) é que o equilíbrio perfeito de subjogo é aquele em que raramente os jogadores irão tomar ação diferente do equilíbrio, e assim depois de uma longa experiência, cada jogador forma expectativas corretas sobre as estratégias de seu oponente e sabe como ele irá se comportar em cada subjogo (mesmo que inicialmente ele não conheça as preferências do mesmo). ) é determinado por indução retroativa, ou seja, partindo dos subjogos de menor extensão para o jogo completo, e inferindo sobre as decisões dos jogadores.
Nesse cenário, nenhum jogador pode criar ameaças para o outro, uma vez que o equilíbrio (A,A) é o que resulta no melhor resultado para ambos, de todas as situações possíveis. Porém, se, por exemplo, o jogador 1 se engana e escolhe B, o jogador 2 pode escolher B também para punir o jogador 1 de não ter escolhido de maneira "correta". Esta ameaça, no entanto, não é crível, porque o jogador 2 também obtém um payoff menor do que se escolhesse A. O resultado, portanto, não depende das expectativas dos jogadores sobre o comportamento e racionalidade do seu oponente.
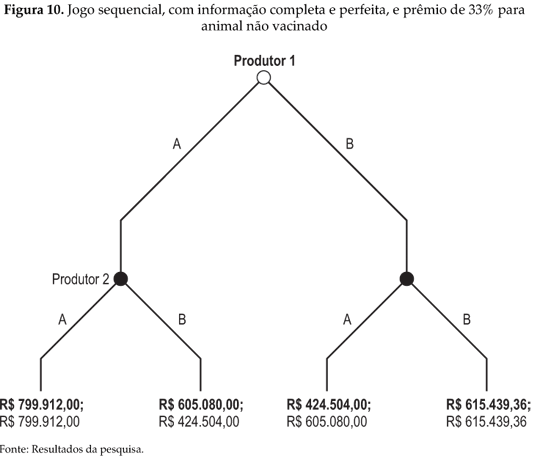
Se considerado, contudo, como simulado no jogo simultâneo, que os produtores obtêm um prêmio de 33% sobre o preço dos animais não vacinados (se ambos não vacinarem), os payoffs do jogo extensivo assumem os valores apresentados na Figura 10.
Por indução retroativa, e se a informação for completa e perfeita, verifica-se (A,A) é o equilíbrio do jogo.
Visualizando o mesmo jogo extensivo na forma estratégica (como na matriz de payoffs da Figura 6), verifica-se que (B,B) também é um equilíbrio de Nash para este jogo, dado que nenhum dos jogadores terá estímulo a desviar individualmente de sua estratégia, dado que se encontram nessa situação. Esse equilíbrio, entretanto, não foi encontrado na forma extensiva, dado que ele não é um Equilíbrio de Nash Perfeito de Subjogos (ENPS), ou seja, ele não é um equilíbrio estável robusto.
Já no caso de prêmio de 50% sobre o preço dos animais para o caso dos produtores decidirem não vacinar, o equilíbrio perfeito de subjogos passa a ser a situação (B,B).
Essa situação, como já discutido, deve preocupar o governo, no sentido de buscar incentivos para que o equilíbrio tenda para a situação (A,A).
4.2.2. Jogo extensivo com informação completa e imperfeita
Um jogo extensivo com informação imperfeita representa uma situação em que cada jogador, quando chamado a jogar, não tem conhecimento sobre as ações tomadas previamente pelo(s) outro(s) jogador(es).
Nesse caso, considerando os dados do cenário base, o resultado encontrado é o mesmo de um jogo simultâneo representado na forma estratégica. Resolvendo o jogo para encontrar o equilíbrio, verifica-se que o único ENPS é a situação (A,A), em que ambos vacinam seus animais.
Se o produtor 2 não tivesse uma estratégia dominante, como no jogo em que um prêmio de 33% é oferecido sobre o preço dos animais não vacinados, a indução retroativa falha e, portanto, não é trivial encontrar o equilíbrio de Nash em estratégias puras. A representação na forma estratégica facilita a determinação do Equilíbrio de Nash, e a matriz de payoffs correspondente à esse jogo é a mesma representada na Figura 6, na simulação de um jogo simultâneo, que determina que (A,A) e (B,B) são equilíbrios de Nash, sendo ambos ENPS.
Apontar, porém, qual dos dois equilíbrios é mais provável de ocorrer, depende das expectativas dos jogadores a respeito da decisão do seu oponente, as quais são baseadas nas deciões tomadas em períodos anteriores. Se o jogador 2 acredita que o jogador 1 escolherá a estratégia B, ele também escolherá B, e o contrário se acreditar que 1 escolherá A.
4.2.3. Jogo estratégico com informação incompleta
Num jogo estratégico com informação incompleta, também chamado de jogo Bayesiano, os jogadores não têm certeza sobre as preferências e/ou função de payoffs de seus oponentes, inferindo, a partir de sinais que o seu oponente demonstra, sobre essas possibilidades. De maneira analítica, o jogador que não tem certeza sobre a função de payoff de seu oponente deve levar em consideração todas as possibilidades para essa variável de decisão, ou seja, deve considerar os tipos de jogador que seu oponente pode ser, ou estados que pode assumir, e as probabilidades de que estes estados sejam verdadeiros. O equilíbrio de Nash, nesse caso, é a melhor resposta de cada jogador à cada "tipo" de oponente (OSBORNE, 2004).
No jogo proposto no presente trabalho, pode ocorrer, por exemplo, de um dos jogadores não conhecer a função de custo de seu oponente. Assim, pode-se pressupor que o jogador 1 não sabe se os custos de produção co2 do jogador 2 são relativamente altos ou baixos. O jogador 2, porém, conhece a função de custo do jogador 1, da mesma forma que ambos conhecem sua própria função de custo. Nesse caso, propõe-se como exemplo para análise o seguinte jogo simultâneo:
Jogadores (i): produtores 1 e 2.
Estados (ou tipos): o conjunto dos possíveis tipos são: custo de produção (co2) elevado para o jogador 2 (y); e custo baixo para o jogador 2 (n).
Ações: adotar (A) ou não adotar (B) as ações de prevenção.
Sinalização11 11 Pode-se dizer que inicialmente ambos os jogadores não conhecem sua função de custo, nem a de seu oponente, ou seja, não sabem se são elevados ou baixos. Após receber um tipo de sinalização, o jogador 2 consegue saber de que situação se trata, ou seja, sabe para ambos os jogadores se eles possuem custos elevados ou baixos; o jogador 1, por sua vez, recebe um sinal não-informativo, do qual não consegue distinguir qual o tipo de função de custo do jogador 2. O jogador 1 somente consegue, por meio do sinal, formar uma crença sobre a chance de seu oponente ter custos elevados ou baixos. Por isso, o jogador 1 precisa tecer suas estratégias para cada tipo de função de custo do jogador 2, e o jogador 2 deve planejar suas ações para cada tipo de sinal que receber. : O jogador 1 (que não conhece os custos de 2) pode receber um sinal chamado z; sua função de sinal τ1 satisfaz τ1(y) = τ1(n) = z; o jogador 2 (que conhece os custos de ambos) recebe um de dois sinais, chamados m e v; a função de sinal τ2 satisfaz τ1(y) = m e τ2(n) = v.
Crenças: o jogador 1 atribui probabilidade ½ para cada estado y e n, depois de receber o sinal z. O jogador 2 atribui probabilidade 1 para o estado y depois de receber o sinal m, e atribui probabilidade 1 para o estado n depois de receber o sinal v; em outras palavras, o jogador 1 acredita com mesma probabilidade que os custos de 2 são altos ou baixos, e o jogador 2 conhece de fato os custos de 1, e sabe de qual estado se trata.
Payoffs: os payoffs de cada jogador i para todos os pares possíveis de ações e estados são apresentados na Figura 11. Como exemplo, pressupõe-se que o jogador 1 não tem certeza se os outros custos de produção de seu oponente é R$ 487,00/cabeça12 12 Custo variável do sistema de recria-engorda referente à região de Umuarama (PR). (co2y, que é o estado em que o custo é mais elevado) ou R$ 320,00/cabeça (co2n, que é o estado em que o custo é mais baixo); já o produtor 2 sabe se o custo de 1 é elevado ou baixo. Considera-se, para as outras variáveis, os mesmos valores adotados no cenário base.
Se o custo do jogador 1 é baixo (R$ 320,00/cabeça), e dado que o jogador 2 tem esse conhecimento, a matriz de payoffs é apresentada na Figura 11. A moldura denominada 2, envolvendo ambos os quadros separadamente, indica que o jogador 2 sabe qual matriz de payoffs é a verdadeira (ou seja, tem conhecimento sobre seu próprio custo). A moldura denominada 1 envolvendo os dois quadros simultaneamente indica que o jogador 1 não sabe qual matriz de payoffs é a verdadeira.
No jogo definido neste cenário, existem dois tipos para o jogador 2 e um tipo para o jogador 1e, desse modo, o equilíbrio de Nash em estratégias puras possui três ações, uma para o jogador 1 e duas para o jogador 2 (que é uma para cada tipo do jogador 2).
Para se encontrar o(s) equilíbrio(s) de Nash desse jogo, construiu-se para o jogador 1 uma matriz com os payoffs esperados a cada ação sua, para os quatro possíveis pares de ações referentes aos dois estados de seu oponente. Na Figura 12, cada linha corresponde a uma ação do jogador 1, e cada coluna corresponde ao par de ações para os dois estados do jogador 2.
No equilíbrio de Nash, a ação do jogador 1 deve ser a melhor resposta, na Figura 12, ao par de ações dos dois tipos de jogador 2; a ação do jogador 2 que tem custo elevado deve ser a melhor resposta na tabela esquerda da Figura 11 à ação do jogador 1; e a ação do jogador 2 que tem custo baixo deve ser a melhor resposta na tabela direita da Figura 11 à ação do jogador 1.
Seguindo essa análise, verifica-se que (A,(AA)) é o único equilíbrio de Nash.
Alterando-se a crença do jogador 1 sobre os custos do jogador 2, ou seja, a probabilidade de o jogador 2 ter custos elevados ou baixos, o resultado não se altera. Para qualquer nível de certeza do produtor 1 sobre a função de custos do produtor 2, o Equilíbrio de Nash será (A,(A,A)).
Desse modo, se um dos jogadores não conhece os custos do seu oponente, mas um deles conhece o de ambos, o equilíbrio do jogo é a situação em que ambos tomam ações preventivas voluntárias contra a febre aftosa. Esse resultado já se era esperado, visto que nas primeiras simulações realizadas, apresentadas no Quadro 1, verificou-se que a variação no custo de produção não altera o equilíbrio do jogo.
Poderia-se simular que o produtor 1 não tem conhecimento sobre o custo de prevenção do jogador 2, para determinar se ocorre alguma alteração no equilíbrio do jogo. Porém, como também verificado nas simulações iniciais, o equilíbrio se altera somente se o custo de prevenção é superior a R$ 164,00/cabeça, o que é um valor consideravelmente elevado para o caso da febre aftosa. Pressupondo que isso possa ocorrer, com um custo de prevenção de R$ 165,00/cabeça, por exemplo, o equilíbrio passa a ser o conjunto de estratégias (A,(B,A)).
Já no caso dos produtores receberem um prêmio de 33% sobre o preço dos animais se não adotarem as medidas preventivas, o resultado do jogo também se altera, passando a ter dois equilíbrios de Nash, os quais são (A,(A,A)) e (B,(B,B)).
Outras possíveis suposições são de que nenhum dos dois jogadores tem certeza sobre a função de custo de seu oponente, cada um conhecendo apenas a sua função de custo; ou ainda que um dos jogadores não tem certeza se o seu oponente conhece sua função de custos. Como nas simulações anteriores, o equilíbrio de Nash desses jogos é a situação em que ambos os jogadores adotam as medidas preventivas. Pressupondo um prêmio de 33% sobre o preço dos animais no caso de nenhum dos produtores vacinar seu rebanho, estes jogos possuem dois equilíbrio de Nash, os quais são ((A,A),(A,A)) e ((B,B),(B,B)).
4.2.4. Jogos Repetitivos
Considerando um jogo estratégico repetitivo (finito ou infinito), e a matriz de payoffs do cenário base (Figura 4), verifica-se que, mesmo que um jogador decida não cooperar no período t (não vacinando seu rebanho), será sempre melhor para o outro jogador adotar as medidas preventivas nos períodos seguintes, e então (A,A) também é o único equilíbrio de Nash do jogo repetitivo.
Já para o jogo apresentado na Figura 6, no qual um prêmio de 33% é oferecido sobre o preço dos animais não vacinados, porém repetitivo (finito ou infinito), o equilíbrio passa a ser a chamada "trigger strategy" para ambos os produtores, em que um jogador escolhe sempre a mesma ação até o momento em que o seu oponente muda sua estratégia13 13 Num jogo repetitivo do tipo "dilema dos prisioneiros", pode-se dizer que um jogador que adota a " trigger strategy" decide cooperar até o momento em que seu oponente coopera, e deixa de cooperar nos períodos subsequentes se este se desvia do resultado cooperativo. .
5. Conclusões
O modelo desenvolvido no presente trabalho mostrou-se adequado para a análise e interpretação de possíveis ações estratégicas associadas a casos de doença em animais cujas implicações econômicas são expressivas e no qual a prevenção da enfermidade seja alvo de controvérsias, envolvendo questões científicas e econômicas. Diversos aspectos, assumindo ou não a intervenção governamental, podem ser explorados para o delineamento de ações estratégicas para o setor.
Nos casos em que a adoção de medidas preventivas dentro de uma determinada atividade produtiva geralmente não é efetivada quando não mandatória, o governo pode utilizar modelos dessa natureza para determinar os incentivos econômicos (multas e/ou indenizações) a serem aplicadas para torná-las efetivas.
Para o caso específico da febre aftosa, verifica-se que a aplicação do modelo parece ser útil e adequada. Ao contrário da hipótese inicial, nenhum dos modelos e extensões desenvolvidos na pesquisa se configuram num equilíbrio do tipo de dilema dos prisioneiros, que requer a intervenção de um terceiro agente para maximizar o bem-estar geral.
O modelo mostrou que, quando não se tem um mercado diferenciado para animal não vacinado, independente do tipo de jogo proposto (simultâneo, seqüencial, com informação perfeita ou imperfeita), o equilíbrio tende para a situação em que ambos os produtores decidem vacinar seu rebanho, sugerindo, portanto, que não existe a necessidade de intervenção do governo para estimular a adoção das medidas preventivas.
Por outro lado, se existir um mercado diferenciado para animais não vacinados, como um prêmio igual ou superior a 33% sobre o preço de mercado do boi gordo (considerando os dados da simulação aqui proposta), a decisão de não vacinar o rebanho passa a ser um equilíbrio do jogo.
Mesmo sem a existência de um mercado diferenciado para a carne de animais não vacinados de origem brasileira, agentes do setor consultados para o presente estudo indicam que existem produtores que não vacinam seu rebanho, ou parte dele. Nesse caso, a atuação governamental pode ser interessante, uma vez que a ocorrência de falhas de mercado é provável.
O que se verifica para o caso brasileiro é que de fato o governo acaba por estabelecer políticas de incentivo para a vacinação efetiva do gado bovino, por meio de multas e indenizações, apesar do modelo aqui desenvolvido mostrar que a melhor decisão para o produtor é adotar medidas preventivas, independente do estímulo do governo.
De fato, a Teoria dos Jogos prevê situações como esta, no qual o modelo teórico/empírico prevê uma situação diferente da realidade. Isso pode ocorrer por três motivos: pouca aderência do modelo à realidade, omissão de fatores importantes para o cômputo dos payoffs ou, ainda, por pressuposição incorreta por parte dos agentes tomadores de decisão (nesse caso, os produtores) dos parâmetros envolvidos na tomada de decisão, que se traduz na falta de racionalidade ao tomar decisões.
Dentre os motivos para a não-vacinação, de acordo com diversos agentes do mercado, têm-se as seguintes constatações:
Não percepção por parte do produtor de um retorno direto e imediato da vacina contra a febre aftosa, como ocorre com outros tipos de medicamentos aplicados nos animais (como de controle parasitário, que faz com que os animais intensifiquem o ganho de peso), o que destimula a vacinação. O retorno da vacina somente será verificado no caso de um surto da doença ocorrer na proximidade da propriedade do produtor, e este ter vacinado seu animal. Em outras palavras, a vacina não agrega valor ao animal, mas sim o risco de contaminação;
Operação relativamente trabalhosa de aplicação da vacina em todos os animais. Na verdade, os custos da vacina e aplicação foram computados e considerados no modelo do presente trabalho, o que mostra que esta razão não é justificada.
Perda de peso dos animais após a aplicação da vacina, decorrente de estresse. Veterinários consultados14 14 BRASIL. Ministério da Agricultura. Departamento de Saúde Animal. 8 maio 2007. afirmam que a perda de peso do animal após a vacinação é mínima e pode ser recuperada facilmente (informação verbal).
Risco de gerar lesões na carcaça do animal e este perder valor comercial. Veterinários consultados também afirmam que as lesões ocorrem somente quando a vacina é aplicada de maneira incorreta e sem os procedimentos higiênicos exigidos. Portanto, esse argumento também não é uma justificativa plausível para a não-vacinação.
Outro fator que pode desestimular a vacinação por parte de alguns produtores é a redução da percepção de risco da doença quando há muito tempo não ocorrem surtos da mesma ou poucos casos recentes aconteceram. De fato, a frequência dos surtos vem diminuindo nos últimos anos, em partes pelo esforço do governo, na divulgação da importância da vacinação e por meio de políticas de estímulo.
Diante dessas constatações, verifica-se certa irracionalidade por parte de alguns produtores ao não adotar medidas preventivas. Assim, o estudo desenvolvido no presente trabalho é importante para que estes possam delinear panoramas de decisão, de forma a identificar as melhores ações a serem tomadas de acordo com a análise de benefício/custo.
Pela ótica do governo, a irracionalidade de alguns produtores mostra que, tomando o exemplo da pecuária nacional, com os valores considerados para o período explicitado no exemplo aplicado, não se pode deixar por conta dos produtores a decisão da vacinação contra a febre aftosa, dado que as suas decisões afetam toda a economia do País.
Mas, sabendo que o equilíbrio não necessita da sua intervenção, o governo pode redirecionar sua estratégia, divulgando modelos de decisão como o desenvolvido no presente trabalho, para que produtores busquem um procedimento de tomada de decisão adequado.
As outras ações do governo de incentivo à vacinação, dentro da linha já adotada de instituição de multas e indenizações, também são válidas, porém, a fiscalização das medidas preventivas deve ser intensificada.
6. Referências Bibliográficas
AGÊNCIA ESTADUAL DE DEFESA SANITÁRIA VEGETAL E ANIMAL IAGRO. Campanhas de vacinação. Disponível em: <http://www.iagro.ms.gov.br/>. Acesso em: 3 jan. 2007.
AGÊNCIA ESTADUAL DE NOTÍCIAS AEN. Governa libera R$ 700 mil para sacrifício de animais. Disponível em: <http://www.bonde.com.br/bondenews/ bondenewsd.php?id=561&dt=20060224>. Acesso em: 10 fev. 2006.
BARRETT, S. Global disease eradication. Journal of the European Economic Association, Milan, v. 1, n. 2-3, p. 591-600, Aug. 2002. Presented at the CONGRESS OF THE EUROPEAN ECONOMIC ASSOCIATION, 17., 2003, Venice.
BARRETT, S. The economics of eradication versus control of infectious diseases. In: WORKSHOP ON THE ECONOMICS OF VACCINATION IN LOW AND MIDDLE INCOME COUNTRIES, 2003, London. Report Disponível em: < http://www.who.int/immunization_financing/analyses/en/economics_of_immunization_workshop.pdf>. Acesso em: 14 nov. 2005.
BAUCH, C.T.; EARN, D.J.D. Vaccination and the theory of games. Proceedings of the National Academy of Sciences of the United States of America PNAS, Stanford, v. 101, n. 36, p. 13391-13394, Sep. 2004.
BLISKA, F. M. M.; PARRÉ, J. L.; GUILHOTO, J. J. M. O Programa de Produção de Carne Qualificada de Bovídeos no Estado de São Paulo sob o enfoque da Teoria dos Jogos. Informações Econômicas, São Paulo v. 28, n. 2, p. 27-36, 1998.
BRASIL. Ministério da Agricultura, Pecuária e Abastecimento. Programa Nacional de Erradicação da Febre Aftosa: relatório anual 2004. Disponível em: <http://www.agricultura.gov.br/pls/portal/docs/PAGE/MAPA/ PROGRAMAS/AREA_ANIMAL/PNEFA/RELATORIO_PNEFA_2004.PDF>. Acesso em: 5 jan. 2006.
BRASIL. Ministério do Desenvolvimento, Indústria e Comércio Exterior MDIC. Aliceweb. Disponível em: <http://www.aliceweb.desenvolvimento.gov.br>. Acesso em: 21 ago. 2007.
EKBOIR, J.; JARVIS, L.S.; SUMNER, D.A.; BERVEJILLO, J.E.; SUTTON, W.R. Changes in foot and mouth disease status and evolving world beef markets. Agribusiness, Hoboken, v. 18, n. 2, p. 213229, 2002. Disponível em: <http://www3.interscience.wiley.com/cgi-bin/fulltext/93514280/ PDFSTART>. Acesso em: 10 dez. 2005
KEELING, M.J.; WOOLHOUSE, M.E.J.; MAY, R.M.; DAVIES, G.; GRENFELL, B.T. Modelling vaccination strategies against foot-and-mouth disease. Nature, New York, v. 421, n. 6919, p. 136-142, Jan. 2003.
MATTOO, A. Discriminatory consequences of non-discriminatory standards. Genebra: World Trade Organization, Trade in Services Division, Sept. 1996. 30 p. (Working Paper, TISD-96-01).
ORGANIZAÇÃO MUNDIAL DE SAÚDE ANIMAL OIE. Official animal health status. Disponível em: <http://www.oie.int>. Acesso em: 3 jan. 2007.
OSBORNE, M.J. An introduction to game theory. New York: Oxford University Press, 2004. 533 p.
RICH, K.M. DISCOSEM: an integrated epidemiological-economic analysis of foot and mouth disease in the southern cone. Urbana: University of Illinois, Regional Economics Applications Laboratory REAL, Nov. 2004. 33 p. (Discussion Paper, REAL 04-T-15).
RICH, K.M.; WINTER-NELSON, A.; BROZOVI'C, N. Modeling regional externalities with heterogeneous incentives and fixed boundaries: applications to foot and mouth disease control in South America. Review of Agricultural Economics, New Jersey, v. 27, n. 3, p. 456464, 2005.
- AGÊNCIA ESTADUAL DE DEFESA SANITÁRIA VEGETAL E ANIMAL IAGRO. Campanhas de vacinação Disponível em: <http://www.iagro.ms.gov.br/>. Acesso em: 3 jan. 2007.
- AGÊNCIA ESTADUAL DE NOTÍCIAS AEN. Governa libera R$ 700 mil para sacrifício de animais Disponível em: <http://www.bonde.com.br/bondenews/ bondenewsd.php?id=561&dt=20060224>. Acesso em: 10 fev. 2006.
- BARRETT, S. Global disease eradication. Journal of the European Economic Association, Milan, v. 1, n. 2-3, p. 591-600, Aug. 2002.
- Presented at the CONGRESS OF THE EUROPEAN ECONOMIC ASSOCIATION, 17., 2003, Venice.
- BARRETT, S. The economics of eradication versus control of infectious diseases. In: WORKSHOP ON THE ECONOMICS OF VACCINATION IN LOW AND MIDDLE INCOME COUNTRIES, 2003, London. Report Disponível em: < http://www.who.int/immunization_financing/analyses/en/economics_of_immunization_workshop.pdf>. Acesso em: 14 nov. 2005.
- BAUCH, C.T.; EARN, D.J.D. Vaccination and the theory of games. Proceedings of the National Academy of Sciences of the United States of America PNAS, Stanford, v. 101, n. 36, p. 13391-13394, Sep. 2004.
- BLISKA, F. M. M.; PARRÉ, J. L.; GUILHOTO, J. J. M. O Programa de Produção de Carne Qualificada de Bovídeos no Estado de São Paulo sob o enfoque da Teoria dos Jogos. Informações Econômicas, São Paulo v. 28, n. 2, p. 27-36, 1998.
- BRASIL. Ministério da Agricultura, Pecuária e Abastecimento. Programa Nacional de Erradicação da Febre Aftosa: relatório anual 2004. Disponível em: <http://www.agricultura.gov.br/pls/portal/docs/PAGE/MAPA/ PROGRAMAS/AREA_ANIMAL/PNEFA/RELATORIO_PNEFA_2004.PDF>. Acesso em: 5 jan. 2006.
- BRASIL. Ministério do Desenvolvimento, Indústria e Comércio Exterior MDIC. Aliceweb Disponível em: <http://www.aliceweb.desenvolvimento.gov.br>. Acesso em: 21 ago. 2007.
- EKBOIR, J.; JARVIS, L.S.; SUMNER, D.A.; BERVEJILLO, J.E.; SUTTON, W.R. Changes in foot and mouth disease status and evolving world beef markets. Agribusiness, Hoboken, v. 18, n. 2, p. 213229, 2002. Disponível em: <http://www3.interscience.wiley.com/cgi-bin/fulltext/93514280/ PDFSTART>. Acesso em: 10 dez. 2005
- KEELING, M.J.; WOOLHOUSE, M.E.J.; MAY, R.M.; DAVIES, G.; GRENFELL, B.T. Modelling vaccination strategies against foot-and-mouth disease. Nature, New York, v. 421, n. 6919, p. 136-142, Jan. 2003.
- MATTOO, A. Discriminatory consequences of non-discriminatory standards Genebra: World Trade Organization, Trade in Services Division, Sept. 1996. 30 p. (Working Paper, TISD-96-01).
- ORGANIZAÇÃO MUNDIAL DE SAÚDE ANIMAL OIE. Official animal health status Disponível em: <http://www.oie.int>. Acesso em: 3 jan. 2007.
- OSBORNE, M.J. An introduction to game theory New York: Oxford University Press, 2004. 533 p.
- RICH, K.M. DISCOSEM: an integrated epidemiological-economic analysis of foot and mouth disease in the southern cone. Urbana: University of Illinois, Regional Economics Applications Laboratory REAL, Nov. 2004. 33 p. (Discussion Paper, REAL 04-T-15).
- RICH, K.M.; WINTER-NELSON, A.; BROZOVI'C, N. Modeling regional externalities with heterogeneous incentives and fixed boundaries: applications to foot and mouth disease control in South America. Review of Agricultural Economics, New Jersey, v. 27, n. 3, p. 456464, 2005.
Datas de Publicação
-
Publicação nesta coleção
09 Nov 2009 -
Data do Fascículo
Jun 2009