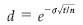Resumos
O objetivo geral deste trabalho é analisar a viabilidade econômicofinanceira de um projeto agroindustrial, através da Teoria de Opções Reais (TOR). A justificativa para utilização da TOR está centrada no fato de que os métodos tradicionais de análise de projetos (VPL e TIR) ignoram duas características importantes: a) a irreversibilidade e b) a possibilidade de adiamento da decisão de investir. Essas características, junto à incerteza sobre o futuro, fazem com que a oportunidade de investimento seja análoga a uma opção financeira. Com o intuito de aplicar estes conceitos, será realizado um estudo de caso, que consiste em um projeto agroindustrial de processamento de frutas, em que se pretende produzir sucos, polpas, geleias, doces e frutas desidratadas. A avaliação pretende demonstrar o valor das flexibilidades operacionais que esse projeto apresenta, como adiar a implementação do mesmo. Para isso, adotou-se a metodologia proposta por Copeland e Antikarov (2001), que adiciona à avaliação tradicional de Fluxo de Caixa Descontado as Opções Reais que o projeto possui. O resultado obtido para o valor presente líquido expandido do projeto, considerando-se as opções reais, para o quarto ano, foi de R$ 891.877,00, aumento de 207% em relação ao valor presente tradicional.
Opções reais; Agronegócio; Viabilidade econômico-financeira; Projetos de investimento
The main objective of this work is to analyze the economical and financial feasibility of an agribusiness project using the Real Options Theory. The justification for using the TOR is centered on the fact that traditional methods of project analysis (NPV and IRR) ignore two important characteristics: a) irreversibility; b) the possibility of postponing the investing decision. These particularities, along with uncertainties about the future and other similarities, allow the investment opportunity to be in many aspects considered analogous to a financial option. In order to apply these concepts, this work presents a case study that is an agribusiness project of fruit processing which produces dehydrated fruits, pulps, juices, jams and candies. The evaluation aims to demonstrate the value of operational flexibilities presented by this project, such as delaying the project implementation. These flexibilities will be evaluated using the methodology proposed by Copeland & Antikarov (2001), which adds the Real Options of the project to the standard discounted cash flow method. The achieved results using the Expanded Net Present Value (ENPV), considering the real options, in the fourth year, was 891,877.00 reais, an increase of 207% compared to the traditional Net Present Value (NPV).
Real options; Agribusiness; Economic and financial viability; Investment projects
Análise de um projeto agroindustrial utilizando a Teoria de Opções Reais: a opção de adiamento
Paula Moreira NardelliI; Marcelo Alvaro da Silva MacedoII
IMestre em Gestão e Estratégia em Negócios pelo PPGEN/UFRuralRJ. E-mail: paulanardelli@hotmail.com
IIProfessor do Programa de Pós-Graduação em Ciências Contábeis da FACC/UFRJ. E-mail: malvaro.facc.ufrj@gmail.com
RESUMO
O objetivo geral deste trabalho é analisar a viabilidade econômicofinanceira de um projeto agroindustrial, através da Teoria de Opções Reais (TOR). A justificativa para utilização da TOR está centrada no fato de que os métodos tradicionais de análise de projetos (VPL e TIR) ignoram duas características importantes: a) a irreversibilidade e b) a possibilidade de adiamento da decisão de investir. Essas características, junto à incerteza sobre o futuro, fazem com que a oportunidade de investimento seja análoga a uma opção financeira. Com o intuito de aplicar estes conceitos, será realizado um estudo de caso, que consiste em um projeto agroindustrial de processamento de frutas, em que se pretende produzir sucos, polpas, geleias, doces e frutas desidratadas. A avaliação pretende demonstrar o valor das flexibilidades operacionais que esse projeto apresenta, como adiar a implementação do mesmo. Para isso, adotou-se a metodologia proposta por Copeland e Antikarov (2001), que adiciona à avaliação tradicional de Fluxo de Caixa Descontado as Opções Reais que o projeto possui. O resultado obtido para o valor presente líquido expandido do projeto, considerando-se as opções reais, para o quarto ano, foi de R$ 891.877,00, aumento de 207% em relação ao valor presente tradicional.
Palavras-chave: Opções reais, Agronegócio, Viabilidade econômico-financeira, Projetos de investimento.
ABSTRACT
The main objective of this work is to analyze the economical and financial feasibility of an agribusiness project using the Real Options Theory. The justification for using the TOR is centered on the fact that traditional methods of project analysis (NPV and IRR) ignore two important characteristics: a) irreversibility; b) the possibility of postponing the investing decision. These particularities, along with uncertainties about the future and other similarities, allow the investment opportunity to be in many aspects considered analogous to a financial option. In order to apply these concepts, this work presents a case study that is an agribusiness project of fruit processing which produces dehydrated fruits, pulps, juices, jams and candies. The evaluation aims to demonstrate the value of operational flexibilities presented by this project, such as delaying the project implementation. These flexibilities will be evaluated using the methodology proposed by Copeland & Antikarov (2001), which adds the Real Options of the project to the standard discounted cash flow method. The achieved results using the Expanded Net Present Value (ENPV), considering the real options, in the fourth year, was 891,877.00 reais, an increase of 207% compared to the traditional Net Present Value (NPV).
Key words: Real options, Agribusiness, Economic and financial viability, Investment projects.
Classificação JEL: G31, D81.
1. Introdução
Devido à globalização e às rápidas alterações que implicam acirrada competitividade empresarial, a gestão de investimentos tem se tornado uma importante componente da vantagem competitiva, estando, ou devendo estar, no foco de muitas organizações.
Logo, a análise sobre oportunidades de investimentos deve considerar que cada decisão de investimento efetivada no presente tem a capacidade de modificar o conjunto de oportunidades disponíveis no futuro.
Desta maneira, o primeiro passo na reorientação do pensamento estratégico é identificar as opções reais que existem nas decisões de investimento. Em outras palavras, deve-se ter um novo entendimento sobre fatores-chave, tais como a irreversibilidade, a incerteza, o timing, a flexibilidade, o risco e a volatilidade, que trará, para as empresas, motivos para uma maior ênfase a seus processos e abordagens sobre análise de investimento.
Assim sendo, considerar uma oportunidade de investimento como uma sucessão de opções de crescimento pode representar a melhor maneira de verificar a viabilidade econômico-financeira de projetos em relação à análise tradicional de investimentos. Isso porque, ao se fazer a avaliação, o questionamento mais apropriado não é qual retorno será obtido deste investimento, mas que opções de crescimento serão criadas por cada investimento sucessivo e qual estratégia de crescimento irá criar o maior valor para a empresa.
Esta mudança de paradigma, no que tange aos questionamentos próprios da análise de viabilidade econômico-financeira, é devida ao fato de que o valor de um projeto não se origina tanto de seu fluxo de caixa direto (atribuído ao mesmo), mas de futuras oportunidades de crescimento que ele poderá criar. Assim, a oportunidade de investimento poderá valer mais que o VPL do projeto.
Neste sentido, surge como alternativa de metodologia de análise a Teoria de Opções Reais (TOR). Esta consegue integrar o orçamento de capital e o planejamento estratégico, na busca pelo objetivo de maximizar o valor do empreendimento. A TOR representa uma estrutura de decisão mais adequada e mais completa, que auxilia no reconhecimento das opções reais implícitas e explícitas relativas ao investimento a ser feito, realçando o valor do projeto (MACEDO, 2003).
Esta abordagem deve ser vista como uma ferramenta de suporte à decisão a ser usada em conjunto com as outras já tradicionalmente utilizadas. O ideal é construí-la sobre a análise de VPL baseada em desconto de fluxo de caixa que as empresas já utilizam, ao invés de abandonar esta metodologia. O apreçamento de opções deve, portanto, ser entendido como um complemento às abordagens existentes de orçamentação de capital, e não um substituto para estas.
Nos últimos anos, as opções reais têm encontrado ampla aceitação onde há alta volatilidade e incerteza, como no agronegócio. O desafio atual, entretanto, é descobrir como institucionalizar o processo de reconhecer, avaliar e exercer as opções presentes em futuros projetos de investimentos, especialmente em mercados com elevada incerteza, mas com grandes promessas de bons resultados a curto e longo prazos.
É neste sentido que está inserido o presente estudo, que tem como objetivo analisar a viabilidade econômico-financeira de um projeto agroindustrial, através da utilização da Teoria de Opções Reais, tratando especificamente a opção de adiamento dos investimentos.
2. Referencial teórico
2.1. Análise de viabilidade econômico-financeira: métodos tradicionais
Um projeto de investimento pode ser resumido em um documento básico, o fluxo de caixa do projeto. O fluxo refere-se a períodos, geralmente anos, que abrangem sua vida útil. Os registros em cada período referem-se aos valores líquidos acumulados durante o período, resultados da diferença entre as entradas e as saídas de caixa, que ocorrem durante o período. O último valor do fluxo de caixa geralmente inclui o valor estimado da venda do projeto ao final da vida útil do investimento, o chamado valor residual, caso exista este valor.
Para avaliar a viabilidade de um projeto, através da análise de seu fluxo de caixa, pode-se utilizar um método denominado de Desconto de Fluxo de Caixa ou Fluxo de Caixa Descontado. Uma característica deste método é que não se podem comparar quantias em instantes de tempo diferentes, uma vez que um mesmo montante tem valores diferentes em períodos diferentes. O método consiste, então, em obter valores equivalentes em um único período.
A base para este método é que o dinheiro tem mais valor hoje que no futuro. Isto ocorre não só pela desvalorização do dinheiro, mas também pelas oportunidades que existem hoje e que podem não existir no futuro, ou ainda pelo custo do capital para a realização do investimento.
Nesse método, os fluxos de caixa futuros são então "penalizados" por um fator, chamado taxa de desconto ou taxa mínima de atratividade (TMA), de forma a refletir essas oportunidades, no pressuposto de que o investimento é irreversível (do tipo "agora ou nunca"), a fim de garantir que as entradas futuras deverão ser suficientes para pagar um empréstimo feito hoje de valor igual ao investimento inicial ou pelo menos igualar os custos de oportunidade do capital.
O fator de penalização sobre qualquer quantia a ser obtida a n períodos futuros é 1/(1+i)n, onde i é a taxa mínima de atratividade. Uma quantia Q a n períodos é, então, equivalente hoje à Q/(1+i)n. De maneira análoga, uma quantia Q hoje é equivalente a uma quantia Q(1+i)n a n períodos futuros.
Logo, com o método de fluxo de caixa descontado, é possível a definição de indicadores relativos a cada alternativa de investimento, que considerem explicitamente o valor do dinheiro no tempo. Os principais são:
• Valor Presente Líquido (VPL): O VPL refere-se à diferença, no início do projeto (data presente), entre o valor presente dos fluxos de caixa futuros gerados pelo projeto e os investimentos feitos. Um projeto viável deve, então, apresentar VPL > 0. A melhor alternativa é a que apresenta maior VPL, entre as que possuem VPL positivo;
• Taxa Interna de Retorno (TIR): O VPL de qualquer projeto diminui com o aumento da taxa de desconto. A TIR é a taxa de desconto que torna nulo o VPL de um determinado projeto, representando, assim, a taxa acima da qual o VPL do investimento torna-se negativo. Ela representa, então, a rentabilidade do projeto, sendo viável todo projeto que apresentar TIR > TMA.
• Período de Payback Descontado (PPD): O PPD representa o período de recuperação do capital investido através da incorporação do valor presente dos fluxos de caixa futuros. Quanto menor o PPD, melhor é o projeto.
Outro aspecto muito importante na análise de viabilidade econômico-financeira é o cálculo do ponto de equilíbrio (P.E.). Este representa o nível de atividade de um projeto necessário para que as receitas possam cobrir os custos totais (fixos e variáveis). Este é tido como um indicador de risco operacional, visto que quanto maior for o P.E., mais difícil será para empresa sair de uma faixa de volume que gera prejuízo (por não cobertura dos custos fixos) para uma faixa de lucro (receitas maiores que os custos).
2.2. Teoria de opções reais
A excessiva preocupação com a análise econômico-financeira, em detrimento de uma visão estratégica integrada, privilegia os investimentos de curto prazo. Isso porque os investimentos de longo prazo, cujos VPLs são penalizados pela incerteza e pela demora do recebimento de fluxos de caixa futuros, acabam sendo sacrificados.
Em outras palavras, existem fatores estratégicos fundamentais para a manutenção ou aumento da competitividade de uma empresa, sem os quais sua rentabilidade futura (e, em última análise, a sua própria sobrevivência) fica comprometida, que podem não estar sendo convenientemente traduzidos em incremento dos fluxos de caixa futuros. Assim sendo, projetos para os quais se calcula VPL baixo, ou mesmo negativo, podem ser adotados por razões estratégicas, e projetos com VPL aparentemente alto podem ser ignorados por não atenderem aos objetivos estratégicos da empresa.
Logo, se torna imprescindível a utilização, na análise de viabilidade econômico-financeira, de uma metodologia que considere explicitamente as questões estratégicas futuras.
Alguns autores, tais como Hayes, Wheelwright e Clark (1988) criticam a maneira como a maioria das empresas elabora projeções dos fluxos de caixa futuros de seus projetos. Consideram "mecânica" a abordagem adotada, que avalia somente as consequências claramente associáveis à decisão de investimento inicial, ignorando as consequências de decisões futuras. Advogam uma perspectiva "orgânica", que assume certa inevitabilidade na maneira como certos eventos geram outros eventos no correr de um projeto, e uma razoável previsibilidade destes eventos a partir do momento em que o projeto tem início.
Estas questões são abordadas por Brennan e Schwartz (1985a), Myers (1987) e Mason e Merton (1985), que definem este problema como de avaliação da flexibilidade gerencial. Assumindo fluxos de caixa predeterminados, a abordagem clássica pode ser caracterizada como estática, pois ignora a possibilidade de adoção de decisões gerenciais por parte dos administradores de um projeto. Tais decisões adiamento do início das operações, alteração dos níveis de produção, expansão ou redução de capacidade, encerramento das atividades etc. poderão certamente ser tomadas após a implantação do projeto, tendo em vista as condições de mercado que se verificarem no correr de sua vida útil. Na opinião de Myers (1987), os métodos de precificação de opções são ferramentas promissoras na análise de questões estratégicas, especialmente a da interdependência sequencial entre projetos. Mason e Merton (1985) e Trigeorgis e Mason (1987) são mais taxativos ao afirmarem que a Teoria das Opções Reais é uma ferramenta adequada para lidar com o problema e resolvê-lo convenientemente.
Brennan e Schwartz (1985b) ressaltam que a análise tradicional desconsidera o fato de que o nível de risco do projeto é afetado pela flexibilidade que as decisões gerenciais proporcionam. Projetos que podem ser alterados (ou mesmo abandonados) diante de condições adversas oferecem menos risco, especialmente se parte do investimento inicial pode ser recuperado.
Myers (1987) ressalta que considerar a oportunidade futura como um segundo estágio do investimento inicial, estimar os fluxos de caixa proporcionados pelos estágios e descontá-los junto à taxa de desconto determinada não leva à resposta correta. O segundo estágio representa uma opção, pois a empresa não é obrigada a realizá-lo; só o fará se o primeiro estágio for concluído de forma a propiciar a realização do segundo e se este continuar atrativo após o término do primeiro. Investir no primeiro estágio significa adquirir um ativo intangível: uma opção de compra sobre o segundo estágio, cujo valor pode superar um VPL negativo do investimento no primeiro. A técnica tradicional de VPL não avalia opções corretamente.
Trigeorgis e Mason (1987) mostram que a aplicação da Teoria de Opções à análise de projetos pode ser feita, de maneira prática e objetiva, numa série de situações em que a flexibilidade gerencial está presente, reconhecendo as oportunidades proporcionadas pelo mercado. Esta aplicação gera o que os autores denominam de VPL expandido, equivalente à soma do VPL tradicional, ou estático, a um prêmio de opção proporcionado pelas oportunidades de flexibilidade gerencial. Os autores concluem que o cálculo convencional de VPL pode subestimar projetos ao ignorar o prêmio de opção, que eventualmente compõe o seu valor total, e que a magnitude desta subavaliação pode ser quantificada pela utilização da Teoria de Opções Reais (TOR).
Portanto, pode ser correto aceitar projetos cujo VPL estático é negativo, se o prêmio de opção existir e exceder esse valor. E, contrariamente ao senso comum, grande incerteza, altas taxas de juros e horizonte de investimento de longo prazo (quando existe a oportunidade de adiá-lo parcialmente) não são fatores que necessariamente reduzem o valor de uma oportunidade de investimento. Os efeitos negativos destes fatores sobre o VPL estático podem ser compensados pelo prêmio de opção proporcionado pela flexibilidade gerencial. Os trabalhos de Myers (1987) e Trigeorgis e Mason (1987) mostram que as restrições à utilização da técnica tradicional na avaliação de investimentos têm fundamento. Assim sendo, a novidade trazida pela TOR é a de indicar que o valor estratégico de um investimento pode ser quantificado pelo valor do prêmio de opção que a flexibilidade gerencial proporciona ao investimento.
Essa realidade é totalmente aplicável na análise de viabilidade econômico-financeira de projetos agropecuários, pois com a aplicação das técnicas convencionais, ignoram-se as possibilidades de decisões futuras causadas pelas incertezas inerentes ao agronegócio, tais como variação de preços e de volume de produção.
Em projetos agropecuários, a incerteza ocorre principalmente com relação à flutuação dos preços futuros das commodities agropecuárias, que afetam bastante o retorno do investimento. Projetos que apresentam um VPL positivo hoje podem apresentar prejuízos num curto espaço de tempo. Os custos também são fonte de incertezas, pois os preços dos insumos específicos para agropecuária (sementes, adubos, defensivos e aluguel da terra) apresentam uma forte correlação com preço do produto a ser explorado. Além disso, outros elementos tais como a falha ou sucesso na adoção de novas tecnologias e as quebras de safras agrícolas devido a problemas climáticos são incertezas naturais em projetos desta natureza.
2.3. Opção de adiar: um caso específico
Este tipo de opção permite a avaliação do adiamento do investimento por determinado tempo, com o intuito de se obterem novas informações relevantes ao projeto.
A opção de adiar é análoga a uma opção de compra americana do valor presente bruto do fluxo de caixa esperado do projeto, com preço de exercício igual ao investimento requerido. Como exemplo, uma empresa que possui uma opção de adiar um investimento não precisa fazê-lo hoje, podendo esperar até a data de vencimento da opção para tomar esta decisão, e somente investirá se as condições futuras forem favoráveis.
A abordagem de opções reais exerce impacto nas decisões sobre análise de investimento, uma vez que pode mudar tais decisões significativamente, caso o valor da opção de esperar seja levado em consideração corretamente (KEMNA, 1993).
A opção de adiar um investimento para explorar uma propriedade rural é uma opção americana de compra. Como a opção de adiar o investimento dá à administração o direito (não a obrigação) de realizar o investimento para explorar a propriedade, um projeto que pode ser adiado tem mais valor do que o mesmo sem a flexibilidade do adiamento.
Isso porque esta opção permite ao administrador beneficiar-se de movimentos favoráveis ao valor do projeto (como aumento de preços do produto a ser gerado), e evitar perdas caso cenários desfavoráveis ocorram. Se a decisão for investir agora, o investidor exerce a opção e incorrerá a um custo de oportunidade igual ao valor da opção.
Por outro lado, a opção pode ser preservada até o ano seguinte, exercendo-a caso a taxa de atratividade do projeto aumente. Evidentemente, as firmas nem sempre têm essa possibilidade, principalmente em mercados com alto poder concorrencial. A firma deve sempre comparar o custo de adiar o risco de entrada de novas firmas no mercado ou a perda de fluxos de caixa com os benefícios de esperar informação nova para subsidiar a decisão de investir.
Cabe ressaltar que, como dito no item 2.2., o valor da opção está diretamente relacionado ao nível de incerteza, quando da existência da flexibilidade de adiamento. Isso porque são as incertezas que trazem valor para as possibilidades de beneficiar-se de movimentos favoráveis e evitar perdas em cenários desfavoráveis.
2.4. O modelo binomial na teoria de opções reais
As diferentes abordagens de valoração de opções reais podem ser separadas de acordo com a forma com que o tempo é considerado: de forma discreta ou contínua. Abordagens "lattice" multinomial constituem a avaliação que consideram tempo discreto, enquanto equações de "solução fechada" (closedform), equações diferenciais estocásticas e simulação de Monte Carlo são abordagens que avaliam em tempo contínuo (MILLER e PARK, 2002).
A abordagem lattice assume que o ativo subjacente segue um processo estocástico discreto, multinomial e multiplicativo ao longo do tempo de maneira a se obter alguma forma de "árvore". O valor da opção é, então, resolvido recursivamente a partir dos nós finais da árvore. A vantagem de sua utilização é o procedimento flexível de avaliação (MILLER e PARK, 2002).
Existem muitos trabalhos na literatura que desenvolveram abordagens lattice na valoração de opções reais. Cox, Ross e Rubinstein (1979) desenvolveram uma abordagem binomial para valorar opções que se tornou bastante utilizada. Apesar de ter sido concebido para avaliar opções financeiras, este modelo é útil para modelar e apreçar opções reais.
O modelo binomial é um modelo de tempo discreto para apreçamento de opções e explica claramente o princípio econômico fundamental da não arbitragem para valoração de opções. A ideia básica é desenvolver um portfolio apropriado para replicar os retornos futuros da opção.
Cox, Ross e Rubinstein (1979) mostraram que para se determinar o valor exato de uma opção de compra (C) é necessário e suficiente que se tenha:
• Preço de exercício (X);
• Preço do ativo subjacente (S);
• Média dos movimentos de subida (u) e de descida (d) no preço do ativo subjacente;
• Taxa de juros (r = 1+ rf), sendo rf a taxa livre de risco.
O modelo binomial assume que:
• O preço do ativo segue um processo multiplicativo binomial em períodos discretos. Assim, para cada período, o ativo (representado por uma ação no momento do desenvolvimento do modelo) pode assumir somente dois valores distintos no tempo. Estes movimentos são descritos como ascendente e descendente pelo fato de representarem um valor maior e outro menor que o anterior;
• A taxa de juros é constante;
• Pode-se emprestar ou tomar emprestado a esta mesma taxa livre de risco.
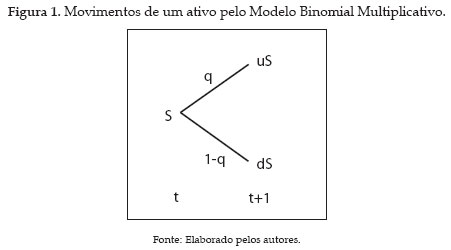
Supondo-se que o preço do ativo no tempo t seja S; no tempo t+1, ela valerá uS, com probabilidade q ou dS com probabilidade (1-q). Os valores de u e d representam as taxas de retorno se o ativo move para cima ou para baixo respectivamente. A Figura 1 a seguir representa de forma esquemática os movimentos supradefinidos:
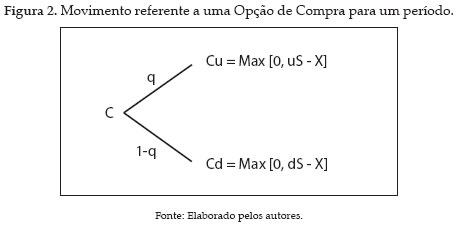
Para valorar uma opção de compra, C, sobre este ativo, Cu e Cd representam o valor da opção ao final de um período, quando o preço do ativo é uS e dS, respectivamente. Sendo X o preço de exercício da opção, os possíveis valores para a opção serão: Cu = Max [uS X, 0] e Cd = Max [dS X, 0], conforme demonstrado na Figura 2:
Segundo Cox, Ross e Rubinstein (1979), as probabilidades objetivas (q e 1 -q) são substituídas por probabilidades intrínsecas ao movimento ascendente e descendente do modelo binomial (p e 1- p), denominadas de probabilidades neutras ao risco. Estas podem ser definidas da seguinte maneira:
Cox, Ross e Rubinstein (1979) chegaram à seguinte equação para calcular o preço de uma opção de compra (sobre um ativo que não paga dividendos) um período antes de sua expiração, em termos de S, X, r, u e d.
em que: r = 1 + taxa livre de risco.
Cox, Ross e Rubinstein (1979) ressaltam as principais características da relação apresentada nesta equação:
• A probabilidade objetiva q não aparece na fórmula. Isto significa que as diferentes visões dos diversos investidores quanto às probabilidades que acreditam com relação ao movimento de subida ou descida da ação não influenciarão o valor da opção;
• O valor da opção não depende das atitudes dos investidores em relação ao risco;
• A única variável aleatória da qual o preço da opção de compra depende é o preço da própria ação (ou do ativo subjacente à opção).
A avaliação de uma opção pelo método binomial, quando existe mais de um período, é uma extensão direta da fórmula para um período. Assim, este método pode avaliar situações com grande número de períodos. Entretanto, à medida que se aumenta a quantidade de períodos, o cálculo das opções torna-se mais trabalhoso.
Outra importante relação apresentada por Cox, Ross e Rubinstein (1979) foi a estimativa dos valores de u e d, os quais se baseiam no desvio padrão da taxa de retorno da ação ou volatilidade do retorno (σ), no número n de intervalos ou períodos até a expiração e no tempo t até a expiração. De outra maneira, t/n representa o tempo transcorrido entre mudanças sucessivas no preço do ativo. As fórmulas apresentadas por estes autores são:
Este será o modelo a ser utilizado para avaliação da opção de adiar no projeto agroindustrial a ser analisado.
3. Metodologia
Nesta investigação serão combinadas algumas modalidades de pesquisas: Pesquisa Descritiva, pois será descrita a realidade, e Pesquisa de Campo, através de um estudo de caso, já que o tema central se encontra em desenvolvimento, e ainda não há muitas informações e trabalhos a respeito da aplicação de Opções Reais em projetos agroindustriais. O uso de estudo de caso se justifica na medida em que este trabalho se constitui numa pesquisa exploratória, pois este tipo de pesquisa, segundo Zaltamn e Burger (1975), se aplica quando as evidências disponíveis são contraditórias ou insuficientes para permitir o estabelecimento de hipóteses formais ou a detecção de novos conceitos.
De acordo com Vergara (2009), uma investigação exploratória é realizada em área na qual há pouco conhecimento acumulado e sistematizado. Andrade (2001) complementa dizendo que esta se configura como a fase preliminar, que busca proporcionar mais informações sobre o assunto que vai se investigar.
Será adotada como estratégia de pesquisa a metodologia de estudo de caso por propor estudar um foco "bem delimitado, devendo ter seus contornos claramente definidos no desenrolar do estudo" (LUDKE e ANDRÉ, 1986, p. 17). Neste sentido, destaca-se a relevância deste método devido à possibilidade de aprofundar no entendimento de uma realidade que possa ser estendida a outras oportunidades futuras de pesquisa a partir do caso em estudo.
Segundo Bourchalat (1961), um caso procura descrever uma situação concreta extraída do mundo dos negócios. Além disso, é uma espécie de elo que une a experiência do executivo em seu trabalho ao pesquisador nos seus esforços de compreender o processo de gestão. De acordo com Yin (1993), os estudos de casos são fortes em realismo e em validade interna. Porém, não apresentam validade estatística para que se possa generalizar os fatos observados, além de serem difíceis de replicações.
Para o desenvolvimento do estudo de caso, será realizada uma coleta de dados quantitativos obtidos durante a pesquisa exploratória e documental. A pesquisa irá se basear em dados coletados de um projeto agroindustrial, onde se pretende fabricar e vender sucos, polpas, geleias, doces e frutas desidratadas, a partir do processamento de frutas. Estas informações servirão de subsídio numérico para a construção do modelo de aplicação da Teoria de Opções Reais, que representa o tratamento dos dados deste trabalho.
Este projeto foi desenvolvido em 2007, para implantação de uma unidade agroindustrial de processamento de frutas, no estado do Rio de Janeiro.
Primeiramente, para se fazer o estudo de viabilidade técnica e econômica, foram levantados dados referentes às possíveis demandas relacionados ao mercado dos produtos à base de frutas, para o cálculo das estimativas de produção, receita e custos diretos e indiretos e a estimativa de investimento. Para isso, foram consultados sites, como por exemplo, da ABNT (Associação Brasileira de Normas Técnicas), BNDES (Banco Nacional de Desenvolvimento Econômico e Social), Bolsa de Gêneros Alimentícios do Rio de Janeiro (BGA- RJ), Brasil Rio Promoções e Empreendimentos Ltda, Ceagesp (Companhia de Entrepostos e Armazéns Gerais de São Paulo), FGV (Fundação Getúlio Vargas) e outras empresas fabricantes de equipamentos e insumos, produtores e cooperativas fornecedoras de matérias-primas.
Para analisar os dados do projeto da unidade agroindustrial de processamento de frutas, serão calculados, pela análise tradicional, os seguintes indicadores: Valor Presente Líquido, Taxa Interna de Retorno, Tempo de Retorno de Capital (período de payback descontado PPD) e Ponto de Equilíbrio.
Para se calcular o valor da opção utilizando o modelo binominal através do método da probabilidade neutra ao risco, será suposto que as oscilações dos preços das matérias-primas respeitam uma distribuição binomial no período de tempo (Dt). Para o cálculo do VPL expandido, serão estimados o período de tempo (Dt), a taxa livre de risco (r) no período considerado e a volatilidade (σ). O passo a passo para os cálculos é descrito a seguir.
As opções calculadas neste trabalho serão: Opção de Adiamento para o período de um, dois, três e quatro anos. Seguem abaixo os passos para o cálculo do valor das opções, segundo Copeland e Antikarov (2001).
1. Primeiro passo: Cálculo do VPL do projeto
Cálculo do VPL do projeto, sem flexibilidades, por meio da metodologia tradicional do fluxo de caixa, descontado à taxa de desconto ajustada ao risco, determinando, desta forma, o valor presente (VP) do projeto.
2. Segundo passo: Modelagem das incertezas que afetam o valor do ativo subjacente e da árvore de eventos
A principal incerteza presente no projeto é a volatilidade dos preços das frutas, que são as principais matérias-primas usadas no projeto. Ela será calculada a partir da série histórica de preços das frutas no período de janeiro de 2000 a agosto de 2008.
Com auxílio do programa Excel, será calculada a volatilidade dos preços das frutas da seguinte maneira, levando-se em consideração suas entressafras:
• Para cada fruta e a cada mês, será multiplicado o seu preço pela sua quantidade anual;
• Com estes resultados, calcula-se o logaritmo neperiano entre o resultado do período sobre o resultado do período anterior;
• Depois, será calculada a média ponderada do logaritmo neperiano para um mesmo período, levando-se em consideração as quantidades de entrada de cada fruta no projeto;
• Assim, calcula-se o desvio padrão dos resultados da média ponderada em todo o período considerado;
• O desvio padrão encontrado será anualizado, multiplicando por raiz quadrada de 12, conforme demonstrado em Hull (2005).
Este desvio padrão é a volatilidade usada para a construção da árvore e, posteriormente, o cálculo do valor da opção. Ou seja, aproxima-se a volatilidade dos fluxos do projeto à volatilidade de preços de seu principal insumo: as frutas.
O valor de referência para a taxa de juros livre de risco é a taxa de poupança. Será feita uma média das taxas anuais de poupança no período de 2000 a 2008, o mesmo período considerado para o cálculo da volatilidade das frutas.
Para se modelar a árvore de eventos, segundo o modelo binomial proposto por Cox, Rox e Rubinstein (1979), serão utilizadas planilhas do Excel. O valor do projeto será determinado para cada nó do evento utilizando-se os valores de u e d, movimentos ascendentes e descendentes, respectivamente. Também serão consideradas a volatilidade do projeto (σ), a taxa de juros livre de risco (r), a probabilidade neutra ao risco p e (1p) e cada ano será um instante de tempo (t).
O resultado desta árvore, ainda sem flexibilidade, deverá ser igual ao resultado calculado no primeiro passo.
3. Terceiro passo: Modelagem da árvore de decisão
Para a modelagem da árvore de decisão, as opções reais presentes no projeto serão consideradas em cada nó de decisão onde elas existam. Segundo Brandão (2002), a árvore binomial transforma-se em árvore de decisão ao incorporarmos as opções reais no projeto.
Portanto, através da árvore de decisão, obtém-se um novo resultado de VP do projeto, considerando a flexibilidade existente.
4. Quarto passo: Análise das opções reais
Após o cálculo do VPL do projeto e o VPL do projeto considerando-se incertezas e flexibilidades, o valor das opções reais será obtido. A diferença entre esse valor presente expandido e o valor presente tradicional será o próprio valor das opções, ou seja, VPL expandido = VPL tradicional + VPL opções reais.
4. Apresentação e análise dos resultados
4.1. Considerações iniciais e análise tradicional
Na análise do projeto da unidade de processamento de frutas, foram utilizados índices tradicionais de viabilidade econômico-financeira, tais como Taxa Interna de Retorno (TIR), Valor Presente Líquido (VPL), Período de Payback Descontado (PPD) e Ponto de Equilíbrio (PE). Foram considerados uma Taxa Mínima de Atratividade (TMA) de 15% a.a., baseada nas taxas existentes no mercado do produto sob análise, e um horizonte de análise de 10 anos.
O projeto da unidade de industrialização tem como objetivo o processamento mensal de frutas em torno de 155.000 kg, produzindo 96.000 kg de derivados de frutas, entre abacaxi desidratado e banana-passa; geléias de abacaxi, maracujá, goiaba, manga e pêssego; doce de banana; polpas de abacaxi, banana, maracujá, goiaba, manga e pêssego; e sucos de abacaxi, maracujá, goiaba, manga e pêssego.
A partir do plano de produção, fez-se o cálculo dos investimentos iniciais da empresa, considerando-se os itens: construção civil de prédios e instalações, máquinas, equipamentos, utensílios e outros necessários para o início do projeto. Esse levantamento foi dimensionado de acordo com a produção pretendida para a indústria. Ainda, considerou-se como zero o custo relativo a terreno e terraplanagem, uma vez que, para este projeto, o terreno foi doação da prefeitura da cidade onde o empreendimento será instalado. O Quadro 1 mostra a descrição dos principais itens referentes ao investimento inicial.
Calculou-se o investimento inicial total, que foi de R$ 2.243.000,00, aproximadamente, suficiente para adquirir máquinas e equipamentos, para fazer as obras civis e para formar um capital de giro necessário para desencadear o negócio. É importante salientar que o investimento em capital de giro foi estimado para cobertura de um mês de operações mais uma reserva técnica de 20% deste valor. Além disso, para os investimentos permanentes, foi estimada uma reserva técnica de 20% de seu valor.
Foram levantados, para o cenário proposto, os custos fixos do projeto, ou seja, aqueles que ocorrem independentemente da produção ou vendas, como, por exemplo, gastos com energia elétrica (onde foram incluídos 18% de impostos), telefonia e água, entre outros, num total de R$ 52.603,54/mês.
Também foram estimados outros custos referentes à operação da fábrica. Em relação à mão de obra, foi dividida em mão de obra direta (funcionários ligados diretamente à área de produção) e mão de obra indireta (funcionários do setor administrativo). Para a mão de obra direta, são necessários 30 colaboradores para as áreas de seleção, recebimento, linha de fabricação, embalagem, congelamento e outros, além de um supervisor de produção e um gerente, totalizando R$ 29.241,00 em salários e encargos. Para a mão de obra indireta, foram estimados 20 colaboradores, entre auxiliares administrativos, faxineiros, vendedores, contador, secretário e outros, somando R$ 21.660,00 (com encargos). Logo, os custos totais com mão de obra são R$ 50.901,00/mês.
Dentro dos custos variáveis, foram levantados os custos com insumos, ou seja, materiais diretos como matérias-primas, materiais secundários, embalagens e demais materiais utilizados na fabricação dos produtos.
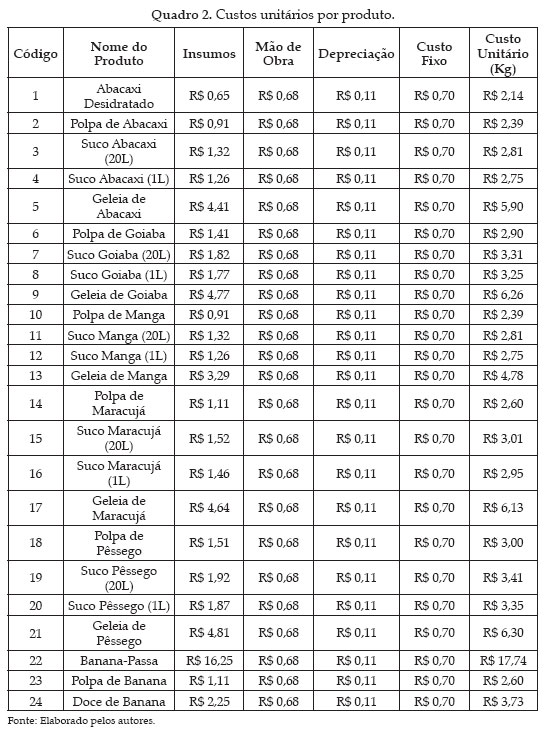
Depois de conhecido o custo de mão de obra e sabendo quanto irá gastar com insumos, calculou-se o custo unitário de produção. Chega-se a ele somando o custo unitário dos materiais diretos com um rateio dos custos fixos, da mão de obra e da depreciação, como mostrado no Quadro 2. Em relação à depreciação, a vida útil foi estimada em 10 anos para os equipamentos, e em 50 anos para as instalações.
Tecnicamente, chegou-se ao preço unitário de venda por embalagem aplicando-se a taxa de marcação aos custos unitários. Esta taxa variou de 50% a 75% e foi obtida levando-se em consideração condições de competitividade dos produtos. Após o levantamento do preço de venda por embalagem, obteve-se a Receita Operacional Mensal, que é considerada entrada de caixa, de R$ 403.261,66/mês. A projeção desta receita foi resultante do potencial de mercado, da capacidade produtiva e da força de vendas da empresa. No Quadro 3, verificam-se os preços de venda e a Receita Operacional Mensal.
Com estas informações, pode-se montar o fluxo de caixa para a análise da viabilidade. O fluxo de caixa anual pode ser visto no Quadro 4 e é o conjunto de entradas (receitas) e saídas (despesas) relativo ao período do projeto.
Para o cálculo deste fluxo de caixa, admitiu-se que foram vendidas 40%, 50%, 55%, 60%, 65%, 70%, 75%, 75%, 80% e 80% referentes à capacidade de produção, respectivamente, nos 10 anos de vida útil do projeto. O fluxo de caixa do ano 0 representa o valor do investimento inicial apresentado no Quadro 1. Foi considerada, ainda, uma necessidade de complementação de capital de giro no ano 1, nos mesmos níveis do que foi feito no ano 0. Para fins de cálculo, estimou-se uma alíquota de imposto de renda da ordem de 15% para os lucros tributáveis da empresa. Um último ponto relevante para a montagem do fluxo de caixa é que a depreciação foi considerada como custo operacional e, assim, relacionada como uma saída no cálculo do fluxo de caixa anual. Porém, como esta tem efeito de economia fiscal, mas não representa uma saída efetiva de caixa, seu valor foi somado ao final do fluxo de cada ano. No ano 10 foi considerada uma recuperação do capital investido (de giro e permanente) da ordem de R$ 1.000.000,00.
Utilizando-se uma TMA de 15% a.a., pode-se calcular o VPL do projeto, que foi de R$ 430.297,10. Além disso, foi calculada a TIR, que ficou em torno de 18,43% a.a.., e o PPD, que foi de nove anos.
Com base nos dados, pode-se concluir, em relação à viabilidade econômico-financeira deste projeto que, considerando-se o VPL e a TIR, o projeto é viável, considerando-se TMA de 15% a.a. e uma vida útil de 10 anos, pois VPL é maior do que zero e a TIR é maior que a taxa mínima de atratividade (TMA). Porém, ressalta-se que o projeto possui um período de recuperação bastante elevado, considerando-se sua vida útil.
Uma análise de sensibilidade foi feita em relação a algumas variáveis. A primeira foi feita em relação ao valor residual do projeto (considerado inicialmente no montante de R$ 1.000.000,00). Percebe-se que, mesmo que este valor seja zerado, o projeto ainda continua viável, com VPL de cerca de R$ 183.000,00 e TIR de pouco mais de 16% a.a. Outra análise se deu em relação aos fluxos de caixa anuais. Percebeu-se que havia a possibilidade de uma redução máxima de 16,1% dos mesmos para que o projeto ainda assim continuasse a ser viável. Isto mostra a folga que os fluxos de caixa têm no sentido de gerar alguma segurança na empresa em relação aos indicadores calculados.
Por fim, a análise de ponto de equilíbrio foi feita a partir dos dados operacionais resumidos no Quadro 5.
Com os valores dos custos fixos totais, a receita operacional e os custos variáveis totais, calculou-se o Ponto de Equilíbrio, que ficou em torno de 34% da capacidade produtiva estimada para o projeto (receita total máxima). Isso implica dizer que, para obter lucro, a operação precisa trabalhar acima de 34% da capacidade produtiva.
Para o ponto de equilíbrio, também foi feita uma análise de sensibilidade. Esta teve como ponto de partida fazer simulações com os valores de algumas variáveis até que o ponto de equilíbrio ficasse no limite máximo (preestabelecido) de 50% da capacidade. Primeiramente, observou-se que os custos fixos poderiam aumentar até 46% dos níveis atuais. Mesmo assim, o projeto ficaria em um nível aceitável de risco (volume do P.E. = 50% da capacidade). O mesmo foi feito em relação aos custos variáveis, e encontrou-se que estes podem crescer no máximo 20% para que o ponto de equilíbrio não ultrapasse a marca de 50% da capacidade. Já em relação à receita total, percebeu-se que a redução máxima aceitável para este nível de risco operacional proposto seria de 12%. Isso quer dizer que perdas de receitas representam problemas sérios para o projeto, visto que este possui maior sensibilidade (menor margem de segurança) em relação a esta variável.
4.2. Análise dos Resultados da Aplicação da TOR
O modelo de Opções Reais utilizado para complementar a análise tradicional permite aos tomadores de decisão avaliar, com base em informações mais completas e levando-se em consideração presença de incertezas e flexibilidades gerenciais, a viabilidade de implantação do projeto.
O cálculo dos indicadores, inclusive o VPL, foi apresentado, em detalhes, no item 4.1., sendo que o VPL encontrado foi de R$ 430.297,10.
Pelo método do VPL, poderia ser indicado o investimento no projeto, já que o mesmo possui VPL positivo. Porém, esse resultado é insuficiente para a tomada de decisão, como se constatou na revisão de literatura, visto que não considera os riscos (volatilidades dos fluxos) e a possibilidade de mudança de decisão ao longo do projeto.
Assumiu-se uma incerteza para o projeto de unidade processadora de frutas: o preço das frutas que são utilizadas como entradas (matéria-prima principal do projeto).
Foi possível observar a incerteza pelas séries históricas de preços das frutas comercializadas no Ceasa-RJ no período de janeiro de 2000 a agosto de 2008 (Fontes: SIMA/RJ e Pesagro-Rio). A partir dessas séries históricas, calculou-se a volatilidade anual dos preços, conforme descrito na metodologia, tendo como valor encontrado 32,21%.
A partir das taxas de poupança anuais do período de 2000 a 2008, foi calculada a taxa livre de risco como sendo a média destas taxas anuais, que ficou em torno de 8,72% a.a.
Desta forma, os dados para a modelagem binomial da opção de adiamento são: VPL = R$ 430.297,10
Investimento Inicial = R$ 2.350.732,09 (Fc da data 0 + VP do investimento em capital de giro da data 1)
Valor Presente dos Fluxos de Caixa Futuros = R$ 2.781.029,19 (VPL + Investimento Inicial)
σ = 32,21% (volatilidade anual)
r = 8,72% (taxa livre de risco)
t = 1 (período de variação dos fluxos)
u = e 32,21 % √ 1 = 1, 38 (taxa de subida dos fluxos)
d = 1/ u = 0,72 (taxa de descida dos fluxos)
p =
=> p =
= 0,55 (prob. de subida dos fluxos)
1-p = 0,45 (prob. de descida dos fluxos)
k = Investimento Inicial x (1 + r)t, sendo os seguintes valores em cada período: para o ano 0 = R$ 2.350.732,09; para o ano 1 = R$ 2.555.715,93; para o ano 2 = R$ 2.778.574,36; para o ano 3 = R$ 3.020.866,04; para o ano 4 = R$ 3.284.285,56.
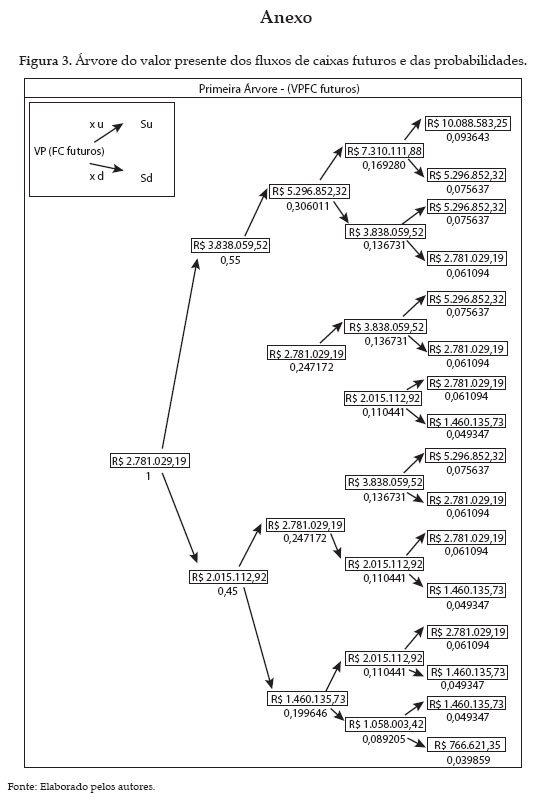
Foram utilizadas as variáveis acima para construção das árvores binomiais e, consequentemente, para o cálculo da Opção de Adiamento, para um, dois, três e quatro anos. A Figura 3 (ver anexo) representa a primeira árvore onde o valor presente do fluxo de caixa futuro é multiplicado pelo movimento ascendente ou descendente e as probabilidades de cada nó são apresentadas.
A ideia, então, é fazer o valor presente dos fluxos de caixa futuros variar de acordo com as taxas binárias de subida e descida, obtidas a partir da volatilidade dos preços das frutas. Depois disso, obtêm-se as diferenças entre estes valores e os de exercício em cada período (k), ou seja, os valores de Su k e Sd k.
Cabe ressaltar que os valores de k (na opção de adiamento) são iguais aos valores do Investimento Inicial levados para a data de análise (corrigidos pela taxa livre de risco), neste caso, para os períodos 1, 2, 3 e 4.
De posse destes valores (S k), obtém-se o máximo entre os mesmos e zero. Tem-se, então, em cada nó da árvore binomial, o quanto o valor presente dos fluxos de caixa futuros ultrapassa o preço de exercício (k).
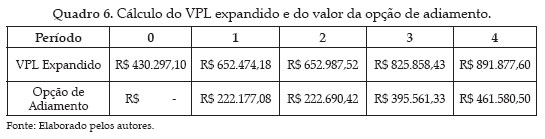
O próximo passo é ponderar a existência de opções reais, ou seja, quando S k é maior que zero, pela sua respectiva probabilidade neutra ao risco (Figura 3). O valor presente da soma destes valores ponderados, em cada período, representa o VPL expandido do projeto, considerando-se a opção de adiar por um, dois, três ou quatro períodos a decisão de investir. No Quadro 6, pode-se observar os VPL expandidos e o valor da opção de adiar, considerando-se que VPL expandido = VPL tradicional + VPL opções reais.
Analisando os resultados apresentados acima, que consideraram a presença de incertezas e flexibilidades gerenciais e complementaram a análise tradicional, verifica-se que há informações mais completas para a tomada de decisão.
Com a incorporação das opções reais na avaliação do projeto, constata-se que o VPL do projeto aumenta no período considerado, constatando a premissa de que um projeto que pode ser adiado tem mais valor do que o mesmo sem a flexibilidade do adiamento, uma vez que o investidor tem a opção de adiar o início do empreendimento, levando-se em consideração os riscos e a possibilidade de mudanças.
O valor presente líquido do projeto é de R$ 430.297, 10; ao incluir o valor da opção de adiamento, temos como VPL expandido R$ 652.474,18 para um ano; R$ 652.987,52 para dois anos; R$ 825.858,43 para três e R$ 891.877,60 para quatro anos, valores superiores aos constatados através da avaliação pelo método tradicional do fluxo de caixa descontado. O aumento decorrente da incorporação das opções reais na análise, para um adiamento de quatro anos, por exemplo, é de 207%.
Para complementar os resultados, procedeu-se uma análise de sensibilidade para os dois principais elementos estimados: a taxa de juros e a volatilidade. Para a taxa de juros, variando seu valor de 10% para cima ou para baixo, observa-se que o VPL expandido tem seu valor majorado ou reduzido em cerca de 1%. Já em relação à volatilidade, quando a mesma é modificada em 10% para cima ou para baixo, o valor do VPL expandido tem variações de 5% a 7%.
5. Conclusão e considerações finais
Através da aplicação da TOR conduzida neste estudo, pôde-se perceber que, em situações nas quais a questão da incerteza é relevante, como é o caso de projetos agroindustriais, é possível quantificar as flexibilidades gerenciais existentes em função da possibilidade de decisões de adiar a implementação de um projeto.
A questão fundamental da análise conduzida é que as incertezas envolvendo variáveis fundamentais para a avaliação do projeto, como por exemplo, o preço das matérias-primas principais, não são consideradas pelo método tradicional do fluxo de caixa descontado. Desta forma, para capturar as incertezas e flexibilidades existentes, o trabalho utilizou a Teoria de Opções Reais, metodologia complementar ao método tradicional de valor presente líquido.
O valor presente líquido do projeto, pela análise tradicional, é de R$430.297,10 e, com a incorporação da opção de adiá-lo, temos o valor expandido, para um, dois, três e quatro anos, respectivamente, R$ 652.474,18, R$ 652.987,52, R$ 825.858,43 e R$ 891.877,60. Dessa forma, pôde-se perceber que, neste projeto, a metodologia tradicional subestimou a riqueza gerada pelo projeto, pois ignorou o valor econômico da opção de adiar o início do empreendimento.
Com esta avaliação, o investidor passa a ter subsídios e informações mais confiáveis para sua tomada de decisão, pois foi criada na análise a possibilidade de adiamento, na qual este investidor poderá aguardar o início do empreendimento, com o intuito de se obter novas informações relevantes ao projeto, somente investindo se as condições futuras forem favoráveis.
Cabe destacar que a aplicação da TOR é totalmente pertinente no ambiente do agronegócio, pois, além de apresentar todas as condições para a implementação da técnica de análise, o setor ainda teria como resposta uma conclusão mais realista sobre a viabilidade econômico-financeira de projetos de investimento. Isso impulsionaria o setor a novos investimentos, pois projetos tradicionalmente não viáveis poderiam mudar de perspectiva, sendo implementados em função de ganhos provenientes das opções reais.
Este trabalho avaliou a opção de adiamento da implantação de uma empresa agroindustrial de processamento de frutas, mas inúmeras outras formas de opções podem ser consideradas, como por exemplo, a opção de abandono, onde o investidor poderá ter uma valiosa opção de abandonar o projeto definitivamente para evitar perdas ainda maiores, quando algum problema maior acontecer ao longo de sua vida útil. Sendo assim, para estudos posteriores, sugere-se incorporar outros tipos de opções.
Ainda, sugere-se, para trabalhos futuros, o desafio de refinamento dos cálculos da volatilidade, onde se possa avaliar, conjuntamente, outras incertezas inerentes ao projeto, além do preço da matéria-prima.
6. Referências Bibliográficas
- ANDRADE, M. M. Como Preparar Trabalhos para Cursos de Pós Graduação 4Ş ed. São Paulo: Atlas, 2001.
- BOURCHALAT, J. La Methode de Cas Paris: Presses Universitaires de France, 1961.
- BRANDÃO, L. Uma aplicação da teoria das Opções Reais em tempo discreto para avaliação de uma concessão rodoviária no Brasil Rio de Janeiro: PUC. 2002. (Tese de Doutorado apresentada ao Programa de Pós-Graduação em Engenharia Industrial. da Pontifícia Universidade Católica do Rio de Janeiro).
- BRENNAN, M. J.; SCHWARTZ, E. S. Evaluating Natural Resource Investments. Journal of Business v. 58, n. 2, p. 135-157, 1985a.
- BRENNAN, M. J.; SCHWARTZ, E. S. A New Approach to Evaluating Natural Resource Investments. Midland Corporate Finance Journal v. 3, nş 1, p. 37-47, 1985b.
- COPELAND, T. E., ANTIKAROV, V. Opções reais: um novo paradigma para reinventar a avaliação de investimentos. Rio de Janeiro: Campus, 2001.
- COX, J.; ROSS, S.; RUBINSTEIN, M. Option Pricing: a simplified approach. Journal of Financial Economics, v. 7, p. 229-264, 1979.
- HAYES, R. H.; WHEELWRIGHT, S. C.; CLARK; K. B. Dinamic Manufacturing: Creating The Learning Organization. New York: The Free Press, 1988.
- HULL, J. C. Fundamentos dos Mercados Futuros e de Opções São Paulo: Bolsa de Mercadorias & Futuros, 2005.
- KEMNA, A. G. Z. Case Studies on Real Options. Financial Management, v. 22, nş 3, p.259-70, 1993.
- LUDKE, M.; ANDRÉ, M. Pesquisa em Educação: abordagens avaliativas. São Paulo: EPU, 1986.
- MACEDO, M. A. S. Estudo da viabilidade econômico-financeira de projetos que utilizam gerenciamento de restrições. In: SIMPÓSIO DE ADMINISTRAÇÃO DA PRODUÇÃO, LOGÍSTICA E OPERAÇÕES INTERNACIONAIS, 6, 2003, São Paulo. Anais do VI SIMPOI. São Paulo: FGVSP, 2003. 1 CD.
- MASON, S. P.; MERTON, R. C. The Role of Contingent Claims Analysis in Corporate Finance. In: ALTMAN, E. I.; SUBRAHMANYAM, M. G. Recent Advances In Corporate Finance Homewood: Irwin, p. 9-54, 1985.
- MILLER, L. T.; PARK, C. S. Decision Making under uncertainty Real Options to the Rescue? The Engineering Economist, v. 47, nş 2, p. 105-150, 2002.
- MYERS, S. C. Finance Theory and Financial Strategy. Midland Corporate Finance Journal v. 5, nş 1, p. 6-13, 1987.
- TRIGEORGIS, L., MASON, S. P. Valuing Managerial Flexibility. Midland Corporate Finance Journal v. 5, nş 1, p. 14-21, 1987.
- VERGARA, S. C. Projetos e Relatórios de Pesquisa em Administração 10Ş ed. São Paulo: Atlas, 2009.
- YIN, R. Applications of Case Study Research Newbury Park: Sage, 1993.
- ZALTAMN, G.; BURGER, P. C. Marketing Research: fundamentals and dynamics. Himdale: Druden Press, 1975.
Datas de Publicação
-
Publicação nesta coleção
07 Mar 2012 -
Data do Fascículo
Dez 2011