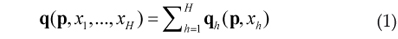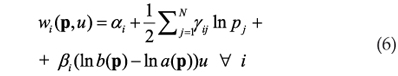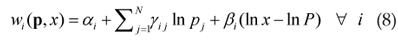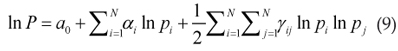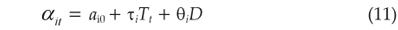Resumos
Especificações alternativas do sistema de demanda quase ideal (AIDS) foram utilizadas para estimar as demandas agregadas das carnes bovina, suína e de frango e outros bens de consumo e as suas elasticidades no Brasil. Detectada a necessidade de se utilizar a variável tendência nas equações dos modelos, observou-se uma tendência de crescimento da demanda por carnes e de decrescimento da demanda por outros bens de consumo. A variável dummy para o Plano Real indicou que o mesmo não afetou as demandas. Com base nas elasticidades próprios-preços Marshallianas, as demandas por carnes são inelásticas e a demanda por outros bens de consumo é elástica. As elasticidades preços-cruzados Marshallianas e Hicksianas confirmaram que as carnes bovina, suína e de frango são bens substitutos. As elasticidades-gasto indicaram que todos os bens são normais, exceto a carne suína que é um bem inferior. Como é provável que o gasto com o consumo das famílias aumente ao longo do tempo, ceteris paribus, as elasticidades gasto indicam que a demanda por carnes perderá importância para os outros bens de consumo, que o consumo de carne bovina perderá importância para a carne de frango e que o consumo de carne de porco perderá importância para as outras carnes.
demanda por carnes; sistema de demanda quase ideal; elasticidade; Brasil
We use alternative specifications of the Almost Ideal Demand System (AIDS) to estimate the aggregate demand in Brazil for beef, pork, chicken, other consumption goods, and their elasticities. We detect the need for using time trend variables in models' equations so that we found an upward trend for the demand of each type of meat and a downward trend for other consumption goods. The dummy variable for the prices stabilization macroeconomic Real Plan indicated it has not changed demands. According to Marshallian own-price elasticities, meat demands are inelastic and demand for other consumption goods is elastic. Cross-price Marshallian and Hicksian elasticities confirm beef, pork and chicken are substitutes. Expenditure elasticities show that all goods are normal, except for pork, which is an inferior good. As personal consumption expenditure is likely to increase over time, ceteris paribus, meat consumption will lose importance to other consumption goods, beef consumption will lose importance to chicken and pork consumption will lose importance to the other two types of meat.
meat demand; almost ideal demand system; elasticity; Brazil
Sistemas de equações de demanda por carnes no Brasil: especificação e estimação1 1 Os autores agradecem o financiamento do CNPq e Fapemig.
Moisés de Andrade Resende FilhoI; Valéria Gama Fully BressanII; Marcelo José BragaIII; Aureliano Angel BressanIV
IProfessor do Departamento de Economia da UnB. E-mail: moisesresende@unb.br
IIProfessor do Departamento de Contabilidade da UFMG. E-mail: vfully@face.ufmg.br
IIIProfessor do Departamento de Economia rural da UFV. E-mail: mjbraga@ufv.br
IVProfessor do Departamento de Administração da UFMG. E-mail: bressan@face.ufmg.br
RESUMO
Especificações alternativas do sistema de demanda quase ideal (AIDS) foram utilizadas para estimar as demandas agregadas das carnes bovina, suína e de frango e outros bens de consumo e as suas elasticidades no Brasil. Detectada a necessidade de se utilizar a variável tendência nas equações dos modelos, observou-se uma tendência de crescimento da demanda por carnes e de decrescimento da demanda por outros bens de consumo. A variável dummy para o Plano Real indicou que o mesmo não afetou as demandas. Com base nas elasticidades próprios-preços Marshallianas, as demandas por carnes são inelásticas e a demanda por outros bens de consumo é elástica. As elasticidades preços-cruzados Marshallianas e Hicksianas confirmaram que as carnes bovina, suína e de frango são bens substitutos. As elasticidades-gasto indicaram que todos os bens são normais, exceto a carne suína que é um bem inferior. Como é provável que o gasto com o consumo das famílias aumente ao longo do tempo, ceteris paribus, as elasticidades gasto indicam que a demanda por carnes perderá importância para os outros bens de consumo, que o consumo de carne bovina perderá importância para a carne de frango e que o consumo de carne de porco perderá importância para as outras carnes.
Palavras-chaves: demanda por carnes, sistema de demanda quase ideal, elasticidade, Brasil.
ABSTRACT
We use alternative specifications of the Almost Ideal Demand System (AIDS) to estimate the aggregate demand in Brazil for beef, pork, chicken, other consumption goods, and their elasticities. We detect the need for using time trend variables in models' equations so that we found an upward trend for the demand of each type of meat and a downward trend for other consumption goods. The dummy variable for the prices stabilization macroeconomic Real Plan indicated it has not changed demands. According to Marshallian own-price elasticities, meat demands are inelastic and demand for other consumption goods is elastic. Cross-price Marshallian and Hicksian elasticities confirm beef, pork and chicken are substitutes. Expenditure elasticities show that all goods are normal, except for pork, which is an inferior good. As personal consumption expenditure is likely to increase over time, ceteris paribus, meat consumption will lose importance to other consumption goods, beef consumption will lose importance to chicken and pork consumption will lose importance to the other two types of meat.
Key-words: meat demand, almost ideal demand system, elasticity, Brazil.
Classificação JEL: C22, Q11, Q13, Q18.
1. Introdução
Em 2007, o Brasil foi responsável por 14,9% da produção de carne bovina, 11,8% da de frango e 3% da produção de carne suína, segundo dados da FAO (2009). Quanto às exportações, naquele mesmo ano, o Brasil foi responsável por 17,4% (com receita de US$ 3,5 bilhões) dos embarques de carne de boi, 30,5% (receita de US$ 4,2 bilhões) da de frango e por 7,8% (ou US$ 1 bilhão em receita) dos envios de carne suína, também segundo dados da FAO (2009). De 1975 a 2008, em média 88%, 86% e 79% da produção total brasileira de carne bovina, de frango e suína foi consumida internamente, fazendo com que o Brasil figurasse como o segundo, terceiro e quarto maior consumidor mundial, respectivamente, dessas carnes (USDA/FAS, 2009). Tais números não só colocam o Brasil como um líder mundial no mercado internacional de carnes como também demonstram que o seu mercado interno, objeto de análise do presente estudo, é extremamente importante.
Estimativas confiáveis da sensibilidade da demanda com respeito a preços, renda e demais fatores são fundamentais para a tomada de decisão nos setores público e privado. Por exemplo, o setor produtor de carnes pode utilizar as elasticidades-renda para antecipar a expansão no consumo de carnes em um cenário de tendência de aumento da renda da população brasileira, ceteris paribus. Ainda, por exemplo, suponha que o setor público estivesse interessado em estimular a substituição da carne vermelha por carne branca via adoção de políticas de taxação ou de subsídio. Se for conhecido que a elasticidade-renda da carne branca é superior à da carne vermelha, em um cenário de aumento da renda da população, ceteris paribus, haverá naturalmente tal substituição sem a necessidade de se adotar qualquer tipo de política (GALLET, 2010).
Apesar da importância do mercado interno brasileiro, existem poucos estudos econométricos sobre a demanda agregada por carnes no Brasil nos últimos vinte anos. Como apresentado a seguir, esses trabalhos podem ser agrupados em dois: os que utilizaram dados agregados de séries temporais e os que utilizaram microdados de seção cruzada (cross-section).
Dentre os trabalhos que utilizam séries temporais, Fernandes et al. (1989) utilizam um modelo Rotterdam de demanda e dados anuais do período entre 1966 e 1975 para estimar a demanda agregada das carnes bovina, de frango e suína. Apesar de o modelo Rotterdam permitir a conexão com a teoria do consumidor, tal estudo utiliza uma série antiga e curta de dados. Bacchi e Barros (1992) estimaram um modelo de ajustamento parcial para a carne bovina com dados anuais de 1957 a 1987 de modo a obterem elasticidades de longo e curto prazo para a demanda por carne bovina no Brasil. Para tanto, estimaram um modelo uniequacional, mas sem explicitamente considerar a teoria do consumidor em sua especificação. Santana (1999) usa uma especificação duplo-logarítmica para estimar um sistema de equações de demanda para as carnes bovina, de frango e suína, utilizando, para tanto, dados anuais de 1990 a 1997. Com isso, toma um período muito curto de tempo (apenas oito observações) e, ainda, não se baseia na teoria do consumidor para especificar o seu modelo.
O segundo grupo de trabalhos relacionado à demanda por carnes no Brasil tem utilizado microdados da POF (Pesquisa de Orçamentos Familiares) conduzida pelo IBGE (Instituto Brasileiro de Geografia e Estatística). Por exemplo, Carvalho (2007) utiliza dados da POF/IBGE para os anos 1987/88, 1995/96 e 2002/03 para estimar um modelo estatístico poligonal com três segmentos, de modo a obter as elasticidades-renda das carnes bovina, de frango e suína no Brasil e nas principais regiões metropolitanas do País. Para tanto, utiliza modelos uniequacionais para estimar curvas de Engel, mas sem se basear na teoria do consumidor para especificá-los. Mais recentemente, Pintos-Payeras (2009) estimou um sistema não linear de demanda quase ideal (AIDS) para grupo de produtos, utilizando a POF/IBGE de 2002/2003. Apesar de a especificação AIDS ser baseada na teoria do consumidor, o referido trabalho não focou especificamente a demanda por carnes, mas 27 grupos de produtos, entre eles os grupos carne de boi de primeira e de segunda, todos os produtos e subprodutos da carne de frango e outras carnes. Apesar de também não focarem especificamente a demanda por carnes, Coelho et al. (2009) utilizaram a POF/IBGE de 2002/2003 para estimar um sistema de demanda para 18 grupos de alimentos, dentre eles os grupos carne de boi de primeira e de segunda, carne de frango e carne suína. Coelho et al. (2009) adotam a especificação do sistema de demanda quadrático quase ideal (QUAIDS), mas utilizando no lugar do índice de preços Translog, o índice de preços de Stone, o mesmo empregado no modelo AIDS linear. Além disso, tratam o problema de consumo zero com a utilização do procedimento em dois estágios de Shonkwiler & Yen.
Os estudos de Pintos-Payeras (2009) e Coelho et al. (2009) apresentam estimativas recentes das elasticidades próprios-preços, elasticidade cruzada e elasticidade-renda para carnes e, por utilizarem microdados, eliminam a possibilidade de viés de agregação2 2 O viés de agregação decorre do fato de as estimativas dos parâmetros dos modelos serem sensíveis ao procedimento utilizado na agregação dos dados. , o que é provável de ocorrer em estudos que utilizam dados agregados de séries temporais (BLUNDELL et al., 1993; DENTON e MOUNTAIN, 2001). Contudo, ao utilizarem dados da POF apenas para o ano 2000/2003, eliminaram a possibilidade de se detectar, por exemplo, o efeito do Plano Real ou de tendência nas demandas causadas por variáveis outras além do preço e renda e que se alteram ao longo do tempo.
Existe uma vasta e crescente literatura internacional devotada à estimação de sistemas de equações de demanda por carnes utilizando dados agregados de séries de tempo3 3 Para um amplo e sistemático levantamento da literatura mundial, vide os trabalhos de meta-análise sobre as elasticidades-preços da demanda por carnes de Gallet (2009) e sobre a elasticidade-renda da demanda de Gallet (2010). sem representantes recentes na literatura nacional. Vide, por exemplo, os trabalhos de Moschini e Meilke (1989), Brester e Schroeder (1995), Piggott et al. (1996), Marsh et al. (2004) e Piggott e Marsh (2004). Assim, há uma lacuna na literatura nacional a ser preenchida.
O presente artigo possui quatro objetivos principais, quais sejam: especificar sistemas de equações de demanda por carne no Brasil com base na teoria do consumidor, estimando-os com o uso de séries de tempo; obter estimativas atualizadas das elasticidades-gasto, próprios-preços e preços-cruzados Marshallianas e Hicksianas para as carnes bovina, suína e de frango; investigar se outros fatores além de preços e renda afetam a demanda agregada por carnes; e investigar se o Plano Real impactou a demanda agregada por carnes. Para tanto, o presente artigo especifica um sistema de equações de demanda por carnes no Brasil, considerando quatro bens segundo o procedimento pioneiro de Brester e Schroeder (1995). Segundo este procedimento, as demandas por carne bovina, de frango e suína são estimadas junto a um bem composto rotulado como "outros bens de consumo da economia". Finalmente, o presente artigo utiliza o procedimento proposto por Berndt e Savin (1975) para testar e corrigir para autocorrelação ou correlação serial dos erros.
O artigo está organizado da seguinte maneira. Além desta seção introdutória, a segunda seção descreve o modelo teórico e os modelos econométricos de demanda por carnes. A terceira seção descreve os dados e os procedimentos utilizados para obtenção das séries gasto e preços para a variável outros bens de consumo. A quarta seção apresenta os resultados dos testes e estimações dos modelos, as estimativas das elasticidades e analisa os resultados. A seção final faz o sumário dos principais resultados obtidos ao longo do artigo e discute algumas implicações dos mesmos para a formulação de ações privadas e de políticas públicas.
2. Modelo de demanda por carnes no Brasil
Nessa seção, primeiro faz-se uma breve apresentação do problema de agregação da demanda dos consumidores para, em seguida, apresentar o desenvolvimento do sistema de demanda quase ideal que permite a exata agregação através dos consumidores e servirá de base para a formulação dos modelos econométricos.
Considera-se uma economia estática4 4 Ou seja, em que não se considera explicitamente o tempo. constituída por H consumidores com relações de preferências contínuas, racionais5 5 Preferências racionais respeitam duas propriedades: completeza e transitividade (MAS-COLELL et al., 1995, p. 42). , localmente não saciadas e, possivelmente, diferentes sobre os N bens dessa economia. Nessa economia, o h-ésimo consumidor possui renda xh e escolhe o quanto consumir de cada bem, resolvendo o problema de maximização de suas preferências, sujeito à observância de sua restrição orçamentária. A solução desse problema é plenamente caracterizada por um vetor N dimensional qh(p, xh) de funções de demandas Marshallianas para cada bem, qih(p, xh) com i = 1, ..., N.
Agregando-se as demandas dos H consumidores, obtém-se o vetor de demandas agregadas da economia como definido em (1).
em que p é um vetor com N números reais estritamente positivos dos preços dos bens da economia.
Pela definição em (1) fica explícito que a demanda agregada por cada bem depende dos preços de todos os bens da economia que são admitidamente os mesmos para cada consumidor e, adicionalmente, da distribuição de renda (x1, ..., xH) da economia.
Mas-Colell et al. (1995, p. 107, proposição 4.B.1.) fornecem as condições necessárias e suficientes para que a demanda agregada dependa tão somente da renda agregada ou, equivalentemente, da renda per capita da economia. Uma vez atendidas tais condições, pode-se estudar as demandas agregadas dos bens como se tivessem sido geradas pelo problema de maximização de um consumidor representativo que maximiza as suas preferências, condicionado a gastar até toda a renda da economia. Essas condições se resumem a que a função de utilidade indireta de cada consumidor, Ψh(p, xh), seja da forma de Gorman:
em que dh(.) é uma função dos preços e que pode variar de consumidor para consumidor; e e(.) é uma função dos preços e que é a mesma para cada consumidor.
Preferências representáveis por funções de utilidade indireta na forma de Gorman (2) exigem curvas de Engel lineares e paralelas e, portanto, são extremamente restritivas. Por exemplo, para que cada consumidor apresentasse preferências representáveis por funções de utilidade indireta na forma de Gorman (2), todos os consumidores deveriam ser idênticos em suas preferências, as quais, adicionalmente, devem ser homotéticas. Outra possibilidade seria a de que os consumidores fossem heterogêneos em suas preferências, desde que as mesmas fossem todas quase-lineares no mesmo bem (MAS-COLELL et al., 1995, p. 108).
Deaton e Muellbauer (1980a) utilizaram condições desenvolvidas por Muellbauer (1975 e 1976) para garantir a existência de um consumidor representativo, as quais são menos restritivas do que se assumir que cada consumidor possua preferências representáveis por funções de utilidade indireta na forma de Gorman (2). Para tanto, a estratégia adotada por Deaton e Muellbauer (1980a), grosso modo, foi a de não partir da imposição de que as demandas agregadas dos bens dependessem unicamente da renda agregada da economia ou da renda per capita, o que abre espaço para que as mesmas dependam de outros parâmetros da distribuição de renda da economia. Com base nisso, Deaton e Muellbauer (1980a) desenvolveram o sistema de demanda quase ideal (Almost Ideal Demand System AIDS) que possibilita a perfeita agregação das demandas dos consumidores. Assim, possibilita transmitir os resultados obtidos com a teoria do consumidor individual para o consumidor representativo da economia sem exigir que os consumidores se comportem tal que as suas curvas de Engel sejam paralelamente lineares. Os cinco passos apresentados a seguir resumem o procedimento adotado por Deaton e Muellbauer (1980a) para desenvolver o sistema AIDS de demanda. Basicamente, o procedimento consiste em se partir de uma função custo/dispêndio e utilizar os resultados da dualidade da teoria do consumidor para se chegar até a formulação das funções de demanda Marshallianas em forma de parcelas do gasto do consumidor.
Primeiro, admite-se que cada consumidor possua preferências racionais que pertencem à classe PIGLOG6 6 Para fins de agregação das demandas dos consumidores, Deaton e Muellbauer (1980a) admitem que a parcela média do gasto para cada bem na economia depende, tão somente, dos preços e do mesmo escalar x 0, que é uma medida de posição da distribuição de renda da economia. Na classe de preferências PIGLOG, x 0 é independente dos preços da economia, dependendo unicamente da distribuição de renda da economia. (Price Independent Generalized Logarithmic) de preferências que são representadas pela função custo7 7 A função custo c( p, u) define, sob os preços dos bens, p, o mínimo gasto necessário para que o consumidor assegure para si o nível de utilidade u. logarítmico (3).
em que u é o valor da utilidade8 8 Em geral, 0 < u < 1, o que permite interpretar a( p) como o custo mínimo necessário a subsistência (quando u = 0) e b( p) como o custo mínimo para o bem-estar pleno (quando u = 1). Vide os casos de exceções à condição 0 < u < 1 no Apêndice de Deaton e Muellbauer (1980a). do consumidor representativo e p é um vetor de preços constituído por N números reais positivos.
O segundo passo consiste em se especificar a função ln a(p) como uma função Translog (4) e a função ln b(p) como a soma de (4) com uma função Cobb-Douglas, como na equação (5). Fazendo isso, garante-se que a função custo (3) será localmente flexível9 9 Uma função custo localmente flexível deve possuir um número de parâmetros o suficiente para permitir que, em qualquer ponto, o seu gradiente e a sua matriz Hessiana possam representar qualquer função custo (DEATON e MUELLBAUER, 1980b). .
Por simples aplicação do lema de Shephard10 10 Pelo lema de Shephard (Mas-Colell et al., 1995: p.68), a derivada parcial da função custo com respeito ao preço do i-ésimo bem gera a função demanda Hicksiana desse bem, ou seja, ∂ c( p, u)/∂ pi = qi( p, u). Multiplicando-se essa igualdade dos dois lados por pi/ c( p, u) e observando-se que a parcela do gasto com o i-ésimo bem é definida por wi = piqi( p, u)/ c( p, u), obtém-se o resultado desejado: wi = ∂ln c( p, u)/∂ln pi . é possível verificar que a parcela compensada do gasto com o i-ésimo bem, wi, pode ser obtida via: wi = ∂ln c(p, u)/∂ln pi . Sendo assim, como terceiro passo aplica-se esse fato à equação (3), o que gera as equações (6) das parcelas compensadas ou Hicksinanas do gasto:
em que wi = piqi(p, u)/c(p, u) e  .
.
Para um consumidor com preferências contínuas e localmente não saciadas, como é o caso, a equivalência entre o problema de maximização da utilidade e o problema de minimização do gasto garante que c(p, Ψ(p, x)) = x (MAS-COLELL et al., 1995, proposição 3.E.1. (i): p. 58), onde x denota o dispêndio ou gasto total do consumidor e Ψ(p, x) é a função utilidade indireta. Aplicando-se o operador logaritmo natural dos dois lados dessa igualdade, segue que ln c(p, Ψ(p, x)) = ln x. Com base nisso, o quarto passo consiste em substituir ln c(p, u) por ln x e u por Ψ(p, x) na função custo (3), para em seguida inverter o resultado, obtendo-se a função utilidade indireta (7).
Como último passo, substitui-se u nas equações (6) por Ψ(p, x) dado pela equação (7). Dessa forma, obtêm-se, finalmente, as equações das parcelas do gasto Marshallianas ou não compensadas do sistema AIDS.
em que P é um índice de preços Translog definido pela equação (9).
em que pj é o preço do j-ésimo bem; e x é o gasto11 11 Nota-se que o gasto se iguala necessariamente à renda do consumidor se o mesmo possui preferências localmente não saciadas. com os N bens.
2.1. Modelo econométrico
Adicionando-se o termo de erro aleatório a cada equação em (8), obtém-se a i-ésima equação do sistema AIDS a ser estimado:
em que qité quantidade de consumo per capita; pité o preço e wit = pitqit/xit é a parcela do gasto com o i-ésimo bem no tempo t;  é o gasto per capita com os N bens no tempo t; e vit denota o termos de erro aleatório da i-ésima equação.
é o gasto per capita com os N bens no tempo t; e vit denota o termos de erro aleatório da i-ésima equação.
Schroeder et al. (2000) sugerem que a pesquisa recente sobre a demanda por carnes nos EUA indica, conclusivamente, que outros fatores em adição a preços e ao gasto devem ser incorporados como variáveis explicativas aos modelos. Assim, esses mesmos autores sugerem que sejam incluídas variáveis explicativas mensurando o nível de informação sobre aspectos de saúde relacionados com a alimentação, a conveniência dos produtos, a segurança e qualidade do alimento, o grau de promoção/propaganda dos produtos e as mudanças demográficas dos consumidores. Diante da indisponibilidade imediata de variáveis como essas no Brasil e objetivando minimizar os problemas decorrentes da omissão de dinâmica nos modelos e da não consideração de não estacionaridades determinísticas nas séries, seguimos o que fizeram Piggott et al. (1996) e Fisher et al. (2001), incluindo deslocadores da demanda via modificações dos interceptos das equações (10), como definido em (11).
em que αit é o intercepto das equações (10) no tempo t; Tt é a variável tendência com valor um para o ano 1975; e D é uma variável dummy com valor zero nos anos de 1995 a 1993 e um nos anos de 1994 em diante, considerado como o período pós Plano Real12 12 O Plano Real é o plano macroeconômico para a estabilização de preços no Brasil que começou a partir de julho de 1994. .
Nota-se que a inclusão da variável tendência nas equações dos modelos permite capturar mudanças estruturais na demanda, mas ao custo de não se ter como identificar os fatores que possam tê-las causado (SCHROEDER et al., 2000).
Propriedades obtidas com a teoria do consumidor foram diretamente impostas aos modelos, como segue. O fato de que toda a renda do consumidor é gasta ou propriedade adding up da demanda exige que a soma das parcelas do gasto seja igual a um, o que é assegurado pela imposição das condições (12); a propriedade de ausência de ilusão monetária ou homogeneidade de grau zero da demanda nos preços e renda é assegurada pelas condições (13); e a simetria da matriz de substituição de Slutsky13 13 Nota-se que, pela teoria do consumidor, a matriz de substituição de Slutsky deve ser também negativa semidefinida. Apesar disso, o sistema AIDS não possibilita a imposição direta das restrições que garantiriam tal propriedade durante o processo de estimação do modelo. Na verdade, a não negatividade da matriz de Slutsky pode ser investigada apenas após a estimação e para cada ponto. Por isso mesmo, o sistema foi rotulado por Deaton e Muellbauer (1980a) como "quase" ideal. é garantida pelas condições (14).
O sistema de equações de demanda foi especificado para um conjunto de quatro bens: carne bovina, carne suína, carne de frango e todos os outros bens de consumo (vide Marsh et al., 2004) para uma aplicação pioneira desse procedimento no contexto de um sistema de equações de demanda Rotterdam para carnes nos EUA).
Caso fosse estimado, como usualmente se faz, um sistema de equações de demanda por carne com apenas três bens (carne bovina, carne suína e de frango), as condições (12) fariam com que potenciais mudanças estruturais para as demandas pelas carnes bovina, suína e de frango necessariamente se anulassem. Por outro lado, a estimação de um sistema de equações com quatro bens possibilita, por exemplo, que a demanda por cada carne apresente mudança estrutural positiva ou negativa. Além disso, tal formulação elimina a possibilidade de haver endogeneidade da variável gasto, o que provável ocorre para um sistema de equações estimado com os três tipos de carnes, uma vez que a variável gasto é o próprio gasto per capita com tais carnes. No sistema de demanda com quatro bens, a variável gasto per capita com consumo é, muito provavelmente, exógena (BRESTER e SCHROEDER, 1995). Finalmente, um sistema com quatro bens permite investigar a possibilidade de substituição entre os tipos de carnes e outros bens de consumo.
2.2. Corrigindo autocorrelação dos erros
Os passos a seguir visam apresentar o procedimento de Berndt e Savin (1975) que foi empregado no presente artigo para testar e, sendo necessário, corrigir a autocorrelação de primeira ordem dos erros dos modelos.
Primeiro, considera-se o vetor de dimensão N × 1 formado pelos erros aleatórios no sistema de demanda (8) definido como: vt = Rvt-1 + τt para t = 2,...,T, onde vt é o vetor N × 1 de erros aleatórios do sistema de equações; a sequência ε2,..., εT consiste de vetores de variáveis aleatórias de dimensão N × 1 com vetor zero de médias e matriz de covariância Σ, independentemente, normalmente e identicamente distribuídos; e R denota uma matriz de autocorrelação com N × N parâmetros desconhecidos.
Berndt e Savin (1975) mostram que, no contexto de um modelo com erros autoregressivos de primeira ordem, a propriedade adding up fará com que a soma dos elementos de cada coluna da matriz R se iguale a uma constante k desconhecida (ou seja, 1'R = k') e a matriz de covariância Σ seja singular, o que exige a eliminação de uma das equações do sistema para que o sistema pudesse ser estimado.
Em seguida, os autores demonstram que as restrições 1'R = k', em que 1 é um vetor N × 1 de uns e k é um vetor N × 1 de elementos com valores iguais a constante k, podem ser transformadas em restrições mais facilmente tratáveis da forma 1' = 0, onde
= 0, onde 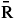 é uma matriz de dimensão N × (N-1) formada pelos elementos Rij - Rin, em que i = 1, ..., N, j = 1,..., n-1; n indexa a última equação do sistema que corresponde à equação eliminada do sistema para contornar o problema de singularidade de Σ; e Rijsão elementos da matriz R. Em seguida, Berndt e Savin (1975) definem
é uma matriz de dimensão N × (N-1) formada pelos elementos Rij - Rin, em que i = 1, ..., N, j = 1,..., n-1; n indexa a última equação do sistema que corresponde à equação eliminada do sistema para contornar o problema de singularidade de Σ; e Rijsão elementos da matriz R. Em seguida, Berndt e Savin (1975) definem 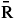 n como a matriz formada pelas primeiras N-1 linhas de
n como a matriz formada pelas primeiras N-1 linhas de 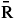 , sendo, portanto, de dimensão (N-1)×(N-1). Como serão os primeiros N-1 elementos de
, sendo, portanto, de dimensão (N-1)×(N-1). Como serão os primeiros N-1 elementos de 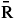 n que serão estimados, e não os elementos de
n que serão estimados, e não os elementos de 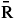 ou R, qualquer restrição sobre
ou R, qualquer restrição sobre 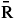 ou R pode ser facilmente imposta a
ou R pode ser facilmente imposta a 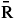 n após a estimação do sistema de equações (PIGGOTT et al., 1996). Dessa forma, a estimação por máxima verossimilhança do sistema constituído pelas N-1 equações será invariante à equação que foi eliminada do sistema original, como desejado.
n após a estimação do sistema de equações (PIGGOTT et al., 1996). Dessa forma, a estimação por máxima verossimilhança do sistema constituído pelas N-1 equações será invariante à equação que foi eliminada do sistema original, como desejado.
Seguindo o que fizeram Piggott et al. (1996), correções para autocorrelação de primeira ordem nos erros foram incorporadas modificando-se o sistema AIDS (10) para:
em que Wt é uma matriz (N-1)×1 de parcelas do gasto observadas para os N-1 bens incluídos no sistema a ser estimado; e Wt(pt, xt) é uma matriz (N-1)×1 de equações de parcelas do gasto do sistema AIDS definidas segundo as equações (10).
No presente estudo, os modelos foram estimados com base em (15), utilizando, para tanto: uma matriz nula
n denominada N-Rmatriz com todos os seus elementos iguais a zero14 14 Nesse caso, não há correção para autocorrelação de primeira ordem. ; uma matriz diagonal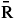 n denominada D-Rmatriz com elementos de mesmo valor compondo a sua diagonal principal e zeros como elementos fora de sua diagonal principal; e uma matriz completa
n denominada D-Rmatriz com elementos de mesmo valor compondo a sua diagonal principal e zeros como elementos fora de sua diagonal principal; e uma matriz completa  n denominada F-Rmatriz composta por elementos que podem assumir qualquer valor real. Cada uma dessas matrizes é de dimensão (N-1)×(N-1).
n denominada F-Rmatriz composta por elementos que podem assumir qualquer valor real. Cada uma dessas matrizes é de dimensão (N-1)×(N-1).
3. Dados
Os modelos foram estimados com dados anuais do período de 1975 a 2008. O conjunto de dados se concentrou nesse intervalo de tempo, pois era importante utilizar séries de tempo longas o suficiente para propiciar a investigação do efeito do Plano Real sobre a demanda por carnes no Brasil e, ainda, garantir a obtenção de modelos estatisticamente significantes. No entanto, caso o objetivo do presente trabalho fosse o de investigar mudanças estruturais das demandas, haveria, possivelmente, a necessidade de se utilizar séries de tempo mais longas.
As séries das quantidades consumidas das carnes bovina, suína e de frango foram obtidas do USDA/FAS (2009) e correspondem ao consumo aparente per capita ao nível de varejo, calculado para cada ano segundo a identidade: consumo aparente da i-ésima carne ≡ produção da carne i + estoque inicial da carne i + quantidade importada da carne i estoque final da carne i exportações da carne i. Em seguida, o consumo aparente por carne foi dividido pela população residente no Brasil em 1° de julho de cada ano do IBGE e obtida no Ipeadata (2009), de modo a gerar as séries de consumo aparente per capita para cada tipo de carne considerado em nossa análise. A Figura 1 apresenta as séries de consumo aparente per capita das carnes bovina, suína e de frango de 1975 a 2008 no Brasil.
Pela Figura 1 se observa que as séries de consumo aparente per capita de cada tipo de carne apresentam tendências diferentes, mas crescentes, e se percebe que o consumo de carne de frango ultrapassa o consumo de carne suína a partir de 1979. Além disso, observa-se que o consumo aparente de carne de frango, que era de 4,51 kg/pessoa em 1975, portanto, quatro vezes ou mais inferior ao consumo aparente de carne bovina (19,71 kg/pessoa), ultrapassa o consumo aparente de carne bovina a partir de 2007. Fenômeno similar ocorre nos EUA por volta de 1991 (SCHROEDER et al., 2000).
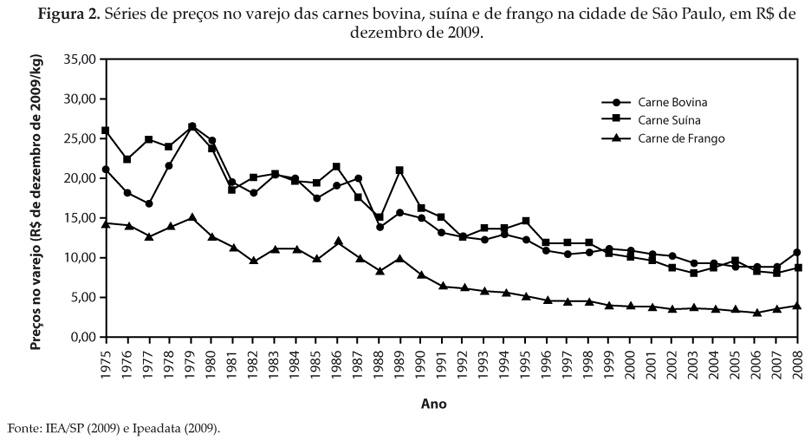
As séries dos preços das carnes bovina, suína e de frango correspondem aos preços no varejo da cidade de São Paulo em R$ por kg, obtidos no IEA/SP (Instituto de Economia Aplicada de São Paulo) (2009). Até onde sabemos, não existem séries de preços de carnes no varejo no Brasil, o que justifica a utilização das séries na cidade de São Paulo, que é seguramente o maior centro consumidor brasileiro. Utilizou-se a série do IGP-DI (Índice Geral de Preços Disponibilidade Interna) da Fundação Getúlio Vargas, disponível no Ipeadata (2009), para deflacionar cada série de preços, tal que todos estivessem em valores constantes de R$ de dezembro de 2009. A Figura 2 apresenta as séries anuais de preços no varejo das carnes bovina, suína e de frango, mensuradas em R$ de dezembro de 2009.
Pela Figura 2 é possível observar a tendência declinante dos preços de cada tipo de carne e a aparente redução da volatilidade dos preços após 1994, ano em que o Plano Real se inicia.
Seguindo o que propuseram Brester e Schroeder (1995), gerou-se a série de preços para a variável outros bens de consumo, com base na série anual do IGP-DI da seguinte maneira: primeiro, gerou-se a série do gasto com todos os outros bens de consumo, exceto carnes, subtraindo-se, para tanto, o gasto per capita com carnes do gasto per capita com consumo que foi gerado a partir da série de consumo das famílias disponibilizada pelo Ipeadata (2009). Segundo, tendo-se as séries das parcelas do gasto referentes ao gasto com carne bovina, suína, de frango e com os outros bens de consumo, gerou-se a série de preços deflacionados dos outros bens de consumo (série p4), resolvendo a igualdade IGP-dit =  para p4t, em que pit e wit são o preço e a parcela do gasto do i-ésimo bem no tempo t.
para p4t, em que pit e wit são o preço e a parcela do gasto do i-ésimo bem no tempo t.
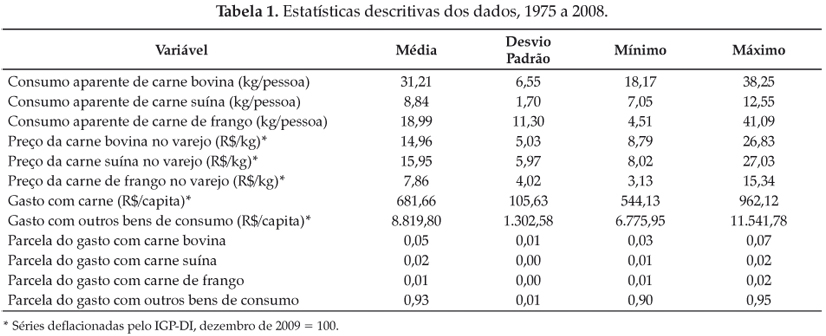
As estatísticas descritivas das séries utilizadas nas estimações dos modelos são apresentadas na Tabela 1.
4. Procedimentos econométricos, resultados e discussão
Nessa seção serão seguidos os seguintes passos: primeiramente, serão descritos os procedimentos utilizados na estimação dos modelos formulados segundo as equações (10), (11) e (15). O segundo passo consistirá em apresentar os testes de raiz unitária dos resíduos dos modelos. Caso se conclua que os resíduos são estacionários, admite-se que as variáveis nos modelos podem ser cointegradas, o que justifica a realização dos passos subsequentes. O terceiro passo consiste na apresentação dos resultados das estimações dos três modelos especificados segundo as equações (10), (11) e (15). No quarto passo, são apresentados os testes de especificação de razão de verossimilhança empregados para selecionar, entre as especificações utilizadas, a preferida. O quinto passo consiste em apresentar e discutir as elasticidades da demanda por carnes obtidas a partir do modelo preferido.
Como a soma das parcelas do gasto (wit) somam sempre um, uma das quatro equações do sistema deve ser retirada de modo a evitar o problema de singularidade da matriz de covariância, o que inviabiliza a estimação (BERNDT e SAVIN, 1975). Assim, a equação da parcela do gasto com outros bens de consumo foi retirada do sistema. Os parâmetros dessa equação podem ser estimados, após a estimação do modelo, utilizando-se as restrições em (12), (13) e (14).
Os modelos (15) foram estimados utilizando-se o método Full Information Maximum Likelihood (FIML) e o método iterativo não linear de regressão aparentemente não relacionada (ITSUR) que são equivalentes no caso de sistemas de equações com erros aparentemente não relacionados (SUR) e normalmente distribuídos (GREENE, 2003, p. 357; BARNET, 1976). Ainda, estimadores FIML são assintoticamente eficientes para modelos simultâneos não lineares, como é o caso, sob a hipótese de que os erros contemporâneos são conjuntamente e normalmente distribuídos (QUANTITATIVE MICRO SOFTWARE, 2010).
Em um recente levantamento sobre o estado da arte na modelagem da demanda do consumidor, Barnet e Serletis (2008) detectaram que ainda faltam trabalhos tratando das modificações necessárias aos métodos de cointegração para modelos lineares de modo a viabilizar a aplicação desses métodos na estimação de sistemas de equações de demanda não lineares. Por conta disso, problemas com a não estacionaridade das séries de tempo (quantidades, preços e gasto) no contexto de estimação de sistemas de equações não lineares têm sido usualmente ignorados ou tratados com a utilização de métodos de cointegração originalmente desenvolvidos para sistemas lineares (BARNET e SERLETIS, 2008).
Métodos que lidam com a não estacionaridade das séries em modelos lineares não podem ser diretamente utilizados em modelos de demanda não lineares (LEWBEL e NG, 2005) como, por exemplo, o sistema AIDS. Com base nisso, ignorou-se o problema de cointegração no presente artigo, admitindo-se que inferências baseadas nos resíduos podem ser confiáveis se os mesmos são estacionários. Nesse sentido, foi adotado o mesmo procedimento de Fisher et al. (2001) e, antes de se efetuar a comparação dos modelos estimados, foram executados testes de raiz unitária dos resíduos dos modelos (15). Tal procedimento está em linha com o método em dois estágios de Engle e Granger (1987), segundo o qual, para que variáveis em modelos lineares possam estar cointegradas é necessário que o resíduo da regressão entre elas seja estacionário.
A Tabela 2 apresenta, baseando-se nos valores críticos obtidos por MacKinnon (1996), os p-valores do teste Dickey-Fuller (ADF) aumentado (DICKEY e FULLER, 1981) e do teste não paramétrico Z(ta) de Phillips (1987) e Phillips e Perron (1988).
Baseando-se nos p-valores apresentados na Tabela 2, conclui-se que a hipótese de existência de raiz unitária nas séries de resíduos é rejeitada em cada modelo estimado ao nível, por exemplo, de 1% de probabilidade. Assim, como os resíduos das equações dos modelos são estacionários, conclui-se que as variáveis nos modelos podem ser cointegradas (FISHER et al., 2001), o que justifica a estimação desses modelos.
Na Tabela 3 são apresentadas as estimativas dos parâmetros, os erros padrão e as medidas da qualidade do ajuste e estatísticas Durbin-Watson dos três modelos de demanda especificados segundo as equações (10), (11) e (15).
Como os resultados apresentados na Tabela 3 demonstram, a maioria das estimativas dos parâmetros para as três especificações dos modelos é estatística e individualmente significante. Por exemplo, todos os parâmetros β são estatística e individualmente significantes para as três especificações. Assim, as estimativas dos betas indicam que as carnes bovina, suína e de frango são bens necessários, uma vez que apresentam β negativos. Já "outros bens de consumo" é um bem de luxo, pois, pela condição (12) segundo a qual a soma dos betas deve ser zero, o seu coeficiente β é positivo (vide detalhes em DEATON e MUELLBAUER, 1980, p. 77).
Observa-se, pela Tabela 3, que os coeficientes da variável tendência (τs) em cada equação dos modelos são estatisticamente, individualmente ou conjuntamente (vide a última coluna da Tabela 4) significantes. Tais resultados confirmam a necessidade de se incorporar a variável tendência nas equações dos modelos de modo a capturar mudanças estruturais causadas por outras variáveis além dos preços e gasto/renda. Contudo, os pequenos valores das estimativas dos seus coeficientes indicam que as demandas por carnes e outros bens de consumo não se alteram muito ao longo do tempo devido a essas outras variáveis. Por exemplo, as estimativas para τb, τp e τc no modelo com F-Rmatriz indicam que, ao longo do tempo, as parcelas do gasto com as carnes bovina, suína e de frango devem crescer 0,0000094 (ou 0,00094%), 0,00038 (ou 0,038%) e 0,00013 (ou 0,013%) ao ano, enquanto que, pela condição adding up em (12), a parcela do gasto com os outros bens de consumo deve decrescer 0,0005194 (ou 0,05194%) ao ano.
A Tabela 3 mostra ainda que a variável dummy para o Plano Real (θ) não é estatística e individualmente significante em nenhuma das equações dos modelos, o que leva à conclusão de que o Plano Real não afetou a demanda por carnes.
A medida utilizada para mensurar o ajustamento das equações dos modelos aos dados foi o R2 Ajustado (vide Tabela 3), que apresentou valores altos para cada equação em todas as especificações dos modelos, indicando haver um bom ajustamento dos modelos aos dados.
As estatísticas Durbin-Watson na Tabela 3 demonstram que a hipótese de autocorrelação de primeira ordem nos erros não pode ser rejeitada para nenhuma das equações do modelo estimado sem correção para autocorrelação (modelo com N-Rmatriz). No entanto, para os modelos com D-Rmatriz e F-Rmatriz o teste de Durbin-Watson não é confiável, uma vez que, em ambos, valores defasados da variável dependente foram utilizados como variável explicativa. Por conta disso, optou-se por utilizar o teste da razão de verossimilhança ajustada, como exposto a seguir, como critério na seleção da melhor especificação entre os modelos.
O teste usual de razão de verossimilhança (teste LR) é, em amostras finitas, viesado a favor da rejeição das restrições impostas aos modelos de demanda (MOSCHINI et al., 1994). Apesar de não haver uma forma única de se ajustar o teste LR com vistas a minimizar tal viés, Moschini et al. (1994) observaram que o método de correção proposto por Italianer (1975) apresenta bom desempenho quando aplicado a modelos não lineares de equações de demanda. A estatística do teste LR ajustado é:
em que M denota o número de equações incluídas na estimação do modelo; T é o tamanho da amostra; ku e kr denotam o número de parâmetros incluídos nos modelos irrestrito e restrito;
LR = 2(LLu − LLr) é a estatística do teste usual de razão de verossimilhança; e LLu e LLr são, respectivamente, os máximos valores da função logaritmo da verossimilhança para os modelos irrestrito e restrito.
A estatística razão da verossimilhança ajustada (LRs) segue assintoticamente uma distribuição qui-quadrado com graus de liberdade iguais à diferença entre o número de parâmetros no modelo irrestrito e restrito. A hipótese nula do teste LR ajustado é de que todos os parâmetros adicionados ao modelo restrito são conjuntamente zeros, ou em outras palavras, o modelo restrito é o verdadeiro modelo. A Tabela 4 apresenta os resultados dos testes de hipóteses com relação à detecção de autocorrelação de primeira ordem nos resíduos e com relação à inclusão ou não da variável tendência no modelo com F-Rmatriz.
Os resultados dos testes de razão da verossimilhança ajustada (LRs), apresentados nas colunas 2 a 4 da Tabela 4, levam às seguintes conclusões15
15
O símbolo f significa "é estritamente preferível a".
com respeito à preferência entre pares de especificações dos modelos: D-Rmatriz N-Rmatriz, F-Rmatriz
N-Rmatriz, F-Rmatriz  D-Rmatriz e F-Rmatriz
D-Rmatriz e F-Rmatriz  N-Rmatriz. Com base nesses resultados, a ordem final de preferência com relação aos modelos é: F-Rmatriz
N-Rmatriz. Com base nesses resultados, a ordem final de preferência com relação aos modelos é: F-Rmatriz  D-Rmatriz
D-Rmatriz  N-Rmatriz, o que implica em concluir que há autocorrelação de primeira ordem dos resíduos, mas que o modelo estimado com F-Rmatriz é capaz de corrigir tal problema.
N-Rmatriz, o que implica em concluir que há autocorrelação de primeira ordem dos resíduos, mas que o modelo estimado com F-Rmatriz é capaz de corrigir tal problema.
Finalmente, na última coluna da Tabela 4, o teste razão da verossimilhança ajustada confirma que o modelo com F-Rmatriz e tendência é o preferível a todos os outros modelos estimados. Tal resultado corrobora a necessidade de se incorporar a variável tendência nas equações dos modelos no sentido de propiciar a detecção de mudanças estruturais causadas por outras variáveis não incluídas nos modelos.
A Tabela 5 apresenta as estimativas das elasticidades-preços Marshalliana e Hicksiana (compensada) e elasticidades-gasto16 16 As elasticidades-preço Marshallianas (η ij) e elasticidades-gasto (η ix) foram calculadas com base nas seguintes fórmulas: em que δ ij é o delta de Kronecker, tal que: δ ij= 1 para i = j, caso contrário, δ ij= 0. As elasticidades-preço Hicksianas ou compensadas foram calculadas com base nas equações de Slutsky na forma de elasticidade: ε ij = η ij + wjη ix ∀ i,j para o sistema AIDS estimado com F-Rmatriz e variável tendência (modelo preferido). As elasticidades na Tabela 5 são médias das elasticidades calculadas em cada observação, as quais são estatística e individualmente significantes pelo teste t ao nível de 5%.
As elasticidades próprios-preços Marshallianas na Tabela 5 das carnes bovina (-0,159), suína (-0,053) e de frango (-0,470) e também para os outros bens de consumo (-1,018), indicam que as demandas por carnes são inelásticas e a demanda por outros bens de consumo é elástica. Santana (1999) estimou elasticidades próprios-preços Marshallianas para a carne bovina e de frango de -0,271 e -0,332. Fernandes et al. (1989) estimaram elasticidades Marshallianas com relação aos próprios preços das carnes bovina, suína e de frango de -0,29, -0,76 e -0,19. Bacchi e Barros (1992) estimaram elasticidades de curto e longo prazo para a demanda por carne bovina com relação ao próprio preço em -0,51 e -1,09. Apesar desses resultados não serem diretamente comparáveis aos obtidos no presente estudo, percebe-se que as suas magnitudes indicam que as estimativas obtidas no presente artigo são plausíveis.
Ainda pela Tabela 5, nota-se que todos os bens, com exceção da carne suína, apresentam elasticidades preços-cruzados Marshallianas, em módulo, inferiores às elasticidades próprios-preços. Para esses bens, confirmam-se as expectativas de que as demandas devem ser mais sensíveis aos próprios preços do que aos preços dos bens correlatos. De toda forma, a não confirmação de tal expectativa para a carne suína não viola qualquer resultado da teoria do consumidor. Nota-se ainda que todas as elasticidades preços-cruzados das carnes são positivas, confirmando que as carnes bovina, suína e de frango são bens substitutos brutos uns dos outros. Além disso, observa-se que a demanda por carne suína (0,069 > 0,015) e a demanda por carne de frango (0,187 > 0,040) são mais sensíveis a variações no preço da carne bovina do que o contrário; e a demanda por carne de frango é mais sensível a variações nos preços da carne suína (0,149 > 0,121) do que o contrário. Dessa forma, em termos de sensibilidade, em relação a variações nos preços das demais carnes, tem-se que: a demanda por carne de frango é mais sensível que a demanda por carne suína, que é mais sensível do que a demanda por carne bovina.
As elasticidades preços-cruzados Marshallianas para cada tipo de carne com relação aos outros bens de consumo são todas positivas, indicando que outros bens de consumo são substitutos brutos das carnes (Tabela 5). Já as elasticidades preços-cruzados Marshallianas dos outros bens de consumo com relação à cada tipo de carne são todas negativas, indicando que cada carne é um complemento bruto de outros bens de consumo. Note-se que esses resultados aparentemente contraditórios em nada violam a teoria do consumidor.
As elasticidades próprios-preços Hicksianas são todas negativas (vide terceira coluna da Tabela 5), como requerido pela teoria do consumidor17 17 A diagonal principal da matriz de substituição de Hicks/Slutsky deve ser composta por números não positivos, como uma das condições necessárias para que a mesma seja semidefinida negativa, ou equivalentemente, para que a função gasto seja côncava (vide proposição 3.G.3 em Mas-Colell et al., 1996). e indicam que as demandas compensadas são inelásticas aos próprios preços. As elasticidades preços-cruzados Hicksianas mostram que as carnes bovina, suína e de frango são substitutos líquidos uns dos outros. De fato, todos os bens são substitutos compensados uns dos outros, com exceção da carne suína que é um complemento líquido de outros bens de consumo e vice-versa.
Finalmente, as elasticidades-gasto na Tabela 5 revelam que: outros bens de consumo são um bem de luxo (ηox = 1,072 > 1); as carnes bovina, suína e de frango são bens necessários (ηkx < 1 para todo k = b, p e c), sendo a carne suína um bem inferior (ηpx = -0,188) e as carnes bovina e de frango, bens normais. Com base nas elasticidades-gasto, um aumento do gasto per capita com consumo acarreta, ceteris paribus, maior aumento na demanda de outros bens de consumo (1,088) que na demanda por carne de frango (0,108); maior aumento na demanda por carne de frango que na demanda por carne bovina (0,073); e redução na demanda por carne suína. Assim, como é provável que o gasto (renda) per capita com consumo aumente ao longo do tempo, é de se esperar que o consumo de carnes perca importância para o consumo de outros bens de consumo (confirmando a lei de Engel para alimentos). Além disso, dentro do grupo carnes, a carne bovina deve perder importância para o consumo das carnes de frango e a carne suína deve perder importância para as outras carnes.
5. Sumário e conclusões
Apesar da importância do mercado interno brasileiro de carnes, existem poucos estudos sobre a demanda agregada por carnes no Brasil. O presente artigo estimou modelos de demanda agregada por carnes e investigou: se outros fatores além de preços e renda afetam a demanda agregada por carnes; e se o Plano Real impactou a demanda agregada por carnes no Brasil. Além disso, o artigo apresentou estimativas das elasticidades da demanda com relação a preços e gasto (renda), o que é fundamental para a tomada de decisão nos setores público e privado. Para tanto, foi empregado o sistema de demanda quase ideal (AIDS) de Deaton e Muellbauer (1980), que possibilita a exata agregação das demandas dos consumidores e a imposição de resultados da teoria do consumidor, como base para a especificação dos modelos de demanda. Os modelos econométricos consideraram um conjunto de quatro bens: carnes bovina, suína e de frango e outros bens de consumo, o que garantiu flexibilidade suficiente para que as mudanças estruturais na demanda por carnes pudessem ser captadas.
Os testes demonstraram que a inclusão da variável tendência nas equações dos modelos era necessária, uma vez que as estimativas dos seus coeficientes foram estatística e individualmente significantes. Assim, detectou-se haver pequenas tendências ao longo do tempo de crescimento das demandas por carnes e de decrescimento da demanda por outros bens de consumo, confirmando que outras variáveis além de preços e gasto afetam a demanda por carnes e, portanto, devem ser mais bem investigadas em pesquisas futuras. Por exemplo, seria importante investigar o grau em que fatores relacionados à preocupação do consumidor com a própria saúde e com a segurança e qualidade do alimento poderiam ser responsáveis pelas tendências detectadas nas demandas por carnes. Detectou-se também, via inclusão de variáveis dummy nas equações dos sistemas de equações que o Plano Real não afetou as demandas por carnes e outros bens de consumo.
As estimativas das elasticidades próprios-preços indicaram que as demandas pelas carnes bovina, suína e de frango são inelásticas e as estimativas das elasticidades preços-cruzados confirmam que as carnes são bens substitutos brutos e líquidos uns dos outros.
Com base nas estimativas das elasticidades-gasto, todos os bens são normais, exceto pela carne suína, que é um bem inferior. Além disso, tais estimativas indicaram que, na medida em que o gasto com consumo das famílias brasileiras cresce, ceteris paribus, o consumo de carnes perderá importância para o consumo de outros bens, corroborando a lei de Engel para alimentos. Dentro do grupo carnes, na medida em que o gasto das famílias com consumo aumenta, ceteris paribus, o consumo de carne bovina deve perder importância para a carne de frango, e o consumo de carne suína deve perder espaço para as carnes de frango e bovina. Diante dessas evidências empíricas, por exemplo, seria importante para o setor de carne suína desenvolver estratégias de marketing no sentido de influenciar sobre a elasticidade-gasto da carne suína, uma vez que é muito provável que o brasileiro identifique a carne suína como uma carne menos saudável que as demais. Por outro lado, se houver alguma intenção de políticas públicas no sentido de se induzir a população brasileira a consumir menos carne suína ou mais carne de frango (carne branca), as elasticidades-gasto demonstram que tais políticas seriam desnecessárias.
6. Referências bibliográficas
- BACCHI, M.R.P. e BARROS, G.S.C. Demanda de carne bovina no mercado brasileiro. Revista de Economia e Sociologia Rural, v. 30, n. 1, p.83-96, 1992.
- BARNET, W.A. e SERLETIS, A. Consumer preferences and demand systems. Journal of Econometrics, v. 147, n. 2, p. 210-224, 2008.
- BARNET, W.A. Maximum likelihood and iterated Aitken estimation of nonlinear systems of equations. Journal of the American Statistical Association, v. 71, n. 354, p. 354-360, 1976.
- BERNDT, E.R. e SAVIN, N.E. Evaluation and hypothesis testing in singular equation systems with autoregressive disturbances. Econometrica, v. 32, n. 5/6, p. 93757, 1975.
- BLUNDELL, R., PASHARDES, P. e WEBER, G. What do we learn about consumer demand patterns form micro data? American Economic Review, v. 83, n. 3, p. 570-597, 1993.
- BRESTER, G.W. e SCHROEDER, T.C. The impacts of brand and generic advertising on meat demand. American Journal of Agricultural Economics, v. 77, n. 4, p. 969-79, 1995.
- CARVALHO, T. Estudo da elasticidade-renda da demanda da carne bovina, suína e de frango no Brasil Dissertação de mestrado. Escola Superior de Agricultura Luiz de Queiroz, Universidade de São Paulo, 2007.
- COELHO, A.B., AGUIAR, D.R.D. e EALES, J.S. Food demand in Brazil: an application of Shonkwiler & Yen two-step estimation method. Estudos Econômicos, v. 40, n. 1, p. 185-211, 2010.
- DEATON, A. e MUELLBAUER, J. An almost ideal demand system American Economic Review, v. 70, n. 3, p. 312-326, 1980a.
- DEATON, A. e MUELLBAUER, J. Economics and consumer behavior New York: Cambridge University Press, 1980b.
- DENTON, F.T. e MOUNTAIN, D.C. Income distribution and aggregation/disaggregation biases in the measurement of consumer demand elasticities. Economics Letters, v. 73, n. 1, p. 21-28.
- DICKEY, D.A. e FULLER, W.A. Likelihood ratio statistics for autoregressive time series with a unit root. Econometrica, v. 49, n. 4, p. 1057-72, 1981.
- ENGLE, R.F. e GRANGER, C.W.J. Cointegration and error correction: representation, estimation and testing. Econometrica, v.55, n. 2, p.251-276, 1987.
- FAO, 2009. FAOSTAT Disponível em <http://faostat.fao.org/>
- FERNANDES, S.A., PANIAGO, E. e LIMA J.E. Análises de políticas relacionadas com a demanda e a oferta de carnes no Brasil. Revista de Economia e Sociologia Rural, v. 27, n. 4, p. 556-561, 1989.
- FISHER, D., FLEISSIG, A.R. e SERLETIS, A. An empirical comparison of flexible demand system functional forms. Journal of Applied Econometrics, v. 16, n. 1, p. 59-80, 2001.
- GALLET, C.A. Meat meets meta: a quantitative review of the price elasticity of meat. American Journal of Agricultural Economics, v. 92, n. 1, p. 258-272, 2009.
- GALLET, C.A.. The income elasticity of meat: a meta analysis. The Autralian Journal of Agricultural and Resource Economics, v. 54, n. 4, p. 477-490, 2010.
- GREENE, W.H. Econometric Analysis, New Jersey: Prentice Hall, 2003.
- IEA/SP, 2009. Preços Mensais no Varejo. Disponível em <http://ciagri.iea.sp.gov.br/bancoiea/Precos_Medios.aspx?cod_sis=4>
- IPEADATA, 2009. Ipeadata Available at <http://www.ipeadata.gov.br/>
- ITALIANER, A. A small-sample correction for the likelihood ratio test. Economics Letters, v. 19, n. 4, p. 315-17, 1975.
- LEWBEL, A., NG, S. Demand systems with nonstationary prices. Review of Economics and Statistics, v. 87, n. 3, p. 479-494, 2005.
- MACKINNON, J.G. Numerical distribution functions for unit root and cointegration tests. Journal of Applied Econometrics, v. 11, n. 6, p. 601-18, 1996.
- MARSH, T.L., SCHROEDER, T.D. e MINTERT, J. Impacts of meat product recalls on consumer demand in the USA. Applied Economics, v. 36, n. 9, p. 897-909, 2004.
- MAS-COLELL, A., WHINSTON, M.D. e GREEN, J.R. Microeconomic Theory, Oxford University Press, 1995.
- MOSCHINI, G. e MEILKE, K.D. Modeling the pattern of structural change in U.S. meat demand. American Journal of Agricultural Economics, v. 71, n. 2, p. 253-261, 1989.
- MOSCHINI, G., MORO, D., GREEN, R.. Maintaining and testing separability in demand system. American Journal of Agricultural Economics, v. 76, n. 1, p. 61-73, 1994.
- MUELLBAUER, J.. Aggregation, income distribution and consumer demand. Review of Economics Studies, v. 84, p. 32-55, 1975.
- MUELLBAUER, J. Community preferences and the representative consumer. Econometrica, v. 44, p. 979-999, 1976.
- PHILLIPS, P.C.B. e PERRON, P. Testing for a unit root in time series regression. Biometrika, v. 75, n. 2, p. 335-46.
- PHILLIPS, P. C. B.. Time series regression with a unit root. Econometrica, v. 55, n. 2, p. 277-301, 1987.
- PIGGOTT, N.E., CHALFANT, J.A., ALSTON, J.M. e GRIFFITH, G.R. Demand response to advertising in the Australian meat industry. American Journal of Agricultural Economics, v. 78, n. 2, p. 268-79, 1996.
- PIGGOTT, N.E. e MARSH, T.L. Does food safety information impact U.S. meat demand? American Journal of Agricultural Economics, v. 86, n. 1, p. 154-74, 2004.
- PINTOS-PAYERAS, J.A. Estimação do sistema de demanda quase ideal para uma cesta ampliada de produtos empregando dados da POF de 2002-2003. Economia Aplicada, v. 13, n. 2, p. 231-255, 2009.
- QUANTITATIVE MICRO SOFTWARE. EViews 7 Command and Programming Reference Irvine, USA: Quantitative Micro Software, 2010.
- SANTANA, A.C. Mudanças recentes nas relações de demanda de carne no Brasil. Revista de Economia e Sociologia Rural, v. 37, n. 2, p. 51-76, 1999.
- SCHROEDER, T.C., MARSH, T.L. e MINTERT, J. Beef demand determinants, Relatório preparado para the National Cattlemen's Beef Association, 2000. Disponível em <http://www.agecon.ksu.edu/ livestock/Extension%20Bulletins/BeefDemandDeterminants.pdf>
- USDA/FAS, 2009. Production, Supply and Demand Online - Downloadable Data Sets Disponível em http://www.fas.usda.gov/psdonline/psdDownload.aspx
Datas de Publicação
-
Publicação nesta coleção
04 Maio 2012 -
Data do Fascículo
Mar 2012