Resumo
O arroz é um alimento básico na dieta do brasileiro; contudo, o lento crescimento de seu consumo tem impactos diretos na expansão do setor. Para compreender os fatores que afetam esse consumo e suas inter-relações com outros alimentos foram estimadas, neste estudo, as elasticidades da demanda por dez alimentos nos domicílios brasileiros, utilizando dados da Pesquisa de Orçamentos Familiares 2008-2009. Para tanto, foi aplicado o modelo Quadratic Almost Ideal Demand System (Quaids) ajustado para o problema do consumo censurado e da endogeneidade das despesas. Os resultados gerais indicam que o arroz apresenta elasticidade-dispêndio menor que a unidade. A elasticidade-renda da demanda reforça esse comportamento de bem necessário, sendo mais elevada em regiões como o Centro-Oeste e o Sudeste. O feijão é um bem complementar ao arroz, ao passo que pão e farinha de mandioca se mostraram como importantes substitutos. Por fim, os resultados encontrados podem ser úteis para dinamizar o consumo domiciliar desse produto, por meio de estratégias que reduzam o preço, com o aumento da produtividade ou alterações tributárias, ou, ainda, estratégias focadas em mercados regionais e que promovam a substituição de outros alimentos pelo cereal.
Palavras-chaves:
Modelo Quaids; arroz; demanda domiciliar; elasticidades
Abstract
Rice is a staple food in the Brazilian diet, but the slow consumption growth has a direct impact on the sector's expansion. In order to understand the factors affecting this consumption and their interrelationships with other food, this paper estimated the elasticities of demand for ten types of food in Brazilian households using microdata of the Household Budget Survey 2008-2009. Therefore, we applied the Quadratic Almost Ideal Demand System model (Quaids) adjusted for censored consumption and endogeneity of total expenditures. The overall results indicate that the rice has elasticity expenditure less than the unity. The income elasticity of demand reinforces this necessary good behavior, being higher in regions like the Midwest and Southeast. It also indicates that beans are complementary to rice, while bread and cassava flour are important substitutes. Finally, these results may be useful to boost household consumption of this product, through strategies that reduce its price, with the productivity increase or tax changes, or strategies focused on regional markets and to promote the substitution of other foods by rice.
Key-words:
Quaids model; rice; household demand; elasticities
1 Introdução
O arroz está presente na alimentação de bilhões de pessoas ao redor do globo. De acordo com a Organização das Nações Unidas para a Alimentação e a Agricultura (Food and Agriculture Organization of The United Nations, 2004Food and Agriculture Organization of the United Nations – FAO. (2004). Ano internacional do arroz. Recuperado em 20 de maio de 2015, de http://www.fao.org/rice2004/es/concept.htm
http://www.fao.org/rice2004/es/concept.h...
), o arroz está profundamente enraizado na herança cultural de muitas sociedades, sendo alimento básico para mais da metade da população mundial. Além disso, esse cereal apresenta-se como uma fonte de nutrientes de relevância crescente em diversos países de baixa renda, sobretudo na África, o que denota sua importância para a segurança alimentar.
No Brasil, a importância do arroz também se faz notar, sendo o principal mercado fora do continente asiático, com produção e consumo em torno de 12 milhões de toneladas em 2014. Os dados da Pesquisa de Orçamento Familiar (POF) de 2008, do Instituto Brasileiro de Geografia e Estatística, podem ser utilizados para ressaltar a significância do arroz no total das calorias ingeridas no domicílio em diferentes unidades da federação, como São Paulo (15%) e Maranhão (39%) (Instituto Brasileiro de Geografia e Estatística, 2015aInstituto Brasileiro de Geografia e Estatística – IBGE. (2015a). Pesquisa de orçamento familiar do IBGE – SIDRA. Rio de Janeiro: IBGE. Recuperado em 20 de maio de 2015, de http://www.sidra.ibge.gov.br/bda/acervo/acervo2.asp?e=v&p=OF&z=t&o=23
http://www.sidra.ibge.gov.br/bda/acervo/...
). Cumpre mencionar ainda que essa participação ganha relevância devido às suas características nutricionais, pois o arroz tem efeito positivo na prevenção de diversas doenças crônicas, como: diabetes e doenças cardiovasculares (Walter et al., 2008Walter, M., Marchezan, E., & Avila, L. A. D. (2008). Arroz: composição e características nutricionais. Ciência Rural, 38(4), 1184-1192. http://dx.doi.org/10.1590/S0103-84782008000400049
http://dx.doi.org/10.1590/S0103-84782008...
). Apesar disso, o consumo segue relativamente estagnado nas últimas duas décadas (Companhia Nacional de Abastecimento, 2015Companhia Nacional de Abastecimento – CONAB. (2015). Quadro de suprimentos. Recuperado em 10 de dezembro de 2015, de http://www.conab.gov.br/conteudos.php?a=1470&t=2
http://www.conab.gov.br/conteudos.php?a=...
), o que tende a afetar negativamente a rentabilidade da cadeia produtiva desse cereal em momentos de forte crescimento da produção. Assim, o setor, recorrentemente, mostra-se como grande demandante de recursos públicos. No período de 2003 a 2011, foram destinados R$ 7,4 bilhões para suporte à produção, estoques e comercialização do grão, que perdeu em recursos recebidos apenas para o milho e para o trigo, conforme aponta Capitani (2013)Capitani, D. H. (2013). Viabilidade de implantação de um contrato futuro de arroz no Brasil (Tese de doutorado). Escola Superior de Agricultura “Luiz de Queiroz”, Universidade de São Paulo, Piracicaba..
Apesar da estabilidade do consumo nacional total, os dados da POF de 2008 mostram significativa variação do consumo regional e maior importância do cereal na dieta das famílias de renda mais baixa (Instituto Brasileiro de Geografia e Estatística, 2015aInstituto Brasileiro de Geografia e Estatística – IBGE. (2015a). Pesquisa de orçamento familiar do IBGE – SIDRA. Rio de Janeiro: IBGE. Recuperado em 20 de maio de 2015, de http://www.sidra.ibge.gov.br/bda/acervo/acervo2.asp?e=v&p=OF&z=t&o=23
http://www.sidra.ibge.gov.br/bda/acervo/...
). Ademais, trabalhos como os de Schlindwein & Kassouf (2007)Schlindwein, M., & Kassouf, A. L. A. (2007). Mudanças no padrão de consumo de alimentos tempo-intensivos e de alimentos poupadores de tempo, por regiões do Brasil. In G. F. Silveira, L. M. Servo, T. Menzes, & S. F. Piola (Orgs.), Gasto e consumo das famílias brasileiras contemporâneas (cap. 14, pp. 423-462). Brasília: Ipea. e Gameiro & Gameiro (2008)Gameiro, A. H., & Gameiro, M. B. P. (2008). O arroz no varejo e os fatores que influenciam o dispêndio das famílias consumidoras. Revista de Economia e Sociologia Rural, Brasília, 46(4), 1043-1066. apontam o impacto da urbanização e a maior participação da mulher no mercado de trabalho como fatores importantes para a queda do consumo domiciliar do alimento. Por sua vez, a distribuição de renda também afeta a demanda de alimentos, conforme mostrado por Ferrario (2013)Ferrario, N. M. (2013). Análise do impacto dos programas de transferência de renda sobre as despesas familiares com o consumo (Tese de doutorado). Escola Superior de Agricultura “Luiz de Queiroz”, Universidade de São Paulo, Piracicaba., havendo um efeito positivo de programas sociais (Bolsa Família e Benefício de Prestação Continuada) no consumo de cereais e de outros componentes da dieta do povo brasileiro.
Neste contexto, a estimação de sistemas de demanda para os alimentos, que considere o arroz e seus potenciais bens substitutos e complementares, se mostra útil para a formulação de políticas públicas ou estratégias setoriais privadas. Através desse método pode-se obter as elasticidades-preço própria e cruzada, bem como a elasticidade-renda por meio de uma estimação conjunta e que considera as restrições advindas da maximização da utilidade sujeita a uma restrição orçamentária, conforme a teoria econômica da escolha do consumidor (Mittal, 2010Mittal, S. (2010). Application of the QUAIDS model to the food sector in India. Journal of Quantitative Economics, 8(1), 42-55.).
Para obter essas elasticidades que auxiliam na compreensão do comportamento do consumidor, um modelo amplamente utilizado na literatura é o modelo Quaids (Quadratic Almost Ideal Demand System), de Banks et al. (1997)Banks, J., Blundell, R., & Lewbel, A. (1997). Quadratic Engel curves and consumer demand. The Review of Economics and Statistics, 79(4), 527-539. http://dx.doi.org/10.1162/003465397557015
http://dx.doi.org/10.1162/00346539755701...
, que é uma versão quadrática do modelo Aids (Almost Ideal Demand System) de Deaton & Muellbauer (1980a)Deaton, A., & Muellbauer, J. (1980a). An almost ideal demand system. The American Economic Review, 70(3), 312-326.. Diversos trabalhos internacionais utilizaram esses modelos para estimação da demanda de alimentos (Alfonzo & Peterson, 2006Alfonzo, L., & Peterson, H. H. (2006). Estimating food demand in Paraguay from household survey data. Agricultural Economics, 34(3), 243-257. http://dx.doi.org/10.1111/j.1574-0864.2006.00122.x
http://dx.doi.org/10.1111/j.1574-0864.20...
; Tafere et al., 2010Tafere, K., Taffesse, A. S., Tamru, S., Tefera, N., & Paulos, Z. (2010). Food demand elasticities in Ethiopia: estimates using household income consumption expenditure (HICE) survey data (Working Paper 11). Washington: International Food Policy Research Institute. Recuperado em 03 de fevereiro de 2015, de http://www.ifpri.org/sites/default/files/publications/esspwp11.pdf
http://www.ifpri.org/sites/default/files...
; Alviola et al., 2010Alviola, P. A., Capps Junior, O., & Wu, X. (2010, july 25-27). Micro-demand system analysis of non-alcoholic beverages in the United States: an application of econometric techniques dealing with censoring. In Proceedings of The Agricultural & Applied Economics Association. Denver-Colorado: AAEA. Recuperado em 05 de fevereiro de 2014, de http://ageconsearch.umn.edu/handle/60462
http://ageconsearch.umn.edu/handle/60462...
; Mittal, 2010Mittal, S. (2010). Application of the QUAIDS model to the food sector in India. Journal of Quantitative Economics, 8(1), 42-55.). Na literatura nacional, também há exemplos da aplicação do modelo Aids na estimação da demanda por pescados (Sonoda, 2006Sonoda, D. Y. (2006). Demanda por pescados no Brasil entre 2002 e 2003 (Tese de doutorado). Escola Superior de Agricultura “Luiz de Queiroz”, Universidade de São Paulo, Piracicaba.), alimentos proteicos (Alves et al., 2007Alves, D., Menezes, T., & Bezerra, F. (2007). Estimação do sistema de demanda censurada para o Brasil:utilizando dados de pseudopainel. In G. F. Silveira, L. M. Servo, T. Menzes & S. F. Piola. (Orgs.), Gasto e consumo das famílias brasileiras contemporâneas (vol. 2, cap. 11, pp. 395-422). Brasília: Ipea.), vinho (Almeida et al., 2015Almeida, A. N., Bragagnolo, C., & Chagas, S. A. L. (2015). A demanda por vinho no brasil: elasticidades no consumo das famílias e determinantes da importação. Revista de Economia e Sociologia Rural, 53(3), 1-11. http://dx.doi.org/10.1590/1234-56781806-9479005303004
http://dx.doi.org/10.1590/1234-56781806-...
) e na análise do padrão de consumo nacional de nutrientes (Rodrigues et al., 2012Rodrigues, C. T., Coelho, A. B., Braga, M. J., & Gomes, A. P. (2012). Demanda por nutrientes nas principais regiões metropolitanas do Brasil no período de 1005-2003. Revista de Economía Aplicada, 16(1), 5-30.). Na sua versão quadrática, podem-se citar a estimação da demanda por alimentos com dados da POF 2002 (Coelho et al., 2010Coelho, A. B., Aguiar, D. R. D., & Eales, J. S. (2010). Food demand in Brazil: an application of Shonkwiler & Yen two-step estimation method. Revista Estudos Econômicos, 40(1), 185-211.) e com dados da POF 2008 por grupos específicos de alimentos (Silva, 2013Silva, M. M. D. C. (2013). Demanda domiciliar por frutas e hortaliças no Brasil (Dissertação de mestrado). Universidade Federal de Viçosa, Viçosa.; Travassos, 2014Travassos, G. F. (2014). Demanda domiciliar por carnes no Brasil: a questão da separabilidade (Dissertação de mestrado). Universidade Federal de Viçosa, Viçosa.), por nutrientes (Pereda & Alves, 2012Pereda, P. C., & Alves, D. C. D. O. (2012). Qualidade alimentar dos brasileiros: teoria e evidência usando demanda por nutrientes. Revista Pesquisa e Planejamento Econômico, 42(2), 239-260.) e por bebidas e cigarros (Almeida & Araújo Junior, 2017Almeida, A. T. C., & Araújo Junior, I. T. (2017). Demanda por bebidas alcoólicas e cigarro no Brasil: elasticidades, micro-simulação e variações no bem estar. Pesquisa e Planejamento Economico, 47(2), 1-11.), dentre outros.
Dessa forma, o presente ensaio tem por objetivo estimar as elasticidades (renda, preço-própria e preço-cruzada) de um sistema de demanda de alimentos para o Brasil. O arroz figura como produto principal desta investigação, com destaque também para os alimentos que apresentam potencial relação de substituição ou complementariedade com esse cereal. Assim sendo, no presente trabalho lança-se mão dos microdados de consumo domiciliar da POF 2008-2009 do Instituto Brasileiro de Geografia e Estatística (2015b)Instituto Brasileiro de Geografia e Estatística – IBGE. (2015b). Microdados da POF 2008-2009 (Pesquisa de Orçamentos Familiares). Rio de Janeiro: IBGE. Recuperado em 03 de setembro de 2015, de http://www.ibge.gov.br/home/estatistica/populacao/condicaodevida/pof/2008_2009/microdados.shtm
http://www.ibge.gov.br/home/estatistica/...
e estima-se um sistema de demanda alimentar através do modelo Quaids. Considera-se que o presente estudo é inédito no que diz respeito ao foco em uma investigação direcionada para o consumo de arroz no Brasil, um dos principais itens que compõe a dieta básica dos brasileiros e, ainda, detém peso relevante no campo produtivo (o cereal ocupa a sexta posição em termos de valor bruto da produção entre as culturas temporárias, perdendo apenas para a soja, a cana-de-açúcar, o milho, mandioca e o feijão, em 2016, de acordo com o Instituto Brasileiro de Geografia e Estatística (2010)Instituto Brasileiro de Geografia e Estatística – IBGE. (2010). Censo populacional 2010. Rio de Janeiro: IBGE. Recuperado em 28 de abril de 2016, de http://www.sidra.ibge.gov.br/bda/popul/default.asp?t=3&z=t&o=25&u1=1&u2=1&u3=1&u4=1&u5=1&u6=1
http://www.sidra.ibge.gov.br/bda/popul/d...
.
Cabe ressaltar que características sociodemográficas, já relatadas como importantes para o consumo do cereal, são incorporadas ao modelo em conformidade com Ray (1983)Ray, R. (1983). Measuring the costs of children: an alternative approach. Journal of Public Economics, 22(1), 89-102. http://dx.doi.org/10.1016/0047-2727(83)90058-0
http://dx.doi.org/10.1016/0047-2727(83)9...
e Poi (2012)Poi, B. P. (2012). Easy demand-system estimation with quaids. The Stata Journal, 12(3), 433-446. http://dx.doi.org/10.1177/1536867X1201200306
http://dx.doi.org/10.1177/1536867X120120...
. Ademais, busca-se contornar dois problemas amplamente relatados na literatura especializada de estimação de sistema de demanda, quais sejam: o problema da potencial endogeneidade da despesa total (Blundell & Robin, 1999Blundell, R., & Robin, J. M. (1999). Estimation in large and disaggregated demand systems: an estimator for conditionally linear systems. Journal of Applied Econometrics, 14(3), 209-232. http://dx.doi.org/10.1002/(SICI)1099-1255(199905/06)14:3<209::AID-JAE532>3.0.CO;2-X
http://dx.doi.org/10.1002/(SICI)1099-125...
) e o problema do consumo zero, isto é, da ausência do consumo de diversos bens do sistema analisado (Shonkwiler & Yen, 1999Shonkwiler, J. S., & Yen, S. T. (1999). Two-step estimation of a censored system of equations. American Journal of Agricultural Economics, 81(4), 972-982. http://dx.doi.org/10.2307/1244339
http://dx.doi.org/10.2307/1244339...
). Assim, o presente trabalho investiga quais os fatores que mais impactam a demanda pelo cereal por meio da pesquisa orçamentária mais recente existente no País, buscando tratar os potenciais problemas econométricos existentes nesses tipos de dados, algo não realizado até então em trabalhos nacionais que trabalharam com a demanda por arroz no domicílio1
1
A questão do consumo zero e endogeneidade do gasto foram tratadas, porém não conjuntamente em trabalhos sobre alimentação no domicílio no Brasil que estimaram a demanda para o arroz entre os alimentos selecionados.
.
O presente artigo está dividido em quatro partes, além desta introdução. A seção dois apresenta o modelo teórico de sistemas de demanda e os potenciais problemas econométricos que surgem na estimação dele. Na seção três, a base de dados e as variáveis utilizadas são explicitadas. A seção quatro expõe os resultados. Por fim, as considerações finais discutem as principais contribuições e limitações do trabalho.
2 Fundamentação teórica conceitual
2.1 Sistemas de demanda
O estudo de sistemas de demanda teve forte impulso por meio do modelo Aids (Almost Ideal Demand System), de Deaton & Muellbauer (1980a)Deaton, A., & Muellbauer, J. (1980a). An almost ideal demand system. The American Economic Review, 70(3), 312-326.. Este modelo é uma aproximação de primeira ordem que relaciona a parcela de gasto com um determinado bem com os preços (preços próprios e dos demais bens do sistema) e com o dispêndio total. Na sequência, o modelo Quadratic Almost Ideal Demand System (Quaids), desenvolvido por Banks et al. (1997)Banks, J., Blundell, R., & Lewbel, A. (1997). Quadratic Engel curves and consumer demand. The Review of Economics and Statistics, 79(4), 527-539. http://dx.doi.org/10.1162/003465397557015
http://dx.doi.org/10.1162/00346539755701...
a partir do modelo Aids, representa um avanço sobre este, pois permite que a relação do logaritmo do dispêndio com o bem possua não linearidade ao incorporar seu termo quadrático na equação. Assim, o Quaids permite considerar curvas de Engel não lineares, ou seja, possibilita que o mesmo bem seja um bem de luxo para alguns níveis de dispêndio (renda) e bem necessário para outros níveis de dispêndio (renda), comportamento bastante plausível para alimentos e não captado por outros modelos.
Especificamente, o modelo Quaids parte da generalização das preferências do tipo Piglog (Price-Independent Generalized Logarithmic) que apresentam funções utilidades indiretas que são lineares no logaritmo da despesa, conforme a equação:
em que ln V é o logaritmo neperiano da função utilidade indireta V; ln m é o logaritmo da despesa total, a(p) e b(p) são funções do vetor de preços p; por sua vez, o termo é a função utilidade indireta de um sistema de demanda Piglog; λ que é função diferenciável e homogênea de grau zero nos preços p2 2 A função utilidade indireta do Quaids é: u*=lny−α0−∑kαklnpk−12∑k∑jγkj*lnpklnpjβ0∏kpkβk−1+λp−1. Em que λp=∑i=1Mλilnpi e ∑iλi=0. Sendo diferente do modelo Aids, apenas pela função ë(p). Quando ë(p) é independente dos preços, esta é equivalente à classe Piglog, que inclui o modelo Aids (Banks et al., 1997). . O termo b((p) é um agregador de preço do tipo Cobb-Douglas:
Por sua vez, ln a(p)3 3 O termoα0, segundo Banks et al. (1997), é definido pelo valor mínimo da despesa total (ln m). é dado por:
O termo , que no caso do modelo Aids é zero, no caso quadrático é definido como:
A partir das substituições destas equações e pela aplicação da identidade de Roy4 4 A identidade de Roy mostra que a demanda Marshalliana para o bem i é o negativo da razão entre as derivadas parciais desta em relação a preço e dispêndio (Deaton & Muellbauer, 1980a, p. 41). na função utilidade indireta, obtém-se a parcela de dispêndio com o i-ésimo bem do sistema:
em que i=1...n são os bens considerados no sistema de demanda; wi é a parcela de gasto da h-ésima família com o bem i, sendo função dos preços (preço próprio e preços dos demais bens do sistema) e da renda total (representada pela despesa deflacionada pelo índice de preços) tanto em nível quanto ao quadrado. Os parâmetros estimados a partir desta equação são utilizados para se obter os cálculos das elasticidades da demanda em relação aos preços e à renda.
Para garantir a consistência com a teoria da demanda, algumas condições são impostas (e testadas) sob os coeficientes do modelo Quaids (aditividade, homogeneidade, simetria e negatividade). A aditividade () é garantida se:
A homogeneidade:
A simetria:
2.2 Quaids com ajustamento para fatores sociodemográficos
A demanda por alimentos não é influenciada apenas por mudanças na renda e nos preços, mas também por fatores sociodemográficos como nível de escolaridade, localização do domicílio rural/urbano, composição etária, mudanças nos gostos e preferências, dentre outros. Diversos trabalhos nacionais (Schlindwein & Kassouf, 2007Schlindwein, M., & Kassouf, A. L. A. (2007). Mudanças no padrão de consumo de alimentos tempo-intensivos e de alimentos poupadores de tempo, por regiões do Brasil. In G. F. Silveira, L. M. Servo, T. Menzes, & S. F. Piola (Orgs.), Gasto e consumo das famílias brasileiras contemporâneas (cap. 14, pp. 423-462). Brasília: Ipea.; Coelho et al., 2010Coelho, A. B., Aguiar, D. R. D., & Eales, J. S. (2010). Food demand in Brazil: an application of Shonkwiler & Yen two-step estimation method. Revista Estudos Econômicos, 40(1), 185-211.; Silva, 2013Silva, M. M. D. C. (2013). Demanda domiciliar por frutas e hortaliças no Brasil (Dissertação de mestrado). Universidade Federal de Viçosa, Viçosa.; Travassos, 2014Travassos, G. F. (2014). Demanda domiciliar por carnes no Brasil: a questão da separabilidade (Dissertação de mestrado). Universidade Federal de Viçosa, Viçosa.) e internacionais (Pollak et al., 1981Pollak, R. A., & Wales, T. J. (1981). Demographic variables in demand analysis. Econometrica, 49(6), 1533-1551. http://dx.doi.org/10.2307/1911416
http://dx.doi.org/10.2307/1911416...
; Ray, 1983Ray, R. (1983). Measuring the costs of children: an alternative approach. Journal of Public Economics, 22(1), 89-102. http://dx.doi.org/10.1016/0047-2727(83)90058-0
http://dx.doi.org/10.1016/0047-2727(83)9...
) reforçam a importância dessas variáveis e apontam que a omissão dessas variáveis pode gerar estimações dos sistemas de demanda com viés.
Poi (2012)Poi, B. P. (2012). Easy demand-system estimation with quaids. The Stata Journal, 12(3), 433-446. http://dx.doi.org/10.1177/1536867X1201200306
http://dx.doi.org/10.1177/1536867X120120...
incorpora fatores sociodemográficos ao modelo Quaids. Para tanto, utiliza o método proposto por Ray (1983)Ray, R. (1983). Measuring the costs of children: an alternative approach. Journal of Public Economics, 22(1), 89-102. http://dx.doi.org/10.1016/0047-2727(83)90058-0
http://dx.doi.org/10.1016/0047-2727(83)9...
em que Z representa um vetor de características sociodemográficas. Assim, admite-se que a função dispêndio ajustada para o vetor Z é dada por:
em que é a função dispêndio do domicílio de referência e, é um fator de escala das características sociodemográficas do domicílio. O primeiro termo do fator de escala dimensiona a resposta do dispêndio a mudanças no vetor Z, independentemente de mudanças no padrão de consumo. O segundo termo controla mudanças nos preços relativos e no padrão de consumo corrente. Ao se introduzir essas variáveis demográficas no modelo Quaids, a equação (5) é alterada para:
em que: é um agregador de preços com ponderação do vetor de variáveis sociodemográficas; , é o fator de escala sociodemográfico, com sendo o vetor de parâmetros dos efeitos das caracteristicas sociodemográficas sobre o dispêndio total a ser estimado; η é o ajuste para mudanças relativas nas despesas com cada bem i; a condição de aditividade requer que ;
Para calcular as elasticidades-preço e dispêndio com base no modelo Quaids deve-se derivar o sistema de equações expresso em (10) em relação ao dispêndio (renda) e aos preços, isto é, em relação a ln m e ln pj. Obtém-se, assim:
Resultando em:
-
elasticidade-dispêndio: ;
-
elasticidade-preço não compensada (Marshalliana): ;
em que é o delta de Kronecker, que toma o valor igual à unidade quando i=j e zero caso contrário. Utiliza-se a equação de Slutsky , parca calcular o conjunto de elasticidades compensadas ().
2.3 O problema do Consumo Zero
Em pesquisas de orçamentos familiares é muito frequente a presença do consumo zero (zero expenditure) de alguns produtos, isto é, não há consumo de alguns dos bens analisados no período investigado. Este consumo zero se deve a três causas principais: i) consumo zero permanente, a família não consome o bem por causas não econômicas, podendo-se citar, por exemplo, os grupos religiosos que não ingerem bebidas alcóolicas independentemente dos preços ou da sua renda; ii) consumo zero como solução ótima, que é um caso típico de solução de canto, isto é, devido a uma escolha da família, dadas suas preferências, preços dos bens e sua restrição orçamentária, ela opta por não adquirir o bem, caso comum para gastos desagregados em alimentos; iii) o consumo zero durante o período analisado, ou seja, a família não comprou o produto no período da pesquisa, podendo adquiri-lo em outro momento, problema comum com alimentos estocáveis, como o arroz (Tafere et al., 2010Tafere, K., Taffesse, A. S., Tamru, S., Tefera, N., & Paulos, Z. (2010). Food demand elasticities in Ethiopia: estimates using household income consumption expenditure (HICE) survey data (Working Paper 11). Washington: International Food Policy Research Institute. Recuperado em 03 de fevereiro de 2015, de http://www.ifpri.org/sites/default/files/publications/esspwp11.pdf
http://www.ifpri.org/sites/default/files...
).
A presença do consumo zero restringe os tipos de métodos econométricos utilizáveis para a correta estimação da demanda, pois a negligência do problema acarreta estimativas viesadas e inconsistentes dos sistemas de demanda. Um procedimento amplamente utilizado para lidar com este problema foi proposto por Shonkwiler & Yen (1999)Shonkwiler, J. S., & Yen, S. T. (1999). Two-step estimation of a censored system of equations. American Journal of Agricultural Economics, 81(4), 972-982. http://dx.doi.org/10.2307/1244339
http://dx.doi.org/10.2307/1244339...
, que consiste em uma estimação em dois estágios do conjunto completo das observações amostrais5
5
O processo de correção aplicado corrige apenas a existência do consumo zero como solução de canto, ou seja, para os potenciais consumidores. O arroz, apesar de ser um alimento estocável, conforme dados da POF está entre os mais consumidos pelos domicílios entrevistados, minimizando o problema da baixa frequência das compras.
. No primeiro estágio estima-se a probabilidade de compra para cada produto do sistema de demanda através de um modelo probit que engloba as características sociodemográficas que afetam a decisão de compra da família. Utiliza-se uma abordagem multivariada para estimação do modelo probit no primeiro estágio, conforme sugerido por Zheng & Henneberry (2010)Zheng, Z., & Henneberry, S. R. (2010). An analysis of food grain consumption in urban Jiangsu Province of China. Journal of Agricultural and Applied Economics, 42(2), 337-355. http://dx.doi.org/10.1017/S1074070800003497
http://dx.doi.org/10.1017/S1074070800003...
e empregado no Brasil por Almeida & Araújo Junior (2017)Almeida, A. T. C., & Araújo Junior, I. T. (2017). Demanda por bebidas alcoólicas e cigarro no Brasil: elasticidades, micro-simulação e variações no bem estar. Pesquisa e Planejamento Economico, 47(2), 1-11.. No segundo estágio, a informação da probabilidade de compra, através da função de densidade de probabilidade (FDP), e a função de distribuição acumulada (FDA), são incorporadas ao modelo Quaids, corrigindo, assim, a estimativa para o problema do consumo zero.
Portanto, no primeiro estágio estima-se um modelo de escolha binária (probit) para todos os bens do sistema de demanda simultaneamente. A variável dependente é o indicador de consumo domiciliar familiar para cada produto, (dih), em que assume o valor da unidade (dih = 1) se o domicílio apresentou despesa positiva com o i-ésimo bem (wih > 0) e zero caso contrário (dih = 0, se wih = 0). Assim, a decisão de consumo é dada pelo probit multivariado, representado por:
dih = 1 se > 0; dih = 0 caso contrário.
Em que o G é o vetor das variáveis explicativas, composto por: despesa total com alimentos (ln m), vetor dos preços dos bens (ln p), o vetor das características sociodemográficas Z, que podem impactar na decisão de consumo domiciliar; θ é o vetor de parâmetros estimados por meio do probit multivariado. O termo de erro padronizado, , assume forma funcional normal multivariada, e r é o coeficiente de correlação entre os termos de erros estocásticos das equações de demanda, o qual será estatisticamente significativo no caso de as decisões de consumo de cada bem não serem independentes do consumo dos demais bens.
Conforme já relatado, a partir das estimativas do probit multivariado calcula-se, para cada bem (i) e cada para cada família (h), a FDA, , e a FDP, , as quais são incorporadas ao modelo Quaids corrigido para o consumo zero, como mostrado a seguir:
em que Whi é o valor observado do dispêndio domiciliar no bem i, whi é valor latente desse dispêndio, que é determinado pelo modelo Quaids (equação 10). O parâmetro τi capta a covariância entre o termo de erro no modelo Quaids e o termo de erro do probit multivariado para as decisões de consumo.
2.4 O problema da endogeneidade das despesas totais
No presente trabalho estima-se um sistema de demanda para os alimentos consumidos no domicílio. Essa abordagem parte da suposição de que o dispêndio com os alimentos considerados seja fracamente separável dos demais gastos das famílias. Isto cria a possibilidade da endogeneidade das despesas totais com alimentos, isto é, pode ser que esse dispêndio total seja determinado ao mesmo tempo que suas parcelas (shares) orçamentárias dos bens específicos no modelo de demanda, o que pode induzir a estimativas inconsistentes dos parâmetros. Para corrigir este problema, Blundell & Robin (1999)Blundell, R., & Robin, J. M. (1999). Estimation in large and disaggregated demand systems: an estimator for conditionally linear systems. Journal of Applied Econometrics, 14(3), 209-232. http://dx.doi.org/10.1002/(SICI)1099-1255(199905/06)14:3<209::AID-JAE532>3.0.CO;2-X
http://dx.doi.org/10.1002/(SICI)1099-125...
propõem a estimação de uma equação na forma reduzida para a despesa total domiciliar com alimentos:
em que: Z e p são, respectivamente, os vetores de variáveis sociodemográficas e de preços (dos bens do sistema); Yh é a renda total domiciliar e ey é a elasticidade renda da despesa restrita (ou despesa total domiciliar) com alimentos (mh).
O resíduo (vh) desta forma reduzida é adicionado como variável explanatória nas equações de parcelas orçamentárias junto ao dispêndio total, contornando o problema de endogeneidade e servindo como teste de exogeneidade do dispêndio domiciliar total nas equações de parcelas orçamentárias (Blundell & Robin, 1999Blundell, R., & Robin, J. M. (1999). Estimation in large and disaggregated demand systems: an estimator for conditionally linear systems. Journal of Applied Econometrics, 14(3), 209-232. http://dx.doi.org/10.1002/(SICI)1099-1255(199905/06)14:3<209::AID-JAE532>3.0.CO;2-X
http://dx.doi.org/10.1002/(SICI)1099-125...
).
2.5 Estimação das equações de parcelas de gastos e das elasticidades no modelo Quaids ajustado
As equações das parcelas de gastos do modelo Quaids ajustado para fatores sociodemográficos, conforme Poi (2012)Poi, B. P. (2012). Easy demand-system estimation with quaids. The Stata Journal, 12(3), 433-446. http://dx.doi.org/10.1177/1536867X1201200306
http://dx.doi.org/10.1177/1536867X120120...
, são adaptadas para levar em consideração as correções para contornar o problema do consumo zero e da endogeneidade do dispêndio total, descritos nas subseções anteriores. Contudo, essas correções fazem com que a condição de aditividade, preconizada pela teoria da demanda, não seja assegurada. Assim, a alternativa proposta por Yen et al. (2003)Yen, S. T., Lin, B. H., & Smallwood, D. M. (2003). Quasi and Simulated-Likelihhod approaches to censored demand systems: Food consumption by food stamp recipients in the United States. American Journal of Agricultural Economics, 85(2), 458-478. http://dx.doi.org/10.1111/1467-8276.00134
http://dx.doi.org/10.1111/1467-8276.0013...
é tratar o n-ésimo bem do sistema como um bem residual, com . O bem de menor interesse na pesquisa foi escolhido como o bem residual (grupo demais bens). A partir dessa restrição, e das demais impostas ao modelo Quaids, estimam-se os parâmetros e pode-se calcular as elasticidades de interesse para o bem residual. Assim, as equações adaptadas, a serem estimadas, são descritas por:
com i =n-1, isto é 1..9, o número total de bens menos um. Por sua vez, ; .
Devido à não linearidade do modelo Quaids, as equações são estimadas por um sistema não linear de regressão aparentemente não relacionada (SUR) utilizando o comando NLSUR do Software Stata. Para tanto, aplica-se o método interated feasible generalized non linear least squares (IFGNLS), que é semelhante às estimações de máxima verossimilhança. A programação desses ajustes para a obtenção dos parâmetros foi feita através da adaptação da function evaluator program, proposta por Poi (2002)Poi, B. P. (2002). From the help desk: demand-system estimation. The Stata Journal, 2(4), 403-410. http://dx.doi.org/10.1177/1536867X0200200406
http://dx.doi.org/10.1177/1536867X020020...
e Poi (2008)Poi, B. P. (2008). Demand-system estimation: update. The Stata Journal, 8(4), 554-556. http://dx.doi.org/10.1177/1536867X0800800407
http://dx.doi.org/10.1177/1536867X080080...
e empregada por Almeida & Araújo Junior (2017)Almeida, A. T. C., & Araújo Junior, I. T. (2017). Demanda por bebidas alcoólicas e cigarro no Brasil: elasticidades, micro-simulação e variações no bem estar. Pesquisa e Planejamento Economico, 47(2), 1-11. para o caso da POF6
6
A function evaluator program considera ajustes no desenho amostral, na despesa censurada e na endogeneidade das despesas totais foi disponibilizada por Almeida e Araújo Jr. (2017).
.
A partir dos parâmetros estimados, compatibilizam-se as elasticidades (apresentadas nas equações 11 e
12) às adaptações do modelo, conforme Zheng & Henneberry (2010)Zheng, Z., & Henneberry, S. R. (2010). An analysis of food grain consumption in urban Jiangsu Province of China. Journal of Agricultural and Applied Economics, 42(2), 337-355. http://dx.doi.org/10.1017/S1074070800003497
http://dx.doi.org/10.1017/S1074070800003...
. Assim, tem-se:
Elasticidade-dispêndio: ;
Elasticidade-preço da demanda não-compensada: . O parâmetro πij é associado ao preço do j-ésimo bem no primeiro estágio (probit multivariado); elasticidade-preço da demanda compensada, pela equação de Slutsky: .
3 Base de dados
O presente trabalho lança mão dos microdados da Pesquisa de Orçamentos Familiares (POF) do Instituto Brasileiro de Geografia e Estatística (IBGE) de 2008-2009, cujo período de referência inicia-se em 19 de maio de 2008 e termina no dia 18 de maio de 2009. A POF é uma pesquisa realizada por amostragem, na qual são investigados os domicílios particulares permanentes. No domicílio, por sua vez, identifica-se a unidade básica da pesquisa – unidade de consumo – que compreende um único morador ou conjunto de moradores que compartilham da mesma fonte de alimentação ou compartilham as despesas com moradia. As informações concernentes aos alimentos destinados ao consumo domiciliar adquiridos pelas famílias encontram-se na Caderneta de Aquisição Coletiva – POF 3, sendo registradas informações como: produto, valor de despesa em Reais, a quantidade e a unidade de medida, o local de compra e a forma de aquisição do produto para um período de sete dias consecutivos7
7
É válido sublinhar que o valor das despesas considerado nesta pesquisa é dado pela soma das despesas não monetárias e das despesas monetárias. Muito embora o peso da despesa não monetária seja maior para os domicílios rurais do que os domicílios situados na área urbana, a estimação de um modelo desconsiderando esse tipo de gasto poderia amplificar o problema do consumo zero na base e, assim, gerar menor robustez para as estimativas obtidas.
(Instituto Brasileiro de Geografia e Estatística, 2015bInstituto Brasileiro de Geografia e Estatística – IBGE. (2015b). Microdados da POF 2008-2009 (Pesquisa de Orçamentos Familiares). Rio de Janeiro: IBGE. Recuperado em 03 de setembro de 2015, de http://www.ibge.gov.br/home/estatistica/populacao/condicaodevida/pof/2008_2009/microdados.shtm
http://www.ibge.gov.br/home/estatistica/...
).
A partir dessa base, são escolhidos os produtos que fazem parte do sistema de demanda tendo por base a relação teórica esperada de complementariedade e substituibilidade com o arroz e a importância dos bens no orçamento das famílias. Assim, os produtos escolhidos foram: arroz, feijão, macarrão, farinha de mandioca, batata, carne de primeira, carne de segunda, frango, pão. Além destes, constituiu-se um agregado chamado “demais produtos”, que contempla todos os demais produtos consumidos nos domicílios. Destaca-se, ainda, que a escolha dos itens alimentares supramencionados, em regra geral, foi feita tendo por base os alimentos identificados na literatura que apresentaram relação significativa estatisticamente com o consumo de arroz no Brasil, como Payeras-Pintos (2009)Payeras-Pintos, J. A. (2009). Estimação do sistema quase ideal de demanda para uma cesta ampliada de produtos empregando dados da POF de 2002-2003. Revista de Economía Aplicada, 13(2), 231-255., Coelho & Aguiar (2007)Coelho, A. B., & Aguiar, D. R. D. (2007). O modelo Quadratic Almost Ideal Demand System (QUAIDS): uma aplicação para o Brasil. In G. F. Silveira, L. M. Servo, T. Menezes, & S. F. Piola (Orgs.), Gasto e consumo das famílias brasileiras contemporâneas (vol. 2, cap. 14, pp. 485-514). Brasília: Ipea. e Coelho et al. (2010)Coelho, A. B., Aguiar, D. R. D., & Eales, J. S. (2010). Food demand in Brazil: an application of Shonkwiler & Yen two-step estimation method. Revista Estudos Econômicos, 40(1), 185-211..
Para consolidação do banco de dados foram excluídas as unidades de consumo com gasto nulo com alimentos no domicílio, bem como aquelas com renda total nula. Na sequência foram excluídos os outliers8 8 Outlier é o share (ou preço) de cada bem que ficou acima de dois desvios-padrão e meio da sua média. , identificados tanto para a parcela de gasto (share), como para os preços (unit value)9 9 O presente trabalho considerou o valor unitário como proxy dos preços (preço=valor/quantidade) e optou por não realizar tratamento de efeito qualidade, isto é, não se corrigiu o potencial problema de endogeneidade dos preços. Isso porque aqui busca-se mensurar as elasticidades para alimentos em nível bastante desagregado e com enfoque no arroz, produto com baixa diferenciação (homogêneo), em que esse potencial problema seria de menor importância conforme trabalhos como: Tafere et al. (2010), Barbosa, Menezes e Andrade (2013), dentre outros. . Assim, o total de domicílios considerados na base de 2008-2009 foi de 44.504. Além dos dados sobre gastos (quantidade e preços) com os alimentos, informações sobre as características sociodemográficas, que potencialmente afetam o consumo alimentar do domicílio, também foram utilizadas para compor o banco de dados.
A Tabela 1 apresenta as estatísticas descritivas das variáveis utilizadas na pesquisa. Há informações sobre a localização do domicílio, com variáveis para as grandes regiões geográficas brasileiras e se o domicílio é urbano ou rural. Completa-se o conjunto de variáveis sociodemográficas com aquelas que se referem às características de cada família. A renda total familiar foi utilizada apenas na regressão que tratou da endogeneidade do dispêndio total. As demais variáveis sociodemográficas foram empregadas tanto no primeiro estágio (probit multivariado) quanto no modelo Quaids propriamente dito.
Na última coluna da Tabela 1 apresenta-se, para cada um dos produtos escolhidos, o percentual de domicílios cujo consumo do referido alimento foi zero. Pode-se notar que é bastante comum a presença de aquisição zero dentre os produtos analisados. No caso do arroz, 63,5% dos domicílios não relataram o consumo do cereal nos dias da pesquisa. Assim sendo, fica patente a importância de se lidar com o problema do consumo zero.
4 Resultados
Na Tabela 2 são apresentados os coeficientes estimados dos parâmetros do modelo Quaids ajustado para o caso do consumo censurado (consumo zero) e da endogeneidade da despesa total com alimentos no domicílio (doravante despesa total restrita). Esses coeficientes são utilizados para se obter as elasticidades de interesse. Cabe reforçar que a interpretação dos resultados do modelo Quaids através das elasticidades é aconselhada pela literatura especializada (Blundell et al., 1993Blundell, R., Pashardes, P., & Weber, G. (1993). What do we learn about consumer demand patterns from micro data? The American Economic Review, 83(3), 570-597.).
Parâmetros do Sistema de Demanda (Quaids) ajustado aos valores censurados e endogeneidade dos gastos totais
Feita essa ressalva, passa-se a analisar a adequação geral dos resultados. De um total de 210 coeficientes diretamente estimados, 119 são estatisticamente significativos, ou seja, quase 57% do total. Além disso, observou-se que o parâmetro que representa o termo quadrático da despesa total com alimentos (λi) foi significativo para quase todas as equações do sistema (com exceção da carne de segunda), o que mostra que a utilização do modelo Quaids é adequada, sendo que ele permite que se capte a não linearidade entre o gasto total com alimentos no domicílio e o consumo desses alimentos. O coeficiente de ajuste das regressões (R2), que mostra o quanto as variáveis independentes de cada equação explicam a dependente, variou de 0,12 no caso da demanda de batata a 0,45 para a demanda de pão. Para o arroz, o coeficiente de determinação foi de 0,28, o terceiro maior dentre as equações dos produtos analisados, superado por alimentos com menor taxa de consumo zero (pão e frango).
O resultado obtido para o parâmetro associado com a correção para o consumo censurado (τi) foi significativo em todas as equações do sistema. Por sua vez, o parâmetro referente à correção da endogeneidade da despesa total restrita () também se mostrou significativo para a maioria das equações (exceções foram as equações da farinha de mandioca, da batata e da carne de primeira). Assim, fica patente que a estratégia de controle desses possíveis vieses se mostra adequada10 10 As estimativas dos estágios prévios ao sistema de demanda estão disponíveis sob demanda aos autores. .
Cumpre mencionar que as variáveis geográficas e socioeconômicas apresentaram expressivo número de coeficientes estatisticamente não nulos, sobretudo na equação da demanda pelo arroz. Por fim, as variáveis relativas a preço, seja próprio, seja dos outros alimentos, bem como a relativa à despesa total, também apresentaram alta frequência de coeficientes diferentes de zero no sistema de demanda. Assim, observa-se que a parcela de gasto domiciliar com cada um desses alimentos está associada a fatores econômicos (preços e despesa total), bem como a fatores sociodemográficos, de maneira que a consideração deste conjunto de variáveis é relevante para uma estimação mais robusta do sistema de demanda.
Na sequência são apresentadas as elasticidades (renda, dispêndio e preço) para todos os alimentos do sistema de demanda. Porém, como o objeto de investigação deste trabalho é o arroz, a análise, nesse caso, será mais detalhada.
4.1 Elasticidades
Apresentam-se, a seguir, as elasticidades (dispêndio restrita, renda e preços da demanda) calculadas na mediana da amostra para minimizar o efeito de valores atípicos. As elasticidades-dispêndio restritas foram estimadas para um intervalo de confiança de 95% do valor da mediana, sendo representados entre parênteses os limites mínimos e entre colchetes os limites máximos para cada bem – as tabelas estão em anexo. Apresentam-se os valores por dez estratos de renda domiciliar per capita e por região geográfica brasileira.
Os resultados da Tabela 3 indicam que o arroz está entre os alimentos consumidos no domicílio com maior elasticidade-dispêndio. Uma elevação de 1% no gasto com alimentos no domicílio faria com que o dispêndio com arroz aumentasse 0,91%. Esse efeito total é similar ao da carne de primeira e maior que para os outros alimentos desagradados, com exceção do grupo “demais bens”. Esses valores são mais elevados do que encontrados em trabalhos nacionais como: Hoffmann (2006Hoffmann, R. (2006). Elasticidades-renda das despesas e do consumo físico de alimentos no Brasil metropolitano 1995-1996. In G. F. Silveira, L. M. Servo, T. Menzes, & S. F. Piola (Orgs.), Gasto e consumo das famílias brasileiras contemporâneas (cap. 7, pp. 197-212). Brasília: Ipea., 2007Hoffmann, R. (2007). Elasticidades-renda das despesas e do consumo de alimentos no Brasil em 2002-2003. In G. F. Silveira, L. M. Servo, T. Menzes, & S. F. Piola (Orgs.), Gasto e consumo das famílias brasileiras contemporâneas (vol. 2, cap. 13, pp. 463-484). Brasília: Ipea., 2010Hoffmann, R. (2010). Estimativas das elasticidades-renda de várias categorias de despesa e de consumo, especialmente alimentos, no Brasil, com base na POF 2008-2009. Revista de Economia Agrícola, São Paulo, 57(2), 49-62.) e Menezes et al. (2006)Menezes, T., Silveira, F. G., Magalhães, L. C. G., Tomich, F. A., Vianna, S. W. (2006). Gastos alimentares nas grandes regiões urbanas do Brasil: aplicação do modelo AID aos microdados da POF 1995/1996 IBGE. In G. F. Silveira, L. M. Servo, T. Menzes, & S. F. Piola (Orgs.), Gasto e consumo das famílias brasileiras contemporâneas (cap. 9, pp. 228-254). Brasília: Ipea.. Duas possíveis causas para a elevada elasticidade-dispêndio (renda) de alimentos como o arroz são aventadas por Coelho & Aguiar (2007)Coelho, A. B., & Aguiar, D. R. D. (2007). O modelo Quadratic Almost Ideal Demand System (QUAIDS): uma aplicação para o Brasil. In G. F. Silveira, L. M. Servo, T. Menezes, & S. F. Piola (Orgs.), Gasto e consumo das famílias brasileiras contemporâneas (vol. 2, cap. 14, pp. 485-514). Brasília: Ipea. e Coelho et al. (2010)Coelho, A. B., Aguiar, D. R. D., & Eales, J. S. (2010). Food demand in Brazil: an application of Shonkwiler & Yen two-step estimation method. Revista Estudos Econômicos, 40(1), 185-211.. A primeira seria o nível de agregação, pois agrupar os consumidores por nível de renda e não fazer a estimação para cada domicílio pode gerar diferenças nas elasticidades encontradas. A segunda causa seria a inclusão de variáveis categóricas para a educação nos dois estágios de estimação, o que poderia gerar estimações de elasticidades-dispêndio (renda) maiores. A hipótese é que há uma relação negativa entre escolaridade e consumo de alimentos básicos e, com a omissão das variáveis educacionais, sua influência seria captada pelas elasticidades-dispêndio (renda), diminuindo as estimativas.
Elasticidade-dispêndio da demanda por alimentos no domicílio por estrato de renda familiar no Brasil, 2008-2009
Em trabalhos com metodologia similar (em termos de agregação e variáveis utilizadas), seja no plano nacional ou internacional, as estimativas para a elasticidade-dispêndio de arroz são condizentes às encontradas no presente estudo. No Brasil podem ser citados: Payeras-Pintos (2009)Payeras-Pintos, J. A. (2009). Estimação do sistema quase ideal de demanda para uma cesta ampliada de produtos empregando dados da POF de 2002-2003. Revista de Economía Aplicada, 13(2), 231-255., 0,46; Barbosa et al. (2013)Barbosa, A. L. N. H., Menezes, T. A., & Andrade, B. C. (2013). Demanda por produtos alimentares nas áreas rurais e urbanas do Brasil. Brasília: Ipea. Recuperado em 25 de março 2014, de http://www.ipea.gov.br/portal/index.php?option=com_content&view=article&id=18336
http://www.ipea.gov.br/portal/index.php?...
1,03; e Coelho & Aguiar (2007)Coelho, A. B., & Aguiar, D. R. D. (2007). O modelo Quadratic Almost Ideal Demand System (QUAIDS): uma aplicação para o Brasil. In G. F. Silveira, L. M. Servo, T. Menezes, & S. F. Piola (Orgs.), Gasto e consumo das famílias brasileiras contemporâneas (vol. 2, cap. 14, pp. 485-514). Brasília: Ipea. 1,26. Em termos internacionais, as elasticidades-dispêndio do arroz da Etiópia (0,88), da China (1,02) e do Japão (entre 1,06 e 1,42) - segundo Erhabor & Ojogho (2011)Erhabor, P. O. I., & Ojogho, O. (2011). Demand analysis for rice in Nigeria. Journal of Food Technology, 9(2), 66-74. http://dx.doi.org/10.3923/jftech.2011.66.74
http://dx.doi.org/10.3923/jftech.2011.66...
, Zheng & Henneberry (2010)Zheng, Z., & Henneberry, S. R. (2010). An analysis of food grain consumption in urban Jiangsu Province of China. Journal of Agricultural and Applied Economics, 42(2), 337-355. http://dx.doi.org/10.1017/S1074070800003497
http://dx.doi.org/10.1017/S1074070800003...
e Chern et al. (2003)Chern, W. S., Ishibashi, K., Taniguhchi, K., & Tokoyama, Y. (2003). Analysis of the food consumption of japanese households (FAO Economic and Social Development, Paper 152). Recuperado em 14 de outubro de 2015, de ftp://ftp.fao.org/docrep/fao/007/ae025e/ae025e00.pdf, respectivamente - reforçam essa similaridade.
Quando se observa a elasticidade-dispêndio restrita para o arroz entre as faixas de renda, nota-se que passa de 0,895 para 0,938 entre os extremos da distribuição, ou seja, há um crescimento no gasto com o produto de 4,84%. Apenas o arroz, a batata e o macarrão têm elasticidade-dispêndio restrita que cresce com a renda. Esse é um resultado não esperado e uma possível explicação seria a diminuição dos preços relativos desses alimentos para as classes de renda mais elevadas que pode se dever às suas características de relativa homogeneidade e não perecibilidade. Assim, seria possível que o preço relativo menor possibilitasse uma elasticidade-dispêndio maior para as classes mais abastadas, pois o aumento do gasto nesses produtos devido ao crescimento da renda é contrabalançado por um preço unitário menor. Contudo, estudos são necessários para compreender como esse preço relativo menor afeta a elasticidade-dispêndio (renda).
A Tabela 4 exibe a elasticidade-dispêndio do arroz por macrorregiões. A partir dela, nota-se que a região Centro-Oeste apresenta a maior elasticidade (0,96), seguida da região Sudeste (0,93). Na sequência, aparecem o Nordeste (0,88), o Norte (0,88) e o Sul com a menor (0,86). Esses resultados são interessantes para o setor produtivo, uma vez que a região Sudeste é a maior do País, abrigando 42% da população brasileira segundo o Censo Populacional de 2010 (Instituto Brasileiro de Geografia e Estatística, 2016Instituto Brasileiro de Geografia e Estatística – IBGE. (2016). PAM 2016 (Pesquisa Agrícola Municipal). Rio de Janeiro: IBGE. Recuperado em 18 de março de 2018, de https://sidra.ibge.gov.br/tabela/1612
https://sidra.ibge.gov.br/tabela/1612...
). O mercado nordestino também é considerável, pois representa 28% da população nacional. Assim, o foco nesses mercados (Sudeste e Nordeste) pode ser benéfico em termos de retorno da propaganda de estímulo ao consumo. Outro ponto interessante é a pequena variabilidade das elasticidades-dispêndio restritas para o arroz entre as macrorregiões, o que indica que seu consumo é disperso em todo o País.
Elasticidade-dispêndio da demanda por alimentos no domicílio para as macrorregiões brasileiras, 2008-2009
A elasticidade-renda indica a sensibilidade do gasto com cada alimento devido a uma variação na renda familiar total, sendo obtida a partir da relação do dispêndio com alimentação domiciliar e da renda familiar total da regressão de endogeneidade do gasto total. Nesta equação, o coeficiente da renda domiciliar total (0,35) indica que uma variação de 1% da renda familiar total eleva o gasto com alimentação no domicílio em 0,35%. A partir dessa relação, a elasticidade-dispêndio é transformada em elasticidade-renda. Os resultados apontam que o arroz é um bem normal, sendo a elasticidade-renda para o Brasil de 0,32, ou seja, um aumento de 1% na renda produz elevação de 0,32% no gasto com o cereal.
A Tabela 5 apresenta a elasticidade-preço da demanda não compensada (Marshalliana) para os dez grupos de alimentos. A diagonal principal representa a elasticidade-preço própria da demanda para cada bem investigado. Os elementos fora da diagonal principal se referem às elasticidades-preço cruzadas, ou seja, a partir desses elementos pode-se identificar como a demanda de i-ésimo bem (arroz, por exemplo) é afetada pela variação no preço do j-ésimo bem (lê-se o efeito dos preços (colunas) sobre a quantidade demandada do bem (linha)). Isto posto, assinala-se que, por meio da elasticidade-preço cruzada Marshalliana, os bens são classificados como substitutos brutos, quando o aumento do preço de j-ésimo bem aumenta a quantidade demandada do i-ésimo bem, ou complementares brutos, quando o aumento do preço de j-ésimo bem reduz a quantidade demandada do i-ésimo bem.
Elasticidades-preços das demandas não compensadas (Marshallianas) para os 10 alimentos avaliados, Brasil, 2008-2009
Os resultados da Tabela 5 mostram que todos os alimentos investigados apresentaram elasticidade-preço próprio negativa, o que indica relação inversa entre a demanda do bem e seu respectivo preço, como postulado pela teoria econômica. A elasticidade-preço da demanda Marshalliana do arroz revela que a sua demanda é elástica, isto é, a variação de 1% no preço do cereal impacta sua demanda de maneira mais do que proporcional (-1,03%). Dentre os alimentos analisados, esse valor só é maior para a farinha de mandioca (-1,49) e para o pão (-1,14).
A elasticidade-preço da demanda do arroz é inferior à encontrada em trabalhos nacionais similares, como: Coelho & Aguiar (2007)Coelho, A. B., & Aguiar, D. R. D. (2007). O modelo Quadratic Almost Ideal Demand System (QUAIDS): uma aplicação para o Brasil. In G. F. Silveira, L. M. Servo, T. Menezes, & S. F. Piola (Orgs.), Gasto e consumo das famílias brasileiras contemporâneas (vol. 2, cap. 14, pp. 485-514). Brasília: Ipea., Coelho et al. (2010)Coelho, A. B., Aguiar, D. R. D., & Eales, J. S. (2010). Food demand in Brazil: an application of Shonkwiler & Yen two-step estimation method. Revista Estudos Econômicos, 40(1), 185-211. e Barbosa et al. (2013)Barbosa, A. L. N. H., Menezes, T. A., & Andrade, B. C. (2013). Demanda por produtos alimentares nas áreas rurais e urbanas do Brasil. Brasília: Ipea. Recuperado em 25 de março 2014, de http://www.ipea.gov.br/portal/index.php?option=com_content&view=article&id=18336
http://www.ipea.gov.br/portal/index.php?...
(-1,66; -1,65 e -1,71 respectivamente). Cumpre reforçar que essas comparações devem ser feitas com cautela, haja vista as diferentes metodologias, bases de dados, agregações e períodos em que os trabalhos foram realizados. Contudo, o resultado apresentado parece ser plausível, pois esses próprios autores não esperavam resultados tão elevados para um alimento essencial como o arroz.
A partir das elasticidades-preço cruzadas pôde-se verificar as relações com os demais grupos de alimentos. Nota-se que o arroz apresentou relações de complementariedade (bruta) com o feijão ( = -0,08). As relações com os outros alimentos é de substituição (bruta) (>0), dentre as quais destacam-se a relação com o pão ( = 0,28), com a farinha de mandioca ( = 0,16), com a batata ( = 0,08) e com o macarrão ( = 0,08), fontes alternativas de carboidratos, conforme identificaram Coelho & Aguiar (2007)Coelho, A. B., & Aguiar, D. R. D. (2007). O modelo Quadratic Almost Ideal Demand System (QUAIDS): uma aplicação para o Brasil. In G. F. Silveira, L. M. Servo, T. Menezes, & S. F. Piola (Orgs.), Gasto e consumo das famílias brasileiras contemporâneas (vol. 2, cap. 14, pp. 485-514). Brasília: Ipea. e Coelho et al. (2010)Coelho, A. B., Aguiar, D. R. D., & Eales, J. S. (2010). Food demand in Brazil: an application of Shonkwiler & Yen two-step estimation method. Revista Estudos Econômicos, 40(1), 185-211.. Essa relação de substituição (bruta) também se verifica com os grupos de carnes, sobretudo com a carne de primeira ( = 0,22) e com o frango ( = 0,16); a relação com a carne de segunda ficou próxima de zero ( = 0,05). A forte relação de substituição com a carne de primeira é um resultado não esperado. Trabalhos como o de Coelho & Aguiar (2007)Coelho, A. B., & Aguiar, D. R. D. (2007). O modelo Quadratic Almost Ideal Demand System (QUAIDS): uma aplicação para o Brasil. In G. F. Silveira, L. M. Servo, T. Menezes, & S. F. Piola (Orgs.), Gasto e consumo das famílias brasileiras contemporâneas (vol. 2, cap. 14, pp. 485-514). Brasília: Ipea. e de Coelho et al. (2010)Coelho, A. B., Aguiar, D. R. D., & Eales, J. S. (2010). Food demand in Brazil: an application of Shonkwiler & Yen two-step estimation method. Revista Estudos Econômicos, 40(1), 185-211. encontraram relação de complementariedade entre arroz e carnes. Assim sendo, esse resultado e seus desdobramentos, apresentados na sequência, devem ser interpretados com cautela, e novos trabalhos devem ser realizados para investigar mais detidamente essa relação.
Quando se investiga essa relação cruzada na equação de cada um dos bens em confronto com o arroz, ou seja, como a variação no preço do arroz afetaria os demais bens, identifica-se que o arroz se mantém como bem complementar ao feijão (= -0,17). Já entre os bens substitutos, a elasticidade cruzada com o arroz se intensifica, principalmente para a farinha de mandioca (= 0,44) e para o pão (= 0,33). Desta forma, há indícios de que políticas de aumento da competitividade, através da redução do preço do arroz, impactariam mais fortemente a demanda por esses alimentos.
Em suma, observando os impactos dos preços sobre a demanda de arroz, parece claro que o feijão, a farinha de mandioca e o pão figuram como importantes produtos relacionados ao consumo do arroz. Por isso, o setor arrozeiro poderia desenvolver estratégias de expansão do consumo que levassem em conta essas inter-relações. Neste caso, poder-se-ia delinear uma política de incentivo ao consumo de feijão, ou, ainda, políticas de geração de novas formas de consumo do arroz que focassem na substituição do pão, produto amplamente consumido nos domicílios brasileiros (Tabela 1) e/ou da farinha de mandioca, produto com consumo mais regionalizado no Nordeste do País e, sobretudo, no caso de famílias de renda mais baixa.
As elasticidades-preço Marshallianas calculadas, na mediana, para dez estratos de renda per capita familiar, para o caso do arroz, são apresentados em forma de duas figuras a seguir. A partir da Figura 1 depreende-se que o arroz é um bem com demanda mais elástica para as famílias de menor renda do País (-1,11). Percebe-se, claramente, que a elasticidade-preço própria vai diminuindo (em módulo), com a demanda de arroz se tornando preço-inelástica (-0,92) no estrato mais elevado de renda. Assim, fica evidente que a demanda do arroz é elástica em relação ao próprio-preço, para a maior parte da população brasileira (mediana de -1,03), exceto para os estratos de renda mais elevados.
Elasticidade- preço própria da demanda não compensada (Marshalliana) para o arroz para dez estratos de renda familiar per capita no Brasil
Quando se analisa a elasticidade preço-cruzada dos outros alimentos em relação ao arroz, algumas informações interessantes emergem (Figura 2). Observa-se, por exemplo, que a relação de complementariedade entre feijão e o arroz mantém-se em todas as faixas de renda, sendo maior, porém, no caso das famílias de menor renda. A carne de segunda, diferentemente do que ocorre para a amostra como um todo, é complementar ao arroz para os dois primeiros estratos de renda, alternando essa situação para o terceiro estrato de renda per capita.
Elasticidade-preço cruzada não compensada (Marshalliana) dos outros alimentos na demanda do arroz entre os dez estratos da renda familiar per capita
Dentre os outros produtos, o macarrão, a batata e o frango apresentam baixo grau de substituição com relação ao arroz para os menores estratos de renda. A elasticidade se eleva para as classes de renda mais alta. Esses alimentos têm seu grau de substituição ao arroz aumentado nos três últimos estratos de renda, em especial no caso da carne de frango, cuja elasticidade preço-cruzada passa de 0,17 no sétimo estrato de renda para 0,31 no décimo. Assim, variações no preço desses bens têm menor impacto na demanda de arroz para as famílias de baixa renda.
A elasticidade-preço cruzada do pão mostra que ele é o principal substituto do arroz para todas as faixas de renda, com elasticidade variando entre 0,23 a 0,39. A carne de primeira também é destaque em termos substitutivos ao arroz, com elasticidade se elevando da menor (0,14) até a maior faixa de renda familiar per capita (0,33).
A farinha de mandioca é, dentre todos os alimentos, a que apresenta menor variação na elasticidade-preço cruzada com o arroz (0,15 a 0,20). Em suma, observa-se que, para as classes de renda mais baixas, a alta no preço de produtos como a farinha de mandioca, a carne de primeira e o pão têm considerável potencial de aumentarem a demanda pelo arroz. A medida que a renda se eleva, os diferentes alimentos aumentam seu grau de substituição ao arroz.
Por fim, as elasticidades-preço da demanda não compensada (Marshalliana) pelo arroz são calculadas, na mediana da amostra, para as macrorregiões do País (Figura 3). Constata-se que as relações de substituição e de complementariedade apresentadas para o País como um todo se mantém nesse recorte, relativamente ao anterior, mas alguns pontos podem ser destacados. Em relação à elasticidade-preço própria, as regiões Norte e Nordeste apresentam valores mais elevados, indicando que eventos que reduzem os preços do cereal impactam mais na demanda dessas regiões.
Elasticidade-preço da demanda não compensada (Marshalliana) do arroz por macrorregião do Brasil
No que tange à relação com os outros alimentos, verifica-se a maior complementariedade do feijão nas regiões Norte e Nordeste. Outro ponto interessante é que a carne bovina de segunda apresentou relação de complementariedade ao arroz no Norte e Nordeste. No caso da região Centro-Oeste, a elasticidade é próxima de zero, diferente do que ocorre nas regiões Sul e Sudeste, onde a relação de substituição é claramente identificada.
A farinha de mandioca apresenta o maior grau de substituibilidade ao arroz nas regiões Norte e Nordeste, conforme era esperado. Já para os casos do pão e do macarrão, o grau de substituição mais elevado em relação ao arroz foi encontrado na região Sul.
Resumindo: as carnes (de primeira, de segunda e de frango) e o macarrão apresentam maior grau de substituição relativamente ao arroz nas regiões Sul e Sudeste. Já nas regiões Norte e Nordeste, o arroz tem maior grau de substituibilidade em relação à farinha de mandioca e de complementariedade em relação ao feijão e à carne de segunda. Esses resultados são importantes, pois facilitam a definição de estratégias de comercialização para os mercados regionais.
5 Considerações finais
Em termos gerais, pôde-se observar a adequação do modelo para estimar as demandas dos alimentos. Identificou-se que os parâmetros que captam a não linearidade do gasto total, bem como aqueles associados à correção do consumo censurado e da endogeneidade da despesa total restrita se mostraram significativos para a maioria das equações. Ademais, verificou-se que as variáveis associadas a fatores sociodemográficos (localização e características do chefe do domicílio) e a fatores econômicos (preços e despesa total restrita) são relevantes na explicação da parcela de gasto domiciliar com os alimentos considerados.
Especificamente para o arroz, a elasticidade-dispêndio, mesmo sendo elevada na comparação com os outros alimentos, denota um comportamento inelástico levando em conta o País como um todo. Na análise considerando a estratificação geográfica, observa-se maior sensibilidade da demanda de arroz ao aumento da despesa com alimentos no domicílio (dispêndio restrito) para as regiões Centro-Oeste, Sudeste e Nordeste, respectivamente. A elasticidade-renda da demanda reforça esse comportamento de bem normal e inelástico para o arroz, sendo cerca de 1/3 da elasticidade-dispêndio restrita.
Na análise da demanda não compensada (Marshalliana) identifica-se que a elasticidade-preço própria do arroz é levemente elástica, sendo o principal componente que afeta a demanda do cereal. As elasticidades-preço cruzadas apontam o feijão como bem complementar ao arroz e os demais bens analisados como substitutos. Nesse contexto, o pão e a farinha de mandioca figuram como importantes substitutos do arroz no consumo domiciliar.
Os exercícios de decompor a demanda Marshalliana por arroz em dez estratos de renda per capita familiar e por macrorregião do País revelam alguns pontos interessantes. Primeiro, identifica-se maior sensibilidade das famílias de menor renda a variações do preço do arroz. Segundo, a relação de substituição com os outros bens se eleva à medida que a renda aumenta. Terceiro, as regiões Norte e Nordeste apresentam elasticidades-preço próprias mais elevadas para o arroz; maior relação de complementariedade do feijão e da carne de segunda e maior grau de substituição da farinha de mandioca. Quarto, para os casos das carnes, do pão e do macarrão, a região Sul apresentou grau de substituição mais elevado na demanda domiciliar pelo arroz.
A principal contribuição deste trabalho está no método com que se estimou as elasticidades da demanda por arroz com os dados da última POF disponível. Considerou-se um modelo que contorna os problemas econométricos inerentes a esse tipo de estudo e levou-se em conta a demanda por outros alimentos importantes na dieta da população brasileira. A análise foi feita controlando diferenças de consumo motivadas por características sociodemográficas das famílias. Os resultados obtidos podem auxiliar a definição de políticas públicas e a construção de estratégias setoriais.
Deve-se destacar que este trabalho contribuiu para o entendimento da demanda alimentar domiciliar no País e, em particular, da demanda por arroz, o que se traduz em um avanço qualitativo nessa literatura, mas alguns pontos merecem atenção. Cabe reforçar que as estimações realizadas se referem ao consumo domiciliar, não sendo incorporada a demanda originada fora do domicílio, que vem crescendo recentemente nos centros urbanos. Além disso, estudos que englobem a demanda pelos diferentes tipos de arroz (integral, orgânico etc.) e questões como efeito-qualidade e desconto por quantidade comprada também podem contribuir para o entendimento mais completo da demanda alimentar no Brasil.
-
1
A questão do consumo zero e endogeneidade do gasto foram tratadas, porém não conjuntamente em trabalhos sobre alimentação no domicílio no Brasil que estimaram a demanda para o arroz entre os alimentos selecionados.
-
2
A função utilidade indireta do Quaids é: . Em que e . Sendo diferente do modelo Aids, apenas pela função ë(p). Quando ë(p) é independente dos preços, esta é equivalente à classe Piglog, que inclui o modelo Aids (Banks et al., 1997Banks, J., Blundell, R., & Lewbel, A. (1997). Quadratic Engel curves and consumer demand. The Review of Economics and Statistics, 79(4), 527-539. http://dx.doi.org/10.1162/003465397557015
http://dx.doi.org/10.1162/00346539755701... ). -
3
O termo, segundo Banks et al. (1997)Banks, J., Blundell, R., & Lewbel, A. (1997). Quadratic Engel curves and consumer demand. The Review of Economics and Statistics, 79(4), 527-539. http://dx.doi.org/10.1162/003465397557015
http://dx.doi.org/10.1162/00346539755701... , é definido pelo valor mínimo da despesa total (ln m). -
4
A identidade de Roy mostra que a demanda Marshalliana para o bem i é o negativo da razão entre as derivadas parciais desta em relação a preço e dispêndio (Deaton & Muellbauer, 1980aDeaton, A., & Muellbauer, J. (1980a). An almost ideal demand system. The American Economic Review, 70(3), 312-326., p. 41).
-
5
O processo de correção aplicado corrige apenas a existência do consumo zero como solução de canto, ou seja, para os potenciais consumidores. O arroz, apesar de ser um alimento estocável, conforme dados da POF está entre os mais consumidos pelos domicílios entrevistados, minimizando o problema da baixa frequência das compras.
-
6
A function evaluator program considera ajustes no desenho amostral, na despesa censurada e na endogeneidade das despesas totais foi disponibilizada por Almeida e Araújo Jr. (2017).
-
7
É válido sublinhar que o valor das despesas considerado nesta pesquisa é dado pela soma das despesas não monetárias e das despesas monetárias. Muito embora o peso da despesa não monetária seja maior para os domicílios rurais do que os domicílios situados na área urbana, a estimação de um modelo desconsiderando esse tipo de gasto poderia amplificar o problema do consumo zero na base e, assim, gerar menor robustez para as estimativas obtidas.
-
8
Outlier é o share (ou preço) de cada bem que ficou acima de dois desvios-padrão e meio da sua média.
-
9
O presente trabalho considerou o valor unitário como proxy dos preços (preço=valor/quantidade) e optou por não realizar tratamento de efeito qualidade, isto é, não se corrigiu o potencial problema de endogeneidade dos preços. Isso porque aqui busca-se mensurar as elasticidades para alimentos em nível bastante desagregado e com enfoque no arroz, produto com baixa diferenciação (homogêneo), em que esse potencial problema seria de menor importância conforme trabalhos como: Tafere et al. (2010)Tafere, K., Taffesse, A. S., Tamru, S., Tefera, N., & Paulos, Z. (2010). Food demand elasticities in Ethiopia: estimates using household income consumption expenditure (HICE) survey data (Working Paper 11). Washington: International Food Policy Research Institute. Recuperado em 03 de fevereiro de 2015, de http://www.ifpri.org/sites/default/files/publications/esspwp11.pdf
http://www.ifpri.org/sites/default/files... , Barbosa, Menezes e Andrade (2013)Barbosa, A. L. N. H., Menezes, T. A., & Andrade, B. C. (2013). Demanda por produtos alimentares nas áreas rurais e urbanas do Brasil. Brasília: Ipea. Recuperado em 25 de março 2014, de http://www.ipea.gov.br/portal/index.php?option=com_content&view=article&id=18336
http://www.ipea.gov.br/portal/index.php?... , dentre outros. -
10
As estimativas dos estágios prévios ao sistema de demanda estão disponíveis sob demanda aos autores.
-
Classificação JEL: D12, R21.
Referências
- Alfonzo, L., & Peterson, H. H. (2006). Estimating food demand in Paraguay from household survey data. Agricultural Economics, 34(3), 243-257. http://dx.doi.org/10.1111/j.1574-0864.2006.00122.x
» http://dx.doi.org/10.1111/j.1574-0864.2006.00122.x - Almeida, A. N., Bragagnolo, C., & Chagas, S. A. L. (2015). A demanda por vinho no brasil: elasticidades no consumo das famílias e determinantes da importação. Revista de Economia e Sociologia Rural, 53(3), 1-11. http://dx.doi.org/10.1590/1234-56781806-9479005303004
» http://dx.doi.org/10.1590/1234-56781806-9479005303004 - Almeida, A. T. C., & Araújo Junior, I. T. (2017). Demanda por bebidas alcoólicas e cigarro no Brasil: elasticidades, micro-simulação e variações no bem estar. Pesquisa e Planejamento Economico, 47(2), 1-11.
- Alves, D., Menezes, T., & Bezerra, F. (2007). Estimação do sistema de demanda censurada para o Brasil:utilizando dados de pseudopainel. In G. F. Silveira, L. M. Servo, T. Menzes & S. F. Piola. (Orgs.), Gasto e consumo das famílias brasileiras contemporâneas (vol. 2, cap. 11, pp. 395-422). Brasília: Ipea.
- Alviola, P. A., Capps Junior, O., & Wu, X. (2010, july 25-27). Micro-demand system analysis of non-alcoholic beverages in the United States: an application of econometric techniques dealing with censoring. In Proceedings of The Agricultural & Applied Economics Association Denver-Colorado: AAEA. Recuperado em 05 de fevereiro de 2014, de http://ageconsearch.umn.edu/handle/60462
» http://ageconsearch.umn.edu/handle/60462 - Banks, J., Blundell, R., & Lewbel, A. (1997). Quadratic Engel curves and consumer demand. The Review of Economics and Statistics, 79(4), 527-539. http://dx.doi.org/10.1162/003465397557015
» http://dx.doi.org/10.1162/003465397557015 - Barbosa, A. L. N. H., Menezes, T. A., & Andrade, B. C. (2013). Demanda por produtos alimentares nas áreas rurais e urbanas do Brasil Brasília: Ipea. Recuperado em 25 de março 2014, de http://www.ipea.gov.br/portal/index.php?option=com_content&view=article&id=18336
» http://www.ipea.gov.br/portal/index.php?option=com_content&view=article&id=18336 - Blundell, R., & Robin, J. M. (1999). Estimation in large and disaggregated demand systems: an estimator for conditionally linear systems. Journal of Applied Econometrics, 14(3), 209-232. http://dx.doi.org/10.1002/(SICI)1099-1255(199905/06)14:3<209::AID-JAE532>3.0.CO;2-X
» http://dx.doi.org/10.1002/(SICI)1099-1255(199905/06)14:3<209::AID-JAE532>3.0.CO;2-X - Blundell, R., Pashardes, P., & Weber, G. (1993). What do we learn about consumer demand patterns from micro data? The American Economic Review, 83(3), 570-597.
- Capitani, D. H. (2013). Viabilidade de implantação de um contrato futuro de arroz no Brasil (Tese de doutorado). Escola Superior de Agricultura “Luiz de Queiroz”, Universidade de São Paulo, Piracicaba.
- Chern, W. S., Ishibashi, K., Taniguhchi, K., & Tokoyama, Y. (2003). Analysis of the food consumption of japanese households (FAO Economic and Social Development, Paper 152). Recuperado em 14 de outubro de 2015, de ftp://ftp.fao.org/docrep/fao/007/ae025e/ae025e00.pdf
- Coelho, A. B., & Aguiar, D. R. D. (2007). O modelo Quadratic Almost Ideal Demand System (QUAIDS): uma aplicação para o Brasil. In G. F. Silveira, L. M. Servo, T. Menezes, & S. F. Piola (Orgs.), Gasto e consumo das famílias brasileiras contemporâneas (vol. 2, cap. 14, pp. 485-514). Brasília: Ipea.
- Coelho, A. B., Aguiar, D. R. D., & Eales, J. S. (2010). Food demand in Brazil: an application of Shonkwiler & Yen two-step estimation method. Revista Estudos Econômicos, 40(1), 185-211.
- Companhia Nacional de Abastecimento – CONAB. (2015). Quadro de suprimentos Recuperado em 10 de dezembro de 2015, de http://www.conab.gov.br/conteudos.php?a=1470&t=2
» http://www.conab.gov.br/conteudos.php?a=1470&t=2 - Deaton, A., & Muellbauer, J. (1980a). An almost ideal demand system. The American Economic Review, 70(3), 312-326.
- Erhabor, P. O. I., & Ojogho, O. (2011). Demand analysis for rice in Nigeria. Journal of Food Technology, 9(2), 66-74. http://dx.doi.org/10.3923/jftech.2011.66.74
» http://dx.doi.org/10.3923/jftech.2011.66.74 - Ferrario, N. M. (2013). Análise do impacto dos programas de transferência de renda sobre as despesas familiares com o consumo (Tese de doutorado). Escola Superior de Agricultura “Luiz de Queiroz”, Universidade de São Paulo, Piracicaba.
- Food and Agriculture Organization of the United Nations – FAO. (2004). Ano internacional do arroz Recuperado em 20 de maio de 2015, de http://www.fao.org/rice2004/es/concept.htm
» http://www.fao.org/rice2004/es/concept.htm - Gameiro, A. H., & Gameiro, M. B. P. (2008). O arroz no varejo e os fatores que influenciam o dispêndio das famílias consumidoras. Revista de Economia e Sociologia Rural, Brasília, 46(4), 1043-1066.
- Hoffmann, R. (2006). Elasticidades-renda das despesas e do consumo físico de alimentos no Brasil metropolitano 1995-1996. In G. F. Silveira, L. M. Servo, T. Menzes, & S. F. Piola (Orgs.), Gasto e consumo das famílias brasileiras contemporâneas (cap. 7, pp. 197-212). Brasília: Ipea.
- Hoffmann, R. (2007). Elasticidades-renda das despesas e do consumo de alimentos no Brasil em 2002-2003. In G. F. Silveira, L. M. Servo, T. Menzes, & S. F. Piola (Orgs.), Gasto e consumo das famílias brasileiras contemporâneas (vol. 2, cap. 13, pp. 463-484). Brasília: Ipea.
- Hoffmann, R. (2010). Estimativas das elasticidades-renda de várias categorias de despesa e de consumo, especialmente alimentos, no Brasil, com base na POF 2008-2009. Revista de Economia Agrícola, São Paulo, 57(2), 49-62.
- Instituto Brasileiro de Geografia e Estatística – IBGE. (2010). Censo populacional 2010 Rio de Janeiro: IBGE. Recuperado em 28 de abril de 2016, de http://www.sidra.ibge.gov.br/bda/popul/default.asp?t=3&z=t&o=25&u1=1&u2=1&u3=1&u4=1&u5=1&u6=1
» http://www.sidra.ibge.gov.br/bda/popul/default.asp?t=3&z=t&o=25&u1=1&u2=1&u3=1&u4=1&u5=1&u6=1 - Instituto Brasileiro de Geografia e Estatística – IBGE. (2015a). Pesquisa de orçamento familiar do IBGE – SIDRA Rio de Janeiro: IBGE. Recuperado em 20 de maio de 2015, de http://www.sidra.ibge.gov.br/bda/acervo/acervo2.asp?e=v&p=OF&z=t&o=23
» http://www.sidra.ibge.gov.br/bda/acervo/acervo2.asp?e=v&p=OF&z=t&o=23 - Instituto Brasileiro de Geografia e Estatística – IBGE. (2015b). Microdados da POF 2008-2009 (Pesquisa de Orçamentos Familiares). Rio de Janeiro: IBGE. Recuperado em 03 de setembro de 2015, de http://www.ibge.gov.br/home/estatistica/populacao/condicaodevida/pof/2008_2009/microdados.shtm
» http://www.ibge.gov.br/home/estatistica/populacao/condicaodevida/pof/2008_2009/microdados.shtm - Instituto Brasileiro de Geografia e Estatística – IBGE. (2016). PAM 2016 (Pesquisa Agrícola Municipal) Rio de Janeiro: IBGE. Recuperado em 18 de março de 2018, de https://sidra.ibge.gov.br/tabela/1612
» https://sidra.ibge.gov.br/tabela/1612 - Menezes, T., Silveira, F. G., Magalhães, L. C. G., Tomich, F. A., Vianna, S. W. (2006). Gastos alimentares nas grandes regiões urbanas do Brasil: aplicação do modelo AID aos microdados da POF 1995/1996 IBGE. In G. F. Silveira, L. M. Servo, T. Menzes, & S. F. Piola (Orgs.), Gasto e consumo das famílias brasileiras contemporâneas (cap. 9, pp. 228-254). Brasília: Ipea.
- Mittal, S. (2010). Application of the QUAIDS model to the food sector in India. Journal of Quantitative Economics, 8(1), 42-55.
- Payeras-Pintos, J. A. (2009). Estimação do sistema quase ideal de demanda para uma cesta ampliada de produtos empregando dados da POF de 2002-2003. Revista de Economía Aplicada, 13(2), 231-255.
- Pereda, P. C., & Alves, D. C. D. O. (2012). Qualidade alimentar dos brasileiros: teoria e evidência usando demanda por nutrientes. Revista Pesquisa e Planejamento Econômico, 42(2), 239-260.
- Poi, B. P. (2002). From the help desk: demand-system estimation. The Stata Journal, 2(4), 403-410. http://dx.doi.org/10.1177/1536867X0200200406
» http://dx.doi.org/10.1177/1536867X0200200406 - Poi, B. P. (2008). Demand-system estimation: update. The Stata Journal, 8(4), 554-556. http://dx.doi.org/10.1177/1536867X0800800407
» http://dx.doi.org/10.1177/1536867X0800800407 - Poi, B. P. (2012). Easy demand-system estimation with quaids. The Stata Journal, 12(3), 433-446. http://dx.doi.org/10.1177/1536867X1201200306
» http://dx.doi.org/10.1177/1536867X1201200306 - Pollak, R. A., & Wales, T. J. (1981). Demographic variables in demand analysis. Econometrica, 49(6), 1533-1551. http://dx.doi.org/10.2307/1911416
» http://dx.doi.org/10.2307/1911416 - Ray, R. (1983). Measuring the costs of children: an alternative approach. Journal of Public Economics, 22(1), 89-102. http://dx.doi.org/10.1016/0047-2727(83)90058-0
» http://dx.doi.org/10.1016/0047-2727(83)90058-0 - Rodrigues, C. T., Coelho, A. B., Braga, M. J., & Gomes, A. P. (2012). Demanda por nutrientes nas principais regiões metropolitanas do Brasil no período de 1005-2003. Revista de Economía Aplicada, 16(1), 5-30.
- Schlindwein, M., & Kassouf, A. L. A. (2007). Mudanças no padrão de consumo de alimentos tempo-intensivos e de alimentos poupadores de tempo, por regiões do Brasil. In G. F. Silveira, L. M. Servo, T. Menzes, & S. F. Piola (Orgs.), Gasto e consumo das famílias brasileiras contemporâneas (cap. 14, pp. 423-462). Brasília: Ipea.
- Shonkwiler, J. S., & Yen, S. T. (1999). Two-step estimation of a censored system of equations. American Journal of Agricultural Economics, 81(4), 972-982. http://dx.doi.org/10.2307/1244339
» http://dx.doi.org/10.2307/1244339 - Silva, M. M. D. C. (2013). Demanda domiciliar por frutas e hortaliças no Brasil (Dissertação de mestrado). Universidade Federal de Viçosa, Viçosa.
- Sonoda, D. Y. (2006). Demanda por pescados no Brasil entre 2002 e 2003 (Tese de doutorado). Escola Superior de Agricultura “Luiz de Queiroz”, Universidade de São Paulo, Piracicaba.
- Tafere, K., Taffesse, A. S., Tamru, S., Tefera, N., & Paulos, Z. (2010). Food demand elasticities in Ethiopia: estimates using household income consumption expenditure (HICE) survey data (Working Paper 11). Washington: International Food Policy Research Institute. Recuperado em 03 de fevereiro de 2015, de http://www.ifpri.org/sites/default/files/publications/esspwp11.pdf
» http://www.ifpri.org/sites/default/files/publications/esspwp11.pdf - Travassos, G. F. (2014). Demanda domiciliar por carnes no Brasil: a questão da separabilidade (Dissertação de mestrado). Universidade Federal de Viçosa, Viçosa.
- Walter, M., Marchezan, E., & Avila, L. A. D. (2008). Arroz: composição e características nutricionais. Ciência Rural, 38(4), 1184-1192. http://dx.doi.org/10.1590/S0103-84782008000400049
» http://dx.doi.org/10.1590/S0103-84782008000400049 - Yen, S. T., Lin, B. H., & Smallwood, D. M. (2003). Quasi and Simulated-Likelihhod approaches to censored demand systems: Food consumption by food stamp recipients in the United States. American Journal of Agricultural Economics, 85(2), 458-478. http://dx.doi.org/10.1111/1467-8276.00134
» http://dx.doi.org/10.1111/1467-8276.00134 - Zheng, Z., & Henneberry, S. R. (2010). An analysis of food grain consumption in urban Jiangsu Province of China. Journal of Agricultural and Applied Economics, 42(2), 337-355. http://dx.doi.org/10.1017/S1074070800003497
» http://dx.doi.org/10.1017/S1074070800003497
Datas de Publicação
-
Publicação nesta coleção
15 Jul 2019 -
Data do Fascículo
Apr-Jun 2019
Histórico
-
Recebido
10 Nov 2016 -
Aceito
27 Maio 2018





 Fonte: Elaboração própria a partir dos microdados da POF 2008-2009.
Fonte: Elaboração própria a partir dos microdados da POF 2008-2009.
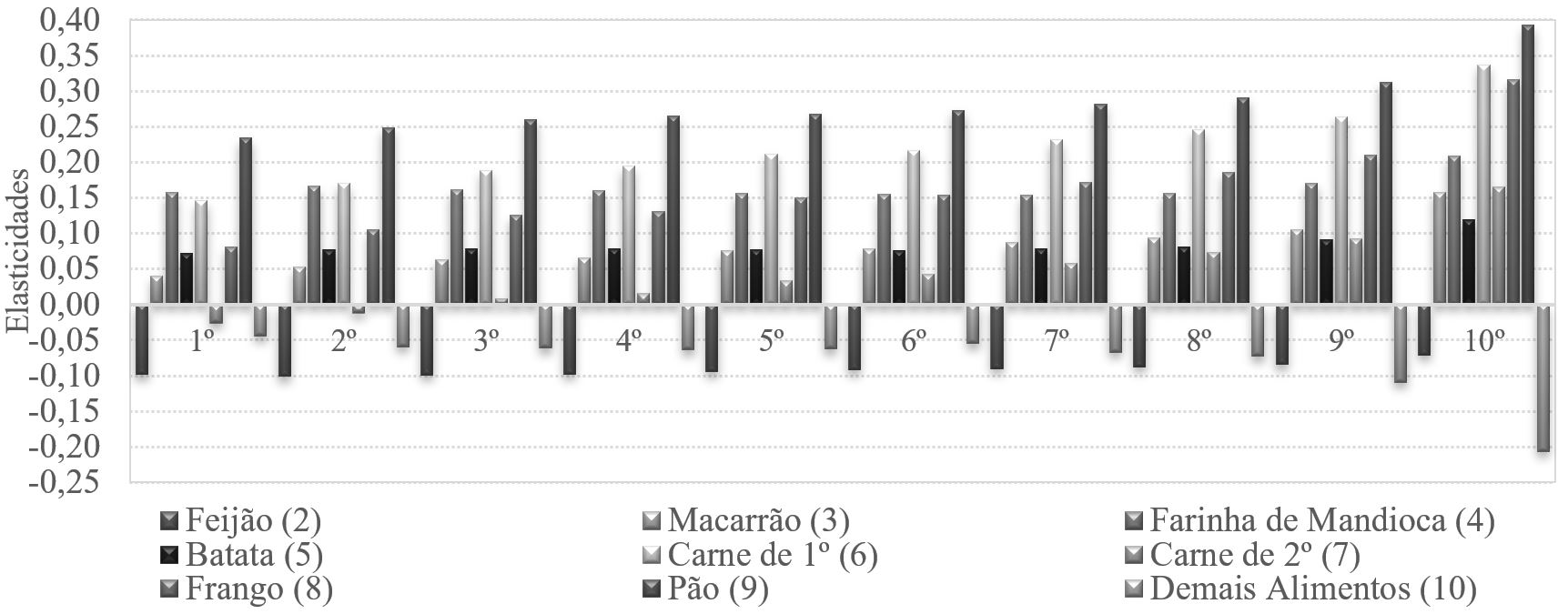 Fonte: Elaboração própria a partir dos microdados da POF 2008-2009.
Fonte: Elaboração própria a partir dos microdados da POF 2008-2009.
 Fonte: Elaboração própria a partir dos microdados da POF 2008-2009.
Fonte: Elaboração própria a partir dos microdados da POF 2008-2009.